Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Macroscopic traffic models are based on the analogy with a continuous one dimensional flow. Conservation of number of cars leads to conservation of mass

$$\displaystyle{ \frac{\partial \rho } {\partial t} + \frac{\partial \rho V } {\partial x} = 0 }$$
(1)

where ρ(t, x) is density and V (t, x) the average velocity of cars. In the kinetic models the continuity equation is supplied with the law of motion given by the Navier–Stokes equation

$$\displaystyle{ \rho \left (\frac{\partial V } {\partial t} + V \frac{\partial V } {\partial x} \right ) = \frac{\partial } {\partial x}\left (\eta \frac{\partial V } {\partial x} \right ) -\frac{\partial p} {\partial x} + X }$$
(2)

where η is viscosity and p the local pressure, being proportional to the variance (“temperature”) of the traffic Θ(x, t), namely the average of the squared differences of the individual cars and the average velocity. The “external forces” in the Kerner-Konhäuser model are represented by driver’s tendency to acquire a safe velocity V e (ρ) with a relaxation time τ,

$$\displaystyle{X =\rho \frac{V _{e}(\rho ) - V } {\tau }.}$$

When Θ = Θ 0 and η = η 0 are supposed constants, the equation of motion (2) simplifies to

$$\displaystyle{ \rho \left (\frac{\partial V } {\partial t} + V \frac{\partial V } {\partial x} \right ) = -\varTheta _{0} \frac{\partial \rho } {\partial x} + \frac{\rho (V _{e}(\rho ) - V )} {\tau } +\eta _{0}\frac{{\partial }^{2}V } {\partial {x}^{2}} }$$
(3)

We look for travelling wave solutions of (1) and (3), then the change of variables \(\xi = x + V _{g}t\) transform (1) into the quadrature which can be immediately solved:

$$\displaystyle{ \rho (V + V _{g}) = Q_{g}. }$$
(4)

Here, the arbitrary constant Q q represents the local flux as measured by an observer moving with the same velocity V g as the travelling wave.

Following [5] introduce adimensional variables

$$\displaystyle{ z =\rho _{\mathit{max}}\xi,\quad v = \frac{V } {V _{\mathit{max}}},\quad v_{g} = \frac{V _{g}} {V _{\mathit{max}}},\quad q_{g} = \frac{Q_{g}} {\rho _{\mathit{max}}V _{\mathit{max}}} }$$
(5)

where ρ max and V max are some maximum reference values of the density depending on the empirical law V e (ρ). Also let

$$\displaystyle{ v_{e}(\rho ) = \frac{V _{e}(\rho )} {V _{\mathit{max}}},\quad \theta _{0} = \frac{\varTheta _{0}} {V _{\mathit{max}}^{2}},\quad \lambda = \frac{V _{\mathit{max}}} {\eta _{0}},\quad \mu = \frac{1} {\rho _{\mathit{max}}\eta _{0}\tau }. }$$
(6)

Here V e (V ) is obtained through V e (ρ) by means of (4). Substitution of (4) into the equation of motion (3) yields dynamical system

$$\displaystyle\begin{array}{rcl} \frac{\mathit{dv}} {\mathit{dz}}& =& y, \\ \frac{\mathit{dy}} {\mathit{dz}}& =& \lambda q_{g}\left [1 - \frac{\theta _{0}} {{(v + v_{g})}^{2}}\right ]y -\mu q_{g}\left (\frac{v_{e}(v) - v} {v + v_{g}} \right ).{}\end{array}$$
(7)

In adimensional form, (4) becomes

$$\displaystyle{ \rho /\rho _{\mathit{max}} = \frac{q_{g}} {v + v_{g}}. }$$
(8)

Here and in what follows, we will take the parameter values λ, μ as given for the model, and will analyze the dynamical behavior with respect to the parameters v g , q g .

2 Fundamental Diagram

Dynamics of (7) depend on the explicit form of the constitutive relationship defined by the fundamental diagram V e (ρ). A typical form of the curve V e (ρ) must meet the following properties that we will state as hypotheses.

  • Hypothesis I. V e (ρ) is a monotone decreasing function defined for ρ ≥ 0 and V e (ρ jam ) = 0 for some ρ jam  > 0.

  • Hypothesis II. V e (ρ) is bounded from below.

  • Hypothesis III. \(\lim _{\rho \rightarrow 0}V _{e}(\rho ) = V _{f} > 0\) and \(\lim {_{\rho \rightarrow 0}\rho }^{2}V _{e}{^\prime}(\rho ) = 0\).

Hypothesis I is explicitly adopted in [2]; ρ jam can be interpreted as jam density where traffic is stuck. The condition V e ′(ρ) = o(ρ 2) in Hypothesis II allows for a plateau in the graph of the curve V e (ρ) for small values of density; V f is then the average velocity in free traffic and can be determined by speed limits.

Historically, diverse fundamental diagrams have been considered. Either fit to empirical data, or deduced from theoretical bases. Some examples are shown in Fig. 1. Explicit formulas are:

  1. 1.

    Greenshields: \(V = V _{\mathit{max}}(1 -\rho /\rho _{\mathit{jam}})\).

  2. 2.

    Greenberg: \(V = V _{\mathit{max}}\ln (\rho _{\mathit{jam}}/\rho )\).

  3. 3.

    Newell: \(V = V _{\mathit{max}}\exp (-\lambda \rho )\).

  4. 4.

    Kerner–Konhäuser: \(V = V _{\mathit{max}}\left ( \frac{1} {1+\exp (\frac{\rho /\rho _{\mathit{max}}-0.25} {0.06} )} - 3.72 \times 1{0}^{-6}\right )\).

Fig. 1
figure 1

Fundamental diagrams of mean velocity V vs. density ρ. (a) Greenshields; (b) Greenberg; (c) Newell; (d) Kerner–Konhäuser

Full size image

It can be verified that all except Newell’s fundmental diagram, satisfy Hypothesis I, and only (3) and (4) satisfy hypothesis II. Kerner-Konhäuser’s can be considered the most accurate fundamental diagram, since it was fitted from a large set of data using double induction detectors. Kerner and Konhäuser [2] and [3] (Greenberg was fitted from 18 data circa 1959). Although Hypothesis III seems reasonable, neither of the fundamental diagrams (1)–(4) satisfy this condition. We argue that it can be mathematically sustained since experimental data are available only for strictly positive ρ; put it in another way, modern technologies such as GPS could be used to get more accurate data for small densities. Thus one can take Kerner–Konhäuser model as an empirical validated for ρ > δ where δ is some positive small density, and modify it in such a way that Hypothesis III is true.

Hypothesis II implies that \(\lim _{\rho \rightarrow \infty }V _{e}(\rho )\) exists. This limit is zero for Newell’s diagram and equals \(-3.72 \times 1{0}^{-6}V _{\mathit{max}}\) for Kerner–Konhäuser’s. Although ρ → ∞ does not make sense physically, it will be useful from a mathematical point of view to allow this limit. This amounts to consider an arbitrary large value of ρ jam (as Newell’s diagram). In fact, in (8) v → −v g as ρ → ∞ and this corresponds to the limit of an observer moving with the wave seeing it standing.

We denote by v e (v) the expression v e (ρ) when ρ is expressed through (8) as a function of v (see 6).

The following properties of v e (v) are readily obtained.

Lemma 1.

Let V e (ρ) satisfy Hypothesis I, II and III. Then v e (v) is a monotone increasing function of v and: (1) \(\lim _{v\rightarrow -v_{g}}v_{e}(v)\) exists; (2) \(\lim _{v\rightarrow -v_{g}}v_{e}{^\prime}(v) = 0\) and, (3) \(\lim _{v\rightarrow \infty }v_{e}(v) = v_{f}\) .

Proof.

Since (4) can be written as

$$\displaystyle{ v + v_{g} = \frac{q_{g}} {\rho /\rho _{\mathit{max}}} }$$
(9)

it follows that ρ∕ρ max is a decreasing function of v, and thus v e (v) is an increasing function of v, for v > −v g . If v → −v g then ρ → ∞ but then \(\lim v_{e}(\rho )\) exists; this proves (1). Using the chain rule

$$\displaystyle{v_{e}{^\prime}(v) = v_{e}{^\prime}(\rho (v))\rho {^\prime}(v) = v_{e}{^\prime}(\rho (v))\left (- \frac{q_{g}/\rho _{\mathit{max}}} {{(v + v_{g})}^{2}}\right ) = -\frac{v_{e}{^\prime}{(\rho )\rho }^{2}} {q_{g}\rho _{\mathit{max}}}}$$

the last term tends to zero by Hypothesis III; this proves (2). Finally if v → ∞ then ρ → 0 but then v e (ρ) → 0. This completes the proof. □ 

The above lemma shows that given “reasonable” fundamental diagram (namely satisfying Hypothesis I–III) function v e (v) is sigmoidal: within the interval [−v g , ∞], v e (v) approaches its limits as v → −v g or ∞, asymptotically flat.

2.1 Critical Points

Critical points of system (7) are given by the equations y = 0 and v e (v) = v. The following results describes a generical situation.

Proposition 1.

Let V e (ρ) satisfy Hypothesis I–III. Then there exists either 1, 2 or 3 critical points of system (7) .

Proof.

Since the graph of v e (v) is sigmoidal, and the critical points are given by the intersection of the graphs of v e (v) and the straight line v = v the result follows. □ 

Figure 2 shows several possibilities for the intersection of the curve v e (v) = v, with 0, 1, 2 or 3 critical points.

Fig. 2
figure 2

Possible intersections v e (v) = v leading to critical points of system (7). Only the graph to the right of the vertical curve \(v = -v_{g}\) must be considered. From left to right from top to bottom, the number of critical points are: zero; one; three and two. A non–generic situation of tangency at the inflection point is not shown

Full size image

3 The Bogdanov–Takens Bifurcation

In this section we will show that the Kerner-Konhäuser ODE (7) undergoes a Bogdanov-Takens (BT) bifurcation. The BT bifurcation occurs in a two parameter dynamical system in the plane (see also it generalization to n-dimensions [1]) when for some value of the parameter vector, the dynamical system has a critical point with a double non–semisimple eigenvalue and some non-degeneracy conditions are satisfied. We state the conditions and its normal form according to Kuznetzov [4].

Theorem 1 (Bogdanov–Takens).

Suppose that a planar system

$$\displaystyle{ \dot{x} = f(x,\alpha ),\quad x \in {\mathbb{R}}^{2},\quad \alpha \in {\mathbb{R}}^{2}, }$$
(10)

with smooth f, has at α = 0 the equilibrium x = 0 with a double zero eigenvalue

$$\displaystyle{\lambda _{1,2}(0) = 0.}$$

Assume that the following genericity conditions are satisfied

  • (BT.0) The Jacobian matrix A(0) = f x (0,0) ≠ 0;

  • (BT.1) a 20 (0) + b 11 (0) ≠ 0;

  • (BT.2) b 20 (0) ≠ 0;

  • (BT.3) The map

    $$\displaystyle{(x,\alpha )\mapsto \left (f(x,\alpha ),\mbox{ tr}\left (\frac{\partial f(x,\alpha )} {\partial x} \right ),\mbox{ det}\left (\frac{\partial f(x,\alpha )} {\partial x} \right )\right )}$$

    is regular at the point (x,α) = (0,0).

    Then there exists smooth invertible transformations smoothly depending on the parameters, a direction–preserving time reparametrization, and smooth invertible parameters changes, which together reduce the system to

    $$\displaystyle\begin{array}{rcl} \dot{\eta }_{1}& =& \eta _{2} {}\end{array}$$
    (11)
    $$\displaystyle\begin{array}{rcl} \dot{\eta }_{2}& =& \beta _{1} +\beta _{2}\eta _{1} +\eta _{ 1}^{2} + s\eta _{ 1}\eta _{2} + O(\vert \vert \eta \vert {\vert }^{3}) {}\end{array}$$
    (12)

    where \(s = \mbox{ sign}[b_{20}(0)(a_{20}(0) + b_{11}(0))] = \pm 1\) .

Remark 1.

The coefficients appearing in the hypotheses (BT.1), (BT.2) are defined as follows: Let v 0, v 1 be generalized right eigenvectors of A 0 = A(0) and w 0, w 1 generalized left eigenvectors, such that A 0 v 0 = 0, A 0 v 1 = v 0 and A T w 1 = 0, A T w 0 = w 1. Then by a linear change of coordinates \(x = y_{1}v_{0} + y_{2}v_{1}\) system (10) can be expanded in a Taylor series as

$$\displaystyle\begin{array}{rcl} \dot{y}_{1}& =& y_{2} + a_{00}(\alpha ) + a_{10}(\alpha )y_{1} + a_{01}(\alpha )y_{2} {}\\ & & +\frac{1} {2}a_{20}(\alpha )y_{1}^{2} + a_{ 11}(\alpha )y_{1}y_{2} + \frac{1} {2}a_{02}(\alpha )y_{2}^{2} + P_{ 1}(y,\alpha ) {}\\ \dot{y}_{2}& =& b_{00}(\alpha ) + b_{10}(\alpha )y_{1} + b_{01}(\alpha )y_{2} {}\\ & & +\frac{1} {2}b_{20}(\alpha )y_{1}^{2} + b_{ 11}(\alpha )y_{1}y_{2} + \frac{1} {2}b_{02}(\alpha )y_{2}^{2} + P_{ 2}(y,\alpha ) {}\\ \end{array}$$

where a kl (α), P 1, 2(y, α) are smooth functions of their arguments and

$$\displaystyle{a_{00}(0) = a_{10}(0) = a_{01}(0) = b_{00}(0) = b_{10}(0) = b_{01}(0) = 0.}$$

Remark 2.

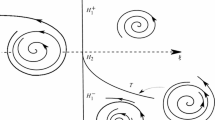
The normal form (12) is a universal unfolding, that is all nearby dynamical systems satisfying the hypotheses of the theorem is topologically equivalent to the normal form with the O( | | η | | 3) terms deleted. Figure 3 shows the different scenarios depending in the parameter space β 1–β 2.

Fig. 3
figure 3

Bogdanov–Takens bifurcation

Full size image

Lemma 2.

Let V e (ρ) satisfy Hypothesis I–III. Suppose that for some values of the parameters v g , q g the curves v e (v) and v = v have a tangency at v = v c . Then there exists θ 0 such that system (7) has a critical point with a double zero eigenvalue and its linear part is not semisimple.

Proof.

The linear part at v c is

$$\displaystyle{A_{0} = \left (\begin{array}{ll} 0 &1 \\ -\frac{q_{g}\mu \left (v_{e}{^\prime}(v_{c})-1\right )} {v+v_{g}} & q_{g}\left (1 - \frac{\theta _{0}} {{(v_{c}+v_{g})}^{2}} \right )\lambda \end{array} \right )}$$

since the curves v = v e (v), v = v have a tangency at v = v c then v e ′(v c ) = 1 and A 0 reduces to

$$\displaystyle{A_{0} = \left (\begin{array}{ll} 0&1 \\ 0&q_{g}\left (1 - \frac{\theta _{0}} {{(v_{c}+v_{g})}^{2}} \right )\lambda \end{array} \right )}$$

choosing \(\theta _{0} = {(v_{c} + v_{g})}^{2}\) reduces to

$$\displaystyle{ A_{0} = \left (\begin{array}{ll} 0&1\\ 0 &0 \end{array} \right ) }$$
(13)

 □ 

Theorem 2.

Let V e (ρ) satisfy Hypothesis I–III. Suppose that for some values of the parameters v g , q g the curves v e (v), v = v have a tangency at v = v c with v e ″(v c ) ≠ 0. Then there exists θ 0 such that system (7) has the linear part (13) . Moreover, if the following generic condition

$$\displaystyle{ \left (\frac{{\partial }^{2}v_{e}} {\partial {v}^{2}} - \frac{{\partial }^{2}v_{e}} {\partial v_{g}\partial v}\right )\frac{\partial v_{e}} {\partial q_{g}} + \frac{{\partial }^{2}v_{e}} {\partial q_{g}\partial v} \frac{\partial v_{e}} {\partial v_{g}}\neq 0 }$$
(14)

is satisfied at the critical value of the point and parameters, then the system undergoes a Bogdanov-Takens bifurcation.

Proof.

According to the remark after the Bogdanov–Takens theorem, the generalized right eigenvectors v 0, v 1 and the generalized left eigenvectors w 1, w 0 as the canonical vectors (1, 0), (0, 1) in \({\mathbb{R}}^{2}\), respectively, and the coordinates (y 1, y 2) as (v, y) coordinates of the dynamical system (7). Then, denoting as f(y 1, y 2) the vector field defining (7), the coefficients appearing in conditions (BT.1), (BT.2) are

$$\displaystyle\begin{array}{rcl} a_{20}(0)& =& \frac{{\partial }^{2}} {\partial y_{1}^{2}}w_{0} \cdot f(y_{1},y_{2}) = \frac{{\partial }^{2}} {\partial {v}^{2}}y = 0 {}\\ b_{20}(0)& =& \frac{{\partial }^{2}} {\partial y_{1}^{2}}w_{1} \cdot f(y_{1},y_{2}) {}\\ & =& \frac{{\partial }^{2}} {\partial {v}^{2}}\left (\lambda q_{g}\left [1 - \frac{\theta _{0}} {{(v + v_{g})}^{2}}\right ]y -\mu q_{g}\left (\frac{v_{e}(v) - v} {v + v_{g}} \right )\right ) = -\mu \frac{q_{g}v_{e}{^\prime}{^\prime}(v_{c})} {v_{c} + v_{g}} {}\\ b_{11}(0)& =& \frac{{\partial }^{2}} {\partial y_{1}\partial y_{2}}w_{1} \cdot f(y_{1},y_{2}) {}\\ & =& \frac{{\partial }^{2}} {\partial y_{1}\partial y_{2}}\left (\lambda q_{g}\left [1 - \frac{\theta _{0}} {{(v + v_{g})}^{2}}\right ]y -\mu q_{g}\left (\frac{v_{e}(v) - v} {v + v_{g}} \right )\right ) = \frac{2\mu q_{g}\theta _{0}} {{(v_{c} + v_{g})}^{3}} {}\\ \end{array}$$

we immediately verify that

$$\displaystyle\begin{array}{rcl} a_{20}(0) + b_{11}(0)& =& \frac{2\mu q_{g}\theta _{0}} {{(v_{c} + v_{g})}^{3}}\neq 0 {}\\ b_{20}& =& -\mu \frac{q_{g}v_{e}{^\prime}{^\prime}(v_{c})} {v_{c} + v_{g}} \neq 0 {}\\ \end{array}$$

the last condition being assumed by hypothesis.

A straightforward computation shows that the matrix of the map in condition (BT.3) at v = v c , y = 0, vg, q g is

$$\displaystyle{\left( \begin{array}{llll} 0 & 1 &0 & 0\\ 0 & 0 & -\frac{\mu q_g {v_e}{^\prime}_{v_g}}{v_c+v_g} & -\frac{\mu q_g {v_e}{^\prime}_{q_g}}{v_c+v_g}\\ \frac{2\lambda q_g}{v_c+v_q} & 0 & \frac{2\lambda q_g}{v_c+v_g} & 0\\ \frac{\mu q_g {v_e}{^\prime}{^\prime}_v}{v_c+v_g} & - \frac{2\lambda q_g}{v_c+v_q} & -\frac{\mu q_g {v_e}{^\prime}_{v_g}}{(v_c+v_g)^2}+ \frac{\mu q_g {v_e}{^\prime}{^\prime}_{v_g,v}}{v_c+v_g} & -\frac{\mu q_g {v_e}{^\prime}_{q_g}}{(v_c+v_g)^2}+ \frac{\mu q_g {v_e}{^\prime}{^\prime}_{q_g,v}}{v_c+v_g} \end{array} \right)}$$

where v e ′, v e ″ denote first and second order partial derivatives with respect to the subindex variables and are evaluated at (q g , v g , v c ). The nonvanishing of the determinant is equivalent to the condition

$$\displaystyle{ ({v_e}{^\prime}{^\prime}_{v} - {v_e}{^\prime}{^\prime}_{v_{g},v}){v_e}{^\prime}_{q_{g}} + {v_e}{^\prime}_{v_{g}}{v_e}{^\prime}{^\prime}_{q_{g},v}\neq 0 }$$
(15)

which is the same as (14). □ 

4 The Kerner-Konhäuser Model

For the Kerner-Konhäuser model one takes

$$\displaystyle{ v_{e}(q_{g},v_{g},v) = \frac{1} {1 +\exp \left [\frac{ \frac{q_{g}} {v+v_{g}}-d_{2}} {d_{3}} \right ]} + d_{1} }$$
(16)

with the empirical values [2]

$$\displaystyle{d_{1} = -3.72 \times 1{0}^{-6},\quad d_{ 2} = 0.25,\quad d_{3} = 0.06}$$

The set of critical points and parameters

$$\displaystyle{\{(q_{g},v_{g},v_{c})\mid v_{e}(v_{c}) - v_{c} = 0\}}$$

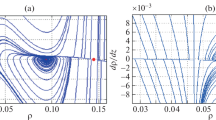
form a three-dimensional surface, given as the zero level set of a function \(F(q_{g},v_{g},v_{c}) = v_{e}(q_{g},v_{g},v_{c}) - v_{c} = 0\). It is shown in Fig. 1. There the vertical axis is \(x = v_{g} + v_{c}\) and we restrict to x > 0.

Fig. 4
figure 4

Surface of critical points and singular locus of the projection. The solid curve is γ

Full size image

The solid curves which will referred as γ are the loci where the projection (v g , q g , v c )↦(v g , q g ) is not surjective, namely the curve defined by the set of equations

$$ \displaystyle\begin{array}{rcl} F(q_{g},v_{g},v_{c})& =& v_{e}(v_{c}) - v_{c} = 0, {}\\ F_{v}(q_{g},v_{g},v_{c})& =& v_{e}{^\prime}(v_{c}) - 1 = 0.\ {}\\ \end{array} $$

These were computed numerically by solving the above equations. Their projections on the q g –v g plane is a cusp curve (see Fig. 4) and characterize the values of parameters (q g , v g ) such that the curve v e (v) is tangent to the graph of the identity. On the other hand the solid curve in the three dimensional space q g –v g –v c (or q g –v g –x) can be lifted to a curve \(\tilde{\gamma }\) in four dimensional space θ 0–q g –v g –v c where \(\theta _{0} = \sqrt{v_{c } + v_{g}}\) and thus γ can be viewed as the projection of \(\tilde{\gamma }\) and represent values (θ 0, q g , v g ) such that the linear part at the critical point has the form (13).

Proposition 2.

The conditions of Theorem  2 are satisfied for the Kerner–Konhäuser model (16) whenever d 1 is small an negative, and d 2 ,d 3 > 0.

Proof.

The condition v e ″(v c ) = 0 reduces to

$$\displaystyle{ {e}^{ \frac{q_{g}} {d_{3}x} }(q_{g} - 2d_{3}x) - {e}^{d_{2}/d_{3}}(q_{g} + 2d_{3}x) = 0, }$$
(17)

and the nondegenericity condition (14) to

$$\displaystyle{ {e}^{ \frac{q_{g}} {d_{3}x} }(q_{g} - d_{3}x) + {e}^{d_{2}/d_{3}}(q_{g} + d_{3}x) = 0. }$$
(18)

The change of variable q g  = zx (recall \(x = v + v_{g}\), thus \(z =\rho /\rho _{\mathit{max}}\)) and reduces each equation to the trivial one x = 0 which is discarded since v ≠ − v g , or

$$\displaystyle\begin{array}{rcl} 2d_{3}{e}^{d_{2}/d_{3} } + (2d_{3} - z){e}^{z/d_{3} } + {e}^{d_{2}/d_{3} }z& =& 0{}\end{array}$$
(19)
$$\displaystyle\begin{array}{rcl} d_{3}{e}^{d_{2}/d_{3} } + (d_{3} - z){e}^{z/d_{3} } + {e}^{d_{2}/d_{3} }z& =& 0{}\end{array}$$
(20)

Taking the difference of these yields \(d_{3}{e}^{z/d_{3}} = -d_{3}{e}^{d_{2}/d_{3}}\). Since all constants d 1, d 2, d 3 are positive, this last equation has no solution for z > 0. □ 

Corollary 1.

The Kerner–Konhäuser model ( 3 ) with the fundamental diagram ( 16 ) under the assumption ( 1 ) has traveling wave solutions in the unbounded domain x ∈ (−∞,∞) and in the bounded domain [0,L] with periodic boundary conditions.

Proof.

From the BT Theorem 2, it follows that there exists Hopf limit cycles (v(z), y(z)), where z = ρ max ξ and \(\xi = x + V _{g}t\) (see (5)). This yields a traveling wave solution of (3) in the form \(V (x,t) = V _{\mathit{max}}v(x + V _{g}t)\). If T is commensurable with L then the traveling wave satisfies also periodic boundary conditions. □