1 Introduction

In this paper, we study the local Hopf bifurcations of codimension one and two and the kind of stability of the Hopf periodic orbits in the dynamics of the Shimizu–Morioka system given by

$$\begin{aligned} \dot{x}=y, \quad \dot{y}=x-\lambda y-xz, \quad \dot{z}=-\alpha z+x^2, \end{aligned}$$
(1)

where \((x,y,z)\in \mathbb R^3\) are the state variables, and \(\alpha \) and \(\lambda \) are real parameters. System (1) is a simplified model proposed in [18] for studying the dynamics of the well-known Lorenz system [9]. Later, the system gained self-interest, and several articles have appeared in the literature, dealing mainly with the chaotic behavior of the solutions and the emergence of strange attractor, see, for instance [6, 17, 18, 20–22]. It was shown in [17] among other properties that system (1) presents Lorenz-like strange attractors, for example, taking \(\alpha =0.45\) and \(\lambda =0.75\) (see Figure 1 of [13]).

In this note, we perform an analytic bifurcation analysis of dynamical aspects of the solutions of system (1), when the parameters vary, aiming to give a contribution to the understanding of its complex behavior. Our approach permits a geometric synthesis of the bifurcation analysis, based on the algebraic expression and geometric location of the codimension \(2\) Hopf point leading to the bifurcation of periodic orbits.

The study presented here is close to those realized in some papers, which was performed in [12] (see also [3]). But our approach is different, mainly in the computations of the Lyapunov coefficients, which are necessary to study the Hopf bifurcations. In [12], the authors study the system

$$\begin{aligned} \dot{x}=y-x, \quad \dot{y}=\beta x-xz, \quad \dot{z}=-\chi z+\eta x^2. \end{aligned}$$

This system and system (1) are equivalent if \(\beta =\lambda =1\) and \(\eta >0\), taking \(\alpha =\chi \) and doing the change of variables \((x,y,z)\mapsto (\sqrt{\eta }\;x, -\sqrt{\eta }\;x+\sqrt{\eta }\;y, z)\) in system (1), but when \(\beta \ne \lambda \) or \(\eta \le 0\), these systems are not equivalent.

Our main result is the following one.

Theorem 1

Let denote \(h(\lambda )=3\,{\lambda }^{4}-5\,{\lambda }^{2}-1\). The following statements hold for system (1):

  1. (a)

    For \(\alpha = \frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (0,\sqrt{2})\), system (1) has two non-hyperbolic singular points \(Q_-\) and \(Q_+\), and if \(h(\lambda )\ne 0\), a one codimension Hopf bifurcation takes place at these points, permitting the existence of limit cycles near them. These cycles on the central manifolds of \(Q_-\) and \(Q_+\) are unstable if \(h(\lambda ) < 0\) and stable if \(h(\lambda ) > 0\).

  2. (b)

    For \(\alpha = \frac{2-\lambda ^2}{\lambda }\) with \(\lambda \in (0,\sqrt{2})\) and \(h(\lambda )= 0\), a two codimension Hopf bifurcation takes place at the points \(Q_-\) and \(Q_+\), with the creation of two limit cycles, one unstable and the other stable on the central manifolds of \(Q_-\) and \(Q_+\) .

The paper is organized as follows. In Sect. 2, through a linear analysis of system (1), we present a study of the bifurcations, which occurs with its singular points. In Sect. 3, we describe a method to compute the focus quantities, related to the stability of the limit cycles, which appear in the Hopf bifurcations. In Sect. 4, we present a brief review of the theory used to study codimension one and two Hopf bifurcations. These methods are used in Sect. 5 to prove statements (a) and (b) of Theorem 1. For some extensions of the Hopf bifurcation, see [1].

2 Analysis of the singular points

The statement (a) and (b) of the next proposition are not new, in fact, they are well known in the literature see, for instance, [5, 13].

Proposition 1

The following statements hold for system (1).

  1. (a)

    For \(\alpha < 0\), the origin of system (1) is the unique hyperbolic singular point. It is a saddle with a one-dimensional stable manifold and two-dimensional unstable manifold;

  2. (b)

    For \(\alpha = 0\), the \(z\)-axis of system (1) is filled of singular points. The origin becomes a non-hyperbolic singular point, and a degenerate pitchfork bifurcation occurs on it. More precisely, for \(\alpha > 0\) sufficiently small, this line of singular points disappear, the origin becomes a hyperbolic saddle with a two-dimensional stable manifold and an one-dimensional unstable manifold, two new singular points \(Q_-\) and \(Q_+\) are created, and they are symmetric with respect to the z-axis. These new equilibria are hyperbolic and asymptotically stable if \(\alpha >\frac{2-\lambda ^2}{\lambda }\) and \(\lambda >0\). For either \(\alpha =\frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (-\infty , -\sqrt{2})\) or \(\alpha <\frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (-\infty , -\sqrt{2})\cup (0,\sqrt{2})\), \(Q_-\) and \(Q_+\) are unstable singular points.

Proof

For \(\alpha < 0\), the origin \((0, 0,0)\) is the unique singular point of system (1) and the eigenvalues of its linear part are

$$\begin{aligned} \sigma _0=-\alpha , \quad \sigma _{\pm }=\frac{-\lambda \pm \sqrt{\lambda ^2+4}}{2}, \end{aligned}$$
(2)

with eigenvectors given by \(v_0=(0, 0, 1)\), \(v_\pm =(1, \sigma _\pm , 0)\), respectively. As the eigenvalues are all reals and \(\alpha <0\), \(\sigma _+\sigma _-<0\), by the Invariant Manifold Theorem and the Hartman Theorem (see for instance [7]), the origin is a hyperbolic saddle with an one-dimensional stable manifold tangent to the line generated by \(v_-\) and a two-dimensional unstable manifold tangent to the plane generated by \(v_0\) and \(v_+\) for all \(\lambda \). Note that for \(\alpha <0\) the solutions in the invariant \(z\)-axis go away from the origin.

If \(\alpha =0\), the invariant \(z\)-axis is filled by singular points of system (1). Then, the origin is a non-isolated degenerate singular point. Moreover, the eigenvalues of the linear part of system (1) at this point are \(0\) and \(\sigma _\pm \).

When the parameter \(\alpha \) crosses the zero value, the vector fields associated with system (1) cross this degenerate situation transversally. On the other words, for \(\alpha >0\), the \(z\)-axis filled of singular points that exist for \(\alpha =0\) disappears, and system (1) has only the singular points

$$\begin{aligned} Q_0=(0,0,0), \quad Q_\pm =(\pm \sqrt{\alpha },0,1). \end{aligned}$$

The eigenvalues of the linear part of system (1) at \(Q_0\) are given in (2), and we have \(\sigma _0<0\) and \(\sigma _-<0\) and \(\sigma _+>0\). Therefore, \(Q_0\) is a hyperbolic saddle with a two-dimensional stable manifold and an one-dimensional unstable manifold for all \(\lambda \). Thus, under the creation and subsequent elimination of the line of singular points when \(\alpha \) crosses the zero value, the origin \(Q_0\) of system (1) gains one dimension in the stable manifold and loses one dimension in the unstable one, as stated in statement (b) of the proposition.

Under the change of coordinates \((x,y,z)\mapsto (-x,-y,z)\), system (1) is invariant. Hence, the kind of stability of the singular point \(Q_+\) follows from the kind of stability of \(Q_-\). The characteristic polynomial of the linear part of system (1) at \(Q_-\) is

$$\begin{aligned} p(\sigma )= -\sigma ^3-(\alpha +\lambda )\sigma ^2 -\alpha \lambda \sigma -2 \alpha . \end{aligned}$$

The rest of proof follows from the next proposition.

Proposition 2

Consider \(\alpha >0\). The singular point \(Q_-\) is asymptotically stable to system (1) if \(\alpha >\frac{2-\lambda ^2}{\lambda }\) and \(\lambda >0\), and unstable if either \(\alpha =\frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (-\infty , -\sqrt{2})\) or \(\alpha <\frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (-\infty , -\sqrt{2})\cup (0,\sqrt{2})\).

Proof

The proof follows easily from the Routh–Hurwitz stability criterion (see [14, p. 58]).

The next proposition is a straightforward consequence of the relations between roots and coefficients of a polynomial in one variable.

Proposition 3

Consider \(\alpha >0\). If \(\alpha = \frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (0,\sqrt{2})\), then the linear part of system (1) at the singular point \(Q_-\) has one negative eigenvalue and two conjugated pure imaginary eigenvalues.

Following [12], the symmetric bifurcation that occurs when the parameter \(\alpha \) crosses the zero value is called degenerate pitchfork bifurcation, due to the line of equilibria which exists for \(\alpha =0\), and it has already been observed in other systems, which also present chaotic behavior (see, for instance, [16, p. 4] and [12]).

3 Center Theorem and focus quantities

In this section, we summarize the method described in [4] (see also [10, 11]) for studying the center problem on a center manifold for vector fields in \(\mathbb R^3\). Let \(X: U\rightarrow \mathbb R^3\) be a real analytic vector field, such that \(DX(0)\) has two pure imaginary eigenvalues and one nonzero. By a linear change of variables and a possible rescaling of the time, the system of differential equations \({\dot{\mathbf{u}} }= X(\mathbf{u})\) can be written as

$$\begin{aligned} \dot{u}&= -v+P(u,v,w)=\tilde{P}(u,v,w), \nonumber \\ \dot{v}&= u+Q(u,v,w)=\tilde{Q}(u,v,w), \nonumber \\ \dot{w}&= \beta w+R(u,v,w)=\tilde{R}(u,v,w), \end{aligned}$$
(3)

where \(\beta \) is a real nonzero number. We denote again by \(X\) this new vector field.

A non-constant \(C^1\) function \(H\) from a neighborhood of the origin of \(\mathbb R^3\) into \(\mathbb R\) is a local first integral of system (3) if it is constant on the orbits of (3), i.e., \(H\) satisfies

$$\begin{aligned} XH=\tilde{P}\frac{\partial H}{\partial u}+\tilde{Q}\frac{\partial H}{\partial v}+\tilde{R}\frac{\partial H}{\partial w}\equiv 0, \end{aligned}$$
(4)

in a neighborhood of the origin. A non-constant formal power series \(H\) in \(u\), \(v\), and \(w\) is a formal first integral for system (3) if when \(\tilde{P}\), \(\tilde{Q}\), and \(\tilde{R}\) are expanded in power series at the origin, every coefficient in the formal power series in (4) is zero. If \(w\) and \(\dot{w} \) do not appear in system (3) the system is in \(\mathbb R^2\), the singular point at the origin is either a focus (every trajectory near the origin spirals toward the origin, or every trajectory does so in reverse time) or a center (a punctured neighborhood is composed entirely of periodic orbits). The problem of distinguishing between these two cases is the center problem. It was solved by Poincaré and Lyapunov in terms of the nonexistence or existence of a local first integral. A proof is given in [15].

From Theorem \(5.1\) page 152 of [7], we know that system (3) admits a local center manifold \(W_\mathrm{{loc}}^c\) at the origin. The following theorem provides one the main tools for detecting a center on a center manifold . See [4] for a proof.

Theorem 2

The following statements are equivalent.

  1. (a)

    The origin is a center for \(X\mid _{W^c_{loc}}\).

  2. (b)

    There is a local analytic first integral at the origin for system (3) of the form \(H(u,v,w) = u^2 +v^2 +\cdots \) (here the dots mean higher-order terms).

  3. (c)

    There is a formal first integral at the origin for system (3) of the form \(H(u,v,w)\) \( = u^2 +v^2 +\cdots \).

The Lyapunov Center Theorem corresponds to the equivalence of statements (a) and (b); for a proof, see also [2]. From this theorem, we can restrict our attention to investigate the conditions for the existence or nonexistence of a first integral of the form \(H(u,v,w) = u^2 +v^2 +\cdots \), which is equivalent to determine necessary and sufficient conditions for the existence of a center or a focus on the local center manifold, respectively.

In what follows, we consider that P, Q, and R in (3) are polynomials. We start by introducing the complex variable \(x = u + iv\). Therefore, the first two equations in (3) are equivalent to the unique equation \(\dot{x} = ix + \cdots \). Adding to this equation its complex conjugate, changing \(\bar{x}\) (where as usual \(\bar{x}\) denote the conjugate of \(x\)) by \(y\), thinking in \(y\) as an independent complex variable, and substituting \(w\) by \(z\), we obtain the following complexification of system (3)

$$\begin{aligned} \dot{x}&= ix+\displaystyle \sum ^{n}_{p+q+r=2}a_{pqr} x^p y^q z^r, \nonumber \\ \dot{y}&= -iy+\displaystyle \sum ^{n}_{p+q+r=2}b_{pqr} x^p y^q z^r, \nonumber \\ \dot{z}&= \beta z+\displaystyle \sum ^{n}_{p+q+r=2}c_{pqr} x^p y^q z^r, \end{aligned}$$
(5)

where \(b_{qpr} = \bar{a}_{pqr}\) and the \(c_{pqr}\) are such that \(\sum ^{n}_{p+q+r=2} c_{pqr} x^p \bar{x}^q w^r\) is real for all \(x\in \mathbb C\) and \(w\in \mathbb R\). Again, we denote by \(X\) the new vector field associated with system (5) on \(\mathbb C^3\). Now, the existence of a first integral \(H(u,v,w) = u^2 + v^2 + \cdots \) for a system (3) is equivalent to the existence of a first integral of the form

$$\begin{aligned} H(x,y,z)=xy+\sum _{j+k+l=3} v_{jkl} x^j y^k z^l \end{aligned}$$
(6)

for system (5).

By computing the coefficients of \(XH\) and equating them to zero, we investigate the existence of a first integral \(H\) for a system (5) . When \(H\) has the form (6), we can calculated explicitly the coefficient \(g_{k_1k_2k_3}\) of \(x^{k1} y^{k2} z^{k3}\) in \(XH\) (see [4]). But when \((k_1,k_2,k_3) = (k, k, 0)\) for a positive integer \(k\), we can solved in a unique way for \(v_{k_1k_2k_3}\) the equation \(g_{k_1k_2k_3}\) = 0 in terms of the known quantities \(v_{\alpha \beta \gamma }\) such that \(\alpha +\beta +\lambda < k_1+k_2+k_3\). Hence, if \(g_{kk0} = 0\) for all \(k\in \mathbb N\), a formal first integral \(H\) exists. When the coefficient \(g_{kk0}\) is nonzero, an obstruction to the existence of the formal series \(H\) occurs. Such a coefficient is called the kth focus quantity.

The focus quantities \(g_{110} = 0\) and \(g_{220}\) are determined in a unique way, but the others depend on the choices made for \(v_{kk0}\), \(k \in \mathbb N\), \(k\ge 2\). Once such computations are made, \(H\) is determined and satisfies

$$\begin{aligned} XH(x,y,z) = g_{220} (xy)^2 + g_{330} (xy)^3 +\cdots . \end{aligned}$$

It follows that if for one choice of the \(v_{kk0}\) at least one focus quantity is nonzero, the same is true for every other choice of the \(v_{kk0}\). A sufficient and necessary condition for the existence of a center on the center manifold is to vanish all focus quantities; otherwise, we have a focus (see [4]).

In rest of this work, we denote the kth focus quantity \(g_{kk0}\) by \(\nu _k\).

4 Hopf bifurcation method

Let \((\theta ,\rho )\) be polar coordinates on the local center manifold \(W_{loc}^c\), such that \(\rho =0\) corresponds to the origin in Cartesian coordinates. Consider system (3) restricted to its local center manifold and let \(\varPi ({\rho })\) the respective Poincaré first return map on a sufficiently short segment of the axis \(\theta =0\) starting at \(\rho =0\). By the \(k\)th Lyapunov coefficient, we mean the coefficient \(l_k\) in the expansion of displacement map \(\varPi (\rho )-\rho \), i.e.,

$$\begin{aligned} \varPi (\rho )-\rho =l_1 \rho +l_2\rho ^2+\cdots . \end{aligned}$$

It follows by the proof of Theorem 6.2.3 of the page \(261\) of [15] that

$$\begin{aligned} l_1\!=\!c_1\nu _1 \ \text{ and } \ l_k\mid _{l_1=\cdots =l_{k-1}=0}\quad =c_k\nu _k\mid _{\nu _1=\cdots =\nu _{k-1}=0},\nonumber \\ \end{aligned}$$
(7)

where \(c_1,\dots , c_k\) are positive constants.

A method to compute the Lyapunov coefficients can be found in the pages 177–181 of [7] or in [8, 12].

A singular point \((x_0, \mu _0)\) of a \(\mu \)-parameter family of vector fields \(X(x,\mu )\) in \(\mathbb R^3\) is called a Hopf point if the Jacobian matrix \(DX(x_0,\mu _0)\) has a real eigenvalue \(\lambda _1\ne 0\) and a pair of purely imaginary eigenvalues \(\lambda _{2,3}=\pm i\omega _0\). There is a two-dimensional center manifold at a Hopf point, and it is invariant by the flow of the system \(\dot{x}=X(x,\mu )\), see [7, p. 152]. If varying the parameters, the complex eigenvalues cross the imaginary axis with nonzero derivative and the Hopf point is called transversal, i.e., if \(\mu \) is one-dimensional parameter, then \(\dfrac{\mathrm{d}\xi }{\mathrm{d}\mu }(\mu _0)\ne 0\) (where \(\xi (\mu ) \pm i \omega (\mu )\) are the conjugated complex eigenvalues of the linear part of \(X(x,\mu )\) at singular point \(x_\mu \) when \(|\mu -\mu _0|\) is enough small). At a neighborhood of transversal Hopf point with \(l_1(\mu _0)\ne 0\) the system \(\dot{x}=X(x,\mu )\), restricted to a center manifold, is orbitally topologically equivalent to the following complex normal form

$$\begin{aligned} \dot{w}=(\xi +i\omega )w+\sigma w|w|^2, \end{aligned}$$

where \(w\in \mathbb C\), \(\sigma =\text{ sign }\;l_1(\mu _0)=\pm 1\), \(l_1(\mu _0)\) the first Lyapunov coefficient at the Hopf point, and \(\xi \), \(\omega \) are real functions having derivatives of arbitrary higher order, which are continuations of \(0\) and \(\omega _0\), see [7, p. 98]. There is one family of stable (unstable) periodic orbits if \(l_1 < 0\) (\(l_1 > 0\)) on the space of phases variables and parameters shrinking to a singular Hopf point.

A Hopf point of codimension \(2\) is a Hopf point where \(l_1 (\mu _0)=0\) and \(l_2(\mu _0)\ne 0\). It is called transversal if the manifolds \(\xi (\mu )=0\) (\(\xi (\mu )\) is the real part of the conjugated complex eigenvalues) and \(l_1(\mu )\) have transversal intersections, i.e., the map \(\mu \mapsto (\xi (\mu ), l_1 (\mu ))\) is regular at \(\mu _0\). The codimension two Hopf bifurcation is also called of Bautin bifurcation or degenerated Hopf bifurcation. The system \(\dot{x}=X(x,\mu )\) restricted to a center manifold at a neighborhood of a transversal Hopf point of codimension \(2\) is orbitally topologically equivalent to

$$\begin{aligned} \dot{w}=(\xi +i\omega _0)w+\tau w|w|^2+\sigma w|w|^4, \end{aligned}$$
(8)

where \(\xi \) and \(\tau \) are the unfolding parameters and \(\sigma = \text{ sign } \;l_2(\mu _0)=\pm 1\), see [7, p. 311]. The bifurcation diagram of system (8) on the space of parameters \((\xi , \tau )\) for \(\sigma =1\) is shown in Fig. 1, where the lines \(H^{\pm }_1=\{\pm \tau >0\}\) correspond to the Hopf bifurcation of codimension one with negative and with positive Lyapunov coefficient, respectively. Along these lines, the singular point has eigenvalues \(\lambda _{1,2} = \pm \omega _0 i\). Moreover, the singular point is stable for \(\xi < 0\) and unstable for \(\xi > 0\). The first Lyapunov coefficient is \(l_1(\xi , \tau ) = \tau \). Therefore, the point of the Hopf bifurcation of codimension two \(H_2\) occurs when \(\xi = \tau = 0\) and separates the two branches, \(H^-_1\) and \(H^+_1\) of \(\tau \)-axis. An unstable limit cycle bifurcates from the singular point if we cross \(H^+_1\) from right to left, while a stable limit cycle appears if we cross \(H^-_1\) in the opposite direction. These limit cycles collide and disappear on the curve

$$\begin{aligned} T=\left\{ (\xi ,\tau )\;:\; 4\xi -\tau ^2=0\right\} , \end{aligned}$$

corresponding to a non-degenerate fold bifurcation of the cycles. Along this curve, the system has a semistable limit cycle of multiplicity one, see [7, p. 311].

Fig. 1
figure 1

Diagram at the point \(H_2\) of a two codimension Hopf bifurcation

Full size image

The bifurcation diagrams for \(\sigma =-1\) can be found in [7], page \(313\), and in [19] .

From (7), the Hopf method described above can be applied changing the Lyapunov coefficients by the focus quantities. Thus, in rest of this paper, we shall use the focus quantities in place of the Lyapunov coefficients to study Hopf bifurcations of codimension one and two.

5 Hopf bifurcation in the Shimizu–Morioka system

In this section, we study the stability of the singular point \(Q_-\) of system (1) under the conditions \(\alpha =\frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (0,\sqrt{2})\) given in Proposition 3, i.e., on the Hopf axis correspondent to the \(\tau \)-axis of Fig. 1. We prove the following theorem.

Theorem 3

Consider the two-parameter family of differential equations (1). The first focus quantity at the point \(Q_-\) for parameter values satisfying \(\alpha = \dfrac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (0,\sqrt{2})\) is given by

$$\begin{aligned} \nu _1(\lambda )=\frac{\lambda \sqrt{2-\lambda ^2} \left( 3 \lambda ^4-5 \lambda ^2-1\right) }{4 \left( \lambda ^4-2 \lambda ^2-4\right) \left( \lambda ^4-2 \lambda ^2-1\right) }. \end{aligned}$$

For \(\lambda \in (0,\sqrt{2})\) such that \(h(\lambda )=3\,{\lambda }^{4}-5\,{\lambda }^{2}-1\) is different from zero, system (1) has a transversal Hopf point at \(Q_-\) for \(\alpha = \dfrac{2-\lambda ^2}{\lambda }\).

Now for the parameter values \(\lambda _c=\sqrt{\dfrac{5+\sqrt{37}}{6}}\) and \(\alpha =\dfrac{7-\sqrt{37}}{\sqrt{6(5+37)}}\), system (1) has a transversal Hopf point of codimension 2 at \(Q_-\), which is unstable because \(\nu _2 > 0\).

Proof

For simplify the computations, we introduce the new parameters \((\beta ,\varepsilon )\) by

$$\begin{aligned} \lambda&= \dfrac{-\varepsilon \left( \beta ^2+\varepsilon ^2+2\right) +\sqrt{\left( -\beta ^2-\varepsilon ^2+2\right) \left( \beta ^4 +\left( \beta ^2+2\right) \varepsilon ^2\right) }}{\beta ^2+\varepsilon ^2},\\ \alpha&= -\varepsilon -\dfrac{\sqrt{\left( -\beta ^2-\varepsilon ^2+2\right) \left( \beta ^4 +\left( \beta ^2+2\right) \varepsilon ^2\right) }}{\beta ^2+\varepsilon ^2-2}. \end{aligned}$$

The Jacobian determinant of this change of parameters in the point \((0,\beta )\) is

$$\begin{aligned} -\frac{2 \beta ^5 \left( \beta ^4-2 \beta ^2-4\right) }{\left( -\beta ^4 \left( \beta ^2-2\right) \right) ^{3/2}}. \end{aligned}$$

Thus, the change of parameters is well defined for \((\varepsilon ,\beta ) \in (-\delta ,\delta )\times (0,\sqrt{2})\), with \(\delta \) enough small. In this new parameters, the linear part of system (1) at the singular point \(Q_-\) has a real eigenvalue and two conjugated complex given by \(\varepsilon \pm i\beta \). Furthermore, the conditions \(\alpha =\frac{2-\lambda ^2}{\lambda }\) and \(\lambda \in (0,\sqrt{2})\) correspond to \(\varepsilon =0\) and \(\beta \in (0,\sqrt{2})\). Hence, in this case, we have

$$\begin{aligned} \alpha =\frac{\beta ^2}{\sqrt{2-\beta ^2}}\quad \text{ and } \quad \lambda =\sqrt{2-\beta ^2} \end{aligned}$$
(9)

in system (1). Now, doing the change of coordinates \((x, y, z)\mapsto (\tilde{x}-\sqrt{\alpha }, \tilde{y}, \tilde{z}+1)\), the singular point \(Q_-\) is translated to the origin \((0,0,0)\). Now, we shall write the linear part of system in the coordinates \((\tilde{x}, \tilde{y}, \tilde{z})\) at the origin in its real Jordan normal form. For this, we introduce the variables \((u, v, w)\) by

$$\begin{aligned}&\left( \begin{array}{c} \tilde{x} \\ \tilde{y} \\ \tilde{z} \end{array}\right) \!=\!\left( \! \begin{array}{ccc} -\dfrac{\beta }{2 \root 4 \of {2-\beta ^2}} &{} \dfrac{1}{2} \root 4 \of {2-\beta ^2} &{} 2 \left( 2-\beta ^2\right) ^{5/4} \\ \frac{1}{2} \beta \root 4 \of {2-\beta ^2} &{} \frac{\beta ^2}{2 \root 4 \of {2-\beta ^2}} &{} -4 \left( 2-\beta ^2\right) ^{3/4}\\ 1 &{} 0 &{} 4 \beta \sqrt{2-\beta ^2} \end{array}\!\right) \nonumber \\&\qquad \qquad \quad \times \left( \begin{array}{c} u \\ v \\ w \end{array}\right) , \end{aligned}$$

and so system (1) becomes

$$\begin{aligned} \dot{u}&= -v -{\dfrac{{\beta }\sqrt{2-{\beta }^{2}} \left( 6+{\beta }^{2} \right) {u}^{2}}{-16-8\,{\beta }^{2}+4\,{\beta }^{4}}}\\&\quad -\,{\dfrac{ \left( -8+2\,{\beta }^{2}+{\beta }^{4} \right) vu}{-8-4\,{\beta }^{2} +2\,{\beta }^{4}}} \\&\quad +\,{\dfrac{2 \left( -2+{\beta }^{2} \right) \left( -8+4\,{\beta }^{2}+{\beta }^{4} \right) wu}{-4-2\,{\beta }^{2}+{ \beta }^{4}}}\\&\quad +\,{\dfrac{\sqrt{2-{\beta }^{2}} \left( -4+{\beta }^{4} \right) {v}^{2}}{\beta (-16-8\,{\beta }^{2}+4\,{\beta }^{4}})} \\&\quad -\,{\dfrac{2\sqrt{2-{\beta }^{2}} \left( 8-8\,{\beta }^{2}+{\beta }^{6} \right) wv}{\beta (-4-2\,{\beta }^{2}+{\beta }^{4})}}\\&\quad +\,{\dfrac{ 4\left( 2-{ \beta }^{2} \right) ^{5/2} \left( -4+4\,{\beta }^{2}+{\beta }^{4} \right) {w}^{2}}{\beta (-4-2\,{\beta }^{2}+{\beta }^{4})}}, \\ \dot{v}&= u+ {\dfrac{ \left( 8+{\beta }^{4} \right) {u}^{2}}{16+8\,{\beta }^{2 }-4\,{\beta }^{4}}}+{\dfrac{\sqrt{2-{\beta }^{2}} \left( 4+{ \beta }^{4} \right) vu}{\beta (-8-4\,{\beta }^{2}+2\,{\beta }^{4})}}\\&\quad -\,{\dfrac{2 \sqrt{2-{\beta }^{2}} \left( -8+8\,{\beta }^{2}-2\,{\beta }^{4}+{\beta }^ {6} \right) wu}{\beta (-4-2\,{\beta }^{2}+{\beta }^{4})}}\\&\quad +\,\dfrac{{\beta }^{2} \left( -2+{\beta }^{2} \right) v^2 }{4(-4-2\,{\beta }^{2}+{\beta }^{4})} \\&\quad -\,{\dfrac{2 \left( -8+8\,{\beta }^{2}-4\,{\beta }^{4}+{\beta }^{6} \right) vw}{-4-2\,{\beta }^{2}+{\beta }^{4}}}\\&\quad +\,{\dfrac{4\left( -2+{\beta }^{2} \right) ^{2} \left( 8-2\,{\beta }^{2}+{\beta }^{4 } \right) {w}^{2}}{-4-2\,{\beta }^{2}+{\beta }^{4}}},\\ \dot{w}&= -{\dfrac{2w}{\beta \sqrt{2-{\beta }^{2}}}}+{\dfrac{ \left( -4+3\,{\beta }^{2} \right) {u}^{2}}{64-32\,{ \beta }^{4}+8\,{\beta }^{6}}}\\&\quad +\,{\dfrac{ \left( -1+{\beta }^{2} \right) vu}{2\beta \sqrt{2-{\beta }^{2}} \left( -4-2\,{\beta }^{2}+{\beta }^{4 } \right) }} \\&\quad +\,{\dfrac{ \left( -4+8\,{\beta }^{2}-3\,{\beta }^{4} \right) wu}{\beta \sqrt{2-{\beta }^{2}} \left( -4-2\,{\beta }^{2}+{\beta }^{4} \right) }}\\&\quad -\,{\dfrac{6 \left( -2+{\beta }^{2} \right) ^{2}{w}^{ 2}}{-4-2\,{\beta }^{2}+{\beta }^{4}}}\\&\quad +\,{\dfrac{{v}^{2}}{32+16\,{ \beta }^{2}-8\,{\beta }^{4}}}+{ \dfrac{2 \left( -2+{\beta }^{2} \right) vw}{-4-2\,{\beta }^{2}+{ \beta }^{4}}}. \end{aligned}$$

Note that the above system is in the form (3). Now, we apply the method described in Sect. 3.

Firstly, we introduce the change of variables \((u, v, w)\mapsto (x,y,z)=(u+iv, u-iv, w)\) with inverse given by \((x,y,z)\mapsto (u,v,w)=\left( \dfrac{1}{2}(x+y),-\dfrac{i}{2}(x-y),z\right) \). Hence, we obtain system (1) in the complex form (5). Again let denote by \(X\) the vector field associated with this last system in complex form and let \(H\) be given by (6). We have that

$$\begin{aligned} XH(x,y,z)=\sum _{m\ge 2} H_m(x,y,z), \end{aligned}$$

where \(H_m\) are homogeneous polynomials of degree \(m\) in the variables \((x,y,z)\). It is easy to see that \(H_2\equiv 0 \). Denoting the coefficients of \(H_m\) by \(g_{jkl}\) with \(j+k+l=m\), we can solve easily the equations \(g_{jkl}=0\) with \(j+k+l=3\) in terms of the coefficients \(\nu _{\alpha \beta \gamma }\) of \(H\) such that \(\alpha +\beta +\gamma \le 3\). For instance, the equation \(g_{003}=0\) is given by

$$\begin{aligned} -\frac{6 \nu _{003}}{\beta \sqrt{2-\beta ^2}}=0, \end{aligned}$$

which solution in terms of the coefficients of \(H\) is \(\nu _{003}=0\). Analogously, we can solve the equations \(g_{jkl}=0\) with \(j+k+l=4\) in terms of the coefficients \(\nu _{\alpha \beta \gamma }\) of \(H\) with \(\alpha +\beta +\gamma \le 4\), except the equation \(g_{220}=0\), because this equation does not depend on the coefficients of \(H\), only on the coefficients of \(X\). Hence, we have that the first focus quantity is \(g_{220}=\nu _1\) given by

$$\begin{aligned} \nu _{1}=\dfrac{ \sqrt{2-\beta ^2} \left( 3 \beta ^4-7 \beta ^2+1\right) \beta }{4 \left( \beta ^4-2 \beta ^2-4\right) \left( \beta ^4-2 \beta ^2-1\right) }. \end{aligned}$$
(10)

Following the above ideas, we obtain the second focus quantity \(g_{330}=\nu _2\), i.e.,

$$\begin{aligned} \nu _2&= \bigg (\sqrt{2-\beta ^2} \left( -162 \beta ^{22}+2268 \beta ^{20}-14289 \beta ^{18}\right. \\&\left. +\,47071 \beta ^{16}-80155 \beta ^{14}\right. \\&+\,63495 \beta ^{12}\!-\!20967 \beta ^{10}\!+\!16999 \beta ^8\!-\!23136 \beta ^6\\&+\,9300 \beta ^4\!+\!9760 \beta ^2\\&\!-\!\left. \,80\right) \bigg )/\bigg (96\beta \left( \beta ^4-2 \beta ^2\!-\!4\right) ^3 \left( \beta ^4\!-\!2 \beta ^2\!-\!1\right) ^2\\&\times \,\left( 9 \beta ^2 \left( \beta ^2-2\right) -4\right) \bigg ). \end{aligned}$$

Note that the polynomial \(\beta ^4-2 \beta ^2-4\) has only two real roots, \(\pm \sqrt{1+\sqrt{5}}\), and so it has negative sign in \((-\sqrt{1+\sqrt{5}}, \sqrt{1+\sqrt{5}})\). Now, the polynomial \(\beta ^4-2 \beta ^2-1\) also has only two real roots, \(\pm \sqrt{1+\sqrt{2}}\), and so it has negative sign in \((-\sqrt{1+\sqrt{2}}, \sqrt{1+\sqrt{2}})\). Therefore, the sign of the first focus quantity is determined by the sign of \(h(\beta )=3 \beta ^4-7 \beta ^2+1\), since we are considering \(\beta \in (0,\sqrt{2})\) and so the denominator of (10) is positive. Observe that, for \(\beta \in (0,\sqrt{2})\), the first focus quantity vanishes on \(\beta _c=\sqrt{\dfrac{1}{6} \left( 7-\sqrt{37}\right) }\), and the second is deferent from zero, i.e., \(\nu _1(\beta _c)=0\) and \(\nu _2(\beta _c)=\dfrac{\sqrt{274249 \sqrt{37}-591726}}{15568}\). Moreover, \(\nu _1>0\) for \(\beta \in (0,\beta _c)\) and \(\nu _1<0\) for \(\beta \in (\beta _c,\sqrt{2})\).

Clearly, in the plane of parameters \((\varepsilon , \beta )\), we have a transversal Hopf point in \(Q_-\) for \(\varepsilon =0\) and \(\beta \in (0,\sqrt{2})\setminus \{\beta _c\}\). Now, as the map \((\varepsilon ,\beta )\mapsto (\varepsilon , \nu _1(\beta ))\) is regular in \((0,\beta _c)\), since

$$\begin{aligned} \dfrac{\hbox {d}\nu _1}{\hbox {d}\beta }(\beta _c)=-\dfrac{\sqrt{37 \left( 14066 \sqrt{37}-84205\right) }}{1946}, \end{aligned}$$

it follows that we have a transversal Hopf point of codimension two in \(Q_-\) for \(\varepsilon =0\) and \(\beta =\beta _c\).

In the parameter \(\lambda \), by (9), the function \(h\) becomes \(h(\lambda )=3\,{\lambda }^{4}-5\,{\lambda }^{2}-1\ne 0\),

$$\begin{aligned} \nu _1(\lambda )=\dfrac{\lambda \sqrt{2-\lambda ^2} \left( 3 \lambda ^4-5 \lambda ^2-1\right) }{4 \left( \lambda ^4-2 \lambda ^2-4\right) \left( \lambda ^4-2 \lambda ^2-1\right) } \end{aligned}$$

and \(\nu _1(\lambda )\) is zero in the \((0,\sqrt{2})\) only for the value \(\lambda _c=\sqrt{\dfrac{5+\sqrt{37}}{6}}\). Moreover, in this point, by (9), \(\alpha =\dfrac{7-\sqrt{37}}{\sqrt{6(5+37)}}\).

The same results stated in Theorem 1 are valid also for the point \(Q_+\), due to the symmetry of the system under the change \((x,y,z)\mapsto (-x,-y,z)\). The statements \(({a})\) and \((b)\) of Theorem 1 follow from the above results.

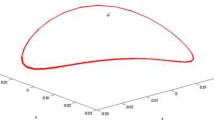
The bifurcation diagram on the space of parameters \((\lambda , \alpha )\) of system (1) on the neighborhood of the two codimension Hopf point \(H_2= \left( \sqrt{\dfrac{5+\sqrt{37}}{6}}, \dfrac{7-\sqrt{37}}{\sqrt{6(5+37)}}\right) \) is described in Fig. 2, where by Sect. 4 the curves \(H^\pm _1\) and \(T\) correspond, respectively, with the curves of Fig.  1. Note that

$$\begin{aligned} H^-_1\cup H_2\cup H^+_1=\left\{ \left( \lambda , \alpha \right) \quad \alpha = \dfrac{2-\lambda ^2}{\lambda },\quad \lambda \in (0,\sqrt{2}) \right\} . \end{aligned}$$
Fig. 2
figure 2

Diagram at the point \(H_2\) of the two codimension Hopf bifurcation of system (1)

Full size image