Abstract
The purpose of this chapter is first to recall some fundamental notions from the theory of crystalline solids (such as direct lattice, unit cell, reciprocal lattice, vectors of the reciprocal lattice, Brillouin zone, etc.) applied to phononic crystals and second to present the most common theoretical tools that have been developed by several authors to study elastic wave propagation in phononic crystals and acoustic metamaterials. These theoretical tools are the plane wave expansion method, the finite-difference time domain method, the multiple scattering theory, and the finite element method. Furthermore, a model reduction method based on Bloch modal analysis is presented. This method applies on top of any of the numerical methods mentioned above. Its purpose is to significantly reduce the size of the final matrix model and hence enable the computation of the band structure at a very fast rate without any noticeable loss in accuracy. The intention in this chapter is to give to the reader the basic elements necessary for the development of his/her own calculation codes. The chapter does not contain all the details of the numerical methods, and the reader is advised to refer to the large bibliography already devoted to this topic.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
10.1 Periodic Structures and Their Properties
Solids possessing crystalline structure are periodic arrays of atoms. The starting point in the description of the symmetry of any periodic arrangement is the concept of a Bravais lattice. A Bravais lattice is defined as an infinite array of discrete points with such an arrangement and orientation that it appears exactly the same from whichever of its points the array is viewed [1]. Mathematically, a Bravais lattice in three dimensions is defined as a collection of points with position vectors \( \vec{R} \) of the form
where \( {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_1},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_2},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_3} \) are any three vectors not all in the same plane and \( n,m,k \) are any three integer numbers. Vectors \( {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_1},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_2},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_3} \) are called primitive vectors of a given Bravais lattice. When any of the primitive vectors are zero, (10.1) also defines a two-dimensional (2D) Bravais lattice, one example of which is shown in Fig. 10.1.
A 2D triangular Bravais lattice. Several possible choices of the primitive vectors \( \overrightarrow {{a_1}} \) and \( \overrightarrow {{a_2}} \) are indicated
It is also worth mentioning that for any given Bravais lattice, the set of primitive vectors is not unique, and there are very many different choices, as shown in Fig. 10.1.
In three dimensions, there exist a total of 14 different Bravais lattices. The symmetry of any physical crystal is described by one of the Bravais lattices plus a basis. The basis consists of identical units (usually made by group of atoms), which are attached to every point of the underlying Bravais lattice. A crystal, whose basis consists of a single atom or ion, is said to have a monatomic Bravais lattice.
Another important concept widely used in the study of crystals is that of a primitive cell. The primitive cell is a volume of space that contains precisely one lattice point and can be translated through all the vectors of a Bravais lattice to fill all the space without overlapping itself or leaving voids. Just as in the case of primitive vectors, there is no unique way of choosing a primitive cell. The most common choice, however, is the Wigner–Seitz cell, which has the full symmetry of the underlying Bravais lattice. The Wigner–Seitz cell about a lattice point also has a property of being closer to that point than to any other lattice point. It can be constructed by drawing lines connecting a given point to nearby lying points, bisecting each line with a plane and taking the smallest polyhedron bounded by these planes.
The Bravais lattice, which is defined in real space, is sometimes referred to as a direct lattice. At the same time, there exist the concepts of a reciprocal space and a reciprocal lattice, which play an extremely important role in virtually any study of wave propagation, diffraction, and other wave phenomena in crystals. For any Bravais lattice, given by a set of vectors \( \vec{R} \) [see (10.1)], and a plane wave \( { \exp }(i\vec{k} \cdot \vec{r}) \), the reciprocal lattice is defined as a set of all wave vectors \( \vec{G} \) that yield plane waves with the periodicity of a given Bravais lattice [1]. Mathematically, a wave vector \( \vec{G} \) belongs to the reciprocal lattice of a Bravais lattice with vectors \( \vec{R} \), if the equation
is true for any \( \vec{r} \) and \( \vec{R} \) of the given Bravais lattice. It follows from (10.2) that a reciprocal lattice can also be viewed as a set of points, whose positions are given by a set of wave vectors \( \vec{G} \) satisfying the condition:
for all \( \vec{R} \) in the Bravais lattice. The reciprocal lattice itself is a Bravais lattice. The primitive vectors \( {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}}_1},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}}_2},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}}_3} \) of the reciprocal lattice are constructed from the primitive vectors \( {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_1},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_2},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}}_3} \) of the direct lattice and given in three dimensions by the following expressions:
As an example, Fig. 10.2 shows a simple-cubic Bravais lattice with a lattice constant \( a \) as well as its reciprocal lattice, which is also a simple-cubic one with a lattice constant \( 2\pi /a \) (as follows from relations (10.4)).
Simple-cubic direct lattice and its reciprocal lattice. The primitive vectors of both lattices are also indicated
Since the reciprocal lattice is a Bravais lattice, one can also find its Wigner–Seitz cell. The Wigner–Seitz cell of a reciprocal lattice is conventionally called a first Brillouin zone (BZ). Planes in k-space, which bisect the lines joining a particular point of a reciprocal lattice with all other points, are known as Bragg planes. Therefore, the first BZ can also be defined as the set of all points in k-space that can be reached from the origin without crossing any Bragg plane. The BZs of higher orders also exist, with the nth BZ defined as the set of points that can be reached from the origin by crossing (n-1) Bragg planes [1]. The first BZ is of great importance in the theory of solids with periodic structures, since the periodicity of the structure allows the description of the properties of the solids within the first BZ. Figure 10.3 shows the first three BZs of the 2D square Bravais lattice. The first BZ has a shape of a square with two high-symmetry directions, which are commonly referred to as ΓX and ΓM.
(a) The first three Brillouin zones of the reciprocal lattice of the 2D square Bravais lattice. The dots indicate reciprocal lattice points, the solid lines indicate Bragg planes, and the digits indicate the order of the corresponding Brillouin zone. (b) The first Brillouin zone with the two high-symmetry directions commonly referred to as ΓX and ΓM. The triangle ΓXM is named the irreducible Brillouin zone
It is well known from quantum mechanics that the energy of an electron in an atom assumes discrete values. However, when the atomic orbitals overlap as the atoms come close together in a solid, the energy levels of the electrons broaden and form continuous regions, also known as energy bands. At the same time, because of the periodicity of the crystal structure, the electronic wave functions undergo strong Bragg reflections at the boundaries of the BZs. The destructive interference of the Bragg-scattered wave functions gives rise to the existence of the energy regions, in which no electronic energy levels exist. Since these regions are not accessible by the electrons, they are also known as forbidden bands. If the forbidden band occurs along the particular direction inside the crystal, it is conventionally called a stop band. If it happens to span all the directions inside the crystal, the term “complete band gap,” or simply band gap, is used instead. The electronic properties of crystalline solids are conveniently described with the help of the band structure plots, which represent energy levels of the electrons of the solid as a function of the direction inside the solid.
The concepts of the direct and reciprocal lattices, BZs and energy bands discussed in this section, are of general nature and can be applied to any periodic system without being limited to atomic crystals. These concepts appear throughout the different chapters of this book.
10.2 Plane Wave Expansion methods
10.2.1 Plane Wave Expansion Method for Bulk Phononic Crystals
We first present with many details the plane wave expansion (PWE) method used for the calculation of the band structures of bulk phononic crystals, i.e., assumed of infinite extent along the three spatial directions. For the sake of simplicity, we limit ourselves to 2D phononic crystals, but the method can be easily extended to 3D structures. Two-dimensional phononic crystals are modeled as periodic arrays of infinite cylinders of different shape (circular, square, etc.) made up of a material A embedded in an infinite matrix B. Elastic materials A and B may be isotropic or of specific crystallographic symmetry. The elastic cylinders are assumed parallel to the \( z \) axis of the Cartesian coordinates system \( (O,x,y,z) \). The intersections of the cylinders axis with the \( (xOy) \) transverse plane form a 2D periodic array and the nearest neighbor distance between cylinders is \( a \). The 2D primitive unit cell may contain one cylinder, or more. The filling factor, \( {f_i} \), of each inclusion is defined as the ratio between the cross-sectional area of a cylinder and the surface of the primitive unit cell (see Fig. 10.4).
Transverse cross section of the (square) array of inclusions . The cylinders are parallel to the z direction. The dotted lines represent the primitive unit cell of the 2D array
In absence of an external force, the equation of propagation of the elastic waves in any composite material is given as
where \( {u_i}(\vec{r},t)(i = 1,2,3) \)) is a component of the elastic displacement field. The elements \( {C_{{ijmn}}}(i,j,m,n = 1,2,3) \) of the elastic stiffness tensor and the mass density \( \rho \) are periodic functions of the position vector, \( \vec{r} = ({\vec{r}_{{_{{//}}}}},z) = (x,y,z). \)
In (10.5), x 1, x 2, x 3,u 1, u 2 and u 3 are equivalent to x, y, z, u x , u y , and u z respectively.
For the sake of clarity, we consider constituent materials of cubic symmetry (but the method could be applied for lower crystallographic symmetry) characterized by the following stiffness tensor:
where the Voigt notation has been used. In this case, (10.5) becomes
For bulk phononic crystals, the elastic constants and the mass density do not depend on \( z \). Then taking advantage of the 2D periodicity in the \( (xOy) \) plane, they can be expanded in Fourier series in the form:
where \( {\vec{G}\prime\prime_{{//}}} \) is a 2D reciprocal lattice vector. One writes, with the help of the Bloch theorem, the elastic displacement field as
where \( \vec{K} = ({\vec{K}_{{//}}},{K_z}) = ({K_x},{K_y},{K_z}) \) is a wave vector, \( \vec{G}^{\prime_{{//}}} \), a 2D reciprocal lattice vector, and \( \omega \) , an angular frequency. Substituting (10.8), (10.9), and (10.10) into (10.5) and posing \( {\vec{G}_{{//}}} = {\vec{G}\prime_{{//}}} + {\vec{G}\prime\prime_{{//}}} \) leads to a set of three coupled equations
where
and G x , G y (resp. \( {\vec{G}\prime_x},{\vec{G}\prime_y} \)) are the components of the \( {\vec{G}_{{//}}} \)(resp. \( {\vec{G}\prime_{{//}}} \)) vectors.
Equation (10.12) can be rewritten as a standard generalized eigenvalue equation in the form
Equation (10.13) is equivalent to \( {\omega^2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}}{\vec{u}_{{\vec{K}}}} = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}}{\vec{u}_{{\vec{K}}}} \), where \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} \) and \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}} \) are square matrices whose size depends on the number of 2D \( {\vec{G}_{{//}}} \) vectors taken into account in the Fourier series. The numerical resolution of this eigenvalue equation is performed along the principal directions of propagation of the \( 2D \) irreducible BZ of the array of inclusions.
If one assumes that the elastic waves propagate only in the transverse plane (xOy), i.e., K z =0, then the elements of the sub-matrices \( {A^{{\left( {13} \right)}}}_{{{{\vec{G}}_{{//}}},{{\vec{G}\prime}_{{//}}}}} \), \( {A^{{\left( {23} \right)}}}_{{{{\vec{G}}_{{//}}},{{\vec{G}\prime}_{{//}}}}} \), \( {A^{{\left( {31} \right)}}}_{{{{\vec{G}}_{{//}}},{{\vec{G}\prime}_{{//}}}}} \), and \( {A^{{\left( {32} \right)}}}_{{{{\vec{G}}_{{//}}},{{\vec{G}\prime}_{{//}}}}} \) vanish and (10.13) can be rewritten as
The matrices involved in (10.14) are super-diagonal, and one can separate this equation into two independent uncoupled eigenvalues equations as follows:
Equation (10.15) leads to XY vibration modes polarized in the transverse plane (xOy) and (10.16) corresponds to Z modes with a displacement field along the z direction. Decoupling of the propagation modes in bulk phononic crystals leads to the diagonalization of matrices of reduced size and then to save computation time.
In order to evaluate the Fourier transform of the elastic constants and the density defined by (10.8) and (10.9), we need to specify the symmetry of the array of inclusions, the shape, and the cross-sectional area of the cylinder inclusion. For example, one considers a square array of cylinders of circular cross section of radius R with a lattice parameter a. Then one inclusion of filling factor \( f = \pi {\left( { \frac{R}{a} } \right)^2} \) is located at the center of the 2D primitive unit cell (Wigner–Seitz cell) and the Fourier coefficients in (10.8) and (10.9) are given as
where \( \zeta \equiv \rho, {C_{{ij}}} \) and \( {A_{\rm{u}}} \) is the area of the 2D primitive unit cell. These Fourier coefficients can be calculated as follows:
But \( \frac{1}{{{A_{\text{u}}}}}\iint\limits_{{\left( \begin{subarray}{l} {\text{primitive}} \\ {\text{unit cell}} \end{subarray} \right)}} {{{\text{e}}^{{ - {\text{i}}{{\vec{G}}_{{//}}} \cdot {{\vec{r}}_{{//}}}}}}{{\text{d}}^2}{{\vec{r}}_{{//}}}} = {\delta_{{{{\vec{G}}_{{//}}},\vec{O}}}} \) where \( \delta \) is the Dirac distribution and (10.18) can be rewritten as
where \( F({\vec{G}_{{//}}}) \) is the structure factor defined as
In (10.20), integration is performed over the cross section of the cylindrical inclusion denoted by (A u.c.). Using the polar coordinates \( {r_{{//}}},{ }\theta \), one shows that
where J 0 and J 1 are Bessel functions of the first kind of orders 0 and 1, \( f = \pi {R^2}/{a^2} \) and \( 0 \le f \le \pi /4 \). The maximum value of f corresponds to the close-packed structure where one cylinder touches another one. Similar calculations lead, for rods of square cross section of width d, to \( F\left( {{{\vec{G}}_{{//}}}} \right) = f\bigg( {\frac{{{ \sin }\left( {{G_x}d/2} \right)}}{{\left( {{G_x}d/2} \right)}}} \bigg)\left( {\frac{{{ \sin }\left( {{G_y}d/2} \right)}}{{\left( {{G_y}d/2} \right)}}} \right) \) where \( f = {d^2}/{a^2} \) and \( 0 \le f \le 1 \).
Note that for \( {\vec{G}_{{//}}} = \vec{0},F({\vec{G}_{{//}}} = \vec{0}) = f\quad {\text{and}} \)
and \( \zeta ({\vec{G}_{{//}}} = {\rm{\vec{0}}}) \) corresponds to the average value of \( \zeta \).
The components of the 2D reciprocal lattice vectors \( {\vec{G}_{{//}}} \) are \( {G_x} = \frac{{2\pi }}{a}{n_x} \) and \( {G_y} = \frac{{2\pi }}{a}{n_y} \) where \( {n_x} \) and \( {n_y} \) are integers. In the course of the numerical resolution of (10.13), we consider \( - {M_x} \leqslant {n_x} \leqslant + {M_x} \) and \( - {M_y} \le {n_y} \le + {M_y} \) (with \( {M_x} \) and \( {M_y} \) positive integers), i.e., \( (2{M_x} + 1)(2{M_y} + 1) \) 2D \( {\vec{G}_{{//}}} \) vectors (\( {G_x} \) and \( {G_y} \) have \( (2{M_x} + 1) \) and \( (2{M_y} + 1) \) different values, respectively) are taken into account. This gives \( 3(2{M_x} + 1)(2{M_y} + 1) \) real eigenfrequencies \( \omega (\vec{K}) \) for a given wave vector \( \vec{K} \) describing the principal directions of propagation in the irreducible BZ. Following the same process, the PWE method can be applied to other symmetries of the array (triangular, honeycomb, etc.) and other shapes of the inclusion (square, rotated square, etc.). The choice of the values of the integers M x , M y is of crucial importance for insuring the convergency of the Fourier series. The convergency is fast when considering constituent materials with closed physical properties but is slower when materials A and B present very different densities and elastic moduli [2]. The PWE method is also useful for computing band structures of phononic crystals made of fluid constituents [3]. In this case, the Fourier transform of the equation of propagation of longitudinal acoustic waves in a heterogeneous periodic fluid leads to a generalized eigenvalue equation similar to (10.16). But the PWE method fails to predict accurately the band structures of mixed phononic crystals made of solid (resp. fluid) inclusions surrounded by a fluid (resp. solid) [4]. Nevertheless, in some particular cases, the PWE method is very well adapted for the calculations of band structures of mixed systems, provided the inclusions can be assumed to be infinitely rigid as it happens in arrays of solid inclusions surrounded with air [5]. On the other hand, the PWE method assumes the phononic crystal to be of infinite extent in the three spatial directions and does not allow the calculation of the reflection and transmission coefficients of elastic waves through phononic crystals of finite thickness.
10.2.2 PWE Method for Phononic Crystal Plates: The Super-Cell Method
To calculate the elastic band structures of 2D phononic crystal plates, one modifies the PWE method presented in Sect. 10.2.1. The phononic crystal plate of thickness, \( {h_2} \), is assumed to be infinite in the \( (xOy) \) plane of the Cartesian coordinates system \( (O,x,y,z) \). The plate is sandwiched between two slabs of thicknesses \( {h_1} \) and \( {h_3} \), made of elastic homogeneous materials C and D (see Fig. 10.5a). In the course of the numerical calculations, one considers the parallelepipedic super-cell depicted in Fig. 10.5b).
(a) 2D phononic crystal plate sandwiched between two slabs of homogeneous materials and (b) 3D super-cell considered in the course of the super-cell PWE computation
The basis of the super-cell in the \( (xOy) \) plane includes that of the 2D primitive unit cell (which may contain one cylinder or more) of the array of inclusions, and its height along the \( z \) direction is \( \ell = {h_1} + {h_2} + {h_3} \). This super-cell is repeated periodically along the \( x \), \( y \), and \( z \) directions. This triple periodicity allows one to develop the elastic constants and the mass density of the constituent materials as Fourier series as
where \( \vec{r} = ({\vec{r}_{{//}}},z) = (x,y,z) \) and \( \vec{G} = ({\vec{G}_{{//}}},{G_z}) = ({G_x},{G_y},{G_z}) \) are 3D position vectors and reciprocal lattice vectors, respectively. Moreover, the elastic displacement field can be written as
The components in the \( (xOy) \) plane of the \( \vec{G} \) vectors depend on the geometry of the array of inclusions while along the \( z \) direction, \( {G_z} = \frac{{2\pi }}{\ell }{n_z} \), where \( {n_z} \) is an integer. The Fourier coefficients in (10.23) are now given as
with \( {V_u} = {A_{\rm{u}}}.\ell \) is the volume of the super-cell.
For a square array of inclusions, the Fourier coefficients become
with
In (10.27), (10.28), and (10.29), the integration is performed over the volume occupied by each material A, C, or D inside the unit cell. In (10.27), \( F({\vec{G}_{{_{{//}}}}}) \) is the structure factor defined by (10.21) for cylindrical inclusions.
As for the bulk phononic crystals, the equation of motion is Fourier transformed by substituting (10.23) and (10.24) in (10.5), and this leads to the following generalized eigenvalue equation:
where
The numerical resolution of this eigenvalue equation is performed along the principal directions of propagation of the 2D irreducible BZ of the array of inclusions while \( {K_z} \) is fixed to any value lower than \( \frac{\pi }{\ell } \). In the course of the numerical calculations, \( {G_x} \), \( {G_y} \), and \( {G_z} \) take respectively \( (2{M_x} + 1) \) , \( (2{M_y} + 1) \), and \( (2{M_z} + 1) \) discrete values, and this leads to \( 3(2{M_x} + 1)(2{M_y} + 1)(2{M_z} + 1) \) eigenfrequencies ω for a given wave vector \( \vec{K} \).
The super-cell method requires an interaction as low as possible between the vibrational modes of neighboring periodically repeated phononic crystal plates. Then, in order to allow the top surface of the plate to be free of stress, medium C should behave, for instance, like vacuum [6]. But as already observed by various authors [6–8], the choice of the physical parameters characterizing vacuum in the course of the PWE computations is of critical importance. Indeed, in the framework of the PWE method, taking abruptly \( {C_{{ij}}} = 0 \) and \( \rho = 0 \) for vacuum leads to numerical instabilities and unphysical results [6–8]. Then vacuum must be modeled as a pseudo-solid material with very low \( {C_{{ij}}} \) and \( \rho \). For the sake of simplicity, this low impedance medium (LIM) is supposed to be elastically isotropic and is characterized by a longitudinal speed of sound \( {C_{\rm{l}}} \), and a transversal speed of sound \( {C_{\rm{t}}} \) or equivalently by two elastic moduli expressed with the Voigt notation as \( {C_{{11}}} = \rho {C_{\ell }}^2 \) and \( {C_{{44}}} = \rho {C_{\rm{t}}}^2 \). The choice of the values of these parameters is governed by the boundary condition between any solid material and vacuum. Indeed, one knows that this interface must be free of stress, and this requires that \( {C_{{11}}} = 0 \) and \( {C_{{44}}} = 0 \) rigorously in vacuum [6]. Then, using the LIM to model vacuum in the PWE computations, the nonvanishing values of these parameters must be as small as possible, and we consider that the ratio between the elastic moduli of the LIM and those of any other solid material constituting the phononic crystal must approach zero. We choose \( {C_{\rm{l}}} \) and \( {C_{\rm{t}}} \) to be much larger than the speeds of sound in usual solid materials in order to limit propagation of acoustic waves to the solid. Large speeds of sound and small elastic moduli impose a choice of a very low mass density for the LIM. More specifically, we choose \( \rho { = 10^{{ - 4}}}{\text{kg}}{{\text{m}}^{{ - 3}}} \) and \( {C_{\rm{l}}} = {C_{\rm{t}}}{ = 10^5}{\text{m}}{{\text{s}}^{{ - 1}}} \), i.e., the acoustic impedances of the LIM are equal to \( 10{\text{kg}}{{\text{m}}^{{ - 2}}}{{\text{s}}^{{ - 1}}} \). With these values, \( {C_{{11}}} = {C_{{44}}}{ = 10^6}{\text{N}}{{\text{m}}^{{ - 2}}} \) and the elastic constants of the LIM are approximately \( {10^4} \) times lower than those of any usual solid material that are typically on the order of \( {10^{{10}}}{\text{N}}{{\text{m}}^{{ - 2}}} \). The values we choose for \( {C_{{11}}} \) and \( {C_{{44}}} \) are a compromise to achieve satisfactory convergence of the SC-PWE method and still satisfy boundary conditions. Values of the elastic constants of the LIM lower than \( {10^4}{\text{N}}{{\text{m}}^{{ - 2}}} \) can have, in some cases, effects on the numerical convergence. We choose \( {C_{{11}}} = {C_{{44}}} \) for convenience. In the course of the PWE calculations, these values of the LIM physical characteristics allow one to model vacuum without numerical difficulties.
In the super-cell, medium D can be either vacuum or a homogeneous material depending on whether one wants to model a phononic crystal plate or a structure made of a phononic crystal plate deposited on a substrate of finite thickness. Computations of dispersion curves of phononic crystal plates with \( {K_z} = 0 \) and with any other nonvanishing value of \( {K_z} \), lower than \( \frac{\pi }{\ell } \), lead to nearly the same result. Indeed, the eigenvalues computed with \( {K_z} = 0 \) and \( {K_z} \ne 0 \) differ only in their third decimal. This indicates that the homogeneous slabs C and D made of the LIM modeling vacuum rigorously provide appropriate decoupling of the plate modes of vibration in the \( z \) direction. Then, the value of \( {K_z} \) may be fixed to zero. Due to this 3D nature, the numerical convergency of the super-cell PWE (SC-PWE) method is relatively slow, and it has been shown that this method is suitable for voids/solid matrix plates but is not reliable for constituent materials with very different physical properties [9]. The SC-PWE method does not to require to write and to satisfy explicitly the boundary conditions at the free surfaces. Nevertheless, other authors have proposed PWE schemes for phononic crystals plates where these boundary conditions are satisfied, but these methods also suffer from convergence difficulties [10].
10.2.3 PWE Method for Complex Band Structures
In classical PWE methods (see Sect. 10.2.1), one calculates a set of real eigenfrequencies \( \omega (\vec{K}) \) for a specific wave vector \( \vec{K} \). That means that only propagating modes with a real wave vector can be deduced from \( \omega (\vec{K}) \) PWE methods. Then an extended PWE method has been proposed that allows the calculation of not only the propagating modes but also the evanescent modes. The wave vector for evanescent waves possesses a nonvanishing imaginary part. We have seen previously that the Fourier transform of the equation of propagation of elastic waves in a phononic crystal leads to the resolution of a generalized eigenvalue equation in the form \( {\omega^2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}}\vec{U} = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}}\vec{U} \). The matrix elements of \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} \) and \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}} \) involve terms depending on the components of the wave vector \( \vec{K} \). It is always possible to rewrite matrix \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} \) as \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} = K_{\alpha }^2\overleftrightarrow{{{A_1}}} + {K_{\alpha }}\overleftrightarrow{{{A_2}}} + \overleftrightarrow{{{A_3}}} \) , where \( {K_{\alpha }} \) is one of the components of the wave vector, and \( \overleftrightarrow{{{A_1}}} \), \( \overleftrightarrow{{{A_2}}} \), and \( \overleftrightarrow{{{A_3}}} \) are matrices of the same size as \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} \). The generalized eigenvalue equation \( {\omega^2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}}\vec{U} = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}}\vec{U} \) may be recast as \( K_{\alpha }^2\overleftrightarrow{{{A_1}}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{U}} = {\omega^2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}}\vec{U} - \overleftrightarrow{{{A_3}}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{U}} - {K_{\alpha }}\overleftrightarrow{{{A_2}}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{U}} \) and one can write
where \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{I}} \) is the identity matrix. Equation (10.31) is nothing else than a generalized eigenvalue equation where the eigenvalues are the component \( {K_{\alpha }} \) of the wave vector. For a specific value of the circular frequency ω, one calculates a set of complex eigenvalues \( {K_{\alpha }} \). This method is named \( \vec{K}(\omega ) \) PWE method. The size of the matrices occurring on the left and right sides of (10.31) is twice that of matrices \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} \) and \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}} \). One may illustrate these general ideas by considering the peculiar case of the Z elastic modes propagating in a bulk 2D phononic crystal made of a square array of lattice parameter a, of cylindrical inclusions embedded in a solid matrix. If one assumes K z = 0, then these modes are given by (10.16), where ω depends on the two variables K x and K y . Consider the propagation of elastic waves along the ΓX direction of the irreducible BZ for which \( {K_y} = 0 \) and \( 0 \le {\text{Re}}({K_x}) \le \frac{\pi }{a} \). Equation (10.16) leads to
and can be rewritten as
Numerical resolution of (10.34) leads to 2N (if N × N is the size of matrices \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{A}} \) and \( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}}{B}} \)) complex values of \( {K_x} = {\text{Re}}({K_x}) - i{\text{Im}}({K_x}) \) for any value of ω. Eigenvalues belonging to the irreducible BZ and corresponding to waves with a vanishing amplitude when \( x \to + \infty \) may be taken into account, i.e., \( 0 \le {\text{Re}}({K_x}) \le \frac{\pi }{a} \) and \( {\text{Im}}({K_x}) \ge 0 \) . Figure 10.6 presents the band structures calculated by both \( \omega (\vec{K}) \) and \( \vec{K}(\omega ) \) methods. This figure shows the ability of the \( \vec{K}(\omega ) \) method to calculate the evanescent modes. Of particular interest is the existence of additional bands (see right panel of Fig. 10.6 for reduced frequency around 1.1) not predicted by the classical \( \omega (\vec{K}) \) PWE method (red dots). These vibrational modes are characterized by a nonvanishing \( {\text{Im}}({K_x}) \).
Band structures along the ΓX direction of the irreducible Brillouin zone for a square array of holes drilled in a Silicon matrix: Red dots: \( \omega (\vec{K}) \) method; Black dots: \( \vec{K}(\omega ) \) method
To apply this, \( \vec{K}(\omega ) \) PWE method requires to consider only one component of the wave vector \( \vec{K} \) as eigenvalue. That needs to keep fixed the other component or to write a linear relation between them. For example, along the ΓM direction in the irreducible BZ of the square array, one can write K x = K y and consider K x as the eigenvalue. In the same way, one can deal with any direction of propagation and not only with the high-symmetry directions. Plotting all the values of K x and K y corresponding to a specific frequency leads to the equi-frequency contour (EFC) of the phononic crystal. Knowing precisely the shape of these EFCs is of fundamental interest when studying focusing or self-collimating of elastic waves by phononic crystals [11]. Moreover, the \( \vec{K}(\omega ) \) PWE method allows to take into account elastic moduli depending on the frequency and should be applied for calculating the band structures of phononic crystals made of viscoelastic materials.
10.3 Finite-Difference Time Domain Method
10.3.1 Calculation of Transmission Coefficients
We present here the basic principles of the finite-difference time domain (FDTD) method applied to the calculation of transmission coefficients of elastic waves through phononic crystals made of nonviscous or nonviscoelastic constituents. The method is based on discretizations of the differential equations of motion on both spatial and time domains. As previously and for the sake of simplicity, we limit ourselves to 2D phononic crystals.
We consider a 2D phononic crystal containing cylindrical inclusions surrounded by a host matrix. Constituent materials are supposed to be isotropic solids or fluids. The inclusions are parallel to the z direction and are arranged periodically in the transverse (x,y) plane. A phononic crystal of finite thickness along the y direction is realized by considering a small number of periods in this direction. The “sample” is bounded by semi-infinite homogeneous media on both sides. The system is infinite in the vertical direction z, and all its physical properties do not depend on z. That means that we propose a strictly 2D FDTD scheme. The probing signal corresponding to a longitudinal wave that propagates along the y direction is launched from the left homogeneous medium (inlet zone) and detected in the right one (outlet zone) (see Fig. 10.7). We just describe here a 2D FDTD scheme just as it has been reported in [12].
Two-dimensional cross section of the FDTD model structure. The cylinders are parallel to the z axis of the Cartesian coordinate system (Oxyz). The lattice parameter is a
The elastic wave equation is given by
with
where t is time, \( \rho (x,y) \) is the mass density, \( \vec{u}(x,y,t) \) is the displacement field, \( \vec{v}(x,y,t) \) is the velocity vector, and \( \bar{\bar{\sigma }}(x,y) \) is the total stress tensor. The nonzero Cartesian components of the 2D stress tensor \( \bar{\bar{\sigma }} \) are
with C 11(x,y), C 44(x,y), C 12(x,y) = C 11(x,y)−2C 44(x,y), the position-dependent elastic moduli. For a given isotropic medium, C11 and C44 are related to the longitudinal C l and transverse C t speeds of sound as C 11 = ρC 2l and C 44 = ρC 2t . A fluid is treated as a solid with zero transverse speed of sound in this 2D FDTD scheme. From (10.37), (10.38), and (10.39), one notes that we consider only modes of vibration analog to XY modes as defined by (10.15) in the preceding section. The FDTD method involves transforming the governing differential equations given by (10.35) and (10.36) in the time domain into finite differences and solving them as one progress in time in small increments. For the implementation of the FDTD method, we divide the computational domain into \( {N_x} \times {N_y} \) sub-domains (grids) with dimensions Δx, Δy. For the time derivative, we use forward difference, with a time interval Δt, and the displacement field is calculated at multiple integers of Δt, whereas the velocity is calculated on a time grid shifted by half the step. The probing signal is launched from the left homogeneous medium and corresponds to a longitudinal wave that propagates along the y direction for increasing y. This can be written as \( F(y,t) = F(y - {C_{\rm{l}}}t) \), where C l is the longitudinal speed of sound in the inlet medium. The initial conditions on the displacement field and the speed vector are such as \( \vec{u}(t = 0) = \left( {\begin{array}{*{20}{c}} {{u_x} = 0} \\ {{u_y} = F(y)} \\ \end{array} } \right) \) and \( \vec{v}\left( {t = \frac{{\Delta t}}{2}} \right) = \left( {\begin{array}{*{20}{c}} {{v_x} = 0} \\ {{v_y} = {{\left. { - {C_l}\frac{{dF(y,t)}}{{dt}}} \right|}_{{ \frac{{t = + \Delta t}}{2} }}}} \\ \end{array} } \right) \).
The stress component \( {\sigma_{{xx}}} \) is calculated at time (n+1) from the components of the displacement field calculated at time t by discretizing (10.37), then
where we define \( {C_{{11}}}\left( {i + \frac{1}{2},j} \right) = \sqrt {{{C_{{11}}}(i + 1,j){C_{{11}}}(i,j)}} \) and \( {C_{{12}}}\left( {i + \frac{1}{2},j} \right) = \sqrt {{{C_{{12}}}(i + 1,j){C_{{12}}}(i,j)}}. \)
Similarly, the components \( {\sigma_{{xy}}} \) and \( {\sigma_{{yy}}} \) are obtained in discretized form as
where we define \( {C_{{44}}}\left( {i,j + \frac{1}{2}} \right) = \sqrt {{{C_{{44}}}(i,j + 1){C_{{44}}}(i,j)}} \).
Using expansions at point (i,j) and time n, (10.35) in component form becomes
where we define \( \rho \left( {i + \frac{1}{2},j + \frac{1}{2}} \right) = \sqrt[4]{{\rho (i,j)\rho (i + 1,j)\rho (i,j + 1)\rho (i + 1,j + 1)}} \).
Finally, the components of the displacement field at time (n+1) are deduced from the same component but evaluated at time n as \( u_x^{{n + 1}}(i,j) = u_x^n(i,j) + \Delta t.v_x^n(i,j) \) and \( u_y^{{n + 1}}(i,j) = u_y^n(i,j) + \Delta t.v_y^n(i,j) \).
Using this iterative procedure, the elastic wave equation is solved numerically, and the components of the time-dependent displacement field are calculated at the exit of the outlet. The component u y (t) is then averaged on a period of the slab along the x direction and Fourier transformed with respect to time. The same procedure is applied when the phononic crystal slab is replaced by a homogeneous medium identical to the inlet and the outlet media. The ratio between the two Fourier-transformed signals (with and without the PC slab) leads to the transmission coefficient. A reliable calculation of the transmission coefficient strongly depends on the choice of the function F(y,t) corresponding to the probing signal. In particular, when considering the propagation through a homogeneous structure, i.e., without the PC slab, the Fourier-transformed signal must vary smoothly with the frequency on a specific frequency range [0,ω max]. This condition can be satisfied by taken into account a sinusoidal function weighted by a Gaussian profile such as \( F(y,t) = F(y - {C_{\rm{l}}}t) = F(Y) = A{ \cos }[{k_0}Y].{ \exp }\left[ { - \frac{{{{({k_0}Y)}^2}}}{2}} \right], \) where \( {k_0}\sim \frac{{{\omega_{{\max }}}}}{{{C_l}}}. \) The choice of this kind of function also allows to mimic the frequency response of a transducer generating pressure waves with a pass band [0,ω max] usually used in ultrasonic measurements.
Periodic boundary conditions are applied along the x direction. That means that the elastic displacement is imposed to be the same on x = 0 and x = L, where L is the width of the FDTD mesh along the x direction for any value of y. For example, one must satisfy for any time step that u y (i max+1, j) = u y (1, j), where the integer i denoting the number of the spatial discretization step along the x direction varies between 1 and i max. For closing the FDTD mesh along the y direction, it is necessary to impose absorbing boundary conditions on y min and y max, where y min and y max denote the entry of the inlet zone and the exit of the outlet zone. Absorbing boundary conditions are implemented in order to prevent reflection from the end elements of the FDTD mesh. First-order Mur’s absorbing conditions [13] are usually used and can be implemented in the FDTD code by satisfying the following formula:
where the integer j denoting the number of the spatial discretization step along the y direction varies between 1 and j max. Same formula should be satisfied for the x component of the displacement field.
Finally, for insuring the numerical stability of the FDTD code, it must be checked that the time step Δt and the discretization meshes Δx and Δy satisfy the following stability criterion [14]:
where C maxl stands for the largest longitudinal speed of sound of the constituent materials involved in the structure.
10.3.2 Band Structure Calculation
In some cases, the PWE method fails to predict accurately the band structure of phononic crystals especially for mixed composites where one of the constituent is a fluid. Tanaka et al. [8] have reported an extension of the FDTD method for the calculation of dispersion relations of acoustic waves in 2D phononic crystals. In contrast with the standard FDTD approach presented in Sect. 10.3.1, the band structure FDTD technique implies a periodic system in the transverse plane xy.
The displacement field, the velocity vector, and the stress tensor must satisfy the Bloch theorem, i.e.,
where \( \vec{r}(x,y) \) is the position vector in the xy plane and \( \vec{K}({K_x},{K_y}) \) is the Bloch wave vector.
\( \vec{U}(\vec{r},t) \), \( \vec{V}(\vec{r},t) \), and \( \overline{\overline \Sigma } (\vec{r},t) \) are spatial periodic functions satisfying \( \vec{U}(\vec{r} + \vec{a}) = \vec{U}(\vec{r}) \), \( \vec{V}(\vec{r} + \vec{a}) = \vec{V}(\vec{r}) \), and \( \overline{\overline \Sigma } (\vec{r} + \vec{a}) = \overline{\overline \Sigma } (\vec{r}) \), where \( \vec{a} \) is the lattice translation vector. One inserts (10.48), (10.49), and (10.50) into the equations of propagation of the elastic waves, i.e., (10.35) and (10.36), and these later become
To solve (10.51), one first specifies a 2D wave vector, \( \vec{K}({K_x},{K_y}) \), along the principal direction of the irreducible BZ. An assumption on the initial displacement \( \vec{U}(\vec{r},t = 0) \) in the form of a delta stimulus at some random location within the unit cell is then made. The equations of motion are then solved by discretizing both space and time. The time evolution of \( \vec{U}(\overrightarrow {{r_i}}, t) \) at several predetermined locations \( \overrightarrow {{r_i}} \) within the unit cell is recorded. Peaks in the frequency space of the Fourier-transformed signals are identified as the eigenfrequencies of the normal modes of the system for a given wave vector, \( \vec{K} \).
10.3.3 Viscoelastic Media
The FDTD method reported in Sect. 10.3.1 is suitable for the calculation of transmission coefficient through phononic crystals made of non-lossy purely elastic material. Nevertheless several experimental studies were devoted to phononic crystals made of viscoelastic materials such as rubber, epoxy. Taking into account the effects of viscoelasticity on the propagation of elastic waves in phononic crystals is of fundamental as well as of practical interest in many areas. In this section, an alternate FDTD scheme where the viscoelastic properties, i.e., time-dependent elastic moduli, are rigorously taken into account is presented. As viscoelastic materials, we consider the general linear viscoelastic fluid (GLVF).
10.3.3.1 Viscoelastic Model
When the GLVF material also is compressible, the components of the total stress tensor are given by
where t is time, \( \vec{v}(\vec{r},t) \) is the velocity vector, \( \vec{D}(\vec{r},t) \) is the rate of deformation tensor given by
and G(t) and K(t) are the steady shear and bulk moduli, respectively.
These moduli can be experimentally determined through rheometry, and the data can be fit in a variety of ways, including the use of mechanical-analog models. A viscoelastic model, or in effect, the behavior pattern it describes, may be illustrated schematically by combinations of springs and dashpots, representing elastic and viscous factors, respectively. Hence, a spring is assumed to reflect the properties of an elastic deformation and similarly a dashpot to depict the characteristics of viscous flow. The generalized Maxwell model, also known as the Maxwell–Weichert model, takes into account the fact that the relaxation does not occur with a single time constant, but with a distribution of relaxation times. The Weichert model shows this by having as many spring–dashpot Maxwell elements as are necessary to accurately represent the distribution (Fig. 10.8
Spring and dashpot illustration of the generalized Maxwell model
). A multiple element Maxwell model is therefore more apt to represent the numerous timescales associated with relaxation in real viscoelastic materials.
For an n-element generalized Maxwell solid model, the extensional modulus E(t) is calculated to be
where \( \{ {E_i},{\tau_i} = 1,2, \ldots, n\} \) are the moduli and relaxation times of the elements, and \( {E_{\infty }} = E(\infty ) \) is the equilibrium extensional modulus.
Introducing \( \alpha (t) = {\alpha_0} + \sum\limits_{{i = 1}}^n {{\alpha_i}{{\text{e}}^{{ - t/{\tau_i}}}}} \) where \( {\alpha_0} = \frac{{{E_{\infty }}}}{{{E_{\rm{sum}}}}} \), \( {\alpha_i} = \frac{{{E_i}}}{{{E_{\rm{sum}}}}} \) (i = 1, 2,.., n), and \( \sum\limits_{{i = 0}}^n {{\alpha_i}} = 1 \), \( {E_{\rm{sum}}} = \sum\limits_{{i = 1}}^n {{E_i}} \), we obtain \( E(t) = {E_{\rm{sum}}}\alpha (t) \).
Consequently, we assume that
In (10.55) and (10.56), \( \upsilon \) is the Poisson’s ratio and λ and μ are the Lamé constant and shear modulus, respectively.
Now we consider a 2D elastic/viscoelastic material, where the system is infinite in the vertical direction z, and none of its properties depends on z (translational invariance). In this case, the Cartesian components of the 2D stress tensor deduced from (10.52) become
For the sake of illustration, let us insert (10.56) into (10.57). Using \( {{\text{C}}_{{11}}} = { 2}\mu + \lambda \), \( {{\text{C}}_{{12}}} = \lambda \), and \( {{\text{C}}_{{44}}} = \mu \), \( {\sigma_{{xx}}}(t) \) becomes
Equation (10.60) involves integrals of the type
in which calculations can be achieved by the following recursive method.
First we assume that for an incident wave that arrives from an elastic medium, we have \( \int_{{ - \infty }}^t \approx \int_0^t \). Then the following variable w = t – t′, (⇒dw = −dt′) leads to
Now we calculate \( Ix{x_i}(t + \Delta t) \).
By changing \( s = w - \Delta t = >\; {\text{d}}s = {\text{d}}w \)
And finally a recursive form for the integral calculation is obtained as
where \( Ix{x_i}(0) = 0 \)
Similar equations are obtained for the yy and xy components.
We can now develop the FDTD method for the generalized Maxwell model.
10.3.3.2 FDTD Method for the Generalized Maxwell Model
As in Sect. 10.3.1, (10.35) stands for the basis equation for implementing the FDTD scheme taking into account the viscoelastic properties of the constituent materials of the 2D phononic crystal. The components of the velocity vector are given in discretized form by (10.43) and (10.44).
The stress component \( {\sigma_{{xx}}} \) is calculated by discretizing (10.60), using expansion at point (i, j) and time (n):
where we define \( {C_{{11}}}(i + 1/2,j) = \sqrt {{{C_{{11}}}(i + 1,j){C_{{11}}}(i,j)}} \), \( {C_{{12}}}(i + 1/2,j) = \sqrt {{{C_{{12}}}(i + 1,j){C_{{12}}}(i,j)}} \), and \( {\alpha_p}(i + 1/2,j) = \sqrt {{{\alpha_p}(i + 1,j){\alpha_p}(i,j)}} \), p = 0,1,2, …,n.
Similarly, the components \( {\sigma_{{yy}}} \) and \( {\sigma_{{xy}}} \) are obtained in discretized form:
where \( {C_{{44}}}(i,j + 1/2) = \sqrt {{{C_{{44}}}(i,j + 1){C_{{44}}}(i,j)}} \) and \( {\alpha_p}(i,j + 1/2) = \sqrt {{{\alpha_p}(i,j + 1){\alpha_p}(i,j)}} \), p = 0,1,2, …,n.
It has to be mentioned that the above way of discretizing the equations ensures second-order accurate central difference for the space derivatives. The field components \( {u_x} \) and \( {u_y} \) have to be centered in different space points. Calculations of transmission coefficients through 2D phononic crystals made of viscoelastic constituents follow the same procedures as in Sect. 10.3.1. These calculations must be done considering the structure depicted in Fig. 10.7 and applying periodic boundary conditions in the x direction and Mur’s absorbing boundary conditions on the two extremities of the discretization mesh along the y direction.
Such calculations for 2D phononic crystals made of steel cylinders embedded in rubber modeled as GLVF were reported in [15, 16]. Results have shown the very good agreement between the numerical predictions and the experimental measurements.
10.4 Multiple Scattering Theory
The multiple scattering theory (MST) was introduced for 3D phononic crystals by three different groups at about the same time [17–19], and its 2D version was developed 3 years later by Prof. Liu’s group in the theoretical work by Mei et al. [20]. The MST is essentially an extension of the Korringa–Kohn–Rostoker (KKR) theory (which is a well-known method used by the solid-state community for electronic band structure calculations) to the case of elastic/acoustic waves. The MST is ideally suited for phononic crystals (both 2D and 3D) in which scattering units have simple symmetries, such as spheres or cylinders. It is also a quickly converging method that takes into account the full vector character of the elastic field and is able to deal with the phononic crystals of any type (e.g., liquid/solid crystals, for which the PWE method fails). We present in this sub-section the main points of the MST in case of the 3D phononic crystals by following the steps along which it was developed by Liu et al. in [18].
In a homogeneous isotropic medium, the elastic wave equation may be written as
where ρ is the density of the medium, λ, μ are its Lamé constants, and \( \vec{u} \) is the displacement field. Because of the spherical symmetry of the scatterers, it is natural to work with the general solution of (10.74) expressed in the spherical coordinates:
where \( {\vec{J}_{{lm\sigma }}}(\vec{r}),{\vec{H}_{{lm\sigma }}}(\vec{r}) \) are defined as follows:
and
where \( \alpha = \omega \sqrt {{{{\rho } \left/ {{(\lambda + 2\mu )}} \right.}}} \), \( \beta = \omega \sqrt {{{{\rho } \left/ {\mu } \right.}}} \), \( {j_l}(x) \) is the spherical Bessel function, \( {h_l}(x) \) is the spherical Hankel function of the first kind, and \( {Y_{{lm}}}(\hat{r}) \) is the usual spherical harmonic with \( \hat{r} \) denoting angular coordinates \( (\theta, \varphi ) \) of \( \vec{r} \) in spherical coordinate system. In (10.75), index σ assumes values from 1 to 3, where \( \sigma = 1 \) indicates the longitudinal wave and \( \sigma = 2,3 \) indicates two transverse waves of different polarizations. In the case when the coefficients \( {b_{{lm\sigma }}} \) in (10.75) are equal to zero, \( \vec{u}(\vec{r}) \) represents an incident wave, and in the case of \( {a_{{lm\sigma }}} = 0 \), \( \vec{u}(\vec{r}) \) represents a scattered wave. Therefore, the wave incident on an ith scatterer is expressed as
where \( {\vec{r}_i} \) indicates some point in space as measured from the center of the ith scatterer. The wave scattered by scatterer i can be expressed as
The first key point of MST is the idea that the wave (10.78) incident on a given scatterer i can be viewed as a sum of the externally incident wave \( \vec{u}_i^{{(0)}}({\vec{r}_i}) \) expressed as
and all other scattered waves except the one scattered by the ith scatterer, which can be expressed as
so that (10.78) can also be written as
Here \( {\vec{r}_i} \) and \( {\vec{r}_j} \) refer to the position of the same point in space and are measured from the centers of scatterers i and j, respectively.
Another crucial point of MST is that for a given scatterer, the scattered field is completely determined from the incident field with the help of the scattering matrix T. In other words, the expansion coefficients \( A = \{ a_{{lm\sigma }}^{j}\} \) and \( B = \{ b_{{lm\sigma }}^{j}\} \) are related through \( T = \{ t_{{lm\sigma l\prime m\prime\sigma \prime}}\} \) as follows:
or more explicitly
For objects of simple geometry, such as spheres or cylinders, the calculation of the scattering matrix T is an exactly solvable boundary-value problem, and this is the origin of MST’s reliability and precision when handling arrangements of scatterers of spherical symmetry. In short, the coefficients \( {t_{{lm\sigma l\prime m\prime\sigma \prime}}} \) are found by applying the boundary conditions that require the continuity of the normal components of both the displacement and the stress vectors at the scatterer–matrix interface. The explicit expressions of the T matrix coefficients for an elastic sphere can be found in [17] (liquid matrix) and in [19] (elastic matrix), and in [20] for an elastic cylinder in an elastic matrix.
The final MST equation is obtained by substituting (10.78), (10.80), (10.81), and (10.83) into (10.82) and reads
where \( {G_{{lm\sigma l\prime m\prime\sigma \prime}}} \) is the so-called vector structure constant, which relates \( \vec{H}_{{lm\sigma }}^j({\vec{r}_j}) \) in (10.81) and \( \vec{J}_{{lm\sigma }}^i({\vec{r}_i}) \) through the relation
(more details can be found in [18]). The normal modes of the system may be obtained by solving the secular equation that follows from (10.84) in the absence of an external incident wave (i.e., when all \( a_{{lm\sigma }}^{{i(0)}} \) are zero):
In case of the periodic system, \( {G_{{lm\sigma l\prime m\prime\sigma \prime}}} \) is modified to take into account the symmetry of the structure. The solutions of (10.85) give the band structure of an elastic periodic system.
To facilitate the direct comparison with the real samples, a successful theory must also be able to calculate the quantities that one measures in a typical experiment, e.g., transmission and reflection coefficients. This is accomplished in the framework of the layer MST, which allows one to calculate the transmission of an elastic wave through a finite slab (with an arbitrary number of layers) of periodically arranged scatterers. The approach starts by calculating the field of the elastic wave scattered (or transmitted) by a single layer of scatterers. Let us assume that the layer of scatterers (elastic spheres) lies completely in the x–y plane and that positions of the scatterers are given by vectors \( \{ {\vec{R}_n}\} \) of a 2D Bravais lattice, which is generated by two primitive vectors \( {\vec{a}_1},{\vec{a}_2} \), i.e.,
where \( {n_1},{n_2} \) are integers. The positive direction of the z-axis is chosen to be to the left of the layer as explained by Fig. 10.9.
Geometry of the layer MST. Vectors \( \overrightarrow {{a_1}} {\text{and}}\overrightarrow {{a_2}} \) are the primitive vectors of the corresponding 2D Bravais lattice
A plane elastic wave \( {\vec{u}^{\rm{in}}}(\vec{r}) \) incident on the layer can be expressed in general as
where \( s = + / - \) indicates waves incident from the left (positive z) and from the right (negative z) respectively, while \( \alpha = 1 \) and \( \beta = 2,3 \) are identical to index σ in (10.75) and distinguish between the longitudinal and the transverse (with two polarizations) waves . Each term in (10.87) can be expressed in terms of the primitive vectors \( {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}}_1},{\vec{b}_2} \) of the 2D reciprocal lattice as follows:
where wave vectors \( \vec{k}_{{\alpha g}}^{\pm } \) and \( \vec{k}_{{\beta g}}^{\pm } \) are given by the expressions
Here \( \vec{g} \) is the 2D reciprocal lattice vector (\( \vec{g} = {m_1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}}_1} + {m_2}{\vec{b}_2} \), where \( {m_1},{m_2} \) are integers), and \( {\vec{k}_{{||}}} \) is a reduced wave vector in the first BZ of the reciprocal lattice. In (10.89a) and (10.89b), \( ({\vec{k}_{{||}}} + \vec{g}) \) simply represents components of wave vectors \( \vec{k}_{{\alpha g}}^{\pm } \) and \( \vec{k}_{{\beta g}}^{\pm } \) that are parallel to the layer of scatterers. These expressions are chosen to simplify subsequent calculations.
Much in the same way, the wave \( {\vec{u}^{\rm{sc}}}(\vec{r}) \) scattered by the layer can be expressed as follows:
Indices α and β have the same meaning as in case of incident wave (10.87). The index \( s = + / - \), however, reverses its meaning and now indicates the scattered waves propagating away from the layer on its right (negative z) and on its left (positive z) correspondingly (see Fig. 10.9).
After lengthy and complicated calculations, one can show (see Ref. [18]) that amplitudes \( \vec{U}_{{\alpha g}}^{{{\rm{sc}},\pm }} \) and \( \vec{U}_{{\beta g}}^{{{\rm{sc}},\pm }} \) of the scattered wave are related to the amplitudes \( \vec{U}_{{\alpha g}}^{{{\rm{in}},\pm }} \) and \( \vec{U}_{{\beta g}}^{{{\rm{in}},\pm }} \) of the incident wave with the help of matrices \( {\mathbf{M}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) (\( s,s\prime = + / - \) and \( \kappa, \kappa \prime = \alpha, \beta \)) as follows:
In the above equations, \( {\mathbf{U}}_{\kappa }^{{{\rm{sc}},\pm }} \) and \( {\mathbf{U}}_{\kappa }^{{{\rm{in}},\pm }} \) are column vectors defined as
where the Tr superscript denotes the operation of transposing. The explicit expressions for the elements of the matrices \( {\mathbf{M}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) are given by Liu et al. [18]. Being very complicated mathematical objects, matrices \( {\mathbf{M}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) nevertheless have simple physical meaning (Fig. 10.10). They are transmission and reflection matrices for incident waves \( {\mathbf{U}}_{\alpha }^{{{\rm{in}},\pm }} \) and \( {\mathbf{U}}_{\beta }^{{{\rm{in}},\pm }} \). For example, by expanding first line in the first matrix equation in (10.91), one obtains
Schematic illustration of the physical significance of the matrices \( {\text{M}}_{{\kappa \kappa \prime}}^{{SS\prime}} \)
Figure 10.10 shows a schematic diagram explaining the physical meaning of matrices contained in the above equation.
Having found transmission and reflection matrices through the single layer, one needs to find a way to calculate similar matrices for a phononic crystal with an arbitrary number of layers. Figure 10.10 shows a schematic diagram explaining the physical meaning of matrices \( {\mathbf{M}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) contained in the above equation. This is accomplished by calculating matrices \( {\mathbf{Q}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) for each of two single layers that are displaced with respect to the x–y plane by vectors \( {{{{{\vec{a}}_3}}} \left/ {2} \right.} \) and \( - {{{{{\vec{a}}_3}}} \left/ {2} \right.} \), where \( {\vec{a}_3} \) is a third primitive vector of the Bravais lattice of the phononic crystal. In other words, \( {\vec{a}_3} \) is a vector by which a single 2D layer of scatterers should be repeated to form the 3D phononic crystal. Matrices \( {\mathbf{Q}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) have the same physical meaning as \( {\mathbf{M}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) and are connected with matrices \( {\mathbf{M}}_{{\kappa \kappa \prime}}^{{ss\prime}} \) by another translation matrix \( \varphi_{\kappa }^s \), whose elements are explicitly expressed in [18]. The transmission and reflection matrices for the pair of two successive layers (denoted by N and N+1) are obtained by combining corresponding matrices \( {\mathbf{Q}}_{{\kappa \kappa \prime}}^{{ss\prime}}(N) \) and \( {\mathbf{Q}}_{{\kappa \kappa \prime}}^{{ss\prime}}(N + 1) \). The essential physics here is that two sets of matrices are combined by taking into account all multiple reflections that the incident wave undergoes between two layers as it propagates through the two-layer system. By repeating this procedure, the transmission and reflection matrices through the slab consisting of \( {2^n} \) layers can be found. The corresponding matrices for the crystal with an arbitrary number of layers can be obtained by combining matrices for the slab with even number of layers and one extra layer.
It also should be noted that in addition to the band structure, which displays normal modes of the system along high-symmetry directions, the MST also allows calculation of the modes along any direction inside the crystal. The geometrical set of all points belonging to a particular mode (which is characterized by a certain frequency) is referred to as an equi-frequency surface or equi-frequency contour for 3D or 2D structures correspondingly.
10.5 Finite Element Method
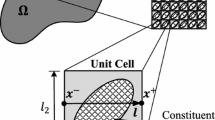
The finite element (FE) method is suitable for the calculation of band structures of phononic crystals, containing several phases or materials. To present the model, a doubly periodic structure is considered. Square-, rectangular-, triangular-, or honeycomb-type structures can be considered, but for the sake of simplicity, only the square array is presented in this section with a 2D mesh. The phononic crystal contains two or more different phases and consists, for instance, in a periodic array of holes in a solid matrix or a periodic array of cylindrical rods or tubes in a solid matrix. The formalism is the same when the periodic structure is all fluid. The structure is supposed to be infinite and periodic in the x-y plane and is infinite and uniform in the third direction. Consequently, the problem is strictly bidimensional, depending only on the x and y coordinates, using plane strain conditions. The whole domain is split into successive cells (Fig. 10.11). Due to the periodicity of the structure, the A1 and A2 lines, parallel to the y axis, and the B1 and B2 lines, parallel to the x axis, limit the unit cell, which is 2d 1 wide in the x direction and 2d 2 wide in the y direction. In Fig. 10.11, corners are marked by letter C.
Schematic description of one unit cell of the doubly periodic structure, used to define the A1, A2, B1, and B2 lines, the C1, C2, C3, and C4 corners, and the phase relation between the lines
Then the structure is excited by a plane monochromatic wave, the direction of incidence of which is marked by an angle θ with respect to the positive y axis. The incident wave is characterized by a real wave vector \( \vec{k} \), of modulus k, the wave number.
Because the structure is assumed to extend from \( - \infty \) to \( + \infty \) in the x and y directions and to be periodic, any space function F (pressure, displacement, electrical potential, etc.) has to satisfy the classical Bloch relation:
Using relation (10.93) allows reducing the model to only one unit cell, which can be meshed using FEs (Fig. 10.11). Writing relation (10.93) between the displacement values for nodes separated by one period provides the boundary conditions between adjacent cells. Using the FE method, a modal analysis is considered, and the whole system of equations is classically
where the unknown is the vector of nodal values of the displacement \( \vec{U} \cdot [{K_{{uu}}}] \) and \( [M] \) are, respectively, the structure stiffness and coherent mass matrices. ω is the angular frequency. \( \vec{F} \)contains the nodal values of the applied forces.
The application of the periodic boundary conditions implies that the phase relation (10.93) between nodal values belonging to the A1 and A2 lines, on the one hand, to the B1 and B2 lines on the other hand, has to be incorporated in the matrix equation (10.94). The unit cell is divided into nine parts: the four lines A1, A2, B1, and B2; the four corners C1, C2, C3, and C4; and the inner domain I. Displacement vector \( \vec{U} \) and force vector \( \vec{F} \) are then split into the corresponding nine parts. Due to relation (10.93), their components have to verify
Then owing to the equilibrium of interconnecting forces between two adjacent cells, relation (10.93) leads to analogous relations for the force vector. \( {\vec{F}_I} \), which corresponds to forces applied to inner nodes, is equal to zero. Defining the reduced vector \( {\vec{U}_R} \) as a vector containing values of the displacement on the A1 and B1 lines, on the C1 corner, and in the inner domain I, relations given in (10.95) imply a simple matrix relation between \( \vec{U} \) and \( {\vec{U}_R} \), which can be written as
In the same way, a matrix relation can be defined between the vector \( \vec{F} \) and the reduced vector \( {\vec{F}_R} \):
Thus, the equation to be solved can be reduced to
Finally, the matrices \( [{K_R}] \) and \( [{M_R}] \) are divided into following four parts, A1, B1, C1, and I and the resulting equation is
A detailed expression of \( [{K_R}] \) and \( [{M_R}] \) are presented in Appendix 2 of [21].
For a given value of the wave number k, the phase shifts of (10.93) and (10.95) are deduced and incorporated in relations (10.96) and (10.97). The resolution of the system (10.99) gives the corresponding eigenvalues ω that are real because the reduced matrices \( [{K_R}] \) and \( [{M_R}] \) are hermitians.
The angular frequency ω is a periodical function of wave vector \( \vec{k} \). Thus, the problem can be reduced to the first BZ. The dispersion curves are built varying \( \vec{k} \) on the first BZ, for a given propagation direction. The whole diagram is deduced using symmetries.
A particular interest is the study of phononic crystal plates, made for instance of arrays of air inclusions drilled in a plate. In that case, a 3D mesh is considered and the structure is supposed to be of finite size along the thickness of the plate, periodic and infinite in the two other directions. Only one unit mesh is considered, and a phase relation is applied on only the four faces of the mesh, defining boundary conditions between adjacent cells. The FE method is accurate for the study of phononic crystal plates because it does not introduce hypothesis on the displacement field or on the characteristics of the medium surrounding the plate [9, 22].
Another way to characterize periodic structures is the scattering or the radiation of plane acoustic waves from immersed passive or active periodic structures at any incidence. Therefore, the calculation of the transmission and reflection coefficients is performed, when N unit cells are taken into account (Fig. 10.12). For this study, the mesh of the N unit cells of the periodic structure is enough, with a small part of the surrounding fluid domain, which can be air, and a harmonic analysis is performed at a given frequency. The general system of equation is
Schematic description of N unit cells (N=6) of the periodic structure, for the calculation of the transmission and reflection coefficients. A small part of the fluid domain is meshed before and after the periodic structure
where the unknown is the vector of nodal values of the displacement \( \vec{U} \) and of the pressure field \( \vec{P} \). \( [H] \) and \( [{M_1}] \) are, respectively, the compressibility and mass matrices for the fluid. [L] is the connectivity matrix at the interface and ρ and c are the density and the sound velocity in the fluid, respectively. \( \vec{\psi } \) contains the nodal values of the pressure normal gradient on the fluid boundaries, on the top and bottom surfaces. In this system, the periodic boundary conditions are introduced as previously by the phase relations between nodes separated by the periodic spacing. Then, the effects of the remaining fluid domain are accounted for by matching the pressure field in the FE mesh with simple PWEs of the incoming and outgoing waves. Writing the continuity equations introduces matrix relations between the nodal values of the pressure on the bottom and top surfaces, which are then incorporated into system (10.100). The resolution of the system gives the pressure in the fluid domain. Then, the transmission and reflection coefficients are calculated.
10.6 Model Reduction for Band Structure Calculations
10.6.1 Background
As thoroughly discussed in previous chapters and sections, the study of wave propagation in phononic crystals, or periodic media in general, utilizes Bloch’s theorem, which allows for the calculation of dispersion curves (frequency band structure) and density of states. Due to crystallographic symmetry, the Bloch wave solution needs to be applied only to a single unit cell in the reciprocal lattice space covering the first BZ [23]. Further utilization of symmetry reduces the solution domain, even more, to the irreducible Brillouin zone (IBZ). As mentioned in previous sections, there are several techniques for band structure calculations for phononic crystals and acoustic metamaterials (which are also applicable to photonic crystals and electromagnetic metamaterials). Some of the methods involve expanding the periodic domain and the wave field using a truncated basis. This provides a means of classification in terms of the type of basis, e.g., the plane wave method (Sect. 10.2) involves a Fourier basis expansion and the FE method (Sect. 10.5) involves a real space basis expansion. The pros and cons of the various methods are discussed in depth in the literature [24].
Regardless of the type of system and type of method used for band structure calculations, the computational effort is usually high because it involves solving a complex eigenvalue problem and doing so numerous times as the value of the wave vector, k, is varied. The size of the problem, and hence the computational load, is particularly high for the following cases: (a) when the unit cell configuration requires a large number of degrees of freedom to be adequately described; (b) when the presence of defects is incorporated in the calculations, thus requiring the modeling of large super-cells; and (c) when a large number of calculations; are needed such as in band structure optimization [25, 26]. All these cases suggest that a fast technique for band structure calculation would be very beneficial.
Some techniques have been developed to expedite band structure calculations; examples include utilization of the multigrid concept [27], development of fast iterative solvers for the Bloch eigenvalue problem [28, 29], and extension of homogenization methods to capture dispersion [30, 31]. In this section, we provide a model reduction method that is based on modal transformation [32, 33]. This method, which is referred to as the reduced Bloch mode expansion (RBME) method, involves carrying out an expansion employing a natural basis composed of a selected reduced set of Bloch eigenfunctionsFootnote 1. This reduced basis is selected within the IBZ at high-symmetry points determined by the crystal structure and group theory (and possibly at additional related points). At each of these high-symmetry points, a number of Bloch eigenfunctions are selected up to the frequency range of interest for the band structure calculations. As mentioned above, it is common to initially discretize the problem at hand using some choice of basis. In this manner, RBME constitutes a secondary expansion using a set of Bloch eigenvectors and hence keeps and builds on any favorable attributes the primary expansion approach might exhibit. The proposed method is in line with the well-known concept of modal analysis, which is widely used in various fields in the physical sciences and engineeringFootnote 2.
In the next section, a description of the RBME process and its application in a discrete setting (e.g., using FEs) is given for a phononic crystal problem. Some results from a case study are also presented to demonstrate the application of the method.
10.6.2 Reduced Bloch Mode Expansion method
The starting point for the RBME method is a discrete generalized eigenvalue problem emerging from the application of Bloch’s theorem applied to a standard periodic unit cell model. This yields an equation of the form
where M and K(k) are the global mass and stiffness matrices, respectively; \( {\mathbf{\tilde{U}}} \) is the discrete Bloch vector, which is periodic in the unit cell domain; k is the wave vector; and \( \omega \) is the frequency. Equation (10.101) is then solved at a reduced set of selected wave vector points (i.e., reduced set of k-points), providing the eigenvectors from which a reduced Bloch modal matrix, denoted \( \Psi \), is formed. Several schemes are available for this selection, the simplest of which is the set of eigenvectors corresponding to the first few branches at the high-symmetry points Γ, X, M for a 2D model and Γ, X, M, R for a 3D model, as illustrated in Fig. 10.13 for square and simple-cubic cells (more details on selection schemes are given in [32]). The matrix \( \Psi \) is then used to expand the eigenvectors \( {\mathbf{\tilde{U}}} \), i.e.,
Unit cell in reciprocal lattice space with the irreducible Brillouin zone, high-symmetry k-points (solid circles) and intermediate k-points (hollow ciircles) shown. (a) 2D square unit cell, (b) 3D simple-cubic unit cell
where \( {\mathbf{\tilde{V}}} \) is a vector of modal coordinates for the unit cell Bloch mode shapes. In (10.102), n and m refer to the number of rows and number of columns for the matrix equation. To enable significant model reduction, the chosen k-point selection scheme has to ensure that \( m < < n \). Substituting (10.102) into (10.101), and premultiplying by the complex transpose of \( \Psi \),
yields a reduced eigenvalue problem of size \( m \times m \),
where \( {\mathbf{\bar{M}}} \) and \( {\mathbf{\bar{K}}}({\mathbf{k}}) \) are reduced generalized mass and stiffness matrices. The eigenvalue problem given in (10.104) can then be solved for the entire region of interest within the IBZ at a significantly lower cost compared to using the full model given in (10.101).
To demonstrate the RBME approach, we consider a linear elastic, isotropic, continuum model of a 2D phononic crystal under plain strain conditions. As an example, a square lattice is considered with a bi-material unit cell. One material phase is chosen to be stiff and dense and the other compliant and light. In particular, a ratio of Young’s moduli of E 2/E 1 = 16 and a ratio of densities of ρ 2/ρ 1 = 8 are chosen. The topology of the material phase distribution in the unit cell is shown in the inset of Fig. 10.14. The unit cell is discretized into 45 × 45 uniformly sized four-node bilinear quadrilateral FEs, i.e., 2,025 elements. With the application of periodic boundary conditions, the number of degrees of freedom is n = 4050. Figure. 10.14 shows the calculated band structure and density of states using two-point expansion, that is, the selection is carried out at the Γ, X, M points in k-space. In the calculations, eight modes were utilized at each of these selection points. As such, a total of 24 eigenvectors (m = 24) were used to form the Bloch modal matrix. The results for the full model are overlaid for comparison indicating excellent agreement, despite a reduction of model size from 4050 to 24 degrees of freedom. For models with a larger number of degrees of freedom, and a calculation with high k-point sampling, two orders of magnitude or greater reduction in computational expense will be achieved (as shown in Fig. 10.15).
Phononic band structure and density of states (DOS) calculated using full model (matrix size: 4,050 × 4,050) and reduced Bloch mode expansion model (matrix size: 24 × 24). The IBZ and eigenvector selection points are shown in the left inset. The 2D unit cell is shown in the right inset; the stiff/dense material phase is in black, and the compliant/light material phase is in white. The finite element method was used for the primary expansion
Computational efficiency: ratio of reduced Bloch mode expansion model to full model calculation times, r, versus number of sampled k-points along the border of the IBZ, n k (for two 2D finite element meshes). The number of elements is denoted by n el
While the focus in this section has been on phononic crystals, the RBME method is also applicable to acoustic metamaterials, to discrete lattice dynamics calculations, and to photonic and electronic band structure calculations. Furthermore, the method is applicable to any type of lattice symmetry.
Notes
- 1.
- 2.
The concept of modal analysis is rooted in the idea of extracting a reduced set of representative information on the dynamical nature of a complex system. This practice is believed to have originated by the Egyptians in around 4700 b.c. in their quest to find effective ways to track the flooding of the Nile and predict celestial events [35].
References
N.W. Ashcroft, N.D. Mermin, Solid State Physics (Saunders College, Philadelphia, 1976)
M. Sigalas, E.N. Economou, Band structure of elastic waves in two dimensional systems. Solid State Commun. 86, 141–143 (1993)
J.O. Vasseur, B. Djafari-Rouhani, L. Dobrzynskiand, P.A. Deymier, Acoustic band gaps in fibre composite materials of boronnitride structure. J. Phys. Condens Matter 9, 7327–7341 (1997)
ZhilinHou, Xiujun Fu, and Youyan Liu, Singularity of the Bloch theorem in the fluid/solid phononic crystal. Phys. Rev. B 73, 024304–024308 (2006)
J.O. Vasseur, P.A. Deymier, A. Khelif, P. Lambin, B. Djafari-Rouhani, A. Akjouj, L. Dobrzynski, N. Fettouhi, J. Zemmouri, Phononic crystal with low filling fraction and absolute acoustic band gap in the audible frequency range: a theoretical and experimental study. Phys. Rev. E 65, 056608 (2002)
B. Manzanares-Martinez, F. Ramos-Mendieta, Surface elastic waves in solid composites of two-dimensional periodicity. Phys. Rev. B 68, 134303 (2003)
C. Goffaux, J.P. Vigneron, Theoretical study of a tunable phononic band gap system. Phys. Rev. B 64, 075118 (2001)
Y. Tanaka, Y. Tomoyasu, S.I. Tamura, Band structure of acoustic waves in phononic lattices: Two-dimensional composites with large acoustic mismatch. Phys. Rev. B 62, 7387 (2000)
J.O. Vasseur, P.A. Deymier, B. Djafari-Rouhani, Y. Pennec, A.-C. Hladky-Hennion, Absolute forbidden bands and waveguiding in two-dimensional phononic crystal plates. Phys. Rev. B 77, 085415 (2008)
C. Charles, B. Bonello, F. Ganot, Propagation of guided elastic waves in 2D phononic crystals. Ultrasonics 44, 1209(E) (2006)
C. Croënne, E.D. Manga, B. Morvan, A. Tinel, B. Dubus, J. Vasseur, A.-C. Hladky-Hennion, Negative refraction of longitudinal waves in a two-dimensional solid-solid phononic crystal. Phys. Rev. B 83, 054301 (2011)
P. Lambin, A. Khelif, J.O. Vasseur, L. Dobrzynski, B. Djafari-Rouhani, Stopping of acoustic waves by sonic polymer-fluid composites. Phys. Rev. E 63, 066605 (2001)
G. Mur, Absorbing boundary conditions for the finite difference approximation of the time-domain electromagnetic field equations. IEEE Trans. Electromagn. Compatibility 23, 377 (1981)
A. Taflove, Computational electrodynamics: the finite difference time domain method (Artech House, Boston, 1995)
B. Merheb, P.A. Deymier, M. Jain, M. Aloshyna-Lesuffleur, S. Mohanty, A. Berker, R.W. Greger, Elastic and viscoelastic effects in rubber/air acoustic band gap structures: a theoretical and experimental study. J. Appl. Phys. 104, 064913 (2008)
B. Merheb, P.A. Deymier, K. Muralidharan, J. Bucay, M. Jain, M. Aloshyna-Lesuffleur, R.W. Greger, S. Mohanty, A. Berker, Viscoelastic effect on acoustic band gaps in polymer-fluid composites. Model. Simul. Mater. Sci. Eng. 17, 075013 (2009)
M. Kafesaki, E.N. Economou, Multiple-scattering theory for three-dimensional periodic acoustic composites. Phys. Rev. B. 60, 11993 (1999)
Z. Liu, C.T. Chan, P. Sheng, A.L. Goertzen, J.H. Page, Elastic wave scattering by periodic structures of spherical objects: theory and experiment. Phys. Rev. B. 62, 2446 (2000)
I.E. Psarobas, N. Stefanou, A. Modinos, Scattering of elastic waves by periodic arrays of spherical bodies. Phys. Rev. B. 62, 278 (2000)
J. Mei, Z. Liu, J. Shi, D. Tian, Theory for elastic wave scattering by a two-dimensional periodical array of cylinders: an ideal approach for band-structure calculations. Phys. Rev. B 67, 245107 (2003)
P. Langlet, A.-C. Hladky-Hennion, J.N. Decarpigny, Analysis of the propagation of plane acoustic waves in passive periodic materials using the finite element method. J. Acoust. Soc. Am. 95, 1792 (1995)
J.O. Vasseur, A.-C. Hladky-Hennion, B. Djafari-Rouhani, F. Duval, B. Dubus, Y. Pennec, Waveguiding in two-dimensional piezoelectric phononic crystal plates. J. Appl. Phys. 101, 114904 (2007)
L. Brillouin, Wave Propagation in Periodic Structures (Dover, New York, 1953)
K. Busch, G. von Freymann, S. Linden, S.F. Mingaleev, L. Tkeshelashvili, M. Wegener, Periodic nanostructures for photonics. Phys. Rep. 444, 101–202 (2007)
O. Sigmund, J.S. Jensen, Systematic design of phononic band-gap materials and structures by topology optimization. Philos. Trans. R. Soc. Lond. A361, 1001–1019 (2003)
O.R. Bilal, M.I. Hussein, Ultrawidephononic band gap for combined in-plane and out-of-plane waves. Phys. Rev. E 84, 065701(R) (2011)
R.L. Chern, C.C. Chang, R.R. Hwang, Large full band gaps for photonic crystals in two dimensions computed by an inverse method with multigrid acceleration. Phys. Rev. E 68, 026704 (2003)
D.C. Dobson, An efficient method for band structure calculations in 2D photonic crystals. J. Comput. Phys. 149, 363–376 (1999)
S.G. Johnson, J.D. Joannopoulos, Photonic crystals: putting a new twist on light. Opt. Express 8, 173 (2001)
T.W. McDevitt, G.M. Hulbert, N. Kikuchi, An assumed strain method for the dispersive global-local modeling of periodic structures. Comput. Methods Appl. Mech. Eng. 190, 6425–6440 (2001)
M.I. Hussein, G.M. Hulbert, Mode-enriched dispersion models of periodic materials within a multiscale mixed finite element framework. Finite Elem. Anal. Des. 42, 602–612 (2006)
M.I. Hussein, Reduced Bloch mode expansion for periodic media band structure calculations. Proc. R. Soc. Lond. A465, 2825–2848 (2009)
Q. Guo, O.R. Bilal, M.I. Hussein, Convergence of the reduced Bloch mode expansion method for electronic band structure calculations,” in Proceedings of Phononics 2011, Paper PHONONICS-2011-0176, Santa Fe, New Mexico, USA, May 29–June 2, 2011, pp. 238–239
M.I. Hussein, Dynamics of banded materials and structures: analysis, design and computation in multiple scales, Ph.D. Thesis, University of Michigan, Ann Arbor, USA, 2004.
O. Døssing, IMAC-XIII keynote address: going beyond modal analysis, or IMAC in a new key. Modal Anal. Int. J. Anal. Exp. Modal Anal. 10, 69 (1995)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Vasseur, J.O., Deymier, P.A., Sukhovich, A., Merheb, B., Hladky-Hennion, AC., Hussein, M.I. (2013). Phononic Band Structures and Transmission Coefficients: Methods and Approaches. In: Deymier, P. (eds) Acoustic Metamaterials and Phononic Crystals. Springer Series in Solid-State Sciences, vol 173. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-31232-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-642-31232-8_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-31231-1
Online ISBN: 978-3-642-31232-8
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)