An isogeometric approach for analysis of phononic crystals and elastic metamaterials with complex geometries

Abstract

An isogeometric analysis (IGA) framework is presented to construct and solve dispersion relations for generating the band structure of periodic materials with complicated geometries representing phononic crystals and elastic metamaterials. As the dispersive properties depend on the microstructural geometry, an accurate representation of microstructural geometrical features is paramount. To this end, the ability of isogeometric analysis to exactly model complex curved geometries is exploited, and wave propagation in infinitely periodic solids is combined with isogeometric analysis. The benefits of IGA are demonstrated by comparing the results to those obtained using standard finite element analysis (FEA). It is shown that the IGA solutions can reach the same level of accuracy as FEA while using significantly fewer degrees of freedom. IGA is applied to phononic crystals and elastic metamaterials and the band structure for a variety of unit cells with complex microstructural geometries is investigated to illustrate the desirable dispersive effects in these metamaterials.

1 Introduction

The design of materials engineered to exhibit exotic mechanical behaviors not found in nature has received much attention in the materials science, physics and engineering communities of late. These meta materials are made up of multiple material phases arranged in topologically complex patterns, resulting in properties that are superior to those of the constituent material phases [1]. Mechanical metamaterials that are designed for enhanced dynamic properties are known as phononic crystals or acoustic/elastic metamaterials and focus on the spectral and spatial manipulation of mechanical waves [2, 3]. These materials are made up of a periodic tessellation of some characteristic unit cell and this periodicity allows their dynamic properties to be contained in a compact band diagram much like the electronic band diagram of atomic crystals. The band structure reveals the effects of dispersion, wherein waves with different frequencies or wavelengths propagate at different speeds. In solids, wave dispersion occurs as a result of the interaction between propagating waves and the material microstructure. While the phenomenon of wave dispersion in solids has been the subject of study for some time [4], the idea of exploiting it by designing materials with tailored band structures is relatively new. Early studies considering the band structure of mechanical waves in solids are those by Sigalas and Economou [5] and Kushwaha et al. [6], the latter of which followed ideas used in the study of photonic band structure. This study revealed that the band structure of a periodic distribution of stiff rods embedded in a soft elastic background medium contained bandgaps, i.e. frequency ranges wherein wave propagation is inhibited. These early studies established the idea that materials could be designed to manipulate mechanical waves, in much the same way as materials are designed to manipulate electromagnetic waves.

The classification as a phononic crystal or acoustic/elastic metamaterial comes down to which dispersive phenomena are exploited for the spectral manipulation of mechanical waves [3]. Phononic crystals rely on the phenomenon of Bragg scattering, which occurs due to a mechanical impedance mismatch between two different constituent materials causing scattering interference [7]. This interference becomes systematic due to the periodic nature of phononic crystals, resulting in strong wave attenuation within certain frequency ranges. Scattering interference is only significant if the wavelength of excitation is of the same order as the scale of the microstructural features, which allows for Bragg scattering effects to be tailored through manipulation of microstructural geometry but restricts the phenomenon to relatively high frequencies. For a Bragg bandgap to occur at a low frequency such as 1 kHz, the wavelength must be of the order of meters, and thus the necessary size of the microstructural features renders the design of phononic crystals with bandgaps at this frequency infeasible. Acoustic/elastic metamaterials exploit the resonant vibration of microstructural features which can result in unusual dynamic behavior such as negative effective properties and the generation of subwavelength bandgaps. This latter phenomenon makes acoustic metamaterials attractive for low frequency wave manipulation, allowing microstructural features to be much smaller than the wavelength of excitation, as has been demonstrated in a number of studies [8,9,10,11,12]. In addition to spectral manipulation, spatial wave manipulation can also be enabled through the exploitation of dispersive effects which cause waves to show different preferential directions of propagation at different frequencies. This frequency dependent directionality is inherent in both phononic crystals and acoustic metamaterials because of the microstructure behaving as a different effective anisotropic medium at different frequencies [13, 14]. Moreover, it has been shown that the wave directionality can be altered by tailoring the microstructural features [15], leading to greater control over spatial wave manipulation. The phenomena of Bragg scattering, local resonance and frequency dependent directionality are all inextricably linked to the geometry of the material microstructure. Therefore, the ability to analyze and design metamaterials with intricate geometrical features is of paramount importance.

Band structure calculations for periodic materials require the construction and solution of dispersion relations which give the nonlinear dependence between frequency and wavenumber. Due to the difficulty of constructing dispersion relations for any domain with reasonable geometrical complexity, analytical methods are scarce and numerical methods such as the plane wave expansion method [16], the finite difference time domain method [17], the method of multiple scales [2], the multiple scattering method [18] or the finite element method [13, 14, 19, 20] are commonly used to obtain the band structure. Among these, the finite element method stands out as one of the most popular due to the ubiquity of finite element solvers and their flexibility in representing different geometric domains. However, for many domains, especially those involving curves, the finite element method relies on geometric approximations, introducing errors in the model that are exacerbated as the details of geometric features become increasingly intricate. Strategies such as mesh refinement or use of higher order elements can mitigate this issue, but at the cost of significantly increasing the number of degrees of freedom needed for an accurate model. Moreover, the generation of an accurate mesh is a nontrivial exercise in itself when geometries are complex. A recent study proposed the use of the extended finite element method (XFEM) to generate the band structure of metamaterials [21]. As XFEM can implicitly account for material interfaces, a uniform mesh can be employed, with the complex geometries of constituents considered using level set functions. This allows for flexibility in considering constituent geometries and circumvents the costly remeshing process, but curved interfaces are still approximated and a relatively fine mesh is needed to resolve these features accurately. Thus, accurate methods of modeling complex geometries are still needed.

Isogeometric analysis (IGA) was introduced by Hughes et al. [22] and employs Non-Uniform Rational B-Splines (NURBS) as the basis for interpolating both geometry and solution spaces. IGA has several advantages over standard finite element analysis (FEA), the first being that IGA can represent the exact geometry of a model derived from computer aided design (CAD) since NURBS are also used to describe geometry in CAD. This means that complex geometries can be easily represented in IGA without introducing errors into the model. In addition, the continuity of IGA bases can be increased efficiently and robustly through k-refinement without altering the geometry in any way [23]. This proves valuable for interpolation of fields that require high-order continuity, and leads to results with higher accuracy [24]. Moreover, even if a solution space requires only $C^{0}$-continuity, higher continuity interpolation may still lead to more accurate results because the increased smoothness of solution spaces can result in significantly better numerical approximations [24, 25]. IGA has been successfully used in the analysis of static problems [22, 26, 27], free and forced vibration of linear and nonlinear cases [28, 29], fluid-structure interaction problems [30], structural optimization [31], and more. All these studies have demonstrated that IGA has superior performance compared to standard FEA. Particularly, for problems involving structural vibrations and wave propagation IGA eliminates some of the deficiencies which are well known in standard FEA, and can obtain significantly more accurate eigenfrequencies compared to FEA with the same number of degrees of freedom [32, 33]. Thus, for band structure calculations IGA offers advantages over FEA, which go beyond the ability to represent complex geometries.

In this study an isogeometric framework for the construction and solution of dispersion relations which generate the band structure of unit cells with complicated geometries is developed. These unit cells may represent phononic crystals or elastic metamaterials as they are governed by the equations of elastodynamics. To the best of the authors’ knowledge, the literature contains no prior studies exploring the use of IGA for band structure calculations and so the implementation details are thoroughly discussed. Beyond being able to represent complicated geometries, the isogeometric framework is attractive due to its seamless integration with CAD, allowing for rapid development of metamaterial designs. It is shown in this study that substantial improvement over FEA is to be gained by using IGA, reflecting the trends discussed in [28, 32, 33]. The band structure for a variety of microstructural unit cell geometries is investigated to illustrate the dispersive effects exploited by phononic crystals and elastic metamaterials including Bragg scattering, local resonance and frequency dependent directionality. By improving the ability to analyze the dispersive properties of solids with intricate periodic microstructural geometries, the isogeometric framework allows for more complex microstructural designs to be considered, furthering the ability to design materials for mechanical wave manipulation. The structure of this paper is as follows: Sect. 2 details the construction of dispersion relations for elastic solids with periodic microstructures, Sect. 3 gives the details of numerical implementation for FEA, Sect. 4 provides some background on IGA and details the numerical implementation of dispersion relations, Sect. 5 covers the solution of dispersion relations and construction of band diagrams, Sect. 6 compares IGA to FEA for a simple example, Sect. 7 presents illustrative results of complex unit cell geometries modeled using IGA, and Sect. 8 provides the important conclusions drawn from this study.

2 Dispersion relations for periodic solids

2.1 Wave propagation in homogeneous elastic solids

Consider a deformable solid body ${\Omega }\subset \mathbb {R}^{3}$ with material points ${\varvec{x}}\in \mathbb {R}^{3}$, material density $\rho \left( {{\varvec{x}},t} \right)$, displacement field ${\varvec{u}}\left( {{\varvec{x}},t} \right)$ and stress field $\varvec{\sigma } \left( {{\varvec{x}},t} \right)$. The governing equations of linear elastodynamics are

$$\begin{aligned} \left. {\begin{array}{l} {{\varvec{\varepsilon }} =\frac{1}{2}\left( {{\varvec{\nabla u}}+ \left( {{\varvec{\nabla u}}} \right) ^{T}} \right) ={\varvec{\nabla }}^{s}{\varvec{u}}} \\ {{\varvec{\sigma }} =\mathbb {C}:{\varvec{\varepsilon }} } \\ {{\varvec{\nabla }} .{\varvec{\sigma }} =\rho \ddot{{\varvec{u}}}} \\ \end{array} } \right\} \hbox { in }\Omega \end{aligned}$$

(1)

where ${\varvec{\nabla }}$ is the gradient operator and $\ddot{\varvec{u}}$ is the acceleration field. The stress ${\varvec{\sigma }}$ is related to the symmetric strain tensor, ${\varvec{\varepsilon }}$, through the fourth order elasticity tensor $\mathbb {C}$. This tensor possesses the important properties of major symmetry, i.e. $\mathbb {C}_{ijkl} =\mathbb {C}_{klij}$, and positive-definiteness. Combining the equations of linear elastodynamics gives the displacement equation of motion

$$\begin{aligned} {\varvec{\nabla }} .\left( {\mathbb {C}^{e}:{\varvec{\nabla }} ^{s}{\varvec{u}}} \right) =\rho \ddot{\varvec{u}} \end{aligned}$$

(2)

In this study, the focus is on the propagation of waves through bulk material rather than the propagation of surface waves. Thus, the solution ${\varvec{u}}\left( {{\varvec{x}},t} \right)$ of Eq. (2) is sought to be in the form of traveling plane waves, i.e.

$$\begin{aligned} {\varvec{u}}\left( {{\varvec{x}},t} \right) ={\varvec{u}}_0 ({\varvec{x}})F\left( {{\varvec{n}}.{\varvec{r}}-ct} \right) \end{aligned}$$

(3)

Equation (4) represents a propagating plane waveform F, where the motion of every material particle along the plane defined by $\phi ({\varvec{x}})={\varvec{n}}.{\varvec{r}}({\varvec{x}})-ct=$ const. is the same and the amplitude of the waveform is given by ${\varvec{u}}_0$ [34]. Here, ${\varvec{n}}$ is the normal to the plane, c is the speed of wave propagation and ${\varvec{r}}={\varvec{x}}-{\varvec{O}}$ is the position of an arbitrary point on the plane. In particular, for complex harmonic waveforms F of constant amplitude the solutions assume the form

$$\begin{aligned} {\varvec{u}}\left( {{\varvec{x}},t} \right)= & {} {\varvec{u}}_0 ({\varvec{x}})\exp \left[ {ik\left( {{\varvec{n}}.{\varvec{r}}-ct} \right) } \right] \nonumber \\= & {} {\varvec{u}}_0 ({\varvec{x}})\exp \left[ {i\left( {{\varvec{k}}.{\varvec{r}}-\omega t} \right) } \right] \end{aligned}$$

(4)

where $\omega =k\times c$ is the radial frequency and k is the wavenumber (inverse of the wavelength), which can be absorbed into the normal vector to create the wave vector ${\varvec{k}}=k{\varvec{n}}$. Inserting the waveform of Eq. (4) into Eq. (2) gives the propagation condition as

$$\begin{aligned} {\varvec{Q}}({\varvec{n}}).{\varvec{u}}_0= & {} \rho c^{2}{\varvec{u}}_0\nonumber \\ Q_{ik}= & {} \mathbb {C}_{ijkl} {{n}}_j {{n}}_l \end{aligned}$$

(5)

where the acoustic tensor ${\varvec{Q}}$ is introduced. The acoustic tensor ${\varvec{Q}}({\varvec{n}})$ depends on the propagation direction ${\varvec{n}}$ and is symmetric and positive definite granted that $\mathbb {C}$ possesses these properties. The necessary and sufficient condition under which harmonic waves of the form given in Eq. (4) can propagate in a body made of elastic material is that $\rho c^{2}$ is an eigenvalue of the acoustic tensor ${\varvec{Q}}$ corresponding to the eigenvector ${\varvec{u}}_0$.

If the material is assumed to be isotropic then $\mathbb {C}_{ijkl} =\lambda \delta _{ij} \delta _{kl} +\mu \left( {\delta _{ik} \delta _{jl} +\delta _{il} \delta _{jk} } \right)$, where $\lambda >0$ and $\mu >0$ are the Lame’s constants, and the acoustic tensor has the form

$$\begin{aligned} {\varvec{Q}}({\varvec{n}})= & {} \left[ {\mu {\varvec{I}}+\left( {\lambda +\mu } \right) \left( {{\varvec{n}}\otimes {\varvec{n}}} \right) } \right] \nonumber \\= & {} \left[ {\mu \left( {{\varvec{I}}-{\varvec{n}}\otimes {\varvec{n}}} \right) +\left( {\lambda +2\mu } \right) \left( {{\varvec{n}}\otimes {\varvec{n}}} \right) } \right] \end{aligned}$$

(6)

where ${\varvec{I}}$ is the second order identity tensor. In this case, ${\varvec{Q}}$ has two distinct eigenvalues $\lambda +2\mu >0$ and $\mu >0$ with the corresponding characteristic spaces being the line spanned by ${\varvec{n}}$ and the plane perpendicular to ${\varvec{n}}$, respectively. Thus, in an isotropic medium two types of harmonic wave modes are possible. The first corresponds to the eigenvalue $\rho c^{2}=\lambda +2\mu$ which has a constant amplitude ${\varvec{u}}_0$ directed along ${\varvec{n}}$, and represents a longitudinal mode. The second corresponds to the eigenvalue $\rho c^{2}=\mu$ which has a constant amplitude ${\varvec{u}}_0$ in the plane perpendicular to ${\varvec{n}}$, and represents a transverse mode. These modes propagate with speed

$$\begin{aligned}&\hbox {Longitudinal mode}:c_l =\sqrt{\frac{\lambda +2\mu }{\rho }}\nonumber \\&\hbox {Transverse mode}:c_t =\sqrt{\frac{\mu }{\rho }} \end{aligned}$$

(7)

If the body is homogeneous, solutions to Eq. (5) hold throughout ${\Omega }$ so that longitudinal and transverse modes are the only possible wave modes. In this case, frequency and wavenumber for a given mode are linearly related through the constant speed $c_l$ or $c_t$, depending on the mode [34].

Fig. 1

Illustration of solid with periodic microstructure and resulting unit cell

2.2 Periodic solids: the Bloch theorem

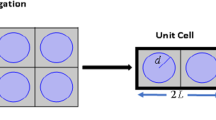
When considering elastic bodies with periodic microstructures, it is commonly assumed that the size of the microstructural unit cell is small enough that the body can be treated as an infinite periodic array of identical unit cells with the same microstructural properties (Fig. 1). The Bloch theorem states that the solutions to linear systems which are periodic in more than one spatial dimensions are in the form of Bloch waves, i.e. the product of a plane wave and a function containing the spatial periodicity [35]. Thus, seeking harmonic plane wave solutions to Eq. (2) for an infinite, perfectly periodic domain ${\Omega }$ is equivalent to seeking periodic harmonic plane wave solutions to Eq. (2) over one unit cell ${\Omega }_{uc}$ (Fig. 1). This leads to Eq. (5) taken over the unit cell domain ${\Omega }_{uc}$ with ${\varvec{u}}_0$ of the form

$$\begin{aligned} {\varvec{u}}_0 ({\varvec{x}})={\varvec{\psi }} ({\varvec{x}})\exp \left[ {i{\varvec{k}}.{\varvec{x}}} \right] \end{aligned}$$

(8)

where the function ${\varvec{\psi }} ({\varvec{x}})$ contains the spatial periodicity and $\exp \left[ {i{\varvec{k}}.{\varvec{x}}} \right]$ describes a plane wave with wave vector k. Since ${\varvec{\psi }} ({\varvec{x}})$ is spatially periodic, ${\varvec{\psi }} \left( {{\varvec{x}}+{\varvec{T}}} \right) ={\varvec{\psi }} ({\varvec{x}})$ where ${\varvec{T}}$ is a translation vector between a point ${\varvec{x}}$ of one unit cell and the same point ${\varvec{x}}^{\prime }$ of another unit cell. Using this condition along with Eq. (8) gives

$$\begin{aligned} {\varvec{u}}_0 \left( {{\varvec{x}}+{\varvec{T}}} \right) ={\varvec{u}}_0 ({\varvec{x}})\exp \left[ {i{\varvec{k}}.{\varvec{T}}} \right] \end{aligned}$$

(9)

which represents kinematic constraints necessary to ensure that ${\varvec{u}}_0$ is periodic. These constraints can be enforced for a unit cell ${\Omega }_{uc}$ by constraining the values of ${\varvec{u}}_0$ on opposite sides of the unit cell boundary $\partial {\Omega }_{uc}$, i.e.

$$\begin{aligned} {\varvec{u}}_0 \left( {{\varvec{x}}^{+}} \right) ={\varvec{u}}_0 \left( {{\varvec{x}}^{-}} \right) \exp \left[ {i{\varvec{k}}.{\varvec{l}}} \right] \end{aligned}$$

(10)

where ${\varvec{x}}^{+}$ and ${\varvec{x}}^{-}$ are points on opposite sides of the unit cell boundary separated by the distance vector ${\varvec{l}}$ (Fig. 1). Considering Eq. (5) over the domain ${\Omega }_{uc}$ along with the constraints in Eq. (10) will give the conditions under which harmonic plane waves can propagate in an infinite periodic domain ${\Omega }$.

2.3 Discretized equations and dispersion relations

When using numerical schemes such as FEA and IGA, the spatial discretization of Eq. (2) for a unit cell domain ${\Omega }_{uc}$ and insertion of harmonic plane wave solutions (Eq. 4) results in the following discrete eigenvalue problem which is analogous to Eq. (5)

$$\begin{aligned} {\varvec{Ku}}_0 =\omega ^{2}{\varvec{Mu}}_0 \end{aligned}$$

(11)

where ${\varvec{K}}$ is the stiffness matrix and ${\varvec{M}}$ is the mass matrix of the discrete system. Equation (11) together with the constraints in Eq. (10) form a constrained eigenvalue problem which gives the conditions under which harmonic plane waves can propagate in an infinite periodic domain. This constrained eigenvalue problem can be transformed into the equivalent unconstrained problem

$$\begin{aligned} \left( {\hat{{\varvec{K}}} ({\varvec{k}})-\omega ^{2}\hat{{\varvec{M}}} ({\varvec{k}})} \right) \hat{{\varvec{u}}} _0 =\mathbf{0} \end{aligned}$$

(12)

where $\hat{{\varvec{K}}}$ and $\hat{{\varvec{M}}}$ are the transformed stiffness and mass matrices, respectively. The final form of this transformed system depends on the spatial discretization, i.e. FEA or IGA, which affects how the constraints can be used to transform the unconstrained eigenvalue problem. The dispersion relations, which represent the relationship between wavenumber ${\varvec{k}}$ and frequency $\omega$, are finally obtained by expressing the eigen-system defined in Eq. (12) as

$$\begin{aligned} {{\mathcal {D}}}\left( {\omega ,{\varvec{k}}} \right) =\det \left[ {\hat{{\varvec{K}}} ({\varvec{k}})-\omega ^{2} \hat{{\varvec{M}}} ({\varvec{k}})} \right] =0 \end{aligned}$$

(13)

Equation (13) implicitly defines the relationship between the wave vector ${\varvec{k}}$ and the corresponding frequency $\omega$. In this study, computational methods based on FEA and IGA are presented to solve Eq. (13) under plane strain assumptions for materials with periodic microstructures.

Fig. 2

Discretized unit cell boundary and degrees of freedom

3 Implementation using standard finite element analysis (FEA)

When using standard finite element analysis, the domain of the unit cell is discretized using isoparametric bilinear four node quadrilateral (Q4) elements. Finite element formulation and implementation details are omitted as they can be found in many standard references, see for instance Ref [36], among others. For a two-dimensional unit cell with discretized boundary nodes as shown in Fig. 2, Eq. (10) results in linear homogeneous multifreedom constraints which can be expressed in master-slave form as

$$\begin{aligned} {\varvec{u}}_0= & {} {\varvec{R}}_{{k}} \hat{{\varvec{u}}} _0 \nonumber \\ {\varvec{R}}_k= & {} \left[ {{\begin{array}{cccc} {\varvec{I}} &{} \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} \\ \mathbf{0} &{} {\varvec{I}} &{} \mathbf{0} &{} \mathbf{0} \\ \mathbf{0} &{} {{\varvec{I}}\exp \left( {2\pi ik_2 l_2 } \right) } &{} \mathbf{0} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} {\varvec{I}} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} {{\varvec{I}}\exp \left( {2\pi ik_1 l_1 } \right) } &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} &{} {\varvec{I}} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} &{} {{\varvec{I}}\exp \left( {2\pi ik_1 l_1 } \right) } \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} &{} {{\varvec{I}}\exp \left[ {2\pi i\left( {k_1 l_1 +k_2 l_2 } \right) } \right] } \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} &{} {{\varvec{I}}\exp \left( {2\pi ik_2 l_2 } \right) } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} {\varvec{u}}_0 =\left[ {{\begin{array}{c} {{\varvec{u}}_i } \\ {{\varvec{u}}_b } \\ {{\varvec{u}}_t } \\ {{\varvec{u}}_l } \\ {{\varvec{u}}_{\varvec{r}} } \\ {{\varvec{u}}_{lb} } \\ {{\varvec{u}}_{rb} } \\ {{\varvec{u}}_{rt} } \\ {{\varvec{u}}_{lt} } \\ \end{array} }} \right] ,\hat{{\varvec{u}}} _0 =\left[ {{\begin{array}{c} {{\varvec{u}}_i } \\ {{\varvec{u}}_b } \\ {{\varvec{u}}_l } \\ {{\varvec{u}}_{lb} } \\ \end{array} }} \right] \end{aligned}$$

where the subscripts i, b, t, l, r, lb, rb, rt, and lt denote degrees of freedom at the interior nodes, bottom surface notes, top surface notes, left surface notes, right surface notes, left-bottom corner node, right-bottom corner node, right-top corner node and left-top corner node, respectively; ${\varvec{I}}$ and 0 are the identity and zero matrices of appropriate dimensions; $\hat{{\varvec{u}}} _0$ represents the master degrees of freedom while ${\varvec{u}}_0$ represents the slave degrees of freedom. The constraint matrix ${\varvec{R}}_k$ contains the homogeneous constraints corresponding to a wave vector ${\varvec{k}}$. Master-slave elimination proceeds by substituting Eq. (14) into Eq. (11) followed by premultiplication by ${\varvec{R}}_k^*$, the Hermetian of ${\varvec{R}}_k$, and yields Eq. (12) with

$$\begin{aligned}&\hat{{\varvec{K}}} ({\varvec{k}})\buildrel \Delta \over = {\varvec{R}}_k^*{\varvec{KR}}_k\nonumber \\&\hat{{\varvec{M}}} ({\varvec{k}})\buildrel \Delta \over = {\varvec{R}}_k^*{\varvec{MR}}_k \end{aligned}$$

(15)

Thus, in standard FEA, the master slave elimination approach results in a condensed eigen-system with only the master degrees of freedom involved.

4 Isogeometric analysis

4.1 B-splines and NURBS

Isogeometric analysis (IGA) uses non-uniform rational B-splines (NURBS) to represent both the geometry and solution spaces in the finite element discretization. A brief overview of B-splines and NURBS is presented in this subsection, further details can be found in Refs [22, 23]. A B-spline curve in 2-D is a parametric curve which can be seen as a mapping from parametric space to physical space as

$$\begin{aligned} {\varvec{x}}(\xi )=\mathop \sum \limits _{i=1}^{n} {{N}}_{i,p} (\xi ){\varvec{B}}_i ,\quad \xi _1 \le \xi \le \xi _{{{n}}+p+1} \end{aligned}$$

(16)

where ${\varvec{x}}(\xi )=\left[ {{{x}}(\xi ),y(\xi )} \right]$ is the position vector which defines coordinates in physical space of a point on the B-spline curve, ${\varvec{B}}_i =\left[ {X_i ,Y_i } \right]$ is the coordinate vector of the ith control point and ${{N}}_{i,p} (\xi )$ is the ith B-spline basis function of order p. The parametric space is defined by coordinate $\xi$ and the discrete set ${\varvec{\xi }}_v =\left\{ {\xi _1 ,\xi _2 ,\ldots ,\xi _{{{n}}+p+1} } \right\}$ is known as a knot vector. Knots $\xi _i$ are arranged in non-decreasing order, i.e.$\xi _i \le \xi _{i+1}$, and the interval $\mathcal {P}=\left[ {\xi _1 ,\xi _{{n}+p+1} } \right]$ is called a patch. The basis functions ${{N}}_{i,p} (\xi )$ can be recursively obtained as [37, 38]

$$\begin{aligned} {{N}}_{i,0} (\xi )= & {} \left\{ {{\begin{array}{ll} 1&{}\hbox { if }\xi _i \le \xi <\xi _{i+1} \\ 0&{}\hbox { otherwise } \\ \end{array} }} \right. ,\qquad p=0.\nonumber \\ {N_{i,p}}\left( \xi \right)= & {} \frac{{\xi - {\xi _i}}}{{{\xi _{i + p}} - {\xi _i}}}{N_{i,p - 1}}\left( \xi \right) \nonumber \\&+ \frac{{{\xi _{i + p + 1}} - \xi }}{{{\xi _{i + p + 1}} - {\xi _{i + 1}}}}{N_{i + 1,p - 1}}\left( \xi \right) ,\qquad p \ge 1 \end{aligned}$$

(17)

In two dimensions, a B-spline surface is parameterized by $\xi$ and $\eta$ and given as

$$\begin{aligned}&{\varvec{x}}\left( {\xi ,\eta } \right) =\mathop \sum \limits _{i=1}^{{n}} \mathop \sum \limits _{j=1}^m {\varvec{B}}_{ij} R_{i,j}^{pq} \left( {\xi ,\eta } \right) ,\nonumber \\&\xi _1 \le \xi \le \xi _{{{n}}+p+1} ,\eta _1 \le \eta \le \eta _{m+q+1} \end{aligned}$$

(18)

where ${\varvec{x}}\left( {\xi ,\eta } \right) =\left[ {{{x}}\left( {\xi ,\eta } \right) ,y\left( {\xi ,\eta } \right) } \right]$ defines the physical coordinate of a B-spline surface point, and ${\varvec{B}}_{ij}$ is the coordinate of the $\left( {i,j} \right)$th control point. The two dimensional basis $R_{i,j}^{pq} \left( {\xi ,\eta } \right)$ is obtained by the tensor product of two B-spline basis functions as

$$\begin{aligned} R_{i,j}^{pq} \left( {\xi ,\eta } \right)= & {} {{N}}_{i,p} (\xi ){{M}}_{j,q} \left( \eta \right) ,\nonumber \\&\xi _1 \le \xi \le \xi _{{{n}}+p+1} ,\nonumber \\&\eta _1 \le \eta \le \eta _{m+q+1} \end{aligned}$$

(19)

where ${M}_{j,q} (\eta )$ is the jth B-spline basis of order q built with knot vector ${\varvec{\eta }} _v =\left[ {\eta _1 ,\ldots ,\eta _{m+q+1} } \right]$ using Eq. (17). The two dimensional parametric region (patch) over which the B-spline surface is defined is $\mathcal {P}=\left[ {\xi _1 ,\xi _{{n}+p+1} } \right] \times \left[ {\eta _1 ,\eta _{m+q+1} } \right]$. Since B-splines use piecewise polynomials, they cannot represent conic curves and surfaces such as circles, ellipses and spheres. However, these conics can be represented using piecewise rational polynomials, which are defined as the ratio between two polynomials. To this end, non-uniform rational B-splines (NURBS) are introduced to describe geometries which cannot be adequately represented using B-splines. A 1-D NURBS basis can be obtained through B-spline bases [22, 37] as

$$\begin{aligned} \bar{{{N}}}_{i,p} (\xi )=\frac{{{N}}_{i,p} (\xi )w_i }{\mathop \sum \nolimits _{{{r}}=1}^{{n}} {{N}}_{{{r}},p} (\xi )w_{{r}} },\xi _1 \le \xi \le \xi _{{{n}}+p+1} \end{aligned}$$

(20)

where $w_{{r}}$ is the weight given to the rth control point. Hence, NURBS curves can be constructed using Eq. (16) but with NURBS bases (Eq. 20) substituted for B-spline bases. Similarly, two-dimensional NURBS bases are defined as

$$\begin{aligned} \bar{R} _{i,j}^{pq} \left( {\xi ,\eta } \right)= & {} \frac{{{N}}_{i,p} (\xi ){{M}}_{j,q} \left( \eta \right) w_{i,j} }{\mathop \sum \nolimits _{s=1}^{{n}} \mathop \sum \nolimits _{t=1}^m {{N}}_{s,p} (\xi )M_{t,q} \left( \eta \right) w_{s,t} }\nonumber \\ \xi _1\le & {} \xi \le \xi _{{{n}}+p+1} \text { and }\eta _1 \le \eta \le \eta _{m+q+1} \end{aligned}$$

(21)

where $w_{s,t}$ is the weight corresponding to control point ${\varvec{B}}_{st}$. Thus, NURBS shapes in 2-D can be constructed using Eq. (18) but with NURBS bases (Eq. 21) substituted for B-spline bases.

4.2 Example: 2-D NURBS object

To illustrate the construction of NURBS geometries, a 2-D square domain with an elliptic void is used as an example (Fig. 3a). The domain is discretized into four patches as shown in Fig. 3b, and because of symmetry, only patch 1 is considered. To model the elliptical boundary, a second or higher order basis is needed. Hence, using Eq. (17) a second order basis ${N}_{i,2} (\xi )$ is defined along the $\xi$-direction with knot vector ${\varvec{\xi }}_v =\left\{ {0,0,0,1,1,1} \right\}$, while a first order basis $M_{j,1} \left( \eta \right)$ is defined along the $\eta$-direction with knot vector ${\varvec{\eta }} _v =\left\{ {0,0,1,1} \right\}$ (Fig. 3c). The control point polygon, i.e. polygon created by considering all control points ${\varvec{B}}_{ij}$ is shown in Fig. 3d, with solid lines representing the $\xi$-direction and dashed lines representing the $\eta$-direction. Note that the meaning of solid lines and dashed lines will remain the same throughout the manuscript. The control points and weights are given in Table 1. Patch 1 is defined by the parametric region $\left[ {0,1} \right] \times \left[ {0,1} \right]$, as shown in Fig. 3e. The NURBS basis $\bar{R} _{i,j}^{pq} \left( {\xi ,\eta } \right)$ is computed using ${{N}}_{i,p}$ and $M_{j,q}$ in Eq. (21) and maps the parametric domain to the physical domain through Eq. (18). The corresponding physical domain of patch 1 is shown in Fig. 3f. Further details about modeling various geometries with NURBS can be found in Ref [23].

Fig. 3

Geometry construction by NURBS basis. In c the knot vectors along two directions are ${\varvec{\xi }}_{v} =\left\{ {0,0,0,1,1,1} \right\}$ and ${\varvec{\eta }}_{v} =\left\{ {0,0,1,1} \right\}$. In d, solid lines represent ${\xi }$-direction and dashed lines represent ${\eta }$-direction. a Geometry, b Discretization with 4 patches, c 1-D B-spline basis, d Control point polygon, e Parametric domain, f Physical domain

4.3 Isogeometric analysis

In isogeometric analysis both the geometry and unknown fields of interest are interpolated using NURBS. Thus, the essential difference between IGA and FEA is the adoption of different shape functions to span the geometry and solution spaces. In IGA, the derivation of weak forms and the finite element discretization remain the same as in FEA. However, in IGA, an “element” is defined as a non-zero knot span for numerical integration purposes [22, 23]. For example, the quarter part shown in Fig. 3f consists of only one element. Furthermore, in IGA the geometry and solution spaces can be enriched by using p-refinement to elevate the order of the basis [37], h-refinement to insert knots [37], or k-refinement to do both [22]. For example, Fig. 4 shows the result of applying k-refinement to the quarter domain of the ellipse in Fig. 3. In Fig. 4a, k-refinement is used to first raise the order of basis along the $\eta$ direction to 2 and then insert new knots in both the $\xi$ and $\eta$ directions (compare to Fig. 3c). This results in a mesh of 6 elements within the 2-D patch. In Fig. 4b, the order of basis along both the $\xi$ and $\eta$ directions is raised to 3 and knots are inserted in both directions, resulting in 12 elements. The advantage of performing k-refinement is that it results in elevation of the basis order of continuity instead of just the basis polynomial order.

Table 1 Control points and weights for quarter part of the elliptical void domain

Fig. 4

B-spline bases and control points after k-refinement. a ${\varvec{\xi }}_v =\left\{ {0,0,0,\frac{1}{3},\frac{2}{3},1,1,1} \right\} , {\varvec{\eta }} _v =\left\{ {0,0,0,\frac{1}{2},1,1,1} \right\} , p=q=2, {{n}}=5, m=4$, b $\xi _v =\left\{ {0,0,0,0,\frac{1}{4},\frac{2}{4},\frac{3}{4},1,1,1,1} \right\} , \eta _v =\left\{ {0,0,0,0,\frac{1}{3},\frac{2}{3},1,1,1,1} \right\} , p=q=3, {{n}}=7, m=6$

Once the NURBS model is generated in geometry space, the isoparametric concept is invoked so that the solution space is spanned by the same NURBS bases, i.e.

$$\begin{aligned} {\varvec{x}}= & {} \mathop \sum \limits _{a=1}^{{{n}}_{cp} } {{N}}_a {\varvec{x}}_a\nonumber \\ {\varvec{u}}= & {} \mathop \sum \limits _{a=1}^{{{n}}_{cp} } {{N}}_a {\varvec{u}}_a \end{aligned}$$

(22)

where ${{n}}_{cp}$ is the number of control points in the model, ${\varvec{x}}_a$ are the control point position vectors, ${\varvec{u}}_a$ are the unknown displacement control variable vectors and ${{N}}_a$ are the NURBS basis functions defined using Eq. (21). Within each IGA element e, the unknown variables are arranged in vector form as

$$\begin{aligned} {\varvec{u}}^{e}=\left[ {{\begin{array}{lllll} {{{u}}_1^e }&{} {v_1^e }&{} \ldots &{} {{{u}}_{({p+1})({q+1})}^e }&{} {v_{({p+1})({q+1})}^e } \\ \end{array} }} \right] ^{T} \end{aligned}$$

(23)

and the NURBS basis functions are assembled into the shape function matrix ${\varvec{N}}^{e}$, with corresponding shape function derivative matrix ${\varvec{B}}^{e}$

$$\begin{aligned} {\varvec{N}}^{e}= & {} \left[ {{\begin{array}{lllll} {{{N}}_1^e }&{} 0&{} \cdots &{} {{{N}}_{({p+1})({q+1})}^e }&{} 0 \\ 0&{} {{{N}}_1^e }&{} \cdots &{} 0&{} {{{N}}_{({p+1})({q+1})}^e } \\ \end{array} }} \right] \nonumber \\ {\varvec{B}}^{e}= & {} \left[ {{\begin{array}{lllll} {{{N}}_{1,{{x}}}^e }&{} 0&{} \cdots &{} {{{N}}_{({p+1})({q+1}),{{x}}}^e }&{} 0 \\ 0&{} {{{N}}_{1,y}^e }&{} \cdots &{} 0&{} {{{N}}_{({p+1})({q+1}),y}^e } \\ {{{N}}_{1,y}^e }&{} {{{N}}_{1,{{x}}}^e }&{} \cdots &{} {{{N}}_{({p+1})({q+1}),y}^e }&{} {{{N}}_{({p+1})({q+1}),{{x}}}^e } \\ \end{array} }} \right] \end{aligned}$$

(24)

where the comma denotes differentiation. The size of ${\varvec{u}}^{e}$ is due to the local support property of NURBS bases, which states that within a given non-zero knot span (IGA element) only $p+1$ basis functions are nonzero, where p is the basis order. Thus, for 2-D elements with bases of order p and q the number of nonzero basis functions is $({p+1})({q+1})$. This can be observed in Fig. 3c where there are $3\times 2=6$ nonzero shape functions. The Galerkin method is invoked so that the weighting function space is spanned by the same NURBS bases. Thus, the stiffness and mass matrices for Eq. (11) are defined using IGA as

$$\begin{aligned} {{\varvec{M}}}= & {} \mathop {{\mathcal {A}}}\limits _{e=1}^{{{n}}_{ele} } {\varvec{M}}^{e},\quad {\varvec{K}}= \mathop {{\mathcal {A}}}\limits _{e=1}^{{{n}}_{ele} } {\varvec{K}}^{e}\nonumber \\ {\varvec{M}}^{e}= & {} \mathop \int \nolimits _{{\Omega }^{e}} \rho h{\varvec{N}}^{eT} {\varvec{N}}^{e}dA,\quad {\varvec{K}}^{e}=\mathop \int \nolimits _{{\Omega }^{e}} h{\varvec{B}}^{eT}{\varvec{CB}}^{e}dA\nonumber \\ {\varvec{C}}= & {} \left[ {{\begin{array}{ccc} {\lambda +2\mu }&{} \lambda &{} 0 \\ \lambda &{} {\lambda +2\mu }&{} 0 \\ 0&{} 0&{} \mu \\ \end{array} }} \right] \end{aligned}$$

(25)

where $\rho$ is the mass density and h is the plane strain thickness. Here, the global displacement vector in Eq. (11) is arranged as ${\varvec{u}}_0 =\left[ {{\begin{array}{lllll} {{{u}}_1 }&{} {v_1 }&{} \cdots &{} {{{u}}_{{{n}}_{cp} } }&{} {v_{{{n}}_{cp} } } \\ \end{array} }} \right] ^{T}$, recalling that ${{n}}_{cp}$ is the number of control points in the entire model.

4.4 Boundary conditions and constraints in IGA

In IGA, the implementation of boundary conditions and constraints is not straightforward due to a number of reasons that warrant further explanation. To illustrate these difficulties, an example consisting of a square unit cell with irregular shaped void shown in Fig. 5 is considered. Four NURBS patches are used to discretize the domain and control points are indicated by black solid squares and labeled as ${{B}}_{ij}^{(k)}$ where the superscript (k) denotes the patch number. Due to symmetry, NURBS information is only provided for patch 1 and patch 3.

The first issue is the continuity of field variables across patch boundaries. In this study, the continuity is ensured, as the control points along the boundary of two adjacent patches are shared leading to ${{C}}^{0}$-continuity of the variables. For instance, the points ${{B}}_{11}^{(1)}$ and ${{B}}_{12}^{(1)}$ (Fig. 5a) are shared between Patch 1 and Patch 4 giving ${{C}}^{0}$-continuity along the patch boundary. It should be mentioned that other techniques for coupling patches exist, for example the use of Nitsche’s method [39]. The second issue is due to the non-interpolatory nature of the NURBS functions. For instance, in a given direction, say $\xi$ or $\eta$, only the two end points are interpolated provided that an open knot vector is used and no interior knot has a multiplicity of p, where p is the degree along this direction [23]. Only at these end points is the data interpolated since only one basis function has value 1 while the other basis functions take the value 0, see Fig. 5b and c. Here, the bases along the $\xi$-direction are such that there is no $\xi \in \left( {0,1} \right)$ at which one basis function reaches 1 while the others vanish. Thus, the NURBS basis functions defined by Eq. (21) are not interpolatory in the interval $\xi \in \left( {0,1} \right)$. The result is that both patch 1 and patch 3 have four control points that are interpolated (${{B}}_{11} , {{B}}_{12} , {{B}}_{41}$ and ${{B}}_{42} )$ and four that are not (${{B}}_{21} , {{B}}_{22} , {{B}}_{31}$ and ${{B}}_{32} )$. Due to this non-interpolatory nature, boundary conditions and constraints cannot be straightforwardly enforced as these conditions are to be prescribed on the physical boundary and not on the control points.

Fig. 5

Geometry of domain with control points and B-spline bases. a NURBS surface with control net, b NURBS surface with control net, c NURBS surface with control net

4.5 Enforcement of periodicity constraints

The constraints in Eq. (10) are enforced on a number of pairs of degrees of freedom which are located at the same position on opposite boundaries. The non-interpolatory nature of NURBS basis functions means that control points on opposite boundaries are not necessarily located at the same position (see, for example, ${{B}}_{32}^{(1)}$ and ${{B}}_{32}^{(3)}$ or ${{B}}_{22}^{(1)}$ and ${{B}}_{22}^{(3)}$ in Fig. 5a). Moreover, the number of control points on opposite boundaries may not be the same, although this can be rectified by performing h-refinement on the different patches. To enforce the constraints in Eq. (10), the following strategy is utilized: (a) constraints at the corners are directly enforced as the corner control points are all interpolated and located at the same positions on opposing boundaries (Fig. 5). (b) Constraints for the rest of the boundary are implemented by first identifying the number of control points on opposing sides, e.g. ${{N}}=2$ for the top and bottom boundaries corresponding to ${{B}}_{32}^{(3)}$ and ${{B}}_{22}^{(3)}$ on the bottom and ${{B}}_{32}^{(1)}$ and ${{B}}_{22}^{(1)}$ on the top in Fig. 5. Next, N equally spaced locations along each opposing boundary are identified in physical coordinates and the corresponding parametric coordinates are obtained by solving the inverse of Eq. (18) using the Newton-Raphson method with $R_{i,j}^{pq}$ replaced by $\bar{R} _{i,j}^{pq}$. The N equally spaced locations are referred to as interpolatory nodes and are shown in Fig. 6 as red circles. Displacement values at the interpolatory nodes can be obtained using Eq. (22) in terms of the parametric coordinates corresponding to the position of an interpolatory node. These values along with the values at the corner control points are related through Eq. (10) to define the global constraint

Fig. 6

Illustration of interpolated boundary—$\blacksquare$ denotes control points; O denotes interpolatory nodes

$$\begin{aligned} {\varvec{\mathcal {C}}}_k {\varvec{u}}_0 =\mathbf{0} \end{aligned}$$

(26)

The matrix ${\varvec{\mathcal {C}}}_k$ contains the shape functions used to find values at interpolatory nodes as well as the discretized relations from Eq. (10). This constraint is enforced using Lagrange multipliers so that the total constrained system involving Eq. (11) is

$$\begin{aligned}&{\varvec{Ku}}_0 -\omega ^{2}{\varvec{Mu}}_0 +{\varvec{\mathcal {C}}}_k^T {\varvec{\lambda }} =\mathbf{0}\nonumber \\&{\varvec{\mathcal {C}}}_k {\varvec{u}}_0 =\mathbf{0} \end{aligned}$$

(27)

where $\varvec{\lambda }$ is the vector of Lagrange multipliers. Finally, Eq. (12) is recovered by writing Eq. (27) in matrix form with

$$\begin{aligned} \hat{{\varvec{K}}} ({\varvec{k}})=\left[ {{\begin{array}{ll} {\varvec{K}}&{} {{\varvec{\mathcal {C}}}_k^T } \\ {{\varvec{\mathcal {C}}}_k }&{} \mathbf{0} \\ \end{array} }} \right] ; \hat{{\varvec{M}}} =\left[ {{\begin{array}{ll} {\varvec{M}}&{} \mathbf{0} \\ \mathbf{0}&{} \mathbf{0} \\ \end{array} }} \right] ;\hat{{\varvec{u}}} _0 =\left[ {{\begin{array}{l} {{\varvec{u}}_0 } \\ {\varvec{\lambda }} \\ \end{array} }} \right] \end{aligned}$$

(28)

For ${\varvec{K}}$ and ${\varvec{M}}$ of dimensions ${{n}}\times {{n}}$ and ${\varvec{\mathcal {C}}}_k$ of dimensions $m\times {{n}}$, the unconstrained eigenvalue problem in Eq. (12), when using the matrices from Eq. (28), has ${{n}}-m$ eigenvalues which are the same as those of the constrained eigenvalue problem and 2m eigenvalues which are infinite [40]. Thus, the lowest ${{n}}-m$ eigenvalues correspond to those of the constrained eigenvalue problem. In this study only square unit cells are considered, but the above described process for enforcing boundary conditions can be easily extended to other unit cell geometries.

5 Computing band structure

In two dimensions, the dispersion relations in Eq. (13) define an eigen-system with three unknowns: (i) the frequency of wave propagation $\omega$ and (ii)–(iii) the components of the wave vector, $k_1$ and $k_2$. To solve this system, the wave vector is prescribed and the frequency of wave propagation is obtained as $\omega =\omega \left( {k_1 ,k_2 } \right)$, which reveals the band structure. For a given wave vector, Eq. (13) has n modal solutions $\omega _q$, along with n corresponding mode shapes $\hat{{\varvec{u}}} _{0q}$, where n is the size of the matrices $\hat{{\varvec{K}}}$ and $\hat{{\varvec{M}}}$. The lowest two modes are identified as acoustic modes, and represent longitudinal and shear waves. Higher modes are referred to as optical modes, and generally represent some combination of longitudinal and shear waves [35]. To investigate the band structure for frequencies of practical interest, only the acoustic modes and a small number of the lowest optical modes are considered. In general, the components of the wave vector can be complex, i.e. $k_\alpha =\mu _\alpha +i\gamma _\alpha$. However, waves propagating without attenuation have real wave numbers [36]. In this study, the aim is to analyze non-attenuating waves, so only the real part of the wavenumber—the phase constant $\mu _\alpha$—is considered. This results in the following form of the dispersion relations

$$\begin{aligned} {{\mathcal {D}}}\left( {\omega _q ,\mu _1 ,\mu _2 } \right)= & {} \det [\hat{{\varvec{K}}} ({\mu _1 ,\mu _2 } )\nonumber \\&-\omega _q^2 \hat{{\varvec{M}}} \left( {\mu _1 ,\mu _2 } \right) ]=0 \end{aligned}$$

(29)

To analyze the band structure, Eq. (29) must be solved for every unique pair of phase constants $\left( {\mu _1 ,\mu _2 } \right) \in \mathrm{R}^{2}$ representing a non-attenuating wave vector. However, by considering the real wave vector components in Eq. (10) it can be observed that

$$\begin{aligned} {\varvec{u}}_0 \left( {{\varvec{x}}^{+}} \right)= & {} {\varvec{u}}_0 \left( {{\varvec{x}}^{-}} \right) \exp \left[ {i\mathop \sum \limits _{\alpha =1}^2 \mu _\alpha l_\alpha } \right] \nonumber \\= & {} {\varvec{u}}_0 \left( {{\varvec{x}}^{-}} \right) \exp \left[ {i\mathop \sum \limits _{\alpha =1}^2 \left( {\mu _\alpha l_\alpha +2\pi } \right) } \right] \end{aligned}$$

(30)

Thus, due to the periodicity of the exponential term the unique phase constants only exist in the range $0\le \mu _\alpha \le 2\pi /l_\alpha$. In solid state physics this range of unique wave numbers is known as the first Brillouin zone (FBZ) and defines a unit cell in the wave number space or the so called reciprocal space [7, 35]. With the frequency defined as a function of the phase constants, a surface can be constructed for each of the n modes $q=1,2,\ldots ,{{n}}$. These surfaces are referred to as dispersion surfaces because they reveal the relationship between frequency and wave number, and each modal dispersion surface represents frequencies at which waves can propagate without attenuation. Thus, the band structure can be visualized by plotting the dispersion surfaces for a number of modes and bandgaps are identified as frequency ranges between consecutive modal dispersion surfaces, i.e. frequency ranges where there is no non-attenuating wave propagation. To investigate wave directionality, contour plots of dispersion curves can be constructed at a given frequency. These contours are known as isofrequency (or equifrequency) contours and give the direction of the group velocity—and thus of energy flow—at a given frequency as the direction normal to the isofrequency contour [41].

For unit cells with geometric symmetries, the range of unique phase constant pairs can be further reduced to what is known as the irreducible Brillouin zone (IBZ) and all the important bandgap information can be investigated by considering only the phase constants on the boundary of the IBZ [35]. This allows one to construct curves by plotting each modal frequency as a function of a scalar arc length parameter describing the position on a curve around the perimeter of the IBZ. Plotting a number of these dispersion curves gives the band diagram, and bandgaps are identified as the spaces between consecutive modal dispersion curves. The construction of dispersion curves is much less computationally expensive than the construction of dispersion surfaces, as it requires far fewer evaluations of the eigenvalue problem (Eq. 29).

Fig. 7

Circular void example geometry, IBZ and meshes. a IBZ, b FEA coarse mesh, c IGA coarse mesh

6 Comparison of FEA and IGA

In this section, implementation of the isogeometric dispersion analysis is validated on a simple example unit cell by comparing the results from FEA and IGA. In addition, this example is used to investigate the effect of k-refinement on the accuracy of the IGA solutions. The improved performance offered by IGA for the calculation of eigenfrequencies which is detailed in Refs [28, 32, 33] is explored here in the context of dispersion relations for periodic solids by performing a mesh refinement study. The material properties used in this and subsequent examples are as follows: $E=3$ GPa, $\nu =0.3$ and $\rho =1000\hbox { kg/m}^{3}$ and represent an epoxy material. All the analyses are carried out in a $\hbox {Matlab}^{{\textregistered }}$ based finite element program CPSSL-FEA developed at the University of Notre Dame. The calculations are performed on a personal computer with a Pentium 3.0 GHz microprocessor. In all of the following results, frequencies are normalized by multiplying by the length of the square unit cell $l=l_1 =l_2$ and dividing by the transverse wave speed $c_t$ in bulk material (Eq. 7).

6.1 Circular void—mesh refinement study

The example problem consists of a square microstructural unit cell with a circular void. The unit cell is 8 mm by 8 mm and the void has a radius of 1 mm, so that 5% of the area of the unit cell is void. The FBZ for the square unit cell is shown in wave number space, defined by coordinate axes $1/l_1$ and $1/l_2$, as the shaded area in Fig. 7a. The point symmetry of the circular void microstructure results in the IBZ enclosed by the points O, A and B in Fig. 7a. The coordinates of points O, A and B are defined in terms of the dimensionless phase constants $({\mu _1 l_1 ,\mu _2 l_2 })$ as $({0,0}), ({\pi ,0})$ and $( {\pi ,\pi } )$, respectively. Figure 7b and c show two meshes created using IGA and FEA with the coarsest mesh. Table 2 lists the NURBS information including the control points, weights and knot vectors of one patch. The whole domain can be seen as an assembly of four such patches, similar to the example shown in Fig. 3. It is clear from Fig. 7 that the FEA discretization of the void does a poor job of representing a circle, while with IGA the circle is exactly represented. Even as the mesh is refined, bilinear finite elements can never exactly represent the circle. While higher order finite elements may be used, a fine mesh is still needed. The IBZ boundary for this example is discretized into 30 points for each of the branches O–A, A–B and B–O, so that 90 eigenvalue analyses are performed in order to compute the band diagram. To compare the results of standard finite element analysis and isogeometric analysis, mesh refinement is carried out and the relative error is calculated for each of the first six dispersion curves using the $L_2$ relative error norm as

$$\begin{aligned} e_q = \left\| \frac{{\varvec{\omega }} _q - {\varvec{\omega }} _q^c }{{\varvec{\omega }} _q^c }\right\| _2 \end{aligned}$$

(31)

Table 2 Control points and weights for left quarter part of the circular void plate

Fig. 8

Results of circular void mesh refinement study for the first six modes at IBZ point A. a Mode 1, b Mode 2, c Mode 3, d Mode 4, e Mode 5, f Mode 6

where $e_q$ is the relative error of mode q and ${\varvec{\omega }} _q$ is the vector of frequencies for mode q, i.e. the qth dispersion curve; ${\varvec{\omega }} _q^c$ is the vector of “converged” frequency values for mode q, which is found using a FEA mesh with 160000 degrees of freedom. The relative errors are plotted in Fig. 8 for different FEA and IGA meshes and for different order bases in IGA. As discussed in [32], regarding the model degrees of freedom as a measure of comparison between IGA and FEA is somewhat misleading due to the increased number of quadrature points which are needed for integration when using higher order basis functions. Nonetheless, comparing model degrees of freedom still gives a good idea of the benefits of using IGA over FEA.

The degrees of freedom reported refer to the size of the transformed mass ($\hat{{\varvec{M}}} )$ and stiffness ($\hat{{\varvec{K}}})$ matrices that are used in the eigenvalue analysis. Thus, for IGA the degrees of freedom include those introduced by using the Lagrange multipliers to enforce the boundary conditions. From this mesh refinement study it can be observed that IGA results are substantially more accurate when using a coarse mesh as compared to FEA. Indeed, an IGA mesh with only around 1000 degrees of freedom has essentially the same accuracy as an FEA mesh with 160000 degrees of freedom. This follows the trends discussed in Refs [28, 32, 33]. To further illustrate this performance, the band structure for the first six modes is shown in Fig. 9 using the FEA mesh with 160000 degrees of freedom and second order IGA mesh with 1000 degrees of freedom.

Fig. 9

Comparison of circular void band structure for the first six modes using FEA and IGA meshes with different degrees of freedom

The bulk of the computational effort for dispersion analysis comes from solving the eigenvalue problem in Eq. (29). Therefore, to better quantify the advantage of using IGA, the time per eigenvalue analysis and the total time spent solving eigenvalue problems are recorded for the FEA mesh with 160000 degrees of freedom and IGA mesh with 1000 degrees of freedom in Table 3. The $\hbox {Matlab}^{{\textregistered }}$ function eigs is used to solve the eigenvalue problem for the lowest six eigenvalues. This result clearly shows the computational advantage of IGA, which is due to the significantly fewer degrees of freedom needed.

Table 3 Time for eigenvalue analyses—circular inclusion meshes

6.2 Circular void—k-refinement

As shown in Fig. 8, k-refinement is also carried out on this example to investigate whether or not the order of continuity used in IGA affects the solution. As k-refinement is utilized, the basis order of continuity is increased along with the polynomial order. While the governing equation (Eq. 2) is second order, higher order bases may offer an advantage by increasing the smoothness of solution spaces, leading to better numerical approximations. From Fig. 8 it can be seen that 3rd order bases converge more rapidly and so are more accurate with coarser meshes than 2nd order, but compared to the relative errors of FEA the difference is negligible. It can also be seen that around 1000 degrees of freedom, both IGA solutions have negligible error (around $10^{-3})$. Figure 10 shows the band structure calculated using 2nd and 3rd order meshes with 1000 degrees of freedom. It is clear from this example that higher continuity offers no further advantage.

Fig. 10

Circular void band structure for different order meshes using 1000 degrees of freedom

Fig. 11

Unit cell geometry, band structure and acoustic mode isofrequency contours for first example problem. a Unit cell geometry, b Band structure, c Transverse mode isofrequency contours, d Longitudinal mode isofrequency contours

7 Numerical examples

In this section, various test cases are presented to demonstrate the important dispersive effects which can be obtained with different microstructural unit cell geometries. Each of these examples highlights a different dispersive phenomenon utilized by phononic crystals and elastic metamaterials. All examples use the epoxy material properties given in Sect. 6 and utilize a square unit cell with FBZ shown in Fig. 7a. Moreover, in order to highlight the efficacy of the proposed isogeometric analysis, the presented examples use unit cells consisting of voids or inclusions with complicated curved geometries that are difficult to represent with standard finite elements. As IGA can accurately represent these microstructural geometries, it is a natural approach for calculating the band structure of such complex microstructural unit cells. While two dimensional examples are considered in the present study, the approach developed herein is readily extendable to three dimensional problems. This simply requires enforcing periodicity constraints over three periodic dimensions in the exact same way as they are enforced over two periodic dimensions herein. Additionally, the correct IBZ must be identified based on the three dimensional unit cell, see e.g. the appendix in [21].

7.1 Bragg scattering

In this example, a phononic crystal with microstructure consisting of a flower shaped inclusion of stiffer material, shown in Fig. 11a, is considered. This geometry is created by using two unique IGA patches and the control points for the patches are given in “Appendix A.1”. The material in the inclusion has an elastic modulus of 5E and a density of $10\rho , E$ and $\rho$ being the epoxy material properties given in Sect. 6. As this microstructural geometry has point symmetry, its IBZ is identical to that shown in Fig. 7a, and the IBZ boundary is discretized in the same way. To construct the isofrequency contours, the first Brillouin zone covering the range $\mu _\alpha l_\alpha \in \left[ {-\pi ,\pi } \right]$ is discretized into a 50 by 50 point mesh. The band structure for this case is shown in Fig. 11b for the two acoustic modes and lowest four optical modes. This band structure reveals a large bandgap between the first and second optical modes and another, smaller bandgap between the third and fourth optical modes. Bandgaps in the higher frequency optical modes are characteristic of Bragg scattering and are due to the mechanical impedance mismatch of the microstructural inclusion. Isofrequency contours of the acoustic modes are given in Fig. 11c and d with the IBZ overlaid. The first mode represents transverse waves while the second represents longitudinal waves. At lower frequencies, the longitudinal mode behaves isotropically and has no preferred direction of propagation, as evidenced by the circular shape of the contours (Fig. 11d). As frequency increases, however, this mode becomes anisotropic, resulting in preferential directions of propagation identified as perpendicular to the flat parts of the contours. In the same way, the transverse mode shows anisotropy, but at all frequencies (Fig. 11c).

Fig. 12

Unit cell geometry, band structure and acoustic mode isofrequency contours for second example problem. a Unit cell geometry, b Band structure, c Transverse mode isofrequency contours, d Longitudinal mode isofrequency contours

7.2 Local resonance

In this example, an elastic metamaterial with unit cell consisting of four curved voids arranged in a windowed frame pattern and shown in Fig. 12a is considered. By arranging the voids in this way, beam-like structures are introduced in the topology of the microstructure that have their own resonant frequencies, and can cause the localization of energy. This geometry is created by using two unique IGA patches and the control points for the patches are given in Appendix A.2. Again, the symmetry results in the IBZ shown in Fig. 7a, and the IBZ boundary is discretized in the same way. For isofrequency contours, the first Brillouin zone is discretized by a 50 by 50 point mesh. The band structure for this example is shown in Fig. 12b. The isofrequency contours for the transverse and longitudinal modes (Fig. 12c, d, respectively) show anisotropy at all frequencies. It can be observed from Fig. 12b that around a normalized frequency of 1.3, the dispersion curves flatten out. As the tangent to a dispersion curve at a particular frequency gives the group velocity, a zero slope means that waves are not propagating and energy is localized. This flattening of dispersion curves is characteristic of local resonance [2] and the fact that this resonance occurs at a relatively low frequency (compare to the bandgaps in Fig. 11b) shows how local resonance effects can be harnessed to manipulate low frequency modes.

Fig. 13

Mode shapes of longitudinal and first optical mode at point A of IBZ for second example problem. a Longitudinal mode near IBZ point A, b First optical mode near IBZ point A

Fig. 14

Unit cell geometry, band structure and acoustic mode isofrequency contours for third example problem. a Unit cell geometry, b Band structure, c Transverse mode isofrequency contours, d Longitudinal mode isofrequency contours

In order to demonstrate that energy is localized through the resonant behavior of the beam-like microstructural features, the mode shapes for the longitudinal mode and first optical mode near point A of the IBZ are shown in Fig. 13. The mode shape is plotted in grey while the undeformed unit cell is plotted in black. The mode shape in Fig. 13a reveals an axial deformation pattern in which the entire unit cell is deforming, indicating the existence of a propagating longitudinal wave. For the mode shape in Fig. 13b, only the beam-like structures are deforming in a rotational pattern while the rest of the unit cell is undeformed, indicating that no wave is passing through the unit cell. Thus, resonance of the beam-like structures has caused the localization of energy and prevented the propagation of waves at this frequency.

7.3 Wave directionality

In the final example, the effect that altering microstructural symmetry has on the directionality of wave propagation is investigated. The unit cell structure is shown in Fig. 14a, and is characterized by an asymmetric shaped void. The control points for the geometry are given in “Appendix A.3”. The change in symmetry alters the IBZ, as the range of unique wave vectors is increased. This can be seen by looking at the acoustic mode isofrequency contours shown in Fig. 14c and d, where the FBZ was again discretized by a 50 by 50 point mesh. From the apparent symmetry of the isofrequency contours, it is clear that the IBZ for this example requires augmenting the IBZ used in previous examples by moving point A from $\left( {\pi ,0} \right)$ to $\left( {\pi ,-\pi } \right)$. For obtaining the band structure, this new IBZ is discretized into 20 points for branch O–A, 30 points for branch A–B and 20 points for branch B–O. The band structure in Fig. 14b does not show any noteworthy behavior as there are no bandgaps or flat regions.

The isofrequency contours reveal anisotropy at all frequencies. However, in both of the previous examples, the transverse mode shows preference toward propagating in the direction along O–B while the longitudinal mode shows preference toward the direction along O–A, at least at higher frequencies. In this example, the preferred direction of propagation for the transverse mode is still along O–B as seen in Fig. 14c. The longitudinal mode, however, clearly changes its preferential direction from along O–A to along O–B, even at the lowest frequencies as seen in Fig. 14d. This example shows how tailoring the features and thus symmetry of the unit cell can allow for greater control over the directions in which waves and thus energy propagate at different frequencies.

Table 4 Control points and weights for Patch 1 in Fig. 16a

Table 5 Control points and weights for Patch 2 in Fig. 16(b)

8 Conclusions

The following are important conclusions which can be drawn from this study:

• (a) It is shown that isogeometric analysis can be used to calculate the dispersive properties of phononic crystals and elastic metamaterials with complex microstructural geometries. This provides a novel and more effective tool for the analysis and thus the design of these materials when considering complex unit cell geometries.

• (b) As the control points in IGA are non-interpolatory, a constraint enforcement technique based on the use of interpolatory nodes and the Lagrange multiplier method is presented to correctly enforce the periodicity constraints in IGA arising from the Bloch theorem.

• (c) The superiority of IGA over FEA which was demonstrated in Refs [28, 32, 33] for structural vibrations and wave propagation problems is demonstrated numerically for the construction and solution of dispersion relations of periodic solids through the use of a mesh refinement study. The ability to exactly represent complex unit cell geometries and to easily increase the basis order means that significantly coarser meshes can be used with IGA to obtain solutions with accuracy comparable to much finer FEA meshes. Thus, the construction of band diagrams requires significantly fewer degrees of freedom when isogeometric analysis is used.

• (d) The efficacy of the proposed isogeometric framework is demonstrated by calculating the band structure of unit cells with intricate curved geometries which result in desirable dispersive phenomena including Bragg scattering, local resonance and frequency-dependent directionality.

• (e) The ability of isogeometric analysis to capture complex geometries using few control points can prove advantageous in a variety of ways. One of these is the use of shape or topology optimization to design unit cells of phononic crystals and acoustic/elastic metamaterials. Not only is there a significant reduction in the number of design variables needed for optimization, but complex geometries can be modeled exactly, opening up new areas of design space. The authors are currently investigating this area.

Fig. 15

Patch discretization of the domain shown in Sect. 7.1

Fig. 16

Control point polygon of two patches in Fig. 15. a Patch 1, b Patch 2

Appendices

Appendix A: Control data for NURBS shapes

1.1 A.1 Geometry from Sect. 7.1

Fig. 17

Patch discretization of the domain shown in Sect. 7.2

Fig. 18

Control point polygon of two patches in Fig. 17. a Patch 1, b Patch 2

Table 6 Control points and weights for Patch 1 in Fig. 18a

Table 7 Control points and weights for Patch 2 in Fig. 18b

The domain in this example is divided into 12 patches as shown in Fig. 15. Only two patches, patch-1 and patch-2, are unique due to symmetry. The control point polygons for the two patches are shown in Fig. 16. Control point data and the corresponding weights for the two patches are provided in Tables 4 and 5, respectively.

Fig. 19

Patch discretization of the domain shown in Sect. 7.3

Fig. 20

Control point polygon of two patches in Fig. 19.a Patch 1, b Patch 2

Table 8 Control points and weights for Patch 1 in Fig. 20a

A.2 Geometry from Sect. 7.2

The domain in this example is divided into 16 patches as shown in Fig. 17. Only two patches, Patch 1 and Patch 2, are unique due to symmetry. The control point polygons for the two patches are shown in Fig. 18. Control point data and the corresponding weights for the two patches are provided in Tables 6 and 7, respectively.

1.1 A.3 Geometry from Sect. 7.3

The domain with asymmetric hole in Example 7.3 is divided into 4 patches as shown in Fig. 19. Only two patches, Patch 1 and Patch 2, are unique due to symmetry. The control point polygons for the two patches are shown in Fig. 20. Control point data and the corresponding weights for the two patches are provided in Tables 8 and 9, respectively.

Table 9 Control points and weights for Patch 2 in Fig. 20b