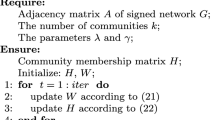Block Modelling and Learning for Structure Analysis of Networks with Positive and Negative Links

Abstract

Currently, many community mining methods for signed networks with positive and negative links have been proposed, however, these methods can only efficiently find the community of signed networks and unable to find other structure, such as bipartite, multipartite and so on. In this study, we present a mathematically principled community mining method for signed networks. Firstly, a probabilistic model is proposed to model the signed networks. Secondly, a variational Bayesian approach is deduced to learn the proximation distribution of model parameters. In our experiments, the proposed method is validated in the synthetic and real-word signed networks. The experimental results show the proposed method not only can efficiently find communities of signed networks but also can find the other structure.

1 Introduction

Signed networks usually are composed of the nodes, positive links and negative links, in which the nodes represent the individuals, the positive links represent like, trust or support relationship and the negative links represent dislike, distrust or oppose relationship [13, 14]. In contrast to the unsigned networks [4, 6, 8], the signed networks may contain more information by extending the single relationship to the positive and negative relationships. Structure analysis is an important problem in the network studies since network structures are closely related to the functions and evolution of systems. Community structure, which is the dense subnetwork within a larger network, is the best-studied structure in networks. In general, the links in communities are dense but the links between communities are sparse [9]. Because there are the negative links in the signed networks, the communities in the signed networks also show another characteristic that is most of the links in communities are the positive links and most of the links between communities are the negative links. To analyze the signed networks, until now, many methods have been proposed to find the communities in the signed networks. The representative methods is as follows: Doreian and Mrvar proposed a frustration-based method (referred to as DM) [3]. Traag et al. proposed a modularity-optimization-based algorithm for signed networks [11]. Yang et al. proposed a fast method based on Markov stochastic process (referred to as FEC) [12]. Anchuri et al. proposed a generalized spectral method for signed network partition [1]. For these methods, their common drawback is it is very difficult to design a good objective. To address the above problems, Zhao et al. proposed an EM-based community detection method for the signed networks [14]. Yang et al. proposed a signed stochastic block model and its variational Bayes learning algorithm for the signed networks [13]. However, these methods mainly focus on the community structure.

Block modelling is a form of statistical inference for the networks. The idea of block modelling for the network analysis is to find the structure of networks by fitting a specific block model to a network. Based on this idea, in this paper, we present a mathematically principled community mining method for signed networks. Firstly, a probabilistic model is proposed to model the signed networks, Secondly, a variational Bayesian approach is deduced to learn the proximation distribution of model parameters. In our experiments, the proposed method is validated in the synthetic and real-word signed networks. The experimental results show the proposed method not only can efficiently find community of signed networks but also can find the other structure.

2 Model and Method

Let $\pmb {a}$ denote the adjacency matrix of the signed network N containing n nodes. The element $a_{ij}$ is equal to 1, −1 or 0 if there is a positive, negative or no link between the node i and the node j. Suppose all of the nodes are divided into K groups and the nodes in the same group have the similar connection patten with the nodes of other groups. The proposed model is defined as follows

$$\begin{aligned} \begin{aligned} X=(K,\pmb {z}, \pmb {\omega },\pmb {\pi }) \end{aligned} \end{aligned}$$

(1)

where K is the number of groups. $\pmb {\omega }$ is a K-dimension vector in which the element $\omega _k$ denotes the probability that a node is assigned to the group k, and $\sum _{k=1}^{K}\omega _k=1$. $\pmb {\pi }$ is a $K\times K\times 3$ matrix, where $\pi _{lq1}$, $\pi _{lq2}$ and $\pi _{lq3}$ denote the probability that there is a positive link, no link or negative link between a pair of nodes in the group l and q, respectively. In addition, the proposed model contains an indicating variable (or latent variable) $\pmb {z}$, which is the $n\times K$ matrix containing the group information of nodes. $z_{ik}=1$ if the node i is assigned to the group k, otherwise $z_{ik}=0$.

Given the parameter $\pmb {\omega }$, the probability distribution of $\pmb {z}$ is as follows

$$\begin{aligned} \begin{aligned} p(\pmb {z}|\pmb {\omega })=\prod _{i=1}^{n}\prod _{k=1}^{K}\omega _{k}^{z_{ik}} \end{aligned} \end{aligned}$$

(2)

Given $\pmb {z}$, $a_{ij}$ follows the following multinomial distribution with parameter $\pmb {\pi }$:

$$\begin{aligned} \begin{gathered} p(a_{ij}|\pmb {z},\pmb {\pi })=\prod _{l,q=1}^{K}\prod _{h=1}^{3}\pi _{lqh}^{z_{il}z_{jq}\delta (a_{ij},2-h)} \end{gathered} \end{aligned}$$

(3)

where $\delta (x,y)$ is Kronecker function, if $x=y$, the function value is 1, otherwise the value is zero.

When the priors of the model parameters $(\pmb {\pi },\pmb {\omega })$ are specified, we can describe the proposed model in a full Bayesian framework. Since $p(z_i|\pmb {\omega })$ and $p(a_{ij}|\pmb {z},\pmb {\pi })$ satisfy the multinomial distribution, respectively, we can select the Dirichlet distribution as their conjugate prior distributions, as follows

$$\begin{aligned} \begin{aligned} p(\pmb {\omega }|\pmb {\rho }^0=\{\rho _1^0,...,\rho _K^0\})=\text {Dir}(\pmb {\omega };\pmb {\rho }^0) \end{aligned} \end{aligned}$$

(4)

$$\begin{aligned} \begin{aligned} p(\pi _{lq}| \pmb {\eta }_{lqh}^{0}=\{\eta _{lq1}^{0},\eta _{lq2}^{0},\eta _{lq3}^{0}\})=\text {Dir}(\pi _{lq};\pmb {\eta }_{lqh}^{0}) \end{aligned} \end{aligned}$$

(5)

where $\pmb {\rho }_q^0$ and $\pmb {\eta }_{lqh}^{0}$ are the hyperparameters. In the full Bayesian framework, the parameters $\pmb {\pi }$ and $\pmb {\omega }$ can be regarded as the random variables which follow the distributions with their respective hyperparameters.

To analyze the structure of network, we need to learn the parameters of model, then analyze the networks based on the learned values of parameters. Since the posterior distribution of $\pmb {z}$, under the condition of data and model parameters, cannot be explicitly derived as an input required, we adopt the variational Bayesian approach [2, 7] to learn the approximate distributions of parameters and variable.

The log-likelihood $\mathcal {L}(N)$ of the network N can be decomposed into two terms

$$\begin{aligned} \begin{aligned} \mathcal {L}(N)=\mathcal {L}(q(\cdot ))+KL(q(\cdot )||p(\cdot |N)) \end{aligned} \end{aligned}$$

(6)

In Eq. 6, $KL(q\parallel p)$ denotes the Kullback-Leibler divergence between the two distributions of $q(\pmb {z},\pmb {\pi },\pmb {\omega })$ and $p(\pmb {z},\pmb {\pi },\pmb {\omega }|N)$. $p(\pmb {z},\pmb {\pi },\pmb {\omega }|N)$ is the true posterior distribution of the variables $\pmb {z}$ and the parameters ($\pmb {\pi },\pmb {\omega }$) given the network N, $q(\pmb {z},\pmb {\pi },\pmb {\omega })$ is an approximation of the true posterior distribution. $\mathcal {L}(q(\cdot ))$ is called the lower bound of $\mathcal {L}(N)$. The Kullback-Leibler vergence satisfies $KL(q\parallel p)\ge 0$, with equality if, and only if, $q(\cdot ) = p(\cdot )$.

The variational approach aims at optimizing a lower bound of $\mathcal {L}(N)$ by approximating the true distributions of the parameters and variable. To obtain a computationally tractable algorithm, we use mean field approximation, in which we assume the posterior $q(\pmb {z},\pmb {\pi },\pmb {\omega })$ is a fully factorized approximation, which is written as follows

$$\begin{aligned} \begin{aligned} q(\pmb {z},\pmb {\pi },\pmb {\omega })=q(\pmb {\pi })q(\pmb {\omega })\prod _{i=1}^{n}q(z_i) \end{aligned} \end{aligned}$$

(7)

where $q(z_i)$, $q(\pmb {\pi })$ and $q(\pmb {\omega })$ denote the distributions of variables $z_i$, $\pmb {\pi }$ and $\pmb {\omega }$, respectively.

Next, we need to seek the distributions of $q(z_i)$, $q(\pmb {\pi })$ and $q(\pmb {\omega })$, which make the lower bound $\mathcal {L}(q(\cdot ))$ largest. This requires us to deduce the expressions of the distributions $q(z_i)$, $q(\pmb {\pi })$ and $q(\pmb {\omega })$.

According to variational Bayes, the optimal distribution $q(z_i)$, $q(\pmb {\omega })$ and $q(\pmb {\pi })$ are the following multinomial or Dirichlet distribution, respectively.

$$\begin{aligned} \begin{aligned} q(z_i)=M(z_i;1,\tau _{i1},...,\tau _{iK}) \end{aligned} \end{aligned}$$

(8)

where $\tau _{ik}$ is the probability of node i belonging to group k, and satisfies:

$$\begin{aligned} \begin{aligned} \tau _{il}\propto&e^{\psi (\rho _l)-\psi (\sum \limits _{l=1}^K \rho _l)}\times \prod _{j\ne i}^n\prod _{q=1}^K\Big (e^{\tau _{jq}\sum \limits _{h=1}^3\delta (a_{ij},2-h)(\psi (\eta _{lqh})-\psi (\sum \limits _{h=1}^3 \eta _{lqh}))}\Big ) \end{aligned} \end{aligned}$$

(9)

where $\psi (\cdot )$ is digamma function.

$$\begin{aligned} \begin{aligned} q(\pmb {\omega })=\text {Dir}(\pmb {\omega };\pmb {\rho }), \qquad \rho _q=\rho _q^0+\sum _{i=1}^n\tau _{iq} \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned}&q(\pmb {\pi })=\prod _{l,q}\text {Dir}(\pmb {\pi }_{lq};\pmb {\eta }_{lq}) \end{aligned} \end{aligned}$$

(11)

For $q \ne l$, the hyperparameter $\eta _{qlh}$ ($h=\{1, 2, 3\}$) is given by

$$\begin{aligned} \begin{aligned} \eta _{lqh}=\eta _{lqh}^{0}+\sum _{i\ne j}^n\tau _{il}\tau _{jq}\delta (a_{ij},2-h) \end{aligned} \end{aligned}$$

(12)

For $\forall q$, the hyperparameter $\eta _{qqh}$ ($h=\{1, 2, 3\}$) is given by

$$\begin{aligned} \begin{aligned} \eta _{qqh}=\eta _{qqh}^{0}+\sum _{i<j}^n\tau _{iq}\tau _{jq}\delta (a_{ij},2-h) \end{aligned} \end{aligned}$$

(13)

The Eqs. 9, 10, 12 and 13, build the main steps of our algorithm. We iterate to update these equations to convergence. Finally, the values of the learned hyperparameters ($\pmb {\tau }, \pmb {\eta }$) can be used to analyze the structure of signed networks. Since the time complexity of the proposed algorithm is mainly determined by calculating Eqs. 9, 10, 12 and 13, the total time complexity of the algorithm is $O(K^2n^2)$.

3 Experiments

The proposed algorithm is called SASN here. SASN is validated in the synthetic and real-world networks in our experiments. We also make comparisons with other four algorithms which are respectively DM [3], SSL [13], FEC [12] and SISN [14]. In our experiments, the normalized mutual information (NMI) [14] is used to evaluate the performance of the algorithms.

Firstly, we generate synthetic networks by the generate model in Ref. [12]. The model parameters are set as follows: $(4,32,32,0.5,0.05*p{-},0)$ and varying $p-$ from 0 to 0.5 with the interval 0.05. The larger the value of $p-$ is, the more the negative links in the communities are. The results of five algorithms running this type of signed networks are shown in Fig. 1. We can see that, all the NMI values of the SASN and SSL are 1 when $p{-}$ varies from 0 to 0.5. This indicates our method and SSL can correctly find the communities in the networks.

Fig. 1.

Results of five algorithms.

Secondly, we generate the networks with coexisting structure. The type of networks is generated according to the following way. First, all the nodes are divided into four groups, each of which includes 32 nodes. Then, the links within or between the groups are generated according to the following $\pi _{a,b}$ value, where a and b denote the labels of groups. $\pi _{11}=\{0.6, 0.1, 0.3\}$, $\pi _{12}=\{0.1, 0.2, 0.7\}$, $\pi _{13}=\{0.1, 0.2, 0.7\}$, $\pi _{14}=\{0.1, 0.2, 0.7\}$, $\pi _{22}=\{0.2, 0.1, 0.7\}$, $\pi _{23}=\{0.01, 0.4, 0.59\}$, $\pi _{24}=\{0.01, 0.4, 0.59\}$, $\pi _{33}=\{0.01, 0.01, 0.98\}$, $\pi _{34}=\{0.01, 0.4, 0.59\}$, $\pi _{44}=\{0.01, 0.01, 0.98\}$, and other $\pi$ is zero. The positive, no and negative links between two nodes within or between groups follow the multinomial distribution with parameter $\pi$. Figure 2 illustrates the adjacency matrix of randomly generated network according to the above parameter set.

Fig. 2.

Adjacency matrix of network.

Fig. 3.

Results of five algorithms.

The results of five algorithms running in this type of signed networks are shown in Fig. 3. The NMI values of the results for the SASN, DM, FEC, SISN and SSL are 1, 0.8641, 0, 0.8827 and 0.8338, respectively. This indicates the SASN has more excellent performance in such networks with the coexisting structure than other four algorithms.

For the real-world signed networks, we select two real-world networks with ground truth community structure to validate the proposed algorithm. The selected signed network are Slovene parliamentary party network (SPPN) [5] and Gahuku-Gama subtribes network (GGSN) [10], respectively. For the SPPN, the nodes in the SPPN are divided into two communities and the results of our algorithm are consistent with their ground truth. For the GGSN, the nodes in the GGSN are divided into three communities and the results of our algorithm are consistent with their ground truth.

4 Conclusions

In this paper, we present a mathematically principled community mining method for the signed network. Firstly, based on block modelling idea, we propose an probability model for the signed network, which can efficiently model the well-known structure. Secondly, we deduce the specific equations of parameters in the variational Bayesian framework. The proposed method is validated in the synthetic and real-world signed networks. The experimental results show the proposed method not only can efficiently find community of signed networks but also can find the other structure.