Keywords

1 Introduction

Communities in networks are defined as the groups of nodes within which the edges are dense but between which the edges are sparse. Community detection in networks attracts many researchers, and many methods for community detection are proposed [1, 4, 9]. Most of the previous research on community detection are for normal networks composed of only one edge type. However, several real relations can be represented as signed networks composed of positive and negative edges. In this paper, we extend the modularity for signed networks in order to detect communities in signed networks. It is composed of positive and negative modularity, and it includes a balancing parameter for the importance of both types of edges.

Moreover, we propose a method for optimizing our modularity, which is an efficient hierarchical agglomeration algorithm for detecting communities in signed networks. It is based on an efficient optimization method for normal networks proposed by Clauset et al. [1].

We apply our method to several signed networks which represent the relationships among users on websites such as Wikipedia, Slashdot and Epinions. We successfully detect communities in large-scale signed networks which have more than 60,000 nodes and more than 600,000 edges. Our method can control the result by adjusting a parameter and it enables us to detect communities and inner factions inside the communities.

2 Related Works

Social relations with friendship and hostility can be represented as signed networks with positive and negative edges. Many attempts have been made for analyzing signed networks. Although structural balance of triangles of positive and negative edges is one of the important topics in signed networks, we will not discuss in this paper. Gomez et al. [5] extended Newman modularity for the analysis of directed and signed networks. Although the proposed modularity is similar to ours, it has the weakness that the balancing factor of positive and negative edges is fixed. Szell et al. [11] analyzes interactions of massive multiplayer online games. The authors claim that reciprocity and clustering coefficient of positive edges are quite different from those of negative edges. They propose STC model for generating triangles from wedges, and the model fit well for the data of online games. Leskovec et al. [6] focus on a task of edge sign prediction, and they propose a method for predicting positive and negative edges based on logistic regression classifier. Maniu et al. [8] built signed network from the interactions of editors in Wikipedia. The dataset called Wikisigned is available at http://konect.uni-koblenz.de/networks/wikisigned-k2. Esmailian et al. [3] discuss the method for detecting communities based on extended Potts Model. Their approach is flow-based, and it is quite different from our modularity optimization-based approach. Influence maximization in signed networks is studied by Li et al. [7], and link recommendation algorithm is proposed by Song et al. [10], which are not focus of this paper.

3 Extended Modularity for Signed Networks

In good partitions of signed networks, positive edges should be dense within communities and sparse between communities, and negative edges should be sparse between communities and dense within communities. We define an extended modularity for undirected signed networks \(Q_{signed}\) as a linear combination of positive and negative modularity.

$$\begin{aligned} Q_{signed} = \alpha Q^{+} - (1 - \alpha ) Q^{-} \end{aligned}$$
(1)

\(Q^{+}\) in Eq. (1) is a positive modularity, which represents the fraction of the positive edges that fall within the given groups minus the expected such fraction if positive edges were distributed at random. This is represented by Eq. (2).

$$\begin{aligned} Q^{+} = \frac{1}{2m^{+}}\sum _{ij}(A^{+}_{ij}-\frac{k^{+}_{i}k^{+}_{j}}{2m^{+}})\delta (c_{i},c_{j}) \end{aligned}$$
(2)

In Eq. (2), \(m^{+}\) is the number of positive edges, \(A^{+}\) is a positive adjacency matrix and \(A^{+}_{ij}\) is its (i, j)-th element.

$$\begin{aligned} A^{+}_{ij} = \left\{ \begin{array}{ll} 1 &{} \ \text {if there is an positive edge between node}\, i \text { and}\, j\\ 0 &{} \ \text {otherwise} \end{array} \right. \end{aligned}$$
(3)

The positive degree \(k^{+}_{i}\) of node i is defined as the number of positive edges that connect to i.

$$\begin{aligned} k^{+}_{i} = \sum _{j}A^{+}_{ij} \end{aligned}$$
(4)

\(Q^{+}\) in Eq. (1) is negative modularity, which is represented by Eq. (5).

$$\begin{aligned} Q^{-} = \frac{1}{2m^{-}}\sum _{ij}(A^{-}_{ij}-\frac{k^{-}_{i}k^{-}_{j}}{2m^{-}})\delta (c_{i},c_{j}) \end{aligned}$$
(5)

In Eq. (5), \(m^{-}\) is the number of negative edges, \(A^{-}\) is a negative adjacency matrix and \(A^{-}_{ij}\) is its (i, j)-th element.

$$\begin{aligned} A^{-}_{ij} = \left\{ \begin{array}{ll} 1 &{} \ \text {there is an negative edge between node}\, i \text { and}\, j\\ 0 &{} \ \text {otherwise} \end{array} \right. \end{aligned}$$
(6)

The negative degree \(k^{-}_{i}\) of node i is defined as the number of negative edges that connect to i.

$$\begin{aligned} k^{-}_{i} = \sum _{j}A^{-}_{ij} \end{aligned}$$
(7)

To simplify the description of our algorithm, we define the following four quantities.

$$\begin{aligned} e^{+}_{ij} = \frac{1}{2m^{+}}\sum _{s \in c_{i}}\sum _{t \in c_{j}}A^{+}_{st} \end{aligned}$$
(8)
$$\begin{aligned} e^{-}_{ij} = \frac{1}{2m^{-}}\sum _{s \in c_{i}}\sum _{t \in c_{j}}A^{-}_{st} \end{aligned}$$
(9)
$$\begin{aligned} a^{+}_{i} = \frac{1}{2m^{+}}\sum _{s \in c_{i}, t \in V}A^{+}_{st} \end{aligned}$$
(10)
$$\begin{aligned} a^{-}_{i} = \frac{1}{2m^{-}}\sum _{s \in c_{i}, t \in V}A^{-}_{st} \end{aligned}$$
(11)

Equation (8) is the fraction of positive edges that connect nodes in community i and nodes in community j, and Eq. (9) is the fraction of negative edges that connect nodes in community i and nodes in community j. Equation (10) is the fraction of positive edges that are attached to nodes in community i, and Eq. (11) is the fraction of negative edges that are attached to nodes in community i.

With the above four quantities, Eqs. (2) and (5) can be simplified as follows:

$$\begin{aligned} Q^{+} = \sum _{i}\{e_{ii}^{+}-(a^{+}_{i})^{2}\} \end{aligned}$$
(12)
$$\begin{aligned} Q^{-} = \sum _{i}\{e_{ii}^{-}-(a^{-}_{i})^{2}\} \end{aligned}$$
(13)
Fig. 1
figure 1

Example of signed network

Full size image
Fig. 2
figure 2

Communities for different \(\alpha \)

Full size image

In good partition of signed networks, the value of \(Q^{+}\) should be large and value of \(Q^{-}\) should be small. In Eq. (1), \(\alpha \) indicates the importance of positive edges and \(1 - \alpha \) indicates the importance of negative edges. The value of \(Q_{signed}\) is less than 1, and it can be negative value.

Other modularities for signed networks are proposed by Gomez et al. [5] and by Traag et al. [12]. In the modularity by Gomez et al., the value of \(\alpha \) is fixed as the proportion of positive edges in the signed network. Parameters are introduced in the modularity by Traag et al. for adjusting the size of communities. They are different from parameter \(\alpha \) in our modularity.

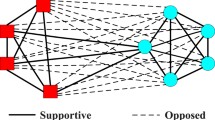
For example, the partition of a signed network (Fig. 1) which gives the largest \(\varDelta Q_{signed}\) depends on the value of \(\alpha \). In this signed network, four kinds of partition can be obtained (Fig. 2). When the value of \(\alpha \) is large, positive edges within communities are more focused. As a result, partitions that include more negative edges within communities are allowed. Conversely, when the value of \(\alpha \) is small, negative edges between communities are more focused. As a result, partitions that include more positive edges between communities are allowed. The modularity by Gomez does not have such flexibility because its parameter is fixed.

4 Method for Optimization

Community detection methods for normal networks cannot be applied directly, because there are negative edges in signed networks. In this paper, we propose a detection method for signed networks based on CNM (the method proposed by Clauset et al.) [1]. By considering the connection patterns of the edges, CNM efficiently calculates the changes in Q that would result from the agglomeration of each pair of communities. CNM cannot be applied directly because there are some connection patterns that do not exist in normal networks. Thus, it is necessary to extend CNM appropriately for signed networks.

In initial state of our method, each node is the sole member of a community. Then, our method calculates changes in \(Q_{signed}\) that would result from the agglomeration of each pair of communities connected by positive or negative edges. Until the largest \(\varDelta Q_{signed}\) becomes negative, it continues agglomeration.

figure a

In line 4 and 6 of Algorithm 1, \(\varDelta Q^{+}_{ij}\) (an element of \(\varDelta Q^{+}\)) and \(\varDelta Q^{-}_{ij}\) (an element of \(\varDelta Q^{-}\)) are defined as follows:

$$\begin{aligned} \varDelta Q^{+}_{ij} = 2(e^{+}_{ij} - a^{+}_{i}a^{+}_{j}) \end{aligned}$$
(14)
$$\begin{aligned} \varDelta Q^{-}_{ij} = 2(e^{-}_{ij} - a^{-}_{i}a^{-}_{j}) \end{aligned}$$
(15)

If node i and j are connected by a positive edge, then we substitute \(e^{+}_{ij} = 1/2m^{+}, e^{-}_{ij} = 0\) for Eqs. (14) and (15). If node i and j are connected by a negative edge, then we substitute \(e^{+}_{ij} = 0, e^{-}_{ij} = 1/2m^{-}\) for Eqs. (14) and (15). Elements of \(\varDelta Q^{+}\) and \(\varDelta Q^{-}\) are as follows:

$$\begin{aligned} \varDelta Q^{+}_{ij} = \left\{ \begin{array}{ll} 1/m^{+} - 2a^{+}_{i}a^{+}_{j} &{} \text {if } A^{+}_{ij} = 1 \\ - 2a^{+}_{i}a^{+}_{j} &{} \text {if } A^{-}_{ij} = 1\\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$
(16)
$$\begin{aligned} \varDelta Q^{-}_{ij} = \left\{ \begin{array}{ll} - 2a^{-}_{i}a^{-}_{j} &{} \text {if } A^{+}_{ij} = 1 \\ 1/m^{-} - 2a^{-}_{i}a^{-}_{j} &{} \text {if } A^{-}_{ij} = 1\\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$
(17)

In line 11–14 of Algorithm 1, the community pair (i, j) that gives the largest increase in \(\varDelta Q_{signed} (=\alpha \varDelta Q^{+}-(1-\alpha )\varDelta Q^{-})\) is agglomerated. Then, we update column i and row i, and remove column j and row j.

In our method, we avoid the calculation of \(e^{+}_{ij}\) and \(e^{-}_{ij}\) in Eqs. (14) and (15) because it is time consuming. Considering edge connection pattern between agglomerated communities i, j and x (Fig. 3), we apply appropriate update of equations for each pattern.

Fig. 3
figure 3

Four connection patterns

Full size image

Update of equations for \(\varDelta Q^{+}\) are as follows:

  1. 1.

    If x is connected to both i and j by positive edges,

    then \(\varDelta Q^{+}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{+}_{ix}= & {} 2(e^{+}_{ix} + e^{+}_{jx} - (a^{+}_{i} + a^{+}_{j}) a^{+}_{x})\nonumber \\= & {} 2(e^{+}_{ix} - a^{+}_{i}a^{+}_{x}) + 2(e^{+}_{jx} - a^{+}_{j}a^{+}_{x}) \nonumber \\= & {} \varDelta Q^{+}_{ix} + \varDelta Q^{+}_{jx} \end{aligned}$$
    (18)

    In this pattern, we need only a simple addition.

  2. 2.

    If x is connected to i but not to j by positive edge,

    then we substitute \(e_{jx}^{+} = 0\) for Eq. (14) and \(\varDelta Q^{+}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{+}_{ix}= & {} 2(e^{+}_{ix} - (a^{+}_{i} + a^{+}_{j}) a^{+}_{x}) \nonumber \\= & {} 2(e^{+}_{ix} - a^{+}_{i}a^{+}_{x}) - 2a^{+}_{j}a^{+}_{x} \nonumber \\= & {} \varDelta Q^{+}_{ix} - 2a^{+}_{j}a^{+}_{x} \end{aligned}$$
    (19)
  3. 3.

    If x is connected to j but not to i by positive edge,

    then we substitute \(e_{ix}^{+} = 0\) for Eq. (14) and \(\varDelta Q^{+}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{+}_{ix} = \varDelta Q^{+}_{jx} - 2a^{+}_{i}a^{+}_{x} \end{aligned}$$
    (20)
  4. 4.

    If x is not connected to i, j by positive edge,

    then we substitute \(e_{ix}^{+} = e_{jx}^{+} = 0\) for Eq. (14) and \(\varDelta Q^{+}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{+}_{ix} = - 2(a^{+}_{i} + a^{+}_{j})a^{+}_{x} \end{aligned}$$
    (21)

    This is the case that i, j and x are connected only by negative edges. In this case, there is no positive edge between i, j and x. This is the specific pattern for signed networks and original CNM does not consider this pattern.

Update equations for \(\varDelta Q^{-}\) are as follows:

  1. 1.

    If x is connected to both i and j by negative edges,

    then \(\varDelta Q^{-}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{-}_{ix} = \varDelta Q^{-}_{ix} + \varDelta Q^{-}_{jx} \end{aligned}$$
    (22)
  2. 2.

    If x is connected to i but not to j by negative edge,

    then we substitute \(e_{jx}^{-} = 0\) for Eq. (15) and \(\varDelta Q^{-}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{-}_{ix} = \varDelta Q^{-}_{ix} - 2a^{-}_{j}a^{-}_{x} \end{aligned}$$
    (23)
  3. 3.

    If x is connected to j but not to i by negative edge,

    then we substitute \(e_{ix}^{-} = 0\) for Eq. (15) and \(\varDelta Q^{-}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{-}_{ix} = \varDelta Q^{-}_{jx} - 2a^{-}_{i}a^{-}_{x} \end{aligned}$$
    (24)
  4. 4.

    If x is not connected to i, j by negative edge,

    then we substitute \(e_{ix}^{-} = e_{jx}^{-} = 0\) for Eq. (15) and \(\varDelta Q^{-}_{ix}\) will be computed as follows:

    $$\begin{aligned} \varDelta Q^{-}_{ix} = - 2(a^{-}_{i} + a^{-}_{j})a^{-}_{x} \end{aligned}$$
    (25)

    This is the case that i, j and x are connected only by positive edges. In this case, there is no negative edge between i, j and x.

These updates are continued until the largest \(\varDelta Q_{signed}\) becomes negative.

Our method reduces computational cost by calculating not the whole \(Q_{signed}\) but \(\varDelta Q_{signed}\) that would result from the agglomeration. In addition, it also reduces computational cost by avoiding to calculate \(e^{+}_{ij}\) and \(e^{-}_{ij}\), which are time consuming. These ingenuities do not affect the resultant value but they significantly improve the efficiency of our method.

5 Experiments

5.1 Synthetic Networks

One way to test our algorithm is to see how well it performs when it is applied to synthetic signed networks. The generated network is composed of 128 nodes which are split into four communities containing 32 nodes each. We regard these four communities as correct answer communities. The purpose of this experiment is to examine whether the answer communities can be extracted. The generation process is the same as the one used in the experiments by Danon et al. [2]. \(p_{1}\) is the noise rate from positive to negative, and \(p_{2}\) is the noise rate from negative to positive.

We detect communities in signed networks (\(p_{1}=p_{2}=0.05\)) by our method. In order to compare the calculation time, we also detect communities with two other methods. The first method is “calculate the whole of \(Q_{signed}\) (not \(\varDelta Q_{signed}\)) after agglomeration”. The second method is “calculate \(\varDelta Q_{signed}\) without using update rules (Eqs. 18–25)”. As a result of these three methods (\(\alpha = 0.5\)), the four communities are detected correctly. The calculation times are shown in Table 1. Our method is quite faster than other two methods.

Table 1 Calculation times
Full size table

In order to examine the impact of \(p_{1}\) and \(p_{2}\), we detect communities in signed networks where we set one parameter as 0.05 and change the other from 0.05 to 0.5. 10 signed networks are generated for each state. We use our method where \(\alpha = 0.2, 0.5, 0.8\) and examine the accuracy of detected communities, which is evaluated by NMI (Normalized Mutual Information) [2].

Fig. 4
figure 4

Results when \(p_{1}\) is changed

Full size image

Figure 4 shows the result when \(p_{2}\) is fixed and \(p_{1}\) is changed, and Fig. 5 shows the result when \(p_{1}\) is fixed and \(p_{2}\) is changed. X-axis is the value of \(p_{1}\)(or \(p_{2}\)), and y-axis is the value of NMI. When \(\alpha \) is large, the value of NMI is also large, but when \(\alpha \) is small, the value of NMI is small.

When \(\alpha \) is small, the negative edges between communities are more focused. The density of positive edge in the answer community is less important than when \(\alpha \) is larger. As a result, it becomes hard to agglomerate a pair within the answer community.

Besides, when \(p_{1}\) (noise rate within the answer community) is large, the value of NMI is relatively larger than the result when \(p_{2}\) (noise rate between answer communities) is large. When \(p_{2}\) is large, the number of positive edges between answer communities increases. Therefore, the chance of agglomeration between answer communities is raised. As a result, detected communities become different from the correct answer, and the value of NMI becomes small.

Fig. 5
figure 5

Results when \(p_{2}\) is changed

Full size image

5.2 Real-World Networks

We use three real-world signed networks for our experiments. Each data can be obtained from Stanford Large Scale Network Dataset (http://snap.stanford.edu/data/index.html) [6]. Original networks are directed signed networks, but we ignore edge direction in our experiments. In addition, we remove nodes with degree 1, so degrees of all nodes are 2 or more. We used the datasets of Wikipedia (4,786 nodes, 76,607 positive edges and 21,849 negative edges), Slashdot (47,726 nodes, 329,873 positive edges and 110,050 negative edges), and Epinions (60,332 nodes, 535,303 positive edges and 109,040 negative edges).

Fig. 6
figure 6

The value of Eq. (26) (red line) and Eq. (27) (blue dotted line) in Epinions

Full size image

We detect communities from these signed networks while changing \(\alpha =0.1,0.2,\ldots ,0.9\). The average calculation time in Wikipedia is 70 s, in Slashdot is 4,800 seconds, in Epinions is 6,500 s. The result of these calculation times show that our optimization method based on CNM is effective for large-scale signed networks which have tens of thousands of nodes and several hundreds of thousands of edges.

The property of positive and negative edges for each \(\alpha \) in Epinions is shown. In Fig. 6, the value of Eq. (26) is represented by continuous line.

$$\begin{aligned} \frac{1}{2m^{+}}\sum _{ij} A^{+}_{ij} (1-\delta (c_{i},c_{j})) \end{aligned}$$
(26)

Equation (26) shows the fraction of positive edges between communities. Therefore, the result is good for positive edges if this value is small.

In Fig. 6, the value of Eq. (27) is represented by dotted line.

$$\begin{aligned} \frac{1}{2m^{-}}\sum _{ij} A^{-}_{ij} \delta (c_{i},c_{j}) \end{aligned}$$
(27)

Equation (27) shows the fraction of negative edges within communities. Therefore, the result is good for negative edges if this value is small.

Fig. 7
figure 7

Fraction of negative edges connected to the largest community

Full size image
Fig. 8
figure 8

Fraction of positive edges connected to the largest community

Full size image

In Fig. 6, when \(\alpha \) is small, the number of positive edges between communities is large but within communities is small. On the other hand, when \(\alpha \) is large, the number of negative edges within community is large but between communities is small.

In addition, Figs. 7 and 8 are about fraction of positive and negative edges connected to the largest community in each result. X-axis is the value of \(\alpha \). Y-axis of Fig. 7 is fraction of negative edges connected to the largest community and y-axis of Fig. 8 is fraction of positive edges connected to the largest community.

In Fig. 7, when \(\alpha \) is small, the largest community tends to gather a lot of negative edges, but when \(\alpha \) is large, it does not gather a lot. On the other hand, in Fig. 8, when \(\alpha \) is small, the largest community tends to gather a lot of positive edges, but when \(\alpha \) is large, it does not gather a lot. Figures 7 and 8 show foes will be placed in different communities, but friends also will be placed in different communities when \(\alpha \) is small. In contrast, friends will be placed in the same community, but foes also will be placed in the same community.

From these results, when \(\alpha \) is small, the number of negative edges within communities is small and between communities is large. It is a good community structure in terms of negative edges. When \(\alpha \) is large, the number of positive edges within communities is large and between communities is small. It is a good community structure in terms of positive edges. Certainly, the parameter \(\alpha \) we introduce works as our intention.

In modularity by Gomez et al., they fix \(\alpha \) to the fraction of positive edges. Generally, in most real world signed networks, the number of positive edges is more than the number of negative edges. Thus, community detection with their modularity will be biased for the result which allows negative edges within communities. According to Traag et al. [12], it is difficult to determine the optimal value of \(\alpha \). It depends on network structure and characteristics required for community structure. Therefore, in order to try several experiments with values of \(\alpha \), the fast optimization method proposed in this paper is important.

We also examine the difference between the result where negative edges are ignored and the results where negative edges are considered. Figure 9 is about the largest community in Wikipedia with \(\alpha =1\) (negative edges are ignored) and communities with \(\alpha =0.5\). Most of nodes in the largest community with \(\alpha =1\) are split into the members of two communities with \(\alpha =0.5\). There are 9,612 positive edges (12.5% of positive edges) and 4,432 negative edges (20.3% of negative edges) between them. Because there are a lot of negative edges between them, they might be hostile each other. However, they are regarded as members of a community when negative edges are ignored. Therefore, both types of edges should be considered appropriately. By adjusting the value of \(\alpha \), we can detect inner factions within communities.

Fig. 9
figure 9

The largest community with \(\alpha =1\) and communities with \(\alpha =0.5\) (wikipedia)

Full size image

6 Conclusion

We have extended signed modularity and CNM in order to detect communities in large-scale signed networks. We detect communities in synthetic signed networks by our method and examined the relationship between \(\alpha \) in our modularity and positive and negative edges in the resultant communities. From the result of real world signed networks, we can say that our method is effective also for large-scale signed networks.