Community Detection Based on Regularized Semi-Nonnegative Matrix Tri-Factorization in Signed Networks

Abstract

Community detection is a fundamental task in the social network analysis field, which is beneficial for many real-world applications such as recommendation systems and telephone fraud detection. Community detection in unsigned networks has been extensively studied, however, few works focus on community detection in signed networks. Under this background, we propose a framework based on regularized semi-nonnegative matrix tri-factorization which maps the signed network from high-dimensional space to low-dimensional space, such that the communities of the signed network can be derived. In addition, to improve the detection accuracy, we introduce a graph regularization to distribute the pair of nodes which are connected with negative links into different communities. The experimental results on both synthetic datasets and real-world datasets verify the effectiveness of the proposed method.

1 Introduction

Community structure is a prominent feature of social networks. Community detection is a fundamental task in the Social Network Analysis (SNA) field that helps us understand the rganizational structure and functional components of a social network [1]. It also promotes other SNA tasks such recommendation systems [1]. Recommendation system is usually based on the users’ past preferences, while community detection provides complementary information for it by deriving user communities. For example, if a community whose users have similar requirements and interests is detected, the telecommunications operator can recommend relevant services to a user according to the subscribed services of other users in the same community, so that better recommendations are made. Moreover, community detection has been applied to some real-world missions [2,3,4]. In the against telephone fraud missions, community detection helps to identify fraudster groups. According to the communication records and other online activities of a suspect, community detection helps the police to have a rough idea of the suspected fraudster group. Besides, in the against terrorism missions, community detection together with other SNA technics plays an important role in terrorist organization identification. Thus, community detection has attracted many attentions.

Various methods have been developed to capture the network structural characteristics during the past years, however, most of them can only deal with networks with only positive links, i.e., unsigned networks [5,6,7]. While many complex systems in the real world are represented by networks with both positive and negative links, i.e., signed networks. The relationships between users in some real-world systems are various, including not only positive relations like friendships, trusts and likes, but also negative relations like antagonisms, distrusts and dislike. For example, we have both contact list and black list in the telephone address book. These systems are modeled as signed networks, whose positive links represent positive relations and negative links represent negative relations [8]. Kunegis et al. [9] shows that negative links have a significant influence on the structure of the social network. However, the existing algorithms developed for unsigned networks cannot handle negative links [10], thus, mining signed networks is still a young field which needs further and separate efforts.

In the unsigned network, a community can be defined as a group of nodes that contact with each other more frequently than with those outside the group [11]. While in the signed network, not only the density of links but also the signs of links are considered. Two principles are developed: (1) within communities the links should be positive and dense and (2) between communities the links should be negative [12]. Community detection in the signed network is to find out antagonistic communities so that entities within the same community have a positive relationship with each other and entities in different communities have a negative relationship with each other. The existence of negative links exerts great challenges on mining communities in signed networks. The negative links may have a stronger influence on the community structure. In other words, a negative link indicates that the connected users have a high probability to belong to different communities while a positive link may not indicate a high probability of the same belongingness. Besides, the real-world systems are often complex, it is natural to have some positive links between communities and some negative links within communities. Thus, how to properly retain or disregard some positive and negative links to find out the communities accurately is a problem. Furthermore, most existing community detection algorithms designed for unsigned networks can only deal with positive links, methods for signed networks are needed. Some strategies based on graph partition have been proposed which solve two optimizations: maximizing the positive links in communities and maximizing the negative links across communities. However, the community detection accuracy is not high.

Keeping the intrinsic properties of communities in the signed network in mind, in this paper we propose a community detection method based on Regularized Semi-Nonnegative Matrix tri-Factorization (ReS-NMF) which considers both link density and link signs. Furthermore, in order to improve the detection accuracy, we introduce a graph regularization to keep all the negative links between communities. The main contributions are summarized as follows:

• 1. We take into account of the mutual influences of positive and negative links in the signed network, build a latent space model to map the signed network from the high-dimensional space to the low-dimensional space, then derive the underlying communities in the new space.

• 2. We investigate the effects of the negative links on the structure of the network. In order to detect the communities more accurately, we introduce a graph regularization to distribute the pair of nodes which are connected by negative links into different communities. Furthermore, we enforce the sparsity constraints on the model to avoid overlapping distributions.

• 3. Experiments are carried out on both synthetic and real-world datasets, the results show the effectiveness of the proposed method.

The rest of this paper is organized below: Section 2 includes a brief review of the related work. The proposed framework is described in details in Section 3. Experimental results on both synthetic and real-world datasets are presented in Section 4. Finally, conclusions are provided in Section 5.

2 Related work

Some algorithms designed for the unsigned network have been extended to derive communities in the signed network. Wu et al. [13] investigated the impacts of the negative links on the network structure and examined the patterns in the spectral space of the adjacency matrix. Kunegis et al. [14] extended the spectral clustering algorithm to deal with negative links by developing the signed graph Laplacian matrix. But it had been proved to have a theoretical weakness when it was extended from 2-way to k-way (k > 2) clustering problem [15]. Anchuri et al. [16] extended modularity [17] to signed modularity to evaluate the quality of community partitions in the signed network. There are also multiobjective optimization based methods developed. In paper [16], Anchuri et al. proposed frustration to access community quality which was defined as the sum of the negative links inside the communities and positive links across communities. The communities were detected by minimizing the frustration. Doreian et al. [8] developed an objective function which is similar to the frustration except that it worked out the weighted sum. In the detection process, the nodes were first randomly distributed to k communities, then the above objective function was optimized by reallocating the nodes to more proper communities. Liu et al. [18] designed two objective functions based on the signed similarity and the natural contradiction between positive and negative links, and developed a multiobjective evolutionary algorithm. The algorithm could handle large-scale signed networks and detect overlapping communities directly. Amelio et al. [19] proposed a multiobjective framework based on genetic algorithm, where the first objective was modularity maximization, and the second was frustration minimization. The multiobjective genetic algorithm evolved a population of candidate solutions by trying to obtain the best trade-off between high modularity and low frustration. Chiang et al. [15] proposed positive ratio cut and negative ratio association to detect communities in the signed network. The positive ratio cut objective was to minimize the positive links between communities relative to the community size, and the negative ratio association objective was to minimize the negative links within each community relative to its size. Some model-based methods also have been proposed. Chen [20] proposed a signed probabilistic mixture model to derive overlapping communities in the signed network. The model generated positive and negative links with different probabilities, and provided soft memberships which indicated the strength of a node belonging to a community. Yang et al. [21] proposed an FEC framework based on random walk model which could be applied to detect communities in both unsigned and signed networks. FEC adopted an agent-based heuristic method, it included two phases - (1) the FC phase computed the transition probability vector and sorted them for each row via random walks, and (2) the EC phase utilized a cutoff criterion to divide the transformed adjacency matrix into two block matrices, which corresponded to two subgraphs. One of the subgraphs was the identified community, and the other was to be processed recursively by the above two phases.

There are some shortcomings in the above methods: (1) The community detection accuracy needs to be improved, more effective and robust methods are needed. (2) Most of them deal with positive and negative links separately by solving the above mentioned objectives, neglecting the mutual influence of positive and negative links. In this paper, we develop a variant of Non-negative Matrix Factorization (NMF) to approximate the adjacency matrix of the signed network with low-dimensional matrices, so that communities can be detected in the latent space. NMF [22] is a popular matrix factorization method where all the elements are restricted to be nonnegative, it performs well in the SNA field [11, 23]. As NMF is limited to deal with matrix with nonnegative matrices, Ding et al. [24] proposed a semi-NMF algorithm which did not require the matrix to be nonnegative, extended the application of NMF ideas. Semi-NMF has been applied to address issues such as nonlinear unmixing of hyperspectral data analysis [25] and motion segmentation [26], achieving good performances. Based on the idea of semi-NMF, we propose semi-Nonnegative Matrix Tri-Factorization (semi-NMTF) to factorize the adjacency matrix of the signed network, map the original network to a low-dimensional space where the underlying structure information is more explicit and clear. Moreover, we introduce a graph regularization to enhance the detection accuracy. And we develop the iterative algorithm to discover communities in the signed network.

3 ReS-NMF framework for community detection in signed networks

In this section, we introduce the definition and main symbols used in this paper, and then describe the proposed method in details.

3.1 Notations

The symbols used in this paper are shown in Table 1. Given a signed network with n nodes which are grouped into k communities. The topology is represented by the adjacency matrix A ∈ R ^n×n where A _{i j} = 1, A _{i j} = −1, and A _{i j} = 0 denote a positive link, a negative link and no link between node i and node j respectively. The matrix A ^p ∈ R ^n×n represents a positive network where $A_{ij}^{p}=1$ denotes a positive link between node i and node j and $A_{ij}^{p}=0$ otherwise. Similarly, A ⁿ ∈ R ^n×n is used to represent a negative network where $A_{ij}^{n}=1$ denotes a negative link and $A_{ij}^{n}=0$ otherwise. It is easy to convert one representation into the other representation with the following rules: A = A ^p − A ⁿ, $A^{p}=\frac {|A|+A}2$, $A^{n}=\frac {|A|-A}2$. The matrix $H\in R_{+}^{n\times k}$ is the community indicator whose element H _{i j} denotes the probability that node i belongs to j-th community. The matrix S ∈ R ^k×k is the association matrix indicating the relationships between communities.

Table 1 Symbol definitions

3.2 Problem statement

With the notations given above, the community detection problem in the signed network is formally defined as follows.

Problem 1

Given a signed network G = (V, E)with adjacency matrix A, positive adjacency matrix A ^p and negative adjacency matrix A ⁿ , find k communities {C ₁,..., C _k }with maximal positive links within communities and maximal negative links across communities, i.e., $\max {\sum }_{ij}A_{ij}^{p}\delta (c_{i},c_{j})$ and $\max {\sum }_{ij}A_{ij}^{n}(1-\delta (c_{i},c_{j}))$ , where δ(c _i , c _j )is the Kronecker delta function which is 1 if node i and node j belong to the same community, 0 otherwise.

The problem is NP-hard, we attempt to solve it by building a latent space model. In the model, a variant of semi-NMF to approximate the adjacency matrix is developed, which maps the network into a low-dimensional space to make the underlying structure information explicit. Besides, we introduce a graph regularization to minimize the number of negative links inside each community, so that negative links between communities are maximized.

3.3 Proposed method

In this subsection, the proposed framework Res-NMF is presented in details.

In paper [24], the 2-factor semi-NMF, i.e., A ≈ F H ^T, was proposed where only H is restricted to be nonnegative, it has been proved useful to capture node similarity and mutual influences between links. However, 2-factor factorization only captures limited features, while 3-factor factorization can capture relations between communities and analyze the network more precisely. Then we propose semi-NMTF to approximate the adjacency matrix of the signed network, i.e., A ≈ H S H ^T, where $H\in R_{+}^{n\times k}$ is the community indicator and S ∈ R ^k×k is the community relationship indicator. The element H _{i j} is nonnegative which denotes the likelihood that node i belongs to the j-th community. If node i belongs to the j-th community, H _{i j} = 1, otherwise, H _{i j} = 0. The positive element S _{i j} of S denotes the positive relationship between i-th community and j-th community, similarly, the negative element denotes the negative relationship. The proposed semi-NMTF is written as follows:

$$ \underset{H\in R^{n\times k}, S\in R^{k\times k}}{\min} \|A-HSH^{T}\|_{F}^{2} ~~s.t.H_{ij}\in\{0,1\}, $$

(1)

where A is the adjacency matrix of the signed network, ∥⋅∥ _F denotes the matrix Frobenius norm which is defined as $\|A\|_{F}=\sqrt {{\sum }_{i=1}^{m}{\sum }_{j=1}^{n}|A_{ij}|^{2}}$.

Besides, the negative links have substantial influence on the community structure. In order to keep negative links between communities, we introduce a graph regularization to minimize the number of negative links inside each community relative to its size. In particular, the regularization is defined as follows:

$$ \min\sum\limits_{j=1}^{k}\frac{{h_{j}^{T}} A^{n} h_{j}}{{h_{j}^{T}} h_{j}}, $$

(2)

where A ⁿ is the adjacency matrix of a negative network, h _j is the j-th vector of matrix H and H = [h ₁;…;h _k ]. The regularization enforces the nodes connected with negative links to be distributed into different communities, then the goal of keeping negative links between communities dense can be achieved.

Because the above optimization problems are NP-hard [1], in this paper, we solve this problem with some relaxations. Suppose the indicator H has the following form:

$$ H_{ij} = \left\{\begin{array}{ll} \sqrt{1/\pi_{j}}~, & node~i\in\pi_{j}\\ 0~, & otherwise \end{array}\right. ~, $$

(3)

where |π _j | is the number of nodes in the j-th community. Then the objective function (1) can be written as follows:

$$ \underset{H\in R^{n\times k}, S\in R^{k\times k}}{\min} \|A-HSH^{T}\|_{F}^{2} ~~s.t.H_{ij}\geq 0, \forall i, j. $$

(4)

Moreover, we observe that $tr(H^{T}A^{n}H)={\sum }_{j=1}^{k}\frac {{h_{j}^{T}} A^{n} h_{j}}{{h_{j}^{T}} h_{j}}$. Then the solution to the optimization problem (2) can be obtained by addressing the following optimization problem:

$$ \underset{H\in R^{n\times k}}{\min}tr(H^{T}A^{n}H)~~s.t.H_{ij}\geq 0, \forall i, j. $$

(5)

Furthermore, in order to make the node try its best to belong to only one community, we introduce l ₁ norm ${\sum }_{j=1}^{n}\|H(j,:)\|_{1}^{2}$ to control the sparsity of the model.

Combining the regularizations into semi-NMTF, the final optimization objective we develop is defined as Formula (6):

$$ \begin{array}{l} \underset{H\in R^{n\times k}, S\in R^{k\times k}}{\min} \|A-HSH^{T}\|_{F}^{2}+\gamma_{1}tr(H^{T}A^{n}H)\\ +\gamma_{2}{\sum}_{j=1}^{n}\|H(j,:)\|_{1}^{2}~~s.t.H_{ij}\geq 0, \forall i, j \end{array} ~, $$

(6)

where γ ₁, γ ₂ are parameters to control the weights of the regularization terms.

3.4 The updating rules

In this section, we discuss how to solve the optimization problem (6). The optimal solution can be achieved using the iterative update algorithm we develop. We define a matrix N _k×k whose elements are 1, let α be the Lagrange matrix for constraint H ≥ 0, then the Lagrangian function can be written as:

$$ \begin{array}{ll} L &=\|A-HSH^{T}\|_{F}^{2}+\gamma_{1}tr(H^{T}A^{n}H)\\ &~+\gamma_{2}{\sum}_{j=1}^{n}\|H(j,:)\|_{1}^{2}-\alpha H \\ &=tr((A-HSH^{T})(A-HSH^{T})^{T})\\ &~+\gamma_{1}tr(H^{T}A^{n}H) +\gamma_{2}tr(HNH^{T})-\alpha H \\ &=-2tr(AHS^{T}H^{T})+tr(HSH^{T}HS^{T}H^{T})-\alpha \\ &~+tr(AA^{T})+\gamma_{1}tr(H^{T}A^{n}H)+\gamma_{2}tr(HNH^{T}) \end{array} . $$

(7)

Then the derivatives of L with respect to H and S are:

$$ \frac{\partial L}{\partial S}=-2H^{T}AH+2H^{T}HSH^{T}H~, $$

(8)

$$ \frac{\partial L}{\partial H}=-4{\Phi}_{1}+4H{\Phi}_{2}+2\gamma_{1}A^{n}H+2\gamma_{2}HN-\alpha~, $$

(9)

where Φ₁ = A H S ^T, Φ₂ = S H ^T H S. Using the KKT conditions that α H = 0, and according to methods in [16], the updating rules are shown as follows:

$$ S\leftarrow (H^{T}H)^{-1}H^{T}AH(H^{T}H)^{-1}~, $$

(10)

$$ H_{ij}\leftarrow H_{ij}\sqrt{\frac{(2{\Phi}_{1}^{+} +2H{\Phi}_{2}^{-})_{ij}}{(2{\Phi}_{1}^{-} +2H{\Phi}_{2}^{+} +\gamma_{1}A^{n}H+\gamma_{2}HN)_{ij}}}~, $$

(11)

where $X_{ij}^{+}=(|X_{ij}|+X_{ij})/2$, $X_{ij}^{-}=(|X_{ij}|-X_{ij})/2$.

With the above updating rules, the optimization algorithm is presented in Algorithm 1. Note that we update one matrix while fixing the other matrices in each step and the iterative process is stopped if these cluster matrices converge or the number of iterative reaches a given threshold.

4 Experiments

In this section, we evaluate the effectiveness of the proposed algorithm in detecting communities from signed social networks. Experiments are carried out on both synthetic and real-world datasets.

4.1 Evaluation measures and baseline methods

In this paper, we apply Normalized Mutual Information (NMI) [27], Purity [28] and Signed Modularity [29] to evaluate the performances of different algorithms. Both NMI and Purity adopt the ground truth as a baseline, the values of the two measures range from 0 to 1 and higher value means better performance. Signed Modularity measures the quality of the derived community structure from the perspective of how far it deviates from a random network, the larger value it is, the stronger the strength of community structure is.

NMI estimates the similarity between the ground truth communities and the detected. Let C and G denote our partition the ground truth respectively, F be the confusion matrix whose element F _{i j} is the number of nodes in community i of the partition C that are also in the community j of the partition G, then NMI is defined as follows:

$$ NMI=\frac{-2{\sum}_{i=1}^{f_{C}}{\sum}_{j=1}^{f_{G}}F_{ij}\log(F_{ij}n/F_{i\cdot}F_{\cdot j})}{{\sum}_{i=1}^{f_{C}}F_{i\cdot}\log(F_{i\cdot}/n)+{\sum}_{j=1}^{f_{G}}F_{\cdot j}\log(F_{\cdot j}/n)}, $$

(12)

where f _C (f _G ) is the number of communities in the partition C(G), F _i⋅(F _⋅j ) is the sum of the elements of F in row i (column j), and n is the number of nodes. If C = G, N M I = 1. If C and G are completely different, N M I = 0.

Purity is measured by computing the number of nodes assigned with the same labels in all communities. Let G = G ₁,..., G _k be the set of communities in the ground truth and G = C ₁,..., C _t be the t communities extracted by different approaches. Purity is defined as:

$$ Purity=\frac{1}{n}\sum\limits_{i=1}^{t}\underset{j}{\max}|C_{i}\cap G_{j}|~, $$

(13)

where n is the number of nodes.

The original Modularity Q is designed for unsigned networks [17], it is defined as the probability of having links falling within communities in the networks minus the expected probability in an equivalent network with the same number of nodes, and links placed at random preserving the nodes degree. However, Q cannot deal with negative links. Gmez et al. [29] developed Signed Modularity as follows:

$$ Q_{s}=\frac{1}{2{\kern-.3pt}w^{+} \!{\kern-.3pt}+{\kern-.3pt}\! 2{\kern-.3pt}w^{-}}\!\sum\limits_{i}\!\sum\limits_{j}\!\left[\!w_{ij}\!{\kern-.5pt}-{\kern-2.5pt}\!\left( \!\frac{w_{i}^{+}{\kern-.75pt}w_{j}^{+}}{2w^{+}}\!{\kern-.5pt}-{\kern-.5pt}\!\frac{w_{i}^{-}{\kern-.75pt}w_{j}^{-}}{2{\kern-.5pt}w^{-}}\!\right)\!\!\right]\!,\delta({\kern-.3pt}c_{i}{\kern-.5pt},{\kern-.75pt} c_{j}{\kern-.4pt}) $$

(14)

where $w_{i}^{+}\left (w_{j}^{+}\right )$ denotes the sum of all positive weights of node i(j), and $w_{i}^{-}(w_{j}^{-})$ represents the sum of all negative weights of node i(j). Besides w ⁺(w ⁻) denotes total positive (negative) strength. If nodes i and j are in the same community, δ(c _i , c _j ) = 1, otherwise, δ(c _i , c _j ) = 0. Normally the larger the value of Q _s is, the better the separation of the community structure is.

In order to measure the effectiveness of ReS-NMF framework, three existing community detection methods for signed networks, i.e., the signed spectral clustering algorithm [14] and FEC algorithm [21], and MEAs-SN algorithm [18] are compared in our experiments.

In peper [14], a signed variant of the graph Laplacian is proposed, then the signed spectral clustering algorithm is developed based on it. In the method, the top k eigenvectors of signed Laplacian matrix associated with the signed network are calculated, then k-means is applied to the eigenvectors to obtain disjoint partitions of the network.

FEC is proposed in [21], it regards the sign and the density of relations as the clustering attributes. The method adopts an agent-based approach for formulating the communities. It contains two main phases: (1) the FC phase transforms the adjacency matrix to compute their transition probability vector and sorts them for each row and (2) the EC phase applies a cutoff criterion to the transformed adjacency matrix and divides it into two block matrices, which correspond to two subgraphs. One of these subgraphs is the identified community, and the other is the matrix to be processed recursively following the above mentioned two phases.

MEAs-SN is a multiobjective evolutionary algorithm proposed in [18], it models community detection problem as a multiobjective problem considering both link density and signs. In the method, signed similarity is extended from the original similarity based on the social balance theory so that it can deal with the negative links. Two objectives are optimized together, one is target to put all positive links in communities while the other is target to keep all negative links between communities.

4.2 Experimental results on synthetic datasets

We first validate ReS-NMF on synthetic datasets. We apply the LFR benchmark to generate synthetic networks for community detection. The LFR benchmark is declared to support some main statistical properties of the real networks. The details of the synthetic networks are shown in Table 2, where DS denotes the datasets, N denotes the number of nodes, PL and NL denote the number of positive links and negative links respectively, and C denotes the number of communities.

Table 2 Details of the synthetic networks

The scores of NMI, Purity and Signed Modularity for different methods on five synthetic datasets are presented in Table 3. Note that all experiment results are averaged over 100 runs. From the results shown in the table, some conclusions can be drawn.

Table 3 NMI, Purity and Signed Modularity for four methods on five datasets, bold emphasis represents the best results

It is evident that the proposed ReS-NMF algorithm performs best among all the methods on all the synthetic datasets. For example, in terms of Network 1, our method can gain more than 78%, 44% and 2% improvements on NMI respectively, over 4%, 5% and 8% improvements on Purity respectively, and nearly 17%, 9% and 9% improvements on Signed Modularity, compared with signed spectral clustering algorithm, FEC algorithm and MEAs-SN algorithm. Furthermore, let us pay attention to Network 2 and Network 3 whose generator parameters are the same apart from mu. With higher mu, the network structure is more fuzzy and the communities are more difficult to detect. It can be observed that our method has a better performance than the others and the performance does not deteriorate as mu increases. Network 4 and Network 5 have more nodes and links than the other networks, and the structures are more complex. It can be seen that on the three evaluation metrics, ReS-NMF also performs better than the other methods. The reasons may be as follows: (1) The ReS-NMF framework maps the signed networks into a low-dimensional space, makes the implicit structures clear in the latent space. (2) The graph regularization contributes to distribute the nodes connected with negative links into correct communities, reducing the wrong partitions.

4.3 Experimental results on real-world datasets

In this subsection, we evaluate ReS-NMF method on real-world datasets. Two widely used real-world signed networks, i.e., the Slovene Parliamentary Party network and the Gahuku-Gama Subtribes network, are employed to validate the effectiveness of our method. Moreover, although ReS-NMF is designed for signed networks, it can also be used to unsigned networks. Therefore, two popular unsigned benchmark networks, the Zachary karate club network and the Dolphin network, are tested.

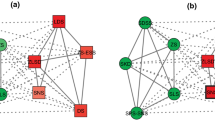
The Slovene Parliamentary Party network describes the relations between ten parties of the Slovene Parliamentary in 1994 [30]. Positive links mean that two parties’ activities are similar, while negative links mean their activities are dissimilar. Figure 1a shows the original topological structure, and the community structure derived by ReS-NMF is shown in Fig. 1b. As can be seen, all parties are separated into two opponent communities. Note that this result is the same as that given by Kropivnik and Mrvar [30].

Fig. 1

a Topological structure of the Slovene Parliamentary Party network. b Community structure obtained by ReS-NMF. In the figures, the thick edges between nodes represent positive links while the thin edges represent negative links. Different node colors in b correspond to different communities

The Gahuku-Gama Subtribes dataset contains 16 tribal groups of the Eastern Central Highlands in New Guinea, the relations between tribal groups can be friendly or antagonistic [31] which are denoted by positive or negative links respectively. The 16 tribal groups are distributed into 3 communities in reality. Figure 2a presents the original topological structure, and the communities obtained by ReS-NMF are shown in Fig. 2b. The community detection result is identical to that in reality.

Fig. 2

a Topological structure of the Gahuku-Gama Subtribes network. b Community structure obtained by ReS-NMF. In the figures, the thick edges between nodes represent friendship while the thin edges represent antagonism. Different node colors in b correspond to different communities

Then we further evaluate the effectiveness of ReS-NMF on unsigned networks. Figure 3 shows the communities found by ReS-NMF for the Zachary karate club network and the Dolphin network. As can be seen, the Zachary karate club network and the dolphin network are divided into two and four communities respectively. The community structures found are meaningful and identical to those in reality.

Fig. 3

a Community structure found by ReS-NMF for Zachary karate club network. b Community structure obtained by ReS-NMF for Dolphin network. Different node colors correspond to different communities

4.4 Parameter study

In this section, we evaluate ReS-NMF in terms of its sensitivity to the regularization parameters γ ₁ and γ ₂. The datasets we use include Network 2 and the Slovene Parliamentary Party network. We systematically test the effect of γ ₁ and γ ₂, where γ ₁ increases from 0.1 to 10 and γ ₂ increases from 0.1 to 8. For each combination of the two parameters, 50 independent runs of ReS-NMF are conducted, and the averaged NMI, Purity and Signed Modularity are shown in Fig. 4.

Fig. 4

Parameter sensitivity evaluation on Network 2 dataset and Slovene Parliamentary Party network

We note that γ ₂ is fixed, with the increase of γ ₁, the performance of ReS-NMF on Network 2 first increases. When γ ₁ > 2, ReS-NMF keeps a relatively stable performance, and when γ ₁ > 8, the values of NMI, Purity and Signed Modularity drop a little. With the fixed γ ₁, we observe that with the increase of γ ₂, the performance on Network 2 first increases correspondingly, when γ ₂ > 4, the performance is relatively stable. It can be observed that our method is relatively stable on γ ₁ and γ ₂ across a wide range. Then we test ReS-NMF on Slovene Parliamentary Party network, across all the values of γ ₁ and γ ₂ in the experiment, the values of NMI and Purity keep to be 1, and Signed Modularity also has stable score. This is because without the help of the regularizations, semi-NMTF can extract the communities of this network accurately. From Fig. 4 we can see that ReS-NMF achieves relatively stable and outstanding performances, and is not sensitive to the regularization parameters.

5 Conclusions

In this paper, we develop a ReS-NMF community detection algorithm for signed networks. The ReS-NMF algorithm captures communities by mapping the signed network into a latent space, moreover, improves the detection accuracy by studying the effects of negative links and enforcing the sparsity constraints on the indicator matrix. Experiments on both synthetic data and real-world data all demonstrate that ReS-NMF has better performance and regularization parameter sensitivity compared with other algorithms. For the future work, we plan to design faster algorithm for regularized matrix factorization.