Hide the Modulus: A Secure Non-Interactive Fully Verifiable Delegation Scheme for Modular Exponentiations via CRT

Abstract

Security protocols using public-key cryptography often requires large number of costly modular exponentiations (MEs). With the proliferation of resource-constrained (mobile) devices and advancements in cloud computing, delegation of such expensive computations to powerful server providers has gained lots of attention. In this paper, we address the problem of verifiably secure delegation of MEs using two servers, where at most one of which is assumed to be malicious (the OMTUP-model). We first show verifiability issues of two recent schemes: We show that a scheme from IndoCrypt 2016 does not offer full verifiability, and that a scheme for n simultaneous MEs from AsiaCCS 2016 is verifiable only with a probability 0.5909 instead of the author’s claim with a probability 0.9955 for $n=10$. Then, we propose the first non-interactive fully verifiable secure delegation scheme by hiding the modulus via Chinese Remainder Theorem (CRT). Our scheme improves also the computational efficiency of the previous schemes considerably. Hence, we provide a lightweight delegation enabling weak clients to securely and verifiably delegate MEs without any expensive local computation (neither online nor offline). The proposed scheme is highly useful for devices having (a) only ultra-lightweight memory, and (b) limited computational power (e.g. sensor nodes, RFID tags).

1 Introduction

Recent advances in mobile computing, internet of things (IoT), and cloud computing makes delegating heavy computational tasks from computationally weak units, devices, or components to a powerful third party servers (also programs and applications) feasible and viable. This enables weak mobile clients with limited memory and computational capabilities (e.g. sensor nodes, smart cards and RFID tags) to be able to utilize several applications of these technologies, which otherwise is difficult and often impossible because of underlying resource-intensive operations and consumption of considerable amount of energy.

Unlike fully homomorphic encryption, secure delegation of expensive cryptographic operations (like MEs modulo a prime number p) is the most practical option along with its little computational costs and applications for critical security applications. However, delegating MEs of the form $u^a\bmod p$ to untrusted servers while ensuring the desired security and privacy properties is highly challenging; i.e. either u or a, or even both (in most privacy enhancing applications), contain sensitive informations, thence required to be properly protected from untrusted servers. Beside these challenges, ensuring the verifiability of the delegated computation is very important. As also pointed out in [8, 11], failure in the verification of a delegated computation has severe consequences especially if the delegated MEs are the core parts of authentication or signature schemes.

Related Work. After the introduction of wallets with observers by Chaum and Pedersen [4], Hohenberger and Lysyanskaya [7] provided the first secure delegation scheme for group exponentiations (GEs) with a verifiability probability 1/2 using two servers, where at most one of them is assumed to be malicious (the OMTUP-model). They also gave the first formal simulation-based security notions for the delegation of GEs in the presence of malicious powerful servers. In ESORICS 2012, Chen et al. [5] improved both the verifiability probability (to 2 / 3) and the computational overhead of [7]. A secure delegation scheme for two simultaneous GEs with a verifiability probability 1/2 is also introduced in [5].

In ESORICS 2014, for the first time Wang et al. [13] proposes a delegation scheme for GEs using a single untrusted server with a verifiability probability 1/2. This scheme involves an online group exponentiation of a small exponent by the delegator; the choice of such a small exponent is subsequently shown to be insecure by Chevalier et al. [6] in ESORICS 2016. Furthermore, it is also shown in [6] essentially that a secure non-interactive (i.e. single-round) delegation with a single untrusted server requires at least an online computation of a GE even without any verifiability if the modulus p is known to the server. Kiraz and Uzunkol [8] introduce the first two-round secure delegation scheme for GEs using a single untrusted server having an adjustable verifiability probability requiring however a huge number of queries to the server. They also provide a delegation scheme for n simultaneous GEs with an adjustable verifiability probability. Cavallo et al. [2] propose subsequently another delegation scheme with a verifiability probability 1/2 again by using a single untrusted server under the assumption that pairs of the form $(u,u^{x})$ are granted at the precomputation for variable base elements u. However, realizing this assumption is difficult (mostly impossible) for resource-constrained devices. In AsiaCCS 2016, Ren et al.[11] proposed the first fully verifiable (with a verifiability probability 1) secure delegation scheme for GEs in the OMTUP-model at the expense of an additional round of communication. They also provide a two-round secure delegation scheme for $n\in \mathbb {Z}^{>1}$ simultaneous GEs which is claimed to have a verifiability probability $1-\frac{1}{2n(n+1)}$.

Kuppusamy and Rangasamy use in INDOCRYPT 2016 [9] for the first time the special ring structure of $\mathbb {Z}_p$ with the aim of eliminating the second round of communication and providing full verifiability simultaneously. They propose a non-interactive efficient secure delegation scheme for MEs using Chinese Remainder Theorem (CRT) in the OMTUP-model which is claimed to satisfy full-verifiability under the intractability of the factorization problem. This approach is also used very recently by Zhou et al. [14] together with disguising the modulus p itself, also assuming the intractability of the factorization problem. They proposed an efficient delegation scheme with an adjustable verifiability probability using a single untrusted server. However, the scheme in [14] does not achieve the desired security properties.

Our Contribution. This paper has the following major goals:

• 1. We analyze two delegation schemes recently proposed at INDOCRYPT 2016 [9] and at AsiaCCS 2016 [11]:

  • (a) We show that the scheme in [9] is unfortunately totally unverifiable, i.e. a malicious server can always cheat the delegator without being noticed, instead of the author’s claim of satisfying the full verifiability.

  • (b) We show that the scheme for n simultaneous MEs in [11] does not achieve the claimed verifiability guarantees; instead of having the verifiability probability $1-\frac{1}{2n(n+1)}$, it only has the verifiability probability at most $1-\frac{n-1}{2(n+1)}$. For instance, it offers a verifiability probability at most $\approx 0.5909$ instead of the author’s claim in [11] offering a verifiability probability $\approx 0.9955$ for $n=10$.

• 2. We propose the first non-interactive fully verifiable secure delegation scheme $\mathsf{HideP}$ for MEs in the OMTUP-model by disguising the prime number p via CRT. $\mathsf{HideP}$ is not only computationally much more efficient than the previous schemes but requires also no interactive round, whence substantially reduces the communication overhead. In particular, hiding p enables the delegator to achieve both non-interactivity and full verifiability at the same time efficiently.

  Note that the delegator of MEs hides the prime modulus p from the servers, and not from a party intended to be communicated (i.e. a weak device (delegator) does not hide p with whom it wants to run a cryptographic protocol). In other words, it solely hides p from the third-party servers to which the computation of MEs is delegated.

• 3. We apply $\mathsf{HideP}$ to speed-up blinded Nyberg-Rueppel signature scheme [10].

We refer the readers to the full version of the paper [12] which provide a delegated preprocessing technique $\mathsf{Rand}$. It eliminates the large memory requirement and reduces substantially the computational cost of the precomputation step. The overall delegation mechanism (i.e. $\mathsf{HideP}$ together with $\mathsf{Rand}$) offers a complete solution for delegating the expensive MEs with full verifiability and security, whence distinguish our mechanism as a highly usable secure delegation primitive for resource-constrained devices.

2 Preliminaries and Security Model

In this section, we first revisit the definitions and the basic notations related to the delegation of MEs. We then give a formal security model by adapting the previous security models of Hohenberger and Lysyanskaya [7] and Cavallo et al. [2]. Lastly, an overview for the requirements of the delegation of a ME¹ is given.

2.1 Preliminaries

We denote by $\mathbb {Z}_m$ the quotient ring $\mathbb {Z}/m\mathbb {Z}$ for a natural number $m\in \mathbb {N}$ with $m>1$. Similarly, $\mathbb {Z}_m^*$ denotes the multiplicative group of $\mathbb {Z}_m$.

Let $\sigma$ be a global security parameter given in a unary representation (e.g. $1^{\sigma }$). Let further p and q be prime numbers with $q\mid (p-1)$ of lengths $\sigma _1$ and $\sigma _2$, respectively. The values $\sigma _1$ and $\sigma _2$ are calculated at the setup of a cryptographic protocol on the input of $\sigma$. Let $\mathbb {G}=<g>$ denote the multiplicative subgroup of $\mathbb {Z}_p^*$ of order q with a fixed generator $g\in \mathbb {G}$.

The process of running a probabilistic algorithm A, which accepts $x_1, x_2,\ldots$ as inputs, and produces an output y, is denoted by $y \leftarrow A(x_1, x_2, \ldots ).$ Let $(z_A, z_B, \mathsf {tr}) \leftarrow (A(x_1, x_2, \ldots ), B(y_1, y_2, \ldots ))$ denote the process of running an interactive protocol between an algorithm A and an algorithm B, where A accepts $x_1, x_2, \ldots$, and B accepts $y_1, y_2, \ldots$ as inputs (possibly together with some random coins) to produce the final output $z_A$ and $z_B$, respectively. We use the expression $\mathsf {tr}$ to represent the sequence of messages exchanged by A and B during protocol execution. By abuse of notation, the expression $y \leftarrow x$ also denotes assigning the value of x to a variable y.

Delegation Mechanism and Protocol Definition. We assume that a delegation mechanism consists of two types of parties called as the client (or delegator) $\mathcal {C}$ (trusted but resource-constrained part) and servers $\mathcal {U}$ (potentially untrusted but powerful part), where $\mathcal {U}$ can consist of one or more parties. Hence, the scenario raises if $\mathcal {C}$ is willing to delegate (or outsource) the computation of certain functions to $\mathcal {U}$. For a given $\sigma ,$ let $\mathsf {F}: \mathsf {Dom(F)} \rightarrow \mathsf {CoDom(F)}$ be a function, where $\mathsf {F}$’s domain is denoted by $\mathsf {Dom(F)}$ and $\mathsf {F}$’s co-domain is denoted by $\mathsf {CoDom(F)}.$ $\mathsf {desc(F)}$ denotes the description of $\mathsf {F}$. We have two cases for $\mathsf {desc(F)}$:

• 1. $\mathsf {desc(F)}$ is known to both $\mathcal {C}$ and $\mathcal {U}$, or

• 2. $\mathsf {desc(F)}$ is known to $\mathcal {C}$, and another description $\mathsf {desc(F')}$ is given to $\mathcal {U}$ such that the function $\mathsf {F}$ can only be obtained from $\mathsf {F}'$ if a trapdoor information $\tau$ is given. By abuse of notation, we sometimes write $\tau (\mathsf {F})=\mathsf {F}'$.

From now on, we concentrate on the second case since we propose a delegation scheme in this scenario. A client-server protocol for the delegated computation of $\mathsf {F}$ is defined as a multiparty communication protocol between $\mathcal {C}$ and $\mathcal {U}$ and denoted by $(\mathcal {C}(1^{\sigma }, \mathsf {desc(F)}, x,\tau ), \mathcal {U}(1^{\sigma }, \mathsf {desc(F')}))$, where the input x and the trapdoor $\tau$ are known only by $\mathcal {C}$. A delegated computation of the value $y = \mathsf {F}(x)$, denoted by

$$ (y_{\mathcal {C}} , y_{\mathcal {S}}, \mathsf {tr}) \leftarrow (\mathcal {C}(1^{\sigma }, \mathsf {desc(F)}, x,\tau ), \mathcal {U}(1^{\sigma }, \mathsf {desc(F')})),$$

which is an execution of the above client-server protocol using independently chosen random bits for $\mathcal {C}$ and $\mathcal {U}.$ At the end of this execution, $\mathcal {C}$ learns $y_{\mathcal {C}}=y,$ $\mathcal {U}$ learns $y_{ \mathcal {U}}$; and $\mathsf {tr}$ is the sequence of messages exchanged by A and B. Note that the execution may happen sequentially or concurrently. In the case of the delegation of MEs, the aim is to always have $y_{ \mathcal {U}}=\emptyset$.

Factorization Problem. We prove some security properties of the proposed scheme later by using the intractability of the factorization problem²: Given a composite integer n, where n is a product of two distinct primes p and q, the factorization problem asks to compute p or q. The formal definition is as follows:

Definition 1

(Factorization Problem) Let $\sigma$ be a security parameter given in unary representation. Let further $\mathcal {A}$ be a probabilistic polynomial-time algorithm. Let further the primes p and q, $p\ne q,$ are obtained by running a modulus generation algorithm $\mathsf {PrimeGen}$ on the input of $\sigma$ with $n=pq$. Run $\mathcal {A}$ with the input n. The adversary $\mathcal {A}$ wins the experiment if it outputs either p or q. We define the advantage of $\mathcal {A}$ as

$$\begin{aligned} \mathsf {Adv}^{\mathsf {Fact}}_{\mathcal {A}}(\sigma )= \mathsf {Prob} \left[ x = p\ or\ x = q : (n,p,q) \leftarrow \mathsf {PrimeGen}(1^{\sigma }) , x \leftarrow \mathcal {A}(n) \right] . \end{aligned}$$

2.2 Security Model

Hohenberger and Lysyanskaya provided first formal simulation-based security notions for secure and verifiable delegation of cryptographic computations in the presence of malicious powerful servers [7]. Different security assumptions for delegation of MEs can be summarized according to [7] as follows:

• One-Untrusted Program (OUP): There exists a single malicious program $\mathcal {U}$ performing the delegated MEs.

• One-Malicious version of a Two-Untrusted Program (OMTUP): There exist two untrusted programs $\mathcal {U}_1$ and $\mathcal {U}_2$ performing the delegated MEs but only one of them behaves maliciously.

• Two-Untrusted Program (TUP): There exist two untrusted programs $\mathcal {U}_1$ and $\mathcal {U}_2$ performing the delegated MEs and both of them may simultaneously behave maliciously, but they do not maliciously collude.

Cavallo et al. [2] gave a formal definition for delegation schemes by relaxing the security definitions first given in [7]. Although the simulation-based security definitions [7] intuitively include (whatever can be efficiently computed about secret values with the protocol’s view can also be efficiently computed without this view [6]) the most direct way of guaranteeing the desired secrecy and verifiability, its formalization is unfortunately highly complex and subtle. Therefore, simpler indistinguishability-based security definitions have been recently used both in [2] and in [6], which, in particular, include the fact that an untrusted server is unable to distinguish which inputs the other parties use.

In this section, we adapt the security definitions of [2] for our security requirements to the OMTUP-model of [7], i.e. the adversary is modeled by a pair of algorithms $\mathcal {A}=(\mathcal {E},\mathcal {U'})$, where $\mathcal {E}$ denotes the adversarial environment and $\mathcal {U}'=(\mathcal {U}_1',\mathcal {U}_2')$ is a malicious adversarial software in place of $\mathcal {U}=(\mathcal {U}_1,\mathcal {U}_2)$, where exactly one of $(\mathcal {U}'_1,\mathcal {U}'_2)$ is assumed to be malicious. In the OMTUP-model we have the fundamental assumption that after interacting with $\mathcal {C}$, any communication between $\mathcal {E}$ and $\mathcal {U}'_1$ or between $\mathcal {E}$ and $\mathcal {U}'_2$ pass solely through the delegator $\mathcal {C}$ [7].

Completeness. If the parties ($\mathcal {C}$,$\mathcal {U}_1$ and $\mathcal {U}_2$) executing the scheme follow the scheme specifications, then $\mathcal {C}'$s output obtained at the end of the execution would be equal to the output obtained by evaluating the function $\mathsf {F}$ on $\mathcal {C}$. The following is the formal definition for completeness:

Definition 2

For the security parameter $\sigma ,$ let $(\mathcal {C}, \mathcal {U}_1, \mathcal {U}_2)$ be a client-server protocol for the delegated computation of a function $\mathsf {F}.$ We say that $(\mathcal {C}, \mathcal {U}_1, \mathcal {U}_2)$ satisfies completeness if for any x in the domain of $\mathsf {F}$, it holds that

$$\mathsf {Prob}[(y_{\mathcal {C}} , y_{\mathcal {S}}, \mathsf {tr}) \leftarrow (\mathcal {C}(1^{\sigma }, \mathsf {desc(F)}, x), \mathcal {U}_i(1^{\sigma }, \mathsf {desc(F')}): y_{\mathcal {C}}= \mathsf {F}(x)] =1. $$

Verifiability. Verifiability means informally that if $\mathcal {C}$ follows the protocol, then the malicious adversary $\mathcal {A}=(\mathcal {E},\mathcal {U}'_i)$, $i=1$ or $i=2$, cannot convince $\mathcal {C}$ to obtain some output $y'$ different from the actual output y at the end of the protocol. The model let further the adversary choose $\mathcal {C}'$s trapdoored input $\tau (\mathsf {F}(x))$ and take part in exponential/polynomial number of protocol executions before it attempts to convince $\mathcal {C}$ with incorrect output values (corresponding to the environmental adversary $\mathcal {E}$).

Definition 3

Let $(\mathcal {C}, \mathcal {U}_1, \mathcal {U}_2)$ be a client-server protocol for the delegated computation of a function $\mathsf {F}$ and $\mathcal {U}'=(\mathcal {U}_1',\mathcal {U}_2')$ be a malicious adversarial software in place of $\mathcal {U}=(\mathcal {U}_1,\mathcal {U}_2)$. We say that $(\mathcal {C}, \mathcal {U}_1, \mathcal {U}_2)$ satisfies $(t_v, \epsilon _v)-$verifiability against a malicious adversary if for any $\mathcal {A}=(\mathcal {E},\mathcal {U}_i')$, either $i=1$ or $i=2$, running in time $t_v,$ it holds that

$$\mathsf {Prob} [\textit{out} \leftarrow \mathsf {VerExp}_{\mathsf {F}',\mathcal {A}}(1^{\sigma }): \textit{out}= 1] \le \epsilon _v, $$

for small $\epsilon _v,$ where experiment $\mathsf {VerExp}$ is defined as follows:

• 1. $i=1$.

• 2. $(a, \tau (\mathsf {F}(x_1)), \mathsf {aux} ) \leftarrow \mathcal {A}(1^{\sigma }, \mathsf {desc(F')} )$

• 3. While $a \ne \mathsf {attack}$ do $(y_i, (a, \tau (\mathsf {F}(x_{i+1})), \mathsf {aux}), \mathsf {tr}_i) \leftarrow (\mathcal {C}(\tau (\mathsf {F}(x_i))), \mathcal {A}(\mathsf {aux}))$ $i \leftarrow i+1$

• 4. $\tau (\mathsf {F}(x)) \leftarrow \mathcal {A}(\mathsf {aux})$

• 5. $(y', \mathsf {aux}, \mathsf {tr}_i) \leftarrow (\mathcal {C}(\tau (\mathsf {F}(x))), \mathcal {A}(\mathsf {aux}))$

• 6. return: 1 if $y' \ne \perp$ and $y' \ne \mathsf {F}(x)$

• 7. return: 0 if $y' = \perp$ or $y' = \mathsf {F}(x)$.

If $\epsilon _v$ is negligibly small for any algorithm A running in time $t_v$, then $(\mathcal {C}, \mathcal {U}_1, \mathcal {U}_2)$ is said to satisfy full verifiability.

Security. Security means informally that if $\mathcal {C}$ follows the protocol, then the malicious adversary$\mathcal {A}=(\mathcal {E},\mathcal {U}'_i)$, $i=1$ or $i=2$, cannot obtain any information about $\mathcal {C}'$s input x. The model let further the adversary choose $\mathcal {C}'$s trapdoored input $\tau (\mathsf {F}(x))$ and take part in exponential/polynomial number of protocol executions before it attempts to obtain useful information about $\mathcal {C}'$s input (corresponding to the environmental adversary $\mathcal {E}$).

Definition 4

Let $(\mathcal {C}, \mathcal {U}_1, \mathcal {U}_2)$ be a client-server protocol for the delegated computation of a function $\mathsf {F}$ and $\mathcal {U}'=(\mathcal {U}_1',\mathcal {U}_2')$ be a malicious adversarial software in place of $\mathcal {U}=(\mathcal {U}_1,\mathcal {U}_2)$. We say that $(\mathcal {C}, \mathcal {U}_1,\mathcal {U}_2)$ satisfies $(t_s, \epsilon _s)-$security against a malicious adversary if for any $\mathcal {A}=(\mathcal {E},\mathcal {U}_i')$, either $i=1$ or $i=2$, running in time $t_s,$ it holds that

$$\mathsf {Prob}[\textit{out} \leftarrow \mathsf {SecExp}_{\mathsf {F}',\mathcal {A}}(1^{\sigma }): \textit{out}= 1] \le \epsilon _s,$$

for negligibly small $\epsilon _s$ for any algorithm A running in time $t_s$, where experiment $\mathsf {SecExp}$ is defined as follows:

• 1. $(a, \tau (\mathsf {F}(x_1)), \mathsf {aux} ) \leftarrow \mathcal {A}(1^{\sigma }, \mathsf {desc(F')} )$

• 2. While $a \ne \mathsf {attack}$ do

  $(y_i, (a, \tau (\mathsf {F}(x_{i+1})), \mathsf {aux}), \cdot ) \leftarrow (\mathcal {C}(\tau (\mathsf {F}(x_i))), \mathcal {A}(\mathsf {aux}))$

  $i \leftarrow i+1$

• 3. $(\tau (\mathsf {F}(x_0)), \tau (\mathsf {F}(x_1)),\mathsf {aux} )\leftarrow \mathcal {A}(\mathsf {aux})$

• 4. $b \leftarrow {0,1}$

• 5. $(y', b', \mathsf {tr}) \leftarrow (\mathcal {C}(\tau (\mathsf {F}(x_b))), \mathcal {A}(\mathsf {aux}))$

• 6. return: 1 if $b=b'$

• 7. return: 0 if $b \ne b'.$

Remark 1

We emphasize that the above security definition corresponds to the OMTUP-model of [7]. As in [7], the adversary $\mathcal {A}$ corresponds to both $\mathcal {E}$ and $\mathcal {U'}$, and can only interact each other over $\mathcal {C}$ after they once begin interacting with $\mathcal {C}.$ The behavior of both parts $(\mathcal {E}$ and $\mathcal {U'}$) is modeled as a single adversary $\mathcal {A}$ by letting the adversary $\mathcal {A}$ submit its own inputs to $\mathcal {C}$ and see/take part in multiple executions of $(\mathcal {C},\mathcal {U}_1,\mathcal {U}_2)$.

Efficiency Metrics. $(\mathcal {C},\mathcal {U}_1,\mathcal {U}_2)$ has efficiency parameters

$$(t_{\mathsf {F}}, t_{m_{\mathcal {C}}},t_{\mathcal {C}}, t_{\mathcal {U}_1}, t_{\mathcal {U}_2}, cc, mc )$$

where $\mathsf {F}$ can be computed using $t_{\mathsf {F}}(\sigma )$ atomic operations, requires $t_{m_{\mathcal {C}}}(\sigma )$ atomic storage for $\mathcal {C}$, $\mathcal {C}$ computes $t_{\mathcal {C}}(\sigma )$ atomic operations, $\mathcal {U}_i$ can be run using $t_{\mathcal {U}_i}(\sigma )$ atomic operations, $\mathcal {C}$ and $\mathcal {U}_i$ exchange a total of at most mc messages of total length at most cc for $i=1,2.$³

2.3 Steps of a Delegation Scheme

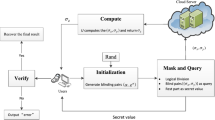
Let p and q be distinct prime numbers. We now give four main steps of a delegation of $u^a\bmod p$ under the OMTUP-model, where $u\in \mathbb {G}$, $a\in \mathbb {Z}_q^*$ and $\mathbb {G}$ is a subgroup of $\mathbb {Z}_p^*$ of order q.

• 1. Precomputation: Invocation of the subroutine $\mathsf{Rand}$: A preprocessing subroutine $\mathsf{Rand}$ is required to randomize u and a and to generate the trapdoor information $\tau$, see the paper’s full version for the details [12].

• 2. Randomizing $a\in \mathbb {Z}_q^*$ and $u\in \mathbb {G}$. The base u and the exponent a are both randomized by $\mathcal {C}$ by performing only modular multiplications (MMs) in $\mathbb {Z}_q^*$ and $\mathbb {G}$ with the values from $\mathsf{Rand}$ using the trapdoor information $\tau$.

• 3. Delegation to servers. The randomized elements are queried to the servers $\mathcal {U}_1$ and $\mathcal {U}_2$ by using $\tau$. For $i=1,2$, $U_{i}(\tau (\alpha ),\tau (h))$ denotes the delegation of $h^{\alpha }\bmod p$ with $\alpha \in \mathbb {Z}_q^*,\ h \in \mathbb {G}$ using the trapdoor information $\tau$ in order to disguise the parameters p, q, whence the concrete description of $\mathbb {G}$.

• 4. Verification of the delegated computation. Upon receiving the outputs of $\mathcal {U}_1$ and $\mathcal {U}_2$, the validity of the delegated computation is verified by comparing the received data with some elements from $\mathsf{Rand}$. If the verification fails, an error message $\perp$ is returned.

• 5. Derandomizing outputs and computing $u^a\bmod p$. If the verification is successful, then $u^a\bmod p$ is computed by $\mathcal {C}$ by performing only MMs.

3 Verifiability Issues in Two Recent Delegation Schemes

In this section, we show two verifiability issues for recently proposed delegation schemes appeared in INDOCRYPT 2016 [9] and AsiaCCS 2016 [11].

3.1 An Attack on the Verifiability of Kuppusamy and Rangasamy’s Scheme from INDOCRYPT 2016

Using CRT, Kuppusamy and Rangasamy proposed a highly efficient secure delegation scheme for MEs in subgroups of $\mathbb {Z}_p^*$ [9]. We now show that the scheme is unfortunately totally unverifiable.

Attack: Let the notation be as in [9]. Assume first that the server $\mathcal {U}_1$ is malicious and $\mathcal {U}_2$ is honest. Since the prime p is public, $\mathcal {U}_1$ can compute $r_1r_2=n/p$, and return the bogus values

$$\begin{aligned} Y_{11}:\equiv D_{11}+ r_1r_2\bmod n, \text{ and } Y_{12}:\equiv D_{12}+r_1r_2\bmod n. \end{aligned}$$

(1)

Now, $\mathcal {U}_1$ can successfully distinguish $D_{11}$ and $D_{12}$ from $D_{13}$ with probability 1 since the first component of $D_{13}$ is an element of $\mathbb {G}$ whereas the first components of $D_{11}$ and $D_{12}$ are elements of $\mathbb {Z}_n$. Afterwards, by the choices of the distinct primes $p, r_1$ and $r_2$, and the properties $Y_{12}\equiv D_{12}\bmod r_2$ and $Y_{11}\equiv D_{11}\bmod r_2$, $\mathcal {U}_1$ can pass the verification step with $Y_{11}$ and $Y_{12}$ instead of using $D_{11}$ and $D_{12}$, respectively. This leads to the bogus final output

$$Y_{12}\cdot D_{21}\cdot D_{13}$$

instead of the actual output $u^a=D_{12}\cdot D_{13}\cdot D_{22}$ given in [9].

Similarly, a malicious $\mathcal {U}_2$ can successfully distinguish $D_{21}$ from $D_{22}$ with probability 1 since the first component of $D_{22}$ is an element of $\mathbb {G}$ whereas the first component of $D_{21}$ is an element of $\mathbb {Z}_n$. Then, $\mathcal {U}_2$ can act as the untrusted server by computing

$$\begin{aligned} Y_{21}\equiv D_{21}+ r_1r_2\bmod r_2. \end{aligned}$$

(2)

Afterwards, by the choices of the distinct primes $p, r_1$ and $r_2$ and the property $Y_{21}\equiv D_{21}\bmod r_2$, $\mathcal {U}_2$ can pass the verification step with the bogus value $Y_{21}$. This results in the output

$$D_{12}\cdot Y_{21}\cdot D_{13}$$

instead of $u^a=D_{12}\cdot D_{13}\cdot D_{21}$ given in [9]. Hence, the scheme in [9] is unfortunately totally unverifiable and the claim regarding full verifiability [9, Thm. 2, pp. 90] does not hold.

3.2 An Attack on the Verifiability of Ren et al.’s Simultaneous Delegation Scheme from AsiaCCS 2016

Ren et al. proposed the first fully verifiable two-round secure delegation scheme for GEs together with a delegation scheme of n simultaneous MEs [11]. We now show that the author’s claim [11, Thm. 4.2, pp. 298] does not hold.

Attack: Let the notation be as in [11]. Assume without loss of generality that the server $\mathcal {U}_2$ is malicious and $\mathcal {U}_1$ is honest. Then, $\mathcal {U}_2$ chooses a random $\theta \in \mathbb {G}$ and sends the bogus value

$$T_{212}\equiv D_{212}\cdot \theta $$

instead of $D_{212}$ after correctly distinguishing $D_{212}$ from $D_{211}$ with probability at least 1/2. Then, $\mathcal {C}$ computes

$$\varTheta :=\theta (\prod _{j=1,i\ne j}^{n}w_j)^{c/t_1}\equiv T_{212}g^{-c}.$$

In order to pass the verification step with $\varTheta \cdot T$ instead of T, $\mathcal {U}_2$ requires to find an output $T_{23j}$ with $T_{23j}\not \in \{D_{22},D_{23i}\}$, i.e. $T_{23j}\equiv D_{23j}\bmod n$ for some $i\ne j$, and sends $\theta \cdot T_{23j}$ instead of $T_{23j}$. Now, since there are $n(n+1)/2$ pairs from the set

$$D:=\{D_{22},D_{231},\cdots ,D_{23n}\}$$

we totally have $n(n-1)$ possibilities for $T_{23j}$ corresponding to a single component of such a pair. If $(\varTheta _1,\varTheta _2)$ is a pair from the set D. Then,

• 1. there exists 2 values for $T_{23j}$ which can be detected by $\mathcal {C}$ corresponding to the single pair with $(\varTheta _1,\varTheta _2)\equiv (D_{22},D_{23i})\bmod p$,

• 2. there exists $n-1$ values of $T_{23j}$ which can be detected by $\mathcal {C}$ corresponding to the pairs of the form $(\varTheta _1,\varTheta _2)$ with $T_1=\varTheta _1\equiv D_{22}$ and $\varTheta _2\not \equiv D_{23i}$,

• 3. there exists $n-1$ values of $T_{23j}$ which can be detected by $\mathcal {C}$ corresponding to the pairs of the form $(\varTheta _1,\varTheta _2)$ with $T_{23j}=\varTheta _1\equiv D_{23i}$ and $\varTheta _2\not \equiv D_{12}$.

Therefore, there exist

$$n(n+1)-2-(n-1)-(n-1)=n(n+1)-2n=n(n-1)$$

possible values for $T_{23j}$ with $T_{23j}\not \in \{D_{22},D_{23i}\}$. Combining with the probability of correctly guessing the position of $D_{232}$, the server $\mathcal {U}_2$ can cheat $\mathcal {C}$ with a probability at least $\frac{n(n-1)}{2n(n+1)}=\frac{n-1}{2(n+1)}$. Hence, the scheme is verifiable with a probability at most $1-\frac{n-1}{2(n+1)}$ instead of the author’s claim that the scheme would be verifiable with a probability $1-\frac{1}{2n(n+1)}$. Thereby it also leads to a bogus output $\theta u_1^{a_1}\cdots u_n^{a_n}.$

For example with $n=10$ and $n=100$, the scheme is verifiable only with probabilities at most $13/22\approx 0.5909$ and $103/202\approx 0.5099$ instead of the claims with probabilities $219/220\approx 0.9955$ and $20199/20200\approx 0.9999$, respectively. Clearly, the verification probability becomes 1/2 if n tends to infinity.

4 $\mathsf{HideP}$: A Secure Fully Verifiable One-Round Delegation Scheme for Modular Exponentiations

In this section, we introduce our secure delegation scheme $\mathsf{HideP}$ in the OMTUP-model.

Let $\mathbb {G}=<g>$ denote the multiplicative subgroup of $\mathbb {Z}_p^*$ of prime order q with a fixed generator $g\in \mathbb {G}$. Our scheme $\mathsf{HideP}$ uses another prime $r\ne p$ of length $\sigma _1$ (e.g. p and r are of about the same size) such that $\mathbb {G}_1$ is a subgroup of prime order $q_1$ of length $\sigma _2$ (e.g. q and $q_1$ are of about the same size). We set $n:=p\cdot r$ and $m:=q_1\cdot q$. Note that $\mathsf{HideP}$ uses the prime number p as a trapdoor information, i.e. p must be kept secret to both $\mathcal {U}_1$ and $\mathcal {U}_2$.

Throughout the section $\mathcal {U}_i(\alpha ,h)$ denotes that $\mathcal {U}_i$ takes $(\alpha ,h)\in \mathbb {Z}_m^*\times \mathbb {Z}_n^*$ as inputs, and outputs $h^{\alpha }\bmod n$ for $i=1,2$, as described in Sect. (2).

4.1 $\mathsf{HideP}$: A Secure Fully Verifiable One-Round Delegation Scheme

Our aim is to delegate $u^a\bmod p$ with $a\in \mathbb {Z}_q^*$ and $u\in \mathbb {G}$.

We now describe our scheme $\mathsf{HideP}$. Public and private parameters of $\mathsf{HideP}$ are given as follows:

Public parameter: n,

Private parameters: Prime numbers p, r, q, and $q_1$, description of the subgroup $\mathbb {G}$ of $\mathbb {Z}_p^*$ of order q, $u\in \mathbb {G}$, $a\in \mathbb {Z}_q^*$..⁴

Additionally, the static values

$$\begin{aligned} Q_r:\equiv r\cdot (r^{-1}\bmod p)\bmod n,\ Q_p:\equiv p\cdot (p^{-1} \bmod r)\bmod n, \end{aligned}$$

(3)

$$\begin{aligned} Q_{q_1}:\equiv q_1\cdot (q_1^{-1}\bmod q)\bmod m, \ Q_q:\equiv q\cdot (q^{-1} \bmod q_1)\bmod m, \end{aligned}$$

(4)

and

$$\begin{aligned} R:\equiv g\cdot Q_r+ g_1\cdot Q_p\bmod n \end{aligned}$$

(5)

are calculated at the initialization of $\mathsf{HideP}$.

Precomputation. Using the existing preprocessing technique or a delegated version $\mathsf{Rand}$ as described in [12]), $\mathcal {C}$ first outputs

$$(G_t\equiv g^t Q_r\bmod n,\ G_{\gamma t}\equiv g^{\gamma t} Q_r\bmod n,\ H_{\gamma t}\equiv g_1^{\gamma t} Q_p\bmod n),$$

$$(H_{t_1}\equiv g_1^{t_1} Q_p\bmod n,\ H_{t_2}\equiv g_1^{t_2} Q_p\bmod n, \ g_1^t \bmod r),$$

and

$$(\gamma ^{-1}\bmod m,\ T_1\equiv t_1Q_q\bmod m,\ T_2\equiv t_2 Q_q\bmod m)$$

for random elements $t_1,t_2,t\in \mathbb {Z}_m^*$ with $t=t_1+t_2$.

Masking. The base u is randomized by $\mathcal {C}$ with

$$\begin{aligned} x_1\equiv u\cdot G_t+H_{t_1}\bmod n, \end{aligned}$$

(6)

$$\begin{aligned} x_2\equiv u G_t+H_{t_2}\bmod n, \end{aligned}$$

(7)

$$\begin{aligned} y\equiv G_{\gamma t}+H_{\gamma t}\bmod n. \end{aligned}$$

(8)

Note that by CRT we have

$$x_1\equiv x_2\equiv u g^{t} \bmod p,\ y\equiv g^{\gamma t}\bmod p,$$

and

$$x_1\equiv g_1^{t_1}\bmod r, x_2\equiv g_1^{t_2}\bmod r, y\equiv g_1^ {\gamma t}\bmod r.$$

Then, the exponent a is first written as the sum of two randomly chosen elements $a_1,a_2\in \mathbb {Z}_m^*$ with $a=a_1+a_2$. Then, the following randomizations are also computed by $\mathcal {C}$

$$\begin{aligned} \alpha _1\equiv a_1\cdot Q_{q_1}+T_1\bmod m, \end{aligned}$$

(9)

$$\begin{aligned} \alpha _2\equiv a_2\cdot Q_{q_1}+T_2\bmod m, \end{aligned}$$

(10)

$$\begin{aligned} \alpha _3\equiv -a\cdot \gamma ^{-1}\bmod m. \end{aligned}$$

(11)

Query to $\mathbf {\mathcal {U}_1}$. $\mathcal {C}$ sends the following queries in random order to $\mathcal {U}_1$:

• 1. $\mathcal {U}_1(\alpha _1,x_1)\longleftarrow X_1\equiv x_1^{\alpha _1}\bmod n,$

• 2. $\mathcal {U}_1(\alpha _3,y)\longleftarrow Y_1\equiv y^{\alpha _3}\bmod n.$

Query to $\mathbf {\mathcal {U}_2}$. Similarly, $\mathcal {C}$ sends the following queries in random order to $\mathcal {U}_2$:

• 1. $\mathcal {U}_2(\alpha _2,x_2)\longleftarrow X_2\equiv x_2^{\alpha _2}\bmod n$,

• 2. $\mathcal {U}_2(\alpha _3,y)\longleftarrow Y_2\equiv y^{\alpha _3}\bmod n.$

Verifying the Correctness of the Outputs of ${\mathbf {\{\mathcal {U}_1, \mathcal {U}_2\}}}$. Upon receiving the queries $X_1$ and $Y_1$ from $\mathcal {U}_1$, and $X_2$ and $Y_2$ from $\mathcal {U}_2$, respectively, $\mathcal {C}$ verifies

$$\begin{aligned} (X_1 \bmod r)\cdot (X_2\bmod r) {\mathop {\equiv }\limits ^{?}}g_1^{t} \end{aligned}$$

(12)

and

$$\begin{aligned} Y_1 {\mathop {\equiv }\limits ^{?}}Y_2\bmod n. \end{aligned}$$

(13)

Recovering $u^a$. If Congruences (12) and (13) hold simultaneously, then $\mathcal {C}$ believes that the values $X_1$, $X_2$, $Y_1$ and $Y_2$ have been computed correctly. It outputs

$$\begin{aligned} u^a\equiv (X_1\bmod p)\cdot (X_2\bmod p)\cdot (Y_1\bmod p). \end{aligned}$$

(14)

If the verification step fails, then $\mathcal {C}$ outputs $\perp$.

5 Security and Efficiency Analysis

In this section, we give the security analysis of $\mathsf{HideP}$ and give a detailed comparison with the previous schemes.

5.1 Security Analysis

Theorem 1

Let $F'$ be given by the exponentiation modulo $n=pr$, where the trapdoor information $\tau$ is given by the primes p and r, $p\ne r$. Let further $(\mathcal {C},\mathcal {U}_1, \mathcal {U}_2)$ be a one-client, two-server, one-round delegation protocol implementation of $\mathsf{HideP}$. Let the adversary be given as $\mathcal {A}=(\mathcal {U}',\mathcal {E})$ in the OMTUP-model (i.e. $\mathcal {U}'=(\mathcal {U}'_1,\mathcal {U}'_2)$ and at most one of $\mathcal {U}'_i$ is malicious with $i=1$ or $i=2$). Then, in the OMTUP-model, the protocol $(\mathcal {C},\mathcal {U}_1, \mathcal {U}_2)$ satisfies

• 1. completeness for $\mathsf{HideP}$,

• 2. security for the exponent a and the exponentiation $u^a$ against any (computationally unrestricted) malicious adversary $\mathcal {A}$, i.e. $\epsilon _s=0$, and security for the base u with $t_s = \mathsf poly(\sigma )$ and $\epsilon _s = \mathsf {Adv}^{\mathsf {Fact}}_{\mathcal {A}'}(\sigma )$,

• 3. full verifiability for any malicious adversary $\mathcal {A}$, where $t_v = \mathsf poly(\sigma )$ and $\epsilon _v = \mathsf {Adv}^{\mathsf {Fact}}_{\mathcal {A}}(\sigma )$, and verifiability for any computationally unrestricted malicious adversary $\mathcal {A}$ with $\epsilon _v=1/2+\epsilon$, where $\epsilon$ is negligibly small in $\sigma$,

• 4. efficiency with parameters where $(\mathsf t_F, t_{m_\mathcal {C}}, t_{\mathcal {C}}, t_{\mathcal {U}_1}, t_{\mathcal {U}_2}, cc, mc),$ where

  • F can be computed by performing $\mathsf t_F = 1$ exponentiation modulo p

  • $\mathcal {C}'s$ memory requirement is $t_{m_\mathcal {C}}$ consists of 1 output of the $\mathsf{Rand}$ scheme,

  • $\mathcal {C}$ can be run by expending $t_{\mathcal {C}}$ atomic operations consisting of 7 modular multiplications and 5 modular reductions (2 multiplications modulo p, 1 multiplication modulo r, 3 multiplications modulo m, 1 multiplication modulo n, 2 reductions modulo r, and 3 reductions modulo p),

  • $\mathcal {U}_i, i = 1, 2$ computes $t_{\mathcal {U}_i} = 2$ exponentiations modulo n for each $i=1,2$,

  • $\mathcal {C}$ and $\mathcal {U}_i$ exchange a total of at most $mc = 4$ messages of total length cc consisting of 2 elements modulo m and 2 elements modulo n for $i=1,2$.

Proof. We first note that the efficiency results can easily be verified by inspecting the description of $\mathsf{HideP}$ for the efficiency parameters given above. Throughout the rest of the proof we assume without loss of generality that $\mathcal {U}_1$ is a malicious server, i.e. adversary is given as $\mathcal {A}=(\mathcal {U}_1,\mathcal {E})$.

Completeness. We first prove the completeness of the verification step. Since the same base y and the exponent $\alpha _3$ are delegated to both $\mathcal {U}_1$ and $\mathcal {U}_2$, the congruence $Y_1\equiv Y_2\equiv y^{\alpha _3}$ holds by the OMTUP assumption. Furthermore, by the choice of $T_1\equiv t_1Q_q$, $T_2\equiv t_2Q_q$, we have the congruences

$$a_1Q_{q_1}+T_1\equiv t_1\bmod q_1,\ a_2Q_{q_1}+T_2\equiv t_2\bmod q_1.$$

Then, together with the equality $t=t_1+t_2$ the following congruence holds:

Hence, the result follows for the verification step. Then, the result follows by the congruences

$$a_1Q_{q_1}+T_1\equiv a_1\bmod q,\ a_2Q_{q_1}+T_2\equiv a_2\bmod q,$$

the equality $a=a_1+a_2$ and Lagrange’s theorem

$$\begin{aligned} (X_1 \cdot X_2\bmod p)\cdot (Y_1\bmod r)&\equiv (x_1^{\alpha _1} \cdot x_2^{\alpha _2}\bmod p) \cdot (y^{\alpha _3}\bmod p)\\&\equiv (ug^{t})^{a_1}\cdot (ug^{t})^{a_2}\cdot g^{-at\gamma \gamma ^{-1}}\bmod p\\&\equiv (ug^{t})^{a_1+a_2}\cdot g^{-at}\bmod p\\&\equiv (ug^{t})^a\cdot g^{-at}\bmod p\\&\equiv u^a\cdot g^{at}\cdot g^{-at}\bmod p\\&\equiv u^a\cdot g^{at-at}\bmod p\\&\equiv u^a\bmod p. \end{aligned}$$

Security. We argue that $\mathsf{HideP}$ satisfies security under the OMTUP-model due to the following observations:

• 1. On a single execution of $(\mathcal {C},\mathcal {U}_1,\mathcal {U}_2)$ the input $(\alpha , x)$ in the query sent by $\mathcal {C}$ to the adversary $\mathcal {A}=(\mathcal {U}_1,\mathcal {E})$ does not leak any information about u, a and $u^a$. The reason is that

  • u is randomized by multiplying with $g^{t}$ which is random. Hence, the adversary $\mathcal {A}$ cannot obtain any useful information about u even if the factors p, r of n are known,

  • a is randomized by $a_1$ and $a_2$ and $a\gamma$. Hence $\mathcal {A}$ cannot obtain any useful information about a by obtaining $a_1$ through $x_1$ and $a\gamma \bmod p$ even if it knows the factors p, r and $q,q_1$ of n and m, respectively.

  • To obtain useful information about $u^a$, $\mathcal {A}$ requires to know $x_2$ which is random and not known by the OMTUP assumption.

• 2. Even if the adversary $\mathcal {A}$ sees multiple executions of $(\mathcal {C},\mathcal {U}_1,\mathcal {U}_2)$ wherein the inputs of $\mathcal {C}$ are adversarially chosen, $\mathcal {A}$ cannot obtain any useful information about the exponent a chosen by $\mathcal {C}$, and the desired exponentiation $u^a$ in a new execution since logical divisions of $a=a_1+a_2$ at each execution involve freshly generated random elements. This implies that $\epsilon _s=0$ for the exponent a and the output $u^a\bmod p$. Assume that $\mathcal {A}$ can break the secrecy of the base u with a non-negligible probability. In particular, it can obtain useful information about both elements $u\cdot G_T$ and $ug^{t}$ with a non-negligible probability, where $G_T\equiv g^{t}\bmod p$ for some t. Then, $\mathcal {A}$ can obtain $\gcd ((uG_T-ug^{t}),n)$. This gives the factors p and r of n with a non-negligible probability as $u\cdot G_T\equiv ug^{t}\bmod p$ holds. This implies that $t_s = \mathsf poly(\sigma )$ and $\epsilon _s$ is at most $\mathsf {Adv}^{\mathsf {Fact}}_{\mathcal {A}}(\sigma )$, i.e. $(\mathcal {C},\mathcal {U}_1,\mathcal {U}_2)$ is a secure implementation of $\mathsf{HideP}$ if the factorization problem is intractable .

In particular, these arguments show that $(\mathcal {C},\mathcal {U}_1, \mathcal {U}_2)$ provides unconditional security for the exponent a and the output $u^a$ against any (computationally unrestricted) adversary and security for the base u against any polynomially bounded adversary.

Verifiability. Since $Y_1$ and $Y_2$ both have the same base and exponent elements, $\mathcal {U}_1$ cannot cheat the delegator $\mathcal {C}$ by manipulating $Y_1$ by the OMTUP assumption. This means that $\mathcal {U}_1$ can only pass the verification step by manipulating the output $X_1$. Hence, the result $\epsilon _p=1/2+\epsilon$ (where $\epsilon$ is negligibly small in the security parameter $\sigma$) holds for any adversary $\mathcal {U}_1$ since $\mathcal {U}_1$ needs to know the correct position of $x_1$ which has at most 1/2. We now show that if there exists an adversary $\mathcal {A}$ that breaks the verifiability property with a non-negligible probability, then $\mathcal {A}$ can be used to effectively solve the factorization problem. Assume now that $\mathcal {U}_1$ as a malicious server passes the verification step with a bogus output $Z_1$ (instead of $X_1=x_1^{\alpha _1}$) with a non-negligible probability. Then, the following congruence must hold for any arbitrary output $X_2$ of the honest server $\mathcal {U}_2$

$$\begin{aligned} Z_1X_2\equiv X_1.X_2\equiv g_1^{t}\bmod r \end{aligned}$$

(15)

with a non-negligible probability. This implies that $\mathcal {U}_1$ can decide whether the congruence $Z_1\equiv X_1\bmod r$ holds with a non-negligible probability. We note that $Z_1\not \equiv 0\bmod r$ as otherwise Congruence 15 cannot hold with $g_1^{t}\not \equiv 0\bmod r$. This implies that $Z_1-X_1\equiv 0\bmod r$ and that $Z_1\not \equiv 0\bmod r$. From the inequality $Z_1-X_1<n$ (when the representatives are considered as integers), it follows that $\mathcal {U}_1$ can compute $\gcd (Z_1-X_1,n)=r$ with a non-negligible probability. Hence, $\mathcal {U}_1$ can obtain information about both the factors p and r of n with a non-negligible probability. This implies that $t_v = \mathsf poly(\sigma )$ and $\epsilon _v$ is at most $\mathsf {Adv}^{\mathsf {Fact}}_{\mathcal {A}}(\sigma )$.    $\square$

Table 1. Comparison of computational and communication costs for $\mathcal {C}$.

Fig. 1.

CPU time: $\mathsf{HideP}$ vs. Computation

Table 2. CPU cost: $\mathsf{HideP}$ vs. Computation

5.2 Comparison

We now compare $\mathsf{HideP}$ with the previous delegation schemes for MEs. We denote by MM a modular multiplication, MI a modular inversion, and MR a modular reduction. Throughout the comparison we make the following assumptions:

• we regard 1 MM modulo n as $\approx 4$ MMs modulo p,

• 1 MM modulo p and 1 MM modulo r cost approximately the same amount of computation,

• 1 MI is at worst 100 times slower than 1 MM (see [8]),

• we regard 1 MR costs approximately 1 MM (e.g. by means of Barret’s or Mongomery’s modular reduction techniques).

We give the delegator’s computational workload in Table 1 by considering the approximate number of MMs modulo p. In particular, Table 1 compares computational cost and communication overhead of $\mathsf{HideP}$ with the previous schemes. It shows that $\mathsf{HideP}$ has not only the best computational cost but requires also only a single round with 4 queries (instead of 2 rounds and 6 queries when compared with the only scheme in the literature satisfying full verifiability [11]) (Table 1).

6 Application: Verifiably Delegated Blind Signatures

Blind signatures were introduced by Chaum [3] and allow a user to obtain the signature of another user in such a way that the signer do not see the actual message to be signed and the user without having knowledge of the signing key is able to get the message signed with that key. Blind signatures are useful in privacy preserving protocols. For example, in e-cash scenario, a bank needs to sign blindly the coins withdrawn by its users. Normally, in blind signature protocols, both the signer and the verifier have to compute MEs using private and public keys, respectively. As an example, delegation of MMs in blinded Nyberg-Rueppel signature scheme [1, 10] using $\mathsf{HideP}$ is depicted in Fig.  2. It is also evidenced from Fig. 1 that the time taken by $\mathsf{HideP}$ is much smaller than that of directly computing $u^a \mod p$, and this gain in CPU time increases rapidly with the size of the modulus. Hence, $\mathsf{HideP}$ becomes more attractive for resource-constrained scenario such as mobile environment when we go for higher security levels.

Fig. 2.

Delegating blinded Nyberg-Rueppel signature

7 Conclusion

In this work, we addressed the problem of secure and verifiable delegation of MEs. We observed that two recent schemes [9, 11] do not satisfy the claimed verifiability probabilities. We presented an efficient non-interactive fully verifiable secure delegation scheme $\mathsf{HideP}$ in the OMTUP-model by disguising the modulus p using CRT. In particular, $\mathsf{HideP}$ is the first non-interactive fully verifiable and the most efficient delegation scheme for modular exponentiations leveraging the properties of $\mathbb {Z}_p$ via CRT. As future works, proposing an efficient fully verifiable delegation scheme without any requirement of online or offline computation of MEs by the delegator (or its impossibility) under the TUP/OUP assumptions could be highly interesting.