Dynamics of a Portable Module Handling System

Abstract

The paper describes a model of a light module handling system (LMHS) developed for IMR (Inspection, Maintenance and Repair) services typically performed for the seabed-located oil and gas production facilities. In order to describe dynamic performance and loads during the operation, the system is characterized by means of a multi-body model consisting both rigid and flexible links. Using the joint coordinates and homogeneous transformations the dynamics can be described by a set of differential equations of the second order and some constraint equations. The system forms several tree-like structures of bodies. The interaction between them takes place on guiding elements and lifting ropes. An important features of the handling system are flexible guide beams and prongs. The flexibility provided by those elements helps to limit some impact loads during the module docking phase. This functionality is modelled by the rigid finite elements. Lifted objects (subsea modules) are described by a set of special elements defining the hydrodynamic interaction. The work will also show some simulation results reflecting a typical operation.

1 Introduction

Subsea modules are complex units installed on the seabed and operated remotely. These units process the natural resources and differ in size and functions. Typically, they serve as separation valves, pumps or compressors, coolers, dischargers or other units. Beside the installation, it is required to perform maintenance on these objects. Despite rough sea conditions, damaged modules must be safely replaced with new ones. To address these challenges, a “small” special module handling system has been developed. Several new functions makes this tool unique. As the majority of subsea modules weight up to 25 tons, the LMHS can be easily applied in existing and future installations. One of the most important futures of the LMHS is its ability to be installed on an “average” supply vessel. No special vessel is required, in contrast to a typical crane-based constructions with detailed specified hull requirements. Moreover, the LMHS can be relocated within 48 h to an another ship (it can be packed in two containers for road transportation).

There are many examples of computational models of offshore systems. Often coupled, complex hydrodynamic motion analyses are conducted for ship cranes and payloads, for example in [1, 3, 4]. Numerical and experimental tests are performed for vessels and equipment where design loads (the wire rope tension) are calculated during installination, such as a 150 ton subsea manifold investigated in [5]. The calculations require hydrodynamic coefficients to be determined by CFD, which is a common practice when ships [9] and lifted objects [7] are analysed. Crane booms are can be very large and its flexibility shall be also considered [6], which makes an additional challenge for designers.

A mathematical model developed is presented in this work. It allows us to calculate dynamic loads acting on the LMHS structure and modules. Assumed vessel and weather criteria can be tested with respect to design criteria. The main goal was to provide a simple, convenient method that allows an engineer to perform qualitative assessment without access to a large and expensive computation systems.

2 LMHS Basic Assumptions and Layout

The design concept considers a safe launch and recovery of subsea modules performed on typical supply vessels having an average performance on moderate sea states. An installation over the vessel side as well as over a moonpool are taken into account. The main components are shown in Fig.  1.

Fig. 1

LMHS - main components, a system with module over deck (CGF frames retracted), b over-boarded position with module launched (CGF frames extracted)

The CGS (cursor guide system) is specially designed to guide the module safely and consist of (Fig. 1b) the following main parts: guide rails (integral part of the slewing column), guide frame, slide frame, two prong beams with prongs. An easy adjustments of prongs towards required module geometry (funnels) is crucial.

3 Mathematical Model

Dynamic analysis must be conducted in order to predict loads and check for the limitations of the LMHS. A mathematical model is developed for that purpose. The LMHS is modelled as a multibody system with both rigid and flexible bodies consisting of multiple, tree-like structures. The flexibility of selected bodies is considered using the rigid finite element method [12].

3.1 Transformation of Coordinates

The inertial coordinate system is designated as $\{0\}$, while the coordinate system $\{p\}$ will be attached to a body (p) (which may be dependent on proceeding bodies in kinematic chain, [2]). The homogeneous transformation matrix to transform coordinates from the coordinate system $\{p\}$ to the inertial system $\{0\}$ denotes $_p ^0 \mathbf {T}$. This matrix depends on all the generalized coordinates of the body (p) in chain, i.e.

$$\begin{aligned} _p ^0 \mathbf {T} = \mathbf {T}^{(p)} \left( \mathbf {q}^{(p)} \right) = \mathbf {T}^{(p-1)} \left( \mathbf {q}^{(p-1)}\right) \cdot \mathbf {T}^{(p)}\left( \tilde{\mathbf {q}}^{(p)} \right) = \mathbf {T}^{(p-1)} \left( \mathbf {q}^{(p-1)}\right) \cdot \prod _{i=1}^{n_p} \mathbf {U}\left( q_i^{(p)}\right) \end{aligned}$$

(1)

where $\mathbf {q}^{(p)} = \begin{bmatrix} q_1^{(p)}&\dots&q_{n_p}^{(p)} \end{bmatrix}^T =\begin{bmatrix} \left( \mathbf {q}^{(p-1)}\right) ^T&\left( \tilde{\mathbf {q}}^{(p)} \right) ^T \end{bmatrix}^T$, $\mathbf {q}^{(p-1)}$ is the vector of generalized coordinates of proceeding body $(p-1)$ in chain, $\tilde{\mathbf {q}}^{(p)}=\begin{bmatrix} \tilde{q}_1^{(p)}&\dots&\tilde{q}_{\tilde{n}_p}^{(p)} \end{bmatrix}^T$ is the vector of generalized coordinates describing the relative motion of the body (p) with respect to $(p-1)$, $n_p$ is the number of generalized coordinates of the body p in kinematic chain, $\mathbf {U}^{(p)}_i \left( \tilde{q}_i^{(p)}\right)$ is transformation matrix which depends only on one generalized coordinate $\tilde{q}_i^{(p)}$, $i=1,\dots ,\tilde{n}_p$, $\tilde{n}_p \le 6$.

For some bodies the vector $\mathbf {q}^{\left( p-1\right) } = \mathbf {\emptyset }$ (no proceeding body - applies to the vessel, guide frame, slide frame and module bodies).

3.2 Generalized Coordinates of the System

In this work we consider that the vessel’s motion can be defined by known functions. For practical reasons we simplify the vessel’s response to a simple harmonic input (see Fig.  3). Therefore the first body’s motion is constrained by the six motion parameters ($x^{(v)}$-surge, $y^{(v)}$-sway, $z^{(v)}$-heave, $\psi ^{(v)}$-yaw, $\theta ^{(v)}$-pitch and $\varphi ^{(v)}$-roll):

$$\begin{aligned} \mathbf {q}^{(v)} \left( t \right) =\begin{bmatrix} x^{(v)}\left( t\right)&y^{(v)}\left( t\right)&z^{(v)}\left( t\right)&\psi ^{(v)} \left( t\right)&\theta ^{(v)}\left( t\right)&\varphi ^{(v)} \left( t\right) \end{bmatrix}^T \end{aligned}$$

(2)

where $x^{(v)}\left( t\right) ,\dots ,\varphi ^{(v)}\left( t\right)$ are known (assumed) functions of time t and other parameters depending on vessel design and operational conditions.

The homogeneous transformation matrix of the vessel, $\mathbf {T}^{(v)}\left( \mathbf {q}^{(v)}\right) = \mathbf {T}^{(v)} \left( \mathbf {q}^{(v)}\left( t\right) \right)$, is also known and can be found for example in [12] where also the detailed approach is presented.

The LMHS column (regarded in this work as a rigid body) may rotate around the vertical axis of a local coordinate system $\{c\}$ (Fig.  1), therefore its vector of generalized coordinates is:

$$\begin{aligned} \tilde{\mathbf {q}}^{(c)}=\begin{bmatrix} \tilde{\psi }_c \end{bmatrix} \end{aligned}$$

(3a)

$$\begin{aligned} \mathbf {q}^{(c)} = \begin{bmatrix} \left. \mathbf {q}^{(v)} \right. ^T&\left. \tilde{\mathbf {q}}^{(c)} \right. ^T \end{bmatrix} \end{aligned}$$

(3b)

while the jib is regarded as a flexible part divided into $n_{f}^{(j)}$ rigid finite elements (rfe) (element $i=0$ is part of the column):

$$\begin{aligned} \tilde{\mathbf {q}}^{(j)} = \begin{bmatrix} \left. \tilde{\mathbf {q}}_1^{(j)} \right. ^T&\dots&\left. \tilde{\mathbf {q}}_{ n_f^{(j)}}^{(j)} \right. ^T \end{bmatrix}^T \end{aligned}$$

(4a)

$$\begin{aligned} \mathbf {q}^{(j)}=\begin{bmatrix} \left. \mathbf {q}^{(v)} \right. ^T&\tilde{\mathbf {q}}^{(c)}&\left. \tilde{\mathbf {q}}^{(j)} \right. ^T \end{bmatrix}^T \end{aligned}$$

(4b)

where $\tilde{\mathbf {q}}_i^{(j)}= \begin{bmatrix} \tilde{\psi }_i^{(j)}&\tilde{\theta }_i^{(j)}&\tilde{\varphi }_i^{(j)} \end{bmatrix}^T$, $\tilde{\psi }_i^{(j)}$, $\dots$, $\tilde{\varphi }_i^{(j)}$ are the rotation angles due to deformation of the i-th rfe with respect to its proceeding body (or rfe), $i = 1,\dots , n_f^{(j)}$. Four winch drums are included in the similar way as the slewing column. The generalized coordinates defining drum rotation can be formulated as (these bodies are added to the slewing column body):

$$\begin{aligned} \left. \mathbf {q}^{(w)}=\begin{bmatrix} \left. \mathbf {q}^{(c)} \right. ^T&\varphi ^{(w)} \end{bmatrix}^T \right| _{w\in \left\{ M, C, G_1, G_2 \right\} } \end{aligned}$$

(5)

where M depicts for main lifting winch (MLW), C stands for cursor guide winch (CGFW) and $G_1$, $G_2$ for the two guide wire winches (GWW #1 and GWW #2).

Guide frame (g) and sliding frame (s) bodies are assumed to be rigid as well and the vectors of generalized coordinates (both $\mathbf {q}^{(g)}$ and $\mathbf {q}^{(s)}$) take the form:

$$\begin{aligned} \mathbf {q}^{(f)} =\begin{bmatrix} x^{(f)}&y^{(f)}&z^{(f)}&\psi ^{(f)}&\theta ^{(f)}&\varphi ^{(f)} \end{bmatrix}^T \text {, } f \in \left\{ g, s \right\} \end{aligned}$$

(6)

and the generalized coordinates for these parts are independent, hence $\mathbf {q}^{(f)} = \tilde{\mathbf {q}}^{(f)}$ and $\mathbf {q}^{(f-1)}=\mathbf {\emptyset }$, $f\in \left\{ g,s\right\}$.

Flexible prong beams $(b_k)$, $k=1,2$ are attached to the sliding frame using hinge connections. The vectors of generalized coordinates are:

$$\begin{aligned} \mathbf {q}^{(b_k)} = \begin{bmatrix} \left. \mathbf {q}^{(s)} \right. ^T&\left. \tilde{\mathbf {q}}^{(b_k)} \right. ^T \end{bmatrix}^T \end{aligned}$$

(7)

where $\tilde{\mathbf {q}}^{(b_k)}= \begin{bmatrix} \left. \tilde{\mathbf {q}}^{(b_k,0)} \right. ^T&\dots&\left. \tilde{\mathbf {q}}^{\left( b_k, n_f^{(b_k)} \right) } \right. ^T \end{bmatrix}^T$,

       $\tilde{\mathbf {q}}^{(b_k,i)}= \left\{ \begin{array}{ll} \begin{bmatrix} \psi ^{(b_k,i)} &{} \theta ^{(b_k,i)} &{} \varphi ^{(b_k,i)} \end{bmatrix}^T &{} \text { for } i=1,\dots ,n_f^{(b_k)} \\ \begin{bmatrix} \psi ^{(b_k,i)} \end{bmatrix} &{} \text { if } i=0 \end{array} \right.$

The module is considered as a single rigid body with six degrees of freedom:

$$\begin{aligned} \mathbf {q}^{(m)} = \begin{bmatrix} x^{(m)}&y^{(m)}&z^{(m)}&\psi ^{(m)}&\theta ^{(m)}&\varphi ^{(m)} \end{bmatrix}^T \end{aligned}$$

(8)

which again yields to $\mathbf {q}^{(m-1)}=\mathbf {\emptyset }$ and its equations of motion are coupled with the LMHS system by wire forces and contact forces between funnels and prongs.

3.3 Guiding Elements

Figure 2 shows guiding elements transmitting loads in the cursor guide system. Figure 2a presents CGF rails, which are an integral part of the slewing structure. CGF rails “constrain” the guide frame body motion (together with the mechanical end-stoppers to limit its vertical motion) using eight wheels: four of them transfer the loads in “Y” direction, and the other four along the “X” direction. The guide frame also posses its own guiding rails - for guiding the sliding frame. The sliding frame (Fig.  2b), is equipped with eight wheels, too. A similar wheel arrangement is used for the slide frame - guide frame interface.

Fig. 2

Guiding elements: a CGF rails, b sliding frame wheels, c prong-module interface

In addition to the wheels, there are also mechanical end-stoppers (indicated Fig. 1b), limiting the movement of guide and sliding frames. When the module is lowered into the sea, the guide frame rests on stoppers, and the sliding frame continues to slide downward, until it reaches the end position (by end stoppers) with fully submerged module. In the other case, whenever the module is handled over the sea/deck, the guide frame is resting on the end-stoppers transferring its weight into the slide frame.

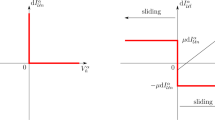
Wheels and stoppers are simulated by introducing a special spring-damping elements, with a non-linear characteristics and arbitrary selected clearances. A proper modelling of the stiffness curve allows us to overcome some numerical difficulties due to changing conditions (sudden contacts) as well as the clearance can be introduced (design constants). Suitable models for such elements are developed, some similar approaches can be found in [10] or [11]. The interaction between the module and prongs is handled similarly. Figure 2c shows contact pairs that guide the module: the upper plate of the prong is working as a stopper, and a soft material forms a spherical shape, that guides the prongs inside the funnels. The upper plate (stopper) plays also other important function - provides required down-force to the module.

3.4 Drive Elements

Slewing column, the jib angle and winches (drum rotations) motions are controlled, which can be realised in the form of kinematic constraints:

$$\begin{aligned} \varphi ^{(i)} = \varphi ^{(i)} \left( t \right) \end{aligned}$$

(9)

where $\varphi ^{(i)} \in \left\{ \tilde{\psi }^{(c)}, \tilde{\varphi }_1^{(j)}, \tilde{\varphi }^{(M)}, \tilde{\varphi }^{(C)} \right\}$ is the appropriate degree of freedom specified in (3a), (4a) or (5).

In order to obtain a desired motion of driven components, additional unknown reactions must be formulated. These driving moments (unknown reactions), ensuring the courses of selected in (9) degrees of freedom, are the components the vector:

$$\begin{aligned} \mathbf {R}_d=\begin{bmatrix} M_c&M_{j_1}&M_{M}&M_C \end{bmatrix}^T \end{aligned}$$

(10)

which must be included in the equations of motion.

3.5 Equations of Motion

The equations of motion for the whole system dynamics can be written in the form:

$$\begin{aligned} \mathbf {A} \ddot{\mathbf {q}} - \mathbf {D}\mathbf {R} = \mathbf {F} \end{aligned}$$

(11a)

$$\begin{aligned} \mathbf {D}^T \ddot{\mathbf {q}} = \mathbf {W} \end{aligned}$$

(11b)

where $\mathbf {A}$ is the inertia matrix (non-diagonal, with variable elements), $\mathbf {q}= \begin{bmatrix} \left. \mathbf {q}^{(H)}\right. ^T&\left. \mathbf {q}^{(f)} \right. ^T&\left. \mathbf {q}^{(s)} \right. ^T&\left. \tilde{\mathbf {q}}^{(b_1)} \right. ^T&\left. \tilde{\mathbf {q}}^{(b_2)} \right. ^T&\left. \mathbf {q}^{(m)} \right. ^T \end{bmatrix}^T$ is the vector of generalized coordinates, $\mathbf {q}^{(H)} = \begin{bmatrix} \left. \mathbf {q}^{(v)}\right. ^T&\tilde{\psi }^{(c)}&\left. \tilde{\mathbf {q}}^{(j)} \right. ^T&\tilde{\varphi }^{(M)}&\tilde{\varphi }^{(C)}&\tilde{\varphi }^{(G_1)}&\tilde{\varphi }^{(G_2)} \end{bmatrix}$, $\mathbf {R}=\begin{bmatrix} \left. \mathbf {R}^{(v)}\right. ^T&\mathbf {R}_d^T \end{bmatrix}^T$ is the vector of unknown reactions, $\mathbf {R}^{(v)}$ is the vector of reactions ensuring realisation of the vessel motion, $\mathbf {D}$ is the constraint coefficient matrix, $\mathbf {F}=\mathbf {F} \left( t,\mathbf {q}, \dot{\mathbf {q}}\right)$, $\mathbf {G}=\mathbf {G} \left( t,\mathbf {q}, \dot{\mathbf {q}}\right)$

When $n_f^{(j)}=n_f^{(b_1)}=n_f^{(b_2)}=0$, Eq. (11) represent a system of minimum $M_{\mathbf {q}}=30$ differential equations and $N_{\mathbf {R}}=10$ constraint equations. The equations are solved by numerical integration using the Runge-Kutta method of the fourth order with fixed time step. The initial conditions were found assuming $\ddot{\mathbf {q}}=\dot{\mathbf {q}}=\mathbf {0}$ in (11) and solving for $\mathbf {q}$ and $\mathbf {R}$ with the Newton’s method [8].

4 Example Simulations

Principal parameters of the vessel, sea conditions and LMHS location considered in example simulations are listed in Table 1.

Table 1 Main parameters of vessel and LMHS

The motion of the vessel is approximated based on available hydrodynamic calculations and shown in Fig. 3.

Fig. 3

Vessel motion assumed, headings $0^\circ , 45^\circ$ and $90^\circ$

Two cases are investigated, where the slewing function is assumed as in Fig. 4a:

• LC-A: operation without the module (governing load case for the CGF winch)

• LC-B: operation with 20 t module (governing loads for the crane structure and MLW drive)

Time histories of calculated slew drive reactions are presented in Fig. 4a. The drive torque equivalent for operation of empty LMHS, despite lower values obtained, is important for dimensioning of the gear box life time (spectrum definition). It’s also important that representative loads acting on CGF rope are determined (Fig. 4b). This allows for dimensioning of the CGF winch drive including fatigue loads for the drive gears as well as for the rope.

Fig. 4

Results for LC-A a slew rotation and moment $M_c$, b CGF winch tension force

Similar results are presented when the module is present, Fig. 5 (same slewing function as in LC-A case). Slew drive moments for three headings are presented in Fig. 5a, where the moment peaks have increased up to 250 kNm which is caused by the module’s inertia forces. The MLW rope tension force is shown in Fig. 5b: it equals the module and all CGF frame masses (i.e. all objects handled by MLW, excluding 20 kN constant tension generated by the CFG winch). Such a winch working mode is typical for the launch and recovery and provides the required down-force level.

Fig. 5

Results for LC-B a slew drive moment $M_c$, b MLW rope force

Module interaction loads with prong sphere (contact forces) are shown in Fig. 6a. Forces presented in Fig. 6b present the contact loads between module funnel and prong vertical stopper. Forces acting on the second prong are similar, some difference is dictated by the prong beam-funnel geometry. The down-force level (the sum of contact forces on both prong stoppers) is an important parameter to consider. If the down-force is not sufficient, the module can slide out from prongs and a dangerous situation may occur (like a damage of the module due to impact with the CGF rails or hull). Therefore, the MLW capacity must be high enough to cover the loads generated by module itself and all cursor guiding elements resting on it.

Fig. 6

Results for LC-B a radial contact force on funnel-prong sphere, b contact force on funnel-vertical prong stopper

5 Conclusions

The numerical model developed and elaborated computer programme enable us to predict the loads in various conditions and configurations. The assumptions made in the project design phase (i.e. design loads) should be confirmed whenever a new installation is planned. Due to various possible vessels, different modules and deck arrangements, detailed engineering must performed for the verification if the governing loads are not exceeded. Winch drives and ropes capacities and life times are also important factors to monitor. For this purpose, as well as due to requirements of an external approval, the developed computer programme could be an useful tool.

The system was developed assuming SWL 25 t and the significant wave height up to 4.5 m. However, due to complexity of module handling operations and variety of possible input parameters (including large variety of module types), it is difficult to asses the limits without running several analyses for each significant input modification. Assisting engineers and vessel managers during such operations was the main motivation behind developing the model presented.