1 Introduction

Coupling multibody system (MBS) formalisms with other fields of engineering is still a challenge for enlarging their scope of applications. In particular, numerous problems involve a dynamic interaction between an articulated system and a granular material such as the dynamics of a vehicle on a sandy soil or the handling of agricultural products, aggregates or ores. In railways, such a kind of problem arises when studying the ballast which plays a key role for the stability of the track. Its dynamic behavior may interact with the dynamics of the train, which is often modeled as a multibody systems, but also with maintenance machines, which constitutes complex articulated systems.

The modeling of the ballast as well as other granular material led to the development of discrete element methods (DEMs) that enable to consider the interactions between each particle of such a media. Two main families can be distinguished. On the one hand, the “Molecular Dynamics” approaches allow particle inter-penetration and often rely on the regularization of contact laws (see for instance [1]). On the other hand, “Contact Dynamics” methods consider rigid contact and impose to solve geometric and dynamic contact equations for the whole media at each time step. In particular, the Non-Smooth Contact Dynamics (NSCD) method proposed by Moreau and Jean [2–5] enables to deal with systems containing a large amount of rigid contacts between particles. It relies on a time-stepping integration scheme based on a \(\theta\)-method that is able to consider several contacts appearing within the same time step. This approach is used for modeling many kinds of applications such as the railway ballast [6, 7]. It differs from event-driven techniques [8, 9] which require one to detect impact events and synchronize the time integrator to make the time step coinciding with each event. This is therefore not adapted for granular materials due to the large number of contacts occurring in such media.

The NSCD approach can be applied for a large range of applications in electronics and mechanics [10, 11]. For multibody systems, Flores et al. [12] dealt with the case of planar multibody systems without bilateral constraints. Non-linear dynamic terms are integrated explicitly while the contact problem is solved using a LCP solver. Chen et al. [13] proposed to split the contribution of smooth forces from contribution of contact and bilateral constraints. The smooth motion is integrated with a generalized-\(\alpha\) time integrator. Bilateral and unilateral constraints are then solved at the velocity level for each time step. Using a Gear–Gupta–Leimkuhler (GGL) method enables one to satisfy constraints both at velocity and position levels [14, 15]. In [11], Akhadkar et al. compared numerical simulations with experimental results for the analysis of an electrical circuit breaker and showed the efficiency of the non-smooth methods. However, in the above-mentioned research, the number of contacts treated in example applications is quite limited. As far as a granular medium is concerned, this may be a limitation.

DEM is particularly suitable for dealing with a very large number of particles and contacts. In a complementary way, MBSs are generally focusing on systems with a smaller number of bodies but with complex interactions in addition to contact such as ball joints, universal joints, etc. For coupling those two domains, a first solution is to resort to co-simulation, which means that the two subsystems are solved using two separate time integration procedures with some exchange of data at synchronization points. For instance, Tijskens et al. [16] coupled DEMeter and LMS VirtualLab Motion for studying the interaction between a wheel loader and a rock pile. Using the same technique, Fleissner et al. [17] studied the impact of a fluid cargo on the truck dynamics by resorting to granular methods implemented in the PASIMODO software coupled to the multibody code SIMPACK. Nevertheless, guaranteeing the numerical stability of such co-simulation techniques is not easy. In particular, Kübler and Schiehlen [18] highlighted that stabilizing the coupling by iterating between the two sub-domains inside each time step is necessary when algebraic loops occur between coupled systems. Granular-multibody couplings via contact constraints are treated in the monolithic approach of Anitescu and Tasora [19] and Tasora et al. [20]. In that case, constraints are solved at velocity level with a stabilizing term at position level to limit drift-off effects. This technique is implemented in CHRONO software [21, 22] to cover various kinds of applications.

In the present paper, we propose a unified modeling method for coupling multibody systems and granular media based on the Non-Smooth Contact Dynamics approach. A monolithic time-stepping scheme is applied to the strongly coupled equations of motion of both particles of the granular media and the multibody system. In this way, the accuracy and stability properties of the time-stepping scheme are preserved when applied to the coupled system. In this work, multibody systems are described using relative coordinates. In case of systems with a tree-like topology, only unilateral constraints arising from contact law must be considered. For mechanisms with kinematic-loops, the resulting bilateral constraints are eliminated at the modeling stage by resorting to the coordinate partitioning technique introduced by Wehage and Haug [9, 23]. Contact constraints between grains and between grains and the multibody system are expressed at the velocity level and are solved together using an iterative procedure. The main idea is to ensure that joint kinematics is accurately modeled and no drift-off effect is observed for the bilateral constraints during the numerical integration. For the granular media, the tolerance on the solution of contact equation may be less strict, as far as the collective behavior of the granular media and its action on the multibody systems are correctly captured.

In the next section, it is explained how the NSCD method is applied to multibody systems. Tree-like structures are first considered before extending the method to closed-loop articulated systems. The time discretization is detailed in the following section. Section 4 describes the implementation of the method by coupling the symbolic multibody software ROBOTRAN with LMGC90 which is dedicated to granular media. In Sect. 5 the slider–crank mechanism with clearance benchmark is solved using the proposed coupling and results are compared with other modeling techniques. Finally, in Sect. 6, as an illustrative application, the tamping of a railway track is presented.

2 Non-smooth contact dynamics formalism

Granular media and articulated systems dynamics are governed by the same basic equations, i.e., the Newton–Euler equations. Nevertheless, the different nature of the system, in particular with respect to the possible interactions between bodies, orientates the modeling to different formalisms. In the present work, relative coordinates are chosen for describing the kinematics of multibody chains. Bilateral constraints are necessary for dealing with systems presenting kinematic loops. This approach leads to a limited number of dynamics equations but which involve rather non-linear terms due to many trigonometric operations. For the granular media, the absolute coordinate approach is more natural since grains are independent from each other and interact via contact conditions only. The non-smooth contact dynamics (NSCD) formalism enables to manage efficiently the large number of interactions that occur between the grains. Since it represents the major part of the computational effort, the main idea of the proposed MBS–DEM coupling consists in extending the NSCD approach to the equations of the multibody systems (an attempt was already proposed here [24]). NSCD is explained in details in [25]. In the present section, NSCD is first summarized by introducing the way it formulates the dynamics equation, the contact condition and the mapping between generalized and local coordinates. Then, NSCD is extended to equations of tree-like MBS, i.e., without bilateral constraints. Finally, it is explained how bilateral constraints present in closed-loop MBS are managed using the coordinate partitioning technique.

2.1 Non-smooth contact dynamics for granular media

As its name suggests, the NSCD approach considers that the velocity can be discontinuous. Consequently, the dynamics equation of the granular media is formulated at the velocity level in terms of differential measures:

$$\begin{aligned} \mathbf{M} _{\mathcal{G}}\, \mathrm {d} \mathbf{v} _{\mathcal{G}}= \mathbf {f} _{\mathcal{G}}( \mathbf{q} _{\mathcal{G}}, \mathbf{v} _{\mathcal{G}} , t)\, \mathrm{d} t + \,\mathrm{d} \mathbf{i} _{\mathcal{U}} \end{aligned}$$
(1)

where

\(\mathbf{q} _{\mathcal{G}}\):

is the vector of generalized coordinates describing the absolute position and the orientation of grains;

\(\mathbf{v} _{\mathcal{G}}\):

is the vector of generalized velocities of grains which is composed of the translation velocities \(\mathbf{v} _{i}\) and the angular velocities \(\boldsymbol{\mathbf{\omega}}_{i}\) of each grain \(i\);

\(\mathbf{M} _{\mathcal{G}}\):

is the mass matrix;

\(\mathbf{f} _{\mathcal{G}}\):

represents the non-linear dynamic terms and the force applied on the system;

\(\mathrm{d} \mathbf{v} _{\mathcal{G}}\):

is the differential measure associated with the velocity;

\(t\):

is the time, \(\mathrm{d} t\) is the corresponding standard Lebesgue measure;

\(\mathrm{d} \mathbf{i} _{\mathcal{U}}\):

is the impulse measure associated with the contact reactions.

Since the configuration of the granular media is described by absolute coordinates, the mass matrix is constant. In the above equation, \(\mathrm{d} \mathbf{v} _{\mathcal{G}}\) encompasses the continuous variation of the velocity and the velocity jumps while \(\mathrm{d} \mathbf{i} _{\mathcal{U}}\) groups the contribution of regular contact forces and impacts:

$$\begin{aligned} &\mathrm{d} \mathbf{v} _{\mathcal{G}}= \dot{ \mathbf{v} } \,\mathrm{d} t + \sum_{i} \bigl( \mathbf{v} _{\mathcal{G}}(t_{i})- \mathbf{v} _{\mathcal{G}}^{-}(t_{i}) \bigr) \delta_{t_{i}} , \end{aligned}$$
(2)
$$\begin{aligned} &{\mathrm{d} } \mathbf{i} _{\mathcal{U}} = \mathbf{r} \, \mathrm{d} t + \sum_{i} \mathbf{p} _{i} \delta_{t_{i}} , \end{aligned}$$
(3)

where

\(\mathbf{r} \):

corresponds to the regular contact forces;

\(\dot{ \mathbf{v} }\, \mathrm{d} t\):

is the continuous variation of the velocity;

\(( \mathbf{v} _{\mathcal{G}}(t_{i})- \mathbf{v} _{\mathcal{G}}^{-}(t_{i}) )\):

is the velocity jump at instant \(t_{i}\);

\(\mathbf{v} _{\mathcal{G}}^{-}(t_{i})\):

is the velocity just before the jump;

\(\delta_{t_{i}}\):

the Dirac delta at instant \(t_{i}\);

\(\mathbf{p} _{i}\):

the impulse that produces the velocity jump.

Equation (1) must be completed by the contact conditions detailed in Sect. 2.2.

2.2 Interaction laws

Interaction laws are expressed in a local frame (\(\hat{n}\), \(\hat {t}_{1}\), \(\hat {t}_{2}\)) at the potential contact point \(P\), which allow to distinguish between the normal direction \(\hat{n}\) and the tangential ones \(\hat {t}_{1}\), \(\hat {t}_{2}\). In the present paper, penetration free conditions are considered for the normal direction and dry friction laws for the tangential direction. They are denoted as the Signorini–Coulomb conditions (Fig. 1) and define the relation between the relative velocity \(\mathbf{V} ^{\alpha}\) of the two particles at the contact point and the impulse measure \(\mathrm{d} \mathbf{I} _{\mathcal{U}}^{\alpha}\) associated with the reaction at contact \(\alpha\).

Fig. 1
figure 1

Left: the Signorini condition imposes a complementarity condition between the normal velocity \(V_{\hat{n}}^{\alpha}\) and the normal reaction \(\mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}}\). Right: the Coulomb condition defines three zones for the magnitude \(\mathrm{d}I^{\alpha}_{\mathcal{U}\hat{t}}\) of the tangential reaction which depends on the magnitude \(V_{\hat{t}}^{\alpha}\) of the tangential velocity, the normal reaction and the friction coefficient \(\mu\)

Full size image

For a contact \(\alpha\), the condition along the normal direction at position level is expressed as follows:

$$ g^{\alpha} \geq0, \quad\mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}} \geq0 , \quad g^{\alpha} \, \mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}}= 0, $$
(4)

with

\(\mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}}\):

the normal component of \(\mathrm{d} \mathbf{I} _{\mathcal{U}}^{\alpha}\);

\(g^{\alpha}\):

the gap between the two particles that may enter in contact.

This equation is completed by the Newton impact law that links the velocities before and after the shock:

$$ V^{\alpha}_{\hat{n}}(t_{i}) = -e V_{\hat{n}}^{\alpha-}(t_{i}) $$
(5)

with

\(V_{\hat{n}}^{\alpha-}(t_{i})\):

the velocity just before the impact;

\(V^{\alpha}_{\hat{n}}\):

the velocity just after;

\(e\in{[0,1]}\):

the restitution coefficient.

Following the Moreau–Jean approach [2–4], the non-penetration condition can be formulated at the velocity and impulse level:

$$ \mbox{if}\ g^{\alpha} \leq0\ \mbox{then}\ V^{\alpha}_{\hat{n}}+e V_{ \hat{n}}^{\alpha-} \geq0, \quad\mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}}\geq0 , \quad \bigl(V^{\alpha}_{\hat{n}}+e V_{\hat{n}}^{\alpha-}\bigr)\,\mathrm{d} {I}^{\alpha}_{\mathcal {U}{n}}= 0. $$
(6)

The Coulomb condition for the tangential direction is also formulated at the velocity and impulse level:

$$ \mbox{if}\ g^{\alpha} \leq0 \mbox{then}\ \big\| \mathrm{d} {\mathbf{I}}^{\alpha}_{\mathcal{U}\hat {t}}\big\| \leq\mu\,\mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}}\ \mbox{and if}\ \mathbf{V}_{\hat {t}}^{\alpha} \neq0 \ \mbox{then}\ \mathrm{d} {\mathbf{I}}^{\alpha }_{\mathcal{U}\hat{t}}= - \mu\, \mathrm{d} {I}^{\alpha}_{\mathcal{U}{n}} {\mathbf{V}}_{\hat{t}}^{\alpha}/ \big\| {\mathbf{V}}_{ \hat{t}}^{\alpha} \big\| $$
(7)

with

\(\mathrm{d} \mathbf{I} ^{\alpha}_{\mathcal {U}\hat{t}}\):

the component of \(\mathrm{d} \mathbf {I} _{\mathcal{U}}^{\alpha}\) in the tangent plane \(\hat {t}_{1}\), \(\hat {t}_{2}\);

\(V_{\hat{t}}^{\alpha}\):

the component of the relative velocity in the tangent plane \(\hat {t}_{1}\), \(\hat {t}_{2}\);

\(\mu\):

the friction coefficient.

2.3 Mapping between coordinate systems

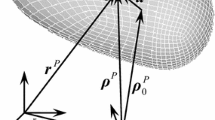
In order to couple the dynamics equation and the contact conditions, the following mapping is defined to link local variables associated with contact \(\alpha\) to generalized coordinates (Fig. 2):

$$ \begin{aligned} & \mathrm{d} \mathbf{i} _{\mathcal{U}}^{\alpha}= \mathbf{H} _{\mathcal{G}}^{\alpha }( \mathbf{q} _{\mathcal{G}})\, \mathrm{d} \mathbf{I} _{\mathcal{U}}^{\alpha}, \\ & \mathbf{V} ^{\alpha}= \mathbf{H} _{\mathcal{G}}^{\alpha}( \mathbf{q} _{\mathcal{G}})^{T} \mathbf{v} _{\mathcal{G}}, \end{aligned} $$
(8)

where

\(\mathrm{d} \mathbf{i} _{\mathcal{U}}^{\alpha}\):

is the contribution of contact \(\alpha\) to \(\mathrm{d} \mathbf {i} _{\mathcal{U}}\);

\(\mathbf{H} ^{\alpha}\):

is the transfer operator between the global and the local frames;

\(\mathbf{H} ^{\alpha T}\):

is the transpose operator of \(\mathbf{H} ^{\alpha}\).

The transfer operators of each contact are assembled in a complete transfer operator \(\mathbf{H} _{\mathcal{G}}( \mathbf {q} _{\mathcal{G}})\) which allows us to write

$$ \begin{aligned} &\mathrm{d} \mathbf{i} _{\mathcal{U}} = \mathbf{H} _{\mathcal{G}}( \mathbf{q} _{\mathcal{G}})\, \mathrm {d} \mathbf{I} _{\mathcal{U}}, \\ & \mathbf{V} = \mathbf{H} _{\mathcal{G}}( \mathbf{q} _{\mathcal{G}})^{T} \mathbf {v} _{\mathcal{G}}, \end{aligned} $$
(9)

where \(\mathrm{d} \mathbf{I} _{\mathcal{U}}\) groups the differential measures \(\mathrm{d} {\mathbf{I}}_{\mathcal{U}}^{\alpha}\) of all contacts \(\alpha\) and \(\mathbf{V} \) the relative velocities \({\mathbf{V}}^{\alpha}\). Using this grouped notation, Eq. (1) becomes

$$\begin{aligned} \mathbf{M} _{\mathcal{G}}\,\mathrm{d} \mathbf{v} _{\mathcal{G}}= \mathbf{f} _{\mathcal{G}}( \mathbf{q} _{\mathcal{G}}, \mathbf {v} _{\mathcal{G}}, t)\, \mathrm{d} t + \mathbf{H} _{\mathcal{G}}\, \mathrm{d} \mathbf{I} _{\mathcal{U}}. \end{aligned}$$
(10)
Fig. 2
figure 2

A global–local mapping enables to formulate the interaction laws in a frame aligned with the direction normal to contact surfaces

Full size image

2.4 NSCD extension to MBS

In order to model contact interactions between multibody systems and granular media, the NSCD formalism is extended to the equations of motion of articulated chains. In the proposed approach, the configuration of the latter is described using relative coordinates, according to the methodology detailed in [26, 27]. Therefore, for a tree-like system (i.e., without any kinematic loop), the dynamics equation for a smooth motion without contact does not involve constraint equations and can be formulated as follows:

$$ \begin{aligned} & \mathbf{M} _{\mathcal{M}}( \mathbf {q} _{\mathcal{M}}) \dot{ \mathbf{v} }_{\mathcal{M}}= \mathbf{f} _{\mathcal{M}}( \mathbf {q} _{\mathcal{M}}, \mathbf{v} _{\mathcal{M}}, t), \\ &\dot{ \mathbf{q} }_{\mathcal{M}}= \mathbf {v} _{\mathcal{M}}, \end{aligned} $$
(11)

where

\(\mathbf{q} _{\mathcal{M}}\):

is the vector of joint position;

\(\mathbf{v} _{\mathcal{M}}\):

is the vector of joint velocities;

\(\mathbf{M} _{\mathcal{M}}\):

is the mass matrix;

\(\mathbf{f} _{\mathcal{M}}\):

groups the non-linear dynamic terms, the forces/torques applied on the system and the joint forces/torques.

Nevertheless, to extend the NSCD formalism to MBS, Eq. (11) is first formulated in terms of differential measures and the contribution of contacts is added in the same way as for Eq. (10) using the impulse measure associated with the contact reactions:

$$\begin{aligned} \mathbf{M} _{\mathcal{M}}( \mathbf{q} _{\mathcal{M}})\, \mathrm{d} \mathbf{v} _{\mathcal{M}}= \mathbf{f} _{\mathcal{M}}( \mathbf {q} _{\mathcal{M}}, \mathbf{v} _{\mathcal{M}}, t)\, \mathrm {d} t + \mathbf{H} _{\mathcal{M}}( \mathbf {q} _{\mathcal{G}}, \mathbf{q} _{\mathcal{M}})\,\mathrm{d} \mathbf{I} _{\mathcal{U}} \end{aligned}$$
(12)

with

\(\mathrm{d} \mathbf{v} _{\mathcal{M}}\):

the differential measure associated with the multibody joint velocity;

\(\mathbf{H} _{\mathcal{M}}\):

the global–local mapping operator that links the multibody generalized coordinates to the contact coordinates.

It is then coupled to Eq. (10), resulting in the following system:

$$\begin{aligned} \left [ \textstyle\begin{array}{cc} \mathbf{M} _{\mathcal{G}} & 0 \\ 0 & \mathbf{M} _{\mathcal{M}}( \mathbf {q} _{\mathcal{M}}) \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \mathrm{d} \mathbf{v} _{\mathcal{G}} \\ \mathrm{d} \mathbf{v} _{\mathcal{M}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \mathbf {f} _{\mathcal{G}}( \mathbf{q} _{\mathcal{G}}, \mathbf{v} _{\mathcal{G}}, t) \\ \mathbf{f} _{\mathcal{M}}( \mathbf{q} _{\mathcal{M}}, \mathbf {v} _{\mathcal{M}}, t) \end{array}\displaystyle \right ]\, \mathrm{d} t + \left [ \textstyle\begin{array}{c} \mathbf{H} _{\mathcal{G}}( \mathbf {q} _{\mathcal{G}}, \mathbf{q} _{\mathcal{M}}) \\ \mathbf{H} _{\mathcal{M}}( \mathbf {q} _{\mathcal{G}}, \mathbf{q} _{\mathcal{M}}) \end{array}\displaystyle \right ]\,\mathrm{d} \mathbf{I} _{\mathcal{U}}. \end{aligned}$$
(13)

This system must be completed by the contact conditions detailed in Sect. 2.2. The two subsystems are thus coupled via the contribution of the contact reaction \(\mathrm{d} \mathbf{I} _{\mathcal{U}}\). The transfer operator \([ \mathbf{H} ]^{T}=[ \mathbf{H} _{\mathcal{G}}^{T}, \mathbf{H} _{\mathcal{M}}^{T}]\) is now composed of two subsets that link local coordinates to the granular coordinates for the first one (\(\mathbf{H} _{\mathcal{G}}\)) and to multibody coordinates for the second one (\(\mathbf{H} _{\mathcal{M}}\)), as illustrated in Fig. 3. For next sections, the dynamics equations represented by Eq. (13) will be written in the following compact form:

$$\begin{aligned} \mathbf{M} ( \mathbf{q} )\, \mathrm{d} \mathbf{v} = \mathbf{f} ( \mathbf{q} , \mathbf{v} , t)\, \mathrm{d} t + \mathbf{H} ( \mathbf{q} )\, \mathrm{d} \mathbf {I} _{\mathcal{U}}. \end{aligned}$$
(14)
Fig. 3
figure 3

The global–local mapping adopted for the granular media coordinates is extended to the multibody coordinates

Full size image

2.5 Extension to systems with bilateral constraints

For systems with kinematic loops, the relative coordinates are not independent anymore but have to satisfy loop-closure conditions. In that case, Eq. (12) is completed by adding the contribution of bilateral constraints:

$$\begin{aligned} & \mathbf{M} _{\mathcal{M}}( \mathbf {q} _{\mathcal{M}})\, \mathrm{d} \mathbf{v} _{\mathcal{M}}= \mathbf{f} _{\mathcal{M}}( \mathbf {q} _{\mathcal{M}}, \mathbf{v} _{\mathcal{M}}, t)\, \mathrm{d} t+ \mathbf{H} _{\mathcal{M}}( \mathbf {q} _{\mathcal{G}}, \mathbf{q} _{\mathcal{M}}) \,\mathrm {d} \mathbf{I} _{\mathcal{U}}+ \mathbf {J} _{\mathcal{B}}^{T}( \mathbf{q} )\, \mathrm{d} \mathbf{I} _{\mathcal{B}}, \end{aligned}$$
(15)
$$\begin{aligned} & \mathbf{h} _{\mathcal{B}}( \mathbf {q} _{\mathcal{M}}) = 0, \end{aligned}$$
(16)

where

\(\mathbf{h} _{\mathcal{B}}( \mathbf {q} _{\mathcal{M}})\):

denotes the bilateral constraints;

\(\mathbf{J} _{\mathcal{B}}( \mathbf {q} _{\mathcal{M}})=\partial \mathbf{h} _{\mathcal{B}}/\partial \mathbf{q} _{\mathcal{M}}\):

is the matrix of bilateral constraint gradient;

\(\mathrm{d} \mathbf{I} _{\mathcal{B}}\):

is the impulse measure of the bilateral constraint forces.

In the present work, the coordinate partitioning technique is used to eliminate the bilateral constraints and to recover a system with a similar form to (12). This technique is detailed in [26] and it is here explained how it is adapted to the NSCD formulation of the dynamics equation. The generalized coordinates and the generalized velocities of the multibody system are split between two sets, the independent ones (\(\mathbf{q} _{\mathcal{M}, u}\), \(\mathbf{v}_{\mathcal{M}, u}\)) and the dependent ones (\(\mathbf{q} _{\mathcal{M}, v}\), \(\mathbf{v}_{\mathcal{M}, v}\)):

$$ \mathbf{q} _{\mathcal{M}}= \left [ \textstyle\begin{array}{c} \mathbf {q} _{\mathcal{M}, u} \\ \mathbf{q} _{\mathcal{M}, v} \end{array}\displaystyle \right ] \quad\mbox{and} \quad \mathbf{v} _{\mathcal{M}}= \left [ \textstyle\begin{array}{c} \mathbf{v}_{\mathcal{M}, u} \\ \mathbf{v}_{\mathcal{M}, v} \end{array}\displaystyle \right ]. $$

The partitioning is not unique but results from the choice of the model designer. A LU factorization of the Jacobian matrix \(\mathbf{J} _{\mathcal{B}}\) can be used to choose a set of independent variables depending on the configuration of the system (see [26]). The impact of the coordinate partitioning on the contact resolution is discussed on the example presented below in Sect. 5.

Applying the partitioning to the dynamics equation (15),

$$ \left [ \textstyle\begin{array}{cc} \mathbf{M} _{\mathcal{M}, uu} & \mathbf{M} _{\mathcal{M}, uv} \\ \mathbf {M} _{\mathcal{M}, vu} & \mathbf{M} _{\mathcal{M}, vv} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \mathrm{d} \mathbf{v}_{\mathcal{M}, u} \\ \mathrm{d} \mathbf{v}_{\mathcal{M}, v} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} \mathbf{f}_{\mathcal{M}, u} \\ \mathbf{f}_{\mathcal{M}, v} \end{array}\displaystyle \right ] \,\mathrm{d} t + \left [ \textstyle\begin{array}{c} \mathbf{H} _{\mathcal{M},u} \\ \mathbf{H} _{\mathcal{M},v} \end{array}\displaystyle \right ]\, \mathrm{d} \mathbf{I} _{\mathcal{U}}+ \left [ \textstyle\begin{array}{c} \mathbf{J} _{\mathcal{B},u}^{T} \\ \mathbf{J} _{\mathcal{B},v}^{T} \end{array}\displaystyle \right ]\, \mathrm{d} \mathbf{I} _{\mathcal{B}} $$
(17)

where \(\mathbf{J} _{\mathcal{B},v}^{T}\) is square and nonsingular. The impulse measures of the bilateral constraints \(\mathrm{d} \mathbf{I} _{\mathcal{B}}\) can be computed from the second line of (17):

$$ \mathrm{d} \mathbf{I} _{\mathcal{B}}= \bigl( \mathbf{J} _{\mathcal{B},v}^{T}\bigr)^{-1} ( \mathbf{M} _{\mathcal{M}, vu} \,\mathrm{d} \mathbf{v}_{\mathcal{M}, u}+ \mathbf {M} _{\mathcal{M}, vv}\, \mathrm{d} \mathbf{v}_{\mathcal{M}, v} - \mathbf{f}_{\mathcal{M}, v}\, \mathrm{d} t - \mathbf {H} _{\mathcal{M},v}\,\mathrm{d} \mathbf{I} _{\mathcal{U}}) . $$
(18)

Dependent positions are computed from the independent positions by solving Eq. (16) (for instance by using an iterative procedure such as the Newton–Raphson algorithm). Dependent velocities can be expressed as a function of independent velocities using the bilateral constraint equation at velocity level:

$$ \mathbf{J} _{\mathcal{B}} \mathbf{v} _{\mathcal{M}}= \left [ \textstyle\begin{array}{cc} \mathbf {J} _{\mathcal{B},u} & \mathbf{J} _{\mathcal{B},v} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \mathbf{v}_{\mathcal{M}, u} \\ \mathbf{v}_{\mathcal{M}, v} \end{array}\displaystyle \right ] = \mathbf{0} , $$
(19)

which gives

$$ \mathbf{v}_{\mathcal{M}, v}= - \mathbf {J} _{\mathcal{B},v}^{-1} \mathbf{J} _{\mathcal{B},u}\mathbf{v} _{\mathcal{M}, u}= \mathbf{B} _{vu}\mathbf{v}_{\mathcal{M}, u}\mathrm{\quad with~} \mathbf{B} _{vu}= - \mathbf {J} _{\mathcal{B},v}^{-1} \mathbf{J} _{\mathcal {B},u}\mathrm{\quad.} $$
(20)

Let us differentiate Eq. (19):

$$ \mathrm{d} \mathbf{J} _{\mathcal{B}} \mathbf {v} _{\mathcal{M}}+ \mathbf{J} _{\mathcal{B}}\, \mathrm{d} \mathbf{v} _{\mathcal{M}}= \mathbf{0} . $$
(21)

Then, observing that \(\mathbf{J} _{\mathcal{B}}( \mathbf{q} _{\mathcal{M}})\) only depends on the position \(\mathbf{q} _{\mathcal{M}}\), its expression is continuous in time and its differential measure is purely diffuse, i.e., \(\mathrm{d} \mathbf {J} _{\mathcal{B}}= \dot{ \mathbf{J} }_{\mathcal{B}}\, \mathrm{d}t\). We obtain

$$ \dot{ \mathbf{J} }_{\mathcal{B}} \mathbf {v} _{\mathcal{M}}\,\mathrm{d}t + \mathbf{J} _{\mathcal{B}}\, \mathrm{d} \mathbf{v} _{\mathcal{M}}= \mathbf{0} , $$
(22)

which can be partitioned as Eq. (19)

$$ \dot{ \mathbf{J} }_{\mathcal{B}} \mathbf {v} _{\mathcal{M}}dt + \left [ \textstyle\begin{array}{cc} \mathbf{J} _{\mathcal {B},u} & \mathbf{J} _{\mathcal{B},v} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \mathrm {d} \mathbf{v}_{\mathcal{M}, u} \\ \mathrm{d} \mathbf{v}_{\mathcal{M}, v} \end{array}\displaystyle \right ] = \mathbf{0} $$
(23)

and finally

$$ \mathrm{d} \mathbf{v}_{\mathcal{M}, v}= - \mathbf{J} _{\mathcal{B},v}^{-1} \dot{ \mathbf {J} }_{\mathcal{B}} \mathbf{v} _{\mathcal{M}}\,\mathrm{d} t + \mathbf{B} _{vu}\,\mathrm{d} \mathbf{v}_{\mathcal{M}, u} = \mathbf{b} \, \mathrm{d} t + \mathbf {B} _{vu}\, \mathrm{d} \mathbf{v}_{\mathcal{M}, u}\quad \mbox{with}\ \mathbf{b} = - \mathbf {J} _{\mathcal{B},v} ^{-1} \dot{ \mathbf{J} }_{\mathcal{B}} \mathbf {v} _{\mathcal{M}}. $$
(24)

Replacing (18), (20) and (24) in the first line of (17):

$$\begin{aligned} & \bigl( \mathbf{M} _{\mathcal{M}, uu}+ \mathbf{B} _{vu}^{T} \mathbf{M} _{\mathcal{M}, vu}+ \mathbf{M} _{\mathcal{M}, uv} \mathbf {B} _{vu}+ \mathbf{B} _{vu}^{T} \mathbf {M} _{\mathcal{M}, vv} \mathbf{B} _{vu}\bigr) \, \mathrm{d} \mathbf{v}_{\mathcal{M}, u} \\ & \quad= \bigl( \mathbf{f}_{\mathcal{M}, u}+ \mathbf{B} _{vu}^{T}\mathbf{f} _{\mathcal{M}, v}- ( \mathbf{M} _{\mathcal{M}, uv}+ \mathbf{B} _{vu}^{T} \mathbf{M} _{\mathcal {M}, vv}) \mathbf{b} \bigr) \,\mathrm{d} t + \bigl( \mathbf{H} _{\mathcal{M},u}+ \mathbf {B} _{vu}^{T} \mathbf{H} _{\mathcal{M},v}\bigr)\, \mathrm {d} \mathbf{I} _{\mathcal{U}}, \end{aligned}$$
(25)

which can be concisely written as

$$ \mathbf{M} _{\mathcal{M}, \text{red}}( \mathbf{q} _{\mathcal{M}, u})\, \mathrm{d} \mathbf{v} _{\mathcal{M}, u}= \mathbf{f} _{\mathcal{M}, \text{red}} ( \mathbf{q} _{\mathcal{M}, u}, \mathbf{v}_{\mathcal{M}, u}, t)\, \mathrm{d} t + \mathbf{H} _{\mathcal{M},\text{red}}( \mathbf {q} _{\mathcal{G}}, \mathbf{q} _{\mathcal{M}, u})\, \mathrm{d} \mathbf{I} _{\mathcal{U}}; $$
(26)

Equation (26) presents the same form as Eq. (12) and can be coupled to equations of the granular media in the same way using the reduced operator \(\mathbf{M} _{\mathcal{M}, \text{red}}\), \({\mathbf{f}}_{\mathcal{M}, \text{red}}\) and \({\mathbf{H}}_{\mathcal{M},\text{red}}\). The bilateral constraints influence the properties of the obtained reduced mass matrix, which may also affect the contact problem as discussed in [28].

Similarly to the case without bilateral constraints, the contact conditions are defined using a global–local mapping depending on the reduced operator \(\mathbf{H} _{\mathcal{M},\text{red}}\):

$$ \begin{aligned} & \mathbf{V} = \mathbf{H} _{\mathcal {M},\text{red}}^{T}\mathbf{v}_{\mathcal{M}, u}, \\ & \mathrm{d} \mathbf{i} _{\mathcal{U}} = \mathbf{H} _{\mathcal{M},\text{red}}\,\mathrm{d} \mathbf {I} _{\mathcal{U}} . \end{aligned} $$
(27)

3 Time discretization

In the proposed approach, the coupled dynamics equation (14) is discretized using a monolithic and implicit scheme. Nevertheless, the non-linear force vector \(\mathbf{f} ( \mathbf {q} , \mathbf{v} ,t)\) is integrated explicitly, following the Moreau time-stepping method [2, 25]:

$$\begin{aligned} & \mathbf{v} _{n+1} = \mathbf{v} _{n} + \mathbf{M} ( \mathbf{q} _{m})^{-1} \bigl(h \mathbf{f} ( \mathbf{q} _{m}, \mathbf{v} _{n}, t) + \mathbf{H} ( \mathbf{q} _{m}) \mathbf{I} _{\mathcal{U},n+1}\bigr) , \end{aligned}$$
(28)
$$\begin{aligned} & \mathbf{q} _{m} = \mathbf{q} _{n} + (1- \theta) h \mathbf{v} _{n}, \end{aligned}$$
(29)
$$\begin{aligned} & \mathbf{q} _{n+1} = \mathbf{q} _{m} + \theta h \mathbf{v} _{n+1}, \end{aligned}$$
(30)

where

\(h\):

is the time step size;

\(n\):

indices denote known values at the beginning of the time step;

\(n+1\):

indices denote unknown values at the end of the time step;

\(h \mathbf{f} ( \mathbf{q} _{m}, \mathbf{v} _{n}, t)\):

approximates \(\int_{t_{n}}^{t_{n+1}} \mathbf{f} ( \mathbf{q} , \mathbf{v} , t) \, \mathrm{d} t \);

\(\mathbf{I} _{\mathcal{U},n+1}\):

approximates \(\int_{t_{n}}^{t_{n+1}}\, \mathrm{d} \mathbf{I} _{\mathcal{U}}\);

\(\mathbf{q} _{m}\):

corresponds to an intermediate position computed explicitly.

In addition, the unknowns \(\mathbf{I} _{\mathcal {U},n+1}\) and \(\mathbf{v} _{n+1}\) must satisfy the contact conditions at velocity level at time \(t_{n+1}\). Since there are generally more contact unknowns than particle degrees of freedom, it is more efficient to solve the contact problem in the local frame. The global–local mapping operator is computed in the \(\mathbf{q} _{m}\) configuration. Thus, by multiplying (28) by \(\mathbf{H} ^{T}( \mathbf{q} _{m})\), the dynamics equation formulated in the local frame can be written as

$$ \mathbf{V} _{n+1} = \mathbf{V} _{\mathrm{free}} + \mathbf{W} \mathbf{I} _{\mathcal{U},n+1} $$
(31)

with

$$\begin{aligned} & \mathbf{V} _{\mathrm{free}} = \mathbf{H} ^{T}( \mathbf{q} _{m}) \bigl( \mathbf{v} _{n} + \mathbf{M} ( \mathbf{q} _{m})^{-1} h \mathbf{f} ( \mathbf{q} _{m}, \mathbf{v} _{n}, t) \bigr) , \\ & \mathbf{W} = \mathbf {H} ^{T}( \mathbf{q} _{m}) \mathbf{M} ^{-1}( \mathbf{q} _{m}) \mathbf{H} ( \mathbf{q} _{m}). \end{aligned}$$

The Signorini–Coulomb condition for a contact \(\alpha\) is discretized as follows:

$$\begin{aligned} \mbox{if}\ g^{\alpha}\leq0 \ \mbox{then}\ &V_{\hat{n},n+1}^{\alpha}+eV_{ \hat{n},n}^{\alpha} \geq0, \quad I_{\hat{n},n+1}^{\alpha}\geq0 , \quad V_{\hat{n},n+1}^{\alpha}~ I_{\hat{n},n+1}^{\alpha}= 0, \\ & \big\| \mathbf{I} _{\hat{t},n+1}^{\alpha}\big\| \leq\mu I_{\hat{n},n+1}^{\alpha}, \\ & \mbox{and}\ \mbox{if}\ \mathbf{V} _{\hat {t},n+1}^{\alpha }\neq \mathbf{0} ,\quad \mathbf{I} _{\hat{t},n+1}^{\alpha}= - \mu I_{\hat{n},n+1}^{\alpha} \mathbf{V} _{\hat {t},n+1}^{\alpha}/ \big\| \mathbf{V} _{\hat{t},n+1}^{\alpha}\big\| . \end{aligned}$$
(32)

The configuration \(\mathbf{q} _{m}\) is used for determining whether contact conditions are active.

Solving Eqs. (31) and (32) requires an iterative process due to their implicit form. It is important to note that the Delassus operator \(\mathbf{W} \) in Eq. (31) couples the unknowns \(\mathbf{V} _{n+1}^{\alpha}\) and \(\mathbf{I} _{\mathcal{U},n+1} ^{\alpha}\) of contact \(\alpha\) with the corresponding unknowns \(\mathbf {V} _{n+1}^{\beta }\) and \(\mathbf{I} _{\mathcal{U},n+1}^{\beta}\) of other contacts \(\beta\). In the proposed approach, an iterative Gauss–Seidel procedure is used: the unknowns of contact \(\alpha\) at iteration \(k+1\) are determined by solving Eqs. (31) and (32) assuming that other contacts \(\beta\) are known. For contacts \(\beta\) which are already computed, the value at iteration \(k+1\) is used while the value at iteration \(k\) is used for contacts that are not solved yet. Equation (31) for iteration \(k+1\) and contact \(\alpha\) is thus expressed as follows:

$$ \mathbf{V} _{n+1, k+1}^{\alpha} = \mathbf{V} _{\mathrm{free}}^{\alpha} + \sum _{ \beta< \alpha} \mathbf{W} ^{\alpha\beta} \mathbf{I} _{\mathcal{U},n+1, k+1} ^{\beta}+ \sum_{ \beta>\alpha} \mathbf{W} ^{\alpha\beta} \mathbf{I} _{\mathcal{U},n+1, k}^{\beta}+ \mathbf{W} ^{\alpha \alpha} \mathbf{I} _{\mathcal{U},n+1, k+1} ^{\alpha}; $$
(33)

\(\mathbf{V} _{n+1, k+1}^{\alpha}\) and \(\mathbf{I} _{\mathcal{U},n+1, k+1}^{\alpha}\) must satisfy Eq. (32) at each iteration.

The Gauss–Seidel procedure may converge slowly with respect to other techniques such as non-smooth Newton algorithms. Nevertheless it is a robust solution well adapted to problems with a large number of contacts. A detailed description and comparison of several solvers is given in [29].

4 Implementation by coupling two dedicated programs

The main steps of the algorithm implementing the monolithic integration scheme of Sect. 3 are described in Algorithm 1. In practice, the algorithm is implemented via the coupling of two software programs:

  • LMGC90Footnote 1 which is oriented towards the modeling of granular media and associated contact problems,

  • ROBOTRANFootnote 2 which is dedicated to the modeling of multibody systems.

Algorithm 1
figure 4

Time integration scheme for the coupled system

Full size image

Those two programs are well proven solutions for each of those modeling fields. They are still actively developed using an open architecture which enables many couplings such as the one presented in this paper. Both are able to deal with research problems as well as industrial applications as shown in next sections. The main idea is to take advantage of the strengths of the two programs to implement the strong coupling strategy presented previously. In particular, ROBOTRAN generates the equation of motion of the MBS in a symbolic form which are easily accessed from the contact solver of LMGC90. This enables to get a monolithic resolution of the contact problem even resorting to two different programs. The Python interfaces available for the two programs allow to set-up and control the simulation in a simple way.

In practice, on the one hand, LMGC90 computes the dynamics of grains, i.e., bodies which are independent from each other and interact via contact constraints only. On the other hand, ROBOTRAN calculates the kinematics and dynamics of articulated chains which contains several bodies connected by joints and that may be in contact with grains also. ROBOTRAN thus deals with the multibody topology, i.e., degrees of freedom and bilateral constraints between bodies of the articulated chains. It also defines the dynamic properties of each body of the chain (mass, inertia matrix, center of mass). All this information is processed by the symbolic engine of ROBOTRAN which thus provides symbolic functions for determining the direct dynamics (generalized mass matrix and dynamics force vector) as well as the mapping from generalized coordinates to positions and velocities of each body.

Each software manages the generalized coordinates of its own components. On the contrary, all the information about contact geometries is collected by LMGC90, both for grains and bodies attached to the multibody chains.

Therefore, for each time step, collision detection is performed by LMGC90, while ROBOTRAN previously determined the absolute positions of contact geometries in the global frame. This operation relies on a two-step process. First, a neighborhood search is carried out to find potential contacts. Then the common plane technique proposed by Cundall [30] is used to check whether contact exists. The different kinds of contacts can be detected in such a way (vertex-to- face, edge-to-edge, etc.). This strategy is suitable for the application presented below which contains convex shapes only. For more complex cases such as non-convex geometries, other techniques are implemented in LMGC90 such as the ones presented in [31].

The computation of the Delassus operator \(\mathbf{W} \) also requires a communication between the two pieces of software. Indeed, for determining the global–local mapping operator \(\mathbf{H} \), ROBOTRAN computes the mapping from the generalized relative coordinates to the absolute position of contact geometries while LMGC90 compute the mapping from this absolute position to the contact frame.

Afterwards, the contact problem is solved by LMGC90 via the Gauss–Seidel procedure. The local reactions are then transposed to the global frame. Finally, LMGC90 computes the position and velocities of grains while ROBOTRAN determines the final positions and velocities of multibody joints.

In the presence of kinematic loops in the multibody topology, bilateral constraints are solved internally by ROBOTRAN on the basis of the coordinate partitioning technique described in Sect. 2.5.

5 Academic example: the slider–crank mechanism

In this section the slider–crank mechanism with a translational clearance joint is modeled using the proposed approach. This benchmark is described in [12, 14] and has been modeled via different approaches. Though it does not involve any granular media, it implies intermittent contacts between the piston and the cylinder.

The system is composed of four bodies: the crank, the connecting rod, the slider (or piston) and the ground (which embed the cylinder). All bodies are considered perfectly rigid. They are connected by perfect hinge joints. The benchmark parameters are defined according to [13]. The geometrical parameters are illustrated in Fig. 4 and mass and inertia are given in Table 1. The center of mass are located at the mid-distances between joints for the crank and the rod and at the center of the body for the slider.

Fig. 4
figure 5

The slider–crank is composed of four rigid bodies (including the ground, dimensions in mm)

Full size image
Table 1 Inertia and mass of bodies of the slider–crank system
Full size table

The simulation of the mechanism starts from the top dead center (all angles set to 0, slider centered in the cylinder) with the following initial absolute angular velocities: crank 150 rad/s, connecting rod −75 rad/s, slider 0 rad/s.

Frictionless contact is considered between the slider and the cylinder with a restitution coefficient \(e=0.4\). The gravity acceleration is opposite to the \(y\) direction and equal to 10 m/s2. The first multibody model of the mechanism is composed of a single chain with three bodies connected by revolute joints (Fig. 5a). The system does not present any kinematic loops and it does not involve any bilateral constraints. Slider–cylinder interactions are accounted by imposing the non-penetration contact conditions between each corner of the slider and the cylinder walls. For the second multibody model, the position and orientation of the slider is defined by absolute coordinate. The slider–rod hinge is modeled by a bilateral constraint which imposes the concordance between positions of the slider center and the rod end (Fig. 5b and c). For this model, the coordinate partitioning technique is used to solve bilateral constraints. Two choices of independent and dependent coordinates are tested. For the first one, the two translational degrees of freedom of the slider are taken as dependent. For the second one, the slider \(y\) translation is set independent and the rotation of the crank is dependent instead.

Fig. 5
figure 6

The slider–crank can be modeled as a linear multibody chain (a) or with a constraint (b and c)

Full size image

The proposed coupling is compared with two other modeling approaches. The first is based on the non-smooth generalized-\(\alpha\) method proposed by Brüls et al. [15]. It is based on absolute nodal coordinates and enforces the joint and contact constraints at position and velocity level simultaneously. The second is a pure LMGC90 implementation of the benchmark. Contact constraints are dealt with the NSCD formalism explained above. Joint constraints are then not eliminated by coordinate partitioning but are imposed at velocity level. The resulting drift-off effect prevents to take time step larger than \(2\cdot10^{-6}\) s.

The motion of the mechanism is simulated for two revolutions of the crank. The slider is first pressed against the upper wall when it leaves the top or the bottom dead center (Fig. 6). Then, due to the gravity, it drops against the bottom wall when slowing down before reaching the opposite dead center. For a \(1\cdot10^{-5}\) s time step, this behavior is correctly reproduced by the proposed method and presents a good match with the two other techniques. The non-penetration condition is well respected and the rebounds due to the restitution coefficient are well captured. It thus enables to take a five time larger time step compared to the pure LMGC90 implementation of the benchmark.

Fig. 6
figure 7

Trajectory of the slider center of the slider–crank benchmark for three modeling approaches: the proposed MBS–DEM coupling, the non-smooth generalized-\(\alpha\) method and a pure LMGC90 implementation of the benchmark

Full size image

Regarding the representation of the multibody system, i.e., using a single multibody chain or introducing a constraint between the rod and the slider, a good match is observed between the different options, provided a small enough time step is used (Fig. 7 left). Nevertheless, for a larger time step (Fig. 7 right), a drift-off effect appears, meaning that the slider penetrates into the wall. This is particularly the case when the mechanism is close to the bottom dead center. This phenomenon appears for all choices of coordinate partitioning but is particularly visible for two of those: the single chain and the cut chain with the two translation joints set as dependent. On the contrary, when the \(y\) translation is set independent, wall penetration is not visible on the graph. In the latter case, the local-global mapping operator \(\mathbf{H} \) along the normal direction depends on the \(y\) translation mainly. It is thus almost linear. For the two other cases, it depends on the rotations of the crank and the rod. This introduces more non-linearities due to trigonometric functions. Evaluating the \(\mathbf{H} \) operator in the intermediate configuration \(\mathbf{q} _{m}\) is thus more penalizing in those cases. This example illustrates how the choice of the coordinate partitioning may affect the results. In some cases, introducing more degrees of freedom and bilateral constraints may be beneficial for the precision of the simulations.

Fig. 7
figure 8

Trajectory of the slider center for different multibody chains and different choices of coordinate partitioning

Full size image

6 Illustrative application: the tamping of railway tracks

The tamping process is a maintenance operation performed on railway infrastructure for restoring a smooth track geometry. While the rail is lift to the desired position, the ballast under the sleeper is compacted by one or several pairs of arms. For each sleeper, the process consists of three main phases: penetration of arms in the ballast, squeezing of arms and lifting out (Fig. 8). The global motion of the tamping tools is combined with a vibration so as to induce a “semi-viscous” state in the ballast which enhances the process. The impact of the vibration can be studied by resorting to the discrete element method and imposing the trajectory of the tamping arms [7]. Nevertheless, considering the motion of the whole machine and the efforts applied in the actuators is of practical interest for constructors and infrastructure managers. The method presented in previous sections enables to establish a coupled model of the tamping machine and the ballast.

Fig. 8
figure 9

The tamping of ballast under each sleeper consists of three main phases: penetration (or diving), squeezing and lifting

Full size image

The tamping unit studied for this illustrative application is inspired by the machine described in the FR2666357 patent [32]. This design presents a specific interest for the present benchmark: the vibration is caused by the rotation of an unbalanced flywheel rather than an eccentric shaft as for other kind of machine. Thus, the oscillations of the arms results from a purely dynamic effect. Kinematics and geometric data were deduced from information given in [32]. Dynamic data was estimated from the main dimensions. Only a single pair of arms is taken into account. Typical operational frequency range for the vibrations lies between 30 and 45 Hz.

From the modeling point of view, a purely planar motion is considered for the tamping machine, without loss of generality, the proposed methodology being able to deal with three-dimensional applications. The model is composed of eight rigid bodies and ten joints (Fig. 9a). The main support is assumed to follow a vertical motion. It is connected to the chassis via linear springs. Other bodies are connected together via perfect hinges. The motion of the arms is driven by an hydraulic actuator modeled as two rigid bodies linked by a prismatic joint. The motion is constrained by two kinematic loops that imposes four algebraic constraints, resulting in six degrees of freedom for the whole multibody system.

Fig. 9
figure 10

The system is modeled with a multibody system (using MBS) and a granular system (using DEM)

Full size image

The ballast grains are modeled by rigid polyhedra with three-dimensional motions. Several stones were digitalised using photogrammetry. Resulting meshes were simplified to convex polyhedra with about 25 vertices. A larger number of grains was generated by scaling the scanned grains so as to respect a realistic ballast granulometry. More than 5000 grains are placed in a \(1.3~\mbox{m} \times0.6~\mbox{m} \times0.6~\mbox{m}\) box bounded by rigid walls (Fig. 9b). A \(0.25~\mbox{m} \times0.6~\mbox{m} \times0.215~\mbox{m}\) rigid parallelepiped represents the sleeper which is maintained in fixed position. Finally, each tamping arm geometry is represented by a cluster of two convex polyhedra attached to the corresponding bodies of the multibody system. The MBS–DEM coupling results from the contact between these parts and the ballast grains. The restitution coefficient between stones and between the ballast and the arms is set to 0. Setting this value is a simple manner to represent the non-linear wave effect that traverses the granular media through the contact network and induces the energy dissipation. This makes sense for such an application where the energy of an impacting stone is directly dissipated in the ballast with a time scale smaller than the considered time step size.

Simple control laws are considered in order to simulate the machine operating the two first steps of a tamping cycle, i.e., the diving followed by the squeezing. Firstly, the diving motion is generated via an external force \(F_{s}\) applied on the support. In the penetration phase, a constant diving force is applied with an additional damping term

$$ F_{s}(t) = F_{s, 1} - C_{s, 1} v_{s} $$
(34)

where \(v_{s}\) is the vertical speed of the support, \(F_{s, 1}\) the magnitude of the downward force and \(C_{s, 1}\) is a damping coefficient. During the squeezing phase, the force applied on the support aims at keeping it at a constant height:

$$ F_{s}(t) = -K_{s, 2} \Delta z_{s} - C_{s, 2} v_{s} $$
(35)

where \(\Delta z_{s}\) is the difference between the vertical position of the support and a fixed targeted position, \(K_{s, 2}\) is a stiffness coefficient and \(C_{s, 2}\) a damping coefficient. Secondly, the squeezing motion of the tamping arms is generated by imposing a joint force \(F_{a}\) between the two bodies that model the hydraulic actuator:

$$ F_{a}(t) = -K_{a} \bigl(x_{a}-L(t)\bigr) - C_{a} v_{a} $$
(36)

where \(x_{a}\) is the elongation of the actuator, \(L(t)\) is the targeted actuator length given as a function of time, \(v_{a}\) is the speed of the actuator rod with respect to the barrel, \(K_{a}\) is a stiffness coefficient and \(C_{a}\) is a damping coefficient.

The main parameters of the model are given in Table 2. For this application, a 0.5 ms time step size is used. Depending on the configuration, a computing time between 160 and 220 hours is needed to simulate 2 s of the real process on a single core.Footnote 3 About 95% of the computational time is spent to solve the contact problem using the Gauss–Seidel procedure. The time to compute the multibody system dynamics is negligible. The restitution time could be reduced by using parallel computing techniques implemented in LMGC90.

Table 2 Main parameters of the tamping operation model
Full size table

Various cases are simulated. Firstly, the tamping operation is simulated for various frequencies: two in the common range (30 Hz and 45 Hz) and one below (15 Hz). In that case, arm vibrations arise from the dynamics due to rotation of the unbalanced flywheel. Secondly, the 15 Hz frequency is also simulated by imposing the vibration of the tamping arms. Here, the main chassis is forced to follow a sinusoidal motion with respect to the support. The amplitude of the imposed motion corresponds to the amplitude of the first case before the machine enters the ballast.

The simulation results highlight the interest of the proposed methodology which enables to account for the dynamics of the machine. We first analyse the diving phase of the cycle plotting the vertical position of the main chassis (Fig. 10) and then we examine the squeezing phase looking at the motion of the hydraulic actuator (Fig. 11).

Fig. 10
figure 11

Diving motion of the tamping unit is affected by the modeling approach. The solid lines refer to simulations accounting for the dynamics of the chassis while, for the dotted line, it is forced to follow a given kinematics

Full size image
Fig. 11
figure 12

Neglecting the dynamics leads to overestimating the squeezing of the tamping arm, which also depends on the frequency. The solid lines refer to simulations accounting for the dynamics of the chassis while, for the dotted line, it is forced to follow a given kinematics

Full size image

Considering the diving motion (Fig. 10) for the two simulations with a 15 Hz vibration frequency, the chassis goes down faster and lower when the vibration motion is imposed (kinematics imposed). The diving depth obtained at 15 Hz with an imposed vibration is similar to the one at 30 Hz and 45 Hz when computing dynamically the vibrations. The performance of the machine is thus overestimated when imposing the kinematics. On the contrary considering the dynamics enables to account for reduction of the vibrations when the tamping arms come into contact with the ballast. For operational purposes, this overestimation of the diving efficiency means that a machine numerically designed to work at 15 Hz will either not penetrate the ballast or require higher pushing load than expected. This will lead to higher ballast degradation.

In the squeezing phase, the motion of the hydraulic cylinder that moves the two arms is analyzed (Fig. 11a). The actuator exerts a force (Fig. 11b) which is proportional to the one applied on the ballast. Again it can be seen that the performances obtained with an imposed vibration motion at 15 Hz are overestimated with respect to the dynamic computation of the vibrations at the same frequency. The ballast is more squeezed (higher elongation of the actuator) with a lower load. The performance obtained by imposing the vibration motion are in an intermediate level between the one obtained at 30 and 45 Hz with a dynamical computation of the vibration. This overestimation could lead to two dramatic consequences if the operational frequency is set to 15 Hz. Firstly the squeezing of the ballast is insufficient and the track is not correctly restored. Secondly the higher force applied on the ballast may increase the ballast degradation, leading to a reduced track lifetime.

7 Conclusions

This paper proposes a strong coupling strategy for the unified modeling of multibody and granular dynamics. The non-smooth contact dynamics approach, initially developed for discrete element methods, is also applied to the equations of multibody systems described by relative coordinates. The equation of motion is formulated in term of differential measures. The coupling between granular and multibody systems is ensured by the contribution of contact impulses. This strategy is able to deal with both tree-like and closed-loop multibody systems. For the latter, the coordinate partitioning technique extended to the differential measure formulation enables to eliminate the bilateral constraints due to kinematic loops.

The proposed algorithm is implemented by coupling two research software packages, i.e., LMGC90 and ROBOTRAN, and applied for two examples.

The method is first compared to other modeling approaches on the academic example of the slider–crank mechanism with translational clearance joint. A good agreement with literature results is obtained. Furthermore, the results demonstrate the ability to solve correctly bilateral constraints, even in the case of high dynamics. On the contrary, a drift-off effect appears at the level of unilateral constraints due to the contact conditions. With the proposed approach, this effect can be controlled by reducing the time step size. It is also impacted by the choice of dependent and independent coordinates required for the coordinate partitioning. Investigating schemes in [14, 15] would provide alternatives in order to reduce the drift-off effect without decreasing too much the step size.

Finally, the interest of the proposed strong coupling methodology is demonstrated for the modeling of the tamping process of railway tracks. The tamping machine is modeled using the multibody formalism and the railway ballast using the discrete element method. This example illustrates the ability to deal with an industrial application involving a large number of grains without any stability problem due to the contact resolution. Furthermore, the need to account for the dynamics of the tamping machine appears clearly. Indeed, imposing its kinematics leads to an overestimation of the performance of the process. In addition, the proposed model properly reproduces the observed phenomena in practice. In particular, the simulation of a machine with higher vibration frequencies shows a better compacting of the ballast and reduced operating forces.

Regarding the perspective of the present work, improvements are possible by using other integration methods such as the generalized-\(\alpha\) scheme. This would enable to deal with stiffer multibody systems. In terms of practical applications, the proposed method opens the way towards the understanding and improvement of many industrial processes. In particular, it would enable railway track specialists to compare different tamping machines, optimize their working parameters such as the squeezing force or diving speed, and finally ensure a longer lifecycle of the railway infrastructure.