Gait Transitions in Artificial Non-standard Snake-Like Locomotion Systems Using Adaptive Control

Abstract

This chapter contributes to the modeling, analysis and control of terrestrial artificial locomotion systems. Inspired by previous models, we set up an unconventional model for a snake-like locomotion systems in form of a chain of visco-elastically interconnected mass points in a plane with passive joints, but – in contrast to literature – active links (time-varying link-length) and rotatable skids to change the movement direction and to avoid obstacles. We investigate this model in a dynamical way and focus on controlling these link lengths to achieve a global movement, steered by the skids. From dynamics, the actuator forces have to adjust the prescribed link length for the locomotion. Since it is impossible to determine the necessary actuator forces a-priori, we apply an adaptive lambda-tracking controller to enable the system to adjust these force outputs on-line on its own. Prescribed motion patterns, i.e. specific gaits, are required to guarantee a controlled movement that differ in the number of resting mass points, the load of actuators and spikes, and the lateral forces of the skids. In contrast to literature, the investigated system of n = 10 mass points exhibit a large variety of possible gaits. To determine the most advantageous gaits, numerical investigations are performed and a weighting function offers a decision of best possible gaits. Using these gaits, a gait transition algorithm, which autonomously changes velocity and number of resting mass points depending on the spike, actuator and lateral skid force load, is presented and tested in numerical simulations.

1 Introduction

Earthworms and snakes serve as a biological inspiration for terrestrial robotic locomotion systems [16]. Most of the works within this field are inspired by the remarkable works of Miller (since 1987, important works e.g. [7, 8]) and Shigeo Hirose [4]. In recent years, most research focussed on fabrication, navigation and control/measurement problems, see [6, 9, 15] from a technical point of view with minor analytical investigations. This is our starting point, to present some modeling and analytical investigations on snake-like systems. For this, we introduce a non-standard mechanical model of a snake-like robots in Sect. 2 in order to extend some models and ideas from worm-like locomotion systems in [13]. Moreover, almost all prototypes use active joints to achieve a special kind of snake locomotion (serpentine movement) [3]. Hence, contrary to literature, we model a snake-like locomotion system using passive joints, active links, spikes and rotatable skids to change the movement direction and to avoid obstacles. To achieve movement, special gaits have to be generated in Sect. 3 and are adaptively tracked in dynamics Sect. 4. Because of an uncertain environment, the snake has to adjust its locomotion pattern, i.e., has to perform a gait shift in Sect. 5. Finally, all theoretic items are tested in simulations in Sect. 6.

2 Kinematic Model

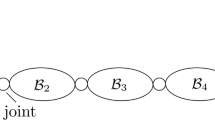
The kinematic model is presented in Fig. 1. It contains several mass points $m_i$ which are connected by links with lengths $r_j$ (hereafter named $l_j$). The unit vector $\vec {e}_{i,i-1}$ points from element $m_i$ to element $m_{i-1}$. Each mass element is equipped with rotatable and spikes skids by the angle $\varGamma _i$ preventing backward displacements. The angle $\varTheta _j$ describes the angle between the x-axis and the link $l_j$, introducing $\gamma _j := \varGamma _j - \varTheta _j$. Each mass element has a skid-fixed coordinate system with $\vec {e}_i$ in tangential and $\vec {g}_i$ in the normal direction, Eq. (1).

Fig. 1

Mass-point model of a snake from [11]

$$\begin{aligned} \vec {e}_i = \quad \cos (\varGamma _i) \vec {e}_x + \sin (\varGamma ) \vec {e}_y\,, \qquad \vec {g}_i = -\sin (\varGamma _i) \vec {e}_x + \cos (\varGamma ) \vec {e}_y \end{aligned}$$

(1)

The positions $\vec {x}_i$ of the mass elements $m_i$ are here (in inertial system):

$$\begin{aligned} \vec {r}_i = x_i \vec {e}_x + y_i \vec {e}_y \end{aligned}$$

(2)

We assume the spiked skids to be ideal, i.e., preventing a backwards movement of the mass element in the skid direction, and a movement laterally to the skid direction, which is hereafter named as no side-slip condition. Therefore, it yields Eq. (3):

$$\begin{aligned} v_{t,i} = \dot{\vec {r}_i} \cdot \vec {e}_i \ge 0\,, \qquad v_{n,i} = \dot{\vec {r}_i} \cdot \vec {g}_i = 0 \end{aligned}$$

(3)

The input variables of the model are the link lengths $l_j(t)$ and the skid angles $\varGamma _i(x_i,y_i)$ which are prescribed as functions of the position $\vec {r}_i$ of mass element $m_i$. According to [11], the kinematic model is (with the special case $\varGamma _0 = \varTheta _1+\gamma _0$):

$$\begin{aligned} \left. \begin{array}{lrcl} &{} \varGamma _i &{} = &{} \varTheta _i+\gamma _i\\ &{} \dot{x}_i &{} = &{} v_i \cos (\varGamma _i)\\ &{} \dot{y}_i &{} = &{} v_i \sin (\varGamma _i)\\ \text {backward:} &{} v_i &{} = &{} \frac{v_{i-1} \cos (\gamma _{i-1}+\varTheta _{i-1}-\varTheta _i) -\dot{l}_i}{\cos (\gamma _i)}\\ \text {- special case:} &{} v_1 &{} = &{} \frac{v_0 \cos (\varGamma _0-\varTheta _1) -\dot{l}_1}{\cos (\gamma _1)}\\ \text {forward:} &{} v_i &{} = &{} \frac{v_{i+1} \cos (\gamma _{i+1}) +\dot{l}_i}{\cos (\gamma _i+\varTheta _i-\varTheta _{i+1})}\\ \text {- special case:} &{} v_0 &{} = &{} \frac{v_1 \cos (\gamma _1) +\dot{l}_1}{\cos (\varGamma _0 -\varTheta _1)}\\ \text {generally:} &{} \dot{\varTheta }_i &{} = &{} \frac{v_{i-1} \sin (\gamma _{i-1}+\varTheta _{i-1}-\varTheta _i)-v_i \sin (\gamma _i)}{l_i(t)} \end{array} \right\} \end{aligned}$$

(4)

Rotatable skids allow for a plane movement. Their angle $\varGamma _i$ referring to the inertial system is a system input for tracking predefined paths. For this, the skid angle of the head segment $\varGamma _0$ is defined as a function of the position and the rearward skid angles. There are several (testing) paths possible, e.g., U-turn, lane change or sinusoid. According to [3], we focus on 4 different types of skid adjusting mechanisms for the rearwards mass elements:

$$ \text {tractrix/exact following/swerve backwards/swerve forwards}. $$

These 4 different skid adjusting mechanisms describe the way in which a mass element $m_i$ follows the predecessor $m_ {i-1}$ and the head segment $m_0$, resp. This may be useful, when traversing an obstacle in order to allow a larger curve radius for rearwards segments.

3 Gaits

To allow a movement of the snake model, the distances between the mass points have to be shortened and lengthened. To guarantee forward movement, at least one mass element has to move forward and at least one has to rest. There are several motion patterns conceivably, so-called gaits. As shown in [12], gaits have to be designed systematically: At first, gaits differ in the number of active spikes $a \in \left\{ 1,\ldots ,n\right\}$ (i.e., resting mass elements). Furthermore, there is a periodic sequence of active spikes $\mathbf {A}(t)$, e.g., for a system with $N=4$ mass points and $a=2$ a possible sequence is $\mathbf {A}(t) = \left\{ 0,1\right\} \rightarrow \left\{ 1,2\right\} \rightarrow \left\{ 2,3\right\} \rightarrow \left\{ 3,0\right\}$, while $\mathbf {A}(t) = \left\{ 0,1\right\} \rightarrow \left\{ 2,3\right\} \rightarrow \left\{ 1,2\right\} \rightarrow \left\{ 3,0\right\}$ is not recommended (no traveling wave). With this knowledge, it can be deduced whether a distance $l_j(t)$ has to be shortened or lengthened at a certain time. Following the recommendation from [12], the sequence of active spike should move to left or to the right, like a worm does. Thus, admissible gaits can be described explicitly by the start sequence $\mathbf {A}_0$ of the resting mass points and the direction dir of the wave of active spikes (“l” for left or “r” for right).

The reference distance functions are built w.r.t. [12]. The time intervals are defined as:

$$\begin{aligned} t \in \left[ p \frac{T}{N}, (p+1) \frac{T}{N} \right] ,\quad p \in \mathbf {N}_0. \end{aligned}$$

To guarantee a smooth movement of the system, i.e., there are no jerks to the mass points, approximations like $\sin ^2(\cdot )$-functions are used for the link lengths, while $\tau = t - p \frac{T}{N}$:

$$\begin{aligned} l_j(\tau ) = l_{0*} + \varepsilon l_0 N f \tau - \frac{1}{2 \pi } \varepsilon l_0 \sin \left( 2 \pi f N \tau \right) , \text { with } \dot{l}_j(\tau ) = \varepsilon l_0 2 N f \sin ^2\left( \pi f N \tau \right) \end{aligned}$$

(5)

• $|\varepsilon | \in (0; 1)$ is the relative factor of the maximum distance change,

• f is the frequency of the $\mathbf {A}(t)$-sequence with its periodic time $T=\frac{1}{f}$, chosen in simulation to avoid a rigid-body-movement of the whole system,

• $l_0>0$ is the initial distance,

• $l_{0*}$ is the distance at the beginning of the time interval $(\tau =0)$, depending on the previous interval either $l_0$, $l_0 (1+\varepsilon )$ or $l_0 (1-\varepsilon )$, [10].

Further investigations in [5] – considering one-dimensional, worm-like locomotion and generation of optimal gaits – have determined the most advantageous gaits regarding the loads of spikes and actuators for a system with $N=10$ mass elements. Hence, these gaits are used for the considerations here and are listed in Table 1.

Table 1 Most advantageous gaits for $N=10$

Fig. 2

Mass element with forces

4 Dynamic Model

To allow the system to shorten and lengthen its links between the mass elements, viscoelastic actuators are assumed between the segments in the following dynamic model. The applied forces are exemplarily given to element i, see Fig. 2. The linear spring forces $F_{c,i}$ and $F_{c,i+1}$ are obtained from the distances between the neighboring mass elements:

$$\begin{aligned} \begin{aligned} \vec {F}_{c,i}&= c_i \cdot \left( ||(\vec {r}_{i-1}-\vec {r}_{i}) ||- l_{0,i} \right) \vec {e}_{i,i-1} \\ \vec {F}_{c,i+1}&= -c_{i+1} \cdot \left( ||(\vec {r}_{i}-\vec {r}_{i+1}) ||- l_{0,i+1} \right) \vec {e}_{i+1,i} \end{aligned} \end{aligned}$$

(6)

The linear damper forces $F_{d,i}$ and $F_{d,i+1}$ are determined (under the assumption of the no side-slip condition, i.e., the normal velocity component $v_{n,i}=0$) using $v_{t,i}$ as the velocity of the mass element $m_i$ in the skid direction ($\vec {e}_i$ direction):

$$\begin{aligned} \begin{aligned} \vec {F}_{d,i}&= d_i \cdot \left[ v_{t,i-1} \cdot \cos (\varGamma _{i-1} - \varTheta _i) - v_{t,i} \cdot \cos (\gamma _i) \right] \vec {e}_{i,i-1} \\ \vec {F}_{d,i+1}&= -d_{i+1} \cdot \left[ v_{t,i} \cdot \cos (\varGamma _{i} - \varTheta _{i+1}) - v_{t,i+1} \cdot \cos (\gamma _{i+1}) \right] \vec {e}_{i+1,i} \end{aligned} \end{aligned}$$

(7)

The weight forces $\vec {F}_{Gx,i}$ and $\vec {F}_{Gy,i}$ are calculated in dependence on the slope angles $\alpha _x$ and $\alpha _y$ (rotation of the plane around x- respectively y-axis):

$$\begin{aligned} \vec {F}_{Gx,i} = - m_i g \sin (\alpha _x) \vec {e}_x \quad \text { and } \quad \vec {F}_{Gy,i} = - m_i g \sin (\alpha _y) \vec {e}_y \end{aligned}$$

(8)

According to [3], Stokes’s friction forces are assumed in the skid direction:

$$\begin{aligned} \vec {F}_{R,i} = - k_{St} v_{t,i} \vec {e}_i \end{aligned}$$

(9)

According to [13], the ideal spikes (spike force $F_{Z}$) have to fulfill:

$$\begin{aligned} \dot{x}_i \ge 0, \qquad F_{Z,i} \ge 0 \quad \text {with complementary-slackness condition} \quad \dot{x}_i \cdot F_{Z,i} = 0\,. \end{aligned}$$

(10)

This condition is fulfilled using Eq. (11), where $\vec {F}_i$ is the sum of all applied forces.

$$\begin{aligned} \vec {F}_{Z,i}(v_{t,i},\vec {F}_i) = \left[ -\frac{1}{2} [1 - \text {sign}(v_{t,i})] [1 - \text {sign}(\vec {F}_i \cdot \vec {e}_i)] \vec {F}_i \cdot \vec {e}_i \right] \vec {e}_i \end{aligned}$$

(11)

Because the skids are considered to be ideal –fulfilling the no side-slip condition– the skid forces are, taking the inertial fraction into account:

$$\begin{aligned} \vec {F}_{K,i} = \left( m_i v_{t,i} \dot{\varGamma }_i - \vec {F}_i \cdot \vec {g}_i \right) \vec {g}_i \end{aligned}$$

(12)

Applied actuators shall generate a movement of the system and serve as inputs to control the distances between the segments. To track a prescribed motion pattern/gait in an uncertain environment, an adaptive $\lambda$-tracking controller is used which generates the necessary actuator forces on its own. Introducing on the error $e_j(t)$:

• $l_j(t) := x_{j-1}(t) - x_j(t)$, the distance between neighboring mass points (outputs);

• $l_{ref,j}(t)$, the predefined reference distance functions of Eq. (5);

• $e_j(t) := l_j(t) - l_{ref,j}(t)$, error of the output;

we apply the controller Eq. (13), see [1, 2]. It contains regular PD-feedback, which adapts the gain of P- and D- elements depending on the 2-norm of the error $\Vert \mathbf {e}(t)\Vert$. The controller’s goal is to track a reference function of the outputs and to keep the error within a certain tolerated accuracy $\lambda$:

$$\begin{aligned} \begin{aligned} \mathbf {e}(t) :=&\; \mathbf {l}(t) - \mathbf {l}_{ref}(t) \\ \mathbf {u}(t) =&\; k(t) \, \mathbf {e}(t) + k(t) \, \kappa \, \dot{\mathbf {e}}(t) = k(t) \cdot \left( \mathbf {e}(t) + \kappa \, \dot{\mathbf {e}}(t) \right) \\ \dot{k}(t) =&{\left\{ \begin{array}{ll} \gamma \cdot ( \Vert \mathbf {e}(t)\Vert - \lambda )^{2}, &{} \Vert \mathbf {e}(t)\Vert \ge \lambda +1 \\ \gamma \cdot ( \Vert \mathbf {e}(t)\Vert - \lambda )^{0.5}, &{} \lambda + 1 > \Vert \mathbf {e}(t)\Vert \ge \lambda \\ 0, &{} (\Vert \mathbf {e}(t)\Vert<\lambda ) \,\, \wedge \,\, (t-t_E<t_d) \\ -\sigma k(t), &{} (\Vert \mathbf {e}(t)\Vert <\lambda ) \,\, \wedge \,\, (t-t_E \ge t_d) \end{array}\right. } \end{aligned} \end{aligned}$$

(13)

with $\gamma> 1,\;\kappa>0,\;\sigma>0,\;t_d \ge 0,\;\lambda \ge 0,\;k_0 > 0$, determined in [5]. Remark: It is obvious that the proposed controller is based on output derivative. This is sometimes quite hard to arrange, see [14] for a way out.

With this relation, Newton’s second law can be applied to get the equations of motion. At first, the following relationships between the skid-fixed and the inertial coordinate system are needed:

$$\begin{aligned} \vec {e}_i = \cos (\varGamma _i)\vec {e}_x + \sin (\varGamma _i)\vec {e}_y \qquad \text {and} \qquad \vec {g}_i = -\sin (\varGamma _i)\vec {e}_x + \cos (\varGamma _i)\vec {e}_y \end{aligned}$$

(14)

Furthermore, by differentiating, we get:

$$\begin{aligned} \dot{\vec {r}}_i = v_{t,i} \vec {e}_i + v_{n,i} \vec {g}_i \qquad \text {and} \qquad \ddot{\vec {r}}_i = \left( \dot{v}_{t,i} - v_{n,i} \dot{\varGamma }_i \right) \vec {e}_i + \left( \dot{v}_{n,i} + v_{t,i} \dot{\varGamma }_i \right) \vec {g}_i \end{aligned}$$

(15)

Summarizing, the differential equation for element $m_i$ in skid coordinates is:

In skid direction $\vec {e}_i$:

$$\begin{aligned} \left. {\begin{aligned} m_0 \left( \dot{v}_{t,0} - v_{n,0} \dot{\varGamma }_0 \right) =&\left( -F_{c,1}-F_{d,1}-u_{1} \right) \cos (\varGamma _0 - \varTheta _{1})+ F_{Z,0} + F_{R,0} \\&+ F_{Gx,0} \cos (\varGamma _0) + F_{Gy,0} \sin (\varGamma _0) \\ m_i \left( \dot{v}_{t,i} - v_{n,i} \dot{\varGamma }_i \right) =&\left( -F_{c,i+1}-F_{d,i+1}-u_{i+1} \right) \cos (\varGamma _i - \varTheta _{i+1})+ F_{Z,i} + F_{R,i} \\&+ \left( F_{c,i}+F_{d,i}+u_{i} \right) \cos (\gamma _i)+ F_{Gx,i} \cos (\varGamma _i) + F_{Gy,i} \sin (\varGamma _i) \\ m_n \left( \dot{v}_{t,n} - v_{n,n} \dot{\varGamma }_n \right) =&\left( F_{c,n}+F_{d,n}+u_{n} \right) \cos (\gamma _n) + F_{Z,n} + F_{R,n}\\&+ F_{Gx,n} \cos (\varGamma _n) + F_{Gy,n} \sin (\varGamma _n) \end{aligned}} \right\} \end{aligned}$$

(16)

Normal to skid direction $\vec {g}_i$:

$$\begin{aligned} \left. {\begin{aligned} m_0 \left( \dot{v}_{n,0} + v_{t,0} \dot{\varGamma }_0 \right) =&\left( +F_{c,1}+F_{d,1}+u_{1} \right) \sin (\varGamma _0 - \varTheta _{1}) + F_{K,0} \\&- F_{Gx,0} \sin (\varGamma _0) + F_{Gy,0} \cos (\varGamma _0) \\ m_i \left( \dot{v}_{n,i} + v_{t,i} \dot{\varGamma }_i \right) =&\left( +F_{c,i+1}+F_{d,i+1}+u_{i+1} \right) \sin (\varGamma _i - \varTheta _{i+1})- F_{Gx,i} \sin (\varGamma _i) \\&+ \left( -F_{c,i}-F_{d,i}-u_{i} \right) \sin (\gamma _i) + F_{K,i} + F_{Gy,i} \cos (\varGamma _i) \\ m_n \left( \dot{v}_{n,n} + v_{t,n} \dot{\varGamma }_n \right) =&\left( -F_{c,n}-F_{d,n}-u_{n} \right) \sin (\gamma _n) + F_{K,n} \\&- F_{Gx,n} \sin (\varGamma _n) + F_{Gy,n} \cos (\varGamma _n) \end{aligned}} \right\} \end{aligned}$$

(17)

5 Gait Transition

In Sect. 3, most advantageous gaits are presented, which have to be autonomously selected to be the best for actual situation. Thinking of an uncertain environment (changing slope, malfunction of actuators, failing of spikes), a gait transition becomes important, because changes result in different loads of (the remaining) actuators, spikes and skids. Hence, the system has to be enabled to react to such changes in switching its gait and frequency on its own. Remark: Analogous example of driving a car – increasing the frequency can be compared to accelerating while gait changing is similar to gear shifting.

The frequency shall only be changed after concluding a single period, i.e., when a part of the sequence $\mathbf {A}(t)$ is finished. Changing the frequency has a large influence on the loads of actuators and spikes. To adjust the frequency, a P-feedback is used. It is possible to weight the load of actuators, spikes and skids against each other using factors $w_{u}$, $w_{Fz}$ and $w_{Fk}$:

$$\begin{aligned}&f_1 = \frac{w_{Fz} f_0 (1 + k_{p,Fz} (F_{z,soll} - F_{z,ist})) + w_{u} f_0 (1 + k_{p,u} (u_{soll} - u_{ist}))}{w_{Fz} + w_u + w_{Fk}} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad +\frac{w_{Fk} f_0 (1 + k_{p,Fk} (F_{k,soll} - F_{k,ist}))}{w_{Fz} + w_u + w_{Fk}} \end{aligned}$$

(18)

with $k_{p,u}$, $k_{p,Fz}$ and $k_{p,Fk}$ as gain parameters for actuators, spikes and skids, $f_0$ as the previous frequency and $f_1$ as the newly adjusted frequency. The set points $u_{set}$, $F_{z,set}$ and $F_{k,set}$ are predefined, while the actual values are within a single period:

$$\begin{aligned} \begin{array}{lll} &{} F_{z,act} = \max \left\{ F_{z,0},F_{z,1},\ldots ,F_{z,9} \right\} \,, \quad &{} F_{k,act} = \max \left\{ F_{k,0},F_{k,1},\ldots ,F_{k,9} \right\} \\ &{} \bar{u}_{j} = \frac{1}{T_{e}} \displaystyle \int \limits _{t-T_{e}}^{t} \! u_{j}(\tau ) \, \mathrm {d} \tau \,, \quad &{} u_{act} = \max \left\{ \bar{u}_1,\bar{u}_2,\ldots ,\bar{u}_9 \right\} \\ \end{array} \end{aligned}$$

(19)

Fig. 3

Algorithm of frequency control and gait transition

The value for the frequency has to be limited to $f_{max}$. Otherwise, there would occur rigid-body-movement, if the frequency exceeded $f_{max}$, according to [13]. During the period of existence of such rigid-body motion, it is uncontrollable in this time-interval. This maximum frequency $f_{max}$, from a kinematical theory according to [13], is given by:

$$\begin{aligned} f_{max}(a) = \sqrt{\frac{g \sin (\alpha )}{2 \pi \varepsilon l_0 N (N-a)}} \end{aligned}$$

(20)

After finishing a total period T, i.e., when the sequence of active spikes would start again, the system changes the number of active spikes a. The model upshifts (decrease the number of active spikes a), if the maximum frequency $f_{max}$ of a gait is reached. It downshifts (increases the number of active spikes a), if the current reference velocity Eq. (21) is also reachable with the next slower gait without exceeding the maximum frequency of the slower gait [13]:

$$\begin{aligned} \bar{v}_{ref}(a,f) = (N-a) \varepsilon l_0 f \end{aligned}$$

(21)

This downshift frequency $f_{min}$ is:

$$\begin{aligned} \bar{v}_{min,a} = \bar{v}_{max,a+1} \quad \Leftrightarrow \quad f_{min} = \frac{N-(a+1)}{N-a} f_{max,a+1} \end{aligned}$$

(22)

After shifting the gait, the frequency has to be adapted to guarantee the same velocity before and after a gait transition. The analogy to car driving is the adaption of the engine speed while shifting. The frequency after the transition is:

$$\begin{aligned} \bar{v}_{new} = \bar{v}_{old} \quad \Leftrightarrow \quad f_{new} = \frac{N-a_{old}}{N-a_{new}} f_{old} \end{aligned}$$

(23)

In Fig. 3, the algorithm of frequency control and gait transition is shown, which is executed after the end of the first single period.

6 Simulation

To demonstrate the functionality of the model, the results of a simulation are shown in Figs. 4, 5 and 6. The model performs a lane change while the rearwards mass elements swerve backwards. In Fig. 5(left) can be seen that the frequency and number of active spikes are adjusted depending on the loads of actuators, spikes and skids, see Fig. 6. Furthermore, the working principle of the adaptive $\lambda$-tracking PD-controller is shown in Fig. 5(right).

Fig. 4

Model movement (left), and skid angles $\varGamma _i$ (right)

Fig. 5

Frequency and number of active spikes (left), gain and error norm (left)

Fig. 6

Actuator forces (left), and spike forces (right)

Fig. 7

Model movement (left), and skid angle $\varGamma _i$(right)

Fig. 8

Frequency and number of active spikes (left), gain and error norm (right)

Fig. 9

Actuator forces (left), and spike forces (right)

7 Conclusion and Outlook

The presented snake-like model consisting of 10 mass points is able to move two-dimensionally by shortening and lengthening its links between each mass point. This is achieved by using viscoelastic actuators which are controlled by an adaptive $\lambda$-tracking PD-controller. To allow lateral movement, spikes respectively skids are mounted at each mass points which are considered as ideal. They inhibit backward movement (spikes) and side-slip (skids) of the mass points. The model is able to adjust the gait and its frequency depending on the loads of actuators, spikes and skids. The gathered knowledge from previous investigations considering one-dimensional worm-like locomotion is transferred to this model, e.g., most advantageous gaits, limitation of actuator forces and using only three different gaits in order to reduce the number of gait shifting. The model is able to use different types of skid adjusting mechanisms, such as tractrix, exact following, swerve backwards and swerve forwards, as well as different curve paths, e.g., U-turns, lane changes and sinusoid.

To conclude the presented work, an example of application is presented hereafter. The model shall move through an environment with obstacles while using different types of skid adjusting mechanisms and curve paths (future work is obviously addressed to path planning). As shown in Fig. 7(left), the model is able to move even through narrow spaces. It adjusts its frequency and gait, see Fig. 8(left). Furthermore, the described adaptive $\lambda$-tracking PD-controller for the actuators works reliably, as one can clearly see in Fig. 8(right). The system loads are presented in Fig. 9.