1 Introduction

Locomotion is the ability to move from place to place. In essence, locomotion of natural or artificial system is the process of producing net motion through proper synchronization of two key elements: (a) internal shape changes, and (b) external medium of contact. By changing its shape, the system exerts some forces (as action) on the surrounding medium of interaction. Consequently, the surrounding medium exerts some forces (as a reaction) onto the system which propel it in the medium. The internal shape changes are mostly cyclic/periodic maneuvers, resulting in a net motion of the system, generally called as gaits or modes of locomotion. In case of limbed locomotion, common modes of locomotion are walking, running, galloping, jumping, etc. While creeping, crawling, undulation, slithering, etc. are the common modes of limbless locomotion [1].

Limbless locomotion is of great interest to researchers in the field of robotics due to its versatility and adaptability. The notable terrestrial limbless locomotion is that of snakes, earthworms, caterpillars, inchworms, etc. The elongated and modular morphology of these organisms makes limbless locomotion even more attractive to robotics researchers. The locomotion of snakes is categorized based on four common types of gaits named as lateral undulation, sidewinding, concertina, and caterpillar/rectilinear [2]. Each type of gait is characterized by a particular cyclic behavior. Generally, snakes easily switch between these gaits based on the characteristics of the medium of interaction. The simple and commonly used gait is the lateral undulatory gait of locomotion, in which waves of lateral bending/undulation propagate along the body from head to tail. Accompanied by the contact of the snake’s skin, which has anisotropic frictional properties, with the ground, these waves result in forward propulsion of the snake. It is revealed from research studies that undulatory locomotion is only possible due to the anisotropic friction properties of belly’s skin of the biological snake [3]. The anisotropic frictional properties of the skin enable the snake to produce high friction in lateral (normal) direction and very small friction in axial (tangential) direction. Thus, the lateral friction is a critical component of undulation in producing effective locomotion.

In snake robots, the lateral undulation has been studied by several researchers [4–9]. The mechanics of undulatory locomotion was explained in the context of multibody systems by J. Ostrowski [4]. Undulatory gait, characterized by a serpenoid curve, was first implemented on a snake robot by S. Hirose in 1973 [5]. The forward propulsion of the robot was obtained by synchronizing the internal shape changes produced by sinusoidal motion of the single degree of freedom yaw joints, with the external contact through passive wheels providing anisotropic friction at the contact point. Over time, due to the increasing interest of researchers in the field of locomotion robots, various other research has been conducted on snake robots related to control, optimization, motion/path planning, etc. [10–15]. Moreover, some multi-modal limbless robots produce multiple gaits in a single robot morphology [16, 17].

Ground-adaptive locomotion is the ability of a system to traverse effectively across various mediums of interaction by adapting its locomotion strategy to the specific characteristics of the medium of interaction. One major area of current research in locomotion robots is the adaptive locomotion in response to changes in the type or characteristics of the surrounding medium of contact. The methods and ways in which the adaptation features are encoded into a locomotion robot depend on the nature and complexity of the system and the surrounding medium [13, 18]. Biological snakes have the natural ability of self adaptation in order to respond to changes in the surrounding medium of contact. Snakes either switch their locomotion gait or adjust the shape parameters of a particular gait to adapt to the characteristics of the ground. As for snake robots, in order to adapt to given surface condition between robot and the surrounding medium, several methods and ways have been presented in the last two decades [13, 19, 20]. Where the complexity level of the algorithms and additional components, required for the system to be adaptive, is reflected from the methods and ways established for adaptive locomotion.

Adaptive locomotion strategies in case of given or changing friction between the robot and surrounding medium of contact are rarely addressed in literature. Therefore, this article presents a simulation study based on the dynamics of the snake-like multibody robotic system that can be used to make the locomotion adaptive and efficient for varying and non-varying friction surfaces. The adaptive and efficient locomotion strategy is only based on the comparison between parameters obtained from dynamic model, without the need for additional algorithms. Furthermore, the research on animal locomotion reveals that the net motion is linearly related to the frequency of internal shape changes [1]. In case of snake locomotion, the speed of propagation (celerity) of the undulatory wave is taken as a reference and the speed of propulsion of the robot is taken as the actual speed of the robot. The idea is to compare these two speeds and then decide the optimum propulsion speed making the robot adaptive to the given surface. This type of model has not yet been developed and may be useful for control and optimization of snake-like robots. Finally, this idea may be applied to the locomotion of other robotic systems such as legged robots, limbless robots, underwater robots, flying robots, etc. [21–23].

This article is organized as follows. Section 2 is devoted to the description of the snake-like multibody robotic system. This section also includes the model of contact and the undulatory gait of locomotion. The concept of ground adaptivity is presented mathematically in Sect. 3. The dynamic model of the system is developed in Sect. 4. In Sect. 5, the simulation is presented and its results are discussed. Finally, Sect. 6 concludes the work presented in this article.

2 Description of the snake-like multibody robotic system

In this article, the snake-like robot is considered as a planar serial chain multibody system consisting of \(p\) number of rigid bodies, called as modules, interconnected by \(p-1\) active revolute yaw joints. Each joint has a single degree of freedom (DoF). All the modules are geometrically identical and each has mass \(m\) and length \(L\). The mass distribution is considered homogeneous, with center of mass (CoM) of each module located at its geometric center. Small passive wheels are attached to each module to provide wheel-ground contact. These passive wheels model the anisotropic friction characteristics of the snakeskin.

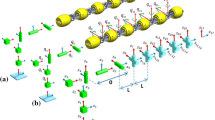
The general topology of the snake-like multibody robotic system is shown in Fig. 1. A Cartesian frame is attached to the joint center of each body. The head (first module) of the robot is selected as a reference body and modules are numbered from head to tail (last module), as depicted in Fig. 1. Based upon the Denavit–Hartenberg (DH) convention, frame \(\mathcal{F}_{j}\) is attached to module \(\mathcal{B}_{j}\) in such a way that the \(z_{j}\)-axis always passes through the joint axis. An outlined frame diagram of the robot is presented in Fig. 2. The joint variables are parameterized by a vector \(q(t)=\left (q_{2}(t),q_{3}(t), \ldots q_{p}(t)\right )^{T}\). The time history of internal joints kinematics \(\left (q(t),\dot{q}(t),\ddot{q}(t)\right )\) is imposed as a function of time and hence is used as an input for the system modeling. As for the body kinematics, the planar velocity of a module \(\mathcal{B}_{j}\) in its body frame \(\mathcal{F}_{j}\) is given by \(V_{j}=\left (V_{jx}, V_{jy}, \Omega _{jz}\right )^{T}\). In the following sections, we model the external contact and the internal shape changes for a snake robot with undulatory locomotion.

Fig. 1
figure 1

Topology of the snake-like robot

Full size image
Fig. 2
figure 2

Outline of snake-like robot with frames

Full size image

2.1 Model of contact

The wheel-ground contact is considered to be the only source of external wrench applied to the system by the surrounding medium. In our two-dimensional system, each module is in contact with the planar ground through a small passive wheel. This provides an anisotropic characteristics of friction, i.e., the axial friction is significantly small as compared to the lateral friction at the point of contact between the wheel and the planar ground. Hence there is no axial friction at the contact point, while the lateral static-kinetic friction exists. The magnitude of the lateral friction force depends upon the mass of the module and the coefficient of lateral friction between the wheel-ground contact, while its direction of application is opposite to the lateral velocity of the module at the contact. The friction is modeled with Coulomb’s law of dry friction. For the purpose of numerical analysis, this static-kinetic model of the lateral friction is given by [24]

$$\begin{aligned} f_{f,j} =\left \{ \textstyle\begin{array}{l@{\quad}l@{\quad}l} -\mu _{s} m g \frac{V_{c,jy}}{\epsilon}& & \text{if} \mid V_{c,jy} \mid \leq \epsilon \\ -\mu _{k} m g \text{ sign}( V_{c,jy})& & \text{if} \mid V_{c,jy} \mid >\epsilon \end{array}\displaystyle , \right . \end{aligned}$$
(1)

where \(\mu _{s}\) and \(\mu _{k}\) are the coefficients of static and kinetic friction, respectively, while \(\epsilon \) is the limit velocity to switch between static and kinetic frictions. \(V_{c,jy}\) is the lateral component of the contact point velocity. Therefore, the contact wrench \(F_{c,j}\) expressed in the local body frame is given by

$$\begin{aligned} \textstyle\begin{array}{l@{\quad}l} F_{c,j} = ^{c}T_{j}^{T} \left ( \textstyle\begin{array}{c} 0 \\ f_{f,j} \\ 0\end{array}\displaystyle \right ) & \text{ with } ^{{c}}{T}_{j}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & 1 & L_{c} \\ 0 & 0 & 1 \end{array}\displaystyle \right ), \end{array}\displaystyle \end{aligned}$$
(2)

where, \(L_{c}\) is the length from body frame to the contact frame.

2.2 Lateral undulation through internal shape changes

In this section, the relation between the parameters of the lateral undulatory wave and that of the internal shape changes is explained. Lateral undulation is a type of snake locomotion characterized by sinusoidal wave like patterns across the body of the snake, propagating from head to tail. Such an undulation can be considered as a one-dimensional traveling wave whose equation is a second-order partial differential equation given as

$$ \frac{\partial ^{2} \kappa (x,t)}{\partial t^{2}}-c^{2} \frac{\partial ^{2} \kappa (x,t)}{\partial x^{2}}=0, $$
(3)

with \((c)\) as the propagation speed, which is also called as celerity of the wave. The solution of the above equation has the following general form

$$ \kappa (x,t)=f(x\pm ct), $$
(4)

which is known as d’Alembert solution. One example of the function \(f\) is given as

$$ \kappa (x,t) = \kappa _{m}\sin \left (kx+\omega t\right ), $$
(5)

which satisfies the wave Equation (3) with \(c=\omega /k\). In case of time-dependent celerity \((c(t))\), Equation (4) takes the following form

$$ \kappa (x,t)=f\left (x\pm \int _{0}^{t} c(\tau )d\tau \right ). $$
(6)

One example of the function \(f\) is given as

$$ \kappa (x,t) = \kappa _{m}\sin \left (kx+\omega (t) t\right ), $$
(7)

with \(c(t)=\omega (t)/k\). Now let us consider the well-known serpenoid curve developed by S. Hirose [5], which is given by

$$ \kappa (s_{o},t) = k\alpha _{o}\sin \left (ks_{o}\right ), $$
(8)

where \(\alpha _{o}\) is the initial winding angle of the curve and \(s_{o}(t)\) is the distance traveled by the curve. In case of time-dependent celerity \((c(t) =\frac{d}{dt}s_{o}(t))\), the above equation can be written as

$$ \kappa (s_{o},t) = k\alpha _{o}\sin \left (k\int _{0}^{t} c(\tau )d \tau \right ). $$
(9)

If the robot is considered as an elongated slender body of length \(l\), it can be modeled as an inextensible planar Kirchhoff beam with yaw deflection [25]. With no side slip, this robot verifies the follow-the-leader approach of snake motion, which is nothing but a one-dimensional traveling wave. Hence in this case, the serpenoid curve (8) takes the following form

$$ \kappa (s,t) = k\alpha _{o}\sin \left (ks\right ), $$
(10)

where \(s(t)=s_{o}(t)+X\) with \(X \in [0,l]\) as a cross-section of the beam. The curvature of the serpenoid curve at any \(X\) is then given by

$$ \kappa (X,t) = k\alpha _{o}\sin \left (k\left (\int _{0}^{t} c(\tau )d \tau +X\right )\right ). $$
(11)

This is in fact the undulatory wave propagating across the length of the robot. The snake-like robot considered in this article consists of rigid bodies serially connected through 1DoF revolute joints. In this case, to shape the body of the snake-like robot over the serpenoid curve (11) through internal shape changes, the relative joint angle between the adjacent bodies is approximated by

$$ q(j,t) = k\alpha _{o}\sin \left (k\left (\int _{0}^{t} c(\tau )d\tau +(j-1)L \right )\right ), \text{ } j=2,3,\ldots ,p, $$
(12)

with

$$ c(\tau )=\frac{\omega (\tau )}{k}. $$
(13)

Keeping \(k\) constant, the joint angle can be written as a sinusoidal wave equation with time-varying angular frequency \((\omega (t))\) as follows

$$ q(j,t) = A\sin \left (\int _{o}^{t}\omega (\tau )d\tau +(j-1)\beta \right ), $$
(14)

with

$$ k=\frac{2\pi K_{n}}{l} \text{, } \beta =\frac{2\pi K_{n}}{p}\text{, } A=k \alpha _{o}, $$
(15)

where \(K_{n}\) is the wave number, \(\alpha _{o}\) is the initial winding angle, \(l\) is the total length of the robot, and \(L\) is the length of a single module. Finally, the complete motion profile of a joint is given as follows

$$\begin{aligned} q(j,t) =& A \sin \left (\int _{o}^{t} \omega (\tau )d\tau + (j-1) \beta \right ), \end{aligned}$$
(16)
$$\begin{aligned} \dot{q}(j,t) =&A \omega (t)\cos \left (\int _{o}^{t} \omega (\tau )d \tau + (j-1)\beta \right ), \end{aligned}$$
(17)
$$\begin{aligned} \ddot{q}(j,t) =&-A \omega ^{2}(t)\sin \left (\int _{o}^{t} \omega ( \tau )d\tau + (j-1)\beta \right ) \\ \text{ }&+A\dot{\omega}(t)\cos \left (\int _{o}^{t} \omega (\tau )d \tau + (j-1)\beta \right ). \end{aligned}$$
(18)

If \(\beta \) is kept constant over time and a time-dependent angular frequency \((\omega (\tau ))\) is assumed, the celerity \((c(\tau ))\) of the undulatory wave changes. The next section relates the celerity of the undulatory wave with the speed of propulsion of the snake-like robot in order to develop a ground-adaptive strategy.

3 Ground-adaptive strategy

The concept of adaptive locomotion is in fact the adaptation of the snake-like robot to the surface conditions for locomotion. In lateral undulation on smooth surfaces, the friction in lateral direction plays a key role in effective locomotion. Because the lateral stick or slip of a module depends on the lateral friction. If there is no lateral slip, the locomotion is perfect and is characterized by follow-the-leader approach. In this approach, each module follows the path of its antecedent module. As the modules are rigid and hence no deformation occurs in the longitudinal direction, the magnitude of axial component (local x-component) of velocity \((V_{jx})\) of each module must satisfy the following condition

$$ |V_{1x}|-|V_{jx}|=0\text{ with } j=1,2,3,\ldots ,p, $$
(19)

where \(V_{1x}\) is the axial component of velocity of the first (head) module, here called as the speed of propulsion of the robot. If the robot propels perfectly, there is no lateral slip \((V_{jy}=0)\) and the energy produced by undulation results in forward thrust of the robot, therefore the speed of propulsion and the celerity \((c)\) of the imposed shape space (i.e., undulatory wave) satisfies the following relation

$$ c-|V_{1x}|=0. $$
(20)

If the locomotion is not perfect, there is a lateral slip of the modules and the lateral velocity of the modules is no longer zero. As a result, the speed of propulsion becomes less than celerity, i.e., Equation (20) is not satisfied.

With this concept, the ground-adaptive strategy can be explained as follows. Let the robot starts moving on a surface with a celerity increasing with time. Initially the robot moves with perfect locomotion satisfying equation (20), i.e., the speed of propulsion of the robot is same as the celerity of undulatory wave. Based upon the surface friction, the robot starts lateral slipping at a certain value of celerity. Equation (20) is then no longer satisfied, which implies that the speed of propulsion of the robot is no longer equal to the celerity. This point is called as point of separation. The strategy is to keep the celerity constant at this point. For a changing surface friction, the strategy is to adjust the celerity in order to reach the separation point. When this strategy is implemented, it makes the locomotion adaptive and efficient by ensuring optimum propulsion speed, i.e., the robot is neither wasting the energy through lateral slip nor under-utilizing it through low speed of propulsion than its optimum value. Such adaptive and efficient locomotion is usually determined through complex control and optimization algorithms, but our proposed algorithm identifies it through Equation (20) or simple computation of the slip factor \((\varepsilon )\) given as follows

$$ \varepsilon = \left (\frac{c-|V_{1x}|}{c}\right )100. $$
(21)

The slip factor requires the value of the speed of propulsion. In the next section, the dynamic model of the robot is developed to compute the speed of propulsion.

4 Dynamic model of snake-like robot

The direct locomotion dynamic model is used to compute the speed of propulsion required for the analysis of the snake-like robot. The general matrix form of such dynamic model for a serial chain multibody system can be written as follows [26]

$$ \mathcal{M}^{+}\dot{\eta}_{1} + M^{T}\ddot{q} + F_{\text{in}}^{+} = F_{ \text{c}}^{+}, $$
(22)

where \(\dot{\eta}_{1}\) is the acceleration of the head of the robot. The “+” as superscript represents a vector/matrix of a composite rigid body. Any composite body \(\mathcal{B}_{j}^{+}\) is a rigid body that is composed of body \(\mathcal{B}_{j}\) and all its successor bodies up to the tail of the snake-like robot, frozen in its current configuration and animated by the motion of body \(\mathcal{B}_{j}\) [26]. The terms of Equation (22) are given as:

$$ \left \{ \textstyle\begin{array}{l} \mathcal{M}^{+}=\mathcal{T}_{1}^{T}\mathcal{M}\mathcal{T}_{1}; \text{ } M^{T} = \mathcal{T}_{1}^{T}\mathcal{M}\mathcal{T}Z; \\ {F}_{\text{in}}^{+} = \mathcal{T}_{1}^{T}\left (\mathcal{M} \mathcal{\dot{T}}_{1}\eta _{1} + \mathcal{M}\mathcal{\dot{T}}Z\dot{q} - F_{ \text{gyr}} \right ); \\ F_{c}^{+} = \mathcal{T}_{1}^{T}F_{\text{c}}, \end{array}\displaystyle \right . $$
(23)

The reader is referred to [26] for detailed expressions and derivations. For our planar system, the vectors/matrices in the above equation are given as follows

$$\begin{aligned} \textstyle\begin{array}{l} T=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & \cdots & 0 \\ ^{2}T_{1} & 0 & 0 & \cdots & 0 \\ 0 & ^{3}T_{2} & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & ^{p}T_{p-1} & 0 \end{array}\displaystyle \right )_{3p\times 3p}\text{ } \mathcal{T}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & \cdots & 0 \\ ^{2}T_{1} & 1 & 0 & \cdots & 0 \\ ^{3}T_{1} & ^{3}T_{2} & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ ^{p}T_{1} & ^{p}T_{2} & \cdots & ^{p}T_{p-1} & 1 \end{array}\displaystyle \right )_{3p\times 3p} \\ \mathcal{T}_{1}=\left ( \textstyle\begin{array}{c} 1 \\ ^{2}T_{1} \\ ^{3}T_{1} \\ \vdots \\ ^{p}T_{1} \end{array}\displaystyle \right )_{3p\times 3} F_{\text{gyr}}=\left ( \textstyle\begin{array}{c} F_{\text{gyr,1}} \\ F_{\text{gyr,2}} \\ \vdots \\ F_{\text{gyr},p} \end{array}\displaystyle \right )_{3p\times 1} \text{ } F_{\text{c}}=\left ( \textstyle\begin{array}{c} F_{\text{c,1}} \\ F_{\text{c,2}} \\ \vdots \\ F_{\text{c},p} \end{array}\displaystyle \right )_{3p\times 1} \\ Z=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} Z_{1} & 0 & \cdots & 0 \\ 0 & Z_{2} & \cdots & 0 \\ \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0& Z_{p} \end{array}\displaystyle \right )_{3p\times p}\text{ } \mathcal{M} = \text{diag}\{ \mathcal{M}_{1}, \mathcal{M}_{2}, \mathcal{M}_{3}, \ldots , \mathcal{M}_{p}\} \end{array}\displaystyle \end{aligned}$$
(24)

The contact wrenches are only due to the wheel-ground contacts. Thus, the vector of contact wrenches \(({F}_{\text{c}})\) is given by Equation (2). Moreover, for planar system, the body parameters are given asFootnote 1

$$\begin{aligned} \textstyle\begin{array}{l} ^{{j}}{T}_{{j-1}}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} cq_{j} & sq_{j} & Lsq_{j} \\ -sq_{j} & cq_{j} & Lcq_{j} \\ 0 & 0 &1 \end{array}\displaystyle \right ),\text{ } ^{{j}}{\dot{T}}_{{j-1}}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} -sq_{j}\dot{q}_{j} & cq_{j}\dot{q}_{j} & Lcq_{j}\dot{q}_{j} \\ -cq_{j}\dot{q}_{j} & -sq_{j}\dot{q}_{j} & -Lsq_{j}\dot{q}_{j} \\ 0 & 0 &0 \end{array}\displaystyle \right ), \\ F_{\text{gyr},j} = \left ( \textstyle\begin{array}{c} mL_{\text{c}}\Omega _{jz}^{2} + m V_{jy} \Omega _{jz} \\ -m V_{jx}\Omega _{jz} \\ -mL_{\text{c}} V_{jx}\Omega _{jz} \end{array}\displaystyle \right ),\text{ } \mathcal{M}_{j} = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} m & 0& 0 \\ 0 & m & mL_{\text{c}} \\ 0 & mL_{\text{c}}& I_{z} \end{array}\displaystyle \right ),\text{ } Z_{j} = \left ( \textstyle\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\displaystyle \right ). \end{array}\displaystyle \end{aligned}$$
(25)

Finally, using the locomotion dynamic model (22), the velocity \((\eta _{1}=(V_{1x},V_{1y},\Omega _{1z})^{T})\) and displacement \((\mathcal{X}_{1}=(x_{1},y_{1},\theta _{1})^{T})\) of the head of the snake-like robot is obtained by time-integration of the following set of equations.

$$ \left \{ \textstyle\begin{array}{l} \dot{\eta}_{1} = \left (\mathcal{M}^{+}\right )^{-1}\left (-M^{T} \ddot{q} - F_{\text{in}}^{+} + F_{\text{c}}^{+}\right ), \\ \mathcal{\dot{X}}_{1}= ^{o}g_{1} \eta _{1}. \end{array}\displaystyle \right . $$
(26)

From this, the coordinates of each module can be computed as

$$\begin{aligned} \textstyle\begin{array}{l} x_{j} = x_{1} + \sum _{k=2}^{j} l\cos (\theta _{k}), \\ y_{j} = y_{1} + \sum _{k=2}^{j} l\sin (\theta _{k}), \\ \theta _{k} = \theta _{1} + \sum _{l=2}^{k} q_{l}, \end{array}\displaystyle \end{aligned}$$
(27)

Moreover, the global frame coordinates \((x,y)\) of the CoM of the whole snake-like robot can be obtained at any instant of time as

$$ (x,y) = \frac{1}{p}\left (\sum _{j=1}^{p} x_{j}, \sum _{j=1}^{p} y_{j}\right ), $$
(28)

The displacement (\(D\)) of the CoM per undulation cycle of the snake-like robot can be written as:

$$ D = \sqrt{(x(T)-x(0))^{2} + (y(T)-y(0))^{2}}, $$
(29)

where \(T\) is the time period of undulation. Therefore, the average velocity (displacement per second) of the CoM is obtained as

$$ \overline{v} = \frac{D}{T}, $$
(30)

5 Simulation results

For the purpose of simulation, the numerical values of input parameters are set as listed in Table 1. The direct dynamic algorithm is coded in Matlab for numerical simulation. The speed of propagation or celerity \((c)\) is changed after one cycle of undulation to compute the average speed of propulsion over one complete cycle. The angular frequency \((\omega )\) is varied from \(20^{o}/\text{ sec}\) to \(3000^{o}/\text{ sec}\). The coefficient of friction is taken as \(\mu _{s} = 0:0.2:1\) with \(\mu _{k} = 0.8\mu _{s}\).

Table 1 Snake-like robot parameters
Full size table

Figure 3 shows the variation in the speed of propulsion \(V_{1x}\) of the robot and the speed of propagation \((c)\) of the undulatory wave vs the variation in the angular frequency \((\omega )\) of the joint motion, for different values of coefficient of friction. The celerity \((c)\) changes linearly with the angular frequency \((\omega )\) and is shown with dotted lines. It is remarkable that the speed of propulsion \((V_{1x})\) is same as the celerity of the traveling wave for a certain range of \(\omega \) which means that with the increase in celerity in this range, the speed of propulsion \((V_{1x})\) also increases at the same rate and thus Equation (20) is fulfilled. Therefore, the locomotion is perfect (no lateral slip) in this range and produces a follow-the-leader motion. As the \(\omega \) crosses this range of perfect locomotion, the rate of increase of the speed of propulsion starts to decrease instead of following the celerity line at the same rate, hence not satisfying Equation (20). This means that the locomotion is no longer perfect and that there is lateral slip.

Fig. 3
figure 3

Speed of propulsion of snake-like robot vs angular frequency of the joints

Full size image

As depicted in Fig. 3, there is a point during locomotion at which the line of speed of propulsion separates from the line of celerity. At this point of separation, the robot is at the verge of lateral slip. In other words, this is the switching point between perfect and imperfect locomotion. It can be said that at this point the robot propels at an optimum speed of propulsion. It is also noteworthy that for different friction surfaces, the point of separation is different. With the increase in the coefficient of friction, the optimum speed of propulsion is also increased, as shown in Fig. 3. Hence at the point of separation, the locomotion is efficient and adaptive to the given surface.

Alternatively, this phenomenon is depicted in Fig. 4 by plotting the slip factor \((\varepsilon )\) vs the angular frequency \((\omega )\). Where, till the point of separation, the slip factor is constant and almost zero. While after the separation point, the slip factor \((\varepsilon )\) increases rapidly and finally almost reaches a maximum value that corresponds to the value for a system with almost zero friction. In other words, at this maximum value, the system has negligible displacement covered compared to the high value of \(\omega \).

Fig. 4
figure 4

Slip factor vs. joint angular frequency

Full size image

Moreover, this trend is also verified by plotting the average velocity of the CoM of the robot vs. the angular frequency \(\omega \) in Fig. 5. Where, the average velocity of the robot linearly increases till the point of separation, while drops nonlinearly afterwards. These results show that the frequency of the cyclic internal motion of joints in locomotion systems can be synchronized with the surface friction for ground adaptivity and efficient locomotion without wastage or under-utilization of energy.

Fig. 5
figure 5

Average velocity of the robot vs. joint angular frequency

Full size image

6 Conclusion

In this paper, the locomotion performance of a snake-like multibody robotic system was studied in the context of ground adaptivity and locomotion efficacy. A relation between the speed of propulsion of robot and the speed of propagation of the lateral undulatory wave was established. Then based on this relation, a strategy for ground adaptivity and efficient locomotion was developed. An algorithm was developed based on the locomotion dynamics of the multibody robotic systems. This algorithm was coded and simulated in Matlab to obtain numerical results. The simulation study revealed that the relation between the speed of propulsion of the robot and the speed of propagation of the undulatory wave can be used to implement the ground-adaptive strategy explained in this article. This work also showed that at the point of separation the speed of propulsion is optimum. Finally, this work opens several avenues for research and further investigation on optimization, control and adaptive locomotion of similar bioinspired locomotion systems on smooth surfaces and any other medium of interaction, e.g., water, air, granular media, etc.