Abstract
This chapter presents an overview of polynomial spline theory, with special emphasis on the B-spline representation, spline approximation properties, and hierarchical spline refinement. We start with the definition of B-splines by means of a recurrence relation, and derive several of their most important properties. In particular, we analyze the piecewise polynomial space they span. Then, we present the construction of a suitable spline quasi-interpolant based on local integrals, in order to show how well any function and its derivatives can be approximated in a given spline space. Finally, we provide a unified treatment of recent results on hierarchical splines. We especially focus on the so-called truncated hierarchical B-splines and their main properties. Our presentation is mainly confined to the univariate spline setting, but we also briefly address the multivariate setting via the tensor-product construction and the multivariate extension of the hierarchical approach.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1.1 Introduction
Splines, in the broad sense of the term, are functions consisting of pieces of smooth functions glued together in a certain smooth way. Besides their theoretical interest, they have application in several branches of the sciences including geometric modeling, signal processing, data analysis, visualization, numerical simulation, and probability, just to mention a few. There is a large variety of spline species, often referred to as the zoo of splines. The most popular species is the one where the pieces are algebraic polynomials and inter-smoothness is imposed by means of equality of derivatives up to a given order. This species will be the topic of the chapter. Several other species can be found in [35, 45] and references therein.
To efficiently deal with splines, one needs a suitable basis for their representation. B-splines turn out to be the most useful spline basis functions because they possess several properties that are important from both theoretical and computational point of view. The construction of B-splines is not confined to the algebraic polynomial case but can be done for many species in the zoo of splines. As it is often the case for important tools or concepts, B-splines have a long history in the sciences. They were already used by Laplace in the early nineteenth century [33], and many of their relevant properties were derived by Chakalov and Popoviciu in the 1930s; see [10] and [37]. However, the modern B-spline theory roots in the seminal works by Schoenberg; see [41, 42] and [15, 16]. There are several ways to define B-splines, based on recurrence, differentiation, divided differences, etc. Each of those definitions has certain advantages according to the problem one has to face. It is impossible to trace all modern works on B-splines, but we refer the reader to Schumaker’s book [45] for an extended bibliography on the topic also beyond the polynomial setting.
This chapter provides an introduction to (polynomial) B-splines, starting from their definition via a recurrence relation. Furthermore, we establish some spline results of interest within the isogeometric analysis (IgA) paradigm. More precisely, the chapter contains
-
a self-contained overview of splines and B-splines;
-
a constructive exploration of approximation properties of spline spaces;
-
a discussion on adaptive spline representations based on hierarchical refinement.
There exists a huge amount of literature about the first two items including some well-established books; see, e.g., [6, 26, 45] and references therein. The hierarchical spline setting received only recently a lot of attention; see, e.g., [22, 51, 53]. The novelties of the chapter can be essentially summarized as follows.
-
Our introduction to B-splines differs somewhat from the standard presentations of the topic. It is mainly based on properties of the dual polynomial functions in the local Marsden identity.
-
Our proof of the approximation properties of a given spline space relies on the explicit construction of a spline quasi-interpolant based on local integrals. For this quasi-interpolant we show error estimates of optimal order to any smooth function and its derivatives.
-
Our presentation of the hierarchical spline setting provides a rather complete and unified treatment of the main properties of both the hierarchical and the truncated hierarchical B-spline basis.
The chapter does not address the geometric modeling aspects of B-splines, explaining why they form the mathematical core of current computer aided design (CAD) systems. For this we refer the reader to the books [13, 27, 38].
Our presentation is mainly confined to the univariate spline setting. Nevertheless, this is the building block of the multivariate setting via the tensor-product construction. Tensor-product B-splines are currently the most common tool in CAD systems and IgA. It is worth mentioning that there are also many other important extensions of the univariate B-spline concepts to the multivariate setting, not restricted to a tensor-product grid; see, for example, [31, 35] and references therein.
The remaining part of the chapter is divided into six sections. The next section is devoted to the definition of B-splines and their main properties, including differentiation and integration formulas, local representation of polynomials, and local linear independence. In Sect. 1.3 we analyze the space spanned by a set of B-splines, and we consider the representation of its elements, knot insertion, and the stability of the B-spline basis. Cardinal B-splines, i.e., B-splines with uniform knots, are of prominent interest in practical applications. They are addressed in Sect. 1.4 where, in particular, the evaluation of their inner products and uniform knot insertion are discussed. In Sect. 1.5, after a general discussion about quasi-interpolants, we present the construction of a new spline quasi-interpolant based on local integrals and we use it to show the approximation properties of the considered spline space. The hierarchical spline approach is the topic of Sect. 1.6, which is mainly devoted to the construction of the truncated hierarchical B-spline basis and the derivation of its main properties, including the so-called preservation of coefficients and the construction of hierarchical quasi-interpolants. Finally, tensor-product B-splines and their hierarchical extension are briefly discussed in Sect. 1.7.
1.2 B-Splines
In this section we introduce one of the most powerful tools in computer-aided geometric design and approximation theory: B-spline functions (in short, B-splines).Footnote 1 They are piecewise polynomials with a certain global smoothness. The positions where the pieces meet are known as knots.
1.2.1 Definition and Basic Properties
In order to define B-splines we need the concept of knot sequences.
Definition 1
A knot sequence ξ is a nondecreasing sequence of real numbers,
The elements ξ i are called knots.
Provided that m ≥ p + 2 we can define B-splines of degree p over the knot-sequence ξ.
Definition 2
Suppose for a nonnegative integer p and some integer j that ξ j ≤ ξ j+1 ≤⋯ ≤ ξ j+p+1 are p + 2 real numbers taken from a knot sequence ξ. The j-th B-spline \(B_{j,p,{\boldsymbol {\xi }}}:{\mathbb {R}}\to {\mathbb {R}}\) of degree p is identically zero if ξ j+p+1 = ξ j and otherwise defined recursively byFootnote 2
starting with
Here we used the convention that fractions with zero denominator have value zero.
We start with some preliminary remarks.
-
For degree 0, the B-spline B j,0,ξ is simply the characteristic function of the half open interval [ξ j, ξ j+1). This implies that a B-spline is continuous except possibly at a knot ξ. We have B j,p,ξ(ξ) = B j,p,ξ(ξ +), where
$$\displaystyle \begin{aligned}x_+:=\lim_{\substack{t\to x \\ t>x}}\ t,\quad x_-:=\lim_{\substack{t\to x \\ t<x}}\ t,\quad x\in{\mathbb{R}}. \end{aligned}$$Thus a B-spline is right continuous, i.e., the value at a point x is obtained by taking the limit from the right.
-
We also use the notation
$$\displaystyle \begin{aligned}B[\xi_j,\ldots ,\xi_{j+p+1}]:=B_{j,p,{\boldsymbol{\xi}}},\end{aligned}$$showing explicitly on which knots the B-spline depends.
-
We say that a knot has multiplicity μ if it occurs exactly μ times in the knot sequence. A knot is called simple, double, triple, … if its multiplicity is equal to 1, 2, 3, …, and a multiple knot in general.
Example 1
A B-spline of degree 1 is also called a linear B-spline or a hat function. The recurrence relation (1.1) takes the form
resulting in
A linear B-spline is discontinuous at a double knot and continuous at a simple knot.
Example 2
A B-spline of degree 2 is also called a quadratic B-spline. Using the recurrence relation (1.1), the three pieces of the quadratic B-spline B j,2,ξ are given by
Example 3
Figure 1.1 illustrates several sets of B-splines of degree p = 1, 2, 3. The same knot sequence is chosen for the different degrees, with only simple knots.
The general explicit expression for a B-spline quickly becomes complicated. Applying the recurrence relation repeatedly we find
where each \(B_{j,p,{\boldsymbol {\xi }}}^{\{i\}}\) is a polynomial of degree p, assumed to be zero if ξ i = ξ i+1. Note that if ξ i = ξ i+1 then B i,0,ξ = 0 and the corresponding polynomial piece is not used. In particular, for the nontrivial cases we have
Furthermore, for the nontrivial cases it follows from Definition 2 that the first and last polynomial pieces in (1.4) are given by
Using induction on the recurrence relation (1.1), we deduce immediately the following basic properties of a B-spline.
-
Local Support. A B-spline is locally supported on the interval given by the extreme knots used in its definition. More precisely,
$$\displaystyle \begin{aligned} B_{j,p,{\boldsymbol{\xi}}}(x)=0, \quad x\notin [\xi_j,\xi_{j+p+1}). \end{aligned} $$(1.6) -
Nonnegativity. A B-spline is nonnegative everywhere, and positive inside its support, i.e.,
$$\displaystyle \begin{aligned} B_{j,p,{\boldsymbol{\xi}}}(x)\ge 0, \quad x\in{\mathbb{R}}, \quad \text{and}\quad B_{j,p,{\boldsymbol{\xi}}}(x)>0, \quad x\in (\xi_j,\xi_{j+p+1}). \end{aligned} $$(1.7) -
Piecewise Structure. A B-spline has a piecewise polynomial structure, i.e.,
$$\displaystyle \begin{aligned} B_{j,p,{\boldsymbol{\xi}}}^{\{i\}}\in{\mathbb{P}}_p, \quad i=j,\ldots,j+p, \end{aligned} $$(1.8)where \({\mathbb {P}}_p\) denotes the space of algebraic polynomials of degree less than or equal to p.
-
Translation and Scaling Invariance. A B-spline is invariant under a translation and/or scaling transformation of its knot sequence, i.e.,
$$\displaystyle \begin{aligned} B_{j,p,\alpha{\boldsymbol{\xi}}+\beta}(\alpha x+\beta)=B_{j,p,{\boldsymbol{\xi}}}(x),\quad \alpha,\beta\in{\mathbb{R}}, \quad \alpha\ne 0, \end{aligned} $$(1.9)where α ξ + β := {αξ i + β}i.
Further properties will be considered in the next sections.
1.2.2 Dual Polynomials
To each B-spline B j,p,ξ of degree p, there corresponds a polynomial ψ j,p,ξ of degree p with roots at the interior knots of the B-spline. We define ψ j,0,ξ := 1 and
This polynomial is called dual polynomial. Many of the B-spline properties can be proved in an elegant way by exploiting a recurrence relation for these dual polynomials.
Theorem 1
For \(p\in {\mathbb {N}}\) , \(x,y\in {\mathbb {R}}\) and ξ j+p > ξ j , we have the dual recurrence relation
and the dual difference formula
Proof
For fixed \(y\in {\mathbb {R}}\) let us define the function \(\ell _y:{\mathbb {R}}\to {\mathbb {R}}\) given by ℓ y(x) := y − x. By linear interpolation, we have
By multiplying both sides with ψ j,p−1,ξ(y) we obtain (1.11). Moreover, (1.12) follows from (1.11) by differentiating with respect to x. □
Proposition 1
The r-th derivative of the dual polynomial ψ j,p,ξ for 0 ≤ r ≤ p can be bounded as follows:
Moreover,
Here we define 00 := 1 if r = p and ξ j+p = ξ j+1.
Proof
Clearly (1.13) holds for all \(p\in {\mathbb {N}}_0\) if r = 0. Using induction on r, p and the product rule for differentiation, we get
and (1.13) follows. The proof of (1.14) is similar. □
1.2.3 Local Marsden Identity and Linear Independence
In this and the following sections (unless specified otherwise) we will extend the knots ξ j ≤⋯ ≤ ξ j+p+1 of B j,p,ξ by defining p extra knots at each end, and we will assume
These extra knots can be defined in any way we like. One possibility is
On such a knot sequence 2p + 1 B-splines B i,p,ξ = B[ξ i, …, ξ i+p+1], i = j − p, …, j + p are well defined.
The following identity was first proved by Marsden [36] and simplifies many dealings with B-splines.
Theorem 2 (Local Marsden Identity)
For j ≤ m ≤ j + p and ξ m < ξ m+1 , we have
If \(B^{\{m\}}_{i,p,{\boldsymbol {\xi }}}\) is the polynomial which is equal to B i,p,ξ(x) for x ∈ [ξ m, ξ m+1) then
Proof
Suppose x ∈ [ξ m, ξ m+1). The equality (1.17) can be proved by induction. It is clearly true for p = 0. Let us now assume it holds for degree p − 1. Then, by means of the dual recurrence (1.11) and the B-spline recurrence relation we obtain
Here we used that \(\frac {x-\xi _i}{\xi _{i+p}-\xi _i}B_{i,p-1,{\boldsymbol {\xi }}}(x)=0\) for i = m − p, m + 1. □
The local Marsden identity immediately leads to the following properties, where we suppose ξ m < ξ m+1 for some j ≤ m ≤ j + p.
-
Local Representation of Monomials. We have for p ≥ k,
$$\displaystyle \begin{aligned} x^k=\sum_{i=m-p}^m\biggl((-1)^k\frac{k!}{p!}D^{p-k}\psi_{i,p,{\boldsymbol{\xi}}}(0)\biggr)B_{i,p,{\boldsymbol{\xi}}}(x), \quad x\in[\xi_m,\xi_{m+1}). \end{aligned} $$(1.19)Proof Fix x ∈ [ξ m, ξ m+1). Differentiating p − k times with respect to y in (1.18) results in
$$\displaystyle \begin{aligned} \frac{(y-x)^k}{k!}=\sum_{i=m-p}^m\left(\frac{1}{p!}D^{p-k}\psi_{i,p,{\boldsymbol{\xi}}}(y)\right)B_{i,p,{\boldsymbol{\xi}}}(x),\quad y \in{\mathbb{R}}, \end{aligned} $$(1.20)for k = 0, 1, …, p. Setting y = 0 in (1.20) results in (1.19). □
-
Local Partition of Unity. Taking k = 0 in (1.19) gives
$$\displaystyle \begin{aligned} \sum_{i=m-p}^m B_{i,p,{\boldsymbol{\xi}}}(x)=1,\quad x\in[\xi_m,\xi_{m+1}). \end{aligned} $$(1.21) -
Local Linear Independence. The two sets \(\{B_{i,p,{\boldsymbol {\xi }}}\}_{i=m-p}^m\) and \(\{\psi _{i,p,{\boldsymbol {\xi }}}\}_{i=m-p}^m\) form both a basis for the polynomial space \({\mathbb {P}}_p\) on any subset of [ξ m, ξ m+1) containing at least p + 1 distinct points.
Proof Let A be a subset of [ξ m, ξ m+1) containing at least p + 1 distinct points. From (1.20) we see that on A every polynomial of degree at most p can be written as a linear combination of the p + 1 polynomials \(B_{i,p,{\boldsymbol {\xi }}}^{\{m\}}\), i = m − p, …, m. Since the dimension of the space \({\mathbb {P}}_p\) on A is p + 1, these polynomials must be linearly independent and a basis. The result for \(\{\psi _{i,p,{\boldsymbol {\xi }}}\}_{i=m-p}^m\) follows by symmetry. □
1.2.4 Smoothness, Differentiation and Integration
The derivative of a B-spline can be expressed by means of a simple difference formula. In the following, we denote the right derivative by D + and the left derivative by D −.
Theorem 3 (Differentiation)
We have
where fractions with zero denominator have value zero.
Proof
If ξ j+p+1 = ξ j then both sides of (1.22) are zero, so we can assume ξ j+p+1 > ξ j. We continue to use the extra knots (1.15). If x < ξ j or x ≥ ξ j+p+1 then both sides of (1.22) are zero. Otherwise x ∈ [ξ m, ξ m+1) for some m with j ≤ m ≤ j + p and it is enough to prove (1.22) for such an interval. Differentiating both sides of (1.17) with respect to x gives
On the other hand, using the local Marsden identity (1.17) for degree p − 1 and the difference formula for dual polynomials (1.12) results in
When comparing this with (1.23) and using the linear independence of the dual polynomials, it follows that (1.22) holds for i = m − p, …, m. In particular, since m − p ≤ j ≤ m, (1.22) holds for i = j. □
Example 4
The differentiation formula (1.22) for p = 2 together with the expression (1.2) immediately gives the piecewise form of the derivative of the quadratic B-spline B j,2,ξ:
This is in agreement with taking the derivative of the piecewise expression (1.3) of B j,2,ξ given in Example 2.
Proposition 2
The r-th derivative of the B-spline B j,p,ξ for 0 ≤ r ≤ p can be bounded as follows. For any x ∈ [ξ m, ξ m+1) with j ≤ m ≤ j + p we have
where
Proof
This holds for r = 0 because of the nonnegativity of B j,p,ξ and the partition of unity property (1.21). By the differentiation formula (1.22) and the local support property (1.6) we have
It follows that
and by induction on r we obtain (1.24). □
Note that the upper bound in (1.24) is well defined since Δ m,k ≥ ξ m+1 − ξ m > 0.
Theorem 4 (Smoothness)
If ξ is a knot of B j,p,ξ of multiplicity μ ≤ p + 1, then
i.e., its derivatives of order 0, 1, …, p − μ are continuous at ξ.
Proof
Suppose ξ is a knot of B j,p,ξ of multiplicity μ. We first consider the smoothness property when μ = p + 1. For x ∈ [ξ j, ξ j+p+1) it follows immediately from (1.4) and (1.5) that
These two B-splines are discontinuous with a jump of absolute size one at the multiple knot showing the smoothness property for μ = p + 1.
Let us now consider the case where B j,p,ξ has an interior knot of multiplicity equal to μ = p, i.e., ξ j < ξ j+1 = ⋯ = ξ j+p < ξ j+p+1. For x ∈ [ξ j, ξ j+p+1) it follows from (1.4) and (1.5) that
The two nontrivial pieces have both value one at the center knot ξ j+1 = ξ j+p, and B j,p,ξ is continuous on \({\mathbb {R}}\). Moreover, the first derivative has a nonzero jump at the center knot.
For the remaining cases we use induction on p to show that B j,p,ξ ∈ C p−μ(ξ). The case p = 1 follows from Example 1. Suppose for some p ≥ 2 that B j,p−1,ξ ∈ C p−1−μ(ξ) at a knot ξ of multiplicity μ. For the multiplicity p case ξ = ξ j = ⋯ = ξ j+p−1 < ξ j+p ≤ ξ j+p+1 we use the recurrence relation
The first term vanishes at x = ξ = ξ j. Since B j+1,p−1,ξ has a knot of multiplicity p − 1 at ξ, it follows from the induction hypothesis that it is continuous there. We conclude that B j,p,ξ is continuous at ξ. The case where the right end knot of B j,p,ξ has multiplicity p is handled similarly. Finally, if μ ≤ p − 1 then both terms in the differentiation formula (1.22) have a knot of multiplicity at most μ at ξ and by the induction hypothesis we obtain D + B j,p,ξ ∈ C p−1−μ(ξ). Moreover, by the recurrence relation and the induction hypothesis it follows that B j,p,ξ is continuous at ξ, and so we also conclude that B j,p,ξ ∈ C p−μ(ξ) if μ ≤ p − 1. This completes the proof. □
The B-spline B j,p,ξ is supported on the interval [ξ j, ξ j+p+1]. Hence, Theorem 4 implies that B j,p,ξ is continuous on \({\mathbb {R}}\) whenever ξ j+p > ξ j and ξ j+p+1 > ξ j+1. Similarly, B j,p,ξ is C r-continuous on \({\mathbb {R}}\) whenever ξ j+p−r+i > ξ j+i for each i = 0, …, r + 1 and − 1 ≤ r < p.
Theorem 5 (Integration)
We have
Proof
This time we define p + 1 extra knots at each end, and we assume
On this knot sequence we consider p + 1 B-splines B i,p+1,ξ, i = j − p − 1, …, j − 1 of degree p + 1. From Theorem 4 we know that these B-splines are continuous on \({\mathbb {R}}\). Therefore, we get for i = j − p − 1, …, j − 1,
where by the local support and the differentiation formula (1.22),
This means that E j = E j−1 = ⋯ = E j−p−1. Moreover, since ξ j−p−1 = ⋯ = ξ j−1, we obtain from (1.28) that
and the integration formula (1.30) follows. □
1.3 Splines
A spline function (in short, spline) is a linear combination of B-splines defined on a given knot sequence with a fixed degree. In this section we analyze the space of splines and discuss several of their properties.
1.3.1 The Spline Space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) and Some Spline Properties
Suppose for integers n > p ≥ 0 that a knot sequence
is given. This knot sequence allows us to define a set of n B-splines of degree p, namely
We consider the space
This is the space of splines spanned by the B-splines in (1.31) over the interval [ξ p+1, ξ n+1], which is called the basic interval.
We now introduce some terminology to identify certain properties of knot sequences which are crucial in the study of the space (1.32).
-
A knot sequence ξ is called (p + 1)-regular if ξ j < ξ j+p+1 for j = 1, …, n. By the local support (1.6) such a knot sequence ensures that all the B-splines in (1.31) are not identically zero.
-
A knot sequence ξ is called (p + 1)-basic if it is (p + 1)-regular with ξ p+1 < ξ p+2 and ξ n < ξ n+1. As we will show later, the B-splines in (1.31) defined on a (p + 1)-basic knot sequence are linearly independent on the basic interval [ξ p+1, ξ n+1].
-
A knot sequence ξ is called (p + 1)-open on an interval [a, b] if it is (p + 1)-regular and it has end knots of multiplicity p + 1, i.e.,
$$\displaystyle \begin{aligned} a:=\xi_1=\cdots=\xi_{p+1}<\xi_{p+2}\le\cdots\le\xi_{n}<\xi_{n+1}=\cdots=\xi_{n+p+1}=:b.\end{aligned} $$(1.33)This sequence is often used in practice. In particular, it turns out to be natural to construct open curves, clamped at two given points. Note that (p + 1)-open implies (p + 1)-basic.
Some further preliminary remarks are in order here.
-
We consider B-splines on a closed basic interval [ξ p+1, ξ n+1]. In order to avoid the asymmetry at the right endpoint we define the B-splines to be left continuous at the right endpoint, i.e., their value at ξ n+1 is obtained by taking the limit from the left:
$$\displaystyle \begin{aligned} B_{j,p,{\boldsymbol{\xi}}}(\xi_{n+1}):=\lim_{\substack{x\to\xi_{n+1} \\ x<\xi_{n+1}}}B_{j,p,{\boldsymbol{\xi}}}(x), \quad j=1,\ldots,n. {} \end{aligned} $$(1.34)Note that for a (p + 1)-open knot sequence the end condition (1.34) means that B n,p,ξ(ξ n+p+1) = 1 and (1.6) has to be modified for this B-spline.
-
We define a multiplicity function \(\mu _{\boldsymbol {\xi }}:{\mathbb {R}}\to {\mathbb {N}}_0\) given by μ ξ(ξ i) = μ i if ξ i ∈ξ occurs exactly μ i ≥ 1 times in ξ, and μ ξ(x) = 0 if x∉ξ. If ξ and \({\tilde {{\boldsymbol {\xi }}}}\) are two knot sequences we say that \({\boldsymbol {\xi }}\subseteq {\tilde {{\boldsymbol {\xi }}}}\) if \(\mu _\xi (x)\le \mu _{{\tilde {{\boldsymbol {\xi }}}}}(x)\) for all \(x\in {\mathbb {R}}\).
-
Without loss of generality, we can always assume that the end knots have multiplicity p + 1. If this is not the case, then we can add extra knots at the ends and assume the extra B-splines to have coefficients zero. This observation simplifies many proofs.
Example 5
Figure 1.2 illustrates all the B-splines of degree p = 3 on a (p + 1)-open knot sequence, where the interior knots are simple.
From the properties of B-splines, we immediately conclude the following properties of the spline representation in (1.32).
-
Smoothness. If ξ is a knot of multiplicity μ then s ∈ C r(ξ) for any \(s\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\), where r + μ = p. This follows from the smoothness property of the B-splines (Theorem 4). The relation between smoothness, multiplicity and degree is as follows:
$$\displaystyle \begin{aligned} \text{``smoothness} + \text{multiplicity}= \text{degree''}. \end{aligned} $$(1.35) -
Local Support. The local support (1.6) of the B-splines implies
$$\displaystyle \begin{aligned} \sum_{j=1}^n c_j B_{j,p,{\boldsymbol{\xi}}}(x)=\sum_{j=m-p}^m c_j B_{j,p,{\boldsymbol{\xi}}}(x), \, x\in [\xi_m,\xi_{m+1}), \, p+1\le m\le n, \end{aligned} $$(1.36)and if ξ m < ξ m+p then
$$\displaystyle \begin{aligned} \sum_{j=1}^n c_j B_{j,p,{\boldsymbol{\xi}}}(\xi_m)=\sum_{j=m-p}^{m-1} c_j B_{j,p,{\boldsymbol{\xi}}}(\xi_m), \quad p+1\le m\le n+1. \end{aligned} $$(1.37) -
Minimal Support. From the smoothness properties it can be proved that if the support of \(s\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) is a proper subset of [ξ j, ξ j+p+1] for some j then s = 0. Therefore, the B-splines have minimal support.
-
Coefficient Recurrence. For x ∈ [ξ p+1, ξ n+1], by the recurrence relation (1.1) we have
$$\displaystyle \begin{aligned} \sum_{j=1}^n c_j B_{j,p,{\boldsymbol{\xi}}}(x)=\sum_{j=2}^n \check{c}_j(x) B_{j,p-1,{\boldsymbol{\xi}}}(x), \end{aligned} $$(1.38)where
$$\displaystyle \begin{aligned} \check{c}_j(x):= \frac{x-\xi_j}{\xi_{j+p}-\xi_j}c_j +\frac{\xi_{j+p}-x}{\xi_{j+p}-\xi_j}c_{j-1}, \end{aligned} $$(1.39)and \(\check {c}_j(x)B_{j,p-1,{\boldsymbol {\xi }}}(x)=0\) if ξ j+p = ξ j.
-
Differentiation. For x ∈ [ξ p+1, ξ n+1], by the differentiation formula (1.22) we have
$$\displaystyle \begin{aligned} D_+\biggl(\sum_{j=1}^n c_j B_{j,p,{\boldsymbol{\xi}}}(x)\biggr)=\sum_{j=2}^n c^{(1)}_j B_{j,p-1,{\boldsymbol{\xi}}}(x), \quad p\geq1, \end{aligned} $$(1.40)where
$$\displaystyle \begin{aligned} c^{(1)}_j := p \biggl(\frac{c_j-c_{j-1}}{\xi_{j+p}-\xi_j}\biggr), \end{aligned} $$(1.41)and fractions with zero denominator have value zero.
-
Linear Independence. If ξ is (p + 1)-basic, then the B-splines in (1.31) are linearly independent on the basic interval. Thus, the spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) is a vector space of dimension n.
Proof We must show that if \(s(x)=\sum _{j=1}^n c_j B_{j,p,{\boldsymbol {\xi }}}(x)=0\) for x ∈ [ξ p+1, ξ n+1] then c j = 0 for all j. Let us fix 1 ≤ j ≤ n. Since ξ is (p + 1)-regular, there is an integer m j with j ≤ m j ≤ j + p such that \(\xi _{m_j}<\xi _{m_j+1}\). Moreover, the assumptions ξ p+1 < ξ p+2 and ξ n < ξ n+1 guarantee that \([\xi _{m_j},\xi _{m_j+1})\) can be chosen in the basic interval. From the local support property (1.36) we know
$$\displaystyle \begin{aligned}s(x)=\sum_{i=m_j-p}^{m_j}c_i B_{i,p,{\boldsymbol{\xi}}}(x)=0,\quad x\in [\xi_{m_j},\xi_{m_j+1}). \end{aligned}$$The local linear independence property (see Sect. 1.2.3) implies \(c_{m_j-p}=\cdots = c_{m_j}=0\), and in particular c j = 0. □
1.3.2 The Piecewise Polynomial Space \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\)
We now prove that the spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) is nothing else than a space of piecewise polynomials of degree p defined by a given sequence of break points and by some prescribed smoothness. The set of knots ξ must be suitably selected according to the break points and the smoothness conditions. Therefore, the B-splines are a basis of such a space of piecewise polynomials.
Let Δ be a sequence of distinct real numbers,
The elements in Δ are called break points. Moreover, let r := (r 1, …, r ℓ) be a vector of integers such that − 1 ≤ r i ≤ p for i = 1, …, ℓ. The space \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\) of piecewise polynomials of degree p with smoothness r over the partition Δ is defined by
Suppose that \(s^{\{i\}}\in {\mathbb {P}}_p\) is the polynomial equal to the restriction of a given function \(s\in {\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\) to the interval [η i, η i+1), i = 0, …, ℓ. Since \(s\in C^{r_i}(\eta _i)\), we have
for some coefficients c i,j. It follows that \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\) is spanned by the set of functions
where the truncated power function \((\cdot )_+^p\) is defined by
and the value at zero is defined by taking the right limit.
It is easy to see that the functions in (1.43) are linearly independent. Indeed, let
On [η 0, η 1) we have \(s(x)=\sum _{j=0}^{p} c_{0,j}\, x^j\) and it follows that c 0,0 = ⋯ = c 0,p = 0. Suppose for some 1 ≤ k ≤ ℓ that c i,j = 0 for i < k. Then, on [η k, η k+1) we have \(s(x)=\sum _{j=r_k+1}^p c_{k,j}(x-\eta _k)^j=0\) showing that all c k,j = 0.
This implies that the set of functions in (1.43) is a basis for \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\), the so-called truncated power basis. As a consequence,
The next theorem shows that the set of B-splines in (1.31) defined over a specific knot sequence ξ forms an alternative basis for \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\). This was first proved by Curry and Schoenberg in [16].
Theorem 6 (Characterization of Spline Space)
The piecewise polynomial space \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\) is characterized in terms of B-splines by
where the knot sequence \({\boldsymbol {\xi }}:=\{\xi _i\}_{i=1}^{n+p+1}\) with \(n:=\dim ({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta ))\) is constructed such that
and
Proof
From the piecewise polynomial and smoothness properties of B-splines it follows that the B-spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) is a subspace of \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\). Moreover, the constructed knot sequence ξ is (p + 1)-basic, so \(\dim ({\mathbb {S}}_{p,{\boldsymbol {\xi }}})=n\) by the linear independence property of B-splines. This implies that \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )={\mathbb {S}}_{p,{\boldsymbol {\xi }}}\). □
Example 6
Consider Δ := {η 0 < η 1 < η 2 < η 3} and the space \({\mathbb {S}}^{\boldsymbol {r}}_3(\varDelta )\) with r = (r 1, r 2) = (2, 1). It follows from Theorem 6 that \({\mathbb {S}}^{\boldsymbol {r}}_3(\varDelta )={\mathbb {S}}_{3,{\boldsymbol {\xi }}}\), where
This knot sequence is 4-open.
Finally, we give a characterization for the space spanned by the r-th derivatives of B-splines for 0 ≤ r ≤ p, i.e.,
Theorem 7 (Characterization of Derivative Spline Space)
Given a knot sequence \({\boldsymbol {\xi }}:=\{\xi _i\}_{i=1}^{n+p+1}\) , we have for 0 ≤ r ≤ p,
where \({\boldsymbol {\xi }}_r:=\{\xi _i\}_{i=r+1}^{n+p+1-r}\).
Proof
The result is obvious for r = 0. Let us now consider the case r = 1, for which we note that
By the differentiation formula (1.40) it is clear that
On the other hand, suppose \(s\in {\mathbb {S}}_{p-1,{\boldsymbol {\xi }}_1}\), represented as \(s=\sum _{j=2}^n d_j B_{j,p-1,{\boldsymbol {\xi }}}\). Then, by using again the differentiation formula, we can write \(s=D_+\big (\sum _{j=1}^n c_j B_{j,p,{\boldsymbol {\xi }}}\big )\), where c 1 can be any real number and
For r > 1 we use the relation \(D_+^r=D_+D_+^{r-1}\). □
By combining Theorems 6 and 7 it follows that for 0 ≤ r ≤ p,
where \({\boldsymbol {r}}-r:=\big (\max (r_1-r,-1),\ldots ,\max (r_\ell -r,-1)\big )\) and the knot sequence ξ is constructed as in Theorem 6.
1.3.3 B-Spline Representation of Polynomials
Polynomials can be represented in terms of B-splines of at least the same degree. We now derive an explicit expression for their B-spline coefficients by using the dual polynomials and the (local) Marsden identity.
Theorem 8 (Marsden Identity)
We have
where ψ j,p,ξ(y) := (y − ξ j+1)⋯(y − ξ j+p) is the polynomial of degree p that is dual to B j,p,ξ.
Proof
This follows immediately from the local version (1.17). Indeed, if x ∈ [ξ p+1, ξ n+1) then x ∈ [ξ m, ξ m+1) for some p + 1 ≤ m ≤ n, and by the local support property (1.36) we get
Taking into account the left continuity of B-splines at the endpoint ξ n+1, see (1.34), we arrive at the Marsden identity (1.45). □
Differentiating p − k times with respect to y in (1.45) results in the following formula.
Corollary 1
For k = 0, 1, …, p we have
Corollary 1 immediately leads to the following properties.
-
Representation of Monomials. For k = 0, 1, …, p we have
$$\displaystyle \begin{aligned} x^k=\sum_{j=1}^n\xi_{j,p,{\boldsymbol{\xi}}}^{\ast,k}B_{j,p,{\boldsymbol{\xi}}}(x), \quad x\in [\xi_{p+1},\xi_{n+1}], \end{aligned} $$(1.47)where
$$\displaystyle \begin{aligned} \xi_{j,p,{\boldsymbol{\xi}}}^{\ast,k}:=(-1)^k\frac{k!}{p!}D^{p-k}\psi_{j,p,{\boldsymbol{\xi}}}(0). \end{aligned} $$(1.48)This follows from (1.46) with y = 0.
-
Partition of Unity. Taking k = 0 in (1.47) gives
$$\displaystyle \begin{aligned} \sum_{j=1}^n B_{j,p,{\boldsymbol{\xi}}}(x)=1, \quad x\in [\xi_{p+1},\xi_{n+1}]. \end{aligned} $$(1.49)Since the B-splines are nonnegative it follows that they form a nonnegative partition of unity on [ξ p+1, ξ n+1].
-
Greville Points. Taking k = 1 in (1.47) gives for p ≥ 1,
$$\displaystyle \begin{aligned} x=\sum_{j=1}^n \xi^\ast_{j,p,{\boldsymbol{\xi}}}B_{j,p,{\boldsymbol{\xi}}}(x), \quad x\in [\xi_{p+1},\xi_{n+1}], \end{aligned} $$(1.50)where
$$\displaystyle \begin{aligned} \xi^\ast_{j,p,{\boldsymbol{\xi}}}:=\xi^{\ast,1}_{j,p,{\boldsymbol{\xi}}}=\frac{\xi_{j+1}+\cdots+\xi_{j+p}}{p}. \end{aligned} $$(1.51)The number \(\xi ^\ast _{j,p,{\boldsymbol {\xi }}}\) is called Greville point.Footnote 3 It is also known as knot average or node.
Example 7
For p = 3 Eq. (1.47) gives
We finally present an expression for the B-spline coefficients of a general polynomial.
Proposition 3 (Representation of Polynomials)
Any polynomial g of degree p can be represented as
where
Proof
The polynomial g can be represented in Taylor form (1.95) as
The result follows when we apply (1.46) with k = p − r. □
Note that, if τ j is a root of ψ j of multiplicity μ j then D r ψ i(τ j) = 0, r = 0, 1, …, μ j − 1 and (1.53) becomes
Example 8
The polynomial g(x) = ax 2 + bx + c can be represented in terms of quadratic B-splines:
From (1.52)–(1.53) with ψ j,2,ξ(y) := (y − ξ j+1)(y − ξ j+2), we obtain that
1.3.4 B-Spline Representation of Splines
In the previous section we have derived an explicit expression for the B-spline coefficients of polynomials; see (1.52). The next theorem extends this result by providing an explicit expression for the B-spline coefficients of any spline in \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\).
Theorem 9 (Representation of B-Spline Coefficients)
Any element s in the space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) can be represented as Footnote 4
where
and where μ j ≥ 0 is the number of times τ j appears in ξ j+1, …, ξ j+p.
Proof
Suppose ξ j ≤ τ j < ξ j+p+1 and let \(I_j:=[\xi _{m_j},\xi _{m_j+1})\) be the interval containing τ j. The restriction of s to I j is a polynomial and so by Proposition 3 we find
Note that since ξ j ≤ τ j < ξ j+p+1 we have j ≤ m j ≤ j + p which implies m j − p ≤ j ≤ m j. By taking i = j in (1.57) and using the local linear independence of the B-splines, we obtain
Since D r ψ j,p,ξ(τ j) = 0 for r < μ j we obtain the top term in (1.56). In the middle term we can replace \(D_+^{p-r}s(\tau _j)\) by D p−r s(τ j) since \(s\in C^{p-\mu _j}(\tau _j)\). The proof of the last term is similar using D − instead of D +. □
Note that the operator Λ j,p,ξ in (1.54) is identical to Λ j,p,ξ in (1.56). However, in the spline case we need the restriction τ j ∈ [ξ j, ξ j+p+1].
Because the set of B-splines \(\{B_{j,p,{\boldsymbol {\xi }}}\}_{j=1}^{n}\) is a basis for the space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\), the coefficients Λ j,p,ξ(s) are uniquely determined for any \(s\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\). Thus, the right-hand side in (1.56) does not depend on the choice of τ j. This is an astonishing property considering the complexity of the expression. For example, one could take the Greville point \(\xi ^\ast _{j,p,{\boldsymbol {\xi }}}\) defined in (1.51) as a valid choice for the point τ j. It is easy to verify that \(\xi ^\ast _{j,p,{\boldsymbol {\xi }}}\in [\xi _j,\xi _{j+p+1}]\), and moreover, \(\xi ^\ast _{j,p,{\boldsymbol {\xi }}}\in (\xi _j,\xi _{j+p+1})\) if B j,p,ξ is a continuous function.
Example 9
We consider the quadratic spline
and we illustrate that some derivative terms in the expression (1.56) can be canceled by specific choices of τ j. Assume for simplicity ξ j < ξ j+1 < ξ j+2 < ξ j+3.
-
If τ j is the Greville point \(\xi ^\ast _{j,2,{\boldsymbol {\xi }}}:=(\xi _{j+1}+\xi _{j+2})/2\), then there is no first derivative term. Indeed, we have
$$\displaystyle \begin{aligned}c_j=\varLambda_{j,2,{\boldsymbol{\xi}}}(s)=s(\xi^\ast_{j,2,{\boldsymbol{\xi}}})-\frac{(\xi_{j+2}-\xi_{j+1})^2}{8}\,D^2s(\xi^\ast_{j,2,{\boldsymbol{\xi}}}). \end{aligned}$$Moreover, since \(s\in {\mathbb {P}}_2\) on [ξ j+1, ξ j+2], we can replace \(D^2s(\xi ^\ast _{j,2,{\boldsymbol {\xi }}})\) by a difference quotient
$$\displaystyle \begin{aligned}D^2s(\xi^\ast_{j,2,{\boldsymbol{\xi}}})=\big(s(\xi_{j+2})-2s(\xi^\ast_{j,2,{\boldsymbol{\xi}}}) +s(\xi_{j+1})\big)\Big/\bigg(\frac{\xi_{j+2}-\xi_{j+1}}{2}\bigg)^2,\end{aligned}$$to obtain
$$\displaystyle \begin{aligned} c_j=-\frac 12s(\xi_{j+1})+2s(\xi^\ast_{j,2,{\boldsymbol{\xi}}})-\frac 12s(\xi_{j+2}). \end{aligned} $$(1.58) -
If τ j is equal to ξ j+1 or ξ j+2, then there is no second derivative term. Indeed, we have
$$\displaystyle \begin{aligned}c_j=\varLambda_{j,2,{\boldsymbol{\xi}}}(s)=s(\tau_j)+\frac{\xi^\ast_{j,2,{\boldsymbol{\xi}}}-\tau_j}{2}\,Ds(\tau_j), \quad \tau_j\in\{\xi_{j+1},\xi_{j+2}\}. \end{aligned}$$A similar property holds for any p: if τ j is chosen as one of the interior knots ξ j+1, …, ξ j+p, then there is no p-th derivative term in the expression of Λ j,p,ξ(s).
1.3.5 Knot Insertion
In this section we are addressing the problem of representing a given spline on a refined knot sequence. In particular, we focus on the special case where only a single knot is inserted. Since any refined knot sequence can be reached by repeatedly inserting one knot at a time, it suffices to deal with this case.
Without loss of generality, we assume that the spline \(s=\sum _{j=1}^n c_j B_{j,p,{\boldsymbol {\xi }}}\) is given on a (p + 1)-basic knot sequence \({\boldsymbol {\xi }}:=\{\xi _i\}_{i=1}^{n+p+1}\). We want to insert a knot ξ in some subinterval [ξ m, ξ m+1) of [ξ p+1, ξ n+1), resulting in a new (p + 1)-basic knot sequence \({\tilde {{\boldsymbol {\xi }}}}:=\{{\tilde {\xi }}_i\}_{i=1}^{n+p+2}\) defined by
The B-spline form of s on the new knot sequence can be computed with the aid of the following procedure introduced by Böhm [3].
Theorem 10 (Knot Insertion)
Let the (p + 1)-basic knot sequence \({\tilde {{\boldsymbol {\xi }}}}:=\{{\tilde {\xi }}_i\}_{i=1}^{n+p+2}\) be obtained from the (p + 1)-basic knot sequence \({\boldsymbol {\xi }}:=\{\xi _i\}_{i=1}^{n+p+1}\) by inserting just one knot ξ, such that ξ m ≤ ξ < ξ m+1 as in (1.59). Then,
where
Proof
From Theorem 6 it follows that \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) is a subspace of \({\mathbb {S}}_{p,{\tilde {{\boldsymbol {\xi }}}}}\), since we have reduced the continuity requirement at ξ m if ξ = ξ m or introduced another segment otherwise. Hence, the B-splines in \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) belong to \({\mathbb {S}}_{p,{\tilde {{\boldsymbol {\xi }}}}}\), and we can write
for some real numbers α i,j,p. Suppose \(s\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) is given by (1.60). Then,
By linear independence of the B-splines in \({\mathbb {S}}_{p,{\tilde {{\boldsymbol {\xi }}}}}\) we obtain
Note that each α i,j,p is independent of the c’s.
Now, consider the function f y(x) := (y − x)p for fixed \(y\in {\mathbb {R}}\). By the Marsden identity (1.45) we have
where
and
Hence, for the function f y(x), the identity (1.62) takes the form
From the relation (1.59) between the knot sequences \({\tilde {{\boldsymbol {\xi }}}}\) and ξ, we deduce that \(\psi _{i,p,{\tilde {{\boldsymbol {\xi }}}}}= \psi _{i,p,{\boldsymbol {\xi }}}\) for i ≤ m − p, and \(\psi _{i,p,{\tilde {{\boldsymbol {\xi }}}}}= \psi _{i-1,p,{\boldsymbol {\xi }}}\) for i > m, and using the dual recurrence relation (1.11) that for m − p < i ≤ m,
Then, (1.61) follows from (1.62) and (1.63). □
When several knots have to be inserted simultaneously, alternative algorithms can be used instead of repeating the single knot insertion procedure given in Theorem 10. In Sect. 1.4.3 we provide such a simultaneous knot insertion algorithm in case of uniform knot sequences. A more general (but also more complex) knot insertion algorithm is known as the Oslo algorithm [11].
-
Convex Combination. From relation (1.61) we see that the coefficients \({\tilde {c}}_i\) are a convex combination of the coefficients c i. In general, the coefficients obtained after repeated knot insertion are a convex combination of the original coefficients.
-
Evaluation. Repeated knot insertion gives rise to an evaluation process for spline functions in B-spline form. Indeed, the evaluation of a spline s at the point x can be achieved by the repeated insertion of x as a knot till it has multiplicity p. Then, assuming that for some m,
$$\displaystyle \begin{aligned}\xi_m<x=\xi_{m+1}=\cdots=\xi_{m+p}<\xi_{m+p+1}, \end{aligned}$$we can conclude from (1.29) and (1.49) that
$$\displaystyle \begin{aligned}B_{j,p,{\boldsymbol{\xi}}}(x)=\begin{cases} 1, & \text{if}\ j=m,\\ 0, & \text{otherwise}, \end{cases} \end{aligned}$$and
$$\displaystyle \begin{aligned}s(x)=\sum_{j=1}^n c_j B_{j,p,{\boldsymbol{\xi}}}(x)= c_{m} B_{m,p,{\boldsymbol{\xi}}}(x)=c_{m}. \end{aligned}$$When comparing (1.61) with (1.39), we observe that single knot insertion is nothing else than applying once the B-spline coefficient recurrence relation. This evaluation procedure is a fast and numerically stable algorithm introduced by de Boor [4].
1.3.6 Condition Number
A basis {B j} of a normed space is said to be stable with respect to a vector norm if there are positive constants K L and K U such that
for all coefficient vectors c := (c j). For simplicity we use the same symbol ∥⋅∥ for the norm in the space and the vector norm. The number
is called the condition number of the basis {B j} with respect to ∥⋅∥.
Such condition numbers give an upper bound for how much an error in coefficients can be magnified in function values and vice versa. Indeed, if f :=∑j c j B j≠0 and g :=∑j d j B j then it follows immediately from (1.64) that
where c := (c j) and d := (d j). Many other applications are given in [5] and it is interesting to have estimates for the size of κ.
We consider the L q-norm for functions and the q-norm for vectors with 1 ≤ q ≤∞. We focus on a scaled version of the B-spline basis defined on [ξ 1, ξ n+p+1],
where γ j,p,ξ := (ξ j+p+1 − ξ j)∕(p + 1); see also (1.30). The knot sequence ξ is assumed to be (p + 1)-basic in order to have linearly independent B-splines. This also ensures that γ j,p,ξ > 0. The q -norm condition number of the basis in (1.66) will be denoted by κ p,q,ξ, i.e.,
The next theorem shows that the scaled B-spline basis above is stable in any L q-norm independently of the knot sequence ξ. It also provides an upper bound for the q-norm condition number which does not depend on ξ. To this end, we first state the Hölder inequality for sums:
where q, q′ are integers so that
In particular, q′ = ∞ if q = 1 and q′ = 2 if q = 2.
Theorem 11
For any p ≥ 0 there exists a positive constant K p depending only on p, such that for any vector c := (c 1, …, c n) and for any 1 ≤ q ≤∞ we have
Proof
We first prove the upper inequality. By using the nonnegative partition of unity property of B-splines, the upper bound for q = ∞ is straightforward. For q = 1, we have
Finally, we consider 1 < q < ∞. By applying the Hölder inequality (1.68) and again the nonnegative partition of unity property of B-splines, we obtain for x ∈ [ξ 1, ξ n+p+1],
Raising both sides of this inequality to the q-th power and integrating gives the inequality
Taking the q-th roots on both sides proves the upper inequality in (1.70).
We now focus on the lower inequality. We extend ξ to a (p + 1)-open knot sequence \(\hat {{\boldsymbol {\xi }}}\) by possibly increasing the multiplicity of ξ 1 and ξ n+p+1 to p + 1. Clearly, the set of B-splines on ξ is a subset of the set of B-splines on \(\hat {{\boldsymbol {\xi }}}\), and any linear combination of the B-splines on ξ is a linear combination of the B-splines on \(\hat {{\boldsymbol {\xi }}}\) where the extra B-splines have coefficients zero. Therefore, without loss of generality, we can assume that the knot sequence is open with the basic interval [ξ 1, ξ n+p+1]. The lower bound then follows from Lemma 5; see Sect. 1.5.3.1. □
Finally, we define a condition number that is independent of the knot sequence,
Theorem 11 shows that
It is known that κ p,q grows like 2p for all 1 ≤ q ≤∞; see [34, 40] where it has been proved that
1.4 Cardinal B-Splines
A particularly interesting case of B-spline functions is obtained when the knot sequence is uniformly spaced. Without loss of generality, we can assume that the knot sequence is given by the set of integers \({\mathbb {Z}}\). It is natural to index the knots as ξ j = j, \(j\in {\mathbb {Z}}\). Due to the translation invariance property (1.9) we have
Therefore, all the B-splines on the knot sequence \({\mathbb {Z}}\) are integer translates of a single function. This motivates the following definition.
Definition 3
The function M p := B[0, 1, …, p + 1] is the cardinal B-spline of degree p.
Example 10
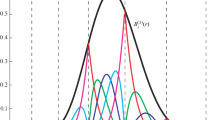
Figure 1.3 illustrates the cardinal B-splines M p for p = 1, …, 5.
1.4.1 Main Properties
Cardinal B-splines possess several interesting features. Of course, they inherit all the properties of general B-splines, and in particular the following ones.
-
Local Support. From (1.6) it follows that the cardinal B-spline M p is locally supported on the interval [0, p + 1].
-
Nonnegativity, Piecewise Structure and Smoothness. From (1.7), (1.8) and (1.26) it follows that the cardinal B-spline M p is a nonnegative, piecewise polynomial of degree p belonging to the class \(C^{p-1}({\mathbb {R}})\).
-
Differentiation and Integration. The formulas (1.22) and (1.30) simplify in the case of cardinal B-splines to
$$\displaystyle \begin{aligned} D_+ M_{p}(x)= M_{p-1}(x)-M_{p-1}(x-1),\quad p\geq1, \end{aligned} $$(1.74)and
$$\displaystyle \begin{aligned} \int_{\mathbb{R}} M_{p}(x)\,\mathrm{d} x = 1. \end{aligned} $$(1.75) -
Recurrence Relation. From Definition 2 we obtain the following recurrence relation for cardinal B-splines,
$$\displaystyle \begin{aligned} M_0(x) &=\begin{cases} 1, &\text{if}\ x\in [0,1), \\ 0,& \text{otherwise}, \end{cases} {} \end{aligned} $$(1.76)$$\displaystyle \begin{aligned} M_{p}(x)&=\frac{x}{p}M_{p-1}(x)+\frac{p+1-x}{p}M_{p-1}(x-1), \quad p\geq 1. {} \end{aligned} $$(1.77)
The uniformity of the knot sequence endows the cardinal B-splines with several additional properties. A key feature is based on convolution.
-
Convolution. The convolution of two functions f and g is defined by
$$\displaystyle \begin{aligned}(f*g)(x):=\int_{\mathbb{R}} f(x-y)g(y)\,\mathrm{d} y.\end{aligned}$$The cardinal B-spline M p can be characterized using convolution by
$$\displaystyle \begin{aligned} M_p(x)=(M_{p-1}*M_0)(x)=\int_{0}^1 M_{p-1}(x-y)\,\mathrm{d} y, \quad p\geq1, \end{aligned} $$(1.78)and
$$\displaystyle \begin{aligned} M_p(x)=\bigl(\overbrace{M_{0} * \cdots * M_{0}}^{p+1}\bigr)(x). \end{aligned} $$(1.79)Proof From (1.74) we deduce
$$\displaystyle \begin{aligned} M_p(x)&=\int_0^x (M_{p-1}(y)- M_{p-1}(y-1))\,\mathrm{d} y\\ &=\int_0^x M_{p-1}(y)\,\mathrm{d} y - \int_{-1}^{x-1} M_{p-1}(y)\,\mathrm{d} y\\ &=\int_{x-1}^x M_{p-1}(y)\,\mathrm{d} y=\int_{0}^1 M_{p-1}(x-y)\,\mathrm{d} y.\end{aligned} $$ -
Fourier Transform. The Fourier transform of a function \(f\in L_2({\mathbb {R}})\) is defined by
$$\displaystyle \begin{aligned}\widehat{f}(\theta):=\int_{\mathbb{R}} f(x)\, {\mathrm{e}}^{-\mathrm{i}\,\theta x}\,\mathrm{d} x,\end{aligned} $$where \(\mathrm {i}:=\sqrt {-1}\) denotes the imaginary unit. The Fourier transform of the cardinal B-spline M p is given by
$$\displaystyle \begin{aligned} \widehat{M_p}(\theta)=\biggl(\frac{1-{\mathrm{e}}^{-\mathrm{i}\,\theta}}{\mathrm{i}\,\theta}\biggr)^{p+1}.\end{aligned} $$(1.80)Proof From (1.76), a direct computation gives
$$\displaystyle \begin{aligned}\widehat{M_0}(\theta)=\frac{1-{\mathrm{e}}^{-\mathrm{i}\,\theta}}{\mathrm{i}\,\theta}.\end{aligned} $$An interesting property of the Fourier transform of a convolution is
$$\displaystyle \begin{aligned} (\widehat{f*g})(\theta)=\widehat{f}(\theta)\widehat{g}(\theta), \quad \forall f,g\in L_2({\mathbb{R}});\end{aligned} $$(1.81)see, e.g., [39]. Hence, by combining (1.81) with (1.79) we deduce that \(\widehat {M_p}(\theta )=\big (\widehat {M_0}(\theta )\big )^{p+1}\), which implies (1.80). □
-
Symmetry. The cardinal B-spline M p is symmetric with respect to the midpoint of its support, namely (p + 1)∕2. More generally,
$$\displaystyle \begin{aligned} D^r M_p\biggl(\frac{p+1}{2}+x\biggr)=(-1)^{r}\,D^r M_p\biggl(\frac{p+1}{2}-x\biggr), \quad r=0,\ldots,p-1,\end{aligned} $$(1.82)and
$$\displaystyle \begin{aligned} D_-^p M_p\biggl(\frac{p+1}{2}+x\biggr)=(-1)^{p}\,D_+^p M_p\biggl(\frac{p+1}{2}-x\biggr). \end{aligned} $$(1.83)Proof It suffices to prove that M p(p + 1 − x) = M p(x). The general result then follows from repeated differentiations. We proceed by induction. It is easy to check that it is true for p = 0. Assuming the symmetry property holds for degree p − 1 and using (1.78), we get
$$\displaystyle \begin{aligned} M_p(p+1-x)&=\int_0^1 M_{p-1}(p+1-x-t)\,\mathrm{d} t =\int_0^1 M_{p-1}(x-1+t)\,\mathrm{d} t\\ &\displaystyle =-\int_1^0 M_{p-1}(x-t)\,\mathrm{d} t =\int_0^1 M_{p-1}(x-t)\,\mathrm{d} t=M_p(x). \end{aligned} $$□
We now focus on the set of integer translates of the cardinal B-spline M p, i.e.,
They have the following properties.
-
Linear Independence. From (1.73) it follows that the integer translates M p(⋅− j), \(j\in {\mathbb {Z}}\), are (locally) linearly independent on \({\mathbb {R}}\). They span the space of piecewise polynomials of degree p and smoothness p − 1 with integer break points; see (1.42).
-
Partition of Unity. From (1.49) and (1.73) we get
$$\displaystyle \begin{aligned}\sum_{j\in{\mathbb{Z}}} M_p(x-j) = 1, \quad x\in{\mathbb{R}}. \end{aligned}$$Due to the local support of cardinal B-splines, the above series reduces to a finite sum for any x. More precisely, referring to (1.21), we have
$$\displaystyle \begin{aligned}\sum_{j=m-p}^{m} M_p(x-j) = 1, \quad x\in[m,m+1). \end{aligned}$$ -
Greville Points. From (1.50)–(1.51) and (1.73) we have
$$\displaystyle \begin{aligned} x=\sum_{j\in{\mathbb{Z}}} \zeta^\ast_{j,p} M_p(x-j), \quad x\in{\mathbb{R}}, \end{aligned}$$with
$$\displaystyle \begin{aligned} \zeta^\ast_{j,p}:=\frac{(1+j)+\cdots+(p+j)}{p}=\frac{p+1}{2}+j. \end{aligned} $$(1.85)
1.4.2 Inner Products
Inner products of cardinal B-splines and their translates can be interpreted as evaluations of higher-degree cardinal B-splines; similar results also hold for their derivatives.Footnote 5
Theorem 12 (Inner Product)
Given p 1, p 2 ≥ 0, we have
Proof
From the symmetry property (1.82)–(1.83) and the convolution relation (1.78) of cardinal B-splines, we get
Finally, again by symmetry of cardinal B-splines, we have
which completes the proof. □
Theorem 13 (Inner Product of Derivatives)
Given p 1 ≥ r 1 ≥ 0 and p 2 ≥ r 2 ≥ 0, we have
Proof
Because of the (anti-)symmetry of higher order derivatives of cardinal B-splines given in (1.82), we have
So, we only have to show one of both equalities in the theorem. This can be proved by induction on the order of derivatives. The base case (r 1 = r 2 = 0) simply follows from Theorem 12. We consider two inductive steps: in the first inductive step we increase the order of derivative of \(M_{p_1}\) by one, i.e., r 1 → r 1 + 1, and in the second inductive step we increase the order of derivative of \(M_{p_2}\) by one, i.e., r 2 → r 2 + 1.
-
1.
(r 1 → r 1 + 1). Using (1.74) and the induction hypothesis, we have
$$\displaystyle \begin{aligned} &\int_{\mathbb{R}} D_+^{r_1+1}M_{p_1}(y)\,D_+^{r_2}M_{p_2}(y+x)\,\mathrm{d} y\\ &\quad = \int_{\mathbb{R}} \bigl(D_+^{r_1}M_{p_1-1}(y)-D_+^{r_1}M_{p_1-1}(y-1)\bigr)\,D_+^{r_2}M_{p_2}(y+x)\,\mathrm{d} y\\ &\quad = \int_{\mathbb{R}} D_+^{r_1}M_{p_1-1}(y) D_+^{r_2}M_{p_2}(y+x)\,\mathrm{d} y\\ &\qquad -\int_{\mathbb{R}} D_+^{r_1}M_{p_1-1}(y-1) D_+^{r_2}M_{p_2}(y+x)\,\mathrm{d} y\\ &\quad = (-1)^{r_1} \bigl(D^{r_1+r_2}M_{p_1+p_2}(p_1+x) - D^{r_1+r_2}M_{p_1+p_2}(p_1+1+x)\bigr) \\ &\quad = (-1)^{r_1+1}\,D^{r_1+r_2+1}M_{p_1+p_2+1}(p_1+1+x). \end{aligned} $$ -
2.
(r 2 → r 2 + 1). This inductive step can be proved in a completely analogous way as the first inductive step. □
Due to the relevance of the set (1.84), the results in Theorems 12 and 13 are of particular interest when we consider integer shifts, i.e., \(x\in {\mathbb {Z}}\). In this case, the above inner products reduce to evaluations of cardinal B-splines and their derivatives at either integer or half-integer points. Moreover, there is a relation with the Greville points (1.85). Indeed, if p 1 = p 2 = p and x = i in Theorem 12, then
A similar relation holds for the inner products of derivatives in Theorem 13. Thanks to the recurrence relation for derivatives (1.74), the inner products of derivatives of cardinal B-splines and its integer translates reduce to evaluations of cardinal B-splines at either integer or half-integer points.
1.4.3 Uniform Knot Insertion
In Sect. 1.3.5 we have seen how to insert a (single) knot into an existing knot sequence without changing the shape of a given spline function defined on that knot sequence. For uniform knot sequences, we can provide a simple alternative algorithm for inserting simultaneously a knot in each knot interval.
Let us consider the B-splines of degree p over the uniform knot sequence given by \({\mathbb {Z}}/2\). In this case, it is natural to index the knots as
From the definition we have \(B_{i,p,{\mathbb {Z}}/2}(x)=M_p(2x-i)\) for \(i\in {\mathbb {Z}}\). Since \({\mathbb {S}}_{p,{\mathbb {Z}}}\subset {\mathbb {S}}_{p,{\mathbb {Z}}/2}\), the cardinal B-spline M p is a refinable function, i.e., it can be written as a linear combination of translated and dilated versions of itself:
We are now looking for a relation between the coefficients of a given spline function corresponding to knots in \({\mathbb {Z}}\) and the coefficients of the same function corresponding to knots in \({\mathbb {Z}}/2\). The following simultaneous knot insertion procedure was introduced by Lane and Riesenfeld [32].
Theorem 14 (Uniform Knot Insertion)
Consider the uniform knot sequences \({\mathbb {Z}}\) and \({\mathbb {Z}}/2\) . Then,
with \({\tilde {c}}_i={\tilde {c}}_i^{[p]}\) defined recursively by
starting from
Proof
For p = 0 we can directly check that
leading to (1.87) with (1.89). We proceed by induction on p. Assume the relation (1.87) with (1.88) holds for cardinal B-splines of degree p − 1. Then, by using the convolution property (1.78) we get
which concludes the proof. □
The knot insertion procedure in Theorem 14 can be geometrically described as follows. First, every coefficient is doubled. Second, a sequence of p sets of coefficients is constructed by taking averages of the previous set of coefficients.
The coefficients {α i,p} in (1.86) can be directly computed from Theorem 14, and we obtain the explicit expression
They are called the subdivision mask of the (uniform) B-spline refinement scheme of degree p.
1.5 Spline Approximation
In this section we discuss how well a sufficiently smooth function can be approximated in the spline space spanned by a given set of B-splines. Exploiting the properties of the B-spline basis presented in the previous sections, we explicitly construct a spline which achieves optimal approximation accuracy for the function and its derivatives, and we determine the corresponding error estimates. The construction method we are going to present is local and linear.
1.5.1 Preliminaries
Let I be a finite interval of the real line. A function \(f:I\to {\mathbb {R}}\) is a piecewise continuous function on I if it is bounded and continuous except at a finite number of points, where the value is obtained by taking the limit either from the left or the right. We denote the space of these functions by C −1(I).
For \(r\in {\mathbb {N}}_0\) and 1 ≤ q ≤∞ the one-dimensional Sobolev spaces are defined by
They are normed spaces with norm
called Sobolev norm. It can be shown that for \(r\in {\mathbb {N}}\) and 1 < q < ∞,
The Hölder inequality for integrals is given by
where I := [a, b] and q, q′ are integers satisfying (1.69).
The Taylor polynomial of degree p at the point a to a function \(f\,{\in }\,W_1^{p+1}([a,b])\) is defined by
and its approximation error can be expressed in integral form for x ∈ [a, b] as
Every polynomial \(g\in {\mathbb {P}}_p\) can be written in Taylor form as \(g={\mathscr {T}}_{a,p}g\).
Theorem 15 (Taylor Interpolation Error)
Let \(f\in W_q^{p+1}([a,b])\) with 1 ≤ q ≤∞, and let \({\mathscr {T}}_{a,p}f\) be the Taylor polynomial of degree p to f at the point a. Then, for any x ∈ [a, b] and 0 ≤ r ≤ p,
and
Proof
By differentiating the integral form of the Taylor approximation error (1.96) and using the Hölder inequality (1.94), we obtain
Since 1∕q + 1∕q′ = 1 and (p − r)q′≥ 0, we obtain (1.97). Finally, taking the L q-norm shows (1.98). □
For the sake of simplicity one can use the following weaker, but simpler upper bound,
1.5.2 Spline Quasi-Interpolation
In general, a spline approximating a function f can be written in terms of B-splines as
for suitable coefficients λ j(f). The spline in (1.100) will be referred to as a quasi-interpolant to f whenever it provides a “reasonable” approximation to f.
Both interpolation and least squares are examples of quasi-interpolation methods. They are global methods since we have to solve an n by n system of linear equations to find their coefficients λ j(f). It follows that the value of the spline (1.100) at a point depends on all the data.
In this section we focus on local linear methods, i.e., methods where each λ j is a linear functional only depending on the values of f in the support of B j,p,ξ. In principle, it suffices to be “near” the support of B j,p,ξ, but we want to keep the presentation as simple as possible. In order to deal with point evaluator functionals we assume here that f ∈ C −1([a, b]), where [a, b] is a bounded interval. We consider a spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\), where the knot sequence ξ is (p + 1)-basic and the basic interval [ξ p+1, ξ n+1] is equal to [a, b].
With the aim of constructing a spline quasi-interpolant with optimal accuracy, we need to introduce some basic approximation properties of quasi-interpolants of the form (1.100). Since we are interested in local methods, we start with the following definition.
Definition 4
We say that a linear functional \(\lambda :C^{-1}([a,b])\to {\mathbb {R}}\) is supported on a nonempty set \({\mathscr {S}}\subset [a,b]\) if λ(f) = 0 for any f ∈ C −1([a, b]) which vanishes on \({\mathscr {S}}\).
Note that the set \({\mathscr {S}}\) in this definition is not uniquely defined and is not necessary minimal.
To construct our quasi-interpolant, we first require linear functionals that are supported on intervals consisting of a few knot intervals. This will ensure that \({\mathscr {Q}} f\) only depends locally on f. To ensure a good approximation power, we also require polynomial reproduction up to a given degree. Finally, to bound the error, a boundedness assumption on the linear functionals is needed. This leads to the following definitions.
Definition 5
The quasi-interpolant \({\mathscr {Q}}\) given by (1.100) is called a local quasi-interpolant if
-
(i)
each λ j is supported on the interval I j, where
$$\displaystyle \begin{aligned} I_j:= [\xi_{j},\xi_{j+p+1}]\cap [a,b], \end{aligned} $$(1.101)such that I j has nonempty interior;
-
(ii)
the λ j are chosen so that (1.100) reproduces \({\mathbb {P}}_l\), i.e.,
$$\displaystyle \begin{aligned} {\mathscr{Q}} g(x)=g(x) \text{ for all }x\in [a,b]\text{ and all }g\in{\mathbb{P}}_l, \end{aligned} $$(1.102)for some l with 0 ≤ l ≤ p.
Definition 6
A local quasi-interpolant \({\mathscr {Q}} \) is called bounded in an L q-norm, 1 ≤ q ≤∞, if there is a constant \(C_{\mathscr {Q}}\) such that for each λ j we have
where
Note that h j,p,ξ is the largest length of a knot interval in the intersection of the basic interval with the support of B j,p,ξ. The requirement (1.101) ensures that the spline in (1.100) provides a local approximation to f. The polynomial reproduction as stated in (1.102) coupled with the boundedness of the linear functionals are the main ingredients to prove the approximation power of any bounded local quasi-interpolant.
We now give both a local and a global version of the approximation power of bounded local quasi-interpolants. To turn a local bound into a global bound we first state the following lemma.
Lemma 1
Suppose that f ∈ L q([ξ p+1, ξ n+1]) for some q, 1 ≤ q < ∞, and that \(m_{i_1},\ldots ,m_{i_2}\) are integers with \(m_{i_1}<\cdots <m_{i_2}\) , \(\xi _{p+1}\le \xi _{m_{i_1}}\) and \(\xi _{m_{i_2}+k}\le \xi _{n+1}\) for some positive integer k and integers i 1 ≤ i 2 . Then,
Proof
Under the stated assumptions, each knot interval in [ξ p+1, ξ n+1] is counted at most k times and moreover all the local intervals \([\xi _{m_j},\xi _{m_j+k}]\) are contained in [ξ p+1, ξ n+1]. The definition of the L q-norm gives immediately (1.105). □
Theorem 16 (Quasi-Interpolation Error)
Let \({\mathscr {Q}}\) be a bounded local quasi-interpolant in an L q -norm, 1 ≤ q ≤∞, as in Definitions 5 and 6 . Let l, p be integers with 0 ≤ l ≤ p. Suppose ξ m < ξ m+1 for some p + 1 ≤ m ≤ n, and let \(f\in W_q^{l+1}(J_m)\) with
Then,
where h m, ξ is the largest length of a knot interval in J m . Moreover, if \(f\in W_{q}^{l+1}([a,b])\) then
where
Proof
Note that f is continuous since l ≥ 0. Suppose x ∈ [ξ m, ξ m+1). By the local partition of unity (1.21) and by (1.103) we have
Since ξ m+1 − ξ m ≤minm−p≤j≤m h j,p,ξ and J m = ∪m−p≤j≤m I j we find
From (1.102) we know that \({\mathscr {Q}}\) reproduces any polynomial \(g\in {\mathbb {P}}_{l}\), and so the triangle inequality gives
Since [ξ m, ξ m+1] ⊂ J m and by (1.108) for any \(g\in {\mathbb {P}}_l\), we have
Let \(a_m:=\max (\xi _{m-p},a)\), and choose \(g:={\mathscr {T}}_{a_m,l}f\), where \({\mathscr {T}}_{a_m,l} f\) is the Taylor polynomial of degree l defined in (1.95) with a = a m. Then, by (1.98) with r = 0 we have
Combining the inequalities (1.109) and (1.110) gives the local bound.
Since each J m is contained in the basic interval [a, b] the global bound follows immediately from the local one and Lemma 1. □
Example 11
Let ξ be a (p + 1)-open knot sequence for p ≥ 1, and consider the operator
where \(\xi ^\ast _{j,p,{\boldsymbol {\xi }}}\) is the j-th Greville point of degree p; see (1.51). This operator is known as the Schoenberg operator, and was introduced in [43, Section 10]. It is a bounded local quasi-interpolant in the L ∞-norm with l = 1 and \(C_{\mathscr {Q}}=1\). Note that \(\xi ^\ast _{j,p,{\boldsymbol {\xi }}}\) belongs to [ξ j+1, ξ j+p]. Therefore, Theorem 16 implies for any \(f\in W_\infty ^2([a,b])\),
The next proposition can be used to find the degree l of polynomials reproduced by a linear quasi-interpolant.
Proposition 4
Let
be n sets of basis functions for \({\mathbb {P}}_l\) , and let
be their B-spline representations. The linear quasi-interpolant (1.100) reproduces \({\mathbb {P}}_l\) provided the corresponding linear functionals satisfy
Proof
On the basic interval, any \(g\in {\mathbb {P}}_l\) can be written both in terms of the φ’s and the B-splines, say
By (1.114) and (1.116) for j = 1, …, n,
By linear independence of the B-splines and choosing j = k we obtain
Similarly, for \({\mathscr {Q}} g\) using (1.116) with j = k,
From the linearity of λ k and (1.115), (1.117) and finally (1.116) again we obtain
□
The next proposition gives a sufficient condition for a quasi-interpolant to reproduce the whole spline space, i.e., to be a projector onto \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\).
Proposition 5
The linear quasi-interpolant (1.100) reproduces the whole spline space, i.e.,
if \({\mathscr {Q}}\) reproduces \({\mathbb {P}}_p\) and each linear functional λ j is supported on one knot interval Footnote 6
Proof
Let j with 1 ≤ j ≤ n be fixed. By the linearity it suffices to prove that
where δ i,j stands for the classical Kronecker delta. On the interval \([\xi _{m_j}^+,\xi _{m_j+1}^-]\) the local support property implies that λ j(B i,p,ξ) = 0 for i∉{m j − p, …, m j}. This follows because we use the left limit at \(\xi _{m_j+1}\) if necessary. Since \(B_{i,p,{\boldsymbol {\xi }}}\in {\mathbb {P}}_p\) on this interval, we have
and by local linear independence of the B-splines we obtain λ k(B i,p,ξ) = δ i,k for k = m j − p, …, m j. In particular, it holds for k = j since the condition (1.119) implies that m j − p ≤ j ≤ m j. □
Example 12
Let p = 2, and let ξ be a 3-open knot sequence with at most double knots in the interior. We consider the operator
where \(\xi ^\ast _{j,2,{\boldsymbol {\xi }}}=(\xi _{j+1}+\xi _{j+2})/2\) is the j-th Greville point of degree 2. It can be checked (see also Example 9) that if we choose a 2,0 = a 2,2 = −1∕2 and a 2,1 = 2 then \({\mathscr {Q}}_{2,{\boldsymbol {\xi }}}\) reproduces \({\mathbb {P}}_2\), i.e., l = 2. Proposition 5 says that it is even a projector on the spline space \({\mathbb {S}}_{2,{\boldsymbol {\xi }}}\). Moreover,
It follows that \({\mathscr {Q}}_{2,{\boldsymbol {\xi }}}\) is a bounded local quasi-interpolant in the L ∞-norm with l = 2 and \(C_{\mathscr {Q}}=3\). In this case, Theorem 16 implies for any \(f\in W_\infty ^3([a,b])\),
showing that the error is \(O(h_{\boldsymbol {\xi }}^3)\).
1.5.3 Approximation Power of Splines
In this section we want to understand how well a function can be approximated by a spline. In order words, we want to investigate the distance between a general function f and the piecewise polynomial space \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )\) defined in (1.42). From Theorem 6 we know that \({\mathbb {S}}^{\boldsymbol {r}}_p(\varDelta )={\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) for a suitable choice of the knot sequence \({\boldsymbol {\xi }}:=\{\xi _i\}_{i=1}^{n+p+1}\). In particular, ξ can be chosen to be (p + 1)-open. Therefore, without loss of generality, we consider the distance between a general function f and the spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) of degree p over the (p + 1)-open knot sequence ξ. For a given f ∈ L q([ξ p+1, ξ n+1]) with 1 ≤ q ≤∞, we define
We are also interested in estimates for the distance between derivatives of f and derivative spline spaces. To this end, in this section we use the simplified notation \(D^rs:=D_+^rs\) for the derivatives of a spline \(s\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) with the usual convention of left continuity at the right endpoint of the basic interval. Note that with such a notation we ensure that D r s(x) exists for all x. In the same spirit, we use the notation \(D^r{\mathbb {S}}_{p,{\boldsymbol {\xi }}}:=D_+^r{\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) for the r-th derivative spline space. We recall from Sect. 1.3.2 that this derivative space is a piecewise polynomial space of degree p − r with a certain smoothness, i.e.,
where the partition Δ consists of the distinct break points in the knot sequence ξ and the smoothness r is related to the multiplicity of the knots, according to the rule in (1.35). This leads to the following more general definition of distance. For a given \(f\in W_{q}^{r}([\xi _{p+1},\xi _{n+1}])\) with 1 ≤ q ≤∞ and 0 ≤ r ≤ p, we define
We will derive the following upper bound for \(\operatorname {dist}_q(D^rf,D^r{\mathbb {S}}_{p,{\boldsymbol {\xi }}})\).
Theorem 17 (Distance to a Function)
For any 0 ≤ r ≤ l ≤ p and \(f\in W_{q}^{l+1}([\xi _{p+1},\xi _{n+1}])\) with 1 ≤ q ≤∞ we have
where h ξ :=maxp+1≤j≤n(ξ j+1 − ξ j) and K is a constant depending only on p.
The distance result will be shown by explicitly constructing a suitable spline quasi-interpolant which achieves this order of approximation; see Theorem 18. For sufficiently smooth f, the upper bound behaves like (h ξ)p+1−r.
1.5.3.1 A Spline Quasi-Interpolant
Given an integer p ≥ 0 and a (p + 1)-open knot sequence ξ, we define a specific spline approximant of degree p over ξ to a given function f. Let \([\xi _{m_{j,p}},\xi _{m_{j,p}+1}]\) be a knot interval of largest length in [ξ j, ξ j+p+1] for any j = 1, …, n and \(h_{j,p,{\boldsymbol {\xi }}}:=\xi _{m_{j,p}+1}-\xi _{m_{j,p}}>0\). The spline approximant to f is constructed as
where
and the coefficients a j,i, i = 0, …, p are such that
where
In the next lemmas we collect some properties for the spline approximation (1.122).
Lemma 2
The above spline approximation is well defined and reproduces polynomials, i.e., for any polynomial \(g\in {\mathbb {P}}_p\) we have
Moreover, it is a projector onto the spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) , i.e., for any spline \(s\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) we have
and, in particular,
Proof
By applying \({\mathscr {L}}_{j,p,{\boldsymbol {\xi }}}\) to the polynomials \(\Big (\frac {x-\xi _{m_{j,p}}}{h_{j,p,{\boldsymbol {\xi }}}}\Big )^r\), r = 0, …, p, the coefficients a j,i are given by the solution of the linear system
where a j := (a j,0, …, a j,p)T, c j := (c j,0,j, …, c j,p,j)T, and H p+1 is a (p + 1) × (p + 1) matrix with elements
for i, r = 0, …, p. This is the well-known Hilbert matrix which is nonsingular and it follows that the spline approximation (1.122) is well defined. From Proposition 4 we deduce that (1.126) holds.
Since we only integrate over one subinterval when we define \({\mathscr {L}}_{j,p,{\boldsymbol {\xi }}}\), we conclude that it reproduces not only polynomials but also splines, and (1.127) follows from Proposition 5. □
Lemma 3
For p ≥ 0 and 1 ≤ q ≤∞ we have for any \(f\in L_q([\xi _{m_{j,p}},\xi _{m_{j,p}+1}])\) ,
where C is a constant depending only on p.
Proof
By (1.20), (1.10) and (1.13) we have
Here we used that \([\xi _{m_{j,p}},\xi _{m_{j,p}+1}]\) is a knot interval of largest length in [ξ j, ξ j+p+1]. Since \(0\le \frac {x-\xi _{m_{j,p}}}{h_{j,p,{\boldsymbol {\xi }}}}\le 1\) for \(x\in [\xi _{m_{j,p}},\xi _{m_{j,p}+1}]\), we get from (1.123),
This gives \(|{\mathscr {L}}_{j,p,{\boldsymbol {\xi }}}(f)|\le Ch_{j,p,{\boldsymbol {\xi }}}^{-1}\|f\|{ }_{L_1([\xi _{m_{j,p}},\xi _{m_{j,p}+1}])}\), where \(C:=\|H_{p+1}^{-1}\|{ }_\infty (p+1)^{p+1}\) only depends on p. By the Hölder inequality (1.94) we arrive at (1.130). □
We now give a bound for the derivative of \({\mathscr {Q}}_{p,{\boldsymbol {\xi }}}f\). To this end, we recall from (1.25) that
and that Δ m,k > 0 for all k if ξ m < ξ m+1.
Lemma 4
Suppose ξ m < ξ m+1 for some p + 1 ≤ m ≤ n, and let f ∈ L q([ξ m−p, ξ m+p+1]) with 1 ≤ q ≤∞. Then, we have for 0 ≤ r ≤ p,
where Δ m,k is defined in (1.25) and C is a constant depending only on p.
Proof
From the quasi-interpolant definition (1.122), the local support property (1.36) and Lemma 3, we have for x ∈ [ξ m, ξ m+1),
Note that [ξ m, ξ m+1] ⊂ [ξ j, ξ j+p+1] for j = m − p, …, m. Since h j,p,ξ is the length of the largest knot interval in [ξ j, ξ j+p+1], we have ξ m+1 − ξ m ≤ h j,p,ξ for j = m − p, …, m. Replacing |D r B j,p,ξ(x)| by the upper bound given in Proposition 2 and taking the L q-norm results in (1.131). □
The next lemma will complete the proof of Theorem 11 related to the condition number. Note that [ξ p+1, ξ n+1] = [ξ 1, ξ n+p+1] because the knot sequence ξ is open.
Lemma 5
For any p ≥ 0, there exists a positive constant K p depending only on p, such that for any vector c := (c 1, …, c n) and for any 1 ≤ q ≤∞ we have
where \(N_{j,p,q,{\boldsymbol {\xi }}}:=\gamma _{j,p,{\boldsymbol {\xi }}}^{-1/q}B_{j,p,{\boldsymbol {\xi }}}\) and γ j,p,ξ := (ξ j+p+1 − ξ j)∕(p + 1).
Proof
Let \(s:=\sum _{j=1}^n \gamma _{j,p,{\boldsymbol {\xi }}}^{-1/q} c_j B_{j,p,{\boldsymbol {\xi }}}\). Observe that (1.128) and (1.130) imply
Since γ j,p,ξ∕h j,p,ξ ≤ 1 we obtain
Raising both sides to the q-th power and summing over j gives
When taking the q-th roots on both sides, we arrive at the inequality in (1.132) with K p := (p + 1)C ≥ (p + 1)1∕q C, which only depends on p. □
1.5.3.2 Distance to a Function
The quasi-interpolant \({\mathscr {Q}}_{p,{\boldsymbol {\xi }}}f\) described in the previous section can be used to obtain an upper bound for the distance between a given function f and the spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) for p ≥ 0, n > p + 1 and \({\boldsymbol {\xi }}:=\{\xi _j\}_{j=1}^{n+p+1}\); see Theorem 18. We recall that the knot sequence ξ is (p + 1)-open. We start by giving a local and global upper bound for (the derivatives of) the difference between f and \({\mathscr {Q}}_{p,{\boldsymbol {\xi }}}f\).
Proposition 6
Suppose ξ m < ξ m+1 for some p + 1 ≤ m ≤ n, and let \(f\in W_q^{l+1}([\xi _{m-p},\xi _{m+p+1}])\) with 0 ≤ l ≤ p and 1 ≤ q ≤∞. If \({\mathscr {Q}}_{p,{\boldsymbol {\xi }}}f\) is defined as in (1.122), then we have for any 0 ≤ r ≤ l,
Here,
Δ m,k is defined in (1.25) and C is a constant depending only on p.
Proof
From Lemma 2 we know that \({\mathscr {Q}}_{p,{\boldsymbol {\xi }}}\) reproduces any polynomial in \({\mathbb {P}}_{l}\), and so the triangle inequality gives
for any \(g\in {\mathbb {P}}_{l}\). Let us now set \(g:={\mathscr {T}}_{\xi _{m},l} f\), where \({\mathscr {T}}_{\xi _{m},l} f\) is the Taylor polynomial of degree l defined in (1.95) with a = ξ m, b = ξ m+1. Then, Eq. (1.99) implies
On the other hand, since f − g ∈ L q([ξ m−p, ξ m+p+1]), it follows from Lemma 4 that
where C is a constant depending only on p. Combining the above three inequalities gives the result. □
We know that the ratio \(\frac {\xi _{m+p+1}-\xi _{m-p}}{\varDelta _{m,k}}\) is well defined because Δ m,k > 0. For a uniform knot sequence
For a general knot sequence it is related to the “local mesh ratio”, i.e., the ratio between the lengths of the largest and smallest knot intervals in a neighborhood of ξ m.
The local error bound in Proposition 6 can be turned into a global one as in the following proposition.
Proposition 7
Let \(f\in W_q^{l+1}([\xi _{p+1},\xi _{n+1}])\) with 0 ≤ l ≤ p and 1 ≤ q ≤∞. If \({\mathscr {Q}}_{p,{\boldsymbol {\xi }}}f\) is defined as in (1.122) then, for any 0 ≤ r ≤ l,
where h ξ :=maxp+1≤j≤n(ξ j+1 − ξ j), and
where Δ m,k is defined in (1.25) and C is a constant depending only on p.
Proof
For q = ∞ the result follows immediately from Proposition 6 by taking into account that ξ is (p + 1)-open. We now assume 1 ≤ q < ∞. Since
the result follows from Lemma 1 and the local error bound in Proposition 6. □
The expression K in the upper bound in Proposition 7 depends on the position of the knots for r > 0. However, for any knot sequence ξ, it is possible to construct a coarser knot sequence ξ ♯ such that the corresponding K only depends on p. This can be obtained by a clever thinning process. The idea of thinning out a knot sequence to get a quasi-uniform sequence is credited to [47]; see [45, Section 6.4] for details. Since ξ ♯ is a subsequence of ξ, we have that \({\mathbb {S}}_{p,{\boldsymbol {\xi }}^\sharp }\) is a subspace of \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\). In particular, for any f ∈ L q([ξ p+1, ξ n+1]) the spline approximation
as defined in (1.122) belongs to the spline space \({\mathbb {S}}_{p,{\boldsymbol {\xi }}}\). This spline quasi-interpolant leads to the following important result.
Theorem 18 (Approximation Error)
Let \(f\in W_{q}^{l+1}([\xi _{p+1},\xi _{n+1}])\) with 1 ≤ q ≤∞ and 0 ≤ l ≤ p. Then, there exists \(s_p\in {\mathbb {S}}_{p,{\boldsymbol {\xi }}}\) such that
where h ξ :=maxp+1≤j≤n(ξ j+1 − ξ j) and K is a constant depending only on p.
The constant K in Theorem 18 grows exponentially with p. However, this dependency on p can be removed in some cases; see [1, Theorem 2] and [52, Theorem 7] for details. Theorem 18 immediately leads to the distance result in Theorem 17.
1.6 Hierarchical Splines and the Truncation Mechanism
The hierarchical spline model is a simple strategy to mix locally spline spaces of different resolution (different mesh size and/or different degree). Hierarchical spline representations are defined in terms of a sequence of nested B-spline bases and a hierarchy of locally refined domains. In this section we define such hierarchical splines and focus on a set of basis functions with properties similar to B-splines.
1.6.1 Hierarchical B-Splines
Let I be a closed interval of the real line, and consider a sequence of strictly nested spline spaces defined on I, say
We assume that each knot sequence involved in (1.135),
is (p + 1)-basic with basic interval I. Nestedness of the spaces is ensured if and only if
Note that (1.136) implies that (ξ ℓ ∩ I) ⊆ (ξ ℓ+1 ∩ I). The assumption of dealing with (p + 1)-basic knot sequences ensures that the corresponding n ℓ B-splines are linearly independent on I. We denote the B-spline basis of the space \({\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\) by
Next, consider a sequence of nested, closed subsets of I,
where Ω ℓ is the union of some closed knot intervals related to the knot sequence ξ ℓ. Note that each Ω ℓ may consist of disjoint intervals. We assume that each connected component of Ω 1 has nonempty interior. The collection of those subsets in (1.138) is denoted by
and will be simply referred to as the domain hierarchy in I. We also set Ω L+1 := ∅. Finally, for a given function f on I, we define its support on Ω as
Given a sequence of spline spaces and bases as in (1.135)–(1.137) and a domain hierarchy as in (1.138)–(1.139), we construct the corresponding set of hierarchical B-splines (in short, HB-splines) as follows.Footnote 7
Definition 7
Given a domain hierarchy Ω, the corresponding set of HB-splines is denoted by \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\) and defined recursively as follows:
-
(i)
\({\mathscr {H}}_1:=\{B_{j,1}\in {\mathscr {B}}_1: \text{supp}_{\boldsymbol {\varOmega }}(B_{j,1})\neq \emptyset \};\)
-
(ii)
for ℓ = 2, …, L:
$$\displaystyle \begin{aligned}{\mathscr{H}}_{\ell}:={\mathscr{H}}_{\ell}^C\cup{\mathscr{H}}_{\ell}^F, \end{aligned}$$where
$$\displaystyle \begin{aligned} {{\mathscr{H}}_{\ell}^C} &:= \{B_{j,k}\in{\mathscr{H}}_{\ell-1}: \text{supp}_{\boldsymbol{\varOmega}}(B_{j,k})\not\subseteq\varOmega_{\ell}\},\\ {\mathscr{H}}_{\ell}^F &:= \{B_{j,\ell}\in{\mathscr{B}}_{\ell}: \text{supp}_{\boldsymbol{\varOmega}}(B_{j,\ell})\subseteq\varOmega_{\ell}\}; \end{aligned} $$ -
(iii)
\({\mathscr {H}}_{{\boldsymbol {\varOmega }}}:={\mathscr {H}}_L\).
To obtain the set of HB-splines, we first take all the B-splines in \({\mathscr {B}}_1\) whose support overlaps Ω 1. Then, we apply a recursive procedure which selects at each level ℓ all the B-splines obtained in the previous step whose support is not entirely contained in Ω ℓ and all the B-splines in \({\mathscr {B}}_\ell \) whose support is entirely contained in Ω ℓ.
Example 13
An example of the recursive definition of HB-splines is illustrated in Fig. 1.4. We consider three nested knot sequences, with knots of multiplicity 4 at the two extrema of the intervals and single knots elsewhere, as in Fig. 1.4a. This allows us to construct the three sets of cubic B-splines shown in Fig. 1.4c, e, g, whose dimensions are n 1 = 10, n 2 = 17 and n 3 = 31, respectively. The domain hierarchy is defined by the subsets Ω 1 = [ξ 4,1, ξ 11,1], Ω 2 = [ξ 8,2, ξ 16,2] and Ω 3 = [ξ 16,3, ξ 24,3], and is shown in Fig. 1.4b. Obviously, \({\mathscr {H}}_1\) coincides with \({\mathscr {B}}_1\). Furthermore, \({\mathscr {H}}_2^C\) is obtained from \({\mathscr {H}}_1\) by removing B 6,1, and \({\mathscr {H}}_2^F=\{B_{8,2},\ldots ,B_{12,2}\}\). Hence, \({\mathscr {H}}_2={\mathscr {H}}_2^C\cup {\mathscr {H}}_2^F\) consists of 9 + 5 = 14 elements. Finally, \({\mathscr {H}}_3^C\) is obtained from \({\mathscr {H}}_2\) by removing B 10,2, and \({\mathscr {H}}_3^F=\{B_{16,3},\ldots ,B_{20,3}\}\). Hence, \({\mathscr {H}}_3={\mathscr {H}}_3^C\cup {\mathscr {H}}_3^F\) consists of 13 + 5 = 18 elements. The sets \({\mathscr {H}}_1\), \({\mathscr {H}}_2\) and \({\mathscr {H}}_3\) are shown in Fig. 1.4d, f, h.
An example of cubic HB-splines where the domain hierarchy consists of three levels. The knot positions are visualized by vertical dotted lines in (c)–(h). (a) Knot sequences. (b) Domain hierarchy. (c) \({\mathscr {B}}_1\). (d) \({\mathscr {H}}_1\). (e) \({\mathscr {B}}_2\). (f) \({\mathscr {H}}_2\). (g) \({\mathscr {B}}_3\). (h) \({\mathscr {H}}_3={\mathscr {H}}_{{ \boldsymbol {\varOmega }}}\)
For each ℓ ∈{1, …, L}, let J ℓ,Ω be the set of indices of the B-splines in \({\mathscr {B}}_\ell \) belonging to \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\), i.e.,
From Definition 7 it follows that
where
Given this index set, we can reconstruct the set of HB-splines as
Since the set of HB-splines is a mixture of standard B-splines, we deduce immediately the following properties.
-
Local Support. An HB-spline is locally supported on an interval that only depends on the level it was introduced in the hierarchical construction and not on the choice of subsets in the domain hierarchy.
-
Nonnegativity. An HB-spline is nonnegative everywhere, and positive inside its support.
-
Piecewise Structure. An HB-spline is a piecewise polynomial, whose degree and smoothness depends on the level it was introduced in the hierarchical construction and the spline space used on that level.
-
Linear Independence. The HB-splines in \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\) are linearly independent on Ω 1.
Proof We first note that if J ℓ,Ω is nonempty then Γ ℓ has nonempty interior for any ℓ; see (1.141) and (1.142). We must prove that if
$$\displaystyle \begin{aligned} s(x)=\sum_{\ell=1}^{L}\sum_{j\in J_{\ell,{\boldsymbol{\varOmega}}}} c_{j,\ell}B_{j,\ell}(x)=0, \quad x\in\varOmega_1, \end{aligned} $$(1.144)then c j,ℓ = 0 for all j and ℓ in (1.144). We know from the local linear independence property that the B-splines B j,1, j ∈ J 1,Ω are linearly independent on Γ 1. Moreover, from (1.141) it follows that only those functions are nonzero on Γ 1. Hence, we conclude that c j,1 = 0 for j ∈ J 1,Ω in (1.144). We can repeat the same argument for the remaining terms in (1.144) going level by level in the hierarchy. Indeed, for ℓ = 2, …, L, the B-splines B j,ℓ, j ∈ J ℓ,Ω are linearly independent on Γ ℓ, and only those functions are nonzero on Γ ℓ except for functions already considered before at previous levels. This implies that c j,ℓ = 0 for j ∈ J ℓ,Ω with ℓ = 2, …, L. □
The space spanned by the HB-splines in \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\) is called the hierarchical spline space on Ω and is denoted by
Such hierarchical space has some interesting properties.
-
Dimension. By the linear independence of the HB-splines, the space \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) is a vector space of dimension \(\sum _{\ell =1}^L |J_{\ell ,{\boldsymbol {\varOmega }}}|\).
-
Nestedness. Let the domain hierarchy \({\tilde {{\boldsymbol {\varOmega }}}}\) be obtained from another domain hierarchy Ω such that \(\varOmega _1={{\tilde {\varOmega }}}_1\) and \(\varOmega _\ell \subseteq {{\tilde {\varOmega }}}_\ell \) for ℓ = 2, …, L. Then, \({\mathbb {S}}_{{\boldsymbol {\varOmega }}} \subseteq {\mathbb {S}}_{{\tilde {{\boldsymbol {\varOmega }}}}}\).
Proof We first note that any B-spline \(B_{j, \ell -1}\in {\mathscr {B}}_{\ell -1}\) whose support is entirely contained in Ω ℓ can be represented exactly in terms of B-splines \(B_{i, \ell }\in {\mathscr {B}}_{\ell }\) whose support is also contained in Ω ℓ. Consider the intermediate spaces \({\mathscr {H}}_\ell \) and \({\tilde {{\mathscr {H}}}}_\ell \) arising in Definition 7. From their construction it directly follows
$$\displaystyle \begin{aligned} \mathrm{span}({\mathscr{H}}_{\ell-1}) \subseteq \mathrm{span}({\mathscr{H}}_{\ell}) \quad \text{and} \quad \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell-1}) \subseteq \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell}).\end{aligned} $$(1.146)We now show that \(\mathrm {span}({\mathscr {H}}_\ell )\subseteq \mathrm {span}({\tilde {{\mathscr {H}}}}_\ell )\) for all ℓ = 1, …, L. This clearly holds for ℓ = 1 since \(\varOmega _1={{\tilde {\varOmega }}}_1\) and hence \({\mathscr {H}}_1={\tilde {{\mathscr {H}}}}_1\). We proceed by induction on ℓ, and assume that the statement is true for ℓ − 1. Then, we have
$$\displaystyle \begin{aligned}\mathrm{span}({\mathscr{H}}_{\ell}^C)\subseteq \mathrm{span}({\mathscr{H}}_{\ell-1})\subseteq \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell-1})\subseteq \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell}), \end{aligned}$$and
$$\displaystyle \begin{aligned}\mathrm{span}({\mathscr{H}}_{\ell}^F)\subseteq \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell}^F)\subseteq \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell}). \end{aligned}$$This implies
$$\displaystyle \begin{aligned}\mathrm{span}({\mathscr{H}}_\ell)=\mathrm{span}({\mathscr{H}}_{\ell}^C)\cup\mathrm{span}({\mathscr{H}}_{\ell}^F)\subseteq \mathrm{span}({\tilde{{\mathscr{H}}}}_{\ell}). \end{aligned}$$As a consequence, \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}=\mathrm {span}({\mathscr {H}}_L)\subseteq \mathrm {span}({\tilde {{\mathscr {H}}}}_L)={\mathbb {S}}_{{\tilde {{\boldsymbol {\varOmega }}}}}\). □
-
Polynomial Embedding. The space \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) contains (at least) all polynomials of degree less than or equal to p 1.
Proof Let g be a polynomial in \({\mathbb {P}}_{p_1}\). From Sect. 1.3.3 we know that g belongs to the coarsest spline space \({\mathbb {S}}_{p_1,{\boldsymbol {\xi }}_1}\) in the sequence (1.135). Hence, taking into account (1.146), we conclude that \(g \in \mathrm {span}({\mathscr {H}}_{1})\subseteq \mathrm {span}({\mathscr {H}}_{L})={\mathbb {S}}_{{\boldsymbol {\varOmega }}}\). □
1.6.2 Truncated Hierarchical B-Splines
HB-splines do not satisfy the partition of unity property. In addition, the number of overlapping basis functions associated with different hierarchical levels easily increases. This motivates the construction of another basis for the hierarchical spline space. The construction is based on the following truncation mechanism [22].
Definition 8
Given ℓ ∈{2, …, L}, let \(s\in {\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\) be represented in the B-spline basis \({\mathscr {B}}_{\ell }\), i.e.,
The truncation of s at level ℓ is defined as the sum of the terms appearing in (1.147) related to the B-splines whose support is not a subset of Ω ℓ, i.e.,
By successively truncating the functions constructed in Definition 7, we obtain the truncated hierarchical B-splines (in short, THB-splines).Footnote 8
Definition 9
Given a domain hierarchy Ω, the corresponding set of THB-splines is denoted by \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) and defined recursively as follows:
-
(i)
\({\mathscr {T}}_1:=\{B_{j,1}\in {\mathscr {B}}_1: \text{supp}_{\boldsymbol {\varOmega }}(B_{j,1})\neq \emptyset \};\)
-
(ii)
for ℓ = 2, …, L:
$$\displaystyle \begin{aligned}{\mathscr{T}}_{\ell}:={\mathscr{T}}_{\ell}^C\cup{\mathscr{T}}_{\ell}^F,\end{aligned} $$where
$$\displaystyle \begin{aligned} {{\mathscr{T}}_{\ell}^C} &:= \{\mathrm{trunc}_{\ell,{\boldsymbol{\varOmega}}}(B^{t}_{j,k,\varOmega_{\ell-1}}): B^{t}_{j,k,\varOmega_{\ell-1}} \in{\mathscr{T}}_{\ell-1},\ \text{supp}_{\boldsymbol{\varOmega}}(B^{t}_{j,k,\varOmega_{\ell-1}})\not\subseteq\varOmega_{\ell}\},\\ {\mathscr{T}}_{\ell}^F &:= \{B_{j,\ell}\in{\mathscr{B}}_{\ell}: \text{supp}_{\boldsymbol{\varOmega}}(B_{j,\ell})\subseteq\varOmega_{\ell}\}; \end{aligned} $$ -
(iii)
\({\mathscr {T}}_{{\boldsymbol {\varOmega }}}:={\mathscr {T}}_L\).
To obtain the THB-splines, we apply a recursive procedure building a set \({\mathscr {T}}_{\ell }\) at level ℓ. This set consists of two subsets, the coarse set \({\mathscr {T}}_{\ell }^C\) and the fine set \({\mathscr {T}}_{\ell }^F\). To construct the elements \(B^{t}_{j,k,\varOmega _{\ell }}\) of \({\mathscr {T}}_{\ell }^C\), we first express any function \(B^{t}_{j,k,\varOmega _{\ell -1}}\in {\mathscr {T}}_{\ell -1}\) with respect to the B-spline basis \({\mathscr {B}}_\ell \), and then we apply the truncation as in (1.148) with \(s=B^{t}_{j,k,\varOmega _{\ell -1}}\). The fine set \({\mathscr {T}}_{\ell }^F\) consists of all B-splines in \({\mathscr {B}}_\ell \) whose support is entirely contained in Ω ℓ, exactly as in the HB-spline case; see Definition 7.
When comparing Definition 9 with Definition 7, we see that the number of THB-splines in the set \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) is equal to the number of HB-splines in the set \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\). In the following, the THB-splines in \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) are denoted by \(B^{T}_{j,\ell ,{\boldsymbol {\varOmega }}}\) for j ∈ J ℓ,Ω and ℓ = 1, …, L.
Example 14
When unrolling the recursive definition of THB-splines for L = 3, we get
Example 15
Figure 1.5 illustrates the truncation mechanism applied to the set of HB-splines depicted in Fig. 1.4 (Example 13). Obviously, \({\mathscr {T}}_1\) coincides with \({\mathscr {H}}_1\). Furthermore, \({\mathscr {T}}_2^C\) is obtained from \({\mathscr {H}}_2^C\) by applying the truncation mechanism to its elements; this only results in a modification of the elements B 4,1, B 5,1, B 7,1 and B 8,1. On the other hand, we have \({\mathscr {T}}_2^F={\mathscr {H}}_2^F\). Finally, \({\mathscr {T}}_3^C\) is obtained from \({\mathscr {H}}_3^C\) by modifying B 4,1, B 5,1, B 7,1, B 8,1 (truncated at level 2) and B 8,2, B 9,2, B 11,2, B 12,2 (truncated at level 3), while \({\mathscr {T}}_3^F={\mathscr {H}}_3^F\). It is clear that \({\mathscr {T}}_\ell ={\mathscr {T}}_{\ell }^C\cup {\mathscr {T}}_{\ell }^F\) and \({\mathscr {H}}_\ell ={\mathscr {H}}_{\ell }^C\cup {\mathscr {H}}_{\ell }^F\) have the same number of elements for ℓ = 2, 3.
HB-splines and THB-splines with respect to the same domain hierarchy as in Fig. 1.4b. (a) \({\mathscr {H}}_1\). (b) \({\mathscr {T}}_1\). (c) \({\mathscr {H}}_2\). (d) \({\mathscr {T}}_2\). (e) \({\mathscr {H}}_3\). (f) \({\mathscr {T}}_3\)
The next properties can be easily deduced from the definition of THB-splines.
-
Relation to HB-Splines. Each THB-spline in \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) is uniquely related to a single HB-spline in \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\) possibly by successive truncations, i.e.,
$$\displaystyle \begin{aligned} B^{T}_{j,\ell,{\boldsymbol{\varOmega}}}=\mathrm{Trunc}_{\ell,{\boldsymbol{\varOmega}}}(B_{j,\ell}), \end{aligned} $$(1.149)where for any \(s\in {\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\) with ℓ = 1, …, L − 1,
$$\displaystyle \begin{aligned}\mathrm{Trunc}_{\ell,{\boldsymbol{\varOmega}}}(s):=\mathrm{trunc}_{L,{\boldsymbol{\varOmega}}}(\mathrm{trunc}_{L-1,{\boldsymbol{\varOmega}}}(\cdots(\mathrm{trunc}_{\ell+1,{\boldsymbol{\varOmega}}}(s))\cdots)), \end{aligned}$$and for any \(s\in {\mathbb {S}}_{p_L,{\boldsymbol {\xi }}_L}\),
$$\displaystyle \begin{aligned}\mathrm{Trunc}_{L,{\boldsymbol{\varOmega}}}(s):=s. \end{aligned}$$From (1.149) in combination with (1.147)–(1.148), it is clear that
$$\displaystyle \begin{aligned} B^{T}_{j,\ell,{\boldsymbol{\varOmega}}}(x)=B_{j,\ell}(x), \quad x\in \varGamma_\ell. \end{aligned} $$(1.150) -
Local Support. From (1.149) it follows that a THB-spline has the same or smaller support than its related HB-spline.
-
Nonnegativity. A THB-spline is nonnegative on Ω 1.
Proof Fix 1 ≤ ℓ 1 < ℓ 2 ≤ L. Because of the nestedness of the spaces in (1.135), we can write the B-spline \(B_{j,\ell _1}\in {\mathscr {B}}_{\ell _1}\) in terms of the B-splines in \({\mathscr {B}}_{\ell _2}\), i.e.,
$$\displaystyle \begin{aligned} \displaystyle B_{j,\ell_1}(x) = \sum_{i=1}^{n_{\ell_2}}c_{i,\ell_2}^{j,\ell_1}B_{i,\ell_2}(x), \quad x\in\varOmega_1. \end{aligned} $$(1.151)From Sect. 1.3.5 we know that the coefficients in (1.151) are all nonnegative in case \(p_{\ell _1}=p_{\ell _2}\). This property holds in general, also when \(p_{\ell _1}<p_{\ell _2}\), and we refer to [12] for its proof. Then, since each THB-spline \(B^{T}_{j,\ell ,{\boldsymbol {\varOmega }}}\) can be deduced from the B-spline B j,ℓ possibly by successive truncations, see (1.149), it follows from (1.147)–(1.148) that \(B^{T}_{j,\ell ,{\boldsymbol {\varOmega }}}\) can be written as a linear combination of B-splines of the finest level L with nonnegative coefficients. This implies that \(B^{T}_{j,\ell ,{\boldsymbol {\varOmega }}}\) is nonnegative. □
-
Linear Independence. The THB-splines in \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) are linearly independent on Ω 1.
Proof We must prove that if
$$\displaystyle \begin{aligned} s(x)=\sum_{\ell=1}^{L}\sum_{j\in J_{\ell,{\boldsymbol{\varOmega}}}} c_{j,\ell}B^{T}_{j,\ell}(x)=0, \quad x\in\varOmega_1, \end{aligned} $$(1.152)then c j,ℓ = 0 for all j and ℓ in (1.152). This can be shown using exactly the same line of arguments as in the case of HB-splines (see (1.144)), taking into account relation (1.150). □
The next theorem shows that the THB-splines in \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) form an alternative basis for the hierarchical spline space \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) in (1.145).
Theorem 19 (Hierarchical Spline Space)
The THB-splines in \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) span the same space as the HB-splines in \({\mathscr {H}}_{{\boldsymbol {\varOmega }}}\) , i.e.,
Proof
Consider the intermediate spaces \({\mathscr {H}}_\ell \) and \({\mathscr {T}}_\ell \) in Definitions 7 and 9, respectively. From their construction it directly follows
We now show that \(\mathrm {span}({\mathscr {H}}_\ell )=\mathrm {span}({\mathscr {T}}_\ell )\) for all ℓ = 1, …, L. This clearly holds for ℓ = 1 since \({\mathscr {H}}_1={\mathscr {T}}_1\). We proceed by induction on ℓ, and assume that the statement is true for ℓ − 1. Then, we have
and
This implies
Finally, since both sets \({\mathscr {H}}_\ell \) and \({\mathscr {T}}_{\ell }\) have the same number of elements and these elements are all linearly independent, it follows that \(\mathrm {span}({\mathscr {H}}_\ell )=\mathrm {span}({\mathscr {T}}_\ell )\). As a consequence, \(\mathrm {span}({\mathscr {H}}_{{\boldsymbol {\varOmega }}})=\mathrm {span}({\mathscr {H}}_L)=\mathrm {span}({\mathscr {T}}_L)=\mathrm {span}({\mathscr {T}}_{{\boldsymbol {\varOmega }}})\). □
The correspondence in (1.149) between the THB-spline \(B^{T}_{j,\ell ,{\boldsymbol {\varOmega }}}\) and a particular B-spline \(B_{j,\ell } \in {\mathscr {B}}_\ell \) has an important consequence, namely the so-called property of preservation of coefficients [23]. This means that the THB-spline representation preserves certain coefficients of functions represented with respect to one of the B-spline bases \({\mathscr {B}}^{\ell }\).
Theorem 20 (Preservation of Coefficients)
Given ℓ ∈{1, …, L}, let the restriction of \(s\in {\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) to Γ ℓ := Ω ℓ ∖ Ω ℓ+1 be represented in the bases \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) and \({\mathscr {B}}_\ell \) , i.e.,
Then,
Proof
We first note that if J ℓ,Ω is nonempty then Γ ℓ has nonempty interior. Assume now that Γ ℓ has nonempty interior. Since \(s\in {\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) and the spline spaces in (1.135) are nested, it is clear that the restriction of s to Γ ℓ can be expressed as a linear combination of the B-splines in \({\mathscr {B}}_\ell \) restricted to Γ ℓ as in (1.154). Let us focus on the sum
and consider three cases.
-
If k > ℓ, then the sum in (1.156) equals zero. Indeed, Definition 9 and (1.149) imply that
$$\displaystyle \begin{aligned}\text{supp}_{{\boldsymbol{\varOmega}}}(B^{T}_{j,k,{\boldsymbol{\varOmega}}})\subseteq \text{supp}_{{\boldsymbol{\varOmega}}}(B_{j,k})\subseteq \varOmega_{k}\subseteq\varOmega_{\ell+1}, \end{aligned}$$and consequently, we have \(\text{supp}_{{\boldsymbol {\varOmega }}}(B^{T}_{j,k,{\boldsymbol {\varOmega }}})\cap \varGamma _\ell =\emptyset \).
-
We now consider the case k = ℓ. From (1.150) it immediately follows
$$\displaystyle \begin{aligned}\sum_{j\in J_{\ell,{\boldsymbol{\varOmega}}}}c_{j,\ell}^{T}B^{T}_{j,\ell,{\boldsymbol{\varOmega}}}(x) =\sum_{j\in J_{\ell,{\boldsymbol{\varOmega}}}}c_{j,\ell}^{T}B_{j,\ell}(x), \quad x\in \varGamma_\ell. \end{aligned}$$ -
Finally, let k < ℓ. In view of the truncation mechanism, we prove that THB-splines introduced at levels less than ℓ in the hierarchy can only contribute in terms of B-splines B i,ℓ with i∉J ℓ,Ω. To this end, let us rewrite the corresponding THB-splines \(B^{T}_{j,k,{\boldsymbol {\varOmega }}}\) in terms of the B-spline basis \({\mathscr {B}}_\ell \),
$$\displaystyle \begin{aligned}B^{T}_{j,k,{\boldsymbol{\varOmega}}}(x)=\sum_{i=1}^{n_\ell}c_{i,\ell}^{j,k}B_{i,\ell}(x), \quad x\in \varGamma_\ell. \end{aligned}$$Due to the definition of \(B^{T}_{j,k,{\boldsymbol {\varOmega }}}\) and the truncation operation (1.148), we have
$$\displaystyle \begin{aligned}c_{i,\ell}^{j,k}=0,\quad \mbox{if}\ \ i\in J_{\ell,{\boldsymbol{\varOmega}}}. \end{aligned}$$Hence, for k < ℓ we arrive at
$$\displaystyle \begin{aligned}\sum_{j\in J_{k,{\boldsymbol{\varOmega}}}}c_{j,k}^{T}B^{T}_{j,k,{\boldsymbol{\varOmega}}}(x) =\sum_{i\not\in J_{\ell,{\boldsymbol{\varOmega}}}} \biggl(\sum_{j\in J_{k,{\boldsymbol{\varOmega}}}}c_{j,k}^{T}c_{i,\ell}^{j,k}\biggr)B_{i,\ell}(x), \quad x\in \varGamma_\ell. \end{aligned}$$
By combining the above three cases and taking into account the local linear independence of B-splines, we obtain the identity (1.154) where
which in particular gives (1.155). □
Thanks to Theorem 20, many interesting features of B-spline representations can be transferred to THB-spline representations.
-
Representation of Polynomials. Any polynomial g of degree p 1 can be represented as
$$\displaystyle \begin{aligned} g(x)=\sum_{\ell=1}^{L}\sum_{\ j\in J_{\ell,{\boldsymbol{\varOmega}}}}\varLambda_{j,p_\ell,{\boldsymbol{\xi}}_\ell}(g)B^{T}_{j,\ell,{\boldsymbol{\varOmega}}}(x),\quad x\in\varOmega_1, \end{aligned} $$(1.157)where \(\varLambda _{j,p_\ell ,{\boldsymbol {\xi }}_\ell }\) is defined in (1.53) with p = p ℓ and ξ = ξ ℓ.
Proof Using the nestedness of the spaces (1.135), it is clear that \(g\in {\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\) for ℓ = 1, …, L and also that \(g\in {\mathbb {S}}_{{\boldsymbol {\varOmega }}}\). Then, consider its representation with respect to \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\) and \({\mathscr {B}}_{\ell }\) for ℓ = 1, …, L. Theorem 20 in combination with Proposition 3 concludes the proof. □
-
Partition of Unity. By (1.49) we have
$$\displaystyle \begin{aligned} \sum_{\ell=1}^{L}\sum_{\ j\in J_{\ell,{\boldsymbol{\varOmega}}}}B^{T}_{j,\ell,{\boldsymbol{\varOmega}}}(x)=1,\quad x\in\varOmega_1. \end{aligned} $$(1.158)Since the THB-splines are nonnegative it follows that they form a nonnegative partition of unity on Ω 1.
-
Greville Points. By (1.50) we have
$$\displaystyle \begin{aligned} x=\sum_{\ell=1}^{L}\sum_{\ j\in J_{\ell,{\boldsymbol{\varOmega}}}}\xi^\ast_{j,p_\ell,{\boldsymbol{\xi}}_\ell}B^{T}_{j,\ell,{\boldsymbol{\varOmega}}}(x), \quad x\in \varOmega_1, \end{aligned} $$(1.159)where \(\xi ^\ast _{j,p_\ell ,{\boldsymbol {\xi }}_\ell }\) are the Greville points defined in (1.51) with p = p ℓ and ξ = ξ ℓ. Note that the Greville points are not necessarily distinct here.
-
Strong Stability. The THB-spline basis is strongly stable with respect to the supremum norm, under mild assumptions on the underlying knot sequences required in the hierarchical construction. We refer the reader to [23] for a proof based on the property of preservation of coefficients. Strong stability in the hierarchical context means that the constants to be considered in the stability relation (1.64) of the basis do not depend on the number of hierarchical levels.
Example 16
The polynomial g(x) = ax 2 + bx + c can be represented in terms of quadratic THB-splines:
From Theorem 20 and Example 8 we obtain that
1.6.3 Quasi-Interpolation in Hierarchical Spaces
The above properties of THB-splines can be exploited to develop a general and very simple procedure for the construction of quasi-interpolants in hierarchical spline spaces [51].
Definition 10
Given for each spline space in (1.135) a quasi-interpolant in B-spline form, i.e.,
the corresponding hierarchical quasi-interpolant in \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) is defined by
According to Definition 10, in order to construct a quasi-interpolant in \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\), it suffices to consider first a quasi-interpolant in each space associated with a particular level in the hierarchy. Then, the coefficients of the proposed hierarchical quasi-interpolant are nothing else than a proper subset of the coefficients of the one-level quasi-interpolants.
We now show how to build hierarchical quasi-interpolants reproducing polynomials of a certain degree p ≤ p 1. As described in Sect. 1.5.2, this is a crucial property feature to ensure good approximation properties.
Theorem 21 (Polynomial Reproduction)
Let \({\mathscr {Q}}_\ell \) be a given sequence of quasi-interpolants as in (1.160), let \({\mathscr {Q}}_{{\boldsymbol {\varOmega }}}\) be the corresponding hierarchical quasi-interpolant as in (1.161), and let p ≤ p 1 . If
then
Proof
Since the spaces in (1.135) are nested, we have p ℓ ≥ p for all ℓ. Let \(g\in {\mathbb {P}}_p\subseteq {\mathbb {P}}_{p_\ell }\subseteq {\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\). Then, this polynomial can be uniquely represented as a linear combination of the B-splines in \({\mathscr {B}}_\ell \),
and since \({\mathscr {Q}}_{\ell }g=g\) we have λ j,ℓ(g) = c j,ℓ. On the other hand, \(g\in {\mathbb {S}}_{{\boldsymbol {\varOmega }}}\), so
From Theorem 20 it follows
implying that \({\mathscr {Q}}_{{\boldsymbol {\varOmega }}} g=g\). □
In the next theorem we present a sufficient condition for constructing quasi-interpolants that are projectors onto \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\).
Theorem 22 (Spline Reproduction)
Let \({\mathscr {Q}}_\ell \) be a given sequence of quasi-interpolants as in (1.160), and let \({\mathscr {Q}}_{{\boldsymbol {\varOmega }}}\) be the corresponding hierarchical quasi-interpolant as in (1.161). Assume
and each λ j,ℓ used in (1.161) is supported on Γ ℓ := Ω ℓ ∖ Ω ℓ+1 . Then,
Proof
Due to the linearity of the quasi-interpolant, it suffices to prove that
where δ r,s stands for the classical Kronecker delta. Let j and ℓ be fixed. To prove (1.163) we consider three cases.
-
If k > ℓ, then \(B^{T}_{i,k,{\boldsymbol {\varOmega }}}(x)=0\) for x ∈ Γ ℓ; see Definition 9. Since λ j,ℓ is only supported on Γ ℓ, it follows from Definition 4 that \(\lambda _{j,\ell }(B^{T}_{i,k,{\boldsymbol {\varOmega }}})=0\).
-
We now consider the case k = ℓ. Since \({\mathscr {Q}}_\ell \) is a projector onto \({\mathbb {S}}_\ell \), we have that λ j,ℓ(B i,ℓ) = δ i,j. From (1.150) and the support restriction of λ j,ℓ, we obtain
$$\displaystyle \begin{aligned}\lambda_{j,\ell}(B^{T}_{i,\ell,{\boldsymbol{\varOmega}}})=\delta_{i,j}, \quad i,j\in J_{\ell,{\boldsymbol{\varOmega}}}. \end{aligned}$$ -
Finally, let k < ℓ. Any \(B^{T}_{i,k,{\boldsymbol {\varOmega }}}\) restricted to Γ ℓ can then be expressed as a linear combination of the B-splines in \({\mathscr {B}}_\ell \) restricted to Γ ℓ, i.e.,
$$\displaystyle \begin{aligned}B^{T}_{i,k,{\boldsymbol{\varOmega}}}(x)=\sum_{r=1}^{n_\ell}c_{r,\ell}^{i,k}B_{r,\ell}(x), \quad x\in \varGamma_\ell, \end{aligned}$$where
$$\displaystyle \begin{aligned}c_{r,\ell}^{i,k}=0,\quad \mbox{if}\ \ r\in J_{\ell, {\boldsymbol{\varOmega}}}, \end{aligned}$$as explained in the third case of the proof of Theorem 20. Thus, by the support restriction of λ j,ℓ, we have for j ∈ J ℓ,Ω,
$$\displaystyle \begin{aligned}\lambda_{j,\ell}(B^{T}_{i,k,{\boldsymbol{\varOmega}}})=\sum_{r=1}^{n_\ell}c_{r,\ell}^{i,k}\lambda_{j,\ell}(B_{r,\ell})= \sum_{r=1}^{n_\ell}c_{r,\ell}^{i,k}\delta_{j,r}=c_{j,\ell}^{i,k}=0. \end{aligned}$$
The above three cases complete the proof. □
Some remarks are in order here.
-
Constraints on ( 1.160 ). The sequence of quasi-interpolants (1.160) considered in Theorem 22 needs to satisfy constraints more restrictive than those in Theorem 21: For each level ℓ, \({\mathscr {Q}}_\ell \) must be a projector onto \({\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\) and each λ j,ℓ, j ∈ J ℓ,Ω, must be supported on Γ ℓ. The former constraint connects the sequence of quasi-interpolants \({\mathscr {Q}}_1,\ldots ,{\mathscr {Q}}_L\) with the sequence of spaces \({\mathbb {S}}_{p_1,{\boldsymbol {\xi }}_1},\ldots ,{\mathbb {S}}_{p_L,{\boldsymbol {\xi }}_L}\) and has a similar counterpart in Theorem 21. The latter constraint links the same sequence of quasi-interpolants with the domain hierarchy Ω. Nevertheless, once a sequence of quasi-interpolants as in (1.160) satisfying the hypotheses of Theorem 22 is available, the construction of a hierarchical quasi-interpolant that is a projector onto \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\) does not require additional efforts compared to a hierarchical quasi-interpolant that just reproduces polynomials.
-
Dual Basis. Let {λ j,ℓ} be a set of linear functionals as in (1.161) that provides a projector onto \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\). Then, because of (1.163), it is a dual basis for the THB-spline basis \({\mathscr {T}}_{{\boldsymbol {\varOmega }}}\).
-
Approximation Power. Polynomial reproduction is one of the key ingredients to show the approximation power of spline quasi-interpolants; see Sect. 1.5.2. Boundedness of a hierarchical quasi-interpolation operator and optimal approximation accuracy can be achieved on domain hierarchies that are nicely graded (i.e., the boundaries of the different Ω ℓ are sufficiently separated). Local error estimates for hierarchical quasi-interpolants of the form (1.161) can be found in [51] with respect to the L ∞-norm, and in [49] with respect to the general L q-norm, 1 ≤ q ≤∞.
Example 17
Let p ℓ = 2, and let ξ ℓ be a 3-open knot sequence with at most double knots in the interior for each ℓ = 1, …, L. Then, we can choose the quasi-interpolants in (1.160) as in Example 12. This leads to the hierarchical quasi-interpolant
where
From Example 12 and Theorem 21 we deduce that this hierarchical quasi-interpolant reproduces the polynomial space \({\mathbb {P}}_2\). If [ξ j+1,ℓ, ξ j+2,ℓ] ⊆ Γ ℓ for each j ∈ J ℓ,Ω, then it actually reproduces the entire hierarchical spline space \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\), according to Theorem 22.
Example 18
Consider the quasi-interpolant constructed in Sect. 1.5.3.1 for each space \({\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\) of level ℓ = 1, …, L. This leads to the hierarchical quasi-interpolant
where \({\mathscr {L}}_{j,p_\ell ,{\boldsymbol {\xi }}_\ell }\) is defined in (1.123) with p = p ℓ and ξ = ξ ℓ; it is supported on a single knot interval \([\xi _{m_{j,p_\ell },\ell },\xi _{m_{j,p_\ell }+1,\ell }]\). From Lemma 2 and Theorem 21 we deduce that this hierarchical quasi-interpolant reproduces the polynomial space \({\mathbb {P}}_{p_1}\). Theorem 22 says that if \([\xi _{m_{j,p_\ell },\ell },\xi _{m_{j,p_\ell }+1,\ell }]\subseteq \varGamma _\ell \) for each j ∈ J ℓ,Ω, then the hierarchical quasi-interpolant reproduces the entire hierarchical spline space \({\mathbb {S}}_{{\boldsymbol {\varOmega }}}\).
The hierarchical quasi-interpolant in Definition 10 can be interpreted as a telescopic approximant, where for each level an approximant of the residual is added.Footnote 9 To show this, we define the following set of indices
Referring to (1.141), it is easy to see that J ℓ,Ω ⊆ K ℓ,Ω, and moreover J L,Ω = K L,Ω.
Theorem 23 (Telescopic Representation)
Let \({\mathscr {Q}}_\ell \) be a given sequence of quasi-interpolants as in (1.160), and let \({\mathscr {Q}}_{{\boldsymbol {\varOmega }}}\) be the corresponding hierarchical quasi-interpolant as in (1.161). Assume
then
where
Proof
Each quasi-interpolant \({\mathscr {Q}}_\ell \), ℓ = 1, …, L, is assumed to be a projector onto the space \({\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\), and because of the nestedness of the spaces \({\mathbb {S}}_{p_\ell ,{\boldsymbol {\xi }}_\ell }\subset {\mathbb {S}}_{p_{\ell +1},{\boldsymbol {\xi }}_{\ell +1}}\), we know that every basis function B j,ℓ can be represented as
where λ k,ℓ+1(B j,ℓ) = 0 if the support of B k,ℓ+1 is not contained in the support of B j,ℓ. By exploiting the definition of the truncated basis (1.149) and (1.167), we obtain
Moreover,
Hence,
We now remark that from the truncation definition (1.148)–(1.149) it follows that \(\lambda _{k,3}(B^{T}_{j,1,{\boldsymbol {\varOmega }}})=0\) for any k ∈ K 3,Ω and j ∈ J 1,Ω, and so
By using similar arguments as before, we can write (1.168) as
and by means of (1.168) and (1.169) we obtain
resulting in
By iterating over all levels in the hierarchy and repeating the same arguments, we get the relation (1.165). □
The telescopic representation in Theorem 23 directly leads to the representation of the hierarchical quasi-interpolant in terms of the HB-spline basis, instead of in terms of the THB-spline basis (see Definition 10), under assumption (1.164). Indeed, as observed in [51], thanks to property (1.167), one can simply replace the index sets K ℓ,Ω by J ℓ,Ω in (1.166) and the relation (1.165) still remains true. This implies that (1.165) can be rewritten as
where
1.7 Tensor-Product Structures and Adaptive Extensions
The most easy way to extend many of the previous results to the multivariate setting is to consider a tensor-product structure. For the sake of simplicity, we briefly focus here on the bivariate setting. The extension to higher dimensions is straightforward; it only requires a more involved indexing notation.
1.7.1 Tensor-Product B-Splines
Given two knot sequences
we define the basic rectangle as
The tensor-product B-splines can be simply constructed as the product of univariate B-splines in each variable, i.e.,
for j k = 1, …, n k and k = 1, 2.
Example 19
Figure 1.6 shows a schematic representation of a tensor-product B-spline basis of bidegree (p 1, p 2) = (3, 3). A (p k + 1)-open knot sequence is chosen in each direction x k, where the interior knots are all simple, and the corresponding univariate B-splines are depicted. Then, the set of tensor-product B-splines is obtained by computing the tensor product of the sets of univariate B-splines in each direction. Contour plots of some bicubic tensor-product B-splines are depicted in Fig. 1.7.
Schematic representation of the (bivariate) tensor-product B-spline basis of bidegree (p 1, p 2) = (3, 3) using a 4-open knot sequence in each direction. The knot lines are visualized by solid lines in the rectangular domain (this is the basic rectangle), and the sets of univariate B-splines are depicted for both directions
Contour plots of some bicubic tensor-product B-splines \(B_{j_1,j_2,3,3,{ \boldsymbol {\xi }}_1,{ \boldsymbol {\xi }}_2}\) defined on the tensor-product mesh given in Fig. 1.6. The bounding box of the support of each B-spline is visualized by solid blue lines. (a) (j 1, j 2) = (3, 3). (b) (j 1, j 2) = (5, 5). (c) (j 1, j 2) = (7, 9)
It is clear that tensor-product B-splines inherit all the nice features of univariate B-splines discussed in Sects. 1.2 and 1.3. In particular, they enjoy the following properties.
-
Local Support. A tensor-product B-spline is locally supported on the rectangle given by the extreme knots used in the definition of its univariate B-splines in each direction. More precisely,
$$\displaystyle \begin{aligned} B_{j_1,j_2,p_1,p_2,{\boldsymbol{\xi}}_1,{\boldsymbol{\xi}}_2}(x_1,x_2)=0, \quad (x_1,x_2)\notin S,\end{aligned} $$(1.173)where
$$\displaystyle \begin{aligned}S:=[\xi_{j_1,1},\xi_{j_1+p_1+1,1})\times[\xi_{j_2,2},\xi_{j_2+p_2+1,2}).\end{aligned} $$ -
Nonnegativity. A tensor-product B-spline is nonnegative everywhere, and positive inside its support, i.e.,
$$\displaystyle \begin{aligned} B_{j_1,j_2,p_1,p_2,{\boldsymbol{\xi}}_1,{\boldsymbol{\xi}}_2}(x_1,x_2)\ge 0, \quad x_1,x_2\in{\mathbb{R}},\end{aligned} $$(1.174)and
 (1.175)
(1.175)where

-
Piecewise Structure. A tensor-product B-spline has a piecewise tensor-product polynomial structure, i.e.,
$$\displaystyle \begin{aligned} B_{j_1,j_2,p_1,p_2,{\boldsymbol{\xi}}_1,{\boldsymbol{\xi}}_2}\in{\mathbb{P}}_{p_1}([\xi_{m_1,1},\xi_{m_1+1,1}))\otimes{\mathbb{P}}_{p_2}([\xi_{m_2,2},\xi_{m_2+1,2})).\end{aligned} $$(1.176) -
Smoothness. If ξ is a knot of \(B_{j_k,p_k,{\boldsymbol {\xi }}_k}\) of multiplicity μ ≤ p k + 1 then \(B_{j_1,j_2,p_1,p_2,{\boldsymbol {\xi }}_1,{\boldsymbol {\xi }}_2}\) belongs to the class \(C^{p_k-\mu }\) across the line x k = ξ for k = 1, 2.
-
Linear Independence. If each ξ k is (p k + 1)-basic for k = 1, 2, then the tensor-product B-splines \(\{B_{j_1,j_2,p_1,p_2,{\boldsymbol {\xi }}_1,{\boldsymbol {\xi }}_2}: j_k=1,\ldots ,n_k, \ k=1,2\}\) are (locally) linearly independent on R.
-
Partition of Unity. We have
$$\displaystyle \begin{aligned} \sum_{j_1=1}^{n_1}\sum_{j_2=1}^{n_2} B_{j_1,j_2,p_1,p_2,{\boldsymbol{\xi}}_1,{\boldsymbol{\xi}}_2}(x_1,x_2)=1, \quad (x_1,x_2)\in R.\end{aligned} $$(1.177)Since the tensor-product B-splines are nonnegative it follows that they form a nonnegative partition of unity on R.
-
Greville Points. For (x 1, x 2) ∈ R and ℓ 1, ℓ 2 ∈{0, 1}, we have
$$\displaystyle \begin{aligned} x_1^{\ell_1}x_2^{\ell_2}=\sum_{j_1=1}^{n_1}\sum_{j_2=1}^{n_2} (\xi^\ast_{j_1,p_1,{\boldsymbol{\xi}}_1})^{\ell_1}(\xi^\ast_{j_2,p_2,{\boldsymbol{\xi}}_2})^{\ell_2} B_{j_1,j_2,p_1,p_2,{\boldsymbol{\xi}}_1,{\boldsymbol{\xi}}_2}(x_1,x_2), \end{aligned} $$(1.178)where \(\xi ^\ast _{j_k,p_k,{\boldsymbol {\xi }}_k}\) is the Greville point defined in (1.51) for the knot sequence ξ k, k = 1, 2.
A tensor-product spline function is defined as
Since the tensor-product B-splines are linearly independent, the space of spline functions has dimension n 1 n 2.
A main advantage of the representation in (1.179) is that its evaluation can be reduced to a sequence of evaluations of univariate spline functions:
or, equivalently,
Note that (1.180) requires n 1 univariate spline evaluations of degree p 2 and one univariate spline evaluation of degree p 1. On the other hand, (1.181) requires n 2 univariate spline evaluations of degree p 1 and one univariate spline evaluation of degree p 2. Thus, it is better to choose one of the two forms according to the minimal computational cost.
Other algorithms in the univariate B-spline setting (like knot insertion) can be extended in a similar way to the tensor-product B-spline setting.
1.7.2 Local Refinement
Despite their simple and elegant formulation, tensor-product B-spline structures have a main drawback. Any refinement of a knot sequence in one direction has a global effect in the other direction, and this prevents doing local refinement as illustrated in Fig. 1.8.
Given an initial tensor-product representation (a), an error estimator indicates regions of the mesh which require further refinement (b). The tensor-product structure necessarily implies a propagation of the refinement (c). Adaptive splines, instead, should provide a proper local control of the refinement procedure (d)
The hierarchical spline model provides a natural strategy to guarantee the locality of the refinement. As explained in Sect. 1.6, hierarchical spline spaces are a mixture of spline spaces of different resolution, localized by the domain hierarchy. Even though the concept of hierarchical splines was detailed in the univariate setting, it can be straightforwardly extended towards the bivariate (and multivariate) setting.
When selecting a sequence of nested tensor-product spline spaces on a common basic rectangle R in place of (1.135) and considering the corresponding tensor-product B-spline bases in place of (1.137), the definitions of tensor-product HB-splines and THB-splines follow verbatim Definitions 7 and 9, respectively. The properties (and their proofs) described in Sect. 1.6 also hold in the tensor-product extension. We refer the reader to [22, 23] for more details on tensor-product THB-splines and their properties. A full treatment of the construction of related hierarchical quasi-interpolants and their approximation properties can be found in [49, 51].
Example 20
An example of a two-dimensional domain hierarchy together with its knot lines is illustrated in Fig. 1.9. We consider a nested sequence of three tensor-product spline spaces defined on a (uniform) knot mesh with open knots along the boundary (Fig. 1.9a). Assume the corresponding basic rectangle is denoted by R. Then, we select the subsets R =: Ω 1 ⊇ Ω 2 ⊇ Ω 3 as a union of mesh elements at each level (Fig. 1.9b), and together they form the domain hierarchy Ω (Fig. 1.9c). On such domain hierarchy, we can define the corresponding HB-splines and THB-splines according to Definitions 7 and 9, respectively. Contour plots of some biquadratic tensor-product THB-splines are depicted in Fig. 1.10. The shape of THB-splines related to coarser levels adapts nicely to the locally refined regions in Ω, as illustrated in Fig. 1.10a, b. THB-splines related to the finest level are nothing else than standard tensor-product B-splines, as illustrated in Fig. 1.10c.
Contour plots of some biquadratic tensor-product THB-splines of different levels defined on the domain hierarchy given in Fig. 1.9. The bounding box of the support of the untruncated version of each THB-spline is visualized by solid blue lines. (a) Level 1. (b) Level 2. (c) Level 3
Finally, we remark that there exist also other adaptive spline models based on local tensor-product structures, like (analysis-suitable) T-splines [2, 46] and LR-splines [9, 17].
Notes
- 1.
The original meaning of the word “spline” is a flexible ruler used to draw curves, mainly in the aircraft and shipbuilding industries. The “B” in B-splines stands for basis or basic.
- 2.
The recurrence relation is due to de Boor, Cox and Mansfield [4, 14]. However, it appears already in works by Popoviciu and Chakalov in the 1930s; see [8] for an account of the early history of splines. For the modern theory of splines we refer the reader to the seminal papers by Schoenberg [41,42,43] and Curry/Schoenberg [15, 16]. In their works, B-splines were defined by divided differences of truncated power functions.
- 3.
- 4.
The value Λ j,p,ξ(s) is known as the de Boor–Fix functional [7] applied to s.
- 5.
- 6.
This notation means that if λ j(f) uses the value of f or one of its derivatives at \(\xi _{m_j}\) (or \(\xi _{m_j+1}\)) then this value is obtained by taking the one sided limit from the right (or the left).
- 7.
- 8.
- 9.
References
L. Beirão da Veiga, A. Buffa, J. Rivas, G. Sangalli, Some estimates for h-p-k-refinement in isogeometric analysis. Numer. Math. 118, 271–305 (2011)
L. Beirão da Veiga, A. Buffa, G. Sangalli, R. Vázquez, Analysis-suitable T-splines of arbitrary degree: definition, linear independence and approximation properties. Math. Models Methods Appl. Sci. 23, 1979–2003 (2013)
W. Böhm, Inserting new knots into B-spline curves. Comput. Aided Des. 12, 199–201 (1980)
C. de Boor, On calculating with B-splines. J. Approx. Theory 6, 50–62 (1972)
C. de Boor, On local linear functionals which vanish at all B-splines but one, in Theory of Approximation with Applications, ed. by A.G. Law, N.B. Sahney (Academic Press, New York, 1976), pp. 120–145
C. de Boor, A Practical Guide to Splines, revised edn. (Springer, New York, 2001)
C. de Boor, G.J. Fix, Spline approximation by quasiinterpolants. J. Approx. Theory 8, 19–45 (1973)
C. de Boor, A. Pinkus, The B-spline recurrence relations of Chakalov and of Popoviciu. J. Approx. Theory 124, 115–123 (2003)
A. Bressan, Some properties of LR-splines. Comput. Aided Geom. Des. 30, 778–794 (2013)
L. Chakalov, On a certain presentation of the Newton divided differences in interpolation theory and its applications. Godishnik na Sofijskiya Universitet, Fiziko-Matematicheski Fakultet 34, 353–394 (1938)
E. Cohen, T. Lyche, R. Riesenfeld, Discrete B-splines and subdivision techniques in computer-aided geometric design and computer graphics. Comput. Graphics Image Process. 14, 87–111 (1980)
E. Cohen, T. Lyche, L.L. Schumaker, Degree raising for splines. J. Approx. Theory 46, 170–181 (1986)
E. Cohen, R.F. Riesenfeld, G. Elber, Geometric Modeling with Splines: An Introduction (A K Peters, Wellesley, 2001)
M.G. Cox, The numerical evaluation of B-splines. J. Inst. Math. Appl. 10, 134–149 (1972)
H.B. Curry, I.J. Schoenberg, On spline distributions and their limits: the Pólya distribution functions. Bull. AMS 53, 1114, Abstract 380t (1947)
H.B. Curry, I.J. Schoenberg, On Pólya frequency functions IV: the fundamental spline functions and their limits. J. Anal. Math. 17, 71–107 (1966)
T. Dokken, T. Lyche, K.F. Pettersen, Polynomial splines over locally refined box-partitions. Comput. Aided Geom. Des. 30, 331–356 (2013)
H.C. Elman, X. Zhang, Algebraic analysis of the hierarchical basis preconditioner. SIAM J. Matrix Anal. Appl. 16, 192–206 (1995)
D.R. Forsey, R.H. Bartels, Hierarchical B-spline refinement. ACM SIGGRAPH Comput. Graph. 22, 205–212 (1988)
D.R. Forsey, R.H. Bartels, Surface fitting with hierarchical splines. ACM Trans. Graph. 14, 134–161 (1995)
C. Garoni, C. Manni, F. Pelosi, S. Serra-Capizzano, H. Speleers, On the spectrum of stiffness matrices arising from isogeometric analysis. Numer. Math. 127, 751–799 (2014)
C. Giannelli, B. Jüttler, H. Speleers, THB-splines: the truncated basis for hierarchical splines. Comput. Aided Geom. Des. 29, 485–498 (2012)
C. Giannelli, B. Jüttler, H. Speleers, Strongly stable bases for adaptively refined multilevel spline spaces. Adv. Comput. Math. 40, 459–490 (2014)
T.N.E. Greville, On the normalisation of the B-splines and the location of the nodes for the case of unequally spaced knots, in Inequalities, ed. by O. Shisha (Academic Press, New York, 1967), pp. 286–290
E. Grinspun, P. Krysl, P. Schröder, CHARMS: a simple framework for adaptive simulation. ACM Trans. Graph. 21, 281–290 (2002)
K. Höllig, J. Hörner, Approximation and Modeling with B-Splines (Society for Industrial and Applied Mathematics, Philadelphia, 2013)
J. Hoschek, D. Lasser, Fundamentals of Computer Aided Geometric Design (A K Peters, Wellesley, 1993)
R. Kraft, Adaptive and linearly independent multilevel B-splines, in Surface Fitting and Multiresolution Methods, ed. by A. Le Méhauté, C. Rabut, L.L. Schumaker (Vanderbilt University Press, Nashville, 1997), pp. 209–218
R. Kraft, Adaptive und linear unabhängige Multilevel B-Splines und ihre Anwendungen, Ph.D. thesis, University of Stuttgart, 1998
P. Krysl, E. Grinspun, P. Schröder, Natural hierarchical refinement for finite element methods. Int. J. Numer. Methods Eng. 56, 1109–1124 (2003)
M.J. Lai, L.L. Schumaker, Spline Functions on Triangulations (Cambridge University Press, Cambridge, 2007)
J.M. Lane, R.F. Riesenfeld, A theoretical development for the computer generation and display of piecewise polynomial surfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2, 35–46 (1980)
P.S. de Laplace, Théorie Analytique des Probabilités, 3rd edn. (Courcier, Paris, 1820)
T. Lyche, A note on the condition numbers of the B-spline bases. J. Approx. Theory 22, 202–205 (1978)
C. Manni, H. Speleers, Standard and non-standard CAGD tools for isogeometric analysis: a tutorial, in IsoGeometric Analysis: A New Paradigm in the Numerical Approximation of PDEs, ed. by A. Buffa, G. Sangalli. Lecture Notes in Mathematics, vol. 2161 (Springer, Cham, 2016), pp. 1–69
M. Marsden, An identity for spline functions and its application to variation diminishing spline approximation. J. Approx. Theory 3, 7–49 (1970)
T. Popoviciu, Sur quelques propriétés des fonctions d’une ou de deux variables réelles, Ph.D. thesis, Presented to the Faculté des Sciences de Paris. Published by Institutul de Arte Grafice Ardealul, Cluj, 1933
H. Prautzsch, W. Böhm, M. Paluszny, Bézier and B-Spline Techniques (Springer, Berlin, 2002)
W. Rudin, Real and Complex Analysis, 3rd edn. (McGraw-Hill, Singapore, 1987)
K. Scherer, A.Y. Shadrin, New upper bound for the B-spline basis condition number: II. A proof of de Boor’s 2k-conjecture. J. Approx. Theory 99, 217–229 (1999)
I.J. Schoenberg, Contributions to the problem of approximation of equidistant data by analytic functions. Part A.–On the problem of smoothing or graduation. A first class of analytic approximation formulae. Q. Appl. Math. 4, 45–99 (1946)
I.J. Schoenberg, Contributions to the problem of approximation of equidistant data by analytic functions. Part B.–On the problem of osculatory interpolation. A second class of analytic approximation formulae. Q. Appl. Math. 4, 112–141 (1946)
I.J. Schoenberg, On spline functions, in Inequalities, ed. by O. Shisha (Academic Press, New York, 1967), pp. 255–286
I.J. Schoenberg, Cardinal interpolation and spline functions. J. Approx. Theory 2, 167–206 (1969)
L.L. Schumaker, Spline Functions: Basic Theory, 3rd edn. (Cambridge University Press, Cambridge, 2007)
T.W. Sederberg, J. Zheng, A. Bakenov, A. Nasri, T-splines and T-NURCCs. ACM Trans. Graph. 22, 477–484 (2003)
A. Sharma, A. Meir, Degree of approximation of spline interpolation. J. Math. Mech. 15, 759–768 (1966)
H. Speleers, Inner products of box splines and their derivatives. BIT Numer. Math. 55, 559–567 (2015)
H. Speleers, Hierarchical spline spaces: quasi-interpolants and local approximation estimates. Adv. Comput. Math. 43, 235–255 (2017)
H. Speleers, P. Dierckx, S. Vandewalle, Quasi-hierarchical Powell–Sabin B-splines. Comput. Aided Geom. Des. 26, 174–191 (2009)
H. Speleers, C. Manni, Effortless quasi-interpolation in hierarchical spaces. Numer. Math. 132, 155–184 (2016)
S. Takacs, T. Takacs, Approximation error estimates and inverse inequalities for B-splines of maximum smoothness. Math. Models Methods Appl. Sci. 26, 1411–1445 (2016)
A.V. Vuong, C. Giannelli, B. Jüttler, B. Simeon, A hierarchical approach to adaptive local refinement in isogeometric analysis. Comput. Methods Appl. Mech. Eng. 200, 3554–3567 (2011)
H. Yserentant, On the multilevel splitting of finite element spaces. Numer. Math. 49, 379–412 (1986)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Lyche, T., Manni, C., Speleers, H. (2018). Foundations of Spline Theory: B-Splines, Spline Approximation, and Hierarchical Refinement. In: Lyche, T., Manni, C., Speleers, H. (eds) Splines and PDEs: From Approximation Theory to Numerical Linear Algebra. Lecture Notes in Mathematics(), vol 2219. Springer, Cham. https://doi.org/10.1007/978-3-319-94911-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-94911-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94910-9
Online ISBN: 978-3-319-94911-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)