1 INTRODUCTION

Expansions on basis splines, also called B-splines, are the well-known and effective computational tool in modern physics that are widely used in applications (see, for example, the review articles [1–3] and references therein). Few programs based on B-spline expansions are available from the Computer Physics Communications [4, 5]. The flexibility of the B-spline basis is defined by the behaviour of piecewise B-spline polynomials which can be readily adjusted with the knot sequence, the order of polynomials and the number of B-splines. Regions with rapidly changing functions may be handled by a corresponding increase of the density of the knot sequence there. It allows to optimize B-splines as a basis set to expand functions and solve systems of differential equations.

Usually, a treatment of B-spline expansions is based on numerical calculations of the Cox-de Boor recursive formula. An efficiency of B-spline methods can be enhanced if the convenient analytical representation of B-spline polynomials for an arbitrary knot sequence and order will be developed. Such development is the main goal of the article. It allows to handle many mathematical operations (product, differentiation, integration and etc.) with B-spline analytically, thus it facilitates and expands applications of the B‑spline methods. A convenient basis for the B-spline analytic representation is given by Bernstein basis functions [6–8] that have the remarkable analytic properties. Bernstein polynomials itself are used in many branches of mathematics, for instance, the approximation theory, the probability theory, for solution of differential equations (see, for example, [9] and references therein) etc. In solution of differential equations a full radial range \([{{r}_{{{\text{min}}}}},{{r}_{{{\text{max}}}}}]\) is mapped on the finite interval \([0,1]\), where expansion on Bernstein basis is used. In this example, the Bernstein basis appears as a global basis for the function decomposition. Usually, the high order of Bernstein basis polynomials must be used in calculations to get the required accuracy for solutions. The piecewise B‑splines are local basis and allow to obtain solutions with relatively small orders of polynomials. Then decomposition on Bernstein polynomials is used only on single subintervals. The combination of both representations allows to keep the flexibility of the local B‑spline expansions and gains a possibility for analytical manipulations based on analytical properties of Bernstein basis polynomials.

The paper is organized as follows. In Section 2 we remind the basic properties of B-spline polynomials and derive their analytic representation via the Bernstein basis functions. In Section 3 some properties of the decomposition are considered and few examples of applications are given. In Appendix A the basic properties of Bernstein basis functions are presented.

2 B-SPLINES DECOMPOSITION

To fix a notation and for a completeness of descriptions, some basic B-spline properties are given below.

2.1 Description of B-Splines

B-splines \(B_{i}^{{(k)}}(r),\)\(i\) = \(1,2, \ldots ,N\) are piecewise polynomial functions of order k, completely defined by a set of points \({\text{\{ }}{{t}_{j}}{\text{\} }}{\text{,}}\)\(j\) = \(1,2, \ldots ,N + k\) which may be in part coincident. The knot sequence \({\text{\{ }}{{t}_{j}}{\text{\} }}\) divides the radial interval [\({{r}_{{{\text{min}}}}}\), \({{r}_{{{\text{max}}}}}\)] into adjacent subintervals

$${{r}_{{\min }}} = {{t}_{1}} \leqslant \ldots \leqslant {{t}_{{N + k}}} = {{r}_{{\max }}}.$$
((1))

The common choice is to make the end-points of the support grid k-fold degenerate

$${{t}_{1}} = \ldots = {{t}_{k}} = {{r}_{{{\text{min}}}}},$$
$${{t}_{{N + 1}}} = \ldots = {{t}_{{N + k}}} = {{r}_{{\max }}}.$$

The knot sequence defines the extent of individual splines. B-splines of the order \(k > 1\) are defined recursively by the Cox-de Boor relation [1]

$$B_{i}^{{(k)}}(r) = \frac{{r - {{t}_{i}}}}{{{{t}_{{i + k - 1}}} - {{t}_{i}}}}B_{i}^{{(k - 1)}}(r) + \frac{{{{t}_{{i + k}}} - r}}{{{{t}_{{i + k}}} - {{t}_{{i + 1}}}}}B_{{i + 1}}^{{(k - 1)}}(r),$$
((2))

supplemented with the definition of B-splines of the order k = 1

$$B_{i}^{{(1)}}(r) = \left\{ \begin{gathered} 1,\,\,\,\,{\text{for}}\,\,\,\,{{t}_{i}} \leqslant r < {{t}_{{i + 1}}} \hfill \\ 0,\,\,\,\,{\text{for}}\,\,\,\,r < {{t}_{i}},r \geqslant {{t}_{{i + 1}}} \hfill \\ \end{gathered} \right..$$
((3))

The recursion (2) is numerically stable and allows to define and manipulate B-splines of arbitrary order and knot point distribution. Each spline \(B_{i}^{{(k)}}(r)\) expands over an interval \([{{t}_{i}},{{t}_{{i + k}}})\), which contains \(k\) subintervals, and is indexed by the knot i, \(i = 1, \ldots ,N\) where it starts. Splines \(B_{i}^{{(k)}}(r)\) are polynomials of the maximum degree n = \(k - 1\). The sum of B-splines represents the partition of the unity for the radial interval \({{r}_{{\min }}} \leqslant r \leqslant {{r}_{{\max }}}\)

$$\sum\limits_{i = 1}^N {B_{i}^{{(k)}}} (r) = 1.$$
((4))

The derivative of a B-spline of the order k can be expressed as a linear combination of B-splines of the order \((k - 1)\). All B-splines are non-negative functions with convex shapes. Thus, the set of B-splines of the order k and the knot sequence \({\text{\{ }}{{t}_{j}}{\text{\} }}\) forms a complete basis for piecewise polynomials of the degree n on the radial interval spanned by the knot sequence. An arbitrary function \(f(r)\) in this interval can be decomposed over B-splines

$$\begin{gathered} f(r) = \sum\limits_{i = 1}^N {{{c}_{i}}B_{i}^{{(k)}}(r)} = \sum\limits_{j = i - k + 1}^i {{{c}_{j}}B_{j}^{{(k)}}(r)} , \\ {\text{for}}\,\,\,\,r \in [{{t}_{i}},{{t}_{{i + 1}}}]. \\ \end{gathered} $$
((5))

Therefore, to calculate a function at any point r only k terms of the sum are needed. The sum includes B-splines that differ from zero in the subinterval i which embraces the point r.

2.2 Derivation of the B-Spline Analytical Representation

B-splines are defined by the non-equidistant grid \({\text{\{ }}{{t}_{j}}{\text{\} }}\). Only for the equidistant grid, the B-spline shapes are the same and consequently translated from one interval to other. In general case to get the analytical presentation is necessary to scale a radial dependence to a variable which is a common for all subintervals. A convenient choice is to define for any subinterval \([{{t}_{i}},{{t}_{{i + 1}}})\) the variable \({{x}_{i}}\) defined as

$$\begin{gathered} {{x}_{i}} = \frac{{r - {{t}_{i}}}}{{{{t}_{{i + 1}}} - {{t}_{i}}}},\,\,\,{\text{for}}\,\,\,\,{{t}_{i}} \leqslant r < {{t}_{{i + 1}}}, \\ 1 - {{x}_{i}} = \frac{{{{t}_{{i + 1}}} - r}}{{{{t}_{{i + 1}}} - {{t}_{i}}}},\,\,\,\,{\text{where}}\,\,\,\,0 \leqslant {{x}_{i}} < 1. \\ \end{gathered} $$
((6))

The subinterval \(i\) can be selected by a projector operator \({{\delta }_{i}} \equiv B_{i}^{{(1)}}(r)\) defined by the expression (3) with property

$${{\delta }_{i}} * {{\delta }_{j}} = \left\{ {\begin{array}{*{20}{c}} {{{\delta }_{i}},}&{i = j} \\ {0,}&{i \ne j} \end{array}} \right..$$
((7))

A set of constant \(z_{{l,m}}^{{i,j}}\) which depends on the grid \({\text{\{ }}{{t}_{j}}{\text{\} }}\) can be defined

$$z_{{l,m}}^{{i,j}} = \frac{{{{t}_{i}} - {{t}_{j}}}}{{{{t}_{l}} - {{t}_{m}}}},\,\,\,\,l \ne m.$$
((8))

It is evident from definition that \(z_{{l,m}}^{{i,i}}\) = 0, and \(z_{{l,m}}^{{l,m}}\) = 1. Using these definitions the factors before B-splines on the right side of Eq. (2) can be written in the following way

$$\frac{{r - {{t}_{i}}}}{{{{t}_{{i + n}}} - {{t}_{i}}}} = \sum\limits_{j = 0}^{n - 1} {{{\delta }_{{i + j}}}} \left( {z_{{i + n,\,i}}^{{i + j,\,i}} + z_{{i + n,\,i}}^{{i + j + 1,\,\,i + j}}{{x}_{{i + j}}}} \right),$$
((9))
$$\begin{gathered} \frac{{{{t}_{{i + n + 1}}} - r}}{{{{t}_{{i + n + 1}}} - {{t}_{{i + 1}}}}} \\ = \sum\limits_{j = 0}^{n - 1} {{{\delta }_{{i + n + 1}}}\left( {z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j + 2}} + z_{{i + n + 1,\,\,i + 1}}^{{i + j + 2,\,\,i + n + 1}}(1 - {{x}_{{j + j + 1}}})} \right)} . \\ \end{gathered} $$
((10))

It is clear from recurrence relation (2) that on any subinterval \((i + j)\) the B-spline can be represented by a sum of products from two factors, \({{x}_{{i + j}}}\) and \((1 - {{x}_{{i + j}}})\), taken in different powers. Functions \(x\), \((1 - x)\) and their product in powers \(l\) and \((m - l)\) can be described by Bernstein basis functions \(b_{1}^{{(1)}}(x),\)\(b_{0}^{{(1)}}(x)\) and \(b_{l}^{{(m)}}(x),\) respectively. The Bernstein basis function \(b_{l}^{{(m)}}(x)\) is the m-th degree polynomial [6, 7] defined by relation

$$b_{l}^{{(m)}}(x) = \left( {\begin{array}{*{20}{c}} m \\ l \end{array}} \right){{x}^{l}}{{(1 - x)}^{{m - l}}},\,\,\,\,0 \leqslant x \leqslant 1,$$
((11))
$$\left( {\begin{array}{*{20}{c}} m \\ l \end{array}} \right) = \frac{{m!}}{{l!(m - l)!}},$$
((12))

for \(l\) = \(0,1, \ldots ,m\) and \(b_{l}^{{(m)}}(x)\) = 0 for \(l < \) 0 or \(l > m.\) These functions form a complete basis over interval \([0,1]\). Some useful properties of these polynomial functions are given in Appendix A. Since an arbitrary Bernstein basis polynomial can be written in terms of Bernstein polynomials of the higher degree (see relation (A.41)), then products of factors xl and (1 – x)(m–l), obtained from the recurrence relation (2), can be reduced to the Bernstein polynomial of the nth degree. Thus B-splines of the order \((n + 1)\) can be presented by an analytic form via Bernstein basis functions of the nth degree

$$B_{i}^{{(n + 1)}}(r) = \sum\limits_{j = 0}^n {{{\delta }_{{i + j}}}} \sum\limits_{l = 0}^n {c_{{j,l}}^{{i,n}}} b_{l}^{{(n)}}({{x}_{{i + j}}}),$$
((13))

where the sum over j is a sum over subintervals within which the B-spline is different from zero, and the sum over l is a sum over different Bernstein basis polynomials of the nth order defined on the subinterval \([{{t}_{{i + j}}},{{t}_{{i + j + 1}}}]\). The aim is to find unknown coefficients \(c_{{j,l}}^{{i,n}}\) that depend only on a distribution of the grid points \({\text{\{ }}{{t}_{j}}{\text{\} }}\) and n- a degree of B-spline polynomials.

The recurrence relation (2) shows that support domain \([{{t}_{i}},{{t}_{{i + 1}}}],\) where a spline \(B_{i}^{{(n + 1)}}(r)\) is non-zero, can be split into three regions: the most left \([{{t}_{i}},{{t}_{{i + 1}}}]\) and the most right \([{{t}_{{i + n}}},{{t}_{{i + n + 1}}}]\) regions, and region between them \([{{t}_{{i + 1}}},{{t}_{{i + n}}}]\). The \(B_{i}^{{(n + 1)}}(r)\) in the most left region \([{{t}_{i}},{{t}_{{i + 1}}}]\) gets the contribution only from \(B_{i}^{{(n)}}(r)\). The \(B_{i}^{{(n + 1)}}(r)\) in the most right region \([{{t}_{{i + n}}},{{t}_{{i + n}}}]\) gets the contribution only from \(B_{{i + 1}}^{{(n)}}(r)\). In the intermediate domain \([{{t}_{{i + 1}}},{{t}_{{i + n}}}]\) both splines \(B_{i}^{{(n)}}(r)\) and \(B_{{i + 1}}^{{(n)}}(r)\) give contributions. We can use decompositions (13) and (9), (10) on the right side of the recurrence relation (2) and write the following expression for B-spline

$$\begin{gathered} B_{i}^{{(n + 1)}}(r) = {{\delta }_{i}}z_{{i + n,i}}^{{i + 1,i}}b_{1}^{{(1)}}({{x}_{i}})\sum\limits_{l = 0}^{n - 1} {c_{{0,l}}^{{i,n - 1}}b_{l}^{{(n - 1)}}} ({{x}_{i}}) \\ + \,\,\sum\limits_{j = 1}^{n - 1} {{{\delta }_{{i + j}}}} \sum\limits_{l = 0}^{n - 1} {c_{{j,l}}^{{i,n - 1}}} b_{l}^{{(n - 1)}}({{x}_{{i + j}}}) \\ \times \,\,\left( {z_{{i + n,i}}^{{i + j,i}} + z_{{i + n,i}}^{{i + j + 1,\,\,i + j}}b_{1}^{{(1)}}({{x}_{{i + j}}})} \right) \\ + \,\,\sum\limits_{j = 1}^{n - 1} {{{\delta }_{{i + j}}}} \sum\limits_{l = 0}^{n - 1} {c_{{j - 1,l}}^{{i + 1,n - 1}}} b_{l}^{{(n - 1)}}({{x}_{{i + j}}}) \\ \times \,\,\left( {z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j + 1}} + z_{{i + n + 1,\,\,i + 1}}^{{i + j + 1,\,\,i + j}}b_{0}^{{(1)}}({{x}_{{i + j}}})} \right) \\ + \,\,{{\delta }_{{i + n}}}z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + n}}b_{0}^{{(1)}}({{x}_{{i + n}}})\sum\limits_{l = 0}^{n - 1} {c_{{n - 1,l}}^{{i + 1,n - 1}}} b_{l}^{{(n - 1)}}({{x}_{{i + n}}}), \\ \end{gathered} $$
((14))

where these three regions are clearly outlined. Since a product of two Bernstein functions is again the Bernstein function of higher order (see Eq. (A.34)), we can write

$$b_{1}^{{(1)}}(x)b_{l}^{{(n - 1)}}(x) = \left( {\tfrac{{l + 1}}{n}} \right)b_{{l + 1}}^{{(n)}}(x),$$
$$b_{0}^{{(1)}}(x)b_{l}^{{(n - 1)}}(x) = \left( {\tfrac{{n - l}}{n}} \right)b_{l}^{{(n)}}(x),$$

and use these expressions in the Eq. (14). Rearranging summation we obtain the expression

$$\begin{gathered} B_{i}^{{(n + 1)}}(r) = {{\delta }_{i}}z_{{i + n,i}}^{{i + 1,i}}\sum\limits_{l = 1}^n {c_{{0,l - 1}}^{{i,n - 1}}} \left( {\frac{l}{n}} \right)b_{l}^{{(n)}}({{x}_{i}}) \\ + \,\,\sum\limits_{j = 1}^{n - 1} {{{\delta }_{{i + j}}}} \sum\limits_{l = 0}^{n - 1} {c_{{j,l}}^{{i,n - 1}}} \\ \times \,\,\left( {z_{{i + n,i}}^{{i + j,i}}b_{l}^{{(n - 1)}}({{x}_{{i + j}}}) + z_{{i + n,i}}^{{i + j + 1,\,\,i + j}}\left( {\frac{{l + 1}}{n}} \right)b_{{l + 1}}^{{(n)}}({{x}_{{i + j}}})} \right) \\ + \,\,\sum\limits_{j = 1}^{n - 1} {{{\delta }_{{i + j}}}} \sum\limits_{l = 0}^{n - 1} {c_{{j - 1,l}}^{{i + 1,n - 1}}} \\ \times \,\,\left( {z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j + 1}}b_{l}^{{(n - 1)}}({{x}_{{i + j}}}) + z_{{i + n + 1,\,\,i + 1}}^{{i + j + 1,\,\,i + j}}\left( {\frac{{n - l}}{n}} \right)b_{l}^{{(n)}}({{x}_{{i + j}}})} \right) \\ + \,\,{{\delta }_{{i + n}}}z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + n}}\sum\limits_{l = 0}^{n - 1} {c_{{n - 1,l}}^{{i + 1,n - 1}}} \left( {\frac{{n - l}}{n}} \right)b_{l}^{{(n)}}({{x}_{{i + n}}}). \\ \end{gathered} $$
((15))

The polynomials \(b_{l}^{{(n - 1)}}(x)\) of the \((n - 1)\) degree from the third and fifth lines (15) can be transformed to the sum of the nth degree polynomials by using the step up relation (A.41). Taking into account this transformation and identities that follow from the definition (8),

$$\begin{gathered} z_{{i + n,i}}^{{i + j + 1,i}} = z_{{i + n,i}}^{{i + j + 1,i + j}} + z_{{i + n,i}}^{{i + j,i}}, \\ z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j}} = z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j + 1}} + z_{{i + n + 1,\,\,i + 1}}^{{i + j + 1,\,\,i + j}}, \\ \end{gathered} $$

Eq. (15) can be reduced to the expression

$$\begin{gathered} B_{i}^{{(n + 1)}}(r) = {{\delta }_{i}}z_{{i + n,i}}^{{i + 1,i}}\left( {c_{{0,n - 1}}^{{i,n - 1}}b_{n}^{{(n)}}({{x}_{i}}) + \sum\limits_{l = 1}^{n - 1} {c_{{0,l - 1}}^{{i,n - 1}}} \left( {\frac{l}{n}} \right)b_{l}^{{(n)}}({{x}_{i}})} \right) \\ + \,\,\sum\limits_{j = 1}^{n - 1} {{{\delta }_{{i + j}}}} \sum\limits_{l = 0}^n {b_{l}^{{(n)}}} ({{x}_{{i + j}}}) \\ \times \,\,\left[ {\left( {\frac{{n - l}}{n}} \right)\left( {z_{{i + n,i}}^{{i + j,i}}c_{{j,l}}^{{i,n - 1}} + z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j}}c_{{j - 1,l}}^{{i + 1,n - 1}}} \right)} \right. \\ \left. { + \,\,\left( {\frac{l}{n}} \right)\left( {z_{{i + n,i}}^{{i + j + 1,i}}c_{{j,l - 1}}^{{i,n - 1}} + z_{{i + n + 1,i + 1}}^{{i + n + 1,\,\,i + j + 1}}c_{{j - 1,l - 1}}^{{i + 1,n - 1}}} \right)} \right] \\ + \,\,{{\delta }_{{i + n}}}z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + n}} \\ \times \,\,\left( {c_{{n - 1,0}}^{{i + 1,n - 1}}b_{0}^{{(n)}}({{x}_{{i + n}}}) + \sum\limits_{l = 1}^{n - 1} {c_{{n - 1,l}}^{{i + 1,n - 1}}} \left( {\frac{{n - l}}{n}} \right)b_{l}^{{(n)}}({{x}_{{i + n}}})} \right), \\ \end{gathered} $$
((16))

which contains only Bernstein basis polynomials of the nth order. To proceed further the initial values of coefficients \(c_{{j,l}}^{{i,n}}\) have to be fixed. From the comparison of the explicit expression of the first order B-spline \(B_{i}^{{(1)}}(r)\) = \({{\delta }_{i}}\) with the decomposition (13) follows that \(c_{{0,0}}^{{i,0}}\) = 1. The second order \(B_{i}^{{(2)}}(r)\) = \({{\delta }_{i}}{{x}_{i}}\) + \({{\delta }_{{i + 1}}}(1 - {{x}_{{i + 1}}})\) leads to following coefficients

$$c_{{0,0}}^{{i,1}} = 0,\,\,\,\,c_{{0,1}}^{{i,1}} = 1,$$
((17))
$$c_{{1,0}}^{{i,1}} = 1,\,\,\,\,c_{{1,1}}^{{i,1}} = 0.$$
((18))

Then, from the first line of Eq. (16) and initial values (17) follow by recursion that only one coefficient \(c_{{0,n}}^{{i,n}}\) is different from zero, and all others are equal to zero

$$\begin{gathered} c_{{0,l}}^{{i,n}} = 0,\,\,\,\,{\text{for}}\,\,\,\,l = 0,1, \ldots ,(n - 1), \\ c_{{0,n}}^{{i,n}} = z_{{i + n,i}}^{{i + 1,i}}c_{{0,n - 1}}^{{i,n - 1}} = z_{{i + n,i}}^{{i + 1,i}}z_{{i + n - 1,i}}^{{i + 1,i}} \ldots z_{{i + 1,i}}^{{i + 1,i}}. \\ \end{gathered} $$
((19))

From the last line of Eq. (16) and initial values (18) follow by recursion the similar conclusion for the coefficient \(c_{{n,l}}^{{i,n}}\)

$$\begin{gathered} c_{{n,0}}^{{i,n}} = z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + n}}c_{{n - 1,0}}^{{i,n - 1}} \\ = z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + n}}z_{{i + n + 1,\,\,i + 2}}^{{i + n + 1,\,\,i + n}} \ldots z_{{i + n + 1,\,\,i + n}}^{{i + n + 1,\,\,i + n}}, \\ c_{{n,l}}^{{i,n}} = 0,\,\,\,\,{\text{for}}\,\,\,l = 1, \ldots ,n \\ \end{gathered} $$
((20))

The rest of coefficients \(c_{{j,l}}^{{i,n}}\) for subintervals \([{{t}_{{i + j}}},{{t}_{{i + j + 1}}}],\)\(j\) = \(1,2, \ldots ,(n - 1)\) and \(l\) = \(0,1, \ldots ,n\) are calculated by the recursion relation

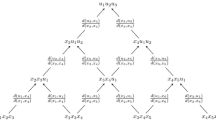
$$\begin{gathered} c_{{j,l}}^{{i,n}} = \left( {\frac{{n - l}}{n}} \right)\left( {z_{{i + n,i}}^{{i + j,i}}c_{{j,l}}^{{i,n - 1}} + z_{{i + n + 1,\,\,i + 1}}^{{i + n + 1,\,\,i + j}}c_{{j - 1,l}}^{{i + 1,n - 1}}} \right) \\ + \,\,\left( {\frac{l}{n}} \right)\left( {z_{{i + n,i}}^{{i + j + 1,\,\,i}}c_{{j,l - 1}}^{{i,n - 1}} + z_{{i + n + 1,i + 1}}^{{i + n + 1,\,\,i + j + 1}}c_{{j - 1,l - 1}}^{{i + 1,n - 1}}} \right). \\ \end{gathered} $$
((21))

Therefore, coefficients \(c_{{j,l}}^{{i,n}}\) in the B-spline decomposition (13) on Bernstein basis functions (12) are obtained by recurrence relations (19)–(21). Coefficients can be calculated if the knot sequence \({\text{\{ }}{{t}_{j}}{\text{\} }}\) are defined. Figure 1 shows the example of a decomposition of the 5th order B-spline on Bernstein polynomials \((c_{{j,l}}^{{i,4}}b_{l}^{{(4)}}),\)\(l = 0, \ldots ,4.\) The B-spline \(B_{i}^{{(5)}}(r)\) is different from zero in the region \([{{t}_{i}},{{t}_{{i + 5}}}].\) On subintervals \([{{t}_{i}},{{t}_{{i + 1}}}]\) and \([{{t}_{{i + 4}}},{{t}_{{i + 5}}}]\) only Bernstein polynomials \(b_{4}^{{(4)}}(x)\) and \(b_{0}^{{(4)}}(x)\) give contributions to the B-spline \(B_{i}^{{(5)}}(r)\). In the region \([{{t}_{{i + 1}}},{{t}_{{i + 4}}}]\) all Bernstein basis functions \(b_{l}^{{(4)}},\)\(l\) = \(0,1, \ldots ,4\) take part in the decomposition (13).

Fig. 1.
figure 1

The B-spline \(B_{i}^{{(5)}}(r)\) (thick solid line) and its decomposition on Bernstein polynomials \((c_{{j,l}}^{{i,4}}b_{l}^{{(4)}})\) (thin solid color lines). The vertical dashed lines show boundaries of subintervals where \(B_{i}^{{(5)}}(r)\) is not equal to zero.

Full size image

3 DISCUSSION AND APPLICATIONS

The analytic properties of Bernstein basis functions \(b_{l}^{{(n)}}(x)\) are very diverse and convenient (see Appendix A). The analytic B-spline representation (13) based on Bernstein basis allows to use these properties in many applications where B-splines appear and perform analytic manipulations. Some examples will be given below.

3.1 Sum Rules

B-splines have many useful properties. Some of them can be used to derive the sum rules for coefficients \(c_{{j,l}}^{{i,n}}\). To get the first one, let multiply (13) on a projector \({{\delta }_{j}}\) and integrate over \({{x}_{j}}\), and then use Eq. (A.38)

$$\int\limits_0^1 {d{{x}_{j}}{{\delta }_{j}}B_{i}^{{(n + 1)}}} (r) = \frac{1}{{n + 1}}\sum\limits_{l = 0}^n {c_{{j - i,l}}^{{i,n}}.} $$
((22))

Using the relation (22) in the expression (4) for an unity partition by B-splines, the sum rule for coefficients \(c_{{j,l}}^{{i,n}}\) can be obtained

$$\frac{1}{{n + 1}}\sum\limits_{i = j - n}^j {\sum\limits_{l = 0}^n {c_{{j - i,l}}^{{i,n}}} } = 1.$$
((23))

To get another sum rule, the property of B-splines [7], that the average value of a B-spline \(B_{i}^{{(n + 1)}}(r)\) over its support interval is independent of i and thus is independent of the choice of the knots, can be used

$$\frac{1}{{({{t}_{{i + n + 1}}} - {{t}_{i}})}}\int\limits_{{{t}_{i}}}^{{{t}_{{i + n + 1}}}} {drB_{i}^{{(n + 1)}}} (r) = \frac{1}{{n + 1}}.$$
((24))

Using in this expression the analytic representation (13) and integrating over r, the next sum rule can be obtained

$$\sum\limits_{j = 0}^n {z_{{i + n + 1,i}}^{{i + j + 1,i + j}}} \sum\limits_{l = 0}^n {c_{{j,l}}^{{i,n}}} = 1.$$
((25))

Sum rules (23) and (25) are the consequence of B‑spline properties and can be used to check the accuracy of calculations.

3.2 Overlap Integrals

In applications the overlap integrals, involving B‑splines and different B-spline derivatives, are necessary. Usually, they are calculated numerically by the Gaussian integration. Using the representation (13) all these overlaps can be calculated analytically. As an example, we calculate overlap integrals between two B-splines, two B-spline derivatives and the B-spline with the B-spline second derivative. These matrices are needed for a construction of the Hamilton matrix in a B-spline basis.

Let consider an overlap integral between two B‑splines, \(B_{{{{i}_{1}}}}^{{(n + 1)}}(r)\) and \(B_{{{{i}_{2}}}}^{{(n + 1)}}(r)\)

$$\left\langle {\left. {B_{{{{i}_{1}}}}^{{(n + 1)}}} \right|B_{{{{i}_{2}}}}^{{(n + 1)}}} \right\rangle = \int\limits_{{{r}_{{\min }}}}^{{{r}_{{\max }}}} {drB_{{{{i}_{1}}}}^{{(n + 1)}}} (r)B_{{{{i}_{2}}}}^{{(n + 1)}}(r).$$
((26))

These overlap integrals are elements of a symmetric banded matrix with indices \(({{i}_{1}},{{i}_{2}}).\) The non-zero elements are only for splines which support domains have a common region. It happens for B-splines with indices \(\left| {{{i}_{1}} - {{i}_{2}}} \right| \leqslant n.\) Since overlap matrix is symmetric, it is enough to consider the case of nonzero overlaps with \(0 \leqslant {{i}_{1}} - {{i}_{2}} \leqslant n.\) The integral (26) becomes the sum of integrals over common subintervals \({{i}_{1}} + {{j}_{1}}\) = \({{i}_{2}} + {{j}_{2}}\) (\({{j}_{1}}\) and \({{j}_{2}}\) numerate subintervals of the B-spline support domains in decomposition (13)). On each subinterval \({{i}_{1}} + {{j}_{1}}\) the integration over r can be scaled to integration over variable \({{x}_{{{{i}_{1}} + {{j}_{1}}}}}\) (see the definition (6)) within interval \([0,1]\), \(dr\) = \({{\Delta }_{{{{i}_{1}} + {{j}_{1}}}}}d{{x}_{{{{i}_{1}} + {{j}_{1}}}}}\), where \({{\Delta }_{{{{i}_{1}} + {{j}_{1}}}}}\) = \({{t}_{{{{i}_{1}} + {{j}_{1}} + 1}}} - {{t}_{{{{i}_{1}} + {{j}_{1}}}}}\). The product of two Bernstein basis functions of the \(n\)th degree under integral expression is reduced to Bernstein basis polynomials of the degree (\(2n\)). The integral of these polynomials over x-variable is equal to factor \({1 \mathord{\left/ {\vphantom {1 {(2n + 1)}}} \right. \kern-0em} {(2n + 1)}}\) (see Eq. (A.38) in the Appendix A). Finally we can write the expression of the overlap integral in the following form

$$\begin{gathered} \left\langle {\left. {B_{{{{i}_{1}}}}^{{(n + 1)}}} \right|B_{{{{i}_{2}}}}^{{(n + 1)}}} \right\rangle \\ = \sum\limits_{{{j}_{1}} = 0}^{n - {{i}_{1}} + {{i}_{2}}} {{{\Delta }_{{{{i}_{1}} + {{j}_{1}}}}}} \sum\limits_{{{l}_{1}},{{l}_{2}} = 0}^n {c_{{{{j}_{1}},{{l}_{1}}}}^{{{{i}_{1}},n}}c_{{{{i}_{1}} - {{i}_{2}} + {{j}_{1}},{{l}_{2}}}}^{{{{i}_{2}},n}}} \left( {\begin{array}{*{20}{c}} n \\ {{{l}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{2}}} \end{array}} \right){{B}_{{{{l}_{1}} + {{l}_{2}}}}}, \\ \end{gathered} $$
((27))

where coefficient \({{B}_{{{{l}_{1}} + {{l}_{2}}}}}\) for overlap of the two B-splines is equal to

$${{B}_{l}} = \frac{1}{{(2n + 1)}}{{\left( {\begin{array}{*{20}{c}} {2n} \\ l \end{array}} \right)}^{{ - 1}}}.$$
((28))

The same procedure can be used to derive overlap integrals for two other cases

$$\begin{gathered} \left\langle {\left. {B_{{{{i}_{1}}}}^{{(n + 1){\kern 1pt} '}}} \right|B_{{{{i}_{2}}}}^{{(n + 1){\kern 1pt} '}}} \right\rangle = \sum\limits_{{{j}_{1}} = 0}^{n - {{i}_{1}} + {{i}_{2}}} {\sum\limits_{{{l}_{1}},{{l}_{2}} = 0}^n {c_{{{{j}_{1}},{{l}_{1}}}}^{{{{i}_{1}},n}}} } c_{{{{i}_{1}} - {{i}_{2}} + {{j}_{1}},{{l}_{2}}}}^{{{{i}_{2}},n}}\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{2}}} \end{array}} \right)\frac{{{{D}_{{{{l}_{1}},{{l}_{2}}}}}}}{{{{\Delta }_{{{{i}_{1}} + {{j}_{1}}}}}}}, \\ \left\langle {\left. {B_{{{{i}_{1}}}}^{{(n + 1)}}} \right|B_{{{{i}_{2}}}}^{{(n + 1){\kern 1pt} {''}}}} \right\rangle = \sum\limits_{{{j}_{1}} = 0}^{n - {{i}_{1}} + {{i}_{2}}} {\sum\limits_{{{l}_{1}},{{l}_{2}} = 0}^n {c_{{{{j}_{1}},{{l}_{1}}}}^{{{{i}_{1}},n}}} } c_{{{{i}_{1}} - {{i}_{2}} + {{j}_{1}},{{l}_{2}}}}^{{{{i}_{2}},n}}\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{2}}} \end{array}} \right)\frac{{{{E}_{{{{l}_{1}},{{l}_{2}}}}}}}{{{{\Delta }_{{{{i}_{1}} + {{j}_{1}}}}}}}, \\ \end{gathered} $$

where for calculations of coefficients \({{D}_{{{{l}_{1}},{{l}_{2}}}}}\) and \({{E}_{{{{l}_{1}},{{l}_{2}}}}}\) are used expressions (A.35) and (A.36) for the first and second derivatives of the Bernstein basis polynomials

$$\begin{gathered} {{D}_{{{{l}_{1}},{{l}_{2}}}}} = \frac{1}{{(2n - 1)}}\left( { - \left( {{{l}_{1}}(n - {{l}_{2}}) + {{l}_{2}}(n - {{l}_{1}})} \right){{{\left( {\begin{array}{*{20}{c}} {2n - 2} \\ {{{l}_{1}} + {{l}_{2}} - 1} \end{array}} \right)}}^{{ - 1}}}} \right. \\ + \,\,\left. {{{l}_{1}}{{l}_{2}}{{{\left( {\begin{array}{*{20}{c}} {2n - 2} \\ {{{l}_{1}} + {{l}_{2}} - 2} \end{array}} \right)}}^{{ - 1}}} + (n - {{l}_{1}})(n - {{l}_{2}}){{{\left( {\begin{array}{*{20}{c}} {2n - 2} \\ {{{l}_{1}} + {{l}_{2}}} \end{array}} \right)}}^{{ - 1}}}} \right), \\ {{E}_{{{{l}_{1}},{{l}_{2}}}}} = \frac{1}{{(2n - 1)}}\left( {(n - {{l}_{2}} - 1)(n - {{l}_{2}}){{{\left( {\begin{array}{*{20}{c}} {2n - 2} \\ {{{l}_{1}} + {{l}_{2}}} \end{array}} \right)}}^{{ - 1}}}} \right. \\ + \,\,\left. {{{l}_{2}}({{l}_{2}} - 1){{{\left( {\begin{array}{*{20}{c}} {2n - 2} \\ {{{l}_{1}} + {{l}_{2}} - 2} \end{array}} \right)}}^{{ - 1}}} - 2{{l}_{2}}(n - {{l}_{2}}){{{\left( {\begin{array}{*{20}{c}} {2n - 2} \\ {{{l}_{1}} + {{l}_{2}} - 1} \end{array}} \right)}}^{{ - 1}}}} \right). \\ \end{gathered} $$

These examples demonstrate the convenience of analytical representation (13) which guarantees the accurate calculations of overlap integrals for any B‑splines without additional troubles connected with numerical realization of an integration process.

3.3 Matrix Elements

Calculations of matrix elements for a function \(f(r)\) between B-splines give another example when analytical representation can be useful and practical. Bernstein polynomials are specially designed to provide an uniform approximation to a continuum function \(f(r)\) within the finite domain. Using the Bernstein polynomials (A.42) the function \(f(r)\) can be approximately written on grid \([{{r}_{{\min }}},{{r}_{{\max }}}]\) as

$$f(r) \simeq \sum\limits_j {{{\delta }_{j}}} {{\mathcal{B}}_{{{{N}_{j}}}}}(f;{{x}_{j}}) = \sum\limits_j {{{\delta }_{j}}} \sum\limits_{l = 0}^{{{N}_{j}}} {{{f}_{{{{N}_{j}},l}}}} b_{l}^{{({{N}_{j}})}}({{x}_{j}}),$$
((29))
$${{f}_{{{{N}_{j}},l}}} = f\left( {{{t}_{j}} + ({{t}_{{j + 1}}} - {{t}_{j}})\frac{l}{{{{N}_{j}}}}} \right),\,\,\,\,{{x}_{j}} = \frac{{r - {{t}_{j}}}}{{{{t}_{{j + 1}}} - {{t}_{j}}}},$$
((30))

where decomposition coefficients \({{f}_{{{{N}_{j}},l}}}\) over the Bernstein basis are known exactly and equal to values of the function \(f(r)\) at points where Bernstein basis functions \(b_{l}^{{({{N}_{j}})}}({{x}_{j}})\) have a maximum. The order \({{N}_{j}}\) of Bernstein basis polynomials defines a precision with which a continuum function \(f(r)\) is approximated on the interval \([{{t}_{j}},{{t}_{{j + 1}}}]\). The matrix elements of the function \(f(r)\) between two B-splines (\(B_{{{{i}_{1}}}}^{{(n + 1)}}(r)\) and \(B_{{{{i}_{2}}}}^{{(n + 1)}}(r)\)) set up the banded symmetric matrix, which has non-zero elements for indices \(\left| {{{i}_{1}} - {{i}_{2}}} \right| \leqslant n,\) corresponding to B-splines with the common support domain. These elements for \(0 \leqslant {{i}_{1}} - {{i}_{2}} \leqslant n\) can be written in following way

$$\begin{gathered} \left\langle {B_{{{{i}_{1}}}}^{{(n + 1)}}\left| f \right|B_{{{{i}_{2}}}}^{{(n + 1)}}} \right\rangle = \int\limits_{{{r}_{{\min }}}}^{{{r}_{{\max }}}} {drB_{{{{i}_{1}}}}^{{(n + 1)}}} (r)f(r)B_{{{{i}_{2}}}}^{{(n + 1)}}(r) \\ = \sum\limits_{{{j}_{1}} = 0}^{n - {{i}_{1}} + {{i}_{2}}} {{{\Delta }_{{{{i}_{1}} + {{j}_{1}}}}}} \sum\limits_{{{l}_{1}},{{l}_{2}} = 0}^n {c_{{{{j}_{1}},{{l}_{1}}}}^{{{{i}_{1}},n}}} c_{{{{i}_{1}} - {{i}_{2}} + {{j}_{1}},{{l}_{2}}}}^{{{{i}_{2}},n}}\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} n \\ {{{l}_{2}}} \end{array}} \right)F_{{{{l}_{1}} + {{l}_{2}}}}^{{{{i}_{1}} + {{j}_{1}}}}, \\ \end{gathered} $$
((31))

where the coefficient \(F_{{{{l}_{1}} + {{l}_{2}}}}^{{{{i}_{1}} + {{j}_{1}}}}\) is a sum of integrals that contain the product of three Bernstein basis functions: two polynomials with degree \(n\) are from the B-spline representation (13) and the third one with degree \({{N}_{j}}\) is from the decomposition (29). The product of these functions transforms to the one Bernstein polynomial with degree \((2n + {{N}_{j}})\) and the integral of a polynomial is defined by the relation (A.38). For the coefficient \(F_{l}^{j},\)\(l\) = \(0,1, \ldots ,2n\) we derive the following expression

$$F_{l}^{j} = \frac{1}{{(2n + {{N}_{j}} + 1)}}\sum\limits_{m = 0}^{{{N}_{j}}} {{{f}_{{{{N}_{j}},m}}}} \frac{{\left( {\begin{array}{*{20}{c}} {{{N}_{j}}} \\ m \end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}} {2n + {{N}_{j}}} \\ {l + m} \end{array}} \right)}}.$$
((32))

This method of calculations is rather flexible. The integration over a radial variable is performed exactly and the total accuracy depends on the precision of function approximation (29) via Bernstein’s polynomials. If necessary, this precision can be easily improved on any interval \([{{t}_{j}},{{t}_{{j + 1}}}]\) by increasing \({{N}_{j}}\). The Weierstrass theorem guarantees an uniform convergence of the approximation (29) to the continuum function \(f(r)\). Monotonic and convex functions yield monotonic and convex approximants, respectively. The Bernstein approximant (29) mimics the behaviour of the function to a remarkable degree. Usually, the convergence of Bernstein polynomials on full interval \([{{r}_{{\min }}},{{r}_{{\max }}}]\) may be slow. In combinations with B-splines, the Bernstein approximation is applied only on single intervals \([{{t}_{j}},{{t}_{{j + 1}}}]\). It reduces the order \({{N}_{j}}\) of the approximating polynomial in comparison to the approximation on the full region. A convergence of the approximation (29) on any interval \([{{t}_{j}},{{t}_{{j + 1}}}]\) can be additionally accelerated by using the iterated Bernstein polynomials [8, 10], see Eqs. (A.43)–(A.48). In this case, factors \(f_{{{{N}_{j}},l}}^{{(k)}}\) or \(f_{{{{N}_{j}},l}}^{{(\infty )}}\) have to be used in Eq. (29) instead of the factor \({{f}_{{{{N}_{j}},l}}}\). In all cases, the same number (\({{N}_{j}}\) + 1) of function calculations is required but the accuracy of approximations is different. Figure 2 shows a relative error \(\left| {{{\left( {f(r) - \mathcal{B}_{{{{N}_{j}}}}^{{(k)}}(f;{{x}_{j}})} \right)} \mathord{\left/ {\vphantom {{\left( {f(r) - \mathcal{B}_{{{{N}_{j}}}}^{{(k)}}(f;{{x}_{j}})} \right)} {f(r)}}} \right. \kern-0em} {f(r)}}} \right|\) for an approximation of the function \(f(r)\) = \({1 \mathord{\left/ {\vphantom {1 {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}}\) by the iterated Bernstein polynomials with the first, second, third iterations (A.45)–(A.47) and the optimal approximation (A.48). The remarkable improvement of the approximation accuracy with increasing the iteration order k is evident. The optimal approximation, which corresponds to the infinite limit of the iteration number, demonstrates the best accuracy. Figure 3 shows the convergence of the optimal approximation for the function \(f(r)\) = \({1 \mathord{\left/ {\vphantom {1 {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}}\) with increasing the number \({{N}_{j}}\). The spectacular increasing of the convergence rate is evident.

Fig. 2.
figure 2

Relative errors for a function approximation by iterated Bernstein polynomials (A.43) with \({{N}_{j}}\) = 10. The upper line (k = 1) is approximation by the classical Bernstein polynomials (A.45). Lines (k = 2, 3) are the second (A.46) and third (A.47) iterations. The line (k = “opt”) is the optimal approximation (A.48). The vertical dashed lines show boundaries of intervals \([{{t}_{j}},{{t}_{{j + 1}}}]\).

Full size image
Fig. 3.
figure 3

Relative errors for the optimal function approximation (A.48) by the iterated Bernstein polynomials. The upper, middle and bottom lines correspond to approximations with \({{N}_{j}}\) = 5, 10 and 15, respectively. The vertical dashed lines show boundaries of the interval \([{{t}_{j}},{{t}_{{j + 1}}}]\).

Full size image

4 CONCLUSIONS

B-splines are one of the most commonly used family of piecewise polynomials, which are well adapted to numerical tasks and have been successfully used for studying the variety of atomic structure and dynamics problems. The recurrence relation (2) is used for B‑spline calculations that are applied for numerical calculations of different matrix elements and overlap matrices.

Here we derive the analytic representation (13) for B-splines of the arbitrary degree \((n + 1)\) and arbitrary sets of the knot sequence via a decomposition on Bernstein basis polynomials \(b_{l}^{{(n)}}(x)\) of the n-th degree. After the knot sequence of B-splines is constructed, the decomposition coefficients \(c_{{j,l}}^{{i,n}}\) must be calculated only once. Bernstein basis polynomials have remarkable analytic properties: product of few polynomials is again Bernstein polynomials with simple proportionality constant, an indefinite integral from Bernstein polynomials is again the sum of these polynomials, definite integral for any Bernstein polynomials of the nth degree are equal to \({1 \mathord{\left/ {\vphantom {1 {(n + 1)}}} \right. \kern-0em} {(n + 1)}},\) and etc. The derived representation allows to use these remarkable analytic properties and perform analytically many mathematical operations with B-splines. Slow convergence of a function approximation by Bernstein polynomials can be overcome by combination of the careful choice of the grid and, if necessary, applications of the iterated Bernstein polynomials. This expands an applicability and enhances a flexibility of B-spline methods. Thus, it opens the way to analytical finite basis-set calculations.