Abstract
The lid-driven cavity is an important fluid mechanical system serving as a benchmark for testing numerical methods and for studying fundamental aspects of incompressible flows in confined volumes which are driven by the tangential motion of a bounding wall. A comprehensive review is provided of lid-driven cavity flows focusing on the evolution of the flow as the Reynolds number is increased. Understanding the flow physics requires to consider pure two-dimensional flows, flows which are periodic in one space direction as well as the full three-dimensional flow. The topics treated range from the characteristic singularities resulting from the discontinuous boundary conditions over flow instabilities and their numerical treatment to the transition to chaos in a fully confined cubical cavity. In addition, the streamline topology of two-dimensional time-dependent and of steady three-dimensional flows are covered, as well as turbulent flow in a square and in a fully confined lid-driven cube. Finally, an overview on various extensions of the lid-driven cavity is given.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
A rectangular or a cubic container are among the most elementary confined geometries within which fluid motion can be studied. The simplest mechanical driving force acting on a viscous fluid with constant density and leaving the simple domain intact is the tangential in-plane motion of a bounding wall. A cuboid of which one of the solid walls moves tangentially to itself is called a lid-driven cavity.
Owing to the simplicity of its setup the lid-driven cavity has been investigated quite extensively. It has been employed as a numerical benchmark problem and as a test bed for studying particular physical effects. Searching the Web of Science for the topic lid-driven yields more than 1800 hits. For these reasons, and because of the rapid evolution of this field of research, a review on lid-driven cavity flows seems justified, given that nearly 20 years have passed since the overview provided by Shankar and Deshpande [293].
After the first numerical investigations of Burggraf [58] and Kawaguti [177] the quest for efficiency and accuracy began with the work of Ghia et al. [122] and Schreiber and Keller [284] who computed the steady two-dimensional flow for Reynolds number up to \(10^4\) in a square cavity bounded by three rigid walls and a lid moving with constant velocity. Koseff and Street carried out a series of experiments on the flow in three-dimensional cavities with different lengths in the third dimension, many of them being summarized in [195]. Stimulated by these experimental results and the remaining open questions, dedicated three-dimensional test cases have been defined and investigated numerically by different research groups with results collected in [95]. After this joint effort, which did not yield very conclusive results for the targeted Reynolds number of \(Re=3200\), a new level of accuracy has been reached for two-dimensional flows by Botella and Peyret [47] who employed spectral methods combined with a dedicated treatment of the singular corners/edges where the moving wall meets with a stationary wall. Their method yields highly accurate numerical solution for the two-dimensional problem up to \(Re=10^3\) (see also [24]). With the progress in computing power and the routine computation of three-dimensional flows, benchmarks for three-dimensional flows became of interest. Applying the method of Botella and Peyret [47] to three-dimensions Albensoeder and Kuhlmann [11] provided highly accurate three-dimensional flow fields for \(Re=10^3\) for different cavity lengths in the spanwise direction and for rigid and periodic boundary conditions at the end walls.
Apart from serving as a numerical benchmark, many fundamental fluid mechanical phenomena arise in the lid-driven cavity problem. An important aspect for an analytical and numerical treatment of the problem are the discontinuous boundary conditions along the edges at which moving and stationary walls meet. This problem is a special case of Taylor’s scraping problem for which he has provided similarity solutions [308, 309]. Along such an edge with discontinuous boundary conditions for the velocity perpendicular to the edge, the vorticity and the pressure diverge at the apex. For two-dimensional flow, closed-form solutions have been obtained (see, e.g., [139]) in terms of a series expansion of the steady flow for small distances from the discontinuous corner. Even a truncated series expansion will capture the leading-order terms of the singular velocity and pressure fields and can be employed to ease convergence of the full numerical problem of solving the Navier–Stokes equations [47]. An artifice to eliminate the singularity is a regularization/smoothing of the discontinuity (see, e.g., [208]). The existence of a singularity in the mathematical problem also indicates the difficulties which arise in experimental realizations of the lid-driven cavity: mathematically the pressure diverges as the singular corners are approached. The decrease of the pressure in the edge at which the wall moves away from the edge will necessarily lead to cavitation in the corner. Furthermore, a gap between a stationary and the moving wall is hard to prevent, leading to pumping and leakage effects [273]. Another peculiarity concerns the viscous flow near the sharp corners made by two stationary walls. Depending on the enclosed angle the flow exhibits a particular asymptotic behavior in form of an infinite sequence of self-similar vortices [231] whose size and intensity decay in geometric progression as the edge is approached. In addition to these local effects, the global vortex structures depend on the motion of the boundaries and the height-to-width ratio of the cavity [254], even in two-dimensional Stokes flow. Solutions to these types of problems can be obtained, apart from numerical methods, by the bi-orthogonal series method [174, 175] or by the use of Greens functions [183]. The theoretical asymptotic treatment of the three-dimensional problem of the local flow near a corner where three plane rigid walls meet is considerably more complicated [128].
Another fundamental aspect of the lid-driven cavity flow concerns the evolution of the two-dimensional flow as the wall velocity increases. According to the Prandtl–Batchelor theorem [29, 267] the steady, two-dimensional flow, in the absence of instabilities, should evolve for large Reynolds numbers to a vortex with an inviscid core of uniform vorticity surrounded by viscous boundary layers which relate the vortex core to the boundary conditions. This tendency was confirmed experimentally [254] and numerically (see, e.g., [104]). However, the two-dimensional steady flow is not stable at high Reynolds numbers [132], and smaller-scale vortices are shed into the cavity from the downstream end of the moving wall when the Reynolds number increases beyond a critical value.
If the two-dimensional cavity problem is extruded in the third dimension, instabilities arise which break the translational symmetry in this third direction, leading to periodic patterns [13]. The spatial and temporal structure of the unstable modes of the linear stability problem depends on the height-to-width ratio (aspect ratio) with the so-called Taylor–Görtler type of mode for unit aspect ratio being the precursor of the three-dimensional unsteady vortices discovered by Koseff and Street [193] for higher Reynolds numbers. Generalizing the single-lid-driven cavity to a cavity with two facing walls which move parallel or antiparallel to each other, the basic two-dimensional flow can loose its uniqueness [14, 201]. Moreover, a rich zoo of three-dimensional flow instabilities can be observed which define the stability balloon [10] of the two-dimensional flow in the parameter space spanned by the aspect ratio and the two wall velocities. In the limit of a shallow two-sided lid-driven cavity, the flow in the bulk of the cavity approximates a class of parallel shear flows (with zero mean).
In cavities with a large span flow patterns can arise in the bulk which are based on the periodic instability of a cavity infinitely extended in the third dimension. The periodic flow patterns in the bulk, however, will be perturbed by the presence of end walls on which no-slip boundary conditions must be satisfied. The end-wall effect associated with the finite span is another topic of interest and related to the Bödewadt boundary layer flow [43]. In very short lid-driven cavities, such as a cube, the end-wall effects become dominant. The flow in these short systems requires a full three-dimensional numerical treatment from the outset. Feldman and Gelfgat [109] discovered the lid-driven flow in a cube to become time-dependent through a subcritical (backward) bifurcation at a Reynolds number of the order of 2000. The intermittency of the chaotic flow immediately above the threshold [200, 220] has only been explained recently by Lopez et al. [221]. Accordingly, different, time-dependent solutions bifurcate subcritically from the steady three-dimensional flow with their upper branches being unstable, except for a very small range of subcritical Reynolds numbers. For still higher Reynolds numbers the flow undergoes a transition to turbulence [209]. Of interest are the particular properties of the turbulent flow which originate from the specific type of driving and the three-dimensional confinement.
Time-dependent, two-dimensional as well as steady, three-dimensional cavity flows have also been employed to study fundamentals of chaotic mixing [81, 169] and to investigate the transport of suspended particles [321]. The advection of fluid and the transport of particles crucially depends on the underlying flow topology. An interesting property of the flow topology at intermediate Reynolds numbers, which affects the mixing, is the coexistence of chaotic and regular streamlines [164, 277].
Many extensions are possible of the problem of rectangular lid-driven cavity flow. A natural extension concerns the variation of the cavity shape. Among those, cavities with triangular cross section have been considered [1, 129, 212], cavities with circular [32] and semi-circular shapes [123, 229], and cavities with geometric inserts making the geometry more complex. Another important extension, is the heat transport when the cavity walls are kept at different temperatures or in the presence of other heat sources (see, e.g., [82, 237, 269]). Finally, combinations of these effects have been considered, including magnetic forces, compressibility effects, and cases in which the cavity is filled with a porous medium or with a non-Newtonian fluid.
2 Governing Equations
We consider the incompressible flow of a Newtonian fluid with constant density \(\rho \) and kinematic viscosity \(\nu \) in a cuboid with dimensions \(L_x \times L_y \times L_z\) as shown in Fig. 1. The Cartesian coordinate system is centered in the cavity. The fluid motion is governed by the incompressible Navier–Stokes equations
where \(\varvec{u} = (u,v,w)\) is the velocity vector in Cartesian coordinates and p the pressure. Length, velocity, time and pressure have been made non-dimensional using the viscous scales L, \(\nu /L\), \(L^2/\nu \) and \(\rho \nu ^2/L^2\), respectively, where L is the length of the sliding lid(s).
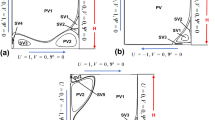
Geometry of the cavities considered with dimensions \(L_x\), \(L_y\) and \(L_z\) in x, y and z direction, respectively. The coordinate origin c (\(\bullet \)) is located in the center of each cavity. For one-sided driving (a) the lid at \(y=L_y/2\) moves with velocity \(U\varvec{e}_x\) in x direction. For two-sided driving (b) the lids at \(x=\pm L_x/2\) move with velocities \(-U_1 \varvec{e}_y\) and \(U_2 \varvec{e}_y\) in y direction, as indicated by the bold grey arrows. The circles (\(\circ \)) indicate the intersection of the axes with the walls. The lateral boundaries are shown in brighter grey. Non-dimensional lengths are given in parentheses
Two driving modes are considered: single-lid motion and double-lid motion. In the latter case two facing walls move in parallel or antiparallel direction. Using the length of the moving lid \(L=L_x\) for the single-lid cavity, and \(L=L_y\) for the double-lid cavity, the velocity boundary conditions on the moving wall(s), Reynolds numbers and cross sectional aspect ratios are defined to conform with the usual conventions
where U, \(U_1\), and \(U_2\) are the velocity magnitudes of the moving lids as indicated in Fig. 1. On all other walls no-slip conditions \(\varvec{u}=0\) are imposed. In addition, it is useful to define the span aspect ratio \(\varLambda =L_z/L\). All data reported hereinafter have been converted to the present scaling and coordinate systems, depending on the driving mode.
3 Corner Singularities
Among the reasons which made the lid-driven cavity one of the most (if not the most) common benchmark in computational fluid dynamics is the combination of its simple geometry and the presence of various corner singularities. The system does not require complicated meshing operations and it allows all kinds of discretization methods to be tested; in addition, only Dirichlet boundary conditions are required to define the mathematical problem. Therefore, all codes can easily be prepared to create a solver for the lid-driven cavity. On the other hand, the singularities which arise at the corners and edges where different walls meet at a sharp angle make the exact solution difficult to approximate and create numerical challenges, in particular, where the geometry changes abruptly and the boundaries move with multi-valued velocities [233].
Several different singularities are encountered in the various lid-driven cavity setups, which can be referred to classical problems of theoretical fluid dynamics. In case of a two-dimensional one-sided cavity the local flow in the edges can be represented by two singular flows (see Fig. 2): Taylor’s scraper problem [308] (top-right zoom-in panel) and viscous corner eddies [231] (bottom-right zoom-in panel). Note the local flows in the singular corners up- and downstream of the moving wall depend on Re, but become equivalent for \(Re\rightarrow 0\). Owing to their significance for two-dimensional and spatially-periodic three-dimensional cavity flows these singularities will be discussed in Sect. 3.1. Other singularities arise when the flow is driven by more than one lid and when the sliding walls share a common edge (see, e.g., [59, 327]), or when only part of a flat wall is moving while the remainder is at rest [232]. Far more complicated than the two-dimensional edge flow is the flow in a corner near the point at which three walls (which may move) meet. This problem has only been investigated in the recent years (see, e.g., [287, 291]). A brief overview of the main achievements is presented in Sect. 3.2.
3.1 Two-dimensional Singularities
The analysis of two-dimensional flows is greatly simplified by the introduction of a stream function \(\psi \) defined such that \(\varvec{u}=\nabla \times (\psi \varvec{e}_z)\). In this representation, the incompressibility constraint is identically satisfied and the Navier–Stokes equation reduces toFootnote 1
Seeking solutions to the singular corner flows in terms of planar polar coordinates \((r,\theta )\) centered at the singular corner enables to treat arbitrary wedge angles. The geometry and notation is sketched in Fig. 3. In the typical asymptotic approach the stream function is represented in form of a power series in r
\(k\in \mathbb {N}\), subject to the normal and tangential velocity boundary conditions
at the two walls (\(i=1,2\)) and the angles \(\theta = \theta _i\), where \(U_i(t)\) refers to the tangential velocity of the i-th wall of the wedge. The smooth functions \(f_k(\theta ,t)\) take care of the azimuthal and time dependence of the flow. The coefficients \(\alpha _k\in \mathbb {C}\) are complex and ordered with respect to their real parts \(1\le \mathfrak {R}{(\alpha _1)}< \mathfrak {R}{(\alpha _2)} < \ldots \) such that the higher k the less singular the k-th term is in (4).
In creeping-flow approximation \((Re \rightarrow 0)\) (3) becomes the biharmonic equation \(\nabla ^4 \psi =0\). The first solutions of the corner flow problem have been obtained for Stokes flow [93, 231, 308] with the understanding that the creeping flow approximation holds true for \(r\vert U\vert /\nu \ll 1\).
When \(U_1=U\) and \(U_2=0\), one of the solid plates is at rest and it is scraped along by the other plate with constant velocity U and at a constant angle \(\phi =\theta _2-\theta _1\) (see Fig. 3 and top-right of Fig. 2). The creeping-flow solution was given by Goodier [131] and Taylor [308, 309]
Further improvements have been obtained by Kondratiev [192], Inouye [157], Moffatt and Duffy [234], Gupta et al. [139], and Hancock et al.[147] who included the effect of the inertial term in (3) on the Taylor’s scraper flow by means of a boundary-layer approach, by corrective terms, or by an expansion of \(\psi \) in powers of Re. More recent advancements are concerned with a generalization of the problem to include non-Newtonian effects [178] or unsteady flows due to a time dependence of the scraping velocities \(U_i\) [48].
Sketch of the Moffatt eddies between two stationary walls enclosing a wedge angle \(\phi =20^\circ \) (adapted from [231]). The numbers indicate relative intensities
The second singular problem to consider is the stationary corner for which \(U_1=U_2=0\). This class of singularity was first pointed out by Rayleigh [272] who considered creeping flows and showed that the homogenous boundary conditions in (5) cannot be satisfied by the ansatz (4) with real exponents. Successively, Dean and Montagnon [93] contributed to the solution of the Stokes-flow problem, which has been completely clarified and explained by Moffatt [231]. Moffatt introduced the notion of an infinite progression of steady viscous eddies located in corners which include at least one solid boundary. The type of eddies which form in the wedge between stationary walls is sketched in Fig. 4. For the important case of a wedge angle \(\phi =\pi /2\) the radial location \(r_{n+1}\) from the origin of the center of an eddy shrinks by a factor of \({\approx }16\) compared to the distance \(r_n\) of the neighboring eddy. Moreover, the intensity measured by the velocity of the eddies falls off by a factor of \({\approx }2000\) between neighboring eddies. This explains the rapid shrinkage and diminishing of succeeding eddies for \(\phi =\pi /2\) as the apex is approached. In the limit of vanishing wedge angle the eddies all have the same radial width of \({\approx }1.39\) times the gap width, while the relative strength between neighboring eddies decays by a factor of about \({\approx }350\) (see also Sect. 5.1). Moffatt [231] also determined the condition \(\phi <146^\circ \) under which this singular vortical pattern is resistant, even though viscosity dampens the strength of the corner eddies.
For the previous case of inhomogeneous boundary conditions with at least one wall moving, a local analysis was sufficient to provide the leading order terms of the expansion (4). For the homogeneous case of stationary walls the situation is different, because the strength of the singular flow must be determined in a global sense by matching the local flow field with the one in the bulk of the cavity. A matching technique and an extension of the series expansion including inertial terms has been proposed by Botella and Peyret [48] and Botella et al. [49].
Asymptotic solutions of this type of wedge-flow problems are of interest also for other configurations. Extensions of Moffatt eddies to non-planar geometries have been investigated by Wakiya [328] and Liu and Joseph [215] who considered axisymmetric conical flows, and by Malhotra et al. [223] who investigated a two-cone geometry. Davis et al. [89] and Davis and O’Neill [87] found viscous eddies also between two spherical surfaces and between a cylinder and a plane, respectively.
3.2 Three-Dimensional Singularities
For three-dimensional flows the stream function formulation cannot always be employed and the full set of equations in primitive variables has to be considered. This complicates the problem which has remained, so far, unresolved.
Several attempts have been made to solve three-dimensional problems which are, in some sense, similar to the corner flow near a moving boundary. The first attempt was made by Hills and Moffatt [150], who considered the honing problem. In the rotary honing problem a blade is held in place at a certain angle \(\alpha \) with respect to a plate rotating with angular velocity \(\varOmega \). The center of rotation can either be on the line of contact between both plates or displaced from it. In creeping flow approximation, Hills and Moffatt [150] derived a solution valid near the center of rotation and found the three-dimensional streamlines to be closed curves whose projections normal to the line of contact correspond to the streamlines of the two-dimensional scraper problem of Taylor. They also extend the analysis to the case in which two stationary intersecting planes are honed by a rotating cone which rotates about the axis defined by the intersection of both stationary planes. For the conical honing, similarity solutions were obtained which are related to the similarity solutions for the two-dimensional wedge problem treated by Moffatt [231].
Motivated by Hills and Moffatt [150] Gomilko et al. [128] investigated the flow near a trihedral corner formed by three mutually orthogonal planes, one of which is sliding or rotating tangentially. Solutions to the Stokes flow problem were represented as a series over spherical harmonics. To find the dominant asymptotic terms a Mellin transformation technique [319] was used. Asymptotic streamline structures near the corner have been obtained for the different modes of wall motion.
Further analyses have been conducted by Shankar [290, 292], who considered the three-dimensional Stokes flow in a semi-infinite wedge. They concluded that, provided the set of eigenfunctions found to be complete and the series representation convergent for the given boundary conditions, there exists and infinite sequence of corner eddies in the neighbourhood of the edge made by the stationary walls for the antisymmetric class of solutions, but not for the symmetric class they found (see also [235, 281]).
Further advancements are due to Leriche and Labrosse [211], who numerically computed the eigenmodes of the Stokes flow in a cubic cavity made by stationary walls using a spectral collocation method. Within the numerical accuracy the authors could not find indications of the existence in a trihedral corner of a three-dimensional analogue of the two-dimensional Moffatt eddies. For the Stokes flow in a trihedral cone, however, Scott [287] numerically found Moffatt-type of modes in form of a two-parameter family of asymptotically dominating flows made by a superposition of symmetric and antisymmetric modes. Antisymmetric modes lead to closed streamlines in the trihedral cone, while in the general case (including symmetric modes) the streamlines are aperiodic. Typically, fluid elements approach the apex of the corner in a spiraling fashion before they turn radially and spiral out. This is illustrated in Fig. 5. A comparison with the results of Leriche and Labrosse [211] is pending. The results of Scott [287] were confirmed by the theoretical analysis of Davis and Smith [88] using three sets of spherical coordinate systems, as in [128].
Example for a typical asymptotic streamline in a trihedral cone, initiated from the bisector plane containing the x axis, under the meridional angle \(\theta =1\) (from the x axis) and with the distance \(r=1\) from the apex. The streamline approaches the trihedral corner along the dotted line and returns along the solid line. The radial coordinate is compressed by scaling with \(r^{1/6}\). The figure is taken from [287]
The asymptotic solution obtained by [128] for a trihedral corner is singular along the edge along which the velocity is discontinuous. Therefore, to eliminate one of the edge singularities of the Navier–Stokes problem in a cuboidal cavity flow, it is not possible to simply subtract the leading-order terms of the two asymptotic solutions which belong to the two corners having a line of discontinuity in common (see also [11]). In principle, an asymptotic matching operation would be required. Moreover, a local asymptotic solution of the trihedral corner flow taking into account inertial effects is still missing.
3.3 Treatment of the Singularities
The singularities inherent to the definition of the lid-driven cavity problem negatively affect the convergence and the accuracy of any approximate numerical solution of the Navier–Stokes equations. To circumvent this problem, leading-order local asymptotic solutions valid near singular corners and edges may be utilized to reduce the singularity of the problem to be solved numerically. Several analytic and numerical strategies have been developed in this direction.
3.3.1 Singularity Annihilation
The method of singularity annihilation relies on an integral-equation formulation of the problem based on a suitably chosen Green’s function. The domain of integration is the whole cavity, except for the singular corners. These can be excluded from the integral if the zeroth- and first-order derivative of the selected Green’s function tends to zero at the moving lid. This method has been successfully applied to Stokes flow involving biharmonic functions [183, 184]. The method involves only little computational load, but the existence of a suitable Green’s function requires that all the singularities are located on a straight or a circular line [52].
3.3.2 Singularity Incorporation
The singularity-incorporation method is a local approach which embodies the asymptotic series defined for the singular corners only in a neighborhood of the singularity. This method has been introduced by Kelmanson [182] and extended in [148] to treat singular creeping flows in channels and corners. The method finds a natural extension and application in combination with the finite-element method, where special functional bases have been adopted near the singularities in order to well approximate the asymptotic expansion [111, 120]. The method also inspired other numerical techniques aimed at matching the local asymptotic with the global numeric solution [112, 222]. The singularity incorporation relies on the knowledge of the singularity, whose leading-order term of the asymptotic expansion for two-dimensional flow is valid within a distance \(r \propto Re^{-1}\). This condition represents a strong limitation for such methods, restricting them to small Reynolds numbers.
3.3.3 Singularity Subtraction
The singularity subtraction method builds on asymptotic expansions about the singular corners. The technique has been introduced by Symm [306] and was extended in [180, 181] to deal with Stokes flows. In the subtraction method the leading-order terms of the singular flow field, denoted \(\varvec{u}_c\), is subtracted from the full solution which is represented as \(\varvec{u} = \varvec{u}_* + \varvec{u}_c\). Therefore, \(\varvec{u}_c\) globally affects the remaining problem of solving for the less singular part of the solution \(\varvec{u}_*\). As a main achievement of the method only a less singular problem for \(\varvec{u}_*\) is left to be computed numerically, instead of the fully singular solution \(\varvec{u}\). This is a crucial advantage for high-order methods for Stokes flows [285, 286] and for Navier–Stokes flows [45,46,47,48,49], since the singularity subtraction leads to a significant improvement of the grid convergence (see Fig. 6). The improved convergence is due to the suppression of spurious modes which would otherwise appear all over the domain and, in particular, on the boundaries (Fig. 7) [285]. Even though these spurious modes are not very evident for local, low-order methods, e.g. classical finite difference or finite volumes, they still condition the accuracy of the numerical solution. An evident demonstration of this problem has been provided by Bruneau and Saad [57], using the finite-volume method on a staggered grid, who addressed the severe singularity in the vorticity (\(\omega \sim r^{-1}\)) as the main cause of the not fully satisfactory grid convergence (see the enstrophy and palinstrophy in Table 7 of [57]).

The figure is taken from [48]
Convergence of the global error of the \(L_2\)-norm of the velocity (a) and the pressure (b) in a one-sided lid-driven square cavity for \(Re=1000\). NS0 indicates results of the direct Navier–Stokes solver. NS1 and NS2 denote the errors for the Navier–Stokes solvers supplied by a first- and a second-order singularity-subtraction method, respectively.

The figure is taken from [285]
Streamlines (streamfunction \(\psi \), left half) and isolines of the vorticity \(\omega \) (right half) of the creeping flow in a two-dimensional square cavity computed using a pseudospectral Chebyshev method employing 11 modes. A comparison is shown between results using a Stokes solver without (a) and with (b) subtraction of the corner singularity. Spurious eddies of numerical origin are evident in (a), but largely suppressed in (b).
3.3.4 Numerical Approaches
Despite the additional computational overhead, the singularity-subtraction method is widely used. All other techniques mentioned above require the knowledge of the full singular asymptotic expansion which, however, is unknown for fully three-dimensional Newtonian cavity-flow problems and also for two-dimensional non-Newtonian cavity flows. It is useful, therefore, to mention other strategies which do not require the a-priori knowledge of the asymptotic edge and corner flows. Among these numerical techniques is the multi-grid approach [53, 122, 145, 330]. It is based on a series of grids on which the solution is alternatingly computed using restriction and prolongation operators. This allows a high resolution near the singularity, while preventing solution blowup on the coarse mesh far from it. Another widely used technique is the application of a-posteriori filtering operators (see, e.g., [47, 323]), which are proven to provide convergence for lid-driven-cavity problems even in terms of the vorticity field [47].
3.3.5 Regularization
Finally, a widely used method to circumvent the singularity problem consists of a suppression or attenuation of the singular component of the corner flow by a modification of the boundary conditions on the moving lid. When the numerical solution to the lid-driven cavity-flow problem is analysed in its spectral components, the multi-valued velocity data at the singular edge lead to the Gibbs phenomenon which spoils the numerical solution by falsely increasing the amplitude of high-wave-number modes (cf. Fig. 7a). The resulting numerically-induced oscillations pose a problem, in particular, for high-order methods. The Gibbs oscillations can be prevented by regularizing the boundary conditions by letting the wall velocity smoothly tend to zero in the vicinity of the singular edge. The regularization function can be polynomial [119, 209, 296], trigonometric [201], or exponential [221]. In any case, the regularized problem is intended to mimic the original singular problem. However, rigorous studies which assess the influence of the regularization on the prediction of flow properties such as, e.g. stability boundaries, are still lacking (see, however, [119]). To illustrate the problem we consider the Hopf bifurcation in the one-sided, lid-driven square cavity: Employing a 4th-order polynomial as regularization, Shen [296] predicts a two-dimensional flow instability for a Reynolds number in the range \(Re\in \) [10000, 10500], whereas for the non-regularized cavity Auteri et al. [24], employing a singularity subtraction method, find the bifurcation to occur at \(Re \in [8017.6,8018.8]\).
4 Numerical Methods
A general discussion of numerical methods for the lid-driven cavity is beyond the scope of this chapter. However, many results presented in the following sections are derived by use of a global linear stability analysis. In the classical approach [61, 99], two computational steps are required: (i) the computation of a basic (reference) state whose stability is to be probed and (ii) the analysis of the dynamics of infinitesimally small perturbations of the basic state. Hereinafter, we are concerned with the stability of stationary basic states. For the stability analysis of time-periodic states, e.g. cavity flows due to an oscillating lid, by use of a Floquet analysis [27, 158] we refer to [39].
4.1 Basic State
The flow at very small Reynolds numbers is unique and reflects the symmetries of the system [207]. Moreover, the flow is stable [289] in the sense that any perturbation of the initial conditions, required for the solution of the governing equations, will decay in time such that the flow always returns to the same basic state. Owing to the growing importance of the nonlinear terms of the Navier–Stokes equations for larger Reynolds numbers the flow may no longer be unique. At the Reynolds number at which new flow states come into existence a bifurcation of solutions occurs. If multiple solutions exist small initial perturbations of a given flow, the basic flow, may be amplified and lead to another flow state. Typically, the basic flow will still exist, but be unstable. The significance of stable and unstable basic flows derives from the fact that stable flows can be observed in experiments, while it may not be possible to observe unstable flows, at least not for an arbitrary long time.
Two methodologies are successfully employed to compute the steady basic state, Newton–Raphson iteration and selective frequency damping. These two methods are, in some, sense complementary regarding their strengths and weaknesses.
4.1.1 Newton–Raphson Iteration
The Newton–Raphson method is usually adopted for the computation of stationary two-dimensional basic states. Due to the local convergence, the Newton–Raphson iteration requires a good initial guess. Therefore, some precursor iterations are often performed by a Picard iteration or by a fixed-point iteration. However, when the initial guess belongs to the basin of attraction of the steady basic-state solution, the Newton–Raphson iteration converges quadratically.
To obtain the steady basic flow, the solution vector \(\varvec{y}=(u,v,w,p)^T\) is iterated \(\varvec{y}^k \rightarrow \varvec{y}^{k+1}= \varvec{y}^k +\delta \varvec{y}\) from an initial guess \(\varvec{y}^0\), where k is the iteration step. Inserting \(\varvec{y}^{k+1}\) in (1) and linearizing the convective terms with respect to the correction \(\delta \varvec{y}\) yields
from which the correction \(\delta \varvec{y}\) is obtained. The \((k+1)\)st Newton-iteration step can be written in compact form
where the Jacobian J is evaluated at the current iteration step k and \(\varvec{f}\left( \varvec{y}^k\right) \) is the non-linear residual of the Navier–Stokes and continuity equations (r.h.s. of (7)).
Besides the advantage of rapid convergence and the drawback of local convergence, it is evident from (8) that the Newton–Raphson method requires the computation and storage of the Jacobian matrix. Hence, this technique does not represent a suitable option for the accurate stability analyses of three-dimensional steady basic states, for which the number of degrees of freedom makes the storage of the Jacobian matrix prohibitively expensive. To overcome this weakness, Jacobian-free approaches have been proposed with the aim of computing \(J\left( \varvec{y}^k\right) \cdot \delta \varvec{y}\) without storing \(J\left( \varvec{y}^k\right) \). The most successful among these methods is the class of so-called Jacobian-free Newton–Krylov (JFNK) methods, which have been reviewed in [191].
4.1.2 Selective Frequency Damping
The selective frequency damping (SFD, [3]) is a technique inspired by control theory, which adds a forcing term to the Navier–Stokes equation in order to drive the system to a certain steady state by means of a low-pass filter which damps unsteady oscillations. In
the forced Navier–Stokes equation (9a) and continuity equation (9b) are augmented with an equation (9c) which rules the damping through the filtered state \(\varvec{\bar{u}}\). When the filtered state \(\varvec{\bar{u}}\) coincides with \(\varvec{u}\), the forcing term \(\chi \left( \varvec{u}-\varvec{\bar{u}}\right) \) as well as \(\partial _t \varvec{\bar{u}}\) vanish, and \(\varvec{u}\) and p become a stationary solution of (1). Two real parameters have been introduced to control the flow: the gain \(\chi > 0\) and the cut-off circular frequency \(\omega _c\) of the filter. Suitable parameters for these variables are related to the physically meaningful growth rate \(\sigma \) and oscillation frequency \(\omega \) of the most dangerous perturbation of the basic state which the filter is supposed to damp. For being successful, the method requires \(\chi >\sigma \) and \(\omega _c<\omega \). If \(\omega \) is known one typically sets \(\omega _c=\omega /2\).
Among the main issues of the selective-frequency-damping method is the growth rate and oscillation frequency of the instability to suppress are often unknown a-priori. This makes difficult the choice of \(\chi \) and \(\omega _c\). Too conservative values for \(\omega _c\) and \(\chi \) results in a very slow rate of convergence, leading to enormous computational costs [219]. To overcome this difficulty, more advanced methods have been proposed, which combine the basic state computed by selective frequency damping with the evaluation of its dominant eigenvalue: Based on the current estimates for \(\sigma \) and \(\omega \) the optimal choice for the control parameters \(\chi \) and \(\omega _c\) is made [173]. Despite the computational overhead in estimating \(\sigma \) and \(\omega \), the advantage in retrieving an optimal convergence rate can be significant. The main advantage of the SFD over the classical Newton method is the selective frequency damping method does not require additional matrices to be allocated and (9) can be solved with a standard projection method.
4.2 Linear Stability Analysis
Once the steady basic state has been computed as described in Sect. 4.1, its stability with respect to infinitesimal perturbations can be investigated by means of a linear stability analysis. To that end the total flow is decomposed
into a steady basic flow (indicated here by the subscript 0) and perturbation quantities (indicated by a prime) which are assumed to be small. Inserting the full flow fields \(\varvec{u}\) and p into the Navier–Stokes equations (1), taking into account that (1) is satisfied by \((\varvec{u}_0,p_0)\) alone, and linearizing the resulting equations with respect to the perturbation quantities yields the linearized Navier–Stokes equations for the perturbations
The perturbation flow is driven by the basic flow through the two advective coupling terms. In short (11) can be written as
where C is the linearized operator which includes convective, viscous and pressure terms of the momentum equation with (12b) enforcing the solenoidal constraint on the perturbation \(\varvec{y}'=(\varvec{u}',p')^T\). Two classes of methods are employed for solving (12a).
Matrix-based methods exploit the steadiness of the basic state. Owing to the linearity in \(\varvec{y}'\) and the homogeneity in t of the perturbation equations, solutions to (12) can be sought in form of so-called normal modes
where c.c. is the complex conjugate and \(\gamma =\sigma +\mathrm{i}\omega \) is a complex growth rate with real growth rate \(\sigma \) and real oscillation frequency \(\omega \). Therefore, a normal-mode type of perturbation (13) will decay or grow exponentially if \(\sigma <0\) or if \(\sigma >0\), respectively. At Reynolds numbers \(Re_n\) at which \(\sigma \) changes its sign the basic flow is neutrally stable with respect to the particular normal mode and a pair of new solutions bifurcates from the basic state. If, at neutral stability \((\sigma =0)\), \(\omega =0\) vanishes, the neutral normal mode is stationary. On the other hand, if \(\omega \ne 0\) the neutral normal mode is oscillatory, leading to a Hopf bifurcation [151]. Among the different possible values \(Re_n\) can take, its minimum value is called the critical Reynolds number \(Re_c\). The exponential time dependence holds true only for infinitesimal perturbations. Once a perturbation has grown to a considerable amplitude the nonlinear terms \(\varvec{u}'\cdot \nabla \varvec{u}'\), which are neglected in (11), have to be taken into account, which typically limits the exponential grow, often leading to a nonlinear saturation of the amplitude of the perturbation flow.
Inserting the ansatz (13) into (12) the problem is reduced to the generalized eigenvalue problem
where \(\tilde{\varvec{y}}=(\tilde{\varvec{u}},\tilde{p})^T\), A is the mass matrix and B includes the operator C and the incompressibility constraint. Since a general perturbation can be represented as a superposition of all possible normal modes, equation (14) must be solved in order to find the eigenpair \((\gamma ,\tilde{\varvec{y}})\) with the maximum possible growth rate \(\sigma \), belonging to most dangerous mode \(\tilde{\varvec{y}}\). A basic flow is linearly stable, if \(\max \sigma <0\), and it is linearly unstable if at least one eigenvalue \(\gamma \) exists for which \(\sigma >0\).
Once the matrices A and B are assembled and stored, the corresponding eigenvalue problem can be solved by means of different techniques, such as Jacobi’s diagonalization method [255], the power method [125], Lanczos’ method [203], Arnoldi’s method [22] or Davidson’s method [84,85,86, 302, 322].
Matrix-free methods intend to solve (12a) directly, without assembling and storing matrices. The very large size of the matrix representation of the linear operator C for three-dimensional meshes and the corresponding prohibitively expensive memory requirements for allocating A and B explain the increasing importance of matrix-free methods for the stability analysis of three-dimensional basic states as compared to matrix-based methods (see, e.g., [25, 219, 260, 261]).
The most popular matrix-free method in fluid dynamics is the time-stepper approach. It was initially proposed by Marcus and Tuckerman [224], then elaborated by Edwards et al. [101], and recently employed by Bagheri et al. [25] for performing the first stability analysis of a three-dimensional basic state. The time-stepping method is based on a projection of (12a) onto a solenoidal velocity-vector space which analytically satisfies (12b). In such a functional space, the system of equations (12) formally reduces to (12a), which admits the solution
where \(\varvec{y}'_0\) is the initial guess of an iteration of (15) and the matrix exponential \(M(\varDelta t) = e^{C\varDelta t}\) is called time propagator or exponential propagator. The advantage of this method is there is no need of ever assembling the matrix \(M(\varDelta t)\). The effect of \(M(\varDelta t)\) on \(\varvec{y}_0\) can be obtained by time-marching (11), projected on the divergence-free vector space of \(\varvec{u}'\). The set of n iterated vectors
spans a Krylov space \(K_n\). The set of Krylov vectors can then be orthogonalized, e.g. within the Arnoldi method. The orthogonal vectors provide good approximations to a subset of the eigenvectors of (14), namely the ones with the maximum absolute eigenvalues \(|\gamma |\). Among these eigenvalues the one with the largest real part has to be found by suitable mappings. Typically, only a relatively small dimension \(n=O(100)\) of the Krylov subspace is required to yield sufficiently accurate results for the largest eigenvalues, their number being limited by the dimension of \(K_n\). Modal and non-modal approaches to global stability analysis have recently been reviewed by Theofilis [312] in a more general context.
5 Two-Dimensional Cavity Flows
The two-dimensional flow in the (x, y) plane can be thought of being embedded in the three-dimensional problem by extruding the two-dimensional flow field \(\varvec{u} = (u,v,0)\) in z direction and by letting \(L_z\rightarrow \infty \). The numerical calculation of two-dimensional cavity flows requires little resources. The system thus provides an efficient test bed for numerical codes and for studying pure two-dimensional flow physics.
5.1 Single-Lid-Driven Cavity
The first numerical investigation of the flow in a single-lid-driven cavity is due to Kawaguti [177], who performed simulations for creeping as well as for nonlinear flows for Reynolds numbers up to \(Re=128\), investigating three aspect ratios \(\varGamma =0.5\), 1 and 2. Only after the more extensive theoretical and numerical study of Burggraf [58] the lid-driven cavity became a benchmark problem for Navier–Stokes solvers [11, 47, 122, 284], as well as a paradigm for investigating vortex dynamics in closed systems. Figure 8 shows a typical plot of the velocity components along the two cavity centerlines for different Reynolds numbers.
Characteristic velocity profiles u(0, y) and v(x, 0) on the two orthogonal centerlines of a square cavity \((\varGamma =1)\) for \(Re=10^2\) (\(\times \), full line), \(10^3\) (\(+\), dashed line) and \(10^4\) (\(\diamond \), dash-dotted line).
Typical streamline patterns of the two-dimensional global recirculating vortex driven by the moving wall for \(Re=1\) and \(Re=8\times 10^3\) are shown in Fig. 9. For \(Re=1\) the streamlines are nearly symmetrical, due to the symmetries of (1) in the Stokes-flow limit \(Re\rightarrow 0\). The streamlines are slightly crowed near the moving lid, where the largest velocities arise, and two separated eddies in the bottom corners are signaled by the two separating streamlines. When the Reynolds number is large \((Re=8\times 10^3)\), inertia terms in (1) destroy the reflectional symmetry with respect to \(x=0\) of the flow. The separated vortices at the bottom become stronger, even a second separated vortex is visible in the bottom right corner of Fig. 9b, and a third separated region is created, for \(Re\gtrsim 1000\), close to the upstream corner of the moving lid near \((x,y)=(-0.5, 0.5)\). For even higher Reynolds numbers the core of the vortex approaches a solid-body rotation with circular streamlines and constant vorticity [29]. This can be seen in Fig. 8 where the velocity profiles become linear in the bulk for high Reynolds numbers.
For shallow cavities \((\varGamma \ll 1)\) and small Reynolds numbers the streamlines become nearly parallel, except for the turning zones near \(x=\pm 0.5\). For deep cavities \((\varGamma \gg 1)\), on the other hand, the flow separates repeatedly. An example with three vortices is shown in Fig. 10. The main vortex, whose core develops circular streamlines for high Reynolds numbers, drives another weaker separated and counter-rotating vortex, and so on. When the strength of the vortices has decayed from the moving wall such that the flow becomes creeping and for \(\varGamma \rightarrow \infty \) the vortices take a self-similar shape, similar to that of the middle eddy in Fig. 10, but symmetric with respect to \(x=0\) (see also Fig. 2 of [254] and [74, 214, 303]). Note the strong asymmetric shape of the streamlines and the curved lines of separation. The asymptotic depth of the eddies far away from the moving wall (in creeping flow) is \(\varDelta y=1.39\) [231].
While the two-dimensional flow for small and moderate Reynolds numbers is steady, it undergoes a Hopf bifurcation and becomes time-dependent for higher Reynolds numbers when inertia effects become larger. The breaking of the time translation symmetry has been initially overlooked for square cavities (see, e.g., [122]). However, Gustafson and Halasi [143] found flow oscillations in time for \(Re=10^4\) and \(\varGamma =2\), and Goodrich et al. [132] bracketed the Reynolds number for the onset of time-dependence for \(\varGamma =2\) to \(Re_c\in [2000,5000]\). Shen [296] further investigated the lid-driven square cavity discovering a Hopf bifurcation for \(\varGamma =1\) with a critical Reynolds number \(Re_c\in [10000,10500]\). The study of Shen [296] has revealed the existence of a complex, time-dependent dynamics in the lid-driven square cavity. However, the results were obtained using a strong regularization of the driving force (see Sect. 3.3.5) by assuming the lid to have a symmetric parabolic velocity profile \(U(x)=Re(1-4x^2)\) which vanishes at the corners \(x=\pm 1/2\). The much more accurate result \(Re_c(\varGamma =1)=8018.2\pm 0.6\) was obtained by Auteri et al. [23]. They used a Galerkin spectral method based on Legendre polynomials to discretize the Navier–Stokes equations, a singularity subtraction method to treat the corner singularities, and bisection to pinpoint the critical threshold. The critical Reynolds number obtained by Auteri et al. [23] is consistent with the results of Nobile [240] (\(Re_c\in [7500,10000]\)) and of Bruneau and Saad [57] (\(Re_c\in [8000,8050]\)) who, in addition, provide extensive benchmark data. For long times the amplitude of oscillation saturates above the threshold. Several authors have accurately reconstructed the corresponding limit cycle in phase space [23, 57, 259]. All these studies have been conducted integrating the time-dependent Navier–Stokes equations. The existence of a Hopf bifurcation for the square cavity has also been confirmed by means of linear stability analyses. These were performed by Poliashenko and Aidun [263] (\(Re_c=7763\pm 2\%\)), followed by Fortin et al. [113] (\(Re_c=8000\)) and Sahin and Owens [280] (\(Re_c=8069.76\)). Even though the critical Reynolds number varies somewhat among the different investigations, a good agreement has been obtained for the critical oscillation frequency \(\omega _c/Re = (2.85\pm 0.02)\). Quite different (and likely less accurate) results for the critical frequency are due to Cazemier et al. [60] who tried to identify the Hopf bifurcation by means of proper orthogonal decomposition (\(Re_c=7819\) and \(\omega _c/Re=3.85\)). The transition to more complicated dynamics is discussed in Sect. 9.1.
5.2 Double-Lid-Driven Cavity
For the double-lid-driven cavity flow the moving walls, the length scale and the aspect ratio \(\varGamma \) are defined differently from the one-sided driving, see (2) and Fig. 1. The flow is driven by two facing walls at \(x=\pm \varGamma /2\) which move with constant velocities \(U_{1,2}\) in parallel or anti-parallel y direction. The problem is characterized by two Reynolds numbers \(Re_i=U_iL_y/\nu \) and the aspect ratio \(\varGamma =L_x/L_y\).
The two-sided lid-driven cavity was introduced by Kelmanson and Lonsdale [183] to study the evolution of the eddy structure in this system as a function of the aspect ratio and the relative motion of the walls. They considered the limit of creeping flow and solved the biharmonic equation for the stream function using and integral-equation technique treating the corner singularities by the singularity annihilation method (Sect. 3.3.1).
Independent of this investigation, Kuhlmann et al. [201] considered the nonlinear Navier–Stokes flow in the two-sided lid-driven cavity for \(\varGamma =1.96\) and found the two-dimensional flow not to be unique. In case of deep cavities \(\varGamma \gtrsim 2\) each moving wall can drive its own (nearly square) vortex. Consider one of these vortices: Downstream from the downstream corner of the respective moving wall, a wall jet is created. The wall jet separates from the downstream stationary wall and re-attaches to the opposite (upstream) stationary wall of the same moving lid due to the suction (strong underpressure) the upstream corner of the moving wall provides. This is similar as for one-sided driving shown in Fig. 10. However, if the Reynolds numbers \(Re_1=Re_2\) are sufficiently large and the walls move in opposite directions (antiparallel wall motion) another flows state exists, in addition. In this new state (Fig. 11a, middle) the wall jet (from each of the two downstream corners) does not separate and can reach to the opposite moving wall, where it gets entrained by the upstream corner flow of the opposite moving wall which is now providing the suction on the wall jet.Footnote 2 Additional flow states for antiparallel wall motion can arise due to breaking of the point reflection symmetry with respect to the center \((x,y)=(0,0)\). For parallel wall motion with \(Re_1=Re_2\) flow multiplicity can also be caused by spontaneous breaking of the reflection symmetry of the flow with respect to \(x=0\).
Flow multiplicity for \(\varGamma =2\). a Three out of the seven different flow states for \(Re_1=Re_2=700\) and anti-parallel wall motion (left up, right down). From top to bottom: point-symmetric two-vortex flow, strongly merged vortex flow and strongly asymmetric vortex flow. b Bifurcation diagram with order parameter \(\xi (Re_1)=\psi (0,0;Re_1)\) for a constant mean Reynolds number \((Re_1+Re_2)/2=700\) [14]
The non-uniqueness of the two-dimensional double-lid-driven cavity flow was studied more systematically by Albensoeder et al. [14]. They found up to seven different two-dimensional steady flow states for the same boundary conditions. Multiplicity is observed for condition near \(Re_1=Re_2\) when both walls move either in parallel or anti-parallel direction. An example is shown in Fig. 11. If the different flow states are characterized by the order parameter \(\xi = \psi (0,0)\), where \(\psi (0,0)\) is the stream function in the center of the cavity, one finds the bifurcation diagram shown in Fig. 11b.
The results of Albensoeder et al. [14] have been extended to higher Reynolds number for parallel and anti-parallel driving by Chen et al. [69, 70], respectively, using an arclength continuation method [179] combined with a stability analysis.
6 Spatially Periodic Lid-Driven Cavity
The incompressible flow in lid-driven cavities is determined by the Reynolds number, the initial, and the boundary conditions. To remove the effects on the flow of the lateral confinement by solid end walls it is useful to let \(\varLambda \rightarrow \infty \) and investigate flows which are periodic in z. Such periodic flows arise due to three-dimensional instabilities of the two-dimensional basic flow and they help understanding the flow in cavities with finite span.
6.1 Single-Lid-Driven Cavity
In a series of publications Koseff et al. [193, 195, 196] experimentally and numerically investigated the lid-driven cavity flow (Fig. 1a) for \(\varGamma =1\) and \(\varLambda =3\). For \(Re=2000\) and 3000 they found three-dimensional vortices aligned with the streamlines of main basic-flow circulation (primary vortex). The streamwise vortices were most pronounced near the separating streamline of the basic flow between the primary vortex and the separated downstream secondary eddy in the corner \((x,y)=(0.5,-0.5)\) (lower right corner in Fig. 9a). The diameter of these streamwise vortices was relatively small compared to the scale L of the flow such that for \(Re=3000\) eight pairs of vortices fit in the span of \(\varLambda =3\), fairly equally spaced. The streamwise vortices were termed Taylor–Görtler-like vortices, because they resemble Görtler vortices [133, 134] and the mean velocity profile in the (x, y) plane is similar to that above a curved concave wall. An example is shown in Fig. 12.
Snapshot of Taylor–Görtler vortices for \(Re=3300\) in a cavity with \(\varGamma =1\) and \(\varLambda =3\), reproduced from Freitas et al. [115]. The flow is illuminated and shown in the plane \(x=0.2\bar{6}\). The lid moves on the upper boundary of the image and perpendicular to the plane shown. The left boundary is made by one end wall, whereas part of the cavity to the right is clipped
The explanation of the Taylor–Görtler-like vortices does not rely on the finite span. The vortices are, however, affected by the presence of the lateral side walls [194] at \(z=\pm \varLambda /2\). To distinguish between the effects on the flow which are introduced by the boundary conditions on the lateral end walls at \(z=\pm \varLambda /2\) and those which are due to the flow in the bulk, i.e. far from the end walls, it is useful to consider the mathematical idealization of an infinitely extended cavity with \(\varLambda \rightarrow \infty \). In this limit the problem becomes homogeneous in z and the side-wall effects are absent. It is expected that the properties of the flow for \(\varLambda \rightarrow \infty \) can be recovered in the bulk of an experimental system, provided the span aspect ratio \(\varLambda \) is sufficiently large.
6.1.1 Flow Stability
For \(\varLambda \rightarrow \infty \) the two-dimensional flow becomes three-dimensional when the Reynolds number is increased beyond a critical threshold. To determine the critical Reynolds number at which the translational symmetry in z is broken we consider infinitesimally small perturbations of the steady two-dimensional basic flow, as in Sect. 4.2. Therefore, the equations governing the deviations \((\varvec{u}',p')\) from the basic flow can be linearized to obtain the linear stability equations (11). Since the basic flow and the coefficients of (11) neither depend on t nor on z, the perturbation flow can be expressed as a normal mode in t and z
Note that (17) differs from the more general form (13), because the homogeneity in z of the problem could be exploited. The linear stability problem reduces to the generalized eigenvalue problem (14) in which the matrix B depends on \(\varvec{u}_0(x,y)\) and on the wavenumber k, which results from the explicit differentiations with respect to z in (11). Hypersurfaces \(Re_n(\varGamma ,k)\) in parameter space along which the growth rate of a particular eigenfunction of the linear stability problem (14) vanishes, i.e. \(\sigma (Re_n,\varGamma ,k)=0\), are called neutral Reynolds numbers (subscript n). Apart from the continuous dependence of the spectrum on k, there also exists a discrete part of the spectrum \(\gamma _m(Re,\varGamma ,k)\) enumerated by the modal index \(m\in \mathbb {N}\). Therefore, \(Re_n(\varGamma ,k,m)\) must be minimized with respect to the continuous wave number k and the discrete index m in order to find the critical Reynolds number for given aspect ratio: \(Re_c(\varGamma ) = \min _{k,m}Re_n(\varGamma ,k,m)\). The critical Reynolds number \(Re_c(\varGamma )\) is the lower envelope of all neutral Reynolds numbers. Note, the condition \(Re > Re_c\) is sufficient for the flow to be three-dimensional.

Symbols indicate results of Ding and Kawahara [97] \((+)\) and Kuhlmann et al. [201] \((*)\) (from Albensoeder et al. [13])
Neutral Reynolds numbers \(Re_n\) (full lines), neutral wave numbers \(k_n\) (dotted lines), and neutral oscillation frequencies \(\omega _n\) (dashed lines) as functions of the aspect ratio \(\varGamma \).
The first linear stability analyses have been carried out for \(\varGamma =1\) by Ding and Kawahara [96, 97] and Ramanan and Homsy [270]. A more complete analysis was presented by Albensoeder et al. [13] who computed the linear stability boundary \(Re_c(\varGamma )\), the critical wavenumber \(k_c(\varGamma )\) and the critical frequency \(\omega _c(\varGamma )\) as functions of the aspect ratio \(\varGamma \). Their results are reproduced in Fig. 13. The critical curve is the envelope of the neutral curves \(Re_n(\varGamma )\) (full lines) which is made from different segments. The four segments represent different perturbation flows (modes) which are denoted \(C_i^\alpha \) [7], where C stands for centrifugal, the superscript \(\alpha =e\) for one-sided driving (einseitig in German) and the subscript enumerates different modes. Also Theofilis et al. [314] considered the linear stability of the periodic cavity flow. The critical Reynolds numbers computed agree with those of [13] for \(\varGamma =1\), but they deviate qualitatively from each other for \(\varGamma \ne 1\), with experiments (see, e.g., [300], and Fig. 24b below) being in favor of the results of Albensoeder et al. [13].
In the important reference case \(\varGamma =1\) the bulk flow instability arises at \(Re_c=786.3\pm 6\) and the critical mode is steady \((\omega _c=0)\) with \(k_c=15.43\pm 0.06\) which is very short wave. This compares well with the experiments of Siegmann-Hegerfeld et al. [300] who find a supercritical bifurcation to Taylor–Görtler vortices at \(Re=791\pm 15\) for \(\varGamma =1\) and \(\varLambda =10.88\). The relative perturbation velocity — the amplitude of the unstable mode remains undetermined in the linear analysis — is highest near the wall at \(x=-0.5\) upstream of the moving wall. The velocity vectors of the critical mode \(C_2^e\) in the plane \(y=0\), parallel to the moving wall, are shown in Fig. 14. The experimental visualization of the flow resulting from the instability is shown in Fig. 15. The short wavelength and the spatial structure of the critical mode \(C_2^e\) are consistent with the early observations of Koseff et al. [196] for much higher Reynolds numbers. The reason for the particularly short spanwise wavelength is the Taylor–Görtler vortices scale with the thickness of the curved boundary layer on the solid walls which is much smaller than the length scale \(L_y\).
The dominant destabilizing interaction mechanism between the basic flow and the critical mode \(C_2^e\) is due to the term \(\varvec{u}'_\perp \cdot \nabla \varvec{u}_0\) in (11), where \(\varvec{u}'_\perp \) is the component of the critical velocity field perpendicular to the basic flow \(\varvec{u}_0\). In plane shear flows the process associated with this term is called lift-up mechanism [204]. In using a local decomposition of the critical mode \(\varvec{u}' = \varvec{u}'_\Vert + \varvec{u}'_\perp \) parallel and normal to the direction of the basic flow, one can show that the lift-up mechanism acts over most parts of the outer streamlines of the basic flow, except near the moving wall. A frequently used scalar measure of this process is the local transfer rate of kinetic energy from the basic state to the three-dimensional perturbation mode (energy per time and volume) given by \(I_2(\varvec{x}) = -\varvec{u}'_\Vert \cdot (\varvec{u}'_\perp \cdot \nabla \varvec{u}_0)/D\) which is shown as grey scale in Fig. 14 and where D is the total rate of dissipation per period of the flow. Additional considerations [13] confirm the centrifugal nature of the instability and justify the name Taylor–Görtler vortices.

The grey scale indicates the local energy production rate \(-\varvec{u}'_\Vert \cdot (\varvec{u}'_\perp \cdot \nabla \varvec{u}_0)/D\) (from Albensoeder et al. [13])
Velocity field of the critical mode \(C_2^e\) (without the basic flow) for \(\varGamma =1\) in the plane \(y=0\). The lid moves from right to left.
Experimental visualization of the Taylor–Görtler vortices for \(\varGamma =1\) and \(Re=850\) in a plane \(x\approx -0.4\) using aluminum flakes. Shown is the central fraction of a finite-length cavity with \(\varLambda =6.55\) (from Albensoeder et al. [13]). The lid at the bottom moves into the plane shown
For other aspect ratios the instability is also centrifugal in nature, but can have different flow structures, wave numbers and time dependence. In total, four different critical modes are destabilized with the other modes \((C_1^e,C_3^e,C_4^e)\) typically having smaller critical wave numbers than the Taylor–Görtler vortices \(C_2^e\) for \(\varGamma =1\) (see Fig. 13). In deep cavities with \(\varGamma >1.207\) the basic vortex flow becomes unstable to a stationary centrifugal mode \(C_4^e\) which makes the vortex wavy along the z direction [13]. Corresponding experiments have been carried out by Siegmann-Hegerfeld et al. [301] for \(\varGamma =1.6\).
In the other limit, for shallow cavities with \(\varGamma \ll 1\), the basic flow in the bulk near \(x=0\) approaches a Couette–Poiseuille flow with zero mean. This shear flow would be linearly stable if the turning zones at \(x=\pm 0.5\) are disregarded. However, near the downstream end of the moving lid a vortex forms, while the flow at the upstream end is of entry-flow type. In such shallow cavities the instability arises as a wave on the downstream located vortex (mode \(C_1^e\)), traveling in z direction with a wavelength that approximately scales with the depth \(\varGamma \) of the layer, a length scale which is more appropriate for shallow cavities than the length scale \(L=L_x\) employed for the single-lid cavity (Fig. 1a). Similarly, the critical Reynolds number approximately scales like \(Re_c \sim \varGamma ^{-1}\) [13], visible by the divergence of \(Re_c\) in Fig. 13 for \(\varGamma \rightarrow 0\).
6.1.2 Nonlinear Three-Dimensional Flow
As the Reynolds number is increased beyond the threshold finite-amplitude flows exist. Since it is computationally quite expensive, there are not many systematic studies on three-dimensional periodic finite-amplitude flows. Another complication is the spatial period \(\lambda =2\pi /k\) of the flow is no longer uniquely determined for \(Re > Re_c\), because Taylor–Görtler vortices out of a whole band of wave numbers are linearly unstable and may saturate, for long times, or vary slowly in z. In an experimental realization the nearly periodic flow in the bulk is also affected by the finite length \(L_z\) of the system.

The resolution of the simulations using a spectral method is \(N_x\times N_y\times N_z=34\times 34\times 25\) (from Albensoeder and Kuhlmann [12])
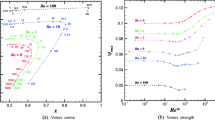
Neutral stability boundary (solid line) and existence boundary of a finite amplitude Taylor–Görtler vortex pair \((\square )\) as functions of the spanwise period \(\varLambda \) (or the wave number \(k=2\pi /\varLambda \)) for \(\varGamma =1\) (square cross section). The length of the error bars indicate the step size and direction of the quasi-static parameter variations of \(\varGamma \) or Re. The dashed and dashed-dotted lines marks the neutral curves for two and three Taylor–Görtler-vortex pairs, respectively.
Albensoeder and Kuhlmann [12] numerically simulated the supercritical three-dimensional flow with saturated amplitude and spanwise periodicity \(\lambda =\varLambda \) in cavities with a square cross section \((\varGamma =1)\). For the wavelength \(\lambda =2\pi /k=0.407\), corresponding to the period of the critical mode \(C_2^e\) of the linear stability analysis, the amplitude of steady periodic Taylor–Görtler vortices was found to depend on the normalized distance \(\epsilon =(Re-Re_c)/Re_c\) from the critical point like \(\sim \epsilon ^{0.345}\). This paradoxical result (the generic exponent is 0.5) can be explained by the range of \(\epsilon \) considered for the fit to determine the exponent and by the bifurcation being supercritical for \(k > k_c\) and subcritical for \(k < k_c\). This peculiar property of the transition is demonstrated by the existence range of Taylor–Görtler vortices shown in Fig. 16. The squares mark the existence boundary of a pair of Taylor–Görtler vortices within a periodic domain of length \(\varLambda \) for given Reynolds number. To find the existence ranges in the \((Re,\varLambda )\) plane both parameters were changed in small steps and the flow was simulated keeping the parameters constant until a steady state was reached [12]. Upon an increase of the spatial period \(\varLambda \) and for \(Re \ge 900\) the single pair of Taylor–Görtler vortices smoothly transforms into a flow with two pairs of Taylor–Görtler vortices. The three rightmost squares in Fig. 16 indicate the vanishing of the fundamental Fourier mode characterizing a single pair of Taylor–Görtler vortices.
Increasing the spatial period \(\varLambda \) flow states with one, two, three, etc. pairs of Taylor–Görtler vortices can arise in the system. The numbers of vortex pairs \(n_\mathrm{TG}\) are given as roman numbers in Fig. 17. The spectrum of the periodic flow contains spatial harmonics m with wavelengths \(\lambda _m = \varLambda /m\). The number of vortex pairs \(n_\mathrm{TG}\) is signaled in the simulations by the lowest harmonic \(m=n_\mathrm{TG}\) present in the spectrum. The symbols in Fig. 17 indicate at which point the amplitude of the fundamental spatial harmonic m vanishes upon a variation of Re (for lower Reynolds numbers) or \(\varLambda \) (for larger Reynolds numbers). As \(\varLambda \) is varied the flow either returns to the steady two-dimensional flow (low Reynolds numbers) or it changes smoothly to a flow state with a different number \(n_\mathrm{TG}\) of Taylor–Görtler vortices. Along line a the amplitude of the Fourier mode \(m=2\) vanishes as \(\varLambda \) is decreased. Along line b the amplitude of the Fourier mode \(m=1\) vanishes as \(\varLambda \) is increased. Between the existence ranges dominated by two and three pairs of Taylor–Görtler vortices the flow for \(Re\ge 850\) is found to be oscillatory (cross-hatched stripes), while between the ranges at which three and four pairs of Taylor–Görtler vortices dominate and \(Re\ge 850\) the flow becomes spatially modulated upon a variation of \(\varLambda \), indicated by the hatched stripes. Along line c the amplitude of mode \(m=4\) vanishes as \(\varLambda \) is decreased.

See text for further explanation (adapted from Albensoeder and Kuhlmann [12])
Nonlinear stability boundaries for one \((\square )\), two \((\lozenge )\), three \((\vartriangle )\) and four (\({\scriptstyle \bigcirc }\)) pairs of Taylor–Görtler vortices (also indicated by roman numbers) in the \((\varLambda ,Re)\) plane. The neutral-stability curves for \(n_\mathrm{TG}=1, ..., 4\) pairs of Taylor–Görtler vortices are shown as full red lines.
Further details on the properties of nonlinear Taylor–Görtler vortices in periodic domains with \(\varGamma =1\) can be found in Albensoeder and Kuhlmann [12]. Numerical simulations for \(Re=1000\) and periodic boundary conditions with \(\varLambda =1\) [80] are consistent with the nonlinear results of Albensoeder and Kuhlmann [12].
6.1.3 Obliquely-Driven Cavity of Infinite Span
A problem related to periodic cavity flow is the lid-driven flow in a duct \((\varLambda \rightarrow \infty )\) in which the lid moves in the same plane as before, but at an angle \(\phi \) with respect to the x axis. This case has been considered by Theofilis et al. [314] for \(\varGamma =1\). Owing to the angle \(\phi \ne 0\) being non-zero and the vanishing pressure gradient in z a net flow exists in direction of the spanwise component of the wall motion. As a result the eigenmodes are typically traveling waves. Theofilis et al. [314] find that for a small deviation of the direction of motion of the lid \((\phi =\pi /8)\) from the classical lid-driven cavity \((\phi =0)\) similar unstable modes exist as for \(\phi =0\). As \(\phi \) increases the eigenmodes become damped substantially with maximum amplification rates at \(Re=900\) and \(Re=1000\) being about a factor of two smaller for \(\phi =\pi /4\) than for \(\phi =\pi /8\). Moreover, the eigenvalues of the most dangerous modes become crowded and are not so well separated as for \(\phi =0\). On a further increase of the angle to \(\phi =3\pi /8\) the growth rates recover, but the range of wavenumbers k for which the growth rate is positive for the above Reynolds numbers is shrinking to a narrow band around \(k\approx 4\) for a whole set of unstable modes. Naturally, the phase velocity \(\omega /k\) of the unstable modes increases as \(\phi \) increases from 0 to \(3\pi /8\).
6.2 Two-Sided Lid-Driven Cavity
The interest in double-lid-driven cavities not only derives from the non-uniqueness of the two-dimensional flow (Sect. 5.2). The system also provides insight into flow instabilities due to the interaction of two vortices confined to a rectangular domain. The perhaps most interesting case is the elliptic instability. The instability can arise when a vortex is strained which, for bipolar strain, makes the streamlines in the vortex core elliptic (similar as in Fig. 11a, middle). Note the scaling and definitions in (2b) and Fig. 1b are used for two-sided driving. The strain can be due to the induced flow caused by the vorticity of other vortices, or by confinement effects due to the boundaries. The mechanism of the instability can be explained in terms of a resonance among two different three-dimensional Kelvin waves traveling about the vortex, where the resonant amplification is communicated by the strain field as part of the two-dimensional basic flow [102, 185, 238]. For the elliptic instability of a single strained vortex in an unbounded domain, see Refs. [31, 102, 153, 262, 329].

The dashed line indicates the main strain direction in \((x,y)=(0,0)\) (from Kuhlmann et al. [201])
Streamlines of the two-dimensional steady flow in an antiparallel lid-driven cavity for \(\varGamma =1.96\) and \(Re_1 = Re_2 = 257\) (critical conditions).
The elliptic instability can arise in the two-sided lid-driven cavity when the lids move in opposite directions, generating two co-rotating vortices. In a certain range of aspect ratios \(\varGamma \) the co-rotating vortices either fully merge to a vortex with elliptic streamlines in the center (Fig. 11a, middle), or they partially merge, creating a free hyperbolic stagnation point in the center \((x,y)=(0,0)\) of the cavity, surrounded by closed streamlines outside of the separatrix (Fig. 18). Both types of flow are characterized by a bipolar strain field with the strain rate being smaller (elliptic point) or larger (hyperbolic point) than the rotation rate of the flow at \((x,y)=(0,0)\).
The elliptic instability (of type E2, see Fig. 20 below) in two-sided lid-driven cavities was first reported by Kuhlmann et al. [201] for \(\varGamma =1.96\) at which the strain in the center of the cavity is so strong that a free hyperbolic stagnation point arises (Fig. 18). Note the flow is still a strained vortex, resulting from a merging of the two vortices driven by each of the moving walls, since closed streamlines arise outside of the separatrix. For periodic boundary conditions in z and anti-parallel wall motion with \(Re:= Re_1 = Re_2\) the instability arises at a relatively small Reynolds number \(Re_c=257\) [8, 201], which is consistent with the experimental value of \(Re_c=275\) which was obtained for a the 4-cell flow in a cavity with \((\varGamma ,\varLambda )=(1.96,6.55)\) [41]. Streaklines of the steady nonlinear four-cell flow which originates from the elliptic instability are shown in Fig. 19a for \(Re = Re_1 = Re_2 = 700\). The steady cuboidal cellular flow is very robust and not much affected by the lateral walls. The cells become time-dependent only at \(Re\approx 850\), the exact value depending on the aspect ratio \(\varGamma \) and the number of cells [41].
Streak lines in the steady cellular flow with four (a) and five (b) convection cells for \(\varGamma =1.96\), \(\varLambda =6.55\) and anti-parallel wall motion with \(Re_1=Re_2=700\) [41]. Top and bottom boundaries of each figure represent the lids moving in and out, respectively, of the plane. The cavity end walls \((z=\pm \varLambda /2)\) are located at the left and the right sides of the figure. The two bright spots in the center and to the right are hot film probes flush mounted to the wall. Equivalent flows which are phase shifted by \(\pi \) (\(\varDelta z=\pi /k\), width of one cell) are not shown
6.2.1 Linear Stability Boundaries
The linear stability of the two-dimensional double-lid-driven cavity flow as function of \(\varGamma \) for anti-parallel wall motion with equal speed \((Re=Re_1=Re_2)\) was investigated by Albensoeder and Kuhlmann [8]. The critical curve shown in Fig. 20 (full line) exhibits a rich behavior. All instabilities are stationary. The aspect ratio ranges for which the elliptic instability mechanism (E1,E2), a centrifugal mechanism (C), and a quadripolar (Q) instability mechanismFootnote 3 dominates are indicated on top of the figure. In addition to the critical wave numbers (dotted lines) experimental results of Blohm et al. [42] are shown as symbols. The stability analysis is complicated by the existence of multiple basic states (Sect. 5.2). Their range of existence is indicated by dashed lines in Fig. 20.

The figure is reproduced from Albensoeder and Kuhlmann [8]
Critical Reynolds numbers \(Re_c\) (envelope of the full lines) and wave numbers \(k_c\) (dotted lines) as functions of the aspect ratio \(\varGamma \). The dashed line indicates the existence range of multiple (three) two-dimensional solutions (see Sect. 5.2). Experimental critical data for \(Re_c\) \((\lozenge )\) and \(k_c\) \((\square )\) have been taken from Blohm et al. [42].
For small aspect ratios the co-rotating vortices due to each moving lid merge to form a single strained vortex. This vortex is unstable to the elliptic instability (type E1). In the extreme case of shallow cavities with \(\varGamma \ll 1\) and \(Re_1=Re_2\) the flow far from the moving walls approaches plane Couette flow with zero mass flux through any plane \(y=\mathrm {const}\). The three-dimensional instability is excited near both symmetrically located turning zones and midway between the two moving walls in the region where the streamline curvature is the highest. As a result of the instability long streaks in y direction are formed. Figure 21a shows the basic flow, the critical mode and the total local energy production rate (color) for \(\varGamma =0.2\).
Basic-state streamlines (full lines), critical mode (arrows) and local energy production rate (color) at the critical Reynolds number for (a) antiparallel wall motion and \(\varGamma =0.2\) (\(Re_c=577.8\), \(k_c=7.578\), mode E1/\(E_1^a\)) [8] and (b) for parallel wall motion and \(\varGamma =0.3\) (\(Re_c=547.6\pm 3.7\), \(k_c=9.018\pm 0.005\), mode \(C^p\)) [9]. The fields are shown in a plane \(z=\mathrm { const}.\) in which the total local production rate takes its absolute maximum. In (a) the local production rate \(-D^{-1} v'u'\partial v_0/\partial x \) is shown. In (b) the total local production rate \(-D^{-1} \varvec{u}' \cdot [\varvec{u}'\cdot \nabla \varvec{u}_0]\) is shown (\(w'=0\) in this plane)

The dotted curve indicates the two-dimensional stability boundary \((k=0)\), see text (from Albensoeder and Kuhlmann [9])
Critical Reynolds number \(Re_c\) (solid line) and wave number \(k_c\) (dashed line) as functions of the aspect ratio \(\varGamma \) for parallel wall motion.
The critical curve (full line) and the critical wave number (dashed line) for parallel wall motion \((Re=Re_1=-Re_2)\) are shown in Fig. 22. The critical curve is continuous for all aspect ratios and the critical mode was denoted \(C^p\) (centrifugal, parallel wall motion) [9]. Plane Poiseuille flow with zero mass flux is approached in the bulk for shallow cavities \((\varGamma \rightarrow 0)\). In this situation the instability is triggered at the downstream end of the moving walls where the basic flow turns inward and returns to the bulk in direction opposite to wall motion. An example is shown in Fig. 21b.
In addition to the three-dimensional instability boundary, also the two-dimensional stability boundary \((k=0)\) is shown in Fig. 22 as a dotted line. It corresponds to the reflection-symmetry breaking instability of the two-dimensional flow (Sect. 5.2). The two-dimensional finite-amplitude flow with broken reflection symmetry is not unique within the regions confined by the dotted lines in Fig. 22. Finite-amplitude two-dimensional flows with broken mirror symmetry exist only within a band of \(\varGamma \) (see also Fig. 6 of [14]).

From Albensoeder and Kuhlmann [10]
Critical surface (stability balloon) of the double-lid-driven cavity shown in the range \(0.3\le \varGamma \le 3\). The colors indicate the most prominent different critical eigenmodes, but not all of them. White lines show Reynolds numbers for which \(Re_1=Re_2\) (anti-parallel wall motion, Fig. 20), \(Re_1=-Re_2\) (parallel wall motion, Fig. 22), and \(Re_2=0\) (one-sided wall motion, Fig. 13).
The linear stability analysis was extended by Albensoeder and Kuhlmann [10] to arbitrary Reynolds numbers \(Re_1\) and \(Re_2\) to find the linear stability balloon in the three-dimensional parameter space spanned by \(Re_1\), \(Re_2\) and \(\varGamma \). It is shown in Fig. 23. Since the linear stability problem is invariant under \((Re_1,Re_2)\rightarrow (Re_2,Re_1)\) and \((Re_1,Re_2)\rightarrow (-Re_1, -Re_2)\) the stability balloon is reflectionally symmetric with respect to the planes \(Re_1=Re_2\) and \(Re_1 = -Re_2\). In the limit \(\varGamma \rightarrow \infty \) the vortex structures driven by the two walls become independent of each other, because the strength of the flow decays from the moving walls towards \(x=0\). Therefore, the flow becomes linearly unstable whenever one of the two Reynolds numbers exceeds the critical Reynolds number for an infinitely deep single-lid-driven cavity. For shallow cavities \((\varGamma \rightarrow 0)\) the situation is more complicated, because the instabilities typically involve the turning zones near \(x=\pm \varGamma /2\). Stability boundaries for various fixed values of \(\varGamma \) and arbitrary Reynolds numbers are provided in [7, 10].
The two volumes in the parameter space in which the basic two-dimensional flow is not unique (Sect. 5.2) are not shown in Fig. 23. These regions arise symmetrically about the planes \(Re_1=Re_2\) (antiparallel driving) and about \(Re_1=-Re_2\) (parallel driving). Only the region of non-uniqueness for antiparallel driving (dashed line in Fig. 20) collides with the stability balloon. Finally, owing to the large (three-dimensional) parameter space only little is known about nonlinear three-dimensional flows for two-sided lid-driven cavities (see, however [41, 277]).
6.2.2 Experimental Stability Results
Some experimental results on the flow stability for large span aspect ratios \(\varLambda \) are available. These are due to Kuhlmann et al. [201], Blohm [40], Blohm and Kuhlmann [41] (see Fig. 19), Siegmann-Hegerfeld [299], and Siegmann-Hegerfeld et al. [300, 301] Experimental critical data of Siegmann-Hegerfeld et al. [300] are shown in Fig. 24 in comparison with numerical linear stability data in the \((Re_1,Re_2)\) plane. According to Albensoeder and Kuhlmann [10] the instabilities arise due to centrifugal (modes C), elliptical (modes E) and quadripolar (modes Q) instability mechanisms. The superscripts p and a stand for parallel and anti-parallel wall motion, respectively. Most experimental data agree with the numerical stability analysis which is based on a finite-volume code with a resolution of \(141\times 141\) grid points in the (x, y) plane [10, 13]. However, for certain modes (\(C_3^e\), \(Q^a\)) the experimental instability boundaries are lower than the numerical ones. The reason could be related to a subcritical bifurcation which was also found numerically for the quadripolar instability mode \(Q^a\) [7]. Moreover, some neutral curves may depend sensitively on aspect ratio \(\varGamma \) (see the different curves in Fig. 24b). Also, the curvature of the moving walls which were experimentally realized by rotating cylinders with large radius may have affected the experimental results.
Experimental critical Reynolds numbers \(Re_{2c}(Re_1)\) (symbols) for \(\varGamma =1\) and \(\varLambda =10.88\) (a) and for \(\varGamma =0.76\) and \(\varLambda =10.43\) (b) according to Siegmann-Hegerfeld et al. [300] in comparison with numerical neutral curves for \(\varLambda \rightarrow \infty \). The labels denote different modes (notation of Albensoeder [7]): \(C^p\) (\(\blacklozenge \), continuous line in (a)), \(C_1^e\) (\(\vartriangleright \)), \(C_2^e\) and \(Q^a\) (\(\blacktriangle \), dash-dotted line in (a)), \(C_3^e\) (\(\circ \), double-dash-dotted line in (a)) and \(E_1^a\) (\(\blacksquare \)). Open symbols denote Hopf bifurcations. The open squares \((\Box )\) are critical data for \(Re_1=0\) of Theofilis et al. [314] with \(Re_{2c}(\varGamma =1)=783\) and \(Re_{2c}(\varGamma =0.76)=825\pm 10\) (from their fig. 14). The neutral curves in (a) have been calculated for \(\varGamma =1\), whereas in (b) numerical neutral curves are shown for \(\varGamma = 0.725\) (dashed lines), \(\varGamma = 0.75\) (continuous lines) and \(\varGamma = 0.787\) (dotted lines). The open diamond in (a) indicates the Reynolds numbers of Fig. 25. Straight dotted lines indicate the limits of parallel and antiparallel wall motion with equal velocity magnitude
Apart from the well-known Taylor–Görtler instability for one-sided driving (mode \(C_2^e\) in Fig. 24a) and the elliptic instability \(E_1^a\) the two counter-rotating vortices for symmetrical and parallel driving can become unstable to the \(C^p\) mode. This mode is illustrated in Fig. 25 which shows streaklines of the steady three-dimensional flow for \(Re_2=-Re_1=250\). The two stationary vortices in the cavity alternatingly extend and shrink in z direction.
Supercritical flow evolving from the \(C^p\) mode for parallel wall motion with \(Re_2=-Re_1=250\), \(\varGamma =1\) and \(\varLambda =10.88\) (from [300]). The walls, located at the top and bottom, move into the plane shown. The flow is visualized by seeding with aluminum flitter and illumination from the right in the plane \(y=0\)
7 Cuboidal Lid-Driven Cavity Flow
Any experimental realization of a closed cavity flow must have a finite length \(L_z\) in spanwise direction. The most natural boundary conditions at \(z=\pm \varLambda \) are no slip boundary conditions \((\varvec{u}=0)\). These conditions strictly prevent the existence of a two-dimensional flow. Therefore, the flow in cuboidal cavities must be three-dimensional, even for very small Reynolds numbers. Here we only consider the single-wall motion such that the scaling (2a) and Fig. 1a apply.
7.1 End-Wall Effects
The presence of end walls suppresses the main swirling motion in their vicinity and a velocity component w in spanwise direction is created whose strength decays towards the bulk. This is similar as in the case of an unbounded vortex with constant vorticity perpendicular to a wall for which Bödewadt [43] has provided similarity solutions for the structure of the boundary layer near the wall. The secondary flow, involving a non-zero wall-normal velocity component w, decays exponentially with the distance from the wall. For the Bödewadt as well as for the cavity flow, the primary vortex flow in the (x, y) plane induces a secondary flow due to an imbalance between pressure forces and centrifugal forces. As a result the wall-induced secondary flow is directed ’inwards’ toward the apparent center of the primary vortex in the vicinity of the end walls. The reduction of the circulation and the secondary flow effect, which leads to a spanwise motion, have experimentally been investigated for different small span aspect ratios \(\varLambda \in [0.25, 1]\) by Prasad and Koseff [268], albeit for relatively high Reynolds numbers larger than \(Re=3200\).
Since the secondary three-dimensional flow in a cuboidal cavity decays away from the end walls, the three-dimensionality of the flow may be neglected in the bulk if the span length \(\varLambda \) is sufficiently large. In that case the three-dimensional instabilities considered in Sect. 6 for an infinitely extended system may be realized in good approximation. However, for short systems with \(\varLambda =O(1)\) the end-wall-induced secondary flow has a profound influence and makes the flow three-dimensional for any Reynolds number.
As the strength of the circulation of the main (primary) flow is significantly reduced by the no-slip end-wall conditions, the circulation in the symmetry plane \(z=0\) of a cubic cavity (\(\varGamma =\varLambda =1\)) is less than the one in a cavity with \(\varGamma =1\) and \(\varLambda =3\) [194]. The vortices generated near the end walls and the global transport due to the secondary flow have been investigated by Chiang and Sheu [75] and Chiang et al. [77]. According to Albensoeder et al. [13] the reduced strength of circulation prevents Taylor–Görtler vortices within a certain distance \(\varDelta z\) from the end walls for Reynolds numbers slightly larger than the critical Reynolds number \(Re_c^\infty \) for an infinitely extended system. This is evident from Fig. 26 showing Taylor–Görtler vortices in cavities with \(\varGamma =1\) and \(\varLambda =6.55\) (a) and \(\varLambda =10.88\) (b). At \(Re=850\) the vortices are steady for \(\varLambda =6.55\), while the vortices drift towards the end walls for \(\varLambda =10.88\). As the Reynolds number is increased the Taylor–Görtler vortices also invade the previously nearly structureless regions near the end walls (in Fig. 26) and the vortices start to drift also for \(\varLambda =6.55\). Obviously, the inhomogeneity in z of the basic flow and the end-wall-induced secondary flow make the Taylor–Görtler vortices travel towards the end walls, with the speed of propagation increasing as the end walls are approached. Such motion of Taylor–Görtler vortices has also been found numerically by Chiang et al. [76] for \(Re=1500\) and \(\varLambda =3\).
Taylor–Görtler vortices for \(\varGamma =1\) and \(Re=850 > Re^\infty _c= 786\). a For \(\varLambda =6.55\) the vortices are steady (from Albensoeder et al. [13]). b For \(\varLambda =10.88\) the vortices drift towards both end walls (from Siegmann-Hegerfeld et al. [300]). The moving lid is located at the bottom of each image and it moves into the plane. The flow is visualized using aluminum flakes and illumination in a layer close to the wall at \(x=-0.5\) (upstream of the moving lid). Note the regions adjacent to the end walls are free from Taylor–Görtler vortices
Figure 27 shows a velocity profile of v in the final state of a three-dimensional numerical simulation [12] for \(\varLambda =6.55\) and \(Re=850\) (full line) corresponding to the flow shown in Fig. 26a. The simulation confirms the localization of the steady Taylor–Görtler vortices in mid-cavity. For comparison, the velocity profile from a nonlinear simulation using periodic boundary condition is shown for the same Reynolds number and a wavelength \(\varLambda =0.407\) corresponding to the critical wave number \(k_c=15.4\) of the linear theory (see Sect. 6.1.1). The wavelength and the peak amplitude of the localized flow pattern agree very well with those for the periodic Taylor–Görtler flow.
Velocity profile \(-u(-0.337,-0.263,z)\) for \(Re=850\) and \(\varGamma =1\). Shown are numerical results of Albensoeder and Kuhlmann [12] for a finite-length cavity and no-slip end walls for \(\varLambda =6.55\) (full line) and for periodic boundary conditions and \(\varLambda =0.407\) (dotted line)
The onset of Taylor–Görtler vortices in cuboidal cavities with \(\varGamma =1\) and moderately large \(\varLambda \) depends both on the Reynolds number and the aspect ratio. Numerically, Albensoeder and Kuhlmann [12] found: When the Reynolds number is reduced quasi-statically for \(\varLambda =6.55\) the Taylor–Görtler vortices break down at \(Re=835\pm 5\), in rough agreement with the experimental value \(Re=810\pm 15\) found by Albensoeder et al. [13]. The value \(Re=835\) is only \({\approx }6\)% larger than the critical Reynolds number \(Re_c^\infty \) for periodic boundary conditions. Similarly, if the span aspect ratio \(\varLambda \) is reduced quasi-statically for \(Re=850\) the Taylor–Görler vortices vanish at \(\varLambda _c(Re=850)=6.1 \pm 0.1\).
For the larger aspect ratio \(\varLambda =10.88\) and for a square cross section \((\varGamma =1)\) Siegmann-Hegerfeld [299] finds Taylor–Görtler vortices drifting from the center \(z=0\) towards the end walls of the cavity immediately from the onset of Taylor–Görtler vortices. This is different form the result for \(\varLambda =6.55\) for which steady localized Taylor–Görtler cells were found numerically and experimentally for \(Re=850\). For \(\varLambda =10.88\) new cells are continuously created at \(z=0\) and annihilated before reaching the end walls at \(z=\pm \varLambda /2\) (see the empty regions in Fig. 26). The drift velocity of the Taylor–Görtler vortices for \(\varLambda =10.88\) depends on the Reynolds number, but it is of the order of O(1) [299]. At \(Re\approx 10^3\), just before time dependence sets in, Taylor–Görtler vortices fill the whole span of the cavity.
The complicated behavior of the system at moderate span aspect ratios is also underlined by the investigation of Aidun et al. [2] for \(\varGamma =1\) and \(\varLambda =3\). Upon a quasi-steady increase of Re they have observed the basic flow to remain stationary up to \(Re\approx 875\pm 50\), beyond which the flow became oscillatory and increasingly complex. They also found multiple steady states in form of cellular patterns at \(Re<500\) which seem to be accessible only by finite-amplitude perturbations of the basic flow. The qualitative nature of the reported behavior indicates there is still much room for precision experiments to clarify the properties of the system under a strong lateral confinement. Moreover, as discussed by Albensoeder et al. [13], the through flow due to the unavoidable gaps between the stationary walls and the moving lid can change the bifurcation scenario.
7.2 Cubic Lid-Driven Cavity
As the aspect ratio \(\varLambda \) is further reduced, the end-wall induced three-dimensional flow is important in the whole cavity, and for \(\varLambda =1\) the periodic Taylor–Görtler instability is absent. Owing to its simple geometry the cubic cavity \(\varGamma =\varLambda =1\) is of particular interest as a benchmark for three-dimensional flows [11], but also regarding the flow physics. Due to the symmetry of the geometry and boundary conditions the flow at lower Reynolds numbers is reflection symmetric with respect to the midplane \(z=0\) (\(Z_2\) symmetry), satisfying
The full three-dimensional nature of the flow is illustrated in Fig. 28 which depicts wall streamlines for \(Re=400\) on all stationary walls. The spiralling-in motion on the end walls \(\overline{DCGH}\) and \(\overline{EFBA}\) and the spanwise dependence of the separation lines marking the corner vortices are clearly seen.
Wall streamlines for cubical cavity flow and \(Re=400\) according to Sheu and Tsai [297]. Shown are the stationary walls which result when removing the lid \(\overline{EFGH}\) and looking down on the bottom wall \(\overline{ABCD}\) with the side walls being unfolded. The lid motion (not shown) is from left to right
As the Reynolds number is increased, it is expected that the reflection symmetry will be lost, the flow become time-dependent, or both. This problem was first tackled by Feldman and Gelfgat [109] who, using finite-volume numerical simulations, found a subcritical oscillatory instability. The critical Reynolds number and oscillation frequency were determined by extrapolation to zero of the subcritical decay rate of the characteristic oscillations. Furthermore, the supercritical oscillatory flow was found to break the reflection symmetry with respect to the midplane \(z=0\). Using a the same subcritical extrapolation, but a more accurate spectral method, Kuhlmann and Albensoeder [200] could pinpoint the critical data to \(Re_c=1919.51\) and \(\omega _c/Re = 0.58611\).
For slightly sub- and supercritical conditions, \(|Re-Re_c|/Re_c\ll 1\), the amplitude of oscillation saturates and remains constant for a very long time. This allows to construct a bifurcation diagram \(A_w(Re)\) by fitting a fourth-order polynomial to the dependence \(Re(A_w)\), where \(A_w\) is the saturated amplitude of the fundamental temporal harmonic oscillation of the spanwise velocity component \(w(\varvec{x}_0)\) evaluated at \((x_0,y_0,z_0)=(-0.32139,-0.35355,0.086824)\). The fit, shown in Fig. 29, indicates the narrow range of hysteresis in Re.

Adapted from Kuhlmann and Albensoeder [200]
Bifurcation diagram showing the amplitude \(A_w\) (diamonds) of the fundamental-frequency oscillation of \(w(-0.32139,-0.35355,0.086824)\) as a function of the Reynolds number. The line is a fit to \(Re(A_w)-Re_c = aA_w^2+bA_w^4\) (\(a = -0.0189977\), \(b = 6.64421 \times 10^{-6}\)). The circle is the linear stability boundary and the asterisk indicates the cyclic-fold bifurcation point \((Re, A_w)=(1906.0, 37.81)\).
Let us call LC1 (limit cycle 1) the solution of the Navier–Stokes equations (1) which bifurcates backwards at \(Re=1919.51\) (Fig. 29). LC1 is symmetric with respect to the mid plane. Thus it cannot explain the broken symmetry observed by Feldman and Gelfgat [109] in their simulations. The reason is the dynamics is more complex. As an example, the time dependence of the total kinetic energy per mass \(E_\mathrm {kin}=(1/2)\int _V \varvec{u}^2\mathrm{d}V\) is shown in Fig. 30 for Reynolds number \(Re=1921\). Starting with the basic flow for \(Re = 1918\) the Reynolds number is increased to \(Re = 1921 > Re_c\) at \(t=0\). Only at \(t\approx 12\) the symmetric oscillations of LC1 are fully developed. After a long period of constant-amplitude oscillation, however, a burst occurs at \(t\approx 18.5\) which involves breaking of the reflection symmetry of LC1. Therefore, LC1 is unstable to symmetry-breaking perturbations. But the asymmetric burst does not lead to an asymmetric flow state with saturated amplitude. Instead, the flow returns close to the unstable steady basic state from which the symmetric oscillations eventually grow again. This scenario repeats itself in an intermittent fashion leading to a chaotic dynamics [200, 220].
Total kinetic energy \(E_\mathrm {kin} = (1/2)\int _V \varvec{u}^2 \mathrm{d}V\) for \(Re=1921\) as a function of time [200]. Note the varying durations of the time periods the system stays close to the basic state (\(E_\mathrm {kin}/Re^2 \approx 0.01913\)), stays close to moderate-amplitude symmetric oscillations (they appear as wide black horizontal bars on the long time scale shown), and of the bursts at the end of the oscillatory period (large-amplitude excursions)
Unstable limit cycles in the intermittent cavity flow for \(Re=1930\) adapted from Loiseau et al. [220]: Basic state BS (small dot at (0, 0)), LC1 (blue), and LC2 (red)
By imposing a symmetry boundary condition on the midplane \(z=0\) Loiseau et al. [220] have been able to identify three different periodic solutions for Re above the onset of time-dependence. The corresponding phase portraits in the plane spanned by the dissipation \(D=\int _V (\nabla \times \varvec{u}')^2\mathrm{d}V\) and the production \(P=-\int _V \varvec{u}' \cdot [(\varvec{u}'\cdot \nabla )\varvec{u}_0]\mathrm{d}V\) are shown in Fig. 31, where \(\varvec{u}_0\) denotes the unstable basic flow and \(\varvec{u}'\) the small but finite amplitude fluctuations. The periodic solutions shown are: (a) the (unstable) steady basic state (BS, dot at \(D=P=0)\), (b) a limit cycle LC1 with low production and dissipation (blue) which bifurcates from the linear instability of the basic state (Fig. 29), and (c) a limit cycle LC2 associated with large production and dissipation (red) which is stabilized by the symmetry constraint. Loiseau et al. [220] explain the intermittent behavior as a wondering of the system in phase space between these invariant objects, which are all unstable. Figure 32 shows snapshots illustrating the oscillatory flow in a state near LC1 (a,b), near LC2 (c), and during the asymmetric breakdown of LC2 (d) after which the flow returns close to the steady basic state.

All figures are taken from Kuhlmann and Albensoeder [200]
Vortex structures in a lid-driven cube for \(Re=1921\), visualized by the Q criterion [171]. Shown are isosurfaces of \(Q=0\). The moving lid is located on the rear side of the cube shown, and it moves downward. a, b Snapshots during different instants of the symmetric oscillations corresponding to LC1. c Snapshot of the stronger symmetric oscillations near LC2. d Snapshot of an asymmetric vortex structure during the breakdown of LC2.
As suggested by Loiseau et al. [220] the intermittent behavior can be better understood by identifying the different unstable solutions of the Navier–Stokes equations. Lopez et al. [221] solved the Navier–Stokes equations in the full three-dimensional space and in the subspace of functions with reflection symmetry about the midplane \(z=0\). The unstable basic state was computed using selective frequency damping (Sect. 4.1.2), while unstable oscillations, corresponding to saddle limit cycles, were accurately located and tracked as function of Re by either restricting the solution to a symmetric subspace (LC2) or by using an edge state technique [283] (LC1). The resulting bifurcation diagram is shown in Fig. 33.
Bifurcation diagram in terms of the standard deviation \(\sigma \) of the kinetic energy (upper panel) and oscillation frequency (lower panel) as functions of the Reynolds number Re (adapted from Lopez et al. [221]). The small numbers shown indicate the number of unstable direction from the solution in the symmetric phase space. See text for further explanations
According to Lopez et al. [221] the steady basic flow (BS) becomes unstable to a symmetric limit cycle LC1 (frequency \(\omega _1\)) through a backward bifurcation at the Hopf bifurcation point \(H_1\) (see also Fig. 29). After turning forward at the cyclic-fold bifucation point \(CF_1\) the solution branch becomes stable but rapidly changes to unstable due to a Neimark–Sacker bifurcation at \(NS_1\). The bifurcating solution QPs is quasi-periodic, symmetric and involves a frequency which is about four times smaller than \(\omega _1\). On the other hand, the quasi-periodic solution branch QPs is connected at \(NS_2\) with the lower-branch of another subcritical limit cycle LC2 which bifurcates from the basic flow at a higher Reynolds number at the Hopf bifurcation point \(H_2\) and with frequency \(\omega _2\). The upper-branch of the limit cycle LC2 is stable in the symmetric subspace and can thus be computed easily [221], but it is unstable to symmetry breaking perturbations. Therefore, for \(Re > Re(NS_1)\), small reflection-symmetric perturbations of the flow corresponding to LC1 grow slowly (the growth rates are quite small) in a quasi-periodic fashion to approach the upper branch of LC2. However, since LC2 is unstable to perturbations which break the reflection symmetry, the flow state is repelled from LC2 involving large-amplitude symmetry-breaking flow structures (burst). Since no stable states seem to exist for \(Re > Re(NS_1)\) the flow remains chaotic in the fashion illustrated in Fig. 30. However, the period of time which the system stays close to LC1 or LC2 shrinks as Re increases rendering the system fully chaotic.
The critical Reynolds numbers \(Re_c=1929\) for the bifurcation point \(H_1\) obtained by Lopez et al. [221], using a spectral truncation \(N=48\) and a smoothing of the corner singularity (Sect. 3.3.5), and the value \(Re_c=1927\) (Richardson extrapolated 1914) obtained by Feldman and Gelfgat [109], using a multi-grid finite-volume technique, differ only slightly from \(Re_c=1919.51\) obtained by Kuhlmann and Albensoeder [200] for a spectral truncation order \(N=128\) and a singularity subtraction method (Sect. 3.3.3).
The subcritical transition to oscillatory flow has been confirmed experimentally by Liberzon et al. [213]. They find the lowest Reynolds number at which oscillations are sustained and the corresponding frequency in rough agreement with the numerical results for LC1. The largest fluctuations of the oscillatory flow in the cavity midplane \(z=0\) were detected in the region between the main vortex and the stationary walls, a behavior also found numerically. But experimental imperfections seem to have prevented uncovering the intermittent scenario found numerically.
7.3 Diagonal Lid Motion
The lid-driven flow in a cuboid whose lid moves diagonally has received some attention. The flow is conceptually very similar to the classical lid-driven cuboidal cavity flow (Sect. 7.2). In view of the complex dynamics in the classical configuration it is of interest to identify similarities and differences. The spanwise periodic version of this problem has been considered by Theofilis et al. [314] (Sect. 6.1.3).
Projected velocity vector field of the steady basic flow in a cube for diagonal lid motion shown a in the diagonal (symmetry) plane for \(Re=700\) and b in the midplane \(y=0\) parallel to the moving lid for \(Re=2000\) (from Povitsky [265]). The lid in (a) is located at the top and it moves from left to right. In (b) the lid moves diagonally from the bottom right to the top left (long arrow). The labels enumerate the vortices
The diagonally-driven cuboidal cavity was introduced by Povitsky [265] as a separated flow in which the flow transverse to the lid motion is particularly strong (see also Povitsky [264]). The steady flow is characterized by a large-scale vortex motion in the diagonal plane. The flow exhibits a reflection symmetry with respect to the diagonal plane, as in the classical case. To illustrate the strong three-dimensional character of the flow in a cube \((\varGamma =\varLambda =1)\) the velocity vector field is shown in Fig. 34. In the diagonal (symmetry) plane the flow at \(Re=700\) (Fig. 34a) turns downward in the 90-degree wedge. Due to the stronger viscous effect the downward motion experiences the flow in the wedge separates earlier than in the classical configuration, and the separated flow readily turns backward. For the larger Reynolds number \(Re=2000\) (Fig. 34b), close to the onset of time dependence, the flow has developed much more fine structure. In the midplane \(y=0\) parallel to the moving wall the separated flow from the downstream wedge (between vortices labelled 3) is opposing the flow driven by the moving wall which has become part of two large scale vortices (indicated by labels 2) due to the strong three-dimensional effect.
Feldman [108] investigated this flow with regard to the onset of time dependence (see also Feldman and Gelfgat [110]). As for the classical case, in which the lid moves parallel to the edges, the first bifurcation is found to be subcritical with a Hopf bifurcation point at \(Re_c=2329\) and a cyclic fold bifurcation point at \(Re=2302\). A more accurate critical Reynolds number \(Re_c=2320\) with \(\omega _c/Re = 0.249\) was obtained by Richardson extrapolation. According to Feldman [108] the perturbation flow has a complicated structure reflecting the complex structure of the basic flow. The essential feature of the oscillatory perturbation flow seems to be a streamwise vortex centered in the midplane whose sense of rotation is alternating with time. Different from the classical case, the upper-branch oscillatory flow violates the reflectional symmetry with respect to the diagonal plane, but satisfies the H symmetry
where \(\check{x}\) and \(\check{y}=y\) are the two orthogonal coordinates in the diagonal plane, \(\check{z}\) the coordinate perpendicular to the \((\check{x},\check{y})\) plane and \(T=2\pi /\omega \) is the period of the flow. The velocities \((\check{u},\check{v},\check{w})\) denote the fluctuating velocity components in the respective \((\check{x},\check{y},\check{z})\) directions. According to Feldman [108] the supercritical H-symmetric oscillatory flow is stable, different from the \(Z_2\)-symmetric flow of LC1 in the classical case.
In yet another variant of cavity flows two facing sidewalls move tangentially and parallel to the edges, but in mutually orthogonal directions. According to Povitsky [266] the two primary vortices, which are essentially oriented orthogonal to each other, lead to a particularly large helicity in the flow which is expected to be beneficial for mixing configurations.
8 Streamline Topology and Mixing
The ease by which the lid-motion can be controlled in experiments, also for time-dependent driving by prescribing any lid-velocity protocol U(t), makes the lid-driven cavity a good test bed for Lagrangian transport. The motion of a fluid element is governed by the advection equation
where \(\varvec{X}=(X,Y,Z)\) is the position vector of the fluid element, \(\varvec{u}=(u,v,w)\) the velocity-vector field of the flow, and the dot denotes the material time derivative.
For a two-dimensional flow a stream function \(\psi \) can be defined such that (20) results in
If, moreover, the flow field [u(X, Y), v(X, Y)] is steady the stream function \(\psi (X,Y)\) takes the role of the Hamiltonian of a dynamical system with one degree of freedom; the streamlines represent trajectories in a two-dimensional phase space spanned by X and Y. The integrable motion in the two-sided lid-driven cavity in the Stokes flow limit has been investigated by Kelmanson and Lonsdale [183] who focused on the eddy genesis when changing the aspect ratio. Further studies of the Stokes flow for two-sided driving are due to Gürcan [141].
The transport is more interesting when the driving becomes time-dependent. In this case the phase space is three-dimensional and the system is non-integrable even in the Stokes-flow limit. As a characteristic property, regular (quasi-periodic) trajectories can co-exists with chaotic ones. Ottino et al. [81, 114, 216, 217, 244, 245] were among the first to investigate the mixing properties in closed boundary-driven systems, focusing on creeping flow conditions. The experimental setup of Leong and Ottino [206] consisted of a double-lid-driven cavity with \(\varGamma =1/1.67\) (see Fig. 1b), open in spanwise (z) direction and \(\varLambda \) large so as to render the flow essentially two-dimensional. The moving boundaries were realized by belts that slide parallel or antiparallel to each other. Marking fluid elements along a line parallel to the x axis initially, the tracers are advected by the flow. After a certain period of time they form patterns, examples of which are shown in Figs. 35a–c for constant wall velocities. The line of marked tracers roles up in a regular fashion. When the wall velocities \(U_{1,2}(t)\) become time-dependent a memoryless sequence of creeping flows is realized, due to the instantaneous character of the Stokes flow. The sequence can range among all possible combinations of the two independent belt velocities: single lid motion (Fig. 35a), double anti-parallel motion (Fig. 35b) and double parallel lid motion (Fig. 35c). Even if the flow is a sequence of instantaneous Stokes flows with regular streamlines, assigning a time-dependent protocol to the two lids may result in chaotic advection of fluid elements. The resulting chaotic mixing is quite striking if one considers that the streamlines are defined instantaneously for each time-step and cannot be chaotic since their phase space is two-dimensional.
For a continuous chaotic dynamics the phase space must have at least three dimensions. It is well understood that the trajectory of a fluid element can be chaotic when it is governed by (20) [20]. For the Stokes flow in the two-sided cavity the non-linear equation (20) reduces to a two-dimensional time-dependent dynamical system (three dimensions in phase space) which allows for chaotic mixing, an example of which is shown in Fig. 35d.

Images are taken from [206]
Mixing in a two-dimensional lid-driven cavity. Shown is the evolution of a line of tracers initially located along the x axis (vertical line) for a steady single lid motion, b steady parallel lid motion, c steady opposing lid motion, and d discontinuous opposing lid motion.
The classic kinematic scenario deals with hyperbolic systemsFootnote 4 dominated by the presence of a chaotic saddle, whose chaotic advection stretches and folds the flow at an exponential rate down to the Batchelor scale [30], at which stretching and molecular diffusion balance. However, this picture is typically complicated by the presence of walls, which destroy the hyperbolicity of the system leading to a decrease of the mixing rate from the ideal exponential to a much slower power-law rate. This reduction is caused by the entrainment of unmixed material from the near-wall regions [315]. Hence, apart from the relevance of Ottino’s results in the context of laminar mixing and microfluidics, where chaotic mixing is the only efficient way to achieve a certain large-scale homogeneity of the transported quantity, studying chaotic advection in closed systems is also intended to provide further insight into the mixing properties of non-hyperbolic systems.
Further efforts in studying mixing in periodically-driven two-dimensional cavities were made by Anderson et al. [18] who characterized the mixing properties of the flow by means of numerical simulations including inertial effects. They focused on the role of Kolmogorov–Arnold–Moser (KAM) tori, which constitute non-chaotic mixing regions in the flow, and discovered that an antiparallel motion of the walls is the only motion which enhances mixing. Other investigations employing the two-sided cavity are concerned with particulate flows (e.g. [331]), where the kinematic template of the flow, i.e. the geometry made by all paths of all fluid elements [20], is coupled with the motion of particles. Surprisingly, when the effective viscosity of the mixture depends on the concentration of the particulate phase an increase of the chaotic advection due to the flow kinematics only (neglecting the particulate phase) does not necessarily enhance the overall mixing of the particle-laden flow. The reason is the mixing can be strongly counteracted by shear migration of particles.
The time-periodic double-lid-driven cavity has been extended numerically and experimentally by Anderson et al. [17, 19]. In their experimental study, Anderson et al. [19] allow the two sliding lids to move tangentially in both, the x- and the z-direction. They confirmed their previous findings about periodic points and the associated poor mixing in their vicinity also for three-dimensional time-periodic flows. It is, however, very challenging to conduct a thorough study of mixing in time-dependent three-dimensional cavities. Even stationary flows can represent an intriguing dynamical systems.
As shown by Bajer [26] incompressible steady three-dimensional flows represent piecewise Hamiltonian systems of 1.5 degrees of freedom. Their kinematics requires a three-dimensional phase space. Therefore, incompressible steady three-dimensional flows typically exhibit chaotic transport. Since pathlines and streamlines coincide for three-dimensional steady flows, we discuss the streamline topology in the following.
Regular and chaotic streamlines of the steady flow in a single-lid-driven cube \((\varGamma =\varLambda =1)\) for \(Re=200\). a Poincaré section on the plane \(x=0\) displaying chaotic (gray dots) and regular (black markers) streamlines. Diamonds indicate the closed elliptic point in the Poincaré plane, corresponding to closed streamlines. b Three-dimensional reconstruction of the outermost surfaces of the main KAM torus \(T_1\) (dark grey) and the 7-periodic KAM torus \(T_7\) (light grey), as well as the 4-periodic closed streamline \(L_4\) (line). Since the flow is mirror symmetric with respect to \(z=0\), only half of the cavity is depicted in (a) and (b)

b Three-dimensional reconstruction of the outermost surfaces of the two point-symmetric period-1 KAM tori (from Romanò et al. [277])
Chaotic (gray) and regular streamlines (purple) in a periodic double-lid-driven cavity with period \(\lambda =2.73\) for \(\varGamma =1.7\) and \(Re= 400\). a Poincaré section on the plane at \(x=0\). Diamonds denote elliptic points corresponding to closed streamlines.
Chiang et al. [76, 78, 79] and Sheu and Tsai [297] were among the first to compute streamlines in genuinely three-dimensional cavity flows. They characterized the main vortex, computed streamtubes of the flow, and related these to the critical topological objects along the cavity walls and in the (mirror-symmetry) midplane of the cavity (\(z=0\)). Attention was focused on the separation and reattachment streamlines as well as on the saddle foci on the walls and on the mirror-symmetry plane. Specifically, Sheu and Tsai [297] computed the distribution of degenerate streamlines on the five steady walls in a cubic single-lid-driven cavity for \(Re=400\) (see Fig. 28). They further characterized the degenerate nodes and saddles on the stationary walls by means of second-order terms of the local Taylor expansion of the velocity field. Additional topological analyses of the streamlines in the corner eddies were carried out by Chiang et al. [79] and Shankar and Deshpande [293].
The investigations of Iwatsu et al. [167], Ishii and Iwatsu [163], Ishii and Adachi [160,161,162] and Ishii et al. [164] had a different focus. They characterized the Lagrangian flow topology by means of Poincaré sections of streamlines and identified regular (KAM tori) and chaotic regions of the flow. By means of compact high-order finite differences they simulated the steady three-dimensional flow in cavities with \(\varLambda =6.55\) (the span aspect ratio in the experiments of Kuhlmann et al. [201]) and \(\varGamma =\lbrace 0.5,1,1.5\rbrace \). For \(Re\in [100,500]\) they identified a 3:1 resonance phenomenon of the main KAM torus. Ishii and Adachi [162] characterized the resonance by means of a normal-form Hamiltonian as proposed by Arnold et al. [21]. Similar topological studies were carried out for \(\varLambda =1\), \(\varGamma =\lbrace 0.4,0.6,1,1.4\rbrace \), and for \(Re\in [100,400]\) [164], for which quite complex flow kinematics were found. Figure 36 shows an example for the coexistence of regular and chaotic streamlines in the cubical single-lid-driven cavity for \(Re=200\). The steady flow has been computed, for reasons of demonstration, using the spectral element code NEK5000 with \(20^3\) 7th-order spectral elements. The streamlines were integrated by a Runge–Kutta Dormand–Prince method with relative and absolute error tolerances of \(10^{-7}\). For further mathematical details on chaotic and regular motion and on the resonance phenomenon the reader is referred to the KAM and Poincaré–Birkhoff theorems [55, 72, 73, 227].
The topology of the flow in a periodic double-lid-driven cavity with \(\varGamma =1.7\) (an example is shown in Fig. 37) has recently been investigated by Romanò et al. [277]. For this aspect ratio, spanwise wavelength \(\varLambda =\lambda _c=2.73\) and for \(Re_1=Re_2=Re\in [Re_c,700]\), where \(Re_c=211.53\) is the critical Reynolds number, the three-dimensional flow is steady in form of periodic cuboidal cells (mode E2 of Fig. 20, see also Fig. 19). The three-dimensional cellular flow is robustly point-symmetric with respect to the center of the cell and mirror-symmetric with respect to the periodic cell-boundaries at \(z=\pm \lambda _c/4\). In this flow Lagrangian chaos sets in globally immediately above the linear stability threshold at which the translation symmetry in z is broken. The sudden appearance of global chaos can be traced back to the breakup of the heteroclinic connection between a spiralling-in and a spiralling-out saddle focus in the supercritical flow and to the abundance of saddle foci with chaotic dynamics right above the critical onset. Increasing the Reynolds number, some of the saddle foci vanish and KAM tori are born and expand until \(Re\approx 400\), beyond which increasing inertial effects smoothly drive the system towards kinematically more chaotic flows. Figure 37a shows a Poincaré section of the streamlines at \(x=0\) for \(Re=400\). Gray dots indicate chaotic streamlines, whereas purple dots refer to regular streamlines. The point-symmetric couple of KAM tori, shown in Fig. 37b for \(Re=400\), shrinks for larger Reynolds numbers until, for \(Re\in (500,700)\), a 2:1 resonance occurs, splitting each of the two KAM tori into a period-1 and a period-2 torus, with the period-2 torus winding about the period-1 torus.
9 Turbulent Flow
Motivated by the early experiments of Koseff et al. (see, e.g., Koseff and Street [193]) benchmark computations using different numerical methods and techniques have been carried out for \(\varGamma =3\) and \(Re=3200\) [95] for which the flow is time-dependent and likely chaotic. At that time the editors of Deville et al. [95] stated:
No definite conclusions about the benchmark solutions can be drawn. Indeed, because of the intricate nature of the time and space behaviours, more work remains to be done ...
This clearly rises the question for the flow properties at higher Reynolds numbers at which the three-dimensional flow becomes chaotic and, eventually, turbulent. The transition scenario for three-dimensional flows is quite different from the scenario in flows restricted to two dimensions.
9.1 Two-Dimensional Flow
It is well established that the flow in a cavity restricted to two dimensions becomes time dependent via a Hopf bifurcation near \(Re\approx 8000\) (Sect. 5.1). Owing to the relatively high Reynolds number and the thin boundary layers associated with it, the correct determination of the onset of oscillations requires a very accurate numerical modeling. Therefore, results on the critical data are scattered. If not mentioned otherwise the following results have been obtained for \(\varGamma =1\).

The lid at the top moves to the left and the vortex street travels counter-clockwise (courtesy F. Auteri, see Auteri et al. [23])
Snapshot of the vorticity field (color) of the oscillatory flow at \(Re=8125>1818 = Re_c\), bandpass filtered in the range \(\omega /Re\in [2.6,3.0]\).
The two-dimensional time-dependent critical mode and the slightly supercritical flow arises in form of a vortex street traveling in streamwise direction within a thin layer between the main vortex and the three separated vortices which are characteristic for the basic flow at high Re. A snapshot of the filtered vorticity field [23] is shown in Fig. 38. The vorticity oscillations are relatively weak on the downstream stationary wall and grow to appreciable amplitude only near the bottom wall, being further enhanced along the wall upstream of the moving lid. Along the moving lid the vortices are stretched and damped before being again injected as perturbations in the boundary layer on the downstream wall. This structure of the slightly supercritical flow has been confirmed by other authors and it was also found in a proper orthogonal decomposition of the flow by Cazemier et al. [60]. Recently, Nuriev et al. [242] computed the linear stability boundary \(Re_c\) of the steady basic flow with a resolution of \(512^2\). The extrapolated critical Reynolds number \(Re_c=8051\) and the oscillation frequency on the finest mesh \(\omega /Re=2.79\) are in good agreement with results of Fortin et al. [113] and Sahin and Owens [280]. Hopf bifurcations of the two-dimensional flow have also been found for deep single-lid-driven cavities with \(\varGamma =1.5\) and 2 [44].
Qualitative bifurcation diagram (adapted from Tiesinga et al. [316])
After the first Hopf bifurcation at \(Re_c\), a second Hopf bifurcation was reported by Auteri et al. [23], Bruneau and Saad [57] and Peng et al. [259] to bifurcate from the basic flow at higher Reynolds numbers for \(\varGamma =1\). The second bifurcation was found to arise near \(Re \approx 10^4\), a Reynolds number at which additional incommensurate frequencies appear in nonlinear flow simulations. However, the frequencies found by the above authors scatter, so that no definitive conclusion can be drawn to date. Tiesinga et al. [316] carried out a bifurcation analysis by computing the most dangerous eigenvalues. They find a succession of Hopf bifurcations within a relatively narrow range of Reynolds numbers and calculated the bifurcations by numerical simulations as shown in Fig. 39. Further Hopf bifurcations arise for Reynolds numbers less than \(Re=11000\), at which Verstappen et al. [324], however, found the flow still to be periodic.
The results of Tiesinga et al. [316] (Fig. 39) suggest that, in a certain range of Re, different oscillatory flows are stable. Cazemier et al. [60] also found multiple Hopf bifurcations and investigated their stability using Floquet theory. Transitions between flows with one and two frequencies were found as well as indications for subharmonic response. This is qualitatively similar to the results of Peng et al. [259] who simulated the two-dimensional flow for Reynolds numbers around \(Re=10^4\) using the marker-and-cell method [149] on a uniform grid with resolution \(100^2\). Varying the Reynolds number Re in small steps, the authors find a supercritical Hof bifurcation at \(Re\approx 7400\). The very low value is due to the moderate resolution used. At criticality, the bifurcating flow has a fundamental frequency \(\omega _1/Re\approx 3.7\), roughly consistent with results from other investigations of the first instability. Near \(Re=10300\) Peng et al. [259] found a succession of flows which are quasi-periodic, subharmonic with a fundamental frequency \(\omega _2\) clearly different from \(\omega _1\), harmonic response, and again subharmonic flow, before the flow turns chaotic. The authors conclude that two oscillatory solution branches exist, belonging to the two fundamental frequencies, because hysteresis was observed upon varying Re. The subharmonic flow may seem to suggest the existence of a Feigenbaum sequence [100], however, no further indications of this scenario were provided.
In his simulation for \(Re=10^4\) Bruneau [56] found two other frequencies \(\omega _{2,3}\) which are commensurate to the main frequency \(\omega _1/Re=3.8\) of the first bifurcation. Similar indications were also detected by Auteri et al. [23] and Peng et al. [259], but owing to the delicacy of the results no definitive conclusion can be drawn, presently. Apart from the oscillatory solution bifurcating from the basic flow at the first critical point, Nuriev et al. [242] also computed other nonlinear flows and detected several new steady solutions of the two-dimensional lid-driven cavity flow. All these latter solution are created by fold bifurcations at \(Re\approx 5800,\ 6360,\ 14190\) and 15270, and all bifurcating solutions were found to be unstable. Nevertheless, it is expected that these unstable solutions play an important role in the dynamical behavior of the system.
When the Reynolds number is increased to \(Re=22000\) the flow is chaotic. Verstappen et al. [324] found the correlation dimension of the chaotic attractor to be approximately 2.8 and a Kolmogorov entropy \(K\approx 3\). The underlying coherent flow structures have been investigated by Cazemier et al. [60] using POD. For an even larger Reynolds number of \(Re=10^5\) Bruneau [56] also finds evidence for the existence of a chaotic attractor. This conclusion was drawn based on different initial conditions evolving to the same statistical state for long times, a conclusion also supported by Garcia [117]. Figure 40 shows snapshots of the vorticity field for \(Re=10^5\).

Results were obtained on \(1024\times 1024\) grid points by Bruneau [56]
Vorticity isolines in a square cavity for \(Re=10^5\) (the lid is on top and moves to the left). Shown are snapshots at \(t=10/Re\) (a) and at \(t=200/Re\) (b) after initialization from rest.
9.2 Three-Dimensional Flow
A detailed view of the first steps towards transition to chaos and turbulence in three dimensions has only recently emerged for the one-sided lid-driven flow in a cube \((\varLambda =\varGamma =1)\) (Sect. 7.2). Two subcritical instabilities near \(Re \approx 2000\) lead to a complicated dynamics characterized by intermittency caused by the unstable basic state and two unstable limit cycles.
Observing the lateral dispersion of dye streaks, Koseff and Street [193] experimentally found the flow in a cavity with \(\varLambda =3\) to become turbulent at \(Re = 6000\) to 8000. They also observed intermittent turbulent burst which become frequent at \(Re = 10^4\). Nevertheless, the Taylor–Görtler vortices were found to exist in the mean even at \(Re = 10^4\). From several investigations, the flow at \(Re = 10^4\) may be called turbulent, because multiple scales are involved in the flow dynamics.
A significant step forward in the simulation of turbulent cavity flows was made by Leriche and Gavrilakis [209]. By direct numerical simulation (DNS) they computed the flow in the cube \((\varGamma =\varLambda =1)\) using a spectral Chebychev-collocation method combined with a projection–diffusion method for the time advancement [210]. The corner singularities along all singular edges of the lid were regularized with a polynomial smoothing. This reduces the mean driving velocity to \({\approx }85\%\) of the original singular problem. Therefore, a Reynolds number \(Re = UL/\nu =12000\) corresponds to a mean Reynolds number \(Re_m=U_m L/\nu = 10200\), where \(U_m\) is the mean lid velocity.
The turbulence was found to be strongly inhomogeneous. With the decomposition \(\varvec{u} = \overline{\varvec{u}} + \varvec{u}'\), where the over-bar denotes time averaging, the Reynolds stresses \(\overline{u'_iu'_j}\) were found to be very small below the moving lid. Furthermore, the volume integral of the total kinetic energy (\(E_\mathrm {kin}/Re^2\) in our scaling) fluctuates with a few percent about its mean value of \({\approx }0.055\) with the mean of the fluctuating kinetic energy being \({\approx }0.0045\).

All figures are adapted from Leriche and Gavrilakis [209]
a Isolines of \((\overline{u}^2 + \overline{v}^2 )^{1/2}\) in the plane \(z=0.2135\). b Isolines of the mean streamwise velocity \(\overline{u}\) slightly below the moving wall at \(y=0.4785\). c Isolines of the energy production term \(-2\overline{v' \varvec{u}' \cdot \nabla \overline{v}}\) in a plane \(y=-0.462\) near the bottom of the cavity; full (dashed) lines indicate positive (negative) values. The plus \((+)\) indicates the monitoring point used for conditional averaging. d Conditional averaged flow field in the plane \(x=0.3865\) close to the downstream wall). The mean Reynolds number is \(Re_m = 10200\).
At the Reynolds number \(Re=12000\) considered the flow is turbulent in part of the cavity with the mean amplitudes of the velocity fluctuations and the mean fluctuating kinetic energy being of the order of a few percent of the respective mean values of the total quantities. The mean flow is symmetric with respect to the midplane \(z=0\) and has a three-dimensional structure in the mean, similar as the one found for steady laminar flow at lower Reynolds numbers. The main global circulation is characterized by a sequence of wall jets as illustrated in Fig. 41a. The mean streamwise velocity \(\overline{u}\) immediately below the moving wall has a clear maximum in the midplane with slower regions in both cavity halves (Fig. 41b). Therefore, the wall jet on the downstream wall is thicker away from the midplane \(z=0\) resulting in two elliptical wall jets [51, 144]. The impingement on \(y=-0.5\) of the wall jet along the downstream wall at \(x=0.5\) generates fluctuations \(v'\). The dominant term of the energy production, contributing the most to \(-2\overline{v' \varvec{u}' \cdot \nabla \overline{v}}\) (Fig. 41c), was found to be \(-2\overline{{v'}^2}(\partial \bar{v}/\partial y)\). This term has a well defined maximum close to the bottom wall at \(y=-0.5\). The time history of this production term measured in the point marked with a plus in Fig. 41c shows very sharp peaks (not shown) which are associated with important turbulence-generating events. This point is exactly located at the border between the mean main circulation and the mean separated downstream corner vortex [51]. Setting a threshold \(-\overline{{v'}^2}(\partial \bar{v}/\partial y) = 0.4 Re^3\) (in our scaling), which is about 50% of the average peak height of this production term, and conditionally averaging the flow only when this threshold is exceeded, reveals a particular mean flow during these events which is shown in Fig. 41d. Apparently, the turbulence generating events are associated with a pair of vortices in each cavity half which are located close to the bottom wall \((y=-0.5)\) near the impingement point of the wall jet on the downstream wall. Leriche and Gavrilakis [209] noted that these pairs of vortices are very similar to vortices caused by the instability of the stagnation point flow on a bluff body [135, 186].

Adapted from Bouffanais et al. [51]
Isolines of the r.m.s. values of fluctuating velocity components for \(Re = 12000\) in the midplane \(z=0\) obtained by a spectral-element DNS. a \((\overline{{u'}^2})^{1/2}\) and b \((\overline{{v'}^2})^{1/2}\). The arrow indicates the lid motion.
The distribution of the root-mean-square values of the fluctuating velocity fields \(u'\) and \(v'\) in the midplane \(z=0\) are shown in Fig. 42. It is clearly seen that the fluctuations are strong in the vicinity of the two separated vortices in both bottom corners. The fluctuations are due to the impingement of the sequence of wall jets on the respective downstream walls. This is also confirmed in Fig. 43 which shows, for \(Re=12000\), an isosurface of \(\bar{\delta } := 2\partial ^2 (\overline{u'_i u'_j})/\partial x_i\partial x_j\) which is a measure for the inhomogeneity of the turbulent flow [51]. Figure 43 also shows the inhomogeneity being largest where the wall jets impinge on the walls near the separated corner vortices and even on the upstream side of the moving wall. The average turbulent energy dissipation rate \(\bar{\epsilon }\) exhibits a similar distribution [51, not shown].

Adapted from a spectral-element LES of Bouffanais et al. [51] using a dynamic mixed model (LES-DMM)
Isosurface of \(\bar{\delta } = 2\partial ^2 \left( \overline{u'_i u'_j}\right) /\partial x_i\partial x_j\) for \(Re=12000\) corresponding to 1% of its maximum value. The arrow indicates the lid motion.

Shown are DNS (black) and LES results (grey) [83]
At \(Re=12000\) the logarithm of the power spectral density (PSD) of the velocity field recorded at \((x,y,z)=(0.3937,-0.4694,-0.16855)\) tends to develop a scaling \(\sim f^{-5/3}\), where f is the frequency.
The relatively low Reynolds number for which simulations have been carried out make a deduction of scaling laws for spectra of energy and other quantities difficult. This difficulty is exacerbated by the non-homogeneous nature of the turbulent flow in which the core of the vortex remains laminar at \(Re=12000\) and by the limited record length of the signals. Nevertheless, a K41 scaling seems to emerge [94, 172] as shown in Fig. 44 for the power spectral density of the velocity measured in the impingement region of the downstream wall jets, where the mean turbulence production attains its maximum value.
The results for \(Re=12000\) have been extended by Patel et al. [257, 258] to the case when two facing walls move in opposite directions (as in Fig. 1b). They carried out a large-eddy simulation (LES) using the dynamic Smagorinsky model (for LES using the dynamic mixed model, see Zang et al. [333]). Furthermore, Leriche [208] extended the Reynolds number range to \(Re=22000\) using a Chebyshev Gauss–Lobatto collocation method for the cubic cavity. Other simulations are due to Verstappen et al. [325] for \(Re=10^4\) and Hossain et al. [152] who simulated the lid-driven flow in a cube for \(Re=10^4\) by a lattice Boltzmann method and by LES with focus on the large scale vortical structures and their representation by POD.
10 Extensions
The lid-driven cavity problem has been specialized, by numerous authors, to take into account additional physical effects which modify the recirculating vortex flow or which are affected by it. Since all these studies cannot be treated comprehensively, this section is intended to give a brief overview of the various topics which have been treated. For an in-depth consideration the reader is referred to the original work.
Since the lid-driven cavity problem is a test bed for numerical methods, it has been used to test a whole range of different numerical procedures. Extending the classical global stability approach, Alizard et al. [15] applied a matrix-free method for the global linear stability analysis to cavity flows in multiple-connected subdomains. Several investigations have also been devoted to the application of lattice-Boltzmann methods to the lid-driven-cavity problem [310], also including the motion of suspended particles [279]. Since the lattice-Boltzmann method seems to overpredict the critical Reynolds number for the onset of two-dimensional flow oscillations [214], particular attention should be paid to the implementation of the boundary conditions. Furthermore, Monte Carlo methods have been applied to micro-cavity flows [105] and molecular dynamics [176] as well as smoothed particle hydrodynamics simulations [189] have been employed to compute lid-driven cavity flows.
Among the obvious parameters affecting the flow is the shape of the cavity. Except for cuboidal shapes and variants thereof [124, 197, 335], including stability analyses [90], also triangular cavities have been investigated [103, 212, 256] and global linear stability analyses have been carried out for periodic flow perturbations in cavities with a triangular cross section [1, 129]. Other cavity shapes investigated range from polar or sectorial cavities [116, 121, 142, 334], trapezoidal cavities [36], flow and stability in circular cavities with part of the bounding circle moving [130], and cavities with an arc-shaped moving wall [165]. Furthermore, toroidal cavity flows and their stability have found consideration [154, 155, 304] as well as cylindrical cavities [336]. To the class of geometry effects also belongs the effect of through flow between moving and stationary walls [273]. The through flow affects the structure and multiplicity of three-dimensional flows and the transition to chaotic dynamics [2, 33]. Apart from the two-sided cavity introduced by Chien et al. [81] for mixing studies and by Kuhlmann et al. [201] to study flow stability, also other wall-motion configuration with up to four adjacent walls moving independently have been investigated [35, 59, 327], even though such cavity flows might be difficult to realize experimentally. With relation to short-dwell coating Gürcan [140] considered two-sided cavities in which the stationary walls are replaced by stress-free surfaces (for Stokes flow see also Gaskell et al. [118]). Yet other geometric complications can be introduced by cavities housing interior bodies and/or partitioners [37, 249, 250]. Such baffled cavity geometries are of interest in mixing [170] (see Sect. 8). Stremler and Chen [305] considered Stokes-flow mixing in a cavity whose lid was sectioned into three parts on each of which the tangential velocity was piecewise constant, but time-dependent (see also McIlhany et al. [226]), while Rao et al. [271] investigated the two-dimensional mixing in Stokes flow due to a time-dependent and spatially periodic wall motion in cavities which are infinitely extended in direction of the wall motion.
Another fundamental extension to the classical lid-driven cavity concerns the effect of thermal convection and heat transfer in addition to the mechanical driving. Experiments have been carried out by Koseff and Street [198] for stratified lid-driven cavity flow, where the moving lid on top is heated and the bottom wall is cooled, for Reynolds numbers ranging from \(10^3\) to \(10^4\) and bulk Richardson numbers in the range of 0.08 to 6.5. Their investigation was extended by Cohen et al. [82] who experimentally studied the turbulent flow under a stable thermal stratification in a nearly cubical lid-driven cavity. For strong stratification the turbulence remaind confined to the moving lid and large-scale internal gravity waves were observed in the regions outside of the large-scale vortex. Two-dimensional numerical investigations of mixed buoyancy-lid-driven flow in rectangular cavities are due to Torrance et al. [318], Iwatsu et al. [168] Mohamad and Viskanta [237] and, for slow mixed convection, by Shankar and Nikiforovich [294]. Isaev et al. [159] investigated the transient behavior of the two-dimensional chaotic flow for \(Re=5\times 10^4\) in a stably stratified square cavity using unsteady Reynolds-averaged Navier–Stokes equations (URANS) which were closed by the shear stress transport model (SST). Mixed buoyancy convection was also studied by Mohamad and Viskanta [236, 237], Prasad and Koseff [269], Oztop and Dagtekin [247] Khanafer et al. [188] and Barletta and Nield [28] and, in three dimensions, by Iwatsu and Hyun [166]. Tiwari and Das [317] put the focus on nanofluids and other authors [62, 64, 65, 68, 71] studied the combined effect of mixed-convection heat transfer and cavity shape, including a wavy bottom contour [187]. The combined effect of heat and mass transfer has been considered by Alleborn et al. [16] in the context of a continuous drying process.
The transient evolution of the cavity flow from rest (start-up) has been studied by Tang et al. [307], Guermond et al. [138], Migeon [228], Migeon et al. [230] and Akyuzlu [4]. Their work focused on the temporal evolution of the flow, depending on the terminal Reynolds number. Cavities with an oscillating floor have been investigated by Vogel et al. [326], who considered flow stability and supercritical flow regimes, among which a time-periodic three-dimensional cellular flow was found to exist. Blackburn and Lopez [38] studied the flow stability in a cavity with an oscillating lid by numerical simulation and Floquet theory. For an aspect ratio of \(\varGamma =0.5\) they found three-dimensional short- and longwave synchronous modes as well as a non-synchronous mode which arises through a Neimark–Sacker bifurcation. They continued their investigations with focus on symmetry breaking and the relation of time-dependent cavity flows to periodic laminar vortex shedding in two-dimensional wakes of symmetric bodies [39]. The effect of lid oscillations was also considered in combination with heat transfer in rectangular [66] and triangular cavities [67]. The two-dimensional time-dependent flow due to harmonic anti-phase oscillations of two facing lids of a square cavity was treated by Noor et al. [241].
The lid-driven cavity flow is closely related to shear-driven flow in an open cavity. If, in particular, the lid is replaced by a liquid–gas interface with high surface tension, tangential temperature gradients can create significant shear stresses on the interface by the thermocapillary effect [288]. Thus, keeping the walls at both ends of the interface at constant temperatures the shear stress becomes constant in the limit of low Prandtl numbers. Schimmel et al. [282] has shown there exists a one-to-one relation between the four three-dimensional flow instabilities in the one-sided lid-driven cavity (see Fig. 13) and the ones in a cavity driven by a constant shear stress. The two-dimensional variant of a shear-driven cavity was used by Romanó and Kuhlmann [276] to study the motion of finite-size particles in the vicinity of the shear stress boundary. The situation becomes more complicated when the surface tension is relaxed (weak) or when an interface is absent. Such open cavities have been considered by many different authors, among which Maull and East [225], Rossiter [278] and Rockwell and Naudascher [274] may be mentioned, to name only a few. Experimentally Neary and Stephanoff [239] found three different flow regimes as a result of the interaction of the shear layer, created by the oncoming flow, with the vortex structures in the open cavity. Faure et al. [106, 107] visualized the flow in open cavities and detected small scale (Görtler) vortices which were traced back to a centrifugal flow instability. In compressible open cavities Brés and Colonius [54] found acoustic (Rossiter) as well as hydrodynamic modes of three-dimensional instability by numerical simulation and stability analysis. The flow stability in shear-driven (as opposed to lid-driven) cavities was also considered by Theofilis [311], Theofilis and Colonius [313], de Vicente et al. [91, 92], and by Liu et al. [218]. Further investigations into the nonlinear regime by large eddy simulations (LES) have been carried out by Larchevêque et al. [205].
Another topic of interest is the motion of finite-size particles in driven cavities. While the motion of suspensions of very small particles has received some attention in the context of mixing (see, e.g., Xu and Gilchrist [331]), the motion of a few large particles has not received much attention. This is certainly related to the difficulty of keeping larger particles suspended for a sufficiently long time and the associated strict conditions on the density matching between particles and the liquid. Nevertheless, Tsorng et al. [320, 321] found a curious particle motion in preferred regions of a lid-driven cavity which they attributed to shear migration. Kuhlmann et al. [202], however, found large density-matched particles can be attracted on a very fast time scale to periodic attractors in a steady three-dimensional cavity flow due to a particle–boundary repulsion effect in conjunction with the topological properties of the flow. The particle attraction in their system is too fast to have been caused by particle inertia. Other investigations of particle motion in cavities are due to Sidik and Attarzadeh [298] and Kosinski et al. [199]. Hafizi et al. [146] considered the particle motion in a semi-elliptical cavity, and Idris et al. [156] studied the particle motion in triangular cavities. Since long-time particle trajectories are difficult to compute due to the possibility of error accumulation, it appears that more work is required to arrive at a reliable prediction of the long-term motion of finite-size particles and to better understand the mixing and segregation of those particles.
Among the many other directions to which the lid-driven cavity-flow problem can be extended is the effect of compressibility, in particular, for shear-driven open cavities. Bergamo et al. [34] have shown that compressibility has a stabilizing effect on the two-dimensional instability of lid-driven cavity flow. This was confirmed by Ohmichi and Suzuki [243] who offered an explanation for the stabilization in terms of baroclinic torque and vorticity dilatation. Magnetohydrodynamic convection in lid-driven cavities including heating has been considered by Chatterjee [63], where the magnetic field was oriented normal to the moving wall. Shatrov et al. [295] investigated the three-dimensional instability of the lid-driven cavity flow in a cavity with a square cross section when the magnetic field is aligned parallel to the moving lid. Typically, the magnetic field suppresses the flow instability, but several instability modes were found at Reynolds numbers of the order of \(Re=O(3\times 10^3)\). Furthermore, different material laws are of interest. Non-Newtonian cavity flows have been considered [136], and elastic instabilities in cavity flows were investigated [137, 251,252,253]. Other investigations were devoted to viscoplastic flow [98] and nematic polymers [332], the latter of which exhibit a sea of defects in the orientation field. Also cavity flows of granular media have been subjects of investigation. For instance, Kneib et al. [190] used a discrete-element method (DEM) to study force fluctuations on the walls. Finally, lid-driven cavity flows have been studied in saturated porous media [5, 248], also including a heated insert [246].
Due to the multitude of publications the coverage of the above specialized fields is far from comprehensive. The reader should also be aware of the large body of literature on cavity flows of nanofluids and on cavity flows which combine various forces such as mixed convection, inserts, internal heat sources, non-Newtonian fluids and/or magnetohydrodynamic effects.
11 Conclusions and Perspectives
The lid-driven cavity problem provides a very rich multitude of fundamental fluid mechanics. Owing to its popularity, also for numerical benchmarking, a wealth of results has been obtained. Nevertheless, quite a number of questions are left open and present challenges for future investigations.
The stability and transition scenario in confined systems is still a huge challenge. In particular, the dependence of the flow on the spanwise confinement, given by the span aspect ratio \(\varLambda \), is largely unexplored. Promising approaches to the global stability analysis of three-dimensional flows in confined geometries are due to Gómez et al. [126, 127], who demonstrated the applicability of matrix-free methods to this class of problems.
Another aspect which has recently received increasing attention is the Lagrangian topology and the characterization of the flow kinematics. These flow properties, along with chaotic and regular regions of the flow, determine the mixing properties. Owing to the high accuracy required, corresponding numerical computations are quite expensive for three-dimensional flows. Only in recent years it has become possible to tackle the problem of streamline topology in steady three-dimensional flows [164, 277].
Related to Lagrangian flow structures, the dynamics of finite-size particles is still an open problem. In confined geometries the particle–wall and particle–particle interaction calls for an accurate treatment which can be extremely expensive computationally if fully resolving methods are employed [275, 276].
For both, to unravel the physics and to test computational techniques, benchmarks are indispensable. As computing power grows and numerical techniques develop, classical benchmarks such as the two-dimensional steady cavity flow can only be a first step. Even if two-dimensional Hopf bifurcations cannot be observed experimentally, because three-dimensional instabilities arise at much lower Reynolds numbers, the sequence of Hopf bifurcations in the two-dimensional lid-driven cavity (Sect. 9.1) provides an interesting scenario of transition to turbulence. Therefore, an accurate prediction of two-dimensional cavity flows at \(Re = O(10^4)\), multiple solutions and bifurcation points remain challenging tasks.
Another demanding test case for advanced numerical methods is the three-dimensional flow in a lid-driven cube. It can be expected that many more distinguished solutions of the Navier–Stokes equations exists for \(Re > 2000\) which can be expected to be unstable, but affect the flow dynamics. Moreover, for three-dimensional turbulent cavity flow at \(Re=10^4\) and higher, it would be useful to define a general test case and observables of interest to be monitored. Thus far, the few available investigations for \(Re=12000\) have yielded an acceptable agreement between spectral and LES results [50].
Yet another candidate for benchmarking is the streamline topology in three-dimensional flows. A well-suited test case seems be the steady flow in a cube at an intermediate Reynolds number, say \(Re=300\), for which the locations and periods of closed streamlines could be compared among different numerical approaches.
Finally, previous investigations have shown that the accuracy of numerical calculations of the lid-driven cavity flow clearly benefits from a dedicated treatment of the inherent singularities, e.g. by use of the singularity subtraction method [47]. Therefore, it can be recommended for future investigations to make use of one of the approaches described to handle the discontinuities of the boundary conditions. Based on the above considerations, it can be expected that the lid-driven cavity problem will remain an important paradigmatic system for fluid mechanics research and for numerical fluid mechanics, in particular, in the foreseeable future.
Notes
- 1.
Here the convective scaling with characteristic velocity U is used to facilitate the mathematical analysis.
- 2.
The deep penetration of the wall jet observed experimentally by Pan and Acrivos [254], which is in contradiction with the results for pure two-dimensional single-lid-driven flows (Sect. 5.1), might have been caused by the strong geometric confinement in z of the flow in their experiments with \(L_z=L_y\).
- 3.
Like the elliptic instability, the quadripolar instability is due to a Kelvin-wave resonance, communicated by a quadripolar strain field [8, 102]. Since the resonance condition in the ideal case of a columnar vortex (see e.g. Chandrasekhar [61]) can only be satisfied for asymptotically large wave number k, the critical wave number in the lid-driven cavity flow is quite large: \(k_c\approx 15\) (see Fig. 20).
- 4.
A dynamical system is called hyperbolic in a linear sense when the Jacobian determining the local linearization of the flow admits non-imaginary eigenvalues.
References
Ahmed, M., Kuhlmann, H.C.: Flow instability in triangular lid-driven cavities with wall motion away from a rectangular corner. Fluid Dyn. Res. 44:025501–1–025501–21, 2012
Aidun, C.K., Triantafillopoulos, N.G., Benson, J.D.: Global stability of a lid-driven cavity with throughflow: flow visualization studies. Phys. Fluids A 3, 2081–2091 (1991)
Åkervik, E., Brandt, L., Henningson, D.S., Hopffner, J., Marxen, O., Schlatter, P.: Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102 (2006)
Akyuzlu, K.M.: A numerical and experimental study of laminar unsteady lid-driven cavity flows. In: Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, pp. IMECE2017–70145. ASME (2017)
Al-Amiri, A.M.: Analysis of momentum and energy transfer in a lid-driven cavity filled with a porous medium. Int. J. Heat Mass Transf. 43, 3513–3527 (2000)
Albensoeder, S.: Zweidimensionale Strömungsmuster in zweiseitig angetriebenen Rechteckbehältern mittels eines Finite-Volumen-Verfahrens (in German). Mathesis, Universität Bremen (1999)
Albensoeder, S.: Lineare und nichtlineare Stabilität inkompressibler Strömungen im zweiseitig angetriebenen Rechteckbehälter (in German). Cuvillier, Göttingen (2004)
Albensoeder, S., Kuhlmann, H.C.: Linear stability of rectangular cavity flows driven by anti-parallel motion of two facing walls. J. Fluid Mech. 458, 153–180 (2002)
Albensoeder, S., Kuhlmann, H.C.: Three-dimensional instability of two counter-rotating vortices in a rectangular cavity driven by parallel wall motion. Eur. J. Mech. B/Fluids 21, 307–316 (2002)
Albensoeder, S., Kuhlmann, H.C.: Stability balloon for the double-lid-driven cavity flow. Phys. Fluids 15, 2453–2456 (2003)
Albensoeder, S., Kuhlmann, H.C.: Accurate three-dimensional lid-driven cavity flow. J. Comput. Phys. 206, 536–558 (2005)
Albensoeder, S., Kuhlmann, H.C.: Nonlinear three-dimensional flow in the lid-driven square cavity. J. Fluid Mech. 569, 465–480 (2006)
Albensoeder, S., Kuhlmann, H.C., Rath, H.J.: Three-dimensional centrifugal-flow instabilities in the lid-driven cavity problem. Phys. Fluids 13, 121–135 (2001)
Albensoeder, S., Kuhlmann, H.C., Rath, H.J.: Multiplicity of steady two-dimensional flows in two-sided lid-driven cavities. Theor. Comput. Fluid Dyn. 14, 223–241 (2001)
Alizard, F., Robinet, J.C., Gloerfelt, X.: A domain decomposition matrix-free method for global linear stability. Comput. Fluids 66, 63–84 (2012)
Alleborn, N., Raszillier, H., Durst, F.: Lid-driven cavity with heat and mass transport. Int. J. Heat Mass Transf. 42, 833–853 (1999)
Anderson, P.D., Galaktionov, O.S., Peters, G.W.M., van de Vosse, F.N., Meijer, H.E.H.: Analysis of mixing in three-dimensional time-periodic cavity flows. J. Fluid Mech. 386, 149–166 (1999)
Anderson, P.D., Galaktionov, O.S., Peters, G.W., van de Vosse, F.N., Meijer, H.E.: Chaotic fluid mixing in non-quasi-static time-periodic cavity flows. Int. J. Heat Fluid Flow 21, 176–185 (2000)
Anderson, P.D., Ternet, D., Peters, W.M., Mejer, H.E.H.: Experimental/numerical analysis of chaotic advection in a three-dimensional cavity. Int. Polym. Process. 21, 412–420 (2006)
Aref, H.: Chaotic advection of fluid particles. Philos. Trans. R. Soc. Lond. Ser. A: Phys. Eng. Sci. 333(1631), 273–288 (1990)
Arnold, V.I., Kozlov, V.V., Neishtadt, A.I.: Mathematical Aspects of Classical and Celestial Mechanics. Springer (2007)
Arnoldi, W.E.: The principle of minimized iterations in the solution of the matrix eigenvalue problem. Quart. Appl. Math. 9, 17–29 (1951)
Auteri, F., Parolini, N., Quartapelle, L.: Numerical investigation on the stability of singular driven cavity flow. J. Comput. Phys. 183, 1–25 (2002)
Auteri, F., Quartapelle, L., Vigevano, L.: Accurate \(\omega \)-\(\psi \) spectral solution of the singular driven cavity problem. J. Comput. Phys. 180, 597–615 (2002)
Bagheri, S., Åkervik, E., Brandt, L., Hennignson, D.S.: Matrix-free methods for the stability and control of boundary layers. AIAA J. 47, 1057–1068 (2009)
Bajer, K.: Hamiltonian formulation of the equations of streamlines in three-dimensional steady flow. Chaos Solitons Fractals 4, 895–911 (1994)
Barkley, D., Henderson, R.D.: Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241 (1996)
Barletta, A., Nield, D.A.: Mixed convection with viscous dissipation and pressure work in a lid-driven square enclosure. Int. J. Heat Mass Transf. 52, 42444253 (2009)
Batchelor, G.K.: On steady laminar flow with closed streamlines at large Reynolds numbers. J. Fluid Mech. 1, 177–190 (1956)
Batchelor, G.K.: Small-scale variation of convected quantities like temperature in turbulent fluid part 1. general discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133 (1959)
Bayly, B.J.: Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57, 2160–2163 (1986)
Belhachmi, Z., Bernardi, C., Karageorghis, A.: Spectral element discretization of the circular driven cavity. part iv. the Navier–Stokes equations. J. Math. Fluid Mech. 6, 121–156 (2004)
Benson, J.D., Aidun, C.K.: Transition to unsteady nonperiodic state in a through-flow lid-driven cavity. Phys. Fluids A 4, 2316–2319 (1992)
Bergamo, L.F., Gennaro, E.M., Theofilis, V., Medeiros, M.A.F.: Compressible modes in a square lid-driven cavity. Aerosp. Sci. Technol. 44, 125–134 (2015)
Beya, B.B., Lili, T.: Three-dimensional incompressible flow in a two-sided non-facing lid-driven cubical cavity. Comptes Rendus Mecanique 336, 863–872 (2008)
Bhattacharya, M., Basak, T., Oztop, H.F., Varol, Y.: Mixed convection and role of multiple solutions in lid-driven trapezoidal enclosures. Int. J. Heat Mass Transf. 63, 366–388 (2013)
Billah, M.M., Rahman, M.M., Sharif, U.M., Rahim, N.A., Saidur, R., Hasanuzzaman, M.: Numerical analysis of fluid flow due to mixed convection in a lid-driven cavity having a heated circular hollow cylinder. Int. Commun. Heat Mass Transf. 38, 1093–1103 (2011)
Blackburn, H.M., Lopez, J.M.: The onset of three-dimensional standing and modulated travelling waves in a periodically driven cavity flow. J. Fluid Mech. 497, 289–317 (2003)
Blackburn, H.M., Lopez, J.M.: Modulated waves in a periodically driven annular cavity. J. Fluid Mech. 667, 336–357 (2011)
Blohm, C.: Experimentelle Untersuchung stationärer und zeitabhängiger Strömungen im zweiseitig angetriebenen Rechteckbehälter (in German). Ph.D thesis, University of Bremen (2001)
Blohm, C., Kuhlmann, H.C.: The two-sided lid-driven cavity: experiments on stationary and time-dependent flows. J. Fluid Mech. 450, 67–95 (2002)
Blohm, C., Albensoeder, S., Kuhlmann, H.C., Broda, M., Rath, H.J.: The two-sided lid-driven cavity: Aspect-ratio dependence of the flow stability. Z. Angew. Math. Mech. 81(Suppl. 3), 781–782 (2001)
Bödewadt, U.T.: Die Drehströmung über festem Grunde. Z. Angew. Math. Mech. 20, 241–253 (1940)
Boppana, V.B.L., Gajjar, J.S.B.: Global flow instability in a lid-driven cavity. Int. J. Numer. Methods Fluids 62, 827–853 (2010)
Botella, O.: On the solution of the Navier–Stokes equations using Chebyshev projection schemes with third-order accuracy in time. Comput. Fluids 26, 107–116 (1997)
Botella, O., Peyret, R.: The Chebyshev approximation for the solution of singular Navier–Stokes problems. In: Numerical Modelling in Continuum Mechanics: Proceedings of the 3rd Summer Conference, pp. 8–11. Prague (1997)
Botella, O., Peyret, R.: Benchmark spectral results on the lid-driven cavity flow. Comput. Fluids 27, 421–433 (1998)
Botella, O., Peyret, R.: Computing singular solutions of the Navier–Stokes equations with the Chebyshev-collocation method. Int. J. Numer. Methods Fluids 36, 125–163 (2001)
Botella, O., Forestier, M.Y., Pasquetti, R., Peyret, R., Sabbah, C.: Chebyshev methods for the Navier-Stokes equations: algorithms and applications. Nonlinear Anal. 47, 4157–4168 (2001)
Bouffanais, R., Deville, M.O., Fischer, P.F., Leriche, E., Weill, D.: Large-eddy simulation of the lid-driven cubic cavity flow by the spectral element method. J. Sci. Comput. 27, 151–162 (2006)
Bouffanais, R., Deville, M.O., Leriche, E.: Large-eddy simulation of the flow in a lid-driven cubical cavity. Phys. Fluids 19, 055108–1–055108–20, (2007)
Boyling, J.B.: A rigidity result for biharmonic functions clamped at a corner. Z. Angew. Math. Phys. 46, 289–294 (1995)
Brandt, A., Livne, O.E.: Multigrid Techniques: 1984 Guide with Applications to Fluid Dynamics, Revised edn. SIAM (2011)
Brés, G.A., Colonius, T.: Three-dimensional instabilities in compressible flow over open cavities. J. Fluid Mech. 599, 309–339 (2008)
Broer, H.W., Huitema, G.B., Sevryuk, M.B.: Quasi-Periodic Motions in Families of Dynamical Systems: Order Amidst Chaos. Springer, Berlin (2009)
Bruneau, C.-H.: Direct Numerical Simulation and Analysis of 2D Turbulent Flows, pp. 33–44. Birkhäuser Basel, Basel, (2007)
Bruneau, C.-H., Saad, M.: The 2d lid-driven cavity problem revisited. Comput. Fluids 35, 326–348 (2006)
Burggraf, O.R.: Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 24, 113–151 (1966)
Cadou, J.M., Guevel, Y., Girault, G.: Numerical tools for the stability analysis of 2D flows: application to the two- and four-sided lid-driven cavity. Fluid Dyn. Res. 44, 031403–1–021403–12 (2012)
Cazemier, W., Verstappen, R.W.C.P., Veldman, A.E.P.: Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys. Fluids 10, 1685–1699 (1998)
Chandrasekhar, S.: Hydrodynamic and Hydromagnetic Stability. Oxford University Press, Oxford (1961)
Chang, M.-H., Cheng, C.-H.: Predictions of lid-driven flow and heat convection in an arc-shape cavity. Int. Commun. Heat. Mass Transfer 26, 829–838 (1999)
Chatterjee, D.: MHD mixed convection in a lid-driven cavity including a heated source. Numer. Heat Transf. A 64, 235–254 (2013)
Chen, C.-L., Cheng, C.-H.: Numerical prediction of buoyancy-induced periodic flow pattern and heat transfer in a lid-driven arc-shape cavity. Numer. Heat Transf. A 44, 645–663 (2003)
Chen, C.-L., Cheng, C.-H.: Experimental and numerical study of mixed convection and flow pattern in a lid-driven arc-shape cavity. Heat Mass Transf. 41, 58–66 (2004)
Chen, C.-L., Cheng, C.-H.: Numerical simulation of periodic mixed convective heat transfer in a rectangular cavity with a vibrating lid. Appl. Therm. Eng. 29, 2855–2862 (2009)
Chen, C.-L., Cheng, C.-H.: Numerical study of the effects of lid oscillation on the periodic flow pattern and convection heat transfer in a triangular cavity. Int. Commun. Heat Mass Transf. 36, 590–596 (2009)
Chen, C.-L., Chung, Y.-C., Lee, T.-F.: Experimental and numerical studies on periodic convection flow and heat transfer in a lid-driven arc-shape cavity. Int. Commun. Heat Mass Transf. 39, 1563–1571 (2012)
Chen, K.-T., Tsai, C.-C., Luo, W.-J., Chen, C.-N.: Multiplicity of steady solutions in a two-sided lid-driven cavity with different aspect ratios. Theor. Comput. Fluid Dyn. 27, 767–776 (2013)
Chen, K.-T., Tsai, C.-C., Luo, W.-J., Lu, C.W., Chen, C.H.: Aspect ratio effect on multiple flow solutions in a two-sided parallel motion lid-driven cavity. J. Mech. 31, 153–160 (2015). ISSN 1811-8216
Cheng, C.-H., Chen, C.-L.: Buoyancy-induced periodic flow and heat transfer in lid-driven cavities with different cross-sectional shapes. Int. Commun. Heat Mass Transf. 32, 483–490 (2005)
Cheng, C.-Q., Sun, Y.-S.: Existence of invariant tori in three-dimensional measure-preserving mappings. Celest. Mech. Dyn. Astron. 47, 275–292 (1989)
Cheng, C.-Q., Sun, Y.-S.: Existence of periodically invariant curves in 3-dimensional measure-preserving mappings. Celest. Mech. Dyn. Astron. 47(3), 293–303 (1989)
Cheng, M., Hung, K.C.: Vortex structure of steady flow in a rectangular cavity. Comput. Fluids 35, 1046–1062 (2006)
Chiang, T.P., Sheu, W.H.: Numerical prediction of eddy structure in a shear-driven cavity. Comput. Mech. 20, 379–396 (1997)
Chiang, T.P., Hwang, R.R., Sheu, W.H.: Finite volume analysis of spiral motion in a rectangular lid-driven cavity. Int. J. Numer. Methods Fluids 23, 325–346 (1996)
Chiang, T.P., Hwang, R.R., Sheu, W.H.: On end-wall corner vortices in a lid-driven cavity. J. Fluids Eng. 119, 201–214 (1997)
Chiang, T.P., Sheu, W.H., Hwang, R.R.: Three-dimensional vortex dynamics in a shear-driven rectangular cavity. Int. J. Comput. Fluid Dyn. 8, 201–214 (1997)
Chiang, T.P., Sheu, W.H., Hwang, R.R.: Effect of Reynolds number on the eddy structure in a lid-driven cavity. Int. J. Numer. Methods Fluids 26, 557–579 (1998)
Chicheportiche, J., Merle, X., Gloerfelt, X., Robinet, J.-C.: Direct numerical simulation and global stability analysis of three-dimensional instabilities in a lid-driven cavity. Comptes Rendus Mecanique 336, 586–591 (2008)
Chien, W.-L., Rising, H., Ottino, J.M.: Laminar mixing and chaotic mixing in several cavity flows. J. Fluid Mech. 170, 355–377 (1986)
Cohen, N., Eidelman, A., Elperin, T., Kleeorin, N., Rogachevskii, I.: Sheared stably stratified turbulence and large-scale waves in a lid driven cavity. Phys. Fluids 26, 105106–1–105106–16 (2014)
Courbebaisse, G., Bouffanais, R., Navarro, L., Leriche, E., Deville, M.: Time-scale joint representation of DNS and LES numerical data. Comput. Fluids 43, 38–45 (2011)
Crouzeix, M., Philippe, B., Sadkane, M.: The Davidson method. SIAM J. Sci. Comput. 15, 62–76 (1994)
Davidson, E.R.: The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 87–94 (1975)
Davidson, E.R.: Matrix eigenvector methods. In: Methods in Computational Molecular Physics, pp. 95–113. Springer, Berlin (1983)
Davis, A.M.J., O’Neill, M.E.: Separation in a slow linear shear flow past a cylinder and a plane. J. Fluid Mech. 81, 551–564 (1977)
Davis, A.M.J., Smith, S.G.L.: Three-dimensional corner eddies in Stokes flow. Fluid Dyn. Res 46, 015509–1–015509–8 (2014)
Davis, A.M.J., O’Neill, M.E., Dorrepaal, J.M., Ranger, K.B.: Separation from the surface of two equal spheres in Stokes flow. J. Fluid Mech. 77, 625–644 (1976)
de Vicente, J., Rodríguez, D., Theofilis, V., Valero, E.: Stability analysis in spanwise-periodic double-sided lid-driven cavity flows with complex cross-sectional profiles. Comput. Fluids 43, 143–153 (2011)
de Vicente, J., Basley, J., Meseguer-Garrido, F., Soria, J., Theofilis, V.: Three-dimensional instabilities over a rectangular open cavity: from linear stability analysis to experimentation. J. Fluid Mech. 748, 189–220 (2014)
de Vicente, J., Basley, J., Meseguer-Garrido, F., Soria, J., Theofilis, V.: Three-dimensional instabilities over a rectangular open cavity: from linear stability analysis to experimentation – ERRATUM. J. Fluid Mech. 751, 747–748 (2014)
Dean, W.R., Montagnon, P.E.: On the steady motion of viscous liquid in a corner. Proc. Camb. Philos. Soc. 45, 389–394 (1949)
Deshpande, M.D., Milton, S.G.: Kolmogorov scales in a driven cavity flow. Fluid Dyn. Res. 22, 359–381 (1998)
Deville, M., Lê, T.-H., Morchoisne, Y.: Numerical Simulation of 3-D Incompressible Unsteady Viscous Laminar Flows. Notes on Numerical Fluid Mechanics, vol. 36. Vieweg, Braunschweig (1992)
Ding, Y., Kawahara, M.: Linear stability of incompressible fluid flow in a cavity using finite element method. Int. J. Numer. Methods Fluids 27, 139–157 (1998)
Ding, Y., Kawahara, M.: Three-dimensional linear stability analysis of incompressible viscous flows using the finite element method. Int. J. Numer. Methods Fluids 31, 451–479 (1999)
dos Santos, D.D., Frey, S., Naccache, M.F., de Souza Mendes, P.R.: Numerical approximations for flow of viscoplastic fluids in a lid-driven cavity. J. Non-Newton. Fluid Mech. 166, 667–679 (2011)
Drazin, P.G., Reid, W.H.: Hydrodynamic Stability. Cambridge University Press, Cambridge (1981)
Eckmann, J.-P.: Roads to turbulence in dissipative dynamical systems. Rev. Mod. Phys. 53, 643–654 (1981)
Edwards, W.S., Tuckerman, L.S., Friesner, R.A., Sorensen, D.C.: Krylov methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 110, 82–102 (1994)
Eloy, C., Le Dizès, S.: Stability of the Rankine vortex in a multipolar strain field. Phys. Fluids 13, 660–676 (2001)
Erturk, E., Gokcol, O.: Fine grid numerical solutions of triangular cavity flow. Eur. Phys. J. Appl. Phys. 38, 97–105 (2007)
Erturk, E., Corke, T.C., Gökçöl, C.: Numerical solutions of 2-d steady incompressible driven cavity flow at high Reynolds numbers. Int. J. Numer. Methods Fluids 48, 747–774 (2005)
Eskandari, M., Nourazar, S.S.: On the time relaxed Monte Carlo computations for the lid-driven micro cavity flow. J. Comput. Phys. 343, 355–367 (2017)
Faure, T., Pastur, L., Lusseyran, F., Fraigneau, Y., Bisch, D.: Three-dimensional centrifugal instabilities development inside a parallelepipedic open cavity of various shape. Exp. Fluids 47, 395–410 (2009)
Faure, T.M., Adrianos, P., Lusseyran, F., Pastur, L.: Visualizations of the flow inside an open cavity at medium range Reynolds numbers. Exp. Fluids 42, 169–184 (2007)
Feldman, Y.: Theoretical analysis of three-dimensional bifurcated flow inside a diagonally lid-driven cavity. Theor. Comput. Fluid Dyn. 29, 245–261 (2015)
Feldman, Y., Gelfgat, A.Y.: Oscillatory instability of a three-dimensional lid-driven flow in a cube. Phys. Fluids 22, 093602-1–093602-9 (2010)
Feldman, Y., Gelfgat, A.Y.: From multi- to single-grid CFD on massively parallel computers: numerical experiments on lid-driven flow in a cube using pressure velocity coupled formulation. Comput. Fluids 46, 218–223, (2011)
Fix, G.J., Gulati, S., Wakoff, G.I.: On the use of singular functions with finite element approximations. J. Comput. Phys. 13, 209–228 (1973)
Floryan, J.M., Czechowski, L.: On the numerical treatment of corner singularity in the vorticity field. J. Comput. Phys. 118, 222–228 (1995)
Fortin, A., Jardak, M., Gervais, J., Pierre, R.: Localization of Hopf bifurcation in fluid flow problems. Int. J. Numer. Methods Fluids 24, 1185–1210 (1997)
Franjione, J.G., Leong, C.-W., Ottino, J.M.: Symmetries within chaos: a route to effective mixing. Phys. Fluids A 1, 1772–1783 (1989)
Freitas, C.J., Street, R.L., Findikakis, A.N., Koseff, J.R.: Numerical simulation of three-dimensional flow in a cavity. Int. J. Numer. Methods Fluids 5, 561–575 (1985)
Fuchs, L., Tillmark, N.: Numerical and experimental study of driven flow in a polar cavity. Int. J. Numer. Methods Fluids 5, 311–329 (1985)
Garcia, S.: The lid-driven square cavity flow: From stationary to time periodic and chaotic. Commun. Comput. Phys. 2, 900–932 (2007)
Gaskell, P.H., Gürcan, F., Savage, M.D., Thompson, H.M.: Stokes flow in a double-lid-driven cavity with free surface side walls. Proc. Inst. Mech. Eng. 212, 387–403 (1998)
Gelfgat, A.Y.: Implementation of arbitrary inner product in the global Galerkin method for incompressible Navier–Stokes equations. J. Comput. Phys. 211, 513–530 (2006)
Georgiou, G.C., Olson, L.G., Schultz, W.W., Sagan, S.: A singular finite element for Stokes flow: the stick-slip problem. Int. J. Numer. Methods Fluids 9, 1353–1367 (1989)
Ghia, U., Goyal, R.K.: Laminar incompressible recirculating flow in a driven cavity of polar cross section. ASME J. Fluids Eng. 99, 774–777 (1977)
Ghia, U., Ghia, K.N., Shin, C.T.: High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 48, 387–411 (1982)
Glowinski, R., Guidoboni, G., Pan, T.-W.: Wall-driven incompressible viscous flow in a two-dimensional semi-circular cavity. J. Comput. Phys. 216, 76–91 (2006)
Gogoi, B.B.: Global 2D stability analysis of the cross lid-driven cavity flow with a streamfunction-vorticity approach. Int. J. Comput. Methods Eng. Sci. Mech. 17, 253–273 (2016)
Golub, H.G., van Loan, H.G.: Matrix Computations. Johns Hopkins University Press (1989)
Gómez, F., Paredes, P., Gómez, R., Theofilis, V.: Global stability of cubic and large aspect ratio three-dimensional lid-driven cavities. In: 42nd AIAA Fluid Dynamics Conference and Exhibit, pp. AIAA 2012–3274, New Orleans, Louisiana. AIAA (2012)
Gómez, F., Gómez, R., Theofilis, V.: On three-dimensional global linear instability analysis of flows with standard aerodynamics codes. Aerosp. Sci. Technol. 32, 223–234 (2014)
Gomilko, A.M., Malyuga, V.S., Meleshko, V.V.: On steady Stokes flow in a trihedral rectangular corner. J. Fluid Mech. 476, 159–177 (2003)
González, L.M., Ahmed, M., Kühnen, J., Kuhlmann, H.C., Theofilis, V.: Three-dimensional flow instability in a lid-driven isosceles triangular cavity. J. Fluid Mech. 675, 369–696 (2011)
González, L.M., Ferrer, E., Díaz-Ojeda, H.R.: Onset of three-dimensional flow instabilities in lid-driven circular cavities. Phys. Fluids 29, 064102–1–064102–16 (2017)
Goodier, J.N.: An analogy between the slow motions of a viscous fluid in two dimensions, and systems of plane stress. Lond. Edinb. Dublin Phil. Mag. J. Sci. 17(113), 554–576 (1934)
Goodrich, J.W., Gustafson, K., Halasi, K.: Hopf bifurcation in the driven cavity. J. Comput. Phys. 90, 219–261 (1990)
Görtler, H.: Über eine dreidimensionale Instabilität laminarer Grenzschichten an konkaven Wänden. Nachrichten von der Akademie der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1, 1–26 (1941)
Görtler, H.: On the three-dimensional instability of laminar boundary layers on concave walls. Technical Report 1375, National Advisory Committee for Aeronautics (1954)
Görtler, H.: Dreidimensionale Instabilität der ebenen Staupunktströmung gegenüber wirbelartigen Strörungen, Fünfzig Jahre Grenzschichtforschung, pp. 304–314. Vieweg, Braunschweig (1955)
Grillet, A.M., Yang, B., Khomami, B., Shaqfeh, E.S.G.: Modeling of viscoelastic lid driven cavity flow using finite element simulations. J. Non-Newton. Fluid Mech. 88, 99–131 (1999)
Grillet, A.M., Shaqfeh, E.S.G., Khomami, B.: Observations of elastic instabilities in lid-driven cavity flow. J. Non-Newton. Fluid Mech. 94, 15–35 (2000)
Guermond, J.-L., Migeon, C., Pineau, G., Quartapelle, L.: Start-up flows in a three-dimensional rectangular driven cavity of aspect ratio 1:1:2 at Re \(=\) 1000. J. Fluid Mech. 450, 169–199 (2002)
Gupta, M.M., Manohar, R.P., Noble, B.: Nature of viscous flows near sharp corners. Comput. Fluids 9, 379–388 (1981)
Gürcan, F.: Effect of the Reynolds number on streamline bifurcations in a double-lid-driven cavity with free surfaces. Comput. Fluids 32, 1283–1298 (2003)
Gürcan, F.: Streamline topologies in Stokes flow within lid-driven cavities. Theor. Comput. Fluid. Dyn. 17, 19–30 (2003)
Gürcan, F., Bilgil, H.: Bifurcations and eddy genesis of Stokes flow within a sectorial cavity. Eur. J. Mech. B/Fluids 39, 42–51 (2013)
Gustafson, K., Halasi, K.: Cavity flow dynamics at higher Reynolds number and higher aspect ratio. J. Comput. Phys. 70, 271–283 (1987)
Habisreutinger, M.A., Bouffanais, R., Leriche, E., Deville, M.O.: A coupled approximate deconvolution and dynamic mixed scale model for large-eddy simulation. J. Comput. Phys. 224, 241–266 (2007)
Hackbusch, W.: On the multi-grid method applied to difference equations. Computing 20, 291–306 (1978)
Hafizi, M.Y.M., Idris, M.S., Ammar, N.M.M.: Study on the behavior of particles in high Reynolds number in semi ellipse lid driven cavity. In: Proceedings of the International Multi-Conference of Engineers and Computer Scientists, vol. 2, 2015
Hancock, C., Lewis, E., Moffatt, H.K.: Effects of inertia in forced corner flows. J. Fluid Mech. 112, 315–327 (1981)
Hansen, E.B., Kelmanson, M.A.: An integral equation justification of the boundary conditions of the driven-cavity problem. Comput. Fluids 23, 225–240 (1994)
Harlow, F.H., Welsh, J.E.: Numerical calculation of the time dependent viscous incompressible flow with free surface. Phys. Fluids 8, 2182–2189 (1965)
Hills, C.P., Moffatt, H.K.: Rotary honing: a variant of the Taylor paint-scraper problem. J. Fluid Mech. 418, 119–135 (2000)
Hopf, E.: Bericht der Math.-Phys. Klasse der Sächsischen Akademie der Wissenschaften zu Leipzig, Abzweigung einer periodischen Lösung von einer stationären Lösung eines Differentialsystems. 94, 1–22 (1942)
Hossain, M.S., Bergstrom, D.J., Chen, X.B.: Visualisation and analysis of large-scale vortex structures in three-dimensional turbulent lid-driven cavity flow. J. Turbul. 16, 901–924 (2015)
Huerre, P., Rossi, M.: Hydrodynamic instabilities in open flows. In: Godréche, C., Manneville, P. (eds.), Hydrodynamics and Nonlinear Instabilities, Chapter 2, pp. 81–294. Cambridge University Press, Cambridge (1998)
Humphrey, J., Cushner, J., Sudarsan, R., Al-Shannag, M., Herrero, J., Giralt, F.: Experimental and numerical investigation of the shear-driven flow in a toroid of square cross-section. In: Lindborg, E., Johansson, A., Eaton, J., Humphrey, J., Kasagi, N., Leschziner, M., Sommerfeld, M. (eds) 2nd International Symposium on Turbulence and Shear Flow Phenomena, vol. III, p. 351, Stockholm, Sweden. Royal Institute of Technology (2001)
Humphrey, J.A.C., Cushner, J., Al-Shannag, M., Herrero, J., Giralt, F.: Shear-driven flow in a toroid of square cross section. ASME J. Fluids Eng. 125, 130–137 (2003)
Idris, M.S., Azwadi, C.S.N., Ammar, N.M.M.; Cubic interpolation profile Navier–Stokes numerical scheme for particle flow behaviour in triangular lid driven cavity. In: 4th International Meeting of Advances in Thermofluids (2012)
Inouye, K.: Ecoulement d’un fluide visqueux dans un angle droit. J. de Mécanique 12, 609–628 (1973)
Iooss, G., Joseph, D.D.: Elementary Stability and Bifurcation Theory. Springer (2012)
Isaev, S.A., Baranov, P.A., Sudakov, A.G., Mordynsky, N.A.: Numerical analysis of vortex dynamics and unsteady turbulent heat transfer in lid-driven square cavity. Thermophys. Aeromech. 15, 463–475 (2008)
Ishii, K., Adachi, S.: Numerical analysis of 3d vortical cavity flow. Proc. Appl. Math. Mech. 6, 871–874 (2006)
Ishii, K., Adachi, S.: Transition of streamline patterns in three-dimensional cavity flows. Theor. Appl. Mech. Japan 59, 203–210 (2010)
Ishii, K., Adachi, S.: Dependence on the aspect ratio of streamline patterns in three-dimensional cavity flows. Theor. Appl. Mech. Japan 60, 51–61 (2011)
Ishii, K., Iwatsu, R.: Numerical simulation of the Lagrangian flow structure in a driven cavity. In: Moffatt, H.K., Tsinober, A. (eds.) Topological Fluid Mechanics, pp. 54–63. Cambridge University Press, Cambridge, U.K. (1990)
Ishii, K., Ota, C., Adachi, S.: Streamlines near a closed curve and chaotic streamlines in steady cavity flows. Proc. IUTAM 5, 173–186 (2012)
Ismael, M.A.: Numerical solution of mixed convection in a lid-driven cavity with arc-shaped moving wall. Eng. Comput. 43, 869–891 (2016)
Iwatsu, R., Hyun, J.M.: Three-dimensional driven-cavity flows with a vertical temperature gradient. Intl J. Heat Mass Transf. 38, 3319–3328 (1995)
Iwatsu, R., Ishii, K., Kawamura, T., Kuwahara, K., Hyun, J.M.: Numerical simulation of three-dimensional flow structure in a driven cavity. Fluid Dyn. Res. 5, 173–189 (1989)
Iwatsu, R., Hyun, J.M., Kuwahara, K.: Mixed convection in a driven cavity with a stable vertical temperature gradient. Intl J. Heat Mass Transf. 36, 1601–1608 (1993)
Jana, S.C., Metcalfe, G., Ottino, J.M.: Experimental and numerical studies of mixing in complex Stokes flow: the vortex mixing flow and multicellular cavity flow. J. Fluid Mech. 269, 199–246 (1994)
Jana, S.C., Tjahjadi, M., Ottino, J.M.: Chaotic mixing of viscous fluids by periodic changes in geometry: baffled cavity flow. AIChE J. 40, 1769–1781 (1994)
Jeong, J., Hussain, F.: On the identification of a vortex. J. Fluid Mech. 285, 69–94 (1995)
Jordan, S.A., Ragab, S.A.: On the unsteady and turbulent characteristics of the three-dimensional shear-driven cavity flow. J. Fluids Eng. 116, 439–449 (1994)
Jordi, B.E., Cotter, C.J., Sherwin, S.J.: An adaptive selective frequency damping method. Phys. Fluids 27, 094104–1–094104–8 (2015)
Joseph, D.D.: The convergence of biorthogonal series for biharmonic and Stokes flow edge problems part I. SIAM J. Appl. Math. 33, 337–347 (1977)
Joseph, D.D., Sturges, L.: The convergence of biorthogonal series for biharmonic and Stokes flow edge problems: part II. SIAM J. Appl. Math. 34, 7–26 (1978)
Kandemir, I., Kaya, A.M.: Molecular dynamics simulation of compressible hot/cold moving lid-driven microcavity flow. Microfluid Nanofluid 12, 509–520 (2012)
Kawaguti, M.: Numerical solution of the Navier-Stokes equations for the flow in a two-dimensional cavity. J. Phys. Soc. Jap. 16, 2307–2315 (1961)
Keiller, R.A., Hinch, E.J.: Corner flow of a suspension of rigid rods. J. Non-Newton. Fluid Mech. 40, 323–335 (1991)
Keller, H.B.: Numerical Solution of Bifurcation and Nonlinear Eigenvalue Problems, pp. 359–384. Academic Press, New York (1977)
Kelmanson, M.A.: An integral equation method for the solution of singular slow flow problems. J. Comput. Phys. 51, 139–158 (1983)
Kelmanson, M.A.: Modified integral equation solution of viscous flows near sharp corners. Comput. Fluids 11, 307–324 (1983)
Kelmanson, M.A.: Solution of nonlinear elliptic equations with boundary singularities by an integral equation method. J. Comput. Phys. 56, 244–258 (1984)
Kelmanson, M.A., Lonsdale, B.: Eddy genesis in the double-lid-driven cavity. Q. J. Mech. Appl. Math. 49, 635–655 (1996)
Kelmanson, M.A., Lonsdale, B.: Annihilation of boundary singularities via suitable Green’s functions. Comput. Math. Appl. 29, 1–7 (1995)
Kelvin, Lord: Vibrations of a columnar vortex. Phil. Mag. 10, 155–168 (1880)
Kerstin, J., Wood, R.T.: On the stability of two-dimensional stagnation flow. J. Fluid Mech. 44, 461–479 (1970)
Khanafer, K.: Comparison of flow and heat transfer characteristics in a lid-driven cavity between flexible and modified geometry of a heated bottom wall. Int. J. Heat Mass Transf. 78, 1032–1041 (2014)
Khanafer, K.M., Al-Amiri, A.M., Pop, I.: Numerical simulation of unsteady mixed convection in a driven cavity using an externally excited sliding lid. Eur. J. Mech. B/Fluids 26, 669–687 (2007)
Khorasanizade, S., Sousa, J.M.M.: A detailed study of lid-driven cavity flow at moderate Reynolds numbers using incompressible SPH. Int. J. Numer. Methods Fluids 76, 653–668 (2014)
Kneib, F., Faug, T., Nicolet, G., Eckert, N., Naaim, M., Dufour, F.: Force fluctuations on a wall in interaction with a granular lid-driven cavity flow. Phys. Rev. E 96, 042906–1–042906–15 (2017)
Knoll, D.A., Keyes, D.E.: Jacobian-free Newton-Krylov methods: a survey of approaches and applications. J. Comput. Phys. 193, 357–397 (2004)
Kondratiev, V.A.: Asymptotics of solutions of the Navier-Stokes equation in a neighbourhood of a corner point. Prikl. Math. Mekh. 31, 119–123 (1967)
Koseff, J.R., Street, R.L.: Visualization studies of a shear driven three-dimensional recirculating flow. J. Fluids Eng. 106, 21–29 (1984)
Koseff, J.R., Street, R.L.: On endwall effects in a lid-driven cavity flow. J. Fluids Eng. 106, 385–389 (1984)
Koseff, J.R., Street, R.L.: The lid-driven cavity flow: a synthesis of qualitative and quantitative observations. J. Fluids Eng. 106, 390–398 (1984)
Koseff, J.R., Street, R.L., Gresho, P.M., Upson, C.D., Humphrey, J.A.C., To, W.-M.: A three-dimensional lid-driven cavity flow: Experiment and simulation. In: Taylor, C. (ed) Proceedings of the 3rd International Conference on Numerical Methods in Laminar and Turbulent Flow, pp. 564–581, Swansea. Pineridge Press (1983)
Koseff, J.R., Prasad, A.K., Perng, C., Street, R.L.: Complex cavities: Are two dimensions sufficient for computation? Phys. Fluids A 2, 619–622 (1990)
Koseff, R.J., Street, R.L.: Circulation structure in a stratified cavity flow. J. Hydraul. Eng. 111, 334–354 (1985)
Kosinski, P., Kosinska, A., Hoffmann, A.C.: Simulation of solid particles behaviour in a driven cavity flow. Powder Technol. 191, 327–339 (2009)
Kuhlmann, H.C., Albensoeder, S.: Stability of the steady three-dimensional lid-driven flow in a cube and the supercritical flow dynamics. Phys. Fluids 26, 024104–1–024104–11 (2014)
Kuhlmann, H.C., Wanschura, M., Rath, H.J.: Flow in two-sided lid-driven cavities: non-uniqueness, instabilities, and cellular structures. J. Fluid Mech. 336, 267–299 (1997)
Kuhlmann, H.C., Romanò, F., Wu, H., Albensoeder, S.: Particle-motion attractors due to particle-boundary interaction in incompressible steady three-dimensional flows. In: Ivey, G., Zhou, T., Jones, N., Draper, S. (eds) The 20th Australasian Fluid Mechanics Conference, p. 102, Paper no. 449. Australasian Fluid Mechanics Society (2016)
Lanczos, C.: An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl Bur. Stand. 45, 255–282 (1950)
Landahl, M.T.: Wave breakdown and turbulence. SIAM J. Appl. Math. 28, 735–756 (1975)
Larchevêque, L., Sagaut, P., Lê, T.-H., Comte, P.: Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number. J. Fluid Mech. 516, 265–301 (2004)
Leong, C.W., Ottino, J.M.: Experiments on mixing due to chaotic advection in a cavity. J. Fluid Mech. 209, 463–499 (1989)
Leray, J.: Etude de diverses equations integrales non lineaires et de quelques problemes que pose l’Hydrodynamique. J. Math. Pures et Appl. 12, 1–82 (1933)
Leriche, E.: Direct numerical simulation in a lid-driven cubical cavity at high Reynolds number by a Chebyshev spectral method. J. Sci. Comput. 27, 335–345 (2006)
Leriche, E., Gavrilakis, S.: Direct numerical simulation of the flow in a lid-driven cubical cavity. Phys. Fluids 12, 1363–1376 (2000)
Leriche, E., Labrosse, G.: High-order direct Stokes solvers with or without temporal splitting: numerical investigations of their comparative properties. SIAM J. Sci. Comput. 22, 1386–1410 (2000)
Leriche, E., Labrosse, G.: Are there localized eddies in the trihedral corners of the Stokes eigenmodes in cubical cavity? Comput. Fluids 43, 98–101 (2011)
Li, M., Tang, T.: Steady viscous flow in a triangular cavity by efficient numerical techniques. Comput. Math. Appl. 31, 55–65 (1996)
Liberzon, A., Feldman, Y., Gelfgat, A.Y.: Experimental observation of the steady-oscillatory transition in a cubic lid-driven cavity. Phys. Fluids 23, 084106–1–084106–7 (2011)
Lin, L.-S., Chen, Y.-C., Lin, C.-A.: Multi relaxation time lattice Boltzmann simulations of deep lid driven cavity flows at different aspect ratios. Comp. Fluids 45, 233–240, (2011)
Liu, C.H., Joseph, D.D.: Stokes flow in conical trenches. SIAM J. Appl. Math. 34, 286–296 (1978)
Liu, M., Muzzio, F.J., Peskin, R.L.: Quantification of mixing in aperiodic chaotic flows. Chaos Solitons Fractals 4, 869–893 (1994)
Liu, M., Peskin, R.L., Muzzio, F.J., Leong, C.W.: Structure of the stretching field in chaotic cavity flows. AIChE J. 40, 1273–1286 (1994)
Liu, Q., Gómez, F., Theofilis, V.: Linear instability analysis of incompressible flow over a cuboid cavity. Procedia IUTAM 14, 511–518 (2015)
Loiseau, J.-C.: Analyse de la stabilité globale et de la dynamique d’écoulements tridimensionnels (Dynamics and global stability analyses of three-dimensional flows). PhD thesis, l’École Nationale Supérieur d’Arts et Métiers (2014)
Loiseau, J.C., Robinet, J.C., Leriche, E.: Intermittency and transition to chaos in the cubical lid-driven cavity flow. Fluid Dyn. Res. 061421–1–061421–11 (2016)
Lopez, J.M., Welfert, B.D., Wu, K., Yalim, J.: Transition to complex dynamics in the cubic lid-driven cavity. Phys. Rev. Fluids 2, 074401–1–074401–23 (2017)
Ma, H., Ruth, D.: A new scheme for vorticity computations near a sharp corner. Comput. Fluids 23, 23–38 (1994)
Malhotra, C.P., Weidman, P.D., Davis, A.M.J.: Nested toroidal vortices between concentric cones. J. Fluid Mech. 522, 117–139 (2005)
Marcus, P.S., Tuckerman, L.S.: Simulation of flow between concentric rotating spheres. part 2. transitions. J. Fluid Mech. 185, 31–65 (1987)
Maull, D.J., East, L.F.: Three-dimensional flow in cavities. J. Fluid Mech. 16, 620–632 (1963)
McIlhany, K.L., Mott, D., Oran, E., Wiggins, S.: Optimizing mixing in lid-driven flow designs through predictions from Eulerian indicators. Phys. Fluids 23, 082005–01–082005–13 (2011)
Mezić, I., Wiggins, S.: On the integrability and perturbation of three-dimensional fluid flows with symmetry. J. Nonlinear Sci. 4, 157–194 (1994)
Migeon, C.: Details on the start-up development of the Taylor–Gortler like vortices inside a square-section lid-driven cavity for \(1,000 \le {R}e \le 3,200\). Exp. Fluids 33, 594–602 (2002)
Migeon, C., Texier, A., Pineau, G.: Effects of lid-driven cavity shape on the flow establishment phase. J. Fluids Struct. 14, 469–488 (2000)
Migeon, C., Pineau, G., Texier, A.: Three-dimensionality development inside standard parallelepipedic lid-driven cavities at \({R}e=1000\). J. Fluids Struct. 17, 717–738 (2003)
Moffatt, H.K.: Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18 (1964)
Moffatt, H.K.: Viscous eddies near a sharp corner. Arch. Mech. Stosow. 16, 365–372 (1964)
Moffatt, H.K.: Singularities in Fluid Dynamics and their Resolution, vol. 1973. Lecture Notes in Mathematics, pp. 157–166. Springer, Berlin (2001)
Moffatt, H.K., Duffy, B.R.: Local similarity solutions and their limitations. J. Fluid Mech. 96, 299–313 (1980)
Moffatt, H.K., Mak, V.: Corner singularities in three-dimensional Stokes flow. In: Durban, D., Pearson, J.R.A. (eds) Symposium on non-linear singularities in deformation and flow, pp. 21–26, Netherland. IUTAM, Kluwer Academic Publishers (1999)
Mohamad, A.A., Viskanta, R.: Transient low Prandtl number fluid convection in a lid-driven cavity. Numer. Heat Transf. A 19, 187–205 (1991)
Mohamad, A.A., Viskanta, R.: Flow and heat transfer in a lid-driven cavity filled with a stably stratified fluid. Appl. Math. Model. 19, 465–472 (1995)
Moore, D.W., Saffman, P.G.: The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346, 413–425 (1975)
Neary, M.D., Stephanoff, D.: Shear-layer-driven transition in a rectangular cavity. Phys. Fluids 30, 2936–2946 (1987)
Nobile, E.: Simulation of time-dependent flow in cavities with the additive-correction multigrid method, part I: mathematical formulation. Numer. Heat Transf. B 30, 341–350 (1996)
Noor, D.Z., Kanna, P.R., Chern, M.-J.: Flow and heat transfer in a driven square cavity with double-sided oscillating lids in anti-phase. Int. J. Heat Mass Transf. 52, 3009–3023 (2009)
Nuriev, A.N., Egorov, A.G., Zaitseva, O.N.: Bifurcation analysis of steady-state flows in the lid-driven cavity. Fluid Dyn. Res. 48, 061405-1–061405-15 (2016)
Ohmichi, Y., Suzuki, K.: Compressibility effects on the first global instability mode of the vortex formed in a regularized lid-driven cavity flow. Comput. Fluids 145, 1–7 (2017)
Ottino, J.M., Leong, C.W., Rising, H., Swanson, P.D.: Morphological structures produced by mixing in chaotic flows. Nature 333, 419–425 (1988)
Ottino, J.M., Muzzio, F.J., Tjahjadi, M., Franjione, J.G., Jana, S.C., Kusch, H.A.: Chaos, symmetry, and self-similarity: exploiting order and disorder in mixing processes. Science 257, 754–760 (1992)
Oztop, H.F.: Combined convection heat transfer in a porous lid-driven enclosure due to heater with finite length. Int. Commun. Heat Mass Transf. 33, 772–779 (2006)
Oztop, H.F., Dagtekin, I.: Mixed convection in two-sided lid-driven differentially heated square cavity. Int. J. Heat Mass Transf. 47, 1761–1769 (2004)
Oztop, H.F., Varol, A.: Combined convection in inclined porous lid-driven enclosures with sinusoidal thermal boundary condition on one wall. Prog. Comput. Fluid Dyn. 9, 127–131 (2009)
Oztop, H.F., Zhao, Z., Yu, B.: Fluid flow due to combined convection in lid-driven enclosure having a circular body. Int. J. Heat Fluid Flow 30, 886–901 (2009)
Oztop, H.F., Zhao, Z., Yu, B.: Conduction-combined forced and natural convection in lid-driven enclosures divided by a vertical solid partitionstar, open. Int. Commun. Heat Mass Transf. 36, 661–668 (2009)
Pakdel, P., McKinley, G.H.: Elastic instability and curved streamlines. Phys. Rev. Lett. 77, 2459–2462 (1996)
Pakdel, P., McKinley, G.H.: Cavity flows of elastic liquids: purely elastic instabilities. Phys. Fluids 10, 1058–1070 (1998)
Pakdel, P., Spiegelberg, S.H., McKinley, G.H.: Cavity flows of elastic liquids: two-dimensional flows. Phys. Fluids 9, 3123–3140 (1997)
Pan, F., Acrivos, A.: Steady flows in rectangular cavities. J. Fluid Mech. 28, 643–655 (1967)
Parlett, B.N.: The Symmetric Eigenvalue Problem. Prentice-Hall, Englewood Cliffs, NJ (1980)
Pasquim, B.M., Mariani, V.C.: Solutions for incompressible viscous flow in a triangular cavity using cartesian grid method. Comput. Model. Eng. Sci. 35, 113–132 (2008)
Patel, D.K., Das, M.K.: LES of incompressible turbulent flow inside a cubical cavity driven by two parallel lids moving in opposite direction. Int. J. Heat Mass Transf. 67, 1039–1053 (2013)
Patel, D.K., Das, M.K., Roy, S.: LES of turbulent flow in a cubical cavity with two parallel lids moving in opposite direction. Int. J. Heat Mass Transf. 72, 37–49 (2014)
Peng, Y.-F., Shiau, Y.-H., Hwang, R.R.: Transition in a 2-D lid-driven cavity flow. Comput. Fluids 32, 337–352 (2003)
Peplinski, A., Schlatter, P., Fischer, P.F. Henningson, D.S. Stability tools for the spectral-element code Nek5000: application to jet-in-crossflow. In: Spectral and High Order Methods for Partial Differential Equations-ICOSAHOM 2012, pp. 349–359. Springer, Berlin (2014)
Peplinski, A., Schlatter, P., Henningson, D.S.: Global stability and optimal perturbation for a jet in cross-flow. Eur. J. Mech. B/Fluids 49, 438–447 (2015)
Pierrehumbert, R.T.: Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157–2159 (1986)
Poliashenko, M., Aidun, C.K.: A direct method for computation of simple bifurcations. J. Comput. Phys. 121, 246–260 (1995)
Povitsky, A.: Three-dimensional flow in cavity at yaw. Technical Report NASA/CR-2001-211232, ICASE Report No. 2001–31, ICASE, NASA Langley Research Center, ICASE, Hampton, Virginia (2001)
Povitsky, A.: Three-dimensional flow in cavity at yaw. Nonlinear Analysis 63, e1573–e1584 (2005)
Povitsky, A.: Three-dimensional flow with elevated helicity in driven cavity by parallel walls moving in perpendicular directions. Phys. Fluids 29, 083601-1–083601-11 (2017)
Prandtl, L.: Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In: Verhdlg. III Intern. Math.-Kongr., pp. 484–491, Leipzig. Teubner (1904)
Prasad, A.K., Koseff, J.R.: Reynolds number and end-wall effects on a lid-driven cavity flow. Phys. Fluids A 1, 208–218 (1989)
Prasad, A.K., Koseff, J.R.: Combined forced and natural convection heat transfer in a deep lid-driven cavity flow. Int. J. Heat Fluid Flow 17, 460–467 (1996)
Ramanan, N., Homsy, G.M.: Linear stability of lid-driven cavity flow. Phys. Fluids 6, 2690–2701 (1994)
Rao, P., Duggleby, A., Stremler, M.A.: Mixing analysis in a lid-driven cavity flow at finite Reynolds numbers. ASME J. Fluids Eng. 134, 041203-1–041203-8 (2012)
Rayleigh, L.: On the dynamics of revolving fluids. In: Scientific Papers VI, pp. 447–453. Cambridge University Press, Cambridge (1920)
Riedler, J., Schneider, W.: Viscous flow in corner regions with a moving wall and leakage of fluid. Acta Mech. 48, 95–102 (1983)
Rockwell, D.D., Naudascher, E.E.: Review – self-sustaining oscillations of flow past cavities. ASME J. Fluids Eng. 100, 152–165 (1978)
Romanò, F., Kuhlmann, H.C.: Numerical investigation of the interaction of a finite-size particle with a tangentially moving boundary. Int. J. Heat Fluid Flow 62(Part A), 75–82 (2016)
Romanò, F., Kuhlmann, H.C.: Particle-boundary interaction in a shear-driven cavity flow. Theor. Comput. Fluid Dyn. 31, 427–445 (2017)
Romanò, F., Albensoeder, S., Kuhlmann, H.C.: Topology of three-dimensional steady cellular flow in a two-sided anti-parallel lid-driven cavity. J. Fluid Mech. 826, 302–334 (2017)
Rossiter, J.E.: Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Technical Report 64037, Royal Aircraft Establishment (1964)
Safdari, A., Kim, K.C.: Lattice Boltzmann simulation of solid particles behavior in a three-dimensional lid-driven cavity flow. Comput. Math. Appl. 68, 606–621 (2014)
Sahin, M., Owens, R.G.: A novel fully-implicit finite volume method applied to the lid-driven cavity problem part ii: linear stability analysis. Int. J. Numer. Methods Fluids 42, 79–88 (2003)
Sano, O., Hasimoto, H.: Three-dimensional Moffatt-type eddies due to a Stokeslet in a corner. J. Phys. Soc. Japan 48, 1763–1768 (1980)
Schimmel, F., Albensoeder, S., Kuhlmann, H.: Stability of thermocapillary-driven flow in rectangular cavities. Proc. Appl. Math. Mech. 5, 583–584 (2005)
Schneider, T.M., Gibson, J.F., Lagha, M., Lillo, F.D., Eckhardt, B.: Laminar-turbulent boundary in plane Couette flow. Phys. Rev. E 78, 037301-1–037301-4 (2008)
Schreiber, R., Keller, H.B.: Driven cavity flows by efficient numerical techniques. J. Comput. Phys. 49, 310–333 (1983)
Schultz, W.W., Lee, N.Y., Boyd, J.P.: Chebyshev pseudosprectral method of viscous flows with corner singularities. J. Sci. Comput. 4, 1–24 (1989)
Schumack, M.R., Schultz, W.W., Boyd, J.P.: Spectral method solution of the Stokes equations on nonstaggered grids. J. Comput. Phys. 94, 30–58 (1991)
Scott, J.F.: Moffatt-type flows in a trihedral cone. J. Fluid Mech. 725, 446–461 (2013)
Scriven, L.E., Sternling, C.V.: The Marangoni effects. Nature 187, 186–188 (1960)
Serrin, J.: On the stability of viscous fluid motions. Arch. Ration. Mech. Anal. 3, 1–13 (1959)
Shankar, P.N.: On Stokes flow in a semi-infinite wedge. J. Fluid Mech. 422, 69–90 (2000)
Shankar, P.N.: Moffatt eddies in the cone. J. Fluid Mech. 539, 113–135 (2005)
Shankar, P.N.: Slow Viscous Flows. Imperial College Press, London (2007)
Shankar, P.N., Deshpande, M.D.: Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136 (2000)
Shankar, P.N., Nikiforovich, E.I.: Slow mixed convection in rectangular containers. J. Fluid Mech. 471, 203–217 (2002)
Shatrov, V., Mutschke, G., Gerbeth, G.: Three-dimensional linear stability analysis of lid-driven magnetohydrodynamic cavity flow. Phys. Fluids 15, 2141–2151 (2003)
Shen, J.: Hopf bifurcation of the unsteady regularized driven cavity flow. J. Comput. Phys. 95, 228–245 (1991)
Sheu, T.W.H., Tsai, S.F.: Flow topology in a steady three-dimensional lid-driven cavity. Comput. Fluids 31, 911–934 (2002)
Sidik, N.A.C., Attarzadeh, S.M.R.: An accurate numerical prediction of solid particle fluid flow in a lid-driven cavity. Int. J. Mech. 5, 123–128 (2011)
Siegmann-Hegerfeld, T.: Wirbelinstabilitäten und Musterbildung in geschlossenen Rechteckbehältern mit tangential bewegten Wänden (in German). PhD thesis, TU Wien (2010)
Siegmann-Hegerfeld, T., Albensoeder, S., Kuhlmann, H.C.: Two- and three-dimensional flows in nearly rectangular cavities driven by collinear motion of two facing walls. Exp. Fluids 45, 781–796 (2008)
Siegmann-Hegerfeld, T., Albensoeder, S., Kuhlmann, H.C.: Three-dimensional flow in a lid-driven cavity with width-to-height ratio of 1.6. Exp. Fluids 54, 1526–1–1526–10 (2013)
Sleijpen, G.L.G., van der Vorst, H.A.: A Jacobi–Davidson iteration method for linear eigenvalue problems. SIAM Rev. 42, 267–293 (2000)
Sousa, R., Poole, R., Afonso, A., Pinho, F., Oliveira, P., Morozov, A., Alves, M.: Lid-driven cavity flow of viscoelastic liquids. J. Non-Newton. Fluid Mech. 234, 129–138 (2016)
Spasov, Y., Herrero, J., Grau, F.X., Giralt, F.: Linear stability analysis and numerical calculations of the lid-driven flow in a toroidally shaped cavity. Phys. Fluids 15, 134–146 (2003)
Stremler, M.A., Chen, J.: Generating topological chaos in lid-driven cavity flow. Phys. Fluids 19, 103602-1–103602-6 (2007)
Symm, G.T.: Treatment of Singularities in the Solution of Laplace’s Equation by an Integral Equation Method. National Physical Laboratory, Division of Numerical Analysis and Computing (1973)
Tang, L.Q., Cheng, T., Tsang, T.T.H.: Transient solutions for three-dimensional lid-driven cavity flows by a least-squares finite element method. Int. J. Numer. Methods Fluids 21, 413–432 (1995)
Taylor, G.I.: Similarity solutions of hydrodynamic problems. In: Aeronautics and Astronautics (Durand Anniversary Volume), pp. 21–28. Pergamon (1960)
Taylor, G.I.: On scraping viscous fluid from a plane surface. In: Batchelor, G.K (ed), The Scientific Papers of Sir Geoffrey Ingram Taylor (1962)
Teixeira, C.M.: Digital physics simulations of lid-driven cavity flow. Int. J. Mod. Phys. C 8, 685–696 (1997)
Theofilis, V.: Globally unstable basic flows in open cavities. In: 6th AIAA/CEAS Aeroacoustics Conference, pp. AIAA 2000–1965, Reston, VA. AIAA (2000)
Theofilis, V.: Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352 (2011)
Theofilis, V., Colonius, T.: An algorithm for the recovery of 2- and 3-D BiGlobal instabilities of compressible flow over 2-D open cavities. In: 33rd Fluid Dynamics Conference and Exhibit, vol. 39, pp. AIAA 2003–4143, Reston, VA. AIAA (2003)
Theofilis, V., Duck, P.W., Owen, J.: Viscous linear stability analysis of rectangular duct and cavity flows. J. Fluid Mech. 505, 249–286 (2004)
Thiffeault, J.-L., Gouillart, E., Dauchot, O.: Moving walls accelerate mixing. Phys. Rev. E 84, 036313-1–036313-8 (2011)
Tiesinga, G., Wubs, F.W., Veldman, A.E.P.: Bifurcation analysis of incompressible flow in a driven cavity by the Newton-Picard method. J. Comput. Appl. Math. 140, 751–772 (2002)
Tiwari, R.K., Das, M.K.: Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Intl J. Heat Mass Transf. 50, 2002–2018 (2007)
Torrance, K., Davis, R., Eike, K., Gill, P., Gutman, D., Hsui, A., Lyons, S., Zien, H.: Cavity flows driven by buoyancy and shear. J. Fluid Mech. 51, 221–231 (1972)
Tranter, C.J.: The use of the Mellin transform in finding the stress distribution in an infinite wedge. Q. J. Mech. Appl. Math. 1, 125–130 (1948)
Tsorng, S.J., Capart, H., Lai, J.S., Young, D.L.: Three-dimensional tracking of the long time trajectories of suspended particles in a lid-driven cavity flow. Exp. Fluids 40, 314–328 (2006)
Tsorng, S.J., Capart, H., Lo, D.C., Lai, J.S., Young, D.L.: Behaviour of macroscopic rigid spheres in lid-driven cavity flow. Int. J. Multiph. Flow 34, 76–101 (2008)
van Lenthe, J.H., Pulay, P.: A space-saving modification of Davidson’s eigenvector algorithm. J. Comput. Chem. 11, 1164–1168 (1990)
Vandeven, H.: Family of spectral filters for discontinous problems. J. Sci. Comput. 6, 159–192 (1991)
Verstappen, R., Wissink, J.G., Veldman, A.E.E.: Direct numerical simulation of driven cavity flows. Appl. Sci. Res. 51, 377–381 (1993)
Verstappen, R., Wissink, J.G., Cazemier, W., Veldman, A.E.P.: Direct numerical simulations of turbulent flow in a driven cavity. Future Gener. Comput. Syst. 10, 345–350 (1994)
Vogel, M.J., Hirsa, A.H., Lopez, J.M.: Spatio-temporal dynamics of a periodically driven cavity flow. J. Fluid Mech. 478, 197–226 (2003)
Wahba, E.M.: Multiplicity of states for two-sided and four-sided lid driven cavity flows. Comput. Fluids 38, 247–253 (2009)
Wakiya, S.: Axisymmetric flow of a viscous fluid near the vertex of a body. J. Fluid Mech. 78, 737–747 (1976)
Waleffe, F.: On the three-dimensional instability of strained vortices. Phys. Fluids A 2, 76–80 (1990)
Wesseling, P.: A Robust and Efficient Multigrid Method, vol. 960, pp. 614–630. Springer, Berlin (1982)
Xu, B., Gilchrist, J.F.: Shear migration and chaotic mixing of particle suspensions in a time-periodic lid-driven cavity. Phys. Fluids 22, 053301-1–053301-7 (2010)
Yang, X., Forest, M.G., Mullins, W., Wang, Q.: 2-D lid-driven cavity flow of nematic polymers: an unsteady sea of defects. Soft Matter 6, 1138–1156 (2010)
Zang, Y., Street, R.L., Koseff, J.R.: A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows. Phys. Fluids A 5, 3186–3196 (1993)
Zang, Y., Street, R.L., Koseff, J.R.: A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33 (1994)
Zhou, Y.C., Patnaik, B.S.V., Wan, D.C., Wei, G.W.: DSC solution for flow in a staggered double lid driven cavity. Int. J. Numer. Methods Eng. 57, 211–234 (2003)
Znaien, J., Speetjens, M.F.M., Trieling, R.R., Clercx, H.J.H.: Observability of periodic lines in three-dimensional lid-driven cylindrical cavity flows. Phys. Rev. E 85, 066320–1–066320–14 (2012)
Acknowledgements
We are very grateful to S. Albensoeder, F. Auteri, O. Botella, R. Bouffanais, C.-H. Bruneau, G. Courbebaisse, J. R. Koseff, E. Leriche, J.-C. Loiseau, J. M. Lopez, H. K. Moffatt, J. M. Ottino, A. Povitsky, W. W. Schultz, J. F. Scott and T. W. H. Sheu, who kindly allowed the reproduction of their figures which have been published earlier.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Kuhlmann, H.C., Romanò, F. (2019). The Lid-Driven Cavity. In: Gelfgat, A. (eds) Computational Modelling of Bifurcations and Instabilities in Fluid Dynamics. Computational Methods in Applied Sciences, vol 50. Springer, Cham. https://doi.org/10.1007/978-3-319-91494-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-91494-7_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-91493-0
Online ISBN: 978-3-319-91494-7
eBook Packages: EngineeringEngineering (R0)