Experimental and numerical study of mixed convection and flow pattern in a lid-driven arc-shape cavity

Abstract

Experimental and numerical study has been performed to investigate the combined effects of lid movement and buoyancy on flow and heat transfer characteristics for the mixed convective flow inside a lid-driven arc-shape cavity. The numerical methodology is based on a numerical grid generation scheme that maps the complex cross section onto a rectangular computation domain. The discretization procedure for the governing equations is based on the finite-volume method. In experiments, steady-state temperature data are measured by T-type thermocouples, and the flow field is visualized by using kerosene smoke. Reynolds number and Grashof number are two major independent parameters representing the effects of lid movement and buoyancy, respectively. Flow pattern, friction factor, and Nusselt numbers are investigated in wide ranges of these independent parameters. Close agreement in the comparison between the predicted and the visualized flow patterns shows the validity of the numerical methods.

1 Introduction

Lid-driven flows in cavities have been interesting topics due to their fundamental natures and relevance to a variety of engineering applications. Examples of such applications can be traced to oil extraction in the grooved wet clutches [1–3], solar collectors [4, 5] and enhancement for thermal performance of heat exchangers [6]. For the related problems, a simple rectangular geometry is often considered for analyzing the momentum and energy transport phenomena inside the cavity. The flow is driven by a moving top wall, and the heat transfer takes place due to a temperature gradient between the top and bottom walls.

An earlier paper of Ghia et al. [7] was devoted to two-dimensional flows in such a rectangular cavity. In the paper, steady two-dimensional solutions were presented and clearly indicated one or more secondary vortices in the flow field at high Reynolds number (Re). However, experimental information was not provided in this paper. A recent study by Prasad and Koseff [8] performed experimental investigation of mixed convection laminar flows inside the two-dimensional rectangular cavities. It was found that the shear flow induced by the moving lid leads to a major vortex flow in the cavity. On the other hand, a buoyancy-driven plume is produced by heating the bottom wall or cooling the top moving lid. This problem of flow driven by a combined effect of a moving lid and the buoyancy has received great attention since the buoyancy may have profound influence on the flow pattern and result in a significant change in the thermal performance in the cavity. However, it appears that only the cavity with a rectangular geometry has been studied thoroughly, and a comprehensive understanding of the flow and heat transfer mechanism in a complex-shape cavity is relatively lacking. In real devices, for example, a wet clutch with lubrication grooves, the cross section shape of the grooves is usually not a perfect rectangle but an arc-shape or other complex areas in accordance with different requirements. These engineering applications lead to the necessity of further study of the flows in the lid-driven complex-shape cavities.

In a recent report, Chen and Cheng [9] presented experimental and numerical information for the natural convection heat transfer in an arc-shape enclosure. Results presented in the report showed that the features of the arc-shape cavity flows are rather different from the rectangular cavity flows. However, the attention of this report was merely focused on the buoyant flows with a stationary lid, and hence the lid movement effects were not investigated.

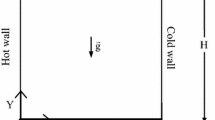
In these circumstances, the present work is aimed at the mixed effects of the lid movement and the buoyancy on flow and heat convection characteristics inside an arc-shape cavity. Both the experimental and the numerical methods are used, and a comparison between the numerical and the experimental data is made for validation. The physical model considered in the investigation is shown in Fig. 1. An arc-shape cavity of height H and width L is placed horizontally. The geometry is essentially two-dimensional since the length of the cavity is in general sufficiently long. A top flat lid maintained at temperature ΔT_L is moving from left to right at a constant speed u₀. The bottom arc-shape wall is heated such that its temperature is fixed at a higher temperature T_H. In this study, the arc-shape wall is part of the profile of a circle according to (x−p)²+(y−q)²=D²/4 with a center located at (p, q) in the Cartesian coordinate. The speed of moving lid (u₀) is a variable in this study. The Re denoting a dimensionless parameter in terms of the lid speed is varied between 100 and 1,500. The temperature difference between the moving lid and the arc-shape wall (T=T_H−T_L) leads to the buoyancy effects. In this study, the Grashof number in terms of the temperature difference ranges from 0 to 10⁷ . Prandtl number (Pr) is assigned to be 0.71 for air herein.

Fig. 1

Schematic of an arc-shape cavity with moving lid.

2 Experimental apparatus

Schematic and dimensions of the tested cavity and the flow visualization apparatus used in this study are shown in Fig. 2. The tested cavity is 63.2 mm wide, 18.5 mm high, and 165 mm long. A polished copper pipe with a thickness of 1.7 mm is properly cut into two parts, and then the smaller part is selected to form the arc-shape bottom wall of the tested cavity. The moving lid is made of a 1.48-mm thick rolling plastic sheet, which is mounted on and driven by two slippery wheels. The driving system of the rolling plastic sheet involves a variable-speed motor, which is connected to one of the slippery wheels through a belt. During operation, the rolling-sheet-and-slippery-wheel assembly is lowered till the rolling sheet covers the arc-shape bottom wall to be the top flat lid. The speed of the top flat lid is dependent on the rotational speed of the motor, which is adjusted to a value of interest prior to the experiment. The uncertainty of the rotational speed of motor is less than 0.58% in the present study. The arc-shape bottom wall is heated by using an electric heater until a sufficiently high steady temperature is reached. The electric heater is designed to comply with the profile of the bottom wall. Temperature of the arc-shape bottom wall is fixed at a constant value by a thermostat connected to the electric heater. In this design, around 75% of the thin moving lid is actually located outside the test section and is cooled by the ambient air. Thus, the lid temperature is maintained at low but constant temperature in experiment. Temperatures of the bottom and the moving lid walls (T_H and T_L) are measured by using four T-type thermocouples and the data are recorded by a data acquisition system for later analysis.

Fig. 2

Flow visualization apparatus. a Dimensions of tested cavity, b Layout of experimental system.

Nowadays, a number of methods have been developed for flow visualization. Smoke method is one of the most widely used techniques for air visualization [10]. In this study, kerosene vapor is produced from liquid kerosene by heating and the kerosene smoke is fed into the cavity through a smoke rake placed beneath the arc-shape bottom wall. The photographs of the visualized flow patterns by smoke lines are taken by using a digital camera and the required lighting is provided by a light unit installed outside the test section. In the experiment, all the properties of the fluid are evaluated at the film temperature.

3 Theoretical analysis

3.1 Governing equations and boundary conditions

The flow and temperature fields are assumed to be two-dimensional and laminar, and the fluid is with constant properties. However, the variation of density in the buoyancy term of the momentum equation is treated by the Boussinesq approximation. Thus, the continuity, momentum and energy equations governing the flow in a cavity are expressed in terms of the Cartesian coordinate as

$$ u_x + v_y = 0 $$

(1)

$$ uu_x + vu_y = - \frac{1} {\rho }p_x + \nu \left( {u_{xx} + u_{yy} } \right) $$

(2)

$$ uv_x + vv_y = - \frac{1} {\rho }p_y + \nu \left( {v_{xx} + v_{yy} } \right) $$

(3)

$$ uT_x + vT_y = \alpha \left( {T_{xx} + T_{yy} } \right) $$

(4)

The stream function-vorticity method is adopted in the study to solve these above equations. The problem is formulated based on a curvilinear coordinate (ξ, η) in term of the vorticity (ω) and stream function (ψ), which are defined as

$$ \omega = v_x - u_y = (\xi _x v_\xi + \eta _x v_\eta ) - (\xi _y u_\xi + \eta _y u_\eta ) $$

(5a)

and

$$ u = \psi _y = \xi _y \psi _\xi + \eta _y \psi _\eta $$

(5b)

$$ v = - \psi _x = - (\xi _x \psi _\xi + \eta _x \psi _\eta ) $$

(5c)

respectively. Meanwhile, the equations have been transformed into dimensionless form by using the following dimensionless quantities:

$$ X = \frac{x} {L},{\enspace} Y = \frac{y} {L},{\enspace} U = \frac{u} {{u_0 }},{\enspace} V = \frac{v} {{u_0 }},{\enspace} \Psi = \frac{\psi } {{u_0 L}},{\enspace} \Omega = \frac{{\omega L}} {{u_0 }},{\enspace} \theta = \frac{{T - T_{\text{L}} }} {{T_{\text{H}} - T_{\text{L}} }}. $$

(6)

Eventually, one obtains the dimensionless governing equations expressed in the stream function-vorticity formulation as

$$ a\Psi _{\eta \eta } - 2b\Psi _{\xi \eta } + c\Psi _{\xi \xi } = - J\Omega $$

(7)

$$ \Psi _\eta \Omega _\xi - \Psi _\xi \Omega _\eta = \frac{{a\Omega _{\eta \eta } - 2b\Omega _{\xi \eta } + c\Omega _{\xi \xi } }} {{J\operatorname{Re} }} + \frac{{Y_\eta \theta _\xi - Y_\xi \theta _\eta }} {{{\text{Gr}}/\operatorname{Re} ^2 }} $$

(8)

$$ \Psi _\eta \theta _\xi - \Psi _\xi \theta _\eta = \frac{{a\theta _{\eta \eta } - 2b\theta _{\xi \eta } + c\theta _{\xi \xi } }} {{J\Pr \operatorname{Re} }} $$

(9)

where a=X ²_η +Y ²_η , b=X_ξX_η+Y_ηY_ξ, c=X ²_ξ +Y ²_ξ , and J=X_ηY_ξ−X_ξY_η.

The dimensionless parameters appearing in the above equations include:

$$ (1)\;{\text{Reynolds}}\;{\text{number:}}\quad \operatorname{Re} = \frac{{u_{0} L}} {\nu } $$

(10)

$$ (2)\;{\text{Grashof}}\;{\text{number:}}\quad {\text{Gr}} = \frac{{g\beta (T_{{\text{H}}} - T_{{\text{L}}} )L^{3} }} {{\nu ^{2} }} $$

(11)

$$ (3)\;{\text{Prandtl}}\;{\text{number:}}\quad \Pr = \frac{\nu } {\alpha } $$

(12)

The boundary conditions for the present problem are given by

$$ {\text{On}}\;{\text{the}}\;{\text{moving}}\;{\text{lid :}}\;U = 1,{\enspace} V = 0,{\enspace} \theta = 0,{\enspace} \Psi = 0,{\enspace} \Omega = - \frac{{X_\xi U_\eta }} {J} $$

(13)

$$ {\text{On}}\;{\text{the}}\;{\text{arc-shape}}\;{\text{wall :}}\;U = 0,{\enspace} V = 0,{\enspace} \theta = 1,{\enspace} \Psi = 0,{\enspace} \Omega = - \frac{{Y_\xi V_\eta - X_\xi U_\eta }} {J} $$

(14)

The governing Eqs.7, 8 and 9, and the boundary conditions, Eqs.13 and 14, are solved by adopting a numerical scheme based on the numerical grid generation scheme and the finite-volume method, which have been described earlier by Chen and Cheng [9]. Further information is available in Ref. [9] and hence will not be provided herein to save space.

4 Results and discussion

4.1 Comparison between experimental and numerical results

Agreement between the numerical predictions and the experimental data is displayed in Table 1 by showing the predicted flow patterns and the flow visualization photographs. The flow visualization photographs are given in the right column of this table, and the numerical predictions are also provided. Based on the numerical predictions, it is observed that for the case at Re=0 and Gr=10⁶ (case 1), two symmetric buoyancy-induced vortices, which are of equal strength while rotating in the opposite directions, occupy the space of the cavity. Apparently, this is referred to a buoyancy-dominated situation since for this case there is no inertial effect. However, as the Re is changed to be 500, only one clockwise vortex prevails in the cavity, and this indicates an inertia-dominated situation. When the value of Re is elevated to be 1,000 while the value of Gr is reduced to zero (case 5), another small counter-clockwise vortex appears adjacent to the bottom wall. All these phenomena predicted by the numerical scheme have been clearly observed by the flow visualization method. Fluid velocity and the strength of the vortex cannot be provided simply based on the photographs of flow visualization. However, inspite of this, the agreement between the numerical and the experimental results is fairly good. Note that in experiments, the Re and the Grashof number are independently adjusted by changing the rotational speed of the motor and the temperature of the arc-shape bottom wall, respectively.

Table 1 Comparisons between experimental and numerical results

According to the experimental information gathered by using the flow visualization apparatus, the flow remains two-dimensional considered in the present study and the three-dimensional effects, such as Taylor-Görtler vortex, are not observed in the ranges of Gr and Re. This may be attributed to the fact that for the cases considered in this study the Grashof and the Reyn olds numbers are relatively low to prevent the three-dimensional effects. Unfortunately, owing to the capacity limit of the experimental system, no experimental observation is performed at a higher Grashof or Re. Further experimental studies are definitely required to clarify the possible three-dimensional unstable flow behavior for a case at higher parameters.

4.2 Flow and thermal fields

Numerical results of flow fields and temperature distributions for various cases are provided in the section. Meanwhile, data of maximum and minimum stream functions are shown in the flow-field plots for a quantitative comparison.

Figure 3 shows the effects of Grashof number on the flow pattern and temperature distribution at Re=1,000. For the case at Gr=0, an inertia-dominated flow pattern with a major clockwise vortex prevailing in the cavity as well as a small counter-clockwise vortex adjacent to the left bottom wall is observed. However, an increase in the Grashof number may cause a significant change in the flow and thermal fields. For example, for the Grashof number ranging between 10⁶ and 5×10⁶, the major vortex is still observed while the small vortex is no longer found. When the value of Gr is further elevated to 10⁷, another counter-clockwise vortex is found in the right bottom area of the cavity. This vortex is expected to grow with Gr toward a full development of the buoyancy-dominated situation. On the other hand, based on the isotherms shown in Fig. 3, it is found that the fluid driven by the moving lid impinges the right corner and resumes the wall temperature in the neighboring area. The fluid motion produces a convective region, which may be identified with a lower local temperature gradient. Extent and strength of the convective region may increase with the Grashof number. At Gr=10⁷, the flow pattern features two vortices which result in two respective convective areas in the cavity. Also note that a higher temperature gradient indicates a higher heat transfer rate. Therefore, based on the density distribution of the isotherms adjacent to the walls, the higher-heat-transfer-rate regions on the walls may be located.

Fig. 3

Effects of Gr on the flow pattern and temperature distribution at Re=1,000.

Effects of Reynolds number on the flow pattern at Gr=0 and 10⁷ are shown in Fig. 4. Note that the case at Gr=0 is referred to a pure inertia-dominated situation. In this situation, a single lid-driven clockwise vortex is expected in the cavity. As the Re is further increased, another counter-clockwise vortex appears adjacent to the bottom wall. The strength and extent of the counter-clockwise vortex grow with the Re. In addition, the transition of the flow pattern from a buoyancy-dominated to an inertia-dominated situation is observed based on the plots given in the right portion of Fig. 4. The case at Gr=10⁷ and Re=100 exhibits a flow pattern very close to the buoyancy-dominated situation, in which two symmetric vortices of equal strength are seen. As the value of Re is elevated toward 1,500 while Gr is fixed at 10⁷, the counter-clockwise vortex grows but the clockwise vortex vanishes. Eventually, an inertia-dominated situation with a clockwise vortex prevailing in the cavity is developed.

Fig. 4

Effects of Re on the flow pattern at Gr=0 and 10⁷.

4.3 Heat transfer performance

The solutions for temperature and velocity distributions enable the heat transfer rate and the friction factor to be further evaluated. Local Nusselt number (Nu _x ) on the moving lid wall is defined by

$$ {\text{Nu}}_x = \frac{{h_x L}} {k} = \left. {\frac{L} {{T_{\text{H}} - T_{\text{L}} }}\frac{{\partial T}} {{\partial y}}} \right|_{{\text{moving lid}}} $$

(15)

where h _x is the local heat transfer coefficient defined by

$$ h_x (T_{\text{H}} - T_{\text{L}} ) = \left. {k\frac{{\partial T}} {{\partial y}}} \right|_{{\text{moving lid}}} $$

(16)

Based on the results of the Nu _x , the average Nusselt number (Nu) on the moving lid wall can then be evaluated by integration as

$$ {\text{Nu}} = \frac{{\bar hL}} {k} = \int\limits_0^1 {{\text{Nu}}_x {\text{d}}X} $$

(17)

where the average heat transfer coefficient $\bar h$ is given by

$$ \bar h = \frac{1} {L}\int\limits_0^L {h_x {\text{d}}X} $$

(18)

Note that the magnitude of the Nu represents the overall heat transfer performance between the top and the bottom walls. On the other hand, local friction factor on the moving lid is defined in terms of the local shear stress on the wall surface as

$$ f_x = \frac{{\tau _x }} {{\rho u_0 ^2 }} = \left. {\frac{\mu } {{\rho u_0 ^2 }}\frac{{\partial u}} {{\partial y}}} \right|_{{\text{moving lid}}} = \left. {\frac{1} {{\operatorname{Re} }}\frac{{X_\xi }} {J}U_\eta } \right|_{{\text{moving lid}}} $$

(19)

Distributions of Nu _x on the moving lid for various Grashof numbers are plotted in Fig. 5. In Fig. 5a, b, the values of Re are fixed at 100 and 1,000, respectively. It has been recognized that a smaller Re leads to a buoyancy-dominated situation, which features a two-symmetric-vortex flow pattern. Therefore, it is expected that at Re=100, the distribution of Nu _x may be more symmetric than that at Re=1,000. The results presented in Fig. 5a reflect this expectation. In general, the magnitude of local Nuincreases with Gr. However, it is interesting to find that for Gr≤10⁵, the local heat transfer rate can be approximated with the pure forced convection data at Gr=0. It is only for Gr≥10⁶ that the local heat transfer rate is appreciably enhanced by the buoyancy. At Re=1,000, the Nu at the left corner of the arc-shape cavity is obviously higher than that at the right corner. This is probably attributed to the fact that at the left corner the buoyancy provides a buoyancy-assisted plume resulting in an increase in local heat transfer. On the contrast, at the right corner a buoyancy-opposed nature of the local flow leads to a reduction of the local heat transfer.

Fig. 5

Distribution of Nu _x on the moving lid. a Re=100, b Re=1,000.

The Nu as a function of the Grashof number at various Re is shown in Fig. 6. It appears that the Grashof number plays an important role in the heat transfer enhancement. In the figure, it is obvious that Nu is independent of Gr when Gr≤10⁵ . However, a significant increase in Nu with Gr is found as Gr>10⁵ . Basically, Nu increases with Re or Gr. The increase in Nu with Gr becomes more significant at a lower Nu.

Fig. 6

Average Nu as a function of Gr at different Re.

Figure 7 displays the Nu as a function of the Re at various Grashof numbers. It is noticed that the effects of the Re are mixed. As Gr≦10⁵, Nu increases with Re monotonically. However, for the curve for a higher Gr, different feature may be observed. At Gr=10⁶, it is seen that the value of Nu decreases first when Re is gradually elevated. The value of Nu reaches a minimum at Re=500 and then increases with Re when Re is further elevated. At Gr=10⁷, the minimum Nuis observed at Re=1,000. As indicated in Fig.3, when the value of Gr is further elevated to 10⁷, another small counter-clockwise vortex is found in the right bottom area of the cavity. This small vortex covering part of the bottom wall provides additional heat transfer resistance to the convection heat transfer from the bottom wall and hence reduces the Nusselt number. It is found that the minimum Nu is actually located in the transition regime between the buoyancy-dominated and the inertia-dominated situations. This phenomenon implies that in the transition regime the flow not only experiences a remarkable change in flow pattern but also a remarkable reduction in heat transfer.

Fig. 7

Average Nu as a function of Re at different Gr.

The distributions of the local friction factor on the moving lid for various Grashof numbers are shown in Fig. 8. For the cases considered in this figure, the value of Re is fixed at 1,000. Results of local friction factor are presented in terms of f _x Re. Note that an increase in Grashof number leads to a decrease in f _x Re in the left portion on the lid wall surface but a slight increase in the right. As Gr is elevated to 10⁷, the value of f _x Re becomes negative in the left portion, and the curve exhibits a nearly anti-symmetric feature in the immediate area of x/L=0.4. The anti-symmetric feature of the curve for Gr=10⁷ may be attributed to the buoyancy-dominated two-symmetric-vortex flow pattern discussed earlier.

Fig. 8

Distribution of local friction factor on the moving lid for various Gr, at Pr=0.71 and Re=1,000.

The present numerical predictions of the flow pattern and heat transfer characteristics have been verified by using the commercial software package, CFD-ACE+ (Version 2003), which is released by CFD Research Corporation, Huntsville, AL, USA. For two typical cases at (Re=100, Gr=10⁷) and (Re=1,500, Gr=10⁷), the flow and temperature fields are predicted by the CFD-ACE+ using a similar grid system. The CFD-ACE+ predictions are compared with the present solutions for these two cases, and the results are given in Table 2. The accuracy of the present study can be found in this table.

Table 2 Comparison between the results obtained by present study and CFD-ACE+, for the cases at (Re=100, Gr=10⁷) and (Re=1,500, Gr=10⁷)

5 Concluding remarks

Experimental and numerical study is conducted to investigate the combined effects of lid movement and buoyancy on flow and heat transfer characteristics for the mixed convective flow inside a lid-driven arc-shape cavity. Flow visualization technique using kerosene smoke is applied to observe the flow pattern. Meanwhile, comparison between the numerical predictions and the visualized flow patterns has been made, and close agreement between these two sets of data for some particular cases has been found.

For an inertia-dominated situation at a lower Grashof number, a major clockwise vortex driven by the moving lid prevails in the cavity, and meanwhile a small counter-clockwise vortex adjacent to the left bottom wall is observed. However, when the Grashof number is increased, the major vortex still exists while the small vortex is no longer found. As the value of Gr is further elevated to a sufficiently high value (say, 10⁷), another counter-clockwise vortex appears in the right bottom area of the cavity, which is expected to grow with Gr. Eventually, this counter-clockwise vortex grows to have nearly the same strength and size as the major clockwise vortex, and then a two-symmetric-vortex flow pattern is formed. The two symmetric vortices, which are of equal strength and size but rotating in the opposite directions, indicate a pure buoyancy-dominated situation.

In general, the magnitude of Nu _x on the surface of the moving lid increases with Gr. However, it is found that for Gr≦10⁵, the local heat transfer rate can be approximated with the pure forced convection data at Gr=0. It is only for Gr≧10⁶ that the local heat transfer rate is appreciably enhanced by the buoyancy. In addition, the Nu _x on the moving lid is higher in the area near the left corner than near the right corner. It is also found that the Nu reaches a minimum value in the transition regime between the buoyancy-dominated and the inertia-dominated situations. This implies that in the transition regime the flow not only experiences a remarkable change in flow pattern but also a remarkable reduction in heat transfer.