Cessation of the lid-driven cavity flow of Newtonian and Bingham fluids

Abstract

We provide benchmark results for a transient variant of the lid-driven cavity problem, where the lid motion is suddenly stopped and the flow is left to decay under the action of viscosity. Results include Newtonian as well as Bingham flows, the latter having finite cessation times, for Reynolds numbers Re ∈ [1, 1000] and Bingham numbers Bn ∈ [0, 10]. The finite-volume method and Papanastasiou regularisation were employed. A combination of Re and Bn, the effective Reynolds number, is shown to convey more information about the flow than either Re or Bn alone. A time scale which characterises the flow independently of the geometry and flow parameters is proposed.

Introduction

Lid-driven cavity flow is a very popular benchmark problem in computational fluid dynamics. A variant of this problem is the transient case where, starting from the steady state, the lid motion is suddenly stopped and the flow is left to gradually cease. Despite its simplicity, a detailed study of this problem is missing from the literature, contrary to its steady-state counterpart.

The viscoplastic version of this problem has been briefly touched upon (Dean and Glowinski 2002; Dean et al. 2007; Muravleva and Muravleva 2009b) as a demonstration test case for new numerical methods. The aim in those studies was to test whether the numerical method could reproduce the theoretical result that viscoplastic flows cease in finite time. When the driving cause of a Newtonian flow (such as a moving boundary or a pressure gradient) is removed, the flow gradually comes to rest under the action of viscosity at a theoretically infinite amount of time. However, with viscoplastic flows, i.e. in flows of materials which exhibit a yield stress, cessation occurs in a finite amount of time. Theoretical upper bounds for the finite cessation times of several simple one-dimensional flows, such as plane and circular Couette flows and plane and axisymmetric Poiseuille flows, were provided by Glowinski (1984), Huilgol et al. (2002) and Muravleva et al. (2010b). Following these theoretical studies, a number of numerical studies appeared in the literature which investigated in great detail the cessation of such one-dimensional flows (Chatzimina et al. 2005; Chatzimina et al. 2007; Zhu and De Kee 2007; Muravleva et al. 2010a, b; Damianou et al. 2014). They showed that the theoretical upper bounds of Glowinski (1984), Huilgol et al. (2002) and Muravleva et al. (2010b) are sharp, i.e. they are very close or coincide with the actual cessation times.

As far as the cessation of two-dimensional flows is concerned, such detailed studies do not appear in the literature, except for a study of the cessation of Bingham flow in ducts of various cross sections by Muravleva and Muravleva (2009a). The cessation of lid-driven cavity flow naturally comes to mind as a two-dimensional test case. In the present study, we attempt a systematic examination of this problem, providing benchmark results for Bingham numbers ranging from 1 to 10 and Reynolds numbers ranging from 1 to 1000. The more fundamental Newtonian flow case is also studied, since benchmark results are also missing from the literature.

The present results show that a simple time scale, calculated from the geometrical parameters of the problem and the fluid properties, is roughly proportional to the cessation time, i.e. it is characteristic of the flow evolution rate. Also, the flow is complex enough to exhibit interesting geometrical features, and we have tried to relate these features to a single dimensionless number, called the effective Reynolds number by Nirmalkar et al. (2013); it is a combination of the classical Reynolds and Bingham numbers. This number is shown to convey more information about the flow than either the Reynolds or Bingham numbers alone, and may deserve more attention in viscoplastic flows in general.

The results were obtained with a finite-volume method (Syrakos et al. 2013, 2014), using the regularisation scheme of Papanastasiou (1987). The rest of this paper is organised as follows: In “Governing equations” the governing equations are presented along with a dedimensionalisation scheme which is useful for interpreting the results. In “Numerical method”, the numerical method is very briefly described. The results for Newtonian flow are presented in “Numerical results for Newtonian flow”. The results for Bingham flow follow in “Numerical results for Bingham flow”, where the accuracy of the numerical method is also discussed. Finally, “Conclusions” summarises the conclusions of this work.

Governing equations

We consider two-dimensional flow in a square cavity with a side of length L. Originally, at time t = 0, the flow is in its steady state, obtained when the top wall (lid) of the cavity moves horizontally towards the right with a uniform velocity U. The steady-state flow, which serves as the initial condition, is a very popular problem in the literature and many published results exist both for Newtonian and Bingham flows—a literature review can be found in our recent work (Syrakos et al. 2014). The present work investigates what happens after the motion of the lid has suddenly been stopped at time t = 0 and the flow is left to gradually decay under the action of viscosity.

The flow, which is assumed to be incompressible and isothermal so that the fluid density ρ is constant, is governed by the continuity and momentum equations:

$$ \nabla \cdot \boldsymbol{\mathrm{u}} \;=\;0 $$

(1)

$$ \rho \left( \frac{\partial{\boldsymbol{\mathrm{u}}}}{\partial{t}} \;+\; \boldsymbol{\mathrm{u}}\cdot \nabla\boldsymbol{\mathrm{u}} \right) \;=\; -\nabla p \;+\; \nabla\cdot\boldsymbol{\tau} $$

(2)

where u = (u, v) is the velocity vector, p is the pressure and τ is the deviatoric stress tensor. For a Bingham fluid of yield stress τ _y and plastic viscosity μ, the stress tensor is related to the velocity field through the following constitutive equation:

$$ \left\{ \begin{array}{ll} \boldsymbol{\dot{\gamma}} \;=\; \boldsymbol{0} \;, \qquad & \tau \leq \tau_{y}\\ \boldsymbol{\tau} \;=\; \left( \frac{\tau_{y}}{\dot{\gamma}} + \mu \right)\boldsymbol{\dot{\gamma}} \;, & \tau > \tau_{y} \end{array} \right. $$

(3)

where $\boldsymbol {\dot {\gamma }}$ is the rate-of-strain tensor, defined as $\boldsymbol {\dot {\gamma }} \equiv \nabla \boldsymbol {\mathrm {u}} + (\nabla \boldsymbol {\mathrm {u}})^{\mathrm {T}}$. The magnitudes of the two tensors are given by $\tau \equiv (\frac {1}{2} \boldsymbol {\tau }:\boldsymbol {\tau })^{1/2}$ and $\dot {\gamma } \equiv (\frac {1}{2} \dot {\boldsymbol {\gamma }}:\dot {\boldsymbol {\gamma }})^{1/2}$. Equation 3 also applies to Newtonian flow, when τ _y = 0. Equations 1, 2 and 3, together with the initial conditions obtained from the corresponding steady-state problems, and the no-slip, zero-velocity wall boundary conditions, were solved for fixed values of ρ = 1, U = 1 and L = 1 units, while τ _y and μ were varied to get the desired Reynolds and Bingham numbers (to be defined shortly).

More insight can be gained from a nondimensional form of the governing equations and of the results. Let therefore lengths and velocities be dedimensionalised by L and U, respectively. Concerning time, one possibility would be to dedimensionalise it by a reference time of T ₁ = L/U. However, in previous studies on cessation (Chatzimina et al. 2005; Muravleva et al. 2010a), the reference time T ₂ = ρ L ²/μ was used instead. This is more convenient for cessation problems and comes from the following reasoning: A characteristic momentum scale for the present problem would be M = ρ U L ³ (a mass ρ L ³ moving with a velocity U).¹ Cessation is caused by the viscous forces acting on the fluid, and a characteristic viscous force would be $F = \mu \frac {U}{L} L^{2}$ (a stress μ U/L acting over a surface L ²). So, a characteristic time of T ₂ = M/F = ρ L ²/μ can be derived, which is the time needed for force F to reduce momentum M to zero in the absence of other forces. One can note, however, that the choice of μ U/L for a characteristic stress is reasonable for Newtonian flows, but for Bingham flows, it seems more appropriate to use τ _y + μ U/L instead. This results in a characteristic time of T ₃ = M/F = ρ U L ²/(τ _y L + μ U). By scaling time by T ₃ and pressure by the characteristic stress τ _y + μ U/L, the following nondimensional form of the momentum equation is obtained, where the tilde (˜) denotes dedimensionalised variables:

$$ \frac{\partial{\tilde{\boldsymbol{\mathrm{u}}}}}{\partial\tilde{t}} + \text{Re}^{*} \,\tilde{\boldsymbol{\mathrm{u}}}\cdot\tilde{\nabla}\tilde{\boldsymbol{\mathrm{u}}} = -\tilde{\nabla} \tilde{p}+ \tilde{\nabla}\cdot\left[ \left( \frac{\text{Bn}}{\text{Bn}+1} \, \frac{1}{\tilde{\dot{\gamma}}} + \frac{1}{\text{Bn}+1} \right) \tilde{\dot{\boldsymbol{\gamma}}} \right] $$

(4)

The dimensionless numbers that appear in the above equation are the Bingham number,

$$ \text{Bn} \;\equiv\; \frac{\tau_{y} L}{\mu U} $$

(5)

which is an indicator of the viscoplasticity of the flow, and the effective Reynolds number (Nirmalkar et al. 2013),

$$ \text{Re}^{*} \;\equiv\; \frac{\rho U^{2}}{\tau_{y} + \mu\frac{U}{L}} $$

(6)

which is an indicator of the inertia of the flow. The latter is defined as the ratio of a characteristic momentum (inertial) flux ρ U ² L ² to a characteristic viscous force (τ _y + μ U/L)L ². The effective Reynolds number is related to the usual Reynolds number Re = ρ U L/μ by Re^∗ = Re/(Bn+1); for Newtonian flow (τ _y = 0), the two are equivalent.

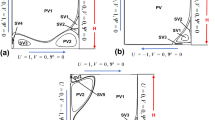
Equation 4 shows that, for a given domain and boundary and initial conditions (in the nondimensional space), the flow is governed only by the two dimensionless numbers Re^∗ and Bn. If these numbers are varied, then only the second (convective) and the last (viscous) terms of Eq. 4 are affected. The viscous term depends only on Bn, and this dependence is modest if Bn is large enough because in that case the terms Bn/(Bn+1)≈1 and 1/(Bn+1)≈0 do not vary much with Bn. Thus, often it will be the case that the main characteristics of the flow depend mostly on Re^∗. This has been observed, for example, by Nirmalkar et al. (2013), but can also be demonstrated in the present case. Figure 1 shows how the position and strength of the vortex that dominates the flow varies with Bn and Re ^∗ in the steady-state case, which serves as initial condition for the present problem. The results of Fig. 1 are taken from Syrakos et al. (2014), but here, they are plotted in terms of Re ^∗ instead of Re. It is interesting to observe that Re ^∗ alone can be used to identify the different flow regimes: Up to Re ^∗≈1, the vortex is very close to the vertical centreline; beyond that, the vortex moves towards the right with its strength constant, up to Re ^∗≈ 60–75; if Re ^∗ is increased further, the vortex moves towards the centre of the cavity and its strength increases. On the other hand, finer details of the flow field, such as the exact vortex position and strength, are determined not only by Re ^∗ alone but also by Bn.

Fig. 1

Vortex position (a) and vortex strength (b) as a function of Bn and Re ^∗ (the latter is shown next to each point in (a)) in the steady-state lid-driven cavity Bingham flow (data taken from Syrakos et al. (2014))

Finally, we note that the characteristic times defined above are related by T ₂ = Re⋅T ₁ and $T_{3} = \text {Re}^{*} \cdot T_{1} = T_{2} / (\text {Bn}+1)$. So, if the corresponding nondimensional time variables are denoted by $\bar {t}$, $\hat {t}$ and $\tilde {t}$ (scaled by T ₁, T ₂ and T ₃, respectively), then $\hat {t} = \bar {t}/\text {Re}$ and $\tilde {t} = \bar {t}/\text {Re}^{*} = (\text {Bn}+1)\hat {t}$. For Newtonian flow, $\hat {t} \equiv \tilde {t}$ and only the notation $\tilde {t}$ will be used.

Numerical method

The constitutive Eq. 3 is discontinuous, having two different branches, each applying to a different state of the material (yielded/unyielded). The easiest and most common way to overcome this difficulty is to approximate Eq. 3 by a regularised constitutive equation which is applicable throughout the domain and approximates unyielded material by a very viscous fluid. This popular approach was also adopted in our previous works (Syrakos et al. 2013, 2014). In particular, we employ the regularisation proposed by Papanastasiou (1987):

$$ \boldsymbol{\tau} \;=\; \left[ \frac{\tau_{y}}{\dot{\gamma}} \left\{ 1-\exp(-m\dot{\gamma})\right\} \,+\, \mu \right] \boldsymbol{\dot{\gamma}} \;=\; \eta(\dot{\gamma}) $$

(7)

where m is a stress growth parameter—the larger this parameter, the better the approximation. According to Eq. 7, the material is everywhere fluid, with effective viscosity $\eta (\dot {\gamma })$. When the shear rate tends to zero, this viscosity does not tend to infinity but to the value

$$ \eta_{0} \;\equiv\; \lim_{\dot{\gamma} \rightarrow 0}\eta \;=\; m\, \tau_{y} \;+\; \mu $$

(8)

This regularisation method was used also in previous one-dimensional studies (Chatzimina et al. 2005, 2007; Zhu and De Kee 2007). A comparison of the results of these studies against those of Muravleva et al. (2010a) and the theoretical bounds shows that values of m of the order of 200–300 lead to accurate prediction of the cessation times for Bingham numbers larger than 0.1. In the present study, we used a value of m = 400.

The equations were solved with the finite-volume method described in our previous work (Syrakos et al. 2013, 2014), extended to include temporal terms in the momentum equation. In particular, the time derivative was approximated using the following second-order accurate backward differentiation formula (Ferziger and Peric 2002):

$$ \left. \frac{\partial{\boldsymbol{\mathrm{u}}}}{\partial{t}} \right|_{t=t_{i}} \;\approx\; \frac{3\boldsymbol{\mathrm{u}}(t_{i}) \;-\; 4\boldsymbol{\mathrm{u}}(t_{i-1}) \;+\; \boldsymbol{\mathrm{u}}(t_{i-2})}{2{\Delta} t} $$

(9)

where t _i is the time after i time steps: t _i = i⋅Δt, Δt being the chosen time step for the simulation. For an accurate simulation, Δt should be smaller when the flow evolves faster, i.e. at lower Reynolds numbers or higher Bingham numbers. However, it will be shown in “Numerical results for Newtonian flow” and “Numerical results for Bingham flow” that if time is dedimensionalised by the time scale T ₃, then the nondimensional time step can be independent of the Reynolds and Bingham numbers. So, a step of ${\Delta } \tilde {t} = 10^{-6}$ was used for the first 400 time steps of each simulation, followed by ${\Delta } \tilde {t} = 4\cdot 10^{-6}$ for the next 400 time steps, and then ${\Delta } \tilde {t} = 1.6\cdot 10^{-5}$ for the rest of the simulation; in this way, the first stages of the flow, when the flow changes rapidly, are modelled accurately.

The scheme is fully implicit, so that the rest of the terms of the momentum equation are all evaluated at the current time t _i by central differences. A modification was made also to the calculation of the mass fluxes via momentum interpolation to account for the transiency of the flow, but this will be described elsewhere. The domain is discretised by a uniform Cartesian grid of 512×512 volumes. The resulting non-linear system of algebraic equations is solved using the SIMPLE algorithm with multigrid acceleration (Syrakos et al. 2013).

Numerical results for Newtonian flow

Despite the popularity of the steady-state Newtonian lid-driven cavity flow problem, it seems that there are no published results for the transient version of the problem where the lid motion is suddenly stopped. This section serves to fill this gap, as well as to provide a useful background for the study of the cessation of Bingham flow in the next section.

The problem was solved for Re = 1, 10, 100 and 1000 (Re≡Re^∗ for Newtonian flow). The flowfields for the extreme cases of Re = 1 and Re = 1000 are visualised in Fig. 2; they are initially very different, but eventually converge to the same pattern. The main feature of the flow is the large vortex in the middle of the cavity, which gradually decays under the action of viscosity. For Re = 1, 10 and 100, the vortex centre is initially located approximately mid-way between the lid and the cavity centre, and for Re = 100, it is also shifted towards the right (Fig. 1a), while for Re = 1000, it is located close to the cavity centre. However, as time passes, all vortex centres converge to the cavity centre, as Fig. 3 shows. By comparing the marked vortex positions, we note that with respect to nondimensional time $\tilde {t}$, the vortex motion evolves at a rate which is roughly independent of the Reynolds number.

Fig. 2

a–h Snapshots of the flowfield for Newtonian flow at Re = 1 (top) and 1000 (bottom), at the times indicated. Contours of nondimensional pressure ($\tilde {p} = p / (\mu U/L)$) are drawn in colour. Superimposed are streamlines, corresponding to values of streamfunction of $\psi = c \cdot \psi _{\max }$ where $\psi _{\max }$ is the instantaneous maximum value of streamfunction (found at the vortex centre) and c takes the values {0, 0.01, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 0.999}. In c, vectors proportional to the pressure force per unit volume −∇p are also drawn. The selected times are such that the instantaneous vortex strength $\psi _{\max }(t)$ is 100, 10, 1 and 0.1 % of the initial strength $\psi _{\max }(t=0)$, respectively (from left to right)

Fig. 3

Trajectories of the vortex centres of Newtonian flow at various Reynolds numbers, indicated at the beginning of each trajectory. The dots (∙) correspond to nondimensional times $\tilde {t}$ = 0, 0.01, 0.02, 0.03, 0.04 and 0.05. The “staircase” appearance of the curves is due to the fact that the vortex centre, at each time instant, is assumed to be located at the grid node where ψ is maximum—therefore, positions can only assume values from a finite set, that of grid node locations

The vortex decay is studied in terms of the vortex strength, that is, the maximum value of the streamfunction ψ, defined by u = −∂ ψ/∂ y, v = ∂ ψ/∂ x with ψ = 0 at the cavity walls. This maximum value $\psi _{\max }$ occurs at the vortex centre and is equal to the rate of flow of fluid through any line joining the vortex centre to any point on the cavity walls. Figure 4 shows how the vortex strength decays with time. If the Reynolds number is decreased by an order of magnitude, then the strength decays an order of magnitude faster as well. This is not surprising, the Reynolds number being an indicator of the ratio of inertial (momentum) fluxes to viscous forces: an order of magnitude decrease in Re implies an order of magnitude relative increase of the viscous forces and of the deceleration they cause. These results are quantified in Table 1. Therefore, the vortex decay rate with respect to $\tilde {t} = \bar {t}/\text {Re}$ is independent of the Reynolds number. This is confirmed by Fig. 4b, which shows that the vortex decay can be described by the following equation:

$$ \frac{\psi_{\max}(\tilde{t}_{2})}{\psi_{\max}(\tilde{t}_{1})} \;=\; e^{-c(\tilde{t}_{2}-\tilde{t}_{1})} \;=\; e^{-c\frac{\mu(t_{2}-t_{1})}{\rho L^{2}}} $$

(10)

where $\tilde {t}_{1}$ and $\tilde {t}_{2}$ are such that $\tilde {t}_{2} > \tilde {t}_{1} > 0.05$, say (at earlier times the decay is faster for Re = 1, 10 and 100). The present results show that c≈52.35, irrespective of Re.

Fig. 4

Vortex strength as a function of time, for Newtonian flow at various Reynolds numbers which are indicated on each curve. The vortex strength is normalised by the initial vortex strength $\psi _{\max }^{0}$ of each case, and time is dedimensionalised by L/U (a) and by ρ L ²/μ (b). Note that the time axis is logarithmic in the left figure and linear in the right figure

Table 1 Time intervals $\delta \bar {t}_{n}$ required for the strength of the main vortex of the cavity to drop from $\psi _{\max } = \psi _{\max }^{0} \cdot 10^{-(n-1)}$ to $\psi _{\max } = \psi _{\max }^{0} \cdot 10^{-n}$, where $\psi _{\max }^{0}$ is the initial vortex strength

The exponential flow decay with respect to $\tilde {t} = t\mu /\rho L^{2}$ suggests that the flow parameters have the following effect: Higher viscosity μ results in faster decay because the viscous, dissipating forces become larger. On the contrary, greater fluid density ρ results in slower decay because the fluid has more inertia and requires larger forces to decelerate. Finally, the effect of the domain dimension L is twofold, hence, L appears squared: (a) increasing the domain size makes the velocity variations occur across larger distances, hence reducing the velocity gradients and the resulting viscous stresses and (b) increasing the dimension L causes a larger increase to the domain volume (proportional to L ³), and hence to the fluid mass and inertia, than to the domain surface (proportional to L ²), and hence to the viscous forces which are the product of viscous stresses and surface areas. This explanation derives from the reasoning behind the dedimensionalisation of time presented in “Governing equations”, where a characteristic time was derived by dividing a characteristic momentum by a characteristic viscous force. It also explains the faster decay observed at the early stages for Re = 1, 10 and 100. At these Reynolds numbers, during the early stages of the flow, the vortex is located close to the lid, and this geometric confinement implies a smaller effective L dimension. Therefore, velocity gradients and associated viscous stresses are larger.

It would be interesting to make a comparison against the decay rates of a couple of simpler, one-dimensional flows: planar Couette flow between infinite parallel plates, located a distance L/2 apart, one of which is stationary while the other moves with velocity U, and flow in a rotating cylinder of radius L/2 and angular velocity 2U/L. The latter is a special case of circular Couette flow where the radius of the inner cylinder is zero. At t = 0, the motion of the plate or cylinder is stopped and the flow gradually decays. These flows bear some resemblance to the present lid-driven cavity flow, if the velocity is zero at the centre of the cavity. They have analytic solutions that can be found, e.g. in Papanastasiou et al. (1999), which have the form of an infinite weighted sum of eigenfunctions that decay at different rates. At long times, the solution is dominated by the eigenfunction of slowest decay. In fact, these eigenfunctions and their decay rates are independent of the initial conditions, so that after a long time, the flow tends to a specific pattern which is independent of the flow history, similarly to the present lid-driven cavity problem. For the Couette flow case, at long times, the velocity profile becomes sinusoidal and decays as $e^{-4\pi ^{2} \tilde {t}}$, corresponding to a decay constant of c = 4π ² = 39.48 in Eq. 10. For the rotating cylinder case, eventually, the velocity profile acquires the form of J ₁, the first-order Bessel function of the first kind, and decays as $e^{-4 {a_{1}^{2}} \tilde {t}}$, where a ₁ = 3.8317 is the first root of J1; the decay constant is $c = 4{a_{1}^{2}} = 58.73$. So, the lid-driven cavity decay constant, c≈52.35, lies between these two. This is not surprising, since the geometry is such that the flow has similarities with both: near the walls the streamlines are straight, like in Couette flow, and near the cavity centre they are circular, like in the cylinder flow.

Figure 5 shows normalised profiles of horizontal velocity u along the vertical lines through the vortex centre, at various times, for Re = 1 and 1000. Sinusoidal and Bessel function J ₁ profiles are included for comparison. The velocity profiles converge as time passes, but they converge more slowly for Re = 1 than for Re = 1000. This is due to the fact that at Re = 1, it takes some time for the vortex to move to the centre of the cavity (Fig. 3), contrary to the Re = 1000 case. The velocities converge to the exact same profile both for Re = 1 and for Re = 1000, which is close to both the sinusoidal and the Bessel function J ₁ profiles; its maximum occurs at y≈0.76.

Fig. 5

Profiles of the x-velocity component along the vertical lines through the vortex centre, normalised by the maximum absolute value along each profile, at various time instances, for Newtonian flow at a Re = 1 and b Re = 1000. The selected time instances are those when the maximum streamfunction has dropped to 100, 50, 10, 1 and 0.1 % of its initial value; see Fig. 2 for the exact times. For comparison, the sine function $\sin (2\pi (y-0.5))$ and the Bessel function J ₁(2a ₁(y−0.5)) profiles are also shown

The convergence of the flow fields of Re = 1 and Re = 1000 as time progresses is not limited to the vertical line through the vortex centre, but it extends to the whole domain, as a comparison between Fig. 2d and h reveals. Similarly to the one-dimensional flows mentioned previously, lid-driven cavity flow eventually becomes dominated by a single eigenfunction, that was shown in Fig. 2d, h, with the slowest decay rate $e^{-52.35\tilde {t}}$. The momentum equation (4), which for Newtonian flow simplifies to

$$ -\tilde{\nabla} \tilde{p} \;=\; \frac{\partial{\tilde{\boldsymbol{\mathrm{u}}}}}{\partial\tilde{t}} \;+\; \text{Re} \,\tilde{\boldsymbol{\mathrm{u}}}\cdot\tilde{\nabla}\tilde{\boldsymbol{\mathrm{u}}} \;-\; \tilde{\nabla}^{2} \tilde{\boldsymbol{\mathrm{u}}} $$

(11)

includes non-linear inertia terms, but these are proportional to the velocity squared and decay faster than the rest of the terms; hence, they can be neglected at large times. Therefore, there is a vector function $\boldsymbol {\phi }(\tilde {x},\tilde {y})$ such that at large times, the velocity field tends asymptotically to

$$ \tilde{\boldsymbol{\mathrm{u}}}(\tilde{x},\tilde{y},\tilde{t}) = \boldsymbol{\phi}(\tilde{x},\tilde{y})\cdot e^{-c\tilde{t}} $$

(12)

Substituting (12) into (11) gives

$$ -\tilde{\nabla} \tilde{p} \;=\; \left( -c \boldsymbol{\phi} \;+\; e^{-c\tilde{t}} \, \text{Re} \, \boldsymbol{\phi} \cdot \tilde{\nabla}\boldsymbol{\phi} \;-\; \tilde{\nabla}^{2} \boldsymbol{\phi} \right) e^{-c\tilde{t}} $$

(13)

So, the term $e^{-c\tilde {t}} \, \text {Re} \,\boldsymbol {\phi }\cdot \tilde {\nabla }\boldsymbol {\phi }$ eventually becomes negligible compared to the other terms in the parentheses, and the momentum equation reduces to

$$ -\tilde{\nabla} \tilde{p} \;=\; \left( -c \boldsymbol{\phi} \;+\; \tilde{\nabla}^{2} \boldsymbol{\phi} \right) e^{-c\tilde{t}} $$

(14)

which is independent of the Reynolds number. At this point, the flow has become dominated by viscous forces. Eq. 14 shows that the pressure gradients also decay at the same rate, $-\tilde {\nabla }\tilde {p} = \boldsymbol {\mathrm {f}}(\tilde {x},\tilde {y}) e^{-c\tilde {t}}$ where $\boldsymbol {\mathrm {f}}(\tilde {x},\tilde {y}) = -c \boldsymbol {\phi } + \tilde {\nabla }^{2} \boldsymbol {\phi }$. Integrating this, we get $\tilde {p} = q(\tilde {x},\tilde {y}) e^{-c\tilde {t}}$, up to a constant, where $\tilde {\nabla } q = -\boldsymbol {\mathrm {f}}$; this is confirmed by Fig. 2.

The initial effects of inertia are evident in the Re = 1000 case. In Fig. 2e–f, the pressure increases radially from the centre of the cavity outwards and is approximately constant along each streamline. Therefore, pressure forces act only as centripetal forces, without affecting the velocity magnitude. Of the acceleration terms of Eq. 11, $\partial \tilde {\boldsymbol {\mathrm {u}}} / \partial \tilde {t}$ is tangential to the streamlines (since the direction of the velocity vector remains nearly constant with time) and expresses the rate of reduction of the velocity magnitude. The other acceleration term, $\text {Re} \,\tilde {\boldsymbol {\mathrm {u}}}\cdot \tilde {\nabla }\tilde {\boldsymbol {\mathrm {u}}}$, expresses the rate of change of velocity as one moves along a streamline at a specific instance in time; since the velocity magnitude does not change much along a streamline (the density of surrounding streamlines is constant), this rate of change concerns mostly the direction, so that $\text {Re} \, \tilde {\boldsymbol {\mathrm {u}}} \cdot \tilde {\nabla } \tilde {\boldsymbol {\mathrm {u}}}$ is a centripetal acceleration. Finally, the viscous term $\tilde {\nabla }^{2} \tilde {\boldsymbol {\mathrm {u}}}$ is still small compared to the inertial terms due to the high Reynolds number Re = 1000. If Eq. 11 is split into radial and circumferential components, we can therefore assume that in the radial direction $-\tilde {\nabla } \tilde {p} \approx \text {Re} \,\tilde {\boldsymbol {\mathrm {u}}} \cdot \tilde {\nabla } \tilde {\boldsymbol {\mathrm {u}}}$, while in the circumferential direction, the deceleration $\partial \tilde {\boldsymbol {\mathrm {u}}} / \partial \tilde {t}$ equals the circumferential component of the viscous force $\tilde {\nabla }^{2} \tilde {\boldsymbol {\mathrm {u}}}$.

Eventually, the flowfield acquires the form shown in Fig. 2d, h, which is Re-independent. Its pressure distribution exhibits alternating highs and lows which appear in pairs, one pair on each side of the cavity. The high is on the upstream side and the low on the downstream side, becoming weaker towards the cavity centre. Figure 2g shows a transitional regime for Re = 1000, where the radial pressure distribution still persists near the centre of the cavity but the alternating pressure pattern has begun forming near the walls. The alternating pressure pattern gives rise to forces shown in Fig. 2c, which in general have a non-zero component tangential to the streamlines, causing acceleration and deceleration of the flow. However, since $\tilde {\nabla } \tilde {p}$ is a conservative vector field derived from the potential function $\tilde {p}$, the line integral $\oint \tilde {\nabla } \tilde {p} \cdot \text {d}\tilde {\mathrm {s}}$ is zero along any closed path. All streamlines of the present flow form closed paths, and the integral $-\oint \tilde {\nabla } \tilde {p} \cdot \text {d}\tilde {\mathrm {s}}$ along a streamline, which is therefore zero, can be interpreted as the total work done by the pressure force on all the particles along the streamline in a small time interval $\text {d}\tilde {t}$, during which each particle moves a small distance $\text {d}\tilde {\mathrm {s}}$ along the streamline. The total pressure work in the cavity is therefore zero, and the flow decays only due to the dissipating action of the viscous forces. Note that the previous argument does not apply to a single fluid particle which completes a closed path along a streamline in a finite time interval $\delta \tilde {t}$: Since pressure differences decay with time, when the fluid particle has returned to its starting position, the pressure there will have changed, and the work of the pressure force on the particle will be non-zero.

Numerical results for Bingham flow

We now turn to the cessation of Bingham flow. Numerical experiments were conducted for the (Re, Bn) pairs shown in Table 2 (Re∈[1,1000], Bn∈[1,10]). The flowfield evolution for selected pairs is shown in Figs. 6, 7, 8 and 9, in order of increasing inertia (Re ^∗). Streamlines are drawn at constant streamfunction intervals of δ ψ = 0.004, which equals the volumetric flow rate between adjacent streamlines; they space out as time passes, reflecting the fact that the flow slows down. The shaded regions denote unyielded material, identified using the usual criterion τ < τ _y (see Burgos et al. (1999) and Syrakos et al. (2014) regarding this choice). The initial flowfields (t = 0) are examined in detail in Syrakos et al. (2014).

Fig. 6

a–h Snapshots of the flowfield for Bn = 10 and Re = 1 (Re ^∗ = 0.09). Time is given as a fraction of the cessation time t _c (the time needed for τ to fall below τ _y everywhere). The lines are lines of constant streamfunction ψ (streamlines), normalised by U L, plotted at intervals of δ ψ = 0.004, with ψ = 0 at the walls. Unyielded areas (τ < τ _y ) are shown shaded

Fig. 7

a–h Snapshots of the flowfield for Bn = 2 and Re = 1 (Re ^∗ = 0.33). Time is given as a fraction of the cessation time t _c (the time needed for τ to fall below τ _y everywhere). The lines are lines of constant streamfunction ψ (streamlines), normalised by U L, plotted at intervals of δ ψ = 0.004, with ψ = 0 at the walls. Unyielded areas (τ < τ _y ) are shown shaded

Fig. 8

a–l Snapshots of the flowfield for Bn = 10 and Re = 1000 (Re ^∗ = 91). Time is given as a fraction of the cessation time t _c (the time needed for τ to fall below τ _y everywhere). The lines are lines of constant streamfunction ψ (streamlines), normalised by U L, plotted at intervals of δ ψ = 0.004, with ψ = 0 at the walls. Unyielded areas (τ < τ _y ) are shown shaded

Fig. 9

a–l Snapshots of the flowfield for Bn = 2 and Re = 1000 (Re ^∗ = 333). Time is given as a fraction of the cessation time t _c (the time needed for τ to fall below τ _y everywhere). The lines are lines of constant streamfunction ψ (streamlines), normalised by U L, plotted at intervals of δ ψ = 0.004, with ψ = 0 at the walls. Unyielded areas (τ < τ _y ) are shown shaded

Table 2 Effective Reynolds numbers Re ^∗ corresponding to the (Re, Bn) combinations used in this study

Unyielded regions fall into two categories. The first category is that of the unyielded regions which are in contact with the cavity walls and therefore contain stagnant material due to the no-slip boundary condition. Initially, these regions are located at the bottom of the cavity, where stresses are low due to the distance from the source of motion (the lid). As time passes and the flow slows down, they expand towards the interior of the cavity. Such unyielded regions develop also at the upper corners of the cavity, where stresses become very low once the lid is stopped because they are circumvented by the main flow (in the Newtonian case, this leads to the development recirculation zones, like at the lower corners—Fig. 2). Eventually, e.g. in Fig. 9l, the stagnant unyielded regions may cover the entire boundary of the cavity. Such zones will henceforth be referred to as “stagnant zones”, following Muravleva (2015). In actual fact, streamlines should not cross into stagnant zones, and so one should keep in mind that the ψ = 0 streamlines, which are shown for completeness in the figures, are a spurious artefact of regularisation, which results in very small but non-zero velocities in the stagnant zones.

The second category is that of the unyielded regions that are not in contact with the walls; they contain material which is not stagnant but moves as a rigid body, as implied by the finite spacing of the enclosed streamlines. Again, following Muravleva (2015), such regions will be referred to as “plug zones”. Plug zones are part of the main vortex, rotating along with it in rigid body rotation; the streamline parts they contain form concentric circular arcs. However, the centre of these arcs will not be the same as the vortex centre, unless the latter is contained within that plug zone as well. As time passes and the flow weakens, the plug zones also expand.

In Figs. 6, 7 and 8, after a short time, the plug zones appear as a pair: a smaller one above the vortex centre and a larger one below the vortex centre. These figures correspond to relatively low Re ^∗ of 0.33, 0.09 and 91, respectively, where the vortex is located close to the lid (Fig. 1a). So, the streamlines have a large radius of curvature inside the upper zone so as to align themselves with the lid, while they have a smaller radius of curvature inside the lower plug zone in order follow the cavity geometry. As long as the two zones have different radii of curvature they cannot come into contact, since a single rigid body can only rotate about a single centre point. Therefore, they are separated by a zone of yielded material. The radii of curvature of the streamlines inside the plug zones gradually change, as their centres of rotation converge towards the vortex centre. Eventually, not long before complete cessation, the two zones merge forming a single aggregate zone that rotates about the vortex centre, which it contains. The streamlines contained entirely within the aggregate plug zone form perfect circles.

On the other hand, if the effective Reynolds number is large, as in Fig. 9 (Re ^∗ = 333), then the vortex centre is close to the cavity centre and equally distant from its walls. This allows the streamlines to have uniform curvature and the plug zones to merge relatively early, forming a single rotating unyielded zone at the centre of the cavity.

Note that, while rotating, a plug zone cannot touch the cavity walls, due to the no-slip boundary condition. Similarly, a moving plug zone cannot touch a stagnant zone. But stagnant zones and plug zones eventually merge, and therefore, this can only happen when the motion of the plug zones has completely stopped. The instance when they merge is in fact the instance of complete flow cessation, t _c. Figures 6h and 7h show that this is nearly, but not exactly, captured by the numerical results; the rotating plug zone starts to merge with the surrounding stagnant zone at a single point, located near its bottom, while the rest of its boundary is still separated from the stagnant zone by a thin layer of yielded material. This is unrealistic and is an artefact of the regularisation method which allows small rates of shear within the unyielded zones; using a higher regularisation parameter m would improve the results. What would actually happen is that, at the same instance when the plug zone ceases to rotate, the (also rotating) thin yielded layer surrounding that zone should vanish everywhere, and the plug zone should merge everywhere with the stagnant zone.

Table 3 lists the computed cessation times t _c. Cessation is assumed to occur when τ < τ _y everywhere in the domain, in accordance with the yield criterion. In Table 3, time is dedimensionalised by T ₁ = L/U, and $\bar {t}_{\text {c}}$ is seen to increase with increasing Reynolds number and decrease with increasing Bingham number. The cessation time can also be derived from the vortex strength: it is the time when the vortex strength has reduced to zero. In Fig. 10, the vortex strength is plotted against $\bar {t}$ for Re = 1 and 100 and for all the Bingham numbers examined. One can notice that the curves for Bn >0 intersect the time axis at precisely the points listed in Table 3. For Bn =0 (Newtonian flow), the strength curve approaches asymptotically the time axis but does not intersect it. As the Bingham number is increased, the flow decelerates more rapidly, while the initial vortex strength is also smaller. Furthermore, comparison between the diagrams for Re = 1 and Re = 100 shows that the deceleration is roughly inversely proportional to the Reynolds number, and the cessation time is roughly proportional to it.

Table 3 Cessation times $\bar {t}_{\text {c}}$ ( = t _c⋅(L/U)⁻¹) for various Reynolds and Bingham numbers. The cessation time is defined as the time elapsed until τ < τ _y everywhere in the domain

Fig. 10

Vortex strength as a function of $\bar {t}$, for various Bingham numbers: a Re = 1; b Re = 100

The cessation times vary by several orders of magnitude among the different test cases studied. However, by dedimensionalising time against a dissipation time scale such as T ₂ or T ₃, as in Fig. 11, the results become rather independent of the Reynolds and Bingham numbers. Figure 11a shows that $\psi _{\max }(\hat {t})$ is roughly independent of the Reynolds number, except when Re ^∗ is high. However, the curves still depend strongly on the Bingham number. Figure 11b shows that if $\psi _{\max }(\tilde {t})$ is plotted instead then the dependence on the Bingham number is much weaker, while the independence on Re is retained. Almost all the cessation times lie in the range $\tilde {t}_{\text {c}} \in [0.013, 0.026]$, the only outliers being the cases (Re =1000, Bn =1) and (Re = 1000, Bn = 2), i.e. the high Re ^∗ cases. It can be conjectured that for these outliers, the high Re ^∗ values make the inertia term in Eq. 4 important at early stages, contrary to the other cases, resulting in a different initial behaviour with smaller deceleration. Nevertheless, the importance of inertia should diminish with time, just like in Newtonian flow analysed in the previous section. This is verified by the results shown in Fig. 12, where the flowfield for Bn = 5 and all Reynolds numbers is depicted. The flow fields can be seen to become more similar as time advances. This is true even for Re = 1000 which is initially very different than the rest: at early stages, the pressure increases radially from the interior of the cavity outwards, but late during the flow evolution pairs of high and low pressure regions appear at the top and bottom of the ring of unyielded material surrounding the plug zone, which resemble the characteristic pressure patterns of the lower Reynolds numbers. Nevertheless, the cessation of Bingham flow occurs in finite time, before a Re-independent flow pattern can be reached, contrary to Newtonian flow.

Fig. 11

Vortex strength as a function of time, dedimensionalised by T ₂ = ρ L ²/μ (a) and T ₃ = ρ U L ²/(τ _y L + μ U) (b), for all combinations of Re and Bn tested. Colours denote the Bingham number: Bn = 0 (black), Bn = 1 (red), Bn = 2 (blue), Bn = 5 (green) and Bn = 10 (purple). Line types denote the Reynolds number: Re = 1 (solid), R e = 100 (chained) and Re = 1000 (dashed). The curves for Re = 10 coincide with those for Re = 1 and are not visible

Fig. 12

a–l Snapshots of the flowfield for Bingham flow at Bn = 5. Each row of figures corresponds to a different Reynolds number: from top to bottom, Re = 1, 10, 100 and 1000. The figures of each row correspond, from left to right, to an early time, an intermediate time, and a late time of the cessation process. Contour plots of nondimensional pressure ($\tilde {p} = p / (\tau _{y} + \mu U/L)$) are drawn in colour. Yield lines (contours of τ = τ _y ) are drawn in thick solid lines. Streamlines are drawn in thin dashed lines, equispaced by $\delta \psi = 0.1\,\psi _{\max }$

The pressure field shown inside the unyielded regions in Fig. 12 should be viewed with scepticism. The Papanastasiou approximation Eq. 7 to the Bingham constitutive Eq. 3 is valid in the yielded zones but not in the unyielded ones, although in the latter, it results in the correct, zero-deformation, velocity field (Frigaard and Nouar 2005) (in the limit $m \to \infty$). But whereas the original Bingham model Eq. 3 leaves the stress tensor undefined in the unyielded regions, the Papanastasiou regularisation, treating all of the material as fluid, results in a unique stress field there. The pressure field shown in Fig. 12, which results from using the Papanastasiou stresses in the momentum (2), cannot be viewed as “correct” but is only one among many possible fields. In fact within the unyielded zones, the physical meaning of pressure is rather ambiguous (see the paper by Huilgol and You (2009) for a discussion).

In addition to inertia, the initial conditions also play an important role for the flow evolution during the early stages. For one thing, the larger the Bingham number, the larger also the percentage of the material that is unyielded to begin with. This leaves less material to become unyielded before cessation and may explain why in Fig. 11b cessation is reached faster when Bn is higher (see also Table 4). So the curves are not completely independent of Bn, but the dependence is nevertheless much weaker than in Fig. 11a. The rate that the material becomes unyielded is of course inversely proportional to the cessation time, and therefore, with respect to nondimensional time $\tilde {t}$, it is also roughly independent of Re and Bn. If m _u is the amount of unyielded material in the cavity, then $dm_{\text {u}}/dt = (dm_{\text {u}}/d\tilde {t}) \!\cdot \! (d\tilde {t}/dt) = (dm_{\text {u}}/d\tilde {t}) \!\cdot \! (1/T_{3})$. Since $dm_{\text {u}}/d\tilde {t}$ is approximately constant, the rate d m _u/d t is inversely proportional to the characteristic time T ₃, i.e. to the ratio of inertia in the cavity to viscous forces.

Table 4 Cessation times $\tilde {t}_{\text {c}}$ ( = t _c⋅[ρ U L ²/(τ _y L + μ U)]⁻¹) for various Reynolds and Bingham numbers. The cessation time is defined as the time elapsed until τ < τ _y everywhere in the domain

A closer look at the cessation times in Table 4 reveals another effect of the initial conditions. One can notice that, if Bn is held fixed and Re varied, $\tilde {t}_{\text {c}}$ begins to increase only after a certain Reynolds number has been exceeded; prior to that, it may also exhibit a minimum. This trend is very similar to the dependency of the initial vortex strength $\psi _{\max }^{0}$ on the Reynolds number, shown in Fig. 1b, and can be explained as follows. Both $\psi _{\max }^{0}$ and $\tilde {t}_{\text {c}}$ are constant up to an effective Reynolds number of Re ^∗≈10. If Re ^∗ is increased further, up to a value of Re ^∗≈70, the vortex moves towards the downstream vertical wall; this confines it geometrically causing its effective diameter to decrease. In turn, this may cause the initial vortex strength to fall, and the cessation time to reduce due to the higher velocity gradients and resulting viscous forces. For Bn ≤1, no such drop is observed as the geometric confinement is very slight. Beyond Re ^∗≈70, the initial vortex position moves towards the cavity centre, relaxing the geometric confinement and lowering the velocity gradients, thus causing an increase to $\psi _{\max }^{0}$ and to $\tilde {t}_{\text {c}}$. Therefore, in Fig. 11b, during early times the vortex strength drops more slowly in the high-Re ^∗ cases than in the low-Re ^∗ ones (the same was observed also for Newtonian flow in Fig. 4b).

Another benefit from using the nondimensional time $\tilde {t}$ is that one can choose the time step ${\Delta } \tilde {t}$ for the simulations independently of Re and Bn. The truncation error that arises from the temporal discretisation is proportional to the square of the time step size (second-order accuracy) and to certain temporal derivatives of the velocity. According to the results presented so far, the flow evolution with respect to $\tilde {t}$ is roughly independent of Re and Bn, so that the derivatives with respect to $\tilde {t}$ can also be assumed to be roughly independent of these numbers. Thus, the truncation error of the discretisation of the dimensionless momentum equation, and the associated discretisation error of the nondimensional flow variables that it produces, will also be roughly independent of Re and Bn.

Since the vortex strength is plotted on a logarithmic axis in Fig. 11b, the curves should become vertical at cessation and intersect with the time axis at the times listed in Table 4. Indeed this is approximately true, but the cessation times cannot be accurately read from Fig. 11b because the curves, although steep, are not completely vertical. This is due to the use of regularisation which treats the unyielded material as a fluid of very high viscosity. In fact, the slope of the curves after cessation can be calculated using the knowledge gained from the study of the Newtonian flow cases. After cessation, the whole of the material is unyielded and the viscosity everywhere tends to the limit value of the Papanastasiou model given by Eq. 8. Therefore, we can assume that the fluid behaves as a Newtonian fluid of that viscosity. The rate of decay of the vortex strength of the unyielded material can then be calculated from Eq. 10, only that η ₀ must be used instead of μ. In other words, time has to be dedimensionalised using a different characteristic time, T ₄ = ρ L ²/η ₀, giving rise to another nondimensional time variable $\check {t} = t/T_{4}$. After some manipulation, it turns out that

$$ T_{4} \;\equiv\; \frac{\rho L^{2}}{\eta_{0}} \;=\; \frac{\text{Re}}{M\!\cdot\! \text{Bn} \,+\, 1} \cdot \frac{L}{U} \;=\; \frac{\text{Re}}{M\!\cdot \text{Bn} \!\,+\, 1} \cdot T_{1} $$

(15)

where M≡m U/L is a nondimensional expression of the regularisation parameter m. Therefore, $\check {t} = t/T_{4} = \bar {t}\cdot (M\!\cdot \!\text {Bn}+1)/\text {Re}$. Assuming that the behaviour of the unyielded fluid is Newtonian, Eq. 10 can be used to calculate the rate of vortex decay:

$$ \frac{\psi_{\max}(\check{t})}{\psi_{\max}(\check{t}_{\text{c}})} \;=\; e^{-52.35(\check{t}-\check{t}_{\text{c}})} $$

(16)

where $\check {t}_{\text {c}}$ is the cessation time and $\check {t} > \check {t}_{\text {c}}$. The validity of this assumption is checked in Fig. 13. It is difficult to discern the various curves, but the important point is that almost all of them follow very closely the above theoretical prediction. The behaviour of the case (Bn = 1, Re = 1000), which corresponds to the highest Re ^∗ tested, is difficult to explain. In the case (Bn = 10, Re = 1000) the slope is steeper at early times because the unyielded “vortex” is confined near the upper right corner of the cavity and has a smaller effective diameter, but as it moves towards the cavity centre, the theoretical rate, Eq. 16, is recovered.

Fig. 13

Vortex strength history after cessation (due to regularisation, the flow never completely ceases): The ratio of current vortex strength $\psi _{\max }(\check {t})$ to the vortex strength at the time of cessation $\psi _{\max }(\check {t}_{\text {c}})$ is plotted against time elapsed since cessation, dedimensionalised by ρ L ²/η ₀. The curves correspond to: Bn = 1, Re = 1 (chained line), Bn = 1, Re = 1000 (double chained line), Bn = 2, Re = 10 (short, dense dashes), Bn = 5, Re = 100 (short, sparse dashes), Bn = 10, Re = 1 (long, sparse dashes) and Bn = 10, Re = 1000 (long, dense dashes). The thick, solid line is the theoretical prediction, Eq. 16

Conclusions

We have investigated the evolution of Newtonian and Bingham flow in a square lid-driven cavity once the driving force (the motion of the lid) has stopped. Contrary to Newtonian flow, Bingham flows cease in a finite amount of time. The effect of the flow configuration and material properties has been investigated by varying the Reynolds number in the range of 1–1000 and the Bingham number in the range of 0–10.

In Newtonian flow, the Reynolds number plays an important role at the early stages of cessation, but eventually, the flow obtains a pattern that is independent of the Reynolds number. The flow decays exponentially with a rate that is proportional to μ/ρ L ². Hence, the rate of decay with respect to the nondimensional time $\hat {t} = t / (\rho L^{2}/\mu )$ is independent of the problem geometric parameters (cavity size and initial lid velocity) and of the fluid properties, and was found to be approximately equal to 52.35.

In Bingham flow, zones of stagnant unyielded material form along the cavity walls and grow inwards, while zones of rotating unyielded material (plug zones) form in the interior of the cavity and grow outwards. The rotating zones decelerate and eventually stop moving at precisely the time when they merge with the outer stagnant zones, at which time the whole of the material in the cavity becomes unyielded and the flow ceases. The time scale of the evolution of the flow is proportional to ρ U L ²/(τ _y L + μ U), so if time is dedimensionalised by this quantity, then the main time-related features of the flow, such as the cessation time, become roughly independent of the geometric parameters of the problem and of the fluid properties.

Bingham flow is governed by two dimensionless parameters, the Reynolds number and the Bingham number, but these two can be combined in a single number, the effective Reynolds number, which is related to the time scale ρ U L ²/(τ _y L + μ U) (note that $\tilde {t} = \bar {t}/\text {Re}^{*}$). The effective Reynolds number is a natural extension of the idea of the Reynolds number to Bingham flows, and often its value alone is sufficient to determine important features of the flow.