A Macro-Based Process for Actively Managing Sovereign Bond Exposures

Abstract

We propose a macro-based yield-curve model for actively managing sovereign bond portfolios. Based on inflation and gross domestic product (GDP) growth expectations and an assumption of the central bank’s policy response function, we project the evolution of the sovereign yield curve. To address constraints on the lower bound of policy rates, we apply the concept of a shadow short rate that is unconstrained by the lower bound. The properties of the model are illustrated for the US, German, UK, and Japanese bond markets. We show that this approach—for naïve assumptions on the evolution of macro variables—has statically significant excess return predictability. Excess return predictability improves with improvements in the quality of inflation and GDP growth expectations.

1 Introduction

The success of any active management approach, that is, any approach that aims at generating outperformance relative to a benchmark, depends crucially on the quality of expectations about the excess returns (the return over and above the short rate) of the managed assets. Only if expected excess returns are fair estimates of subsequently realised excess returns, is added value from active management possible.

To derive expectations on the excess returns of sovereign bonds of different maturities, we propose a macro-based yield-curve model in which we assume that current bond yields are determined—amongst other factors—by expected macroeconomic developments and their future values can be estimated by projecting these macro expectations forward. The link between macroeconomic variables and bond yields is evident by decomposing the yield into two components:

• The short-rate expectations component. This part of the yield on a long-dated bond reflects the expected return from rolling investments in the short rate through to the maturity of the long bond. As argued below, this component is closely related to macroeconomic conditions; and

• The term premium component. This part is the remainder, or the actual yield on the long-dated bond less the short-rate expectations component. The term premium reflects the additional return that investors demand for investing in the long-dated bond over and above the expected return from rolling investments in the short rate.

The sovereign short rate is assumed to be the monetary policy rate of the central bank , which in turn is assumed to be set in reaction to prevailing and expected macroeconomic developments. The central bank sets its policy rate based on its policy objectives, for example, full employment and price stability for the US Fed. Policy makers would tend to reduce the rate if consumer price inflation or employment is expected to undershoot their targets and increase the rate if inflation or employment is expected to overshoot. The conduct of monetary policy therefore ensures a link between the yields of long-dated bonds (notably the short-rate expectations component) and macroeconomic developments. We model this link through a modified Taylor (1993) rule.

In the aftermath of the Great Financial Crisis, the so-called zero lower bound, which describes the situation in which the central bank is unwilling or unable to set a negative policy rate, resulted in the policy rate being maintained at a level above where it would ideally be based purely on the inflation and employment objectives of the central bank . This introduces an additional challenge in the modelling of the policy rate as the policy rate is insensitive to improvement/deterioration in macroeconomic variables in the short run. This challenge is addressed by the introduction of a shadow short rate that can be negative while the actual policy rate remains above or at zero. The shadow short remains responsive to changes in macroeconomic conditions, while the actual monetary policy rate remains at its lower bound. Eventually, after sufficient improvement in macroeconomic conditions, the shadow short rate will increase sufficiently to allow the actual policy rate to “lift-off” from its lower bound.

Over the past few years, a rich literature on zero-lower-bound modelling has emerged; see among others Bauer and Rudebusch (2016), Christensen and Rudebusch (2014), Feunou et al. (2015), Krippner (2013, 2014, 2015b), Wu and Xia (2016) for the US market, and Lemke and Vladu (2016) for the Euro area. Loosely speaking, this literature adopts the concept of a shadow short rate, in the spirit of Black (1995), as an unconstrained random variable that maps to the observed short rate via a static truncation function. These approaches are static with regard to the applied truncation function that does not depend on the state of the economy. This has often led empirical studies to uncover a somewhat counterintuitive time-series trajectory for the shadow short rate process on US data (see, e.g. Krippner 2014, 2015a). For example, the estimated US shadow short rate path has been difficult to reconcile with survey- and market-based expectations of the policy rate path generally agreed among investment professionals, where the Fed eased or tightened policy stance through unconventional programmes (i.e. forward guidance and large-scale asset purchase programmes). These discrepancies motivated Krippner (2014) to advocate the use of two-factor models, instead of the more commonly applied three-factor models (Wu and Xia 2016).

We use a flexible three-factor model proposed by Coche et al. (2017b) that produces an economically intuitive shadow short rate path before, during, and after the zero-lower-bound period. This approach rests on a flexible truncation function, where the mapping from the unobserved shadow short rate to the observed short rate depends on the state of the economy, via the term structure of the yield curve.

The remainder of this chapter is organised as follows. Section 5.2 introduces the model set-up and Sect. 5.3 presents the data and discusses the estimation technique. A detailed assessment of the model’s excess return predictability is presented in Sect. 5.4. Section 5.5 discusses the relevance of possible sources of excess return predictability and offers some thoughts on the application of the proposed model for real-world portfolio management. Section 5.6 concludes.

2 Model Set-Up

The macro-based yield-curve projections are based on a variation of the widely used dynamic Nelson-Siegel model proposed by Diebold and Li (2006), with three modifications. First, instead of the factor-loading structure of the original model of Nelson and Siegel (1987), we use a rotated version with the first factor being the short rate. Second, in order to better capture the dynamics of this factor near the effective lower bound, we use a shadow rate concept. Third, we model the dynamics of the shadow short rate factor using a modified version of the Taylor rule. These modifications are discussed below in detail.

Equation 5.1 shows the rotated loading structure for yield-curve factors β_t as proposed by Nyholm (2015). Consequently, the estimated factors proxy the short rate, slope, and curvature of a yield-curve structure y_t at a time t opposed to the long-term rate, slope, and curvature in the classical Nelson-Siegel loadings. We deviate from Nyholm (2015), in assuming the functional relationship between factors and yields in the shadow rate space rather than in the observed-rate space. Thus yields ${\tilde{y}}_t$ and factors ${\tilde{\beta}}_t$ represent shadow values. τ denotes maturity, and we set parameter λ to 0.71:

$$ {\tilde{y}}_t\left(\tau \right)={\tilde{\beta}}_{t,0}+{\tilde{\beta}}_{t,1}\left(1-\frac{1-{e}^{\lambda\ \tau }}{e^{\lambda\ \tau }}\right)+{\tilde{\beta}}_{t,2}\left(\frac{1-{e}^{\lambda\ \tau }}{e^{\lambda\ \tau }}-{e}^{\lambda\ \tau}\right) $$

(5.1)

The link between the observed space and the shadow space is provided by the flexible truncation function in Eq. 5.2, with parameter A dependent on the curve’s slope and curvature. Here ${\overline{y}}_t\left(\tau \right)$ denotes the estimated observed yields and y_L is the assumed effective lower bound.

$$ {\overline{y}}_t\left(\tau \right)={y}_L+\frac{{\tilde{y}}_t\left(\tau \right)-{y}_L}{1-{e}^{-\mathrm{A}\left({\tilde{\beta}}_t\right)\kern0.28em \left({\tilde{y}}_t\left(\tau \right)-{y}_L\right)}} $$

(5.2)

We base our model choice of A on the premise that once the observed rate is close to the effective lower bound, the shadow rate goes deeper into negative territory with a flattening of the observed curve as longer-maturity yields get pushed down against the lower bound in the expectation that the short rate will remain at the zero bound for an extended period (factor β_{t, 1} decreasing) and lower observed curvature (β_{t, 2} decreases) and vice versa. This premise is reflected in Eq. 5.3 using the product of two hyperbolic tangent functions. Consequently, parameter A is allowed to fluctuate between K and K + 4 as a function of slope and curvature as illustrated in Fig. 5.1. The exact nature of the dependence is controlled in addition by parameters p₁, p₂, q₁, and q₂.

$$ {\displaystyle \begin{array}{c}\mathrm{A}\left({\tilde{\beta}}_t\right)=\kern0.5em \frac{\tanh \left({p}_1\left({\tilde{\beta}}_{t,1}+\min \left({\tilde{\beta}}_{t,0}-{y}_L,0\right)\right)+{q}_1\right)+3}{2}\\ {}\times \frac{\tanh \left({p}_2{\tilde{\beta}}_{t,2}+{q}_2\right)+3}{2}+K\end{array}} $$

(5.3)

Fig. 5.1

Illustration of parameter A

Illustration of how parameter A fluctuates as a function of observed slope and curvature given p₁ = 1, q₁ = 3, p₂ = 1, and q₂ =  − 3. The x-axis shows possible values of the observed slope in the range between −2 and 8, and the y-axis values for the observed curvature in the range between −8 and 4. Different pairs of slope and curvature values, in combination with the short rate being anchored to the effective lower bound, imply different yield-curve shapes, four of which are depicted in inset figures. In addition, the coloured areas indicate the values that parameter A takes as a function of slope and curvature. The corresponding numerical values can be read from the legend on the right

In Eq. 5.3, the observed slope is proxied by the sum of the lower-bound constrained shadow short rate and the shadow slope (${\tilde{\beta}}_{t,1}+\min \left({\tilde{\beta}}_{t,0}-{y}_L,0\right)$).

The set-up in Eqs. 5.1 to 5.3 follows closely the model proposed in Coche et al. (2017b), which provides the arbitrage-free version of the above specifications, and also shows that the implied shadow rate dynamics are broadly in line with the rate dynamics of the Krippner (2014) two-factor model as long as the rates are close to the effective lower bound but that under normal yield-curve environments, the three-factor Nelson-Siegel specification has a superior fit to observed yields.

With regard to the time-series dynamics of the shadow short rate, we deviate from the autoregressive specification in Diebold and Li (2006) by assuming a modified Taylor rule (Eq. 5.4 below) with a contemporaneous dependence of the short-rate factor on inflation expectations ${\pi}_t^e-$ relative to a target inflation π^∗ and output gap x_t as well as a policy inertia term (${d}_0\ {\tilde{\beta}}_{t-1,0}$).

$$ {\tilde{\beta}}_{t,0}^{US}={a}_0+{b}_0\left({\pi}_t^e-{\pi}^{\ast}\right)+{c}_0{x}_t+{d}_0{\tilde{\beta}}_{t-1,0}^{US}+{\epsilon}_{t,0} $$

(5.4)

While Eq. 5.4 represents the choice of the short-rate dynamics for the US market (with a similar specification for Japan), the US shadow short rate is introduced as an additional explanatory variable in the short-rate dynamics of the German and UK markets.

$$ {\tilde{\beta}}_{t,0}={a}_0+{b}_0\left({\pi}_t^e-{\pi}^{\ast}\right)+{c}_0{x}_t+{d}_0{\tilde{\beta}}_{t-1,0}+{e}_0{\beta}_{t,0}^{US}+{\epsilon}_{t,0} $$

(5.4a)

where superscripts UK and EA are omitted for simplicity.

For the slope factor, we assume an autoregressive model with exogenous variables (ARX) specification with the output gap x_t as an explanatory variable (Eq. 5.5), and for the curvature factor, we assume it follows a simple autoregressive process (Eq. 5.6).

$$ {\tilde{\beta}}_{t,1}={a}_1+{c}_1{x}_t+{d}_1\ {\tilde{\beta}}_{t-1,1}+{\epsilon}_{t,1} $$

(5.5)

$$ {\tilde{\beta}}_{t,2}={a}_2+{d}_2\ {\tilde{\beta}}_{t-1,2}+{\epsilon}_{t,2} $$

(5.6)

As there are contemporaneous relationships between the first two factors and the output gap and inflation, projections of these macro variables are required. Either judgement-based or model-based projections for these macro variables can be used. The model-based projection of inflation is based on an autoregressive process of order p on monthly inflation rates from which expectations on year-on-year inflation rates ${\pi}_t^e-$ are derived.

The model-based projection of the output gap x_t = GDP_t/PGDP_t − 1 assumes separate processes for the growth rates of GDP and potential GDP. That is, we assume that the GDP growth rate follows again an autoregressive process of order p. The growth rate of potential output R_t,PGDP is modelled as an exponentially smoothed average of actual realised GDP growth rates R_t-1,GDP and the previous period’s output gap (Eq. 5.7).

$$ {R}_{t, PGDP}=\left(1-w\right){R}_{t-1, PGDP}+w\kern0.28em {R}_{t-1, GDP}+v\kern0.28em {x}_{t-1} $$

(5.7)

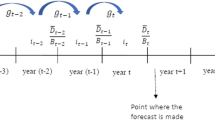
An illustration of this stepwise approach to the projection of yield-curve factors is provided in Fig. 5.2.

Fig. 5.2

Illustration of factor projection

3 Data and Estimation

Table 5.1 summarises the data sources for growth, inflation, and the yield curve used for the model estimation. In order to obtain long data histories, various sources are combined for some of the series. Combined series are in particular used for the euro area where German inflation and growth data are used as proxies prior to 1995. Furthermore, the German government yields are used as proxy for euro-area yields.

Table 5.1 Data sources

As the model is estimated on the basis of monthly data, frequency adjustment of quarterly GDP data is performed using industrial production as an instrument variable. As shown in Eq. 5.8, the proxied monthly GDP growth rates ${r}_{GDP}^M$ correspond to the monthly growth rates of industrial production ${r}_{IP}^M$ plus an adjustment term which ensures that the aggregated monthly GDP growth rate corresponds to the observed quarterly growth rate ${r}_{GDP}^Q.$

$$ {r}_{GDP}^M={r}_{IP}^M+\frac{r_{GDP}^Q-\sum {r}_{IP}^M}{3} $$

(5.8)

The shadow rate curves (Eqs. 5.1 to 5.3) are estimated statically—thus for each month individually—by minimising the sum of squared deviations of estimated yields ${\overline{y}}_t\left(\tau \right)$ from observed yields y_t(τ). For this, we assume a fixed set of parameters p₁ = 1, q₁ = 3, p₂ = 1, q₂ =  − 3 and K = 0. The effective lower bound y_L is set to the minimum observed short rate minus 0.25. The resulting estimates of shadow rate factors are shown in Fig. 5.3.

Fig. 5.3

Evolution of estimate shadow-curve factors. The units of the Y-axis are %

The model equations governing the time-series dynamics (Eqs. 5.4 to 5.6) are estimated individually using maximum likelihood estimation on the full data history. For the estimation of the modified Taylor rule (Eqs. 5.4 and 5.4a), we omit the explicit policy targets π^∗, which thereby are assumed to be reflected in the estimated intercepts. Table 5.2 provides the estimated parameters.

Table 5.2 Coefficient estimates governing the time-series dynamics (Eqs. 5.4 to 5.6)

4 Excess Return Predictability

In this section, we perform an assessment of the model’s excess return pre dictability, which goes beyond the standard criteria typically used for the assessment of yield-curve models such as root-mean-squared errors and mean absolute deviations (e.g. Diebold and Li 2006; Johannsen and Mertens 2016). Notably, we first analyse predictability over time, that is, the extent to which a signal S_t derived from the model at time t predicts a bond’s excess return realised over the subsequent 12 months. Second, we analyse the model’s cross-sectional properties by constructing portfolios of US, German, UK, and Japanese bonds using bond rankings based on the model signals.

Two signals are extracted from the model. The first is the expected return for different (constant) maturity zero-coupon bonds calculated based on the projected evolution of the yield curve.¹ The second is the term premium estimated from the prevailing yield at a given maturity and the projected short rate over the maturity. We compare the predictive power of these signals to the carry signal, which has been shown to imply predictive power for a number of markets including government bonds (e.g. Koijen et al. 2016). Carry is calculated as the yield plus the return component from rolling down an unchanged yield curve.

The model performance is analysed under two macro assumptions: first, that inflation and GDP growth are mean reverting, and second, under the assumption of perfect foresight on these macro variables. For the mean-reverting macro assumption, inflation and GDP growth revert to equilibrium values in an autoregressive process. For the perfect foresight macro assumption, we use the subsequently realised 12-month-ahead inflation and GDP growth.

We backtest asset-return predictability both in sample and out of sample. For the in-sample backtest, we use a long data history going back to 1953 for the US and to 1970 for the German, UK, and Japanese markets. Subsequently, we assess the bias of the in-sample results by successively re-estimating model parameters in an out-of-sample setting starting in 1990.

4.1 In-Sample Backtesting

For the in-sample assessment of the model, we estimate the parameters making use of the full data history.

To analyse the model properties with regard to predicting the excess return over time, we present regression statistics in Table 5.3. For this, a regression of signal S_{i, t} —either the term premium or expected excess return—for bond i is performed on the excess returns R_{i, t → t + k} earned by the bond over the subsequent k = 12 months.

$$ {R}_{i,t\to t+k}=a+b\times {S}_{i,t}+{\epsilon}_{t\to t+k} $$

(5.9)

Table 5.3 In-sample backtest full period

In the calculation of t-statistics, the Hansen and Hodrick (1980) correction is applied to account for overlapping data windows. In addition, accuracy and F1 score measures are reported to assess the quality of the approach to correctly predict the sign of excess returns. Accuracy is defined as the ratio of correctly forecasted signs (i.e. forecasted and realised excess return either both positive or both negative) to total observations. The F1 score (Rijsbergen 1979) considers both the forecast precision P (defined as true positives as a percentage of predicted positives) and recall R (defined as true positives as a percentage of actual positives). Based on this, the F1 score is defined as 2PR/(P + R).²

Table 5.3 shows the regression statistics for both macro assumptions. Under the assumption of mean-reverting macro, the expected return signal produces R²s in the range between 4% and 21%. The weakest results are observed for the German curve and the strongest results for Japan. The regression coefficients are statistically significant for the UK and Japan curves, weakly significant for the US curve, and not significant for the German curve. Switching the signal to term premium implies generally higher R²s and higher significance levels.

Under the assumption of perfect macro foresight, the model shows substantially increased explanatory power and statistical significance. The regression coefficients are significant at high confidence levels consistently across maturities and markets, and R²s increase to between 11% and 53%. Also accuracy and F1 scores improve for all maturities. Under this assumption, the term premium and expected return signals show broadly comparable characteristics.

Table 5.4 offers a comparison of the model’s properties to the carry signal. Over the full period and across all markets and maturities (left panel of Table 5.4; period consistent with the in-sample period used for Table 5.3), carry has a signal quality comparable with the model under the mean-reverting macro assumption. However, under the perfect macro foresight assumption, the model clearly shows superior properties in terms of significance levels and R²s. Also the model shows generally better Accuracy and F1 scores (with the exception of Japan). It is noted here that the results for the model are subject to in-sample bias, while the model-free carry signal is not. To correct for this, we perform below (see Table 5.7) a proper out-of-sample analysis, to be compared with the right panel of Table 5.4.

Table 5.4 Carry

To test the model’s cross-sectional properties and the model’s fitness to serve as a basis for portfolio construction, we assess the effectiveness of a number of duration-neutral strategies. To this end, the model is used to choose from 10 bonds, with maturities ranging from one to ten years for each of the four government bond markets, a universe of 40 bonds in total. In each month over the full sample, the 40 bonds are ranked using one of the term premium, the expected return, or the carry signal. On the basis of this ranking, five portfolios—representing distinct investment strategies—are constructed:

• Three quantile portfolios that comprise the lower third of the ranked bonds (Portfolio P1), the middle third (P2), and the upper third (P3).³ The bonds within each quantile portfolio are equally weighted. As the bonds are duration adjusted, each quantile portfolio has duration equal to one.

• One long-short difference portfolio of the highest signal quantile portfolio (P3) minus the lowest signal quantile portfolio (P1). This long-short portfolio has zero duration.

• One long-short factor portfolio similar to Asness et al. (2013), where the weight w_{i, t} of bond i is determined according to its signal rank. With this portfolio, the sum of the long positions is 1 and the sum of the short positions is −1 and the sum of all weights is zero. This long-short portfolio has zero duration.

  $$ {w}_{i,t}=\frac{\mathit{\operatorname{rank}}\left({S}_{i,t}\right)-{\sum}_i\mathit{\operatorname{rank}}\left({S}_{i,t}\right)/N}{\sum_i\left[\left|\mathit{\operatorname{rank}}\left({S}_{i,t}\right)-{\sum}_i\mathit{\operatorname{rank}}\left({S}_{i,t}\right)/N\right|\right]/2} $$

  (5.10)

Bonds in these portfolios are duration adjusted to have duration equal to one. For example, the duration-adjusted two-year bond has a 50% weight to the two-year bond and a 50% weight to cash, while the duration-adjusted five-year bond has 20% weight to the five-year bond and an 80% weight to cash. As a result, and noting that cash has zero excess return, the excess return on (say) the five-year duration-adjusted bond is 20% of the excess return on the five-year unadjusted bond.

Each portfolio is re-constructed on a monthly basis based on signals for the 40 bonds at the end of each month. Based on the re-constructed portfolios at the end of the month, the returns for the five portfolios/strategies is determined for the subsequent month.

The performance of the five portfolios/strategies is compared with an equally weighted benchmark of all 40 bonds. The benchmark is also used to estimate the portfolio’s alphas and betas and to calculate tracking error and the information ratio. For the monthly rebalancing of the five portfolios as well as the benchmark, transaction costs of 2.5 basis points are assumed on each round trip (buy and sell).

Each portfolio is comprised of bonds denominated in different currencies. Assuming hedging costs reflect short-rate differentials, the excess return a bond earns over the short rate in its domestic currency is the excess return that a foreign exchanged (FX)-hedged investment in that bond will earn reflected in any base currency. The excess returns presented below reflect FX-hedged returns.

There is evidence of excess return predictability across all signals. Tables 5.5 and 5.6 show increasing excess return with signal strength, with the mean excess returns of P3 portfolios consistently higher than those of P2 portfolios that in turn are consistently higher than those of P1 portfolios. At the same time, the P3 portfolios appear to be riskier with higher volatilities, Sharpe ratios, and higher betas in regressions of excess returns on the benchmark. The quantile portfolios based on the expected return signal show the greatest spread in betas with 0.7 for the P1 and 1.3 for the P3 portfolio. The P3 portfolios based on the term premium signal (under both the mean reverting and perfect macro foresight scenarios) and expected return signal (under the perfect macro foresight scenario) show significant positive alphas.

Table 5.5 In-sample backtest expected return—part 1

Table 5.6 In-sample backtest expected return—part 2

Also the results for long-short portfolios, the difference portfolios (P3 − P1) and the factor portfolios, indicate excess return predictability, with statistically significant mean excess returns and significant, positive alphas. At the same time, despite these being zero-duration portfolios, all long-short portfolios show significant, positive betas. Compared with the carry signal, the term premium signal with mean-reverting macro variables implies higher levels of alphas and betas and higher significance levels.

Results under the perfect macro foresight assumption indicate the scope for further improvements in alpha and risk-adjusted returns based on accurate macroeconomic forecasts. The alphas of the difference portfolio are higher by 12 and 16 basis points, respectively, for the expected return and term premium signals. The information ratios increase from 0.28 to 0.44 and from 0.48 to 0.58 for the expected return and term premium signals, respectively.

Figure 5.4 shows the evolution of the cumulative excess return of the factor portfolio over time. This portfolio shows a meaningful increase in the cumulative excess return after 1970 (the point in time when data on all four markets is available; prior to this, only US data is available). In contrast, the cumulative return of the carry-based strategy shows a continuous increase only from the early 1980s onwards, possibly coinciding with start of the secular decline in interest rates (see Coche et al. 2017a).

Fig. 5.4

Cumulative return of factor portfolios

4.2 Out-of-Sample Backtesting

To better assess the suitability of the model to support real-world decision-making, we repeat the analysis of time-series properties by successively re-estimating model parameters in an out-of-sample setting. That is, starting in January 1990, monthly re-estimations of the model parameters are performed, and expected returns and term premia are calculated on the basis of market information available at that point in time.⁴ As before, the projection horizon to derive the return expectations is the subsequent 12 months. Results of this analysis are shown in Table 5.7.

Table 5.7 Out-of-sample backtest (1990 to 2016)

The properties of the term premium signal in the out-of-sample setting are broadly in line with the in-sample forecasts over the same period. Comparing Tables 5.7 and 5.8 of the Annex with in-sample statistics starting in 1990, we find that the level and significance of coefficients in the regressions of the term premium on excess returns are of similar magnitude, both for mean reverting and perfect foresight macro. Further, R²s, accuracy numbers and F1 scores are comparable. However, the statistical significance and explanatory power of the expected return signal appears to be weaker in the out-of-sample setting.

Compared with the carry signal (right panel of Table 5.4), the expected return and the term premium signals both under the mean reverting and under the perfect foresight macro scenarios show higher significance levels and higher explanatory power.

5 Discussion

Asset prices are driven by a wide range of factors. The role of the active portfolio manager is to develop a good understanding of these return drivers in order to understand and manage the risks embedded in the portfolio and to seek to add value (outperformance) relative to the benchmark.

Macroeconomic cycles—with fluctuations in inflation and the output gap—and future prospects for the economy have a fundamental influence on bond prices. Data relating bond prices to the macroeconomic state of the economy is available over many decades—and this relationship is captured by the model we have presented.

We have shown that with perfect foresight on macro developments, the model can generate statistically significant excess returns. Nevertheless, the model also generates significant excess returns with a naïve (AR1) projection of macro variables—this is less expected and while the backtested results of the model are very encouraging, we need to guard against being overconfident in the ability of generating excess returns solely on the basis of a model. We should recognise that financial markets in general—and G7 government bond markets in particular—are likely to be, to a high degree, informationally efficient, with a large number of sophisticated players seeking to maximise profit. Thus, there should be no easy opportunities to outperform. This leads us to question the excess return generated by the model in our out-of-sample backtesting. We contemplate three possible explanations:

• (1) Data mining—that is, we have changed the model specification until we found one that “works”;

• (2) The model has identified risk factors that can be exploited for generating higher return by earning the risk premiums associated with these factors; and

• (3) The model has identified inefficiencies in the market that can be exploited for generating excess return without additional risk.

A model that only works because of data mining is a useless model as it will stop working going forward. The economic rationale underpinning the model specifications adopted in this chapter (e.g. a Taylor rule approach for the short rate) and the fact that the “no-model” carry signal also generates excess return provide considerable confidence that data mining is not the dominant source of excess return predictability.

It is healthy to be sceptical of the suggestions that we have found a formula to generate excess returns without assuming additional risk in the very efficient government bond markets we are analysing. We would therefore lean towards the suggestion that the model exploits one or multiple risk premiums in generating excess returns.

Risk premiums are time-varying and not perfectly correlated across different markets. A signal (such as carry or the model expected return) that picks up on the size of the risk premium can then be used to take on additional (duration) risk when such risk is most rewarded and shed risk when it is poorly rewarded. We note the counter-cyclical nature of this strategy as more exposure is taken at a time when other investors shy away from assuming such exposure.

The results of backtesting the model show that excess returns could have been generated if we had had perfect foresight on macroeconomic developments. This is reassuring as it confirms that macro fundamentals are one driver of bond prices. Unfortunately, real-world portfolio managers do not have perfect foresight, and accurately forecasting the future state of the economy may be as challenging as accurately forecasting future bond prices. While portfolio managers will have developed their own view on the evolution of the economy, the market will already have “priced-in” some form of consensus view of future macroeconomic development into current bond prices, making outperformance difficult even with a well-informed outlook on the macro economy.

In using the model, we also need to recognise that the relationship between the state of the economy and bond prices may have evolved over time. Over the past 30 years we have witnessed a dramatic fall in yield levels in developed markets, it is believed that the real neutral rate has also fallen over this period.⁵ Furthermore, the recovery following the 2007–2008 financial crisis has been particularly shallow and government bond markets have been distorted by large-scale purchases of longer-maturity bonds, with the specific objective of reducing long-term financing costs (i.e. reducing long-term yields and compressing the term premium).

For the above reasons, the model will always remain only one input to our active investment decision-making process—with the final decision ultimately being a judgement call made by the portfolio manager.⁶ While model signals are not automatically implemented, the model signal provides a valuable indicator of current over- or under-valuation of bonds in a historical context and serves as a cornerstone for the financial market discussion and the investment decision-making that follows.

Beyond forecasting the return on bonds of different maturity, the shadow short rate modelling framework can provide the portfolio manager with some insight into the normalisation or “lift-off” of the policy rate, as progress towards the central bank’s macroeconomic policy objectives results in the shadow short rate approaching the lower bound (from below) and eventually in an increase in the actual policy rate.

In this chapter, we focused on the application of the macro-based yield-curve model to support active decision-making within and across government bond markets. For the cross-market positions, we assumed that currency hedging costs are closely matched by short-rate differentials. The model could be extended to account for deviations from the covered interest rate parity in which the currency hedging cost differs from short-rate differential. The model could also be extended to model currency movements—which are in part conditioned by the evolution of short-rate differentials that is already modelled.

6 Conclusions

Active portfolio management is a difficult task, in particular, if it aims at outperforming a benchmark of securities in deep, liquid, and well-researched fixed-income markets. While current bond prices are observable, their future values are not. Expectations about the horizon value of bonds are thus required. In this chapter, we propose a model that estimates these future values by connecting a modified Taylor rule with a rotated Nelson-Siegel yield-curve model. This set-up evaluates a central bank’s interest rate target in response to economic and inflation developments. Furthermore, the chosen approach allows for modelling a negative “shadow short rate” even when the actual policy rate is restricted by the zero lower bound. From the estimates of the monetary policy rate, the yield-curve model dynamically constructs the level, slope, and curvature of future term structures. By comparing the current bond prices with the future projections of these prices, return and term premium estimates are developed.

We show that there is value to be had from using the model’s expected return and term premium signals to guide portfolio construction even under the naïve mean-reverting macro data assumption. The value of using the model to guide portfolio construction increases significantly with perfect foresight on the evolution of macro data. This result supports the integration of macro forecasts into the investment decision-making process.

Annex

Table 5.8 In-sample backtest (1990 to 2016)