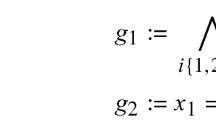Distributed Hybrid Control Synthesis for Multi-Agent Systems from High-Level Specifications

Abstract

Current control applications necessitate in many cases the consideration of systems with multiple interconnected components. These components/agents may need to fulfill high-level tasks at a discrete planning layer and also coupled constraints at the continuous control layer. Toward this end, the need for combined decentralized control at the continuous layer and planning at the discrete layer becomes apparent. While there are approaches that handle the problem in a top-down centralized manner, decentralized bottom-up approaches have not been pursued to the same extent. We present here some of our results for the problem of combined, hybrid control and task planning from high-level specifications for multi-agent systems in a bottom-up manner. In the first part, we present some initial results on extending the necessary notion of abstractions to multi-agent systems in a distributed fashion. We then consider a setup where agents are assigned individual tasks in the form of linear temporal logic (LTL) formulas and derive local task planning strategies for each agent. In the last part, the problem of combined distributed task planning and control under coupled continuous constraints is further considered.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We consider multi-agent systems that need to fulfill high-level tasks, e.g., to periodically reach a given subset of states, or to reach a certain set of states in a particular order, and also undergo dynamically coupled constraints, e.g., to maintain connectivity, or avoid collisions. Toward this end, the need for combined decentralized control at the continuous layer and planning at the discrete layer becomes apparent. While there are approaches that handle the problem in a top-down centralized manner, decentralized bottom-up approaches have not been pursued to the same extent. We present here some of our results for the problem of hybrid control synthesis of multi-agent systems under high-level specifications in a bottom-up manner. This approach can enhance various system properties, such as reducing the computational complexity induced by the number of agents, improving modularity in terms of new agents entering the system, and incorporating fault tolerance, robustness, and adaptability to changes in the workspace.

The next part focuses on distributed abstractions of the multi-agent system. We assume that the agents’ dynamics consist of feedback interconnection terms, which represent dynamically coupled constraints of the multi-agent system, and additional bounded input terms, which we call free inputs and provide the ability for motion planning under the coupled constraints. For the derivation of the symbolic models, we quantify admissible space-time discretizations in order to capture reachability properties of the original system. We provide sufficient conditions which establish that the abstraction of our original system is well posed, in the sense that the finite transition system which serves as an abstract model for the motion capabilities of each agent has at least one outgoing transition for every discrete state. Each agent’s abstract model is based on the knowledge of its neighbors’ discrete positions and the transitions are performed through the selection of appropriate hybrid control laws in place of the agent’s free input, which enables the manipulation of the coupling terms and can drive the agent to its possible successor states. In addition, the derived discretizations include parameters whose tuning enables multiple transitions and provides quantifiable motion planning capabilities for the system. Finally, the corresponding results are generalized by allowing for a varying degree of decentralization i.e., by building each agent’s abstract model based on the knowledge of its neighbors’ discrete positions up to a tunable distance in the communication graph.

In the next part, we deal with dependent temporal logic specifications at the discrete planning level. Namely, the agents’ behaviors are limited by mutually independent temporal logic constraints, allowing to express safety, surveillance, sequencing, or reachability properties of their traces, and, at the same time, a part of the specification expresses the agents’ tasks in terms of the services to be provided along the trace. These may impose requests for the other agent’s collaborations. We propose a two-phase solution based on automata-based model checking, in which the planning procedure for the two types of specifications is systematically decoupled. While this procedure significantly reduces the cost in the case of sparse dependencies, it meets the complexity the centralized solution at worst case. We introduce an additional iterative limited horizon planning technique as a complementary technique.

We then tackle the multi-agent control problem under local temporal logic tasks and continuous-time constraints. The local tasks are dependent due to collaborative services, while at the same time the agents are subject to dynamic constraints with their neighboring agents. Thus, integration of the continuous motion control with the high-level discrete network structure control is essential. Particularly, the agents are subject to relative-distance constraints which relate to the need of maintaining connectivity of the overall network. The local tasks capture the temporal requirements on the agent’s actions, while the relative-distance constraints impose requirements on the collective motion of the whole team. Our approach to the problem involves an offline and an online step. In the offline step, we synthesize a high-level plan in the form of a sequence of services for each of the agents. In the online step, we dynamically switch between the high-level plans through leader election and choose the associated continuous controllers. The whole team then follows the leader toward until its next service is provided and then a new leader is selected. It is guaranteed that each agent’s local task will be accomplished and the communication network remains connected at all time.

2 Decentralized Abstractions

2.1 Introduction

In this section, we focus on multi-agent systems with continuous dynamics consisting of feedback terms, which induce coupling constraints, and bounded additive inputs, which provide the agents’ control capabilities. The feedback interconnection between the agents can represent internal dynamics of the system, or alternatively, a control design guaranteeing certain system properties (e.g., network connectivity or collision avoidance), which appears often in the multi-agent literature. The results are based on our recent works [3] and [4], which provide sufficient conditions for the existence of distributed discrete models for multi-agent systems with coupled dynamics. In particular, our main goal is to obtain a partition of the workspace into cells and select a transition time step, in order to derive for each agent an abstract discrete model with at least one outgoing transition from each discrete state. Compositional approaches for symbolic models of interconnected systems have been also studied in the recent works [7, 17, 19, 20], and [21], and are primarily focused on the discrete time case.

2.2 Problem Formulation

We consider multi-agent systems of the form

$$\begin{aligned} \dot{x}_{i}=f_{i}(x_{i},\mathbf {x}_j)+v_{i},x_i\in \mathbf {R}^n, i\in \mathscr {N}, \end{aligned}$$

(12.1)

where $\mathscr {N}:=\{1,\ldots ,N\}$ stands for the agents’ set. Each agent is assumed to have a fixed number $N_i$ of neighbors $j_1,\ldots ,j_{N_i}$. The dynamics in (12.1) are decentralized and consist for each $i\in \mathscr {N}$ of a feedback term $f_{i}(\cdot )$, which depends on i’s state $x_i$ and the states of its neighbors, which are compactly denoted by $\mathbf {x}_j(=\mathbf {x}_{j(i)}):=(x_{j_{1}},\ldots ,x_{j_{N_i}})$, and an additional input term $v_{i}$, which we call free input. We assume that the feedback terms $f_{i}(\cdot )$ are globally bounded, namely, there exists a constant $M>0$ such that

$$\begin{aligned} |f_{i}(x_{i},\mathbf {x}_j)|\leqslant M, \forall (x_{i},\mathbf {x}_j)\in \mathbf {R}^{(N_i+1)n} \end{aligned}$$

(12.2)

and that they are globally Lipschitz. Thus, there exist constants $L_1,L_2>0$, such that

$$\begin{aligned} |f_{i}(x_{i},\mathbf {x}_j)-f_{i}(x_{i},\mathbf {y}_j)|\leqslant L_1 |(x_{i},\mathbf {x}_j)-(x_{i},\mathbf {y}_j)|, \end{aligned}$$

(12.3)

$$\begin{aligned} |f_{i}(x_{i},\mathbf {x}_j)-f_{i}(y_{i},\mathbf {x}_j)| \leqslant L_2 |(x_{i},\mathbf {x}_j)-(y_{i},\mathbf {x}_j)|, \end{aligned}$$

(12.4)

for all $x_{i},y_{i} \in \mathbf R^n$, $\mathbf {x}_j,\mathbf {y}_j\in \mathbf R^{N_in}$ and $i\in \mathscr {N}$. Furthermore, we consider piecewise continuous free inputs $v_{i}$ that satisfy the bound

$$\begin{aligned} |v_{i}(t)|\leqslant v_{\max },\forall t\geqslant 0, i\in \mathscr {N}. \end{aligned}$$

(12.5)

The coupling terms $f_i(x_i,\mathbf {x}_j)$ are encountered in a large set of multi-agent protocols [16], including consensus, connectivity maintenance, collision avoidance, and formation control. In addition, (12.1) may represent internal dynamics of the system as for instance in the case of smart buildings (see e.g., [1]). It is also assumed that the maximum magnitude of the feedback terms is higher than that of the free inputs, namely, that $v_{\max }<M$. This assumption is in part motivated by the fact that we are primarily interested in maintaining the property that the feedback is designed for, and secondarily, in exploiting the free inputs in order to accomplish high-level tasks. A class of multi-agent systems of the form (12.1) which justifies this assumption has been studied in our companion work [5], which is focused on robust network connectivity maintenance by means of bounded feedback laws. It is worthwhile mentioning that all these assumptions are removed in [6], where the discrete models are built online over a bounded time horizon, and require only forward completeness of the system’s trajectories.

In what follows, we consider a cell decomposition $\mathbf S=\{S_{l}\}_{l\in \mathscr {I}}$ of the state space $\mathbf R^n$, which can be regarded as a partition of $\mathbf R^n$, and a time step $\delta t>0$. We will refer to this selection as a space and time discretization. Given the indices $\mathscr {I}$ of a decomposition, we use the notation $\mathbf {l}_i=(l_i,l_{j_1},\ldots ,$ $l_{j_{N_i}})\in \mathscr {I}^{N_i+1}$ to denote the indices of the cells where agent i and its neighbors belong and call it the cell configuration of i. Our goal is to build an individual transition system of each agent i with state set the cells of the decomposition, actions determined through the possible cells of its neighbors, and transition relation specified as follows. Given the initial cells of agent i and its neighbors, it is possible for i to perform a transition to a final cell, if for all states in its initial cell there exists a free input, such that its trajectory will reach the final cell at time $\delta t$, for all possible initial states of its neighbors in their cells, and their corresponding free inputs.

For the synthesis of high-level plans, we require the discretization to be well posed, in the sense that for each agent and any initial cell it is possible to perform a transition to at least one final cell. In order to illustrate the concept of a well-posed space-time discretization, consider the cell decompositions depicted in Fig. 12.1 and a time step $\delta t$. For both decompositions in the figure we depict a cell configuration of agent i and represent the endpoints of agent’s i trajectories at time $\delta t$ through the tips of the arrows. In the left decomposition, we select three distinct initial conditions of i and observe that the corresponding reachable sets at $\delta t$ lie in different cells. Thus, given this cell configuration of i it is not possible to find a cell in the decomposition which is reachable from every point in the initial cell, and we conclude that the discretization is not well posed for the system. In the right figure, we observe however that for the three distinct initial positions in cell $S_{l_i}$, it is possible to drive agent i to cell $S_{l_i'}$ at time $\delta t$. We assume that this is possible for all initial conditions in this cell and irrespectively of the initial conditions of i’s neighbors in their cells and the inputs they choose. By additionally assuming this property for all configurations of the agents, we establish a well posed discretization for the system.

Fig. 12.1

Illustration of a non-well posed (A) and a well posed (B) discretization

2.3 Derivation of Well-Posed Discretizations

In order to enable the desired transitions of each agent in the presence of the coupling terms $f_{i}(\cdot )$, we assign hybrid control laws to the free inputs $v_{i}$. We next provide the specific feedback laws that are utilized therefore. Consider first a cell decomposition $\mathbf S=\{S_{l}\}_{l\in \mathscr {I}}$ of $\mathbf R^n$ and a time step $\delta t$. For each agent $i\in \mathscr {N}$ and cell configuration $\mathbf {l}_i=(l_i,l_{j_1},\ldots ,l_{j_{N_i}})$ of i select an $N_i+1$-tuple of reference points $(x_{i,G},\mathbf {x}_{j,G})\in S_{l_{i}}\times (S_{l_{j_1}}\times \cdots \times S_{l_{j_{N_i}}})$ and define $F_{i,\mathbf {l}_i}(x_i):=f_i(x_i,\mathbf {x}_{j,G})$, $x_i\in \mathbf R^n$. Also, let $z_i(\cdot )$ be the solution of the initial value problem $\dot{z}_i=F_{i,\mathbf {l}_i}(z_i)$, $z_i(0)=x_{i,G}$, which we call the reference trajectory of i. This trajectory is obtained by “freezing” agent i’s neighbors at their corresponding reference points through the feedback term

$$\begin{aligned} k_{i,\mathbf {l}_i,1}(t,x_{i},\mathbf {x}_j):=f_i(z_i(t),\mathbf {x}_{j,G})-f_i(x_i,\mathbf {x}_j), \end{aligned}$$

(12.6)

in place of the agent’s free input $v_i$. Also, by selecting a vector $w_i$ from the set

$$\begin{aligned} W:=B(\lambda v_{\max }),\lambda \in (0,1), \end{aligned}$$

(12.7)

(the ball with radius $\lambda v_{\max }$ in $\mathbf R^n$) and assuming that we can superpose to the reference trajectory the motion of i with constant speed $w_i$, namely, move along the curve $\bar{x}_i(\cdot )$ defined as $\bar{x}_i(t):=z_i(t)+tw_i$, $t\geqslant 0$, we can reach the point x inside the depicted ball in Fig. 12.2 at time $\delta t$ from the reference point $x_{i,G}$. The parameter $\lambda$ in (12.7) stands for the part of the free input that is used to increase the transition choices from the given cell configuration. In a similar way, it is possible to reach any point inside the ball by a different selection of $w_i$. This ball has radius

$$\begin{aligned} r:=\lambda v_{\max }\delta t, \end{aligned}$$

(12.8)

namely, the distance that the agent can cross in time $\delta t$ by exploiting the part of the free input that is available for reachability purposes. For the abstraction, we require the ability to perform a transition to each cell which has nonempty intersection with $B(z_i(\delta t);r)$. These transitions are enabled via the feedback laws

$$\begin{aligned} k_{i,\mathbf {l}_i}(t,x_i,\mathbf {x}_j;x_{i0},w_i): =k_{i,\mathbf {l}_i,1}(t,x_i,\mathbf {x}_j)+k_{i,\mathbf {l}_i,2}(x_{i0})+k_{i,\mathbf {l}_i,3}(w_i), \end{aligned}$$

(12.9)

parameterized by $x_{i0}\in S_{l_i}$, $w_i\in W$, where $k_{i,\mathbf {l}_i,1}(\cdot )$ is given in (12.6) and with

$$\begin{aligned} k_{i,\mathbf {l}_i,2}(x_{i0}):= \frac{1}{\delta t}(x_{i,G}-x_{i0}),\quad k_{i,\mathbf {l}_i,3}(w_i):= w_i, \quad x_{i0}\in S_{l_i},w_i\in W. \end{aligned}$$

(12.10)

In order to perform for instance a transition to the cell where the point x in Fig. 12.2 belongs, we require that the feedback law $k_{i,\mathbf {l}_i}(\cdot )$ drives agent i to the endpoint of the curve $\bar{x}_i(\cdot )$ from each initial condition in $S_{l_i}$. This is accomplished by exploiting the extra terms $k_{i,\mathbf {l}_i,2}(\cdot )$ and $k_{i,\mathbf {l}_i,3}(\cdot )$. The derivation of well-posed discretizations is additionally based on the choice of cell decompositions and associated time steps $\delta t$ which ensure that the magnitude of the feedback law apart from the term $w_i$ in $k_{i,\mathbf {l}_i,3}(\cdot )$ does not exceed $(1-\lambda )v_{\max }$. Thus, due to (12.7), which implies that $|w_i|\leqslant \lambda v_{\max }$, it follows that the total magnitude of the applied control law will be consistent with assumption (12.5) on the free inputs’ bound. Notice also that due to the assumption $v_{\max } < M$, it is in principle not possible to cancel the interconnection terms. Furthermore, the control laws $k_{i,\mathbf {l}_i}(\cdot )$ are decentralized, since they only use information of agent i’s neighbors states and they depend on the cell configuration $\mathbf {l}_i$, through the reference points $(x_{i,G},\mathbf {x}_{j,G})$ which are involved in (12.6) and (12.10).

Fig. 12.2

Consider any point x inside the ball with center $z_i(\delta t)$. Then, the control law $k_{i,\mathbf {l}_i}(\cdot )$ ensures that for each initial condition $x_{i0}\in S_{l_i}$, agent’s i trajectory $x_i(\cdot )$ will reach x at time $\delta t$. Thus, since $x\in S_{l_i'}$, we obtain a transition to $S_{l_i'}$

Based on the control laws in (12.9) and assuming given a space-time discretization $\mathbf S-\delta t$, we derive the transition system $TS_i:=(Q_i,Act_i,\longrightarrow _i)$ of each agent, where $Q_i$ is a set of states, $Act_i$ is a set of actions, and $\longrightarrow _i$ is a transition relation with $\longrightarrow _i\subset Q_i\times Act_i\times Q_i$. In particular, $TS_i$ is given by $Q_i:=\mathscr {I}$, i.e., the cells of the decomposition, $Act_i:=\mathscr {I}^{N_i+1}$ and the transition relation $\longrightarrow _i$ defined as follows: given $l_i\in \mathscr {I}$, $\mathbf {l}_i=(l_i,l_{j_1},\ldots ,l_{j_{N_i}})$ and $l_i'\in \mathscr {I}$, we enable the transition $(l_i,\mathbf {l}_i,l_i')\in \longrightarrow _i$, if there exists a parameter $w_i$, such that the control law $k_{i,\mathbf {l}_i}(\cdot )$ in (12.9) guarantees that the agent will reach cell $S_{l_i'}$ at $\delta t$, from any initial condition in its cell, based only on the fact that its neighbors belong to the corresponding cells in $\mathbf {l}_i$. By denoting $\mathrm{Post}_i(l_i;\mathbf {l}_i):=\{l_i'\in \mathscr {I}:(l_i,\mathbf {l}_i,l_i')\in \longrightarrow _i\}$, it follows that the discretization is well posed iff for each agent $i\in \mathscr {N}$ and cell configuration $\mathbf {l}_i=(l_i,l_{j_1},\ldots ,l_{j_{N_i}})$ it holds $\mathrm{Post}_i(l_i;\mathbf {l}_i)\ne \emptyset$. In particular we have the following result.

Theorem 12.1

Consider a cell decomposition $\mathbf S$ of   $\mathbf R^n$ with diameter $d_{\max }$, a time step $\delta t$, the parameter $\lambda \in (0,1)$ and define $L:=\max \{3L_{2}+4L_{1}\sqrt{N_i},i\in \mathscr {N}\}$, with $L_1$ and $L_2$ as given in (12.3) and (12.4). We assume that $d_{\max }\in \left( 0,\frac{(1-\lambda )^2 v_{\max }^{2}}{4ML}\right]$ and $\delta t \in \left[ \frac{(1-\lambda )v_{\max }-\sqrt{(1-\lambda )^2 v_{\max }^{2}-4MLd_{\max }}}{2ML},\frac{(1-\lambda )v_{\max }+\sqrt{(1-\lambda )^2 v_{\max }^{2}-4MLd_{\max }}}{2ML}\right]$. Then, the space-time discretization is well posed for (12.1). In particular, for each agent $i\in \mathscr {N}$ and cell configuration $\mathbf {l}_i=(l_i,l_{j_1},\ldots ,l_{j_{N_i}})$, it holds $\mathrm{Post}_i(l_i;\mathbf {l}_i)=\{l\in \mathscr {I}:S_l\cap B(z_i(\delta t);r)\ne \emptyset \}$, with $z_i(\cdot )$ denoting the corresponding reference trajectory of i and r as in (12.8).

2.4 Abstractions of Varying Decentralization Degree

We next present a generalization of the previous approach, where each agent’s abstract model has been based on the knowledge of the discrete positions of its neighbors, by allowing the agent to have this information for all members of the network up to a certain distance in the communication graph. The latter provides an improved estimate of the potential evolution of its neighbors and allows for more accurate discrete agent models, due to the reduction of the control magnitude which is required for the manipulation of the coupling terms. Therefore we introduce also some extra notation. Given $m\geqslant 1$, we denote by $\mathscr {N}_i^m$ the set of agents from which i is reachable through a path of length m and not by a shorter one, excluding also the possibility to reach itself through a cycle. We also define the set $\bar{\mathscr {N}}_i^m:=\bigcup _{\ell =1}^m\mathscr {N}_i^{\ell }\cup \{i\}$, namely, the set of all agents from which i is reachable by a path of length at most m, including i, and call it the m-neighbor set of i (see Fig. 12.3).

Fig. 12.3

This figure illustrates 7 agents of a network. The sets $\mathscr {N}_1^m$, $\bar{\mathscr {N}}_1^m$ of agent 1 up to paths of length $m=3$ are: $\bar{\mathscr {N}}_1^1=\{1,5\}, \; \mathscr {N}_1^1=\{5\}$; $\bar{\mathscr {N}}_1^2=\{1,2,5,6\}, \; \mathscr {N}_1^2=\{2,6\}$; $\bar{\mathscr {N}}_1^3=\{1,2,3,5,6,7\}, \; \mathscr {N}_1^3=\{3,7\}$

The derivation of the discrete models is based as previously on the design of appropriate hybrid feedback laws in place of the $v_{i}$’s, which enable the desired transitions. We, therefore, provide a modification of the control law (12.6) which is based on a more accurate estimation for the evolution of agent i’s neighbors. In particular, select an ordered tuple of indices $\mathbf {l}_i$ corresponding to the cells where the agents in i’s m-neighbor set belong, and assume without any loss of generality that $\mathscr {N}_i^{m+1}\ne \emptyset$. Also, choose a reference point $x_{\ell ,G}$ from the cell of each agent in $\bar{\mathscr {N}}_i^m$ and consider the initial value problem (IVP) $\dot{z}_{\ell }(t) = f_{\ell }(z_{\ell }(t),z_{j(\ell )_1}(t),\ldots ,z_{j(\ell )_{N_{\ell }}}(t))$, $t\geqslant 0$, $\ell \in \bar{\mathscr {N}}_i^{m-1}$, $z_{\ell }(0)= x_{\ell ,G}$, for all $\ell \in \bar{\mathscr {N}}_i^{m-1}$, with the terms $z_{\ell }(\cdot )$, $\ell \in \mathscr {N}_i^{m}$ defined as $z_{\ell }(t):=x_{\ell ,G}$, for all $t\geqslant 0$, $\ell \in \mathscr {N}_i^{m}$. This IVP provides a solution of the unforced, i.e., without free inputs subsystem formed by the m-neighbor set of agent i. In addition, the agents are initiated from their reference points in their cells and the neighbors precisely m hops away are considered fixed at their corresponding reference points for all times. In analogy to the previous section, we will call the ith component $z_i(\cdot )$ of the solution to the IVP the reference trajectory of i. We also compactly denote as $\mathbf {z}_j(\cdot ):=(z_{j_1}(\cdot ),\ldots ,z_{j_{N_i}}(\cdot ))$ the corresponding components of i’s neighbors. The key part in this modification is that the latter provide a more accurate estimate of the neighbors’ possible evolution over the time interval $[0,\delta t]$. Thus, by replacing the feedback component in (12.6) by $k_{i,\mathbf {l}_i,1}(t,x_{i},\mathbf {x}_j):= f_i(z_i(t),\mathbf {z}_j(t))-f_i(x_i,\mathbf {x}_j), t\in [0,\infty ),(x_i,\mathbf {x}_j)\in \mathbf R^{(N_i+1)n}$, we can exploit the control law in (12.9) to obtain analogous transition capabilities as in the previous section. It is noted that this selection reduces the control effort which is required to compensate for the evolution of i’s neighbors and leads to improved discretizations. Sufficient conditions for the derivation of well posed discretizations along the lines of Theorem 12.1 can be found in [4].

3 Multi-agent Plan Synthesis

In this section, we focus on task and motion planning for a multi-agent system that has already been abstracted as a discrete, finite, state-transition system using the technique introduced in Sect. 12.2, or similar. In contrast to Sect. 12.4, the agents here are dependent on each other in terms of their LTL specifications that capture potentially collaborative tasks, whereas we assume that they can communicate in a limited way and they are not subject to relative-distance constraints. Next to the task specifications, each agent is subject to an independent motion specification, also given in LTL. We tackle high-computational demands associated with centralized planning via introducing a two-phase procedure that largely decouples task planning and motion planning. Moreover, we discuss that the solution can benefit further from utilizing receding horizon planning approach. This section, thus, overviews results presented in [23] and [22] and introduces their integration into a single task and motion planning technique. An interested reader is referred to [23] and [22] for full technical details on task and motion planning decomposition and receding horizon planning, respectively.

3.1 Problem Formulation

Similarly as in the previous sections, we consider a team of N possibly heterogeneous, autonomous agents with unique identities (IDs) $i\in \mathscr {N}=\{1,\ldots ,N\}$. However, here the agent i’s capabilities are modeled through finite transition systems (TS)

$$ T_i = (S_i, s_{\textit{init,i}},{A_i},\rightarrow _i, \varPi _i, L_i, \varSigma _i, \mathscr {L}_i, \textit{Sync}_i), $$

where the set of states $S_i$ of the TS represent discrete states of the agent i (e.g., the location of the agent in the environment that is partitioned into a finite number of cells), and $s_{ init,i } \in S_i$ is the agent i’s initial state (e.g., its initial cell). The actions $A_i$ abstract the agent’s low-level controllers, and a transition $s \xrightarrow {\alpha }_i s'$ from $s\in S_i$ to $s' \in S_i$ correspond to the agent’s capability to execute the action $\alpha \in A_i$ (e.g., to move between two cells of the environment). We note that a transition duration is arbitrary and unknown prior its execution. Atomic propositions $\varPi _i$ together with the labeling function $L_i: S_i \rightarrow 2^{\varPi _i}$ are used to mark interesting properties of the system states (e.g., a cell is safe). Labeling function $\mathscr {L}_i: Act \rightarrow 2^{\varSigma _i} \cup \mathscr {E}_i$ associates each action $\alpha \in A_i$ with a set of services of interest $\sigma \in 2^{\varSigma _i}$ that are provided upon its execution (e.g., an object pick-up), or with a special silent service set $\mathscr {E}_i = \{\varepsilon _i\}$, $\varepsilon _i \not \in \varSigma _i$, indicating that no service of interest is provided upon the execution of action $\alpha$. Traces of the transition system are infinite alternating sequences of states and actions that start in the initial state and follow the transition function. Intuitively, they provide abstractions of the agent’s long-term behaviors (e.g., the agent’s trajectories in the environment). A trace $\tau _i = s_{i,1}\alpha _{i,1}s_{i,2}\alpha _{i,2}\ldots$ produces words $w(\tau _i) = L(s_{i,1})L(s_{i,2})\ldots$, and $\omega (\tau _i) = \mathscr {L}(\alpha _{i,1})\mathscr {L}(\alpha _{i,2})\ldots$ representing the sequences of state properties that hold true, and services that are provided, respectively.

The agents can communicate, and in particular they all follow this synchronization protocol: An agent i can send a synchronization request $sync_i(I)$ to a subset of agents $\{i\} \subseteq I \subseteq \mathscr {N}$ notifying that it is ready to synchronize. Then, before proceeding with execution of any action $\alpha \in Act_i$, it waits in its current state to receive $sync_{i'}(I)$ from each $i' \in I$. Assuming lossless communication and instant synchronization upon receiving the needed synchronization requests, the agents can this way enforce waiting for each other and executing actions simultaneously. We denote by $Sync _i = \{sync_i(I) \mid \{i\} \subseteq I \subseteq \mathscr {N}\}$ the set of all synchronization requests of agent i.

Each agent $i \in \mathscr {N}$ is given a specification that consists of

• a motion specification $\phi _i$, which is an LTL$_{\setminus \mathsf X}$ formula over $\varPi _i$ that captures requirements on the states the agent passes through, such as safety, reachability, persistent surveillance, and their combination. The motion specification is interpreted over the word $w(\tau _i)$; and

• a task specification $\psi _i$, which is an LTL formula over ${\varSigma } = \bigcup _{i' \in \mathscr {N}} \varSigma _{i'}$ that captures requirements on services provided along the system execution. In contrast to the motion specification, the task specification is collaborative and yields dependencies between the agents. Each task specification is interpreted over the set of all words $\omega (\tau _i')$, $i' \in \mathscr {N}$. In particular, agent i decides whether $\psi _i$ is satisfied from its local point of view by looking at the subsequence of non-silent services, i.e., services of interest of $\omega (\tau _i)$ and the services provided by the remainder of the team at the corresponding times.

Problem 12.1

Consider a set of agents $\mathscr {N} = \{1,\ldots ,N\}$, each of which is modeled as a transition system $T_i = (S_i, s_{\textit{init,i}},{A_i},\rightarrow _i, \varPi _i, L_i, \varSigma _i, \mathscr {L}_i, Sync _i)$, and assigned a task in the form of an LTL$_{\setminus X}$ formula $\phi _i$ over $\varPi _i$ and $\psi _i$ over $\varSigma = \bigcup _{i' \in \mathscr {N}} \varSigma _{i'}$. For each $i \in \mathscr {N}$ find a plan, i.e., (i) a trace $\tau _i = s_{i,1}\alpha _{i,1}s_{i,2}\alpha _{i,2}\ldots$ of $T_i$ and (ii) a synchronization sequence $\gamma _i = r_{i,1}r_{i,2}\ldots$ over $\textit{Sync}_i$ with the property that the set of induced behaviors is nonempty, and both $\phi _i$ and $\psi _i$ are satisfied from the agent i’s viewpoint.

As each LTL formula can be translated into a BA, from now on, we pose the problem equivalently with the motion specification of each agent i given as a BA $B_i^\phi = (Q_i^\phi , q_{ init, i }^\phi , \delta _i^\phi , 2^{{\varPi _i}}, F_i^\phi )$, and the task one as a BA $B_i^\psi = (Q_i^\psi , q_{ init, i }^\psi , \delta _i^\psi , 2^{\varSigma }, F_i^\psi )$.

3.2 Problem Solution

Even though the agents’ motion specifications are mutually independent, each of them is dependent on the respective agent’s task specification, which is dependent on the task specifications of the other agents. As a result, the procedure of synthesizing the desired N strategies cannot be decentralized in an obvious way. However, one can quite easily obtain a centralized solution when viewing the problem as a synthesis of a single team plan. A major drawback of the centralized solution is the state-space explosion, which makes it practically intractable. We aim to decentralize the solution as much as possible. Namely, we aim to separate the synthesis of service plans yielding the local satisfaction of the task specifications from the syntheses of traces that guarantee the motion specifications. Our approach is to precompute possible traces and represent them efficiently, while abstracting away the features that are not significant for the synthesis of action plans. This abstraction serves as a guidance for the action and synchronization planning, which, by construction, allows for finding a trace complying with both the synthesized action and synchronization plans and the motion specification.

3.2.1 Preprocessing the Motion Specifications

Consider for now a single agent $i \in \mathscr {N}$, and its motion specification BA $B_ i^\phi$. We slightly modify the classical construction of a product automaton of $T_ i$ and $B_ i^\phi$ to obtain a BA that represents the traces of $T_ i$ accepted by $B_ i^\phi$, and furthermore explicitly captures the services provided along the trace.

Definition 12.1

(Motion product) The motion product of a TS $T_i$, and a BA $B_ i$ is a BA $P_i = (Q_{i}, q_{ init,i }, \delta _{i}, 2^{\varSigma _i} \cup 2^{\mathscr {E}_i}, F_{i})$, where $Q_{i} = S_i \times Q_i^\phi$; $q_{ init,i } = (s_{ init,i },q_{ init,i }^\phi )$; $((s,q),\mathscr {L}_i(\alpha ),(s',q')) \in \delta _{i}$ if and only if $s,\xrightarrow {\alpha }_i s'$, and $(q,L_i(s),q') \in \delta _i^\phi$; and $F_{i} = \{(s,q) \mid q \in F_i^\phi \}$.

We introduce a way to reduce the size of the motion product by removing all states and transitions that are insignificant with respect to the local satisfaction of the task specification, and hence with respect to the collaboration with others. Specifically, the significant states are only the ones that have an outgoing transition labeled with $\mathscr {L}_i(\alpha ) \ne \mathscr {E}_i$.

First, we remove all insignificant non-accepting states and their incoming and outgoing transitions and we replace each state with a set of transitions leading directly from the state’s predecessors to its successors, i.e., we concatenate the incoming and the outgoing transitions. The labels of the new transitions differ: if both labels of the concatenated incoming and outgoing transition are $\mathscr {E}_i$, then the new label will stay $\mathscr {E}_i$ to indicate that the transition represents a sequence of actions that are not interesting with respect to the local satisfaction of task specifications. On the other hand, if the label $\sigma$ of the incoming transition belongs to $2^{\varSigma _i}$, we use the action $\sigma$ as the label for the new transition. Each path between two significant states in $P_i$ then maps onto a path between the same states in the reduced motion product and the sequences of non-silent services read on the labels of the transitions of the two paths are equal; and vice versa. Second, we handle the insignificant accepting states similarly to the non-accepting ones, however, we do not remove the states whose predecessors include a significant state in order to preserve the accepting condition. Moreover, we remove all states from which none of the accepting states is reachable, and we can keep only one copy of duplicate states that have analogous incoming and outgoing edges. An example of the reduction is given in Fig. 12.4.

Fig. 12.4

An example of a part of a product automaton $P_i$ (top), and the corresponding part of the reduced product automaton $\ddot{P_i}$ (bottom)

There is a correspondence between the infinite runs of $P_i$ and the infinite runs of the reduced motion product, which we denote by $\ddot{P_i}$: for each run of $P_i$ there exists a run of $\ddot{P_i}$, such that the states of the latter one are a subsequence of the states of the former one, the sequences of non-silent services read on the labels of the transitions of the two runs are equal, and that the latter one is acceptable if and only if the former one is accepting; and vice versa. This correspondence will allow us to reconstruct a desired run of $P_i$ from a run of $\ddot{P_i}$, as we will discuss in Sect. 12.3.2.3.

3.2.2 Preprocessing the Task Specifications

The next two steps of the solution follow similar ideas as in Sect. 12.3.2.1: We build a local task and motion product $\bar{P_i}$ of the reduced motion product $\ddot{P_i}$ and the task specification BA $B_ i^\psi$ for each agent i separately, to capture the admissible traces of i that comply both with its motion and task specification. At this stage, the other agents’ collaboration capabilities are not included, yet. We again remove insignificant states, which are now ones that do not have an outgoing dependent transition, i.e., a transition labeled with a non-silent service $\sigma \in \varSigma \setminus \varSigma _i$. We thus reduce $\bar{P_i}$ to $\widehat{P_i}$. Similarly as before, there is a correspondence between the infinite runs of $\bar{P}_i$ and the infinite runs of $\widehat{P}_i$: for each run of $\bar{P}_i$ there exists a run of $\widehat{P}_i$, such that the states of the latter one are a subsequence of the states of the former one, the sequences of services read on the labels of the transitions leading from the significant states of the two runs are equal, and that the latter one is acceptable if and only if the former one is accepting; and vice versa.

Finally, we build the global product P of the reduced task and motion product automata $\widehat{P}_1, \ldots \widehat{P}_N$. Each accepting run of the global product P maps directly on the accepting runs of the reduced task and motion product automata and vice versa, for each collection of accepting runs of the reduced task and motion product automata, there exists an accepting run of the global product P.

3.2.3 Plan Synthesis

The final step of our solution is the generation of the plan in P and its mapping onto a trace $\tau _i$ of $T_ i$ and a synchronization sequence $\gamma _i$ over ${Sync_i}$, for all $i \in \mathscr {N}$. Using standard graph algorithms (see, e.g.,  [2]), we find an accepting run $q_1 q_2 \ldots$ over a word $\sigma _1\sigma _2\ldots$ in P, where $q_j = (\widehat{q}_{1,j},\ldots ,\widehat{q}_{N,j}, k)$, for all $j \geqslant 1$. For each agent $i\in \mathscr {N}$, we can project this accepting run onto the states of $\widehat{P}_i$, and then, due to the above discussed correspondences between runs of the product automata, we can also find sequences of the states in $\bar{P}_i$, $\ddot{P}_i$, $P_i$, such that the projection from an accepting run of $P_i$ onto the states of $T_i$ yield the desired trace $\tau _i$ (and also the desired sequence of services $\sigma _{i,1}\sigma _{i,2}\ldots$). The synchronization sequence $\gamma _i$ is constructed by setting $r_{i,j}$ to be the set of agents that need to collaborate on executing the transition from $s_{i,j}$ to $s_{i,j+1}$ in order to provide the service $\sigma _{i,j}$.

3.2.4 Receding Horizon Approach

Although we have reduced the size of each local product automaton before constructing the global product P, an additional improvement can be achieved by decomposing the infinite-horizon planning into an infinite sequence of finite-horizon planning problem that can further significantly reduce the size of the global product P.

In particular, following the ideas from [22], we propose to (1) partition the agents into classes based on their dependency observed in $\widehat{P}_1, \ldots , \widehat{P}_N$ within a horizon H; and then for each of the classes separately: (2) build a product automaton up to a predefined horizon h and synthesize a plan that leads to progress in satisfaction of the task specifications; (3) execute part of the plan till the first non-silent service is provided and repeat steps (1), (2), (3).

The benefit of the receding horizon approach reaches beyond tackling the tractability of multi-agent plan synthesis. It builds on Event-Triggered synchronization, and hence, it is especially useful in cases where the agents travel at different speeds than originally assumed.

3.2.5 Complexity

In the worst case, our solution meets the complexity of the centralized solution. However, this is often not the case. Since the size of the global product is highly dependent on the number of dependent services available in the agents’ workspace, our solution is particularly suitable for systems with complex motion capabilities, sparsely distributed services of interest, and occasional needs for collaboration.

4 Decentralized Control Under Local Tasks and Coupled Constraints

In this section, we tackle the multi-agent control problem under local LTL tasks from the bottom-up perspective. We aim for a decentralized solution while taking into account the constraints that the agents can exchange messages only if they are close enough. Following the hierarchical approach to LTL planning, we first generate for each agent a sequence of actions as a high-level plan that, if followed, guarantees the accomplishment of the respective agent’s LTL task. Second, we merge and implement the synthesized plans in real time, upon the run of the system. Namely, we introduce a distributed continuous controller for the leader–follower scheme, where the current leader guides itself and the followers toward the satisfaction of the leader’s task. At the same time, the connectivity of the multi-agent system is maintained. By a systematic leader reelection, we ensure that each agent’s task will be met in long term. This section is a brief summary of the results from the conference publication [11] and an extended study of related problems can be found in [12].

4.1 Related Work

The consideration of relative-distance constraints is closely related to the connectivity of the multi-agent network in robotic tasks [18]. As pointed out in [13, 24], maintaining this connectivity is of great importance for the stability, safety, and integrity of the overall team, for global objectives like rendezvous, formation, and flocking. Very often the connectivity of underlying interaction graphs is imposed by assumption rather than treated as an extra control objective. Here, the proposed distributed motion controller guarantees global convergence and the satisfaction of relative-distance constraints for all time. Moreover, different from [8] where a satisfying discrete plan is enough, the proposed initial plan synthesis algorithm here minimizes a cost of a satisfying plan, along with the communication constraints. Lastly, the same bottom-up planning problem from LTL specifications are considered in [23], where it is assumed that the agents are synchronized in their discrete abstractions and the proposed solutions rely on construction of the synchronized product system between the agents, or at least of its part. In contrast, in this work, we avoid the product construction completely. Compared with [15], these coordination policies are fully distributed and can be applied to agents with limited communication capabilities.

4.2 Problem Formulation

In mathematical terms, we consider a team of N autonomous agents with unique identities (IDs) $i\in \mathscr {N}=\{1,\ldots ,N\}$. They all satisfy the single-integrator dynamics $\dot{x}_i(t) = u_i(t)$, where $x_i(t), \, u_i(t) \in \mathbf {R}^2$ are the respective state and the control input of agent i at time $t>0$. The agents are modeled as point masses without volume. Each agent has a limited communication radius of $r>0$. Namely, agent i can communicate directly with agent j if $\Vert x_i(t)-x_{j}(t)\Vert \leqslant r$ or indirectly via a chain of connected robots. We assume that initially all agents are connected.

Each robot $i\in \mathscr {N}$ has a local task $\varphi _i$ specified over $\varSigma _i=\{\sigma _{ih},h\in \{1,\cdots ,M_i\}\}$, which is a set of services that robot i can provide at different regions $\mathscr {R}_i=\{R_{ig},g\in \{1,\cdots ,K_i\}\}$. Note that $R_{ig}=\{y\in \mathbf {R}^2|\Vert y-c_{ig}\Vert \leqslant r_{ig}\}$ is a circular area with the center $c_{ig}$ and radius $r_{ig}$. Furthermore, some of the services in $\varSigma _i$ can be provided solely by the agent i, while others require cooperation with some other agents. A service $\sigma _{ih}$ is provided if the agent’s relevant service-providing action $\pi _{ih}$ and the corresponding cooperating agents’ actions $\bigwedge _{i' \in C_{ih}} \varpi _{i'ih}$ are executed at the same time, i.e., $\sigma _{ih} = \pi _{ih} \wedge \bigwedge _{i' \in C_{ih}} \varpi _{i'ih}$. Lastly, a LTL task $\varphi _i$ is fulfilled if the sequence of services provided by robot i satisfies $\varphi _i$. Thus, the problem is to synthesize the control input $u_i$, time sequence of executed actions $T_{i}^A$ and the associated sequence of actions $A_i$ for each robot $i\in \mathscr {N}$.

4.3 Solution Outline

Our approach to the problem involves an offline and an online step. In the offline step, we synthesize a high-level plan in the form of a sequence of services for each of the agents. In the online step, we dynamically switch between the high-level plans through leader election and choose the associated continuous controllers. The whole team then follows the leader towards until its next service is provided and then a new leader is selected.

4.3.1 Offline Discrete Plan Synthesis

Given an agent $i \in \mathscr {N}$, a set of services $\varSigma _i$, and an LTL formula $\varphi _i$ over $\varSigma _i$, a high-level plan for i can be computed via standard model-checking methods [2, 10]. Roughly, by translating $\varphi _i$ into a equivalent Büchi automaton and by consecutive analysis of the automaton, a sequence of services with the prefix–suffix format $\varOmega _i = \sigma _{i1} \ldots \sigma _{ip_i}(\sigma _{ip_i+1} \ldots \sigma _{is_i})^\omega$, such that $\varOmega _i \models \varphi _i$ can be found, where $\sigma _{i1}$ can be independent or dependent services for robot $i\in \mathscr {N}$.

4.3.2 Dynamic Leader Selection

In this part, we describe how to elect a leader from the team in a repetitive online procedure, such that each of the agents is elected as a leader infinitely often. Intuitively, each agent $i\in \mathscr {N}$ is assigned a value that represents the agent’s urge to provide the next service in its high-level plan. Using ideas from bully leader election algorithm [9], an agent with the strongest urge is always elected as a leader within the connectivity graph.

Particularly, let i be a fixed agent, t the current time and $\sigma _{i1}\ldots \sigma _{ik}$ a prefix of services of the high-level plan $\varOmega _i$ that have been provided till t. Moreover, let $\tau _{i\lambda }$ denote the time, when the latest service, i.e., $\sigma _{i\lambda }=\sigma _{ik}$ was provided, or $\tau _{i\lambda }=0$ in case no service prefix of $\varOmega _i$ has been provided, yet. Using $\tau _{i\lambda }$, we could define agent i’s urge at time t as a tuple $\varUpsilon _i(t) = (t- \tau _{i\lambda } ,\, i)$. Furthermore, to compare the agents’ urges at time t, we use lexicographical ordering: $\varUpsilon _i(t) > \varUpsilon _j(t)$ if and only if (1) $t - \tau _{i\lambda } > t - \tau _{j\lambda }$, or (2) $t - \tau _{i\lambda }$ = $t - \tau _{j\lambda }$, and $i > j$. Note that $i \ne j$ implies that $\varUpsilon _i(t) \ne \varUpsilon _j(t)$, for all $t\geqslant 0$. As a result, the defined ordering is a linear ordering and at any time t, there exists exactly one agent i maximizing its urge $\varUpsilon _i(t)$. As a result, there is always a single agent that has the highest urge within $\mathscr {N}$ for any given time t. The robot with the highest urge is selected as the leader, which has the opportunity to execute its local plan $\varOmega _i$. However, due to the relative-distance constraints and the depended services, it can not simply move there without adopting a collaborative motion controller described below.

4.3.3 Collaborative Controller Design

Let us first introduce the notion of agents’ connectivity graph that will allow us to handle the constraints imposed on communication between the agents. Recall that each agent has a limited communication radius $r>0$. Moreover, let $\varepsilon \in (0,\,r)$ be a given constant, which plays an important role for the edge definition. In particular, let $G(t)=(\mathscr {N}, E(t))$ denote the undirected time-varying connectivity graph formed by the agents, where $E(t)\subseteq \mathscr {N}\times \mathscr {N}$ is the edge set for $t \geqslant 0$. At time $t=0$, we set $E(0)=\{(i,\,j)|\Vert x_i(0)-x_j(0)\Vert < r \}$.At time $t > 0$, $(i,\, j)\in E(t)$ if and only if one of the following conditions hold: (i) $\Vert x_i(t)-x_j(t)\Vert \leqslant r -\varepsilon$, or (ii) $r -\varepsilon <\Vert x_i(t)-x_j(t)\Vert \leqslant r$ and $(i,j) \in E(t^-)$, where $t^-<t$ and $|t-t^-|\rightarrow 0$. Note that the condition (ii) in the above definition guarantees that a new edge will only be added when the distance between two unconnected agents decreases below $r -\varepsilon$.

Now consider the following problem: given a leader $\ell \in \mathscr {N}$ at time t and a goal region $R_{\ell g}\in \mathscr {R}_{\ell }$, propose a decentralized continuous controller that (1) $G(t')$ remains connected for all $t' \in [t,\,\overline{t}]$; (2) guarantees that all agents $i\in \mathscr {N}$ reach $R_{\ell g}$ at a finite time $\overline{t}<\infty$. Both objectives are critical to ensure sequential satisfaction of $\varphi _i$ for each $i \in \mathscr {N}$.

Denote by $x_{ij}(t)=x_i(t)-x_j(t)$ the pairwise relative position between neighboring agents, $\forall (i,\,j)\in E(t)$. Thus $\Vert x_{ij}(t)\Vert ^2=\big (x_i(t)-x_j(t)\big )^T\big (x_i(t)-x_j(t)\big )$ denotes the corresponding distance. We propose the following continuous controller:

$$\begin{aligned} u_i(t)=-b_i\big (x_i-c_{ig}\big )-\sum _{j\in \mathscr {N}_i(t)}\frac{2r^2}{(r^2-\Vert x_{ij}\Vert ^2)^2}(x_i-x_j), \end{aligned}$$

(12.11)

where $b_i\in \{0,\,1\}$ indicates if agent i is the leader; $c_{ig}\in \mathbf {R}^2$ is the center of the next goal region for agent i; $b_i$ and $c_{ig}$ are derived from the leader selection scheme earlier. It can be seen that the above controller is fully distributed as it only depends $x_i$ and $x_j$, $\forall j\in \mathscr {N}_i(t)$.

Given the controller (12.11), we can prove the following two important properties of the complete system: Assume that G(t) is connected at $t=T_1$ and agent $\ell \in \mathscr {N}$ is the fixed leader for all $t\geqslant T_1$. By applying the controller in (12.11), the following two statements hold:

• The graph G(t) remains connected and $E(T_1)\subseteq E(t)$ for $t\geqslant T_1$.

• There exist a finite time $T_1\leqslant \overline{t}<+\infty$, $x_i(\overline{t}) \in R_{\ell g},\, \forall i\in \mathscr {N}.$

To briefly prove the above two statements, we consider the following potential function of the complete system:

$$\begin{aligned} V(t)=\frac{1}{2}\sum _{i=1}^{N}\sum _{j\in \mathscr {N}_i(t)}\phi (\Vert x_{ij}\Vert ) + \frac{1}{2}\sum _{i=1}^{N} b_i (x_i-c_{ig})^T(x_i-c_{ig}), \end{aligned}$$

(12.12)

where the potential function $\phi \big (\Vert x_{ij}\Vert \big )=\frac{\Vert x_{ij}\Vert ^2}{r^2-\Vert x_{ij}\Vert ^2}$ for $\Vert x_{ij}\Vert \in [0,\, r)$, and thus V(t) is positive semidefinite. Assume that G(t) remains invariant during $[t_1,\, t_2)\subseteq [T_1,\,\infty )$. The time derivative of (12.12) during $[t_1, t_2)$ is given by

$$\begin{aligned} \dot{V}(t)= & {} -\sum _{i=1,\, i\ne \ell }^{N} \Vert \sum _{j\in \mathscr {N}_i(t)} \nabla _{x_i}\phi (\Vert x_{ij}\Vert )\Vert ^2 \nonumber \\&\qquad -\Vert (x_\ell -c_{\ell g})+\sum _{j\in \mathscr {N}_{\ell }(t)} \nabla _{x_{\ell }}\phi (\Vert x_{\ell j}\Vert )\,\Vert ^2\leqslant 0. \end{aligned}$$

(12.13)

Thus $V(t)\leqslant V(0)<+\infty$ for $t\in [t_1,\,t_2)$. It means that during $[t_1,\, t_2)$, no existing edge can have a length close to r, i.e., no existing edge will be lost by the definition of an edge. On the other hand, assume a new edge $(p,\,q)$ is added to the graph G(t) at $t=t_2$, where $p,\, q\in \mathscr {N}$. It holds that $\Vert x_{pq}(t_2)\Vert \leqslant r-\varepsilon$ and $\phi (\Vert x_{pq}(t_2)\Vert )=\frac{r-\varepsilon }{\varepsilon (2r-\varepsilon )}<+\infty$ since $0<\varepsilon <r$. Denote the set of newly added edges at $t=t_2$ as $\widehat{E}\subset \mathscr {N}\times \mathscr {N}$. Let $V(t_2^+)$ and $V(t_2^-)$ be the value of function from (12.12) before and after adding the set of new edges to G(t) at $t=t_2$. We get $V(t_2^+) \leqslant V(t_2^-) + |\widehat{E}|\, \frac{r-\varepsilon }{\varepsilon (2r-\varepsilon )}<+\infty$. As a result, $V(t)<+\infty$ for $t\in [T_1,\, \infty )$. Since one existing edge $(i,\,j)\in E(t)$ will be lost only if $x_{ij}(t)=r$, it implies that $\phi (\Vert x_{ij}\Vert )\rightarrow +\infty$, i.e., $V(t)\rightarrow +\infty$ by (12.12). By contradiction, we can conclude that new edges will be added but no existing edges will be lost. This proves the first statement above.

Regarding the second statement, we need to show that all agents converge to the goal region of the leader in finite time. By (12.13), $\dot{V}(t)\leqslant 0$ for $t\geqslant T_1$ and $\dot{V}(t)=0$ when the following conditions hold: (i) for $i \ne \ell$ and $i\in \mathscr {N}$, it holds that $\sum _{j\in \mathscr {N}_i(t)}h_{ij}(x_i-x_j)=0$; and (ii) for the leader $\ell \in \mathscr {N}$, it holds that $(x_\ell -c_{\ell g})+\sum _{j\in \mathscr {N}_{\ell }(t)} h_{ij}(x_\ell -x_j)=0$, where $h_{ij}=\frac{2r^2}{(r^2-\Vert x_{ij}\Vert ^2)^2}$, $\forall (i,\,j)\in E(t)$. Then we can combine the above two conditions into $H\otimes I_2 \cdot \mathbf {x} + (\mathbf {x}-\mathbf {c}) =0$, where H is a $N\times N$ matrix satisfying $H(i,i)=\sum _{j\in \mathscr {N}_i}h_{ij}$ and $H(i,j)=-h_{ij}$, where $i\ne j\in \mathscr {N}$. Note that H is positive-semidefinite with a single eigenvalue at the origin, of which the corresponding eigenvector is the unit column vector of length N. Thus, the only equilibrium is $\mathbf {x}=\mathbf {c}$, i.e., $x_i=c_{\ell g}$, $\forall i\in \mathscr {N}$. By LaSalle’s Invariance principle [14], there exists $\overline{t}<+\infty$ that $x_i(\overline{t})\in R_{\ell g}$, $\forall i\in \mathscr {N}$.

4.3.4 Integrated System

The integrated system combines the leader selection scheme from Sect. 12.4.3.2 and the continuous control scheme from Sect. 12.4.3.3, such that the discrete plan $\varOmega _i$ synthesized in Sect. 12.4.3.1 can be executed. Particularly, via communicating and comparing the urge function $\varUpsilon _{i}$ among all robots, one robot with the highest urge is selected as the leader, denoted by $\ell \in \mathscr {N}$. Then robot $\ell$ finds its next goal region according to its plan $\varOmega _i$ as $R_{\ell g}$. After that, all robots applies the control input from (12.11) where the leader $\ell$ sets $b_{\ell }=1$ while the rest sets $b_i=0$, $\forall i\in \mathscr {N}$ and $i\ne \ell$. Consequently, as proven in Sect. 12.4.3.3, there exists a finite time that all robots are within the region $R_{\ell g}$, where robot $\ell$ can provide action $\pi _{\ell h}$and its collaborating robots can provide the action $\overline{\omega }_{\ell ' \ell h}$, $\forall \ell '\in C_{\ell h}$. As a result, the service $\sigma _{\ell h}$ is provided at region $R_{\ell g}$. Afterward, the urge function of robot $\ell$ is updated and a new leader is selected for the team. This process repeats itself indefinitely such that all robots can fulfill its local task. Detailed algorithms can be found in [11].

4.3.5 Simulation

We simulate a system of 4 robots $(R_1, R_2, R_3, R_4)$ with regions of interested in a $4\times 4$ m workspace as shown in Fig. 12.5. They initially start from positions (0.0, 0.0), (1.0, 0.0), (2.0, 0.0), (3.0, 0.0) and they all have the communication radius 1.5 m. Furthermore, each robot is assigned a local service task. For instance, the local task for robot 1 is to provide services sequentially in the circular region (1.0, 1.0, 0.2) and the circular region (3.0, 1.0, 0.2), where the service at region (3.0, 1.0, 0.2) requires collaboration from other robots. The tasks of other robots are defined similarly. We apply the proposed control and coordination framework as described above. The resulting trajectories of all robots are shown in Fig. 12.5, which verify that all local tasks are satisfied. Moreover, the relative distances between initially connected neighboring robots, i.e., $(R_1,R_2),(R_2,R_3),(R_3,R_4)$, are also shown in Fig. 12.5, all of which stay below the communication radius 1.5 m at all time. More numerical examples are given in [11].

Fig. 12.5

Left: trajectories of 4 robots that satisfy their local service tasks. Right: the relative distances of initially connected neighboring robots

4.4 Conclusion and Future Work

To summarize, in this section we present the decentralized control scheme of a team of agents that are assigned local tasks expressed as LTL formulas. The solution follows the automata-theoretic approach to LTL model checking, however, it avoids the computationally demanding construction of synchronized product system between the agents. The decentralized coordination among the agents relies on a dynamic leader–follower scheme, to guarantee the low-level connectivity maintenance at all times and a progress toward the satisfaction of the leader’s task. By a systematic leader switching, we ensure that each agent’s task will be accomplished.