An Overview of Synchrony in Coupled Cell Networks

Abstract

One of the key aspects in the theory of coupled cell networks concerns the existence of synchrony subspaces. That is, subspaces defined in terms of equalities between cell coordinates which are flow-invariant for all coupled cell systems that respect a given coupled cell network structure. We review some recent concepts and results concerning synchrony subspaces on coupled cell networks. The existence of such subspaces naturally restricts the dynamics that can occur at the coupled cell systems, as in general it is the case for any dynamical system admitting flow-invariant spaces. We focus at some of the aspects that make important and special the existence of synchrony subspaces for coupled cell systems. Namely, their existence depend on the network structure and not on the specific form of the differential equations that are chosen to govern the dynamics; the solutions of the restricted coupled cell systems represent dynamics where groups of cells are dynamically behaving exactly in the same way; the restricted coupled cell systems are again coupled cell systems that are consistent with a network structure with a fewer cells. We review some results on how synchrony changes, or it is combined, in evolving networks. More precisely, in networks where their topology changes with time, either to a rewiring of a link, appearance or removal of a link or a node, or by merging smaller networks into larger ones. Finally, we consider the complement network of a network remarking that both networks have the same set of synchrony subspaces.

1 Introduction

Many real life phenomena can be dynamically modeled through differential equations that can be interpreted as coupled cell systems – that is – equations consistent with a network graph structure where nodes (the cells) symbolize dynamics of smaller dynamical systems and edges represent interactions (the couplings) between those nodes. The collective dynamics of the time evolution at nodes then gives the dynamics on the network. In the analysis of the collective dynamics it is often crucial and of interest to observe the dynamical behavior of the individual nodes, comparing and finding features such as synchrony or specified phase-relations in periodic solutions. We follow here the theory of coupled cell networks formalized by Stewart et al. [28, 31, 44] and Field [23]. A key advantage of these formalisms is that it allows theoretical deduction of collective dynamics based only on the network structure, without referring to specific dynamics at every cell.

Different factors can contribute for the decision of modelling through network equations. One such factor can be derived from the intrinsic form of the phenomena that is is being modelled in the mathematical language. As an example, network of symmetrically coupled cells can be used to model central pattern generators for quadruped locomotion, see Golubitsky et al. [17, 29]. We are interested in networks associated with directed graphs meaning that the interactions are directional. For example, in a social network representing trade among nations, the interactions are directional and the graph representing such interactions must be directed. Moreover, many interactions are valued, indicating for example the strength of interaction between the social nodes or there can be more than one type of interaction (multirelational networks). See for example Wasserman and Faust [45]. The theory of coupled cell networks that we are following considers networks represented by directed graphs that can have more than one edge type, multi-edges and self-loops. Graphically, each edge type is represented by a different symbol.

Coupled Cell Networks and Coupled Cell Systems

A network is said to be regular if all cells are identical (have the same internal dynamics), all edges are of the same type and all cells receive the same number of input edges – the valency of the network. More generally, a network such that each subnetwork formed by the network cells and the network edges of a given type is regular, is said to be homogeneous. To each such subnetwork is associated an adjacency matrix, with rows and columns indexed by the network cells, with nonnegative integers entries, where the entry ij is m if there are m edges of that given type from cell j to cell i. Thus an homogeneous network with k edges types can be described through k (adjacency) matrices.

Fig. 1

A five-cell network N which is regular of valency two: all the cells and all the edges are represented by the same cell and edge symbol, respectively, since the cells are identical and the edges are of the same type; all the cells receive two input edges

Example 1

The network N of Fig. 1 is an example of a five-cell regular network of valency two with adjacency matrix

$$ \left( \begin{array}{ccccc} 0&{} 1 &{} 0 &{} 1 &{} 0 \\ 1&{} 0 &{} 0 &{} 1 &{} 0 \\ 1&{} 0 &{} 0 &{} 0 &{} 1 \\ 1&{} 1 &{} 0 &{} 0 &{} 0 \\ 1&{} 0 &{} 1 &{} 0 &{} 0 \end{array} \right) \, . $$

The associated coupled cell systems satisfy the following general form:

$$ \begin{array}{l} \dot{x}_1 =f(x_1,\overline{x_2,x_4}) \\ \dot{x}_2 =f(x_2,\overline{x_1,x_4}) \\ \dot{x}_3 =f(x_3,\overline{x_1,x_5}) \\ \dot{x}_4 =f(x_4,\overline{x_1,x_2}) \\ \dot{x}_5 =f(x_5,\overline{x_1,x_3}) \end{array} $$

where $f:\, (\mathrm{\mathbf R}^k)^3 \rightarrow \mathrm{\mathbf R}^k$, for $k \in \mathrm{\mathbf N}$, is a smooth function. The overbar indicates that f is invariant under the permutation of the variables and translates the fact that all the interactions (edges) between cells are of the same type. The same function f is used to describe the time evolution of each cell state for two reasons: the same symbol is used to represent all the cells which indicates that the cells are identical; each cell receives two interactions and so the equations for each cell are identical up to the input variables.

When studying the dynamics of coupled cell systems, obviously it has to be taken into account the underlined network structure, which in particular, can force dynamics that would be highly nongeneric in the context of general dynamical systems. One such example is the occurrence of flow-invariant spaces.

Synchrony Subspaces

One widely observed and most studied collective dynamics in coupled dynamical systems is the synchronization, where phase trajectories of two or more coupled units coincide over time. For importance of synchronization and its ubiquitous presence in nature, we refer to [15, 41] and references therein. In [40], Pikovsky et al. propose to study various synchronization phenomena using a common framework based on modern nonlinear dynamics, where a variety of approaches using coupled periodic and coupled chaotic systems is discussed. Restrepo et al. in [42] point out the crucial effect of network structure on the emergence of collective synchronization in heterogeneous systems, in terms of eigenvalues of network adjacency matrices.

Conditions for the occurrence of robust patterns of partial synchronization in terms of network structure, have been established in Stewart et al. [44] and Golubitsky et al. [31]. In the theory of coupled cell networks the synchronization of two or more cells corresponds to the flow-invariance of the subspace of the total phase space given by the identification of the phase space of those cells. These are called synchrony subspaces and have the amazing property that their existence, implying flow-invariance for the associated coupled cell systems, depends only on the network structure. In fact, by [31, 44] synchrony subspaces are in one-to-one correspondence with the equivalence relations on the network set of cells that satisfy certain properties in which case they are called balanced. Equivalently, synchrony subspaces are in one-to-one correspondence with the polydiagonals (subspaces of $\mathrm{\mathbf R}^n$, if the original network has n cells, defined by equalities of coordinates) that are left invariant under the network adjacency matrix, or the adjacency matrices if the network has more than one edge type.

Example 2

Consider the five-cell regular network N of Fig. 1 with set of cells $C = \{ 1, \ldots , 5\}$ and total phase space $(\mathrm{\mathbf R}^k)^5$. The polydiagonal subspace $\varDelta =\{ \mathbf{x} \in (\mathrm{\mathbf R}^k)^5 :\ x_1=x_2,\, x_3 = x_5\}$ is a synchrony subspace for the coupled cell systems associated to N. This is easily verified using the general form of the equations of the admissible vector fields for N, presented in Example 1. With the identification of $x_1$ with $x_2$ and of $x_3$ with $x_5$, the equations for $\dot{x}_1$ and $\dot{x}_2$ coincide and the equations for $\dot{x}_3$ and $\dot{x}_5$ also coincide. Thus a trajectory with initial condition in $\varDelta$ will remain in $\varDelta$ for all time. Equivalently, from the results of [31, 44], $\varDelta$ is a synchrony subspace since the polydiagonal subspace $\{ \mathbf{x} \in \mathrm{\mathbf R}^5 :\ x_1=x_2,\, x_3 = x_5\}$ is left invariant under the adjacency matrix of N, presented in Example 1.

Symmetry and Synchrony

Symmetric networks are a special class of networks. The symmetry group of a network is the group of the isomorphisms of the network graph. Equivalently, the symmetry group of the network corresponds to the group of the $n \times n$ permutation matrices (if the network has n cells) that commute with the adjacency matrix or the adjacency matrices of the network. Coupled cell systems associated with symmetric networks inherit the network symmetry – that is – they are equivariant under the network symmetry group, considering the natural action by permutation of the network cell coordinates. In this case, there are two main aspects that determine the form of the coupled cell systems - the network and the symmetry. That is, the coupled cell systems are equivariant under the network symmetry group and are also constrained by the network structure. For any isotropy subgroup for the action of the network group of symmetries, the corresponding fixed-point subspace is flow-invariant and it is a polydiagonal, since the action is by permutation of the network coordinates, thus it is a synchrony subspace. But, there can be more additional synchrony subspaces whose existence is not predicted by the symmetry. This comes from the fact that the coupled cell systems are not only equivariant but they also have form consistent with the network. More precisely, the linear space of smooth vector fields with structure consistent with the symmetric network may form a proper subspace of the linear space of the smooth equivariant vector fields. See Antoneli and Stewart [12,13,14]. It is then possible that dynamics that are non-generic from the symmetric point of view, are generic for a given symmetric network structure. That is, dynamics can occur in a robust way for coupled cell systems that have form consistent with a specific network structure, but that would not be expected if we were working in the context of generic smooth equivariant vector fields. See for example Golubitsky et al. [25]. See also Dias and Lamb [19], Paiva [39, Chap. 7], Dias and Paiva [21] and Golubitsky and Lauterbach [24].

An important class of non-symmetric networks that lies between the class of general networks and the class of symmetric networks, where group theoretic methods still apply, are the networks with interior symmetries. In this case, there is a group of permutations of a subset S of the cells (and edges directed to S) that partially preserves the network structure (including cell-types and edges-types) and its action is again by permutation of the network cell coordinates. In other words, the cells in S together with all the edges directed to them form a subnetwork which possesses a non-trivial group of symmetry $\Sigma _S \subseteq \mathbf{S}_n$. For example, in Fig. 2, the network at the left has exact $\mathbf {S}_3$-symmetry, whereas the network on the right has $\mathbf {S}_3$-interior symmetry on the set of cells $S = \{1,2,3\}$. This notion was introduced and investigated by Golubitsky, Pivato and Stewart [26].

Fig. 2

(left) Network with exact $\mathbf {S}_3$-symmetry. (right) Network with $\mathbf {S}_3$-interior symmetry on the set of cells $\{1,2,3\}$

In coupled cell systems, the local bifurcations from a synchronous equilibrium can be classified into synchrony-breaking bifurcations or synchrony-preserving bifurcations. The synchrony-breaking bifurcations occur when a synchronous state looses stability and bifurcates to a state with less synchrony. This is in parallel with the concept of symmetry-breaking bifurcations in symmetric coupled cell systems, see Golubitsky and Stewart [27]. In [26] it is obtained analogues of the Equivariant Branching Lemma [30, Theorem XIII 3.3] and the Equivariant Hopf Theorem [30, Theorem XVI 4.1] for coupled cell systems with interior symmetries.The analogue of the Equivariant Branching Lemma is a natural generalization of the symmetric case. However, in the Equivariant Hopf Theorem, it is proved the existence of states whose linearizations on certain subsets of cells, near bifurcation, are superpositions of synchronous states with states having ‘spatial symmetries’. (In the full symmetric case, the Equivariant Hopf Theorem guarantees the existence of states with certain spatio-temporal symmetries.) More recently, in Antoneli, Dias and Paiva [10, Theorem 4.8], the Equivariant Hopf Theorem for networks with interior symmetries of [26] is extended obtaining the full analogue of the Equivariant Hopf Theorem for networks with symmetries. More precisely, it is guaranteed the existence of states whose linearizations on certain subsets of cells, near bifurcation, are superpositions of synchronous states with states having spatio-temporal symmetries, that is, corresponding to “interiorly” $\mathbf{C}$-axial subgroups of $\Sigma _{S}\times \mathbf {S}^1$. See also Antoneli, Dias and Paiva [11].

Applying the Equivariant Hopf Theorem to a smooth one-parameter family of coupled cell systems with structure consistent with the network at the left of Fig. 2 which has exact $\mathbf {S}_3$-symmetry, assuming a codimension-one interior symmetry-breaking Hopf bifurcation occurs at an equilibrium with $\mathbf {S}_3$-symmetry, then generically we obtain three branches of small amplitude periodic solutions. One branch corresponds to periodic solutions with exact spatial $\mathbf{Z}_2$-symmetry where two cells undergo oscillations that are identical and in phase, and the third (from the set $\{1,2,3\}$) behaving differently. There are two more branches of periodic solutions with spatio-temporal symmetries $\tilde{\mathbf{Z}}_3$ and $\tilde{\mathbf{Z}}_2$: on one branch the oscillations have the same waveform for each cell in the set $\{1,2,3\}$, but are phase-shifted by one third of the period; at the other branch, two cells have identical waveforms but are one half of the period out of phase, and the third cell (from the set $\{1,2,3\}$) has the double frequency. The three groups $\mathbf{Z}_2$, $\tilde{\mathbf{Z}}_3$ and $\tilde{\mathbf{Z}}_2$ correspond to the three (conjugacy classes of) isotropy subgroups of the standard action of $\mathbf{S}_3 \times \mathbf{S}^1$ on $\mathbf{C}\oplus \mathbf{C}$. For details see for example Golubitsky, Stewart and Schaeffer [30, Chaps. XVI, XVIII]. Applying the Equivariant Hopf Theorem with Interior Symmetries of [10], now taking a smooth one-parameter family of coupled cell systems with structure consistent with the network at the right of Fig. 2 which has interior $\mathbf {S}_3$-symmetry on the set of cells $S = \{1,2,3\}$, assuming a codimension-one interior symmetry-breaking Hopf bifurcation occurs at an equilibrium with $\mathbf {S}_3$-symmetry, then generically we obtain as well three branches of small amplitude periodic solutions, corresponding to the three groups $\mathbf{Z}_2$, $\tilde{\mathbf{Z}}_3$ and $\tilde{\mathbf{Z}}_2$, but now the linearizations of the periodic states on the subsets of cells, near bifurcation, are superpositions of synchronous states with states having those spatio-temporal symmetries. See the numerical simulations in [10, Sect. 4.4] illustrating the periodic solutions guaranteed by the Equivariant Hopf Theorem with exact and interior $\mathbf{S}_3$-symmetry in coupled cell systems of four cells with structure consistent with the networks of Fig. 2, respectively, choosing the internal phase space of all four cells to be $\mathbf{C}\cong \mathrm{\mathbf R}^2$. We reproduce here in Fig. 3 results of numerical simulations obtaining periodic solutions with (interior) $\tilde{\mathbf{Z}}_2$-symmetry: it is superimposed the time series of all four cells, which are identified by colours: cell 1 is blue, cell 2 is red, cell 3 is green, and cell 4 is black. The upper panels show the first components and the lower panels show the second components. The left panels refer to network with exact $\mathbf {S}_3$-symmetry and the panels on the right refer to network with $\mathbf {S}_3$-interior symmetry.

Fig. 3

Solutions with $\tilde{\mathrm{\mathbf Z}}_2$ (interior) symmetry. (left) Network with exact $\mathbf {S}_3$-symmetry. (right) Network with $\mathbf {S}_3$-interior symmetry. Figure taken from [10]

Quotients and Inflations

Synchrony subspaces have a major impact at the dynamics of the coupled cell systems associated with a given network. An important aspect of the existence of synchrony subspaces is that the restriction of the coupled cell systems to a synchrony subspace are again coupled cell systems in a lower-dimensional phase space, now associated with a network with fewer cells – the quotient network of the given network by the synchrony subspace. The fact that the restricted systems are consistent with a network structure implies constrains at the dynamics that can occur for those systems and thus for the initial coupled cell systems. Although, the restrictions to the synchrony subspaces do not give all the dynamics for the original network, they give full information concerning the dynamics of the original coupled cell systems at those synchrony subspaces. See for example Aguiar et al. [4, 5]. Moreover, it can happen that the quotient network has been already explored from the dynamical point of view in several contexts. If that is the case, the known dynamics of the quotient network can be lifted to the original network dynamics. Examples of specific structures than can be explored are: existence of global (quotient) network symmetries implying that the associated coupled cell systems are symmetric under a permutation symmetry group – these impose strong constrains at the dynamics that can occur, see for example Golubitsky and Stewart [27, 28] and references therein; known classifications of classes of networks with certain structures, see for example Leite and Golubitsky [35].

It is known that flow-invariant spaces favour the existence of non-generic dynamical behaviour like heteroclinic cycles and networks, which lead to complicated dynamics. It follows that, knowing the set of all synchrony subspaces of a coupled cell network, can help to detect the possibility of the associated coupled cell systems to support heteroclinic behaviour. Besides this, in Aguiar et al. [1], it is also explored the process reverse to the quotient of a network: coupled cell networks supporting heteroclinic networks are constructed by lifting coupled cell dynamics supporting heteroclinic behaviour and associated with smaller networks. That is, networks with a few number of cells (and supporting heteroclinic connections) are inflated and combined in a way that they are quotient networks of bigger networks supporting heteroclinic networks.

Example 3

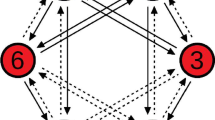
In Fig. 4 we show a six-cell network M for which the five-cell network N of Fig. 1 is a quotient network by the synchrony subspace defined by the cell coordinates equality $x_1 = x_6$. More precisely, the general form of the coupled cell systems associated with M is:

$$ \begin{array}{l} \dot{x}_1 =f(x_1,\overline{x_2,x_4}) \\ \dot{x}_2 =f(x_2,\overline{x_6,x_4}) \\ \dot{x}_3 =f(x_3,\overline{x_6,x_5}) \\ \dot{x}_4 =f(x_4,\overline{x_1,x_2}) \\ \dot{x}_5 =f(x_5,\overline{x_1,x_3}) \\ \dot{x}_6 =f(x_6,\overline{x_2,x_4}) \\ \end{array} $$

where as before, $f:\, (\mathrm{\mathbf R}^k)^3 \rightarrow \mathrm{\mathbf R}^k$ is any smooth function and the overbar indicates that f is invariant under the permutation of the variables. Restricting these equations to the synchrony subspace $\{ \mathbf{x}: \ x_1 = x_6\}$, we obtain the general form of the coupled cell systems associated with the network N of Fig. 1 (see Example 1). Equivalently, the network M in Fig. 4 is an inflation of the five-cell network N of Fig. 1 at cell 1, where cell 1 is inflated to cells 1 and 6.

Fig. 4

A network M which has the network N of Fig. 1 as a quotient by the synchrony subspace defined by the cell coordinates equality $x_1 = x_6$. We also say that the six-cell network M is a simple inflation of the network N of Fig. 1 at cell 1, where cell 1 is inflated to cells 1 and 6

2 Enumeration of Inflations

In general, a given network can be the quotient network of many different networks. In Aguiar et al. [4, 5] it is considered the inverse problem: given a network N provide a systematic way of enumerating the networks that admit N as a quotient network. Those networks are called inflations (Aguiar et al. [1]) or lifts (Dias and Moreira [20]) of N.

2.1 Inflating (Lifting) a Network

An inflation (lift) M of N can be interpreted as enlarging the network N in the number of cells, preserving the valency, where each cell of N corresponds to the identification of a certain set of cells in the inflation M. In order that an n-cell network M is a lift of N, given any two cells that were identified, they must receive the same number of directed edges from cells of each class of identified cells.

An inflation is said to be a simple inflation if there is just one cell that is inflated.

Example 4

If we take the five-cell regular network in Fig. 1, then one of its six-cell (simple) inflations is the network in Fig. 4 where cell 1 of N is inflated to cells 1 and 6 of M. Observe that in N, cell 1 receives two directed edges, one from cell 4 and one from cell 2, and sends two directed edges to cells 5 and 3. The network in Fig. 4 is an inflation of N since: cells 1 and 6, both receive one directed edge from each of the cells 4 and 2; there is a directed edge from one of the cells in the class $\{1,6\}$ to both cells 5 and 3 – a directed edge from cell 1 to cell 5 and a directed edge from cell 6 to cell 3.

Using the theory of coupled cell networks [31, 44], one way to enumerate all the possible inflation networks M, for a fixed N and a fixed polydiagonal, is through the construction of the possible $n \times n$ (adjacency) matrices leaving invariant the fixed polydiagonal and whose restrictions to the polydiagonal are similar to the adjacency matrix of the network N. The methods of enumeration presented by Aguiar et al. [4, 5] explore precisely this approach and are developed for regular networks. (See also Dias and Moreira [20].) In fact, these methods trivially extend to homogeneous networks. Recall that an homogeneous network can be seen as a directed graph with more than one edge type, where the subnetworks on the same network set of cells, considered for each edge-type, are regular. Finding the set of synchrony subspaces of an homogeneous network is equivalent to find the common synchrony subspaces of all these subnetworks. Moreover, if the network is not homogeneous, now the subnetworks to be considered are in some way homogeneous and then the question is again reduced to consider homogeneous networks, and then, regular networks, see Aguiar and Dias [2].

2.2 Inflating (Lifting) a Bifurcation

Consider a coupled cell system with structure consistent with a regular network M, depending on a real bifurcation parameter and assume that a codimension-one steady-state or Hopf bifurcation occurs at a full synchronous equilibrium $X_0$ which, after an affine change of coordinates, we can assume is the null steady-state solution $X_0$. Note that, the full diagonal space is always a synchrony subspace of a regular network. In Aguiar et al. [5] it is addressed the problem of how a steady-state or Hopf bifurcation occurring at a quotient network N of M lifts to M. Every bifurcating solution for the quotient lifts to a bifurcation solution for the inflation network where cells that were identified in the quotient are synchronized. But it can occur that new bifurcating solutions appear for the inflation network M where cells that were identified in the quotient are not synchronized. In Aguiar et al. [5], examples are given of five-cell networks with the three-cell bidirectional ring as quotient, where bifurcations within the ring dynamics lead to solutions that break synchrony in the five-cell network. One of those is the network of Fig. 1.

Results in Leite and Golubitsky [35] and Golubitsky and Lauterbach [24] relate the eigenvalues of the Jacobian $J_M$ of a coupled cell system consistent with a network M at $X_0$ with the eigenvalues of the adjacency matrix of M. In order for bifurcations within the quotient network N to lead to nonsynchronous solutions in the larger network M, the center subspace of $J_M$ must be larger than the center subspace of $J_N$. Results are presented in [5] that relate the eigenvalues of the adjacency matrix of the network M with those of the adjacency matrix of the quotient N which provide an easy way to identify networks M for which the dimension of the center subspaces of $J_M$ and $J_N$ are the same. Each one-parameter steady-state (or Hopf) bifurcation supported by the coupled cell systems for M (or for N) is associated with a degeneracy condition corresponding to a zero (or imaginary) eigenvalue of $J_M$ (or $J_N$) that depends at the eigenvalues of the adjacency matrix of M (or N). The eigenvalues of the adjacency matrix of any inflation M of N are the eigenvalues of N plus other eigenvalues, following the terminology [20], the extra eigenvalues. A degeneracy condition implying a steady-state or Hopf bifurcation of M (or N) is associated at least with an eigenvalue of the adjacency matrix of the network M (or N). That is, the critical eigenvalues of $J_M$ (or $J_N$) are directly associated with the eigenvalues of the adjacency matrix of M (or N). It is then easy to see that if the real parts of the extra eigenvalues of the adjacency matrix of an inflation M of N are distinct from the real parts of the ‘critical’ eigenvalues of the adjacency matrix of N then the coupled cell systems associated with the inflation network M will have no additional branches of steady-state solutions (or periodic solutions in the Hopf case), for the fixed imposed bifurcation degeneracy condition. As an example, in [5] it is proved that, up to isomorphism, there are two four-cell and twelve five-cell networks admitting the three-cell bidirectional ring quotient network, and from these it is shown that only two such networks can exhibit branches of steady-state solutions not predicted by bifurcation in the three-cell bidirectional ring. In fact, generically, the coupled cell systems associated with these two networks have additional branches, and one of these two networks is precisely the network in Fig. 1. More recently some progress has been achieved at this problem. See Dias and Moreira [20] and Moreira [37].

3 The Lattice of Synchrony Subspaces of a Network

As mentioned above, following Stewart et al. [44] and Golubitsky et al. [31], a synchrony subspace of a network is a subspace given by the identification of the phase space of groups of cells (polydiagonal) that is left invariant under any coupled cell system that has form consistent with the network.

By Stewart [43] (see also Aldis [9]) the set of synchrony subspaces associated with a network, taking the relation of inclusion $\subseteq$, is a complete lattice. Recall that a lattice is a partially ordered set such that every pair of elements has a unique least upper bound or join, and a unique greatest lower bound or meet. Moreover, a complete lattice X is a lattice where every subset $Y \subseteq X$ has a unique least upper bound or join, and a unique greatest lower bound or meet. We remark that for a regular network there are always two trivial synchrony subspaces, the total asynchronous and the full synchronous polydiagonal subspaces, corresponding, respectively, to the top and bottom elements of the lattice.

In [2], Aguiar and Dias describe how to obtain the lattice of synchrony subspaces of a given network. As shown, this reduces basically to the problem of how to obtain the lattice of synchrony subspaces of regular networks, and more generally, to identical-cell identical-edge coupled networks. For a regular network the lattice of synchrony subspaces is obtained based on the eigenvalue structure of the network adjacency matrix. It is presented an algorithm that generates the lattice of synchrony subspaces for a regular network. See also the work of Kamei [33], on the class of regular networks where the adjacency matrix has only simple eigenvalues, Kamei and Cock [34] for a computer algorithm searching for all possible balanced equivalence relations using symbolic matrix computations, and Moreira [38] where the lattice of synchrony subspaces of a regular network is obtained using a special class of Jordan subspaces of the network adjacency matrix.

Example 5

The lattice of synchrony subspaces of the network in Fig. 1 was obtained by running the algorithm presented in [2]. The nontrivial synchrony subspaces are listed in Table 1. The trivial synchrony subspaces for the network are the total asynchronous polydiagonal space and full synchronous polydiagonal space $\{ \mathbf{x}:\ x_1 = x_2 = x_3 = x_4 = x_5\}$, that we will represent by P and $\varDelta _0$, respectively. A representation of the lattice is presented in Fig. 5.

Table 1 Nontrivial synchrony subspaces for the network of Fig. 1. The trivial synchrony subspaces for the network are the total asynchronous polydiagonal space and the full synchronous polydiagonal space $\{\mathbf{x}:\ x_1 = x_2 = x_3 = x_4 = x_5\}$

Fig. 5

The lattice of synchrony subspaces for the five-cell regular network N of Fig. 1: the nontrivial synchrony subspaces $\varDelta _i$, for $i=1, \ldots , 16$, are listed in Table 1. The top element is the total phase space P (the total asynchronous polydiagonal space) and the bottom element $\varDelta _0$ is the full synchronous polydiagonal space

4 Evolution of Synchrony

Most real world networks are evolving networks, that is, their topology evolves with time, either due to a rewiring of a link, the appearance or disappearance of a link or node, or by a merging of small networks into a larger one. The dynamics of network topology reflects frequent changes in the interactions among network components and translates into a rich variety of evolutionary patterns. Evolution of network topology can be described by a sequence of static networks and the topology of the networks can be regarded as a discrete dynamical system. Evolving networks are ubiquitous in nature and science. See Albert et al. [8] and Dorogovtsev et al. [22], and references therein for examples in many diverse fields.

For the different definitions of synchronization, there is a vast literature on how synchronizability varies with the changes of the network structure. As examples, we refer to the works of Atay and Biyikoglu [16], Chen and Duan [18], Lu et al. [36], Hagberg and Schult [32].

In the context of coupled cell systems, since, as mentioned earlier, the connecting topology of a network dictates the lattice of synchrony subspaces, we expect changes at the corresponding lattice, if the underlying topology changes. In this perspective, the work in Aguiar et al. [6] considers structural changes in the network topology caused by unary network operations, such as deletion and addition of cells or edges, and rewirings of edges, describing which synchrony subspaces are inherited by the new network structure. The works in Aguiar and Ruan [7] and Aguiar and Dias [3] focus on evolving networks where new networks are formed by combining existing ones using binary network operations - the join and the coalescence operations and the direct and tensor product operations, respectively. Results are obtained relating the set of synchrony subspaces of the component networks and the resulting network.

4.1 Inflation

Equivalently to the definition seen before, an inflation (or lift) of a k-cell network N is any network M with $n >k$ cells such that M admits a synchrony subspace where each coupled cell system associated with M restricted to the synchrony subspace is a coupled cell system now consistent with the network N.

Example 6

The network M in Fig. 4 is a six-cell (simple) inflation of the five-cell network in Fig. 1, where cell 1 of N is inflated to cells 1 and 6 of M. From the definition of inflation, it follows that $\tilde{\varDelta }_0 = \{ \mathbf{x}:\ x_1 = x_6\}$ is a synchrony subspace of M. Moreover, it follows also that there is a one-to-one correspondence between the synchrony subspaces of network N and the synchrony subspaces of network M that are contained in $\tilde{\varDelta }_0$. More concretely, for every nontrivial synchrony subspace $\varDelta _i$, $i=1,\ldots ,16$, for N (recall Table 1), the subspace $\tilde{\varDelta }_i$, defined by the coordinate equality conditions that define $\varDelta _i$ together with the coordinate equality condition $x_1 = x_6$, is a synchrony subspace of M. The nontrivial synchrony subspaces of M are listed in Table 2.

Table 2 Nontrivial synchrony subspaces of the network M of Fig. 4. The network M is an inflation of the five-cell network N of Fig. 1 where cell 1 is inflated to cells 1 and 6. The synchrony subspaces of the network M that are contained in the synchrony subspace $\tilde{\varDelta }_0$ are in one-to-one correspondence with the synchrony subspaces of the network N that are listed in Table 1

4.2 Rewiring

A rewiring of a network occurs when at least one edge of a network is replaced by another edge of the same type and with the same head cell.

Let R be the network obtained by rewiring a edge of a network N. Suppose the rewiring operation replaces an input edge to a cell c from a cell d with one input edge from a cell a. By Lemma 3.10 in Aguiar et al. [6], a polydiagonal $\varDelta$ is simultaneously a synchrony subspace of M and R if and only if, in the definition of $\varDelta$, either there is the coordinate equality condition $d=a$ or there is no coordinate equality condition involving c.

Next we present an example with a rewiring of multiple edges.

Example 7

The network R of Fig. 6 is a rewiring of network M of Fig. 4, where the directed edges, from cell 2 to cell 1 and from cell 4 to cell 6, are replaced by the directed edges, from cell 6 to cell 1 and from cell 1 to cell 6, respectively. It follows from Lemma 3.23 of [6] that the synchrony subspaces of R that are inherited from M are such that in their definition one of the following three conditions holds:

• there is no coordinate equality condition involving $x_1$ and $x_6$;

• the only coordinate equality condition involving $x_1$ and $x_6$ is $x_1=x_6$, and for all $i \ne 1,6$ and $j \in \{2,4\}$, if there is the coordinate equality condition $x_j=x_i$ then there is also the coordinate equality condition $x_k=x_i$ for all $k \in \{2,4\} \setminus \{j\}$;

• for all i and for all $j \in \{1,4\}$ if there is the coordinate equality condition $x_j=x_i$ then there is also the coordinate equality condition $x_k=x_i$ for all $k \in \{1,4\}\setminus \{j\}$. Moreover, for all i and for all $j \in \{2,6\}$ if there is the coordinate equality condition $x_j=x_i$ then there is also the coordinate equality condition $x_k=x_i$ for all $k \in \{2,6\}\setminus \{j\}$.

We have then that the synchrony subspaces for R that are inherited from M are the synchrony subspaces $\tilde{\varDelta }_{3}$, $\tilde{\varDelta }_{5}$, $\tilde{\varDelta }_{8}$, $\tilde{\varDelta }_{12}$, $\tilde{\varDelta }_{16}$, $\tilde{\varDelta }_{19}$, $\tilde{\varDelta }_{20}$ and $\tilde{\varDelta }_{23}$ from Table 2.

Fig. 6

Network R is a rewiring of network M of Fig. 4, where the directed edges, from cell 2 to cell 1 and from cell 4 to cell 6, are replaced by the directed edges, from cell 6 to cell 1 and from cell 1 to cell 6, respectively

4.3 Product

In [3], Aguiar and Dias consider two product operations on identical-edge networks: the cartesian and the Kronecker (tensor) product.

Definition 1

Let $N_1$ and $N_2$ be two identical-edge networks. Assume that $N_i$ has set of cells $C_i = \{ 1, \ldots , r_i\}$ and set of arrows $E_i$, for $i=1,2$. Consider the cartesian product $C_1 \times C_2$ and denote by ij the element (i, j) in $C_1 \times C_2$.

(i) The cartesian product of $N_1$ and $N_2$, denoted by $N_1 \boxtimes N_2$, is the network with set of cells $C_1 \times C_2$ and two edge types such that there is an edge from cell ij to cell kl if and only if:

$$\begin{aligned} i=k \text{ and } (j,l) \in E_2, \text{ or } j=l \text{ and } (i,k) \in E_1\, . \end{aligned}$$

(1)

The edge type of the edges from cells ij to cells il are of distinct type of the edge type of the edges from cells ij to cell kj.

(ii) The Kronecker product of $N_1$ and $N_2$, denoted by $N_1 \otimes N_2$, is the network with set of cells $C_1 \times C_2$ and such that there is an arrow from cell ij to cell kl if and only if:

$$\begin{aligned} (i,k) \in E_1 \text{ and } (j,l) \in E_2\, . \end{aligned}$$

(2)

See Fig. 7 for an example of two networks $N_1$ and $N_2$, and the product networks $N_1 \boxtimes N_2, N_1 \otimes N_2$.

Fig. 7

From left to right: (up) networks $N_1, N_2$, (down) the cartesian product $N_1 \boxtimes N_2$ and the Kronecker product $N_1 \otimes N_2$

The results in [3] establish an inclusion relation between the lattices of synchrony subspaces for the cartesian and Kronecker products of networks. Specifically, it is proved, in Proposition 4.5, that, for any two identical-edge networks $N_1$ and $N_2$, every synchrony subspace of the cartesian product $N_1 \boxtimes N_2$ is a synchrony subspace of the Kronecker product $N_1 \otimes N_2$. For the case of regular synchrony subspaces, that is synchrony subspaces of the tensor product $P_1 \otimes P_2$, of the total phase spaces $P_1$ and $P_2$ of $N_1$ and $N_2$, respectively, of the form $S_1 \otimes S_2$, with $S_i$ a synchrony subspace of $P_i$, $i=1,2$, the results in [3] show equality. That is, the lattice of the regular synchrony subspaces of $N_1 \boxtimes N_2$ is the lattice of the regular synchrony subspaces of $N_1\otimes N_2$.

Moreover, in [3] it is shown how to obtain the lattice of regular synchrony subspaces of a product network from the lattices of synchrony subspaces of the component networks. Specifically, it is proved that a tensor of subspaces is of synchrony of the product network if and only if the subspaces involved in the tensor are synchrony subspaces for the component networks of the product. It is also shown that, in general, there are (irregular) synchrony subspaces for the product network that are not described by the synchrony subspaces for the component networks, concluding that, in general, it is not possible to obtain the all synchrony lattice for the product network from the corresponding lattices for the component networks.

Example 8

The network R of Fig. 6 is the cartesian product of networks $R_1$ and $R_2$ of Fig. 8, that is, $R=R_1 \boxtimes R_2$. (Here we are assuming a slightly different definition of the cartesian product presented in [3], since both edge types of $R_1$ and $R_2$ lead to just one edge-type in R. However, Theorem 6.5 in [3] that we apply next still holds in this case.) From [3, Theorem 6.5], the lattice of regular synchrony subspaces for R is given by the tensor product of the lattice of synchrony subspaces for $R_1$ and the lattice of synchrony subspaces for $R_2$. Given that the synchrony subspaces for $R_1$ are the trivial ones and that the two nontrivial synchrony subspaces for $R_2$ are defined by the coordinate equality condition $d_1=d_2$ and $d_1=d_3$, respectively, the nontrivial regular synchrony subspaces for R are thus the subspaces $\tilde{\varDelta }_{3}$, $\tilde{\varDelta }_{8}$, $\tilde{\varDelta }_{12}$, $\tilde{\varDelta }_{16}$, $\tilde{\varDelta }_{19}$ and $\tilde{\varDelta }_{23}$ from Table 2.

Fig. 8

Networks $R_1$ and $R_2$ such that the network R of Fig. 6 is the cartesian product of $R_1$ and $R_2$

4.4 f-Join

The usual definition of join of graphs is given by the disjoint union of all graphs together with additional arrows added between every two cells from distinct graphs. In [7], Aguiar and Ruan introduce a generalized version of join on coupled cell networks.

Recall that a multimap is a generalized notion of map, where an element from the domain is assigned to a set of values from the range. Let $\tilde{C}_1\subset C_1$ and $\tilde{C}_2\subset C_2$ be non-empty subsets of cells. Denote by $P(\tilde{C}_2)$ the set of all subsets of $\tilde{C}_2$. Consider a multimap f from $\tilde{C}_1$ to $\tilde{C}_2$ given by

$$\begin{aligned} \begin{array}{l} f:\tilde{C}_1\rightarrow P(\tilde{C}_2) \\ c\mapsto f(c)\subset \tilde{C}_2. \end{array} \end{aligned}$$

(3)

In [7], the f-join of two networks is defined as follows.

Definition 2

Let $N_1$ and $N_2$ be two identical-edge networks with set of cells $C_1$ and $C_2$, respectively, such that the cells in $C_1 \cup C_2$ are all of the same type and $C_1 \cap C_2 = \emptyset$. Let $E_1$ and $E_2$ be the set of edges of $C_1$ and $C_2$, respectively. A network N is called the f-join of $N_1$ and $N_2$, denoted by $N= N_1 *_f N_2$, if

• the set of cells of N is given by $C_1 \cup C_2$;

• the set of edges of N is given by $E_1 \cup E_2 \cup F$, where $F = \{(c,d), (d,c): c \in \tilde{C}_1 \wedge d\in f(c) \}$ and f is defined by (3);

• if the edges in $N_1$ and $N_2$ are of the same type then any two edges $e_1$ and $e_2$ in N are of the same type; otherwise two edges $e_1$ and $e_2$ in N are of the same type if and only if they both are edges in $E_1$, in $E_2$ or in F.

Note that, if $\tilde{C}_1=C_1$, $\tilde{C}_2=C_2$ and $f(c)\equiv C_2$ for all $c\in C_1$, then $N_1 *_f N_2$ is the join of $N_1$ and $N_2$, as defined for graphs.

Example 9

The network R of Fig. 6 may be seen as the f-join of two copies, $R_3$ and $R_4$, of the network $R_2$ on the right of Fig. 8, see Fig. 9. That is, $R =R_3 *_f R_4$ where $f:\{4,1,5\} \rightarrow P(\{2,6,3\})$ is the multimap such that $f(4)=\{2\}$, $f(1)=\{6\}$, and $f(5)=\{3\}$.

Fig. 9

The networks $R_3$ and $R_4$ such that the network R of Fig. 6 is the f-join of $R_3$ and $R_4$ where $f:\, \{4,1,5\} \rightarrow P(\{2,6,3\})$ with $f(4)=\{2\}$, $f(1)=\{6\}$, and $f(5)=\{3\}$

According to Definition 4.6 in [7], we can classify the synchrony subspaces of R into non-bipartite, pairing bipartite and non-pairing bipartite. A synchrony subspace is non-bipartite if, in its definition, there is no coordinate equality condition involving one cell in $R_3$ and one cell in $R_4$. A bipartite synchrony subspace is pairing bipartite if, in its definition, every coordinate equality condition involves one cell of $R_3$ and one cell of $R_4$ and for each cell there is at most one coordinate equality condition involving that cell, otherwise the synchrony subspace is said non-pairing bipartite.

The results in Theorem 4.17 of [7] characterize all the synchrony subspaces of $R =R_3 *_f R_4$. The non-bipartite and the pairing bipartite synchrony subspaces are easily obtained from these results, the synchrony subspaces of $R_3$ and $R_4$ and the interior symmetries of R.

The network $R_3$ has only two nontrivial synchrony subspaces, defined by the coordinate equality condition $x_1=x_4$ and $x_4=x_5$, respectively. Analogously, the network $R_4$ has only two nontrivial synchrony subspaces, defined by the coordinate equality condition $x_2=x_6$ and $x_2=x_3$, respectively.

Given a synchrony subspace $S_1$ for $R_3$ and a synchrony subspace $S_2$ for $R_4$, consider the polydiagonal of the total phase space of R defined by the conjunction of the coordinate equality conditions that define $S_1$ with the coordinate equality conditions that define $S_2$. From the results in Theorem 4.17 of [7], every non-bipartite synchrony subspace of R is such a polydiagonal subspace with the additional condition that if the coordinate equality conditions that define $S_1$ include $x_1=x_4$ then the coordinate equality conditions that define $S_2$ must include $x_2=x_6$ and if the coordinate equality conditions that define $S_1$ include $x_4=x_5$ then the coordinate equality conditions that define $S_2$ must include $x_2=x_3$. We have then that the non-bipartite synchrony subspaces for R are $\tilde{\varDelta }_{6}$, $\tilde{\varDelta }_{19}$ and $\tilde{\varDelta }_{23}$ from Table 2.

From the results in Theorem 4.17 of [7], every pairing bipartite synchrony subspace of R is given by some interior symmetry $\sigma$ of R, where $\sigma$ is a product of disjoint transpositions $\tau _i=(c_i,d_i)$ for $c_i\in \{4,1,5\}$, $d_i\in \{2,6,3\}$. There are five such interior symmetries of R: $\sigma _1=(12)$, $\sigma _2=(46)$, $\sigma _3=(12)(46)$, $\sigma _4=(16)(24)$, and $\sigma _5=(16)(24)(35)$. We have then that the pairing bipartite synchrony subspaces for R are $\{\mathbf{x}:\ x_1 = x_2\}$, $\{\mathbf{x}:\ x_4 = x_6\}$ and $\{\mathbf{x}:\ x_1 = x_2,\ x_4 = x_6\}$ and the synchrony subspaces $\tilde{\varDelta }_{3}$ and $\tilde{\varDelta }_{8}$ from Table 2.

5 Complement Network

Suppose that N is a directed graph with n nodes and just with one edge-type, no multiarrows and no self loops. In graph theory, the usual definitions of the complement and converse graphs of G are the following:

(i) The complement of N is a directed graph $\overline{N}$ on the same set of nodes such that: a directed edge from node i to node j is present in $\overline{N}$ if it does not exist at N; a directed edge from node i to node j is not present in $\overline{N}$ if it exists at N. Graphically, if we take N and fill in all missing directed edges in order to obtain a complete graph (a simple directed graph in which every pair of distinct nodes is connected by a unique bidirectional edge), then $\overline{N}$ is obtained by removing the directed edges belonging to N. The sum of the $n \times n$ adjacency matrices of N and $\overline{N}$ is the $n \times n$ matrix with zero at the diagonal entries and 1 elsewhere and so it commutes with all $n \times n$ permutation matrices.

(ii) The converse of N is the graph with the same set of nodes as N and obtained from N by reversing the directions of all edges of N. The $n \times n$ adjacency matrix of the converse of N is the transpose of the adjacency matrix of N and so the sum of the two adjacency matrices, of N and its converse, is symmetric (it coincides with its transpose).

As an example of possible interpretation of the complement and converse graphs of a graph in the context of social networks is the following. The converse of a directed graph might be helpful in thinking about relations that have “opposites”. The complement of a directed graph might be used to represent the absence of a tie. See for example Wasserman and Faust [45, p. 135].

Example 10

In Fig. 10 we show the complement (on the left) and the converse (on the right) of the five-cell network of Fig. 1.

Fig. 10

The complement (on the left) and the converse (on the right) of the five-cell network of Fig. 1

Motivated by this, we define now the complement network of a network with n nodes that can have multiarrows, self-loops and more that one type of directed edges, preserving the fact that the sum of the adjacency matrices of the network and its complement, for each type of edges, is a matrix that commutes with all $n \times n$ permutation matrices – it can be seen as the adjacency matrix of an all-to-all coupling n-cell network. In doing that, if the network corresponds to a directed graph just with one type of edges, no multiarrows and no self loops, then we recover the usual definition of the complement graph as just recalled above.

Definition 3

Let N be an identical-edge n-cell network with the set of cells $C = \{1, \ldots , n\}$ and adjacency matrix $M_N = [a_{ij}]$. Let $l = \max \{a_{ii}:\ i =1, \ldots , n\}$ and $m = \max \{a_{ij}:\ i,j =1, \ldots , n;\, i\not = j\}$. We define the complement network $\overline{N}$ to be the network with the set of cells C and the adjacency matrix $M_{\overline{N}}$ where $M_N + M_{\overline{N}}$ has at the diagonal entries 2l and m elsewhere. Graphically, if we take N and fill in all missing directed edges in order to obtain a graph where every cell has 2l self-loops and every two distinct cells have m bidirectional edges, then $\overline{N}$ is obtained by removing the directed edges belonging to G.

Example 11

In Fig. 11 we show a three-cell network with multiarrows and self loops at the left and its complement at the right.

Fig. 11

A regular three-cell network with multiarrows and self loops at the left and its complement at the right

As happens for the network N of Fig. 1 and its converse in Fig. 10, the converse of an homogeneous (regular) network may not be an homogeneous (regular) network. It follows, in particular, that, in general, a network N and its converse network do not have the same lattice of synchrony subspaces. Nevertheless, a network N and its converse have the same group of symmetries (but not necessarily the same group of interior symmetries).

For the complement network, we have the following:

Theorem 1

Let N be an identical-edge network. Then, we have the following:

(i) If N is regular then the complement network $\overline{N}$ is regular.

(ii) The networks N and $\overline{N}$ have the same lattice of synchrony subspaces.

(iii) The networks N and $\overline{N}$have the same group of symmetries.

Proof

Let N be an identical-edge n-cell network with the set of cells $C = \{1, \ldots , n\}$ and adjacency matrix $M_N = [a_{ij}]$. Let $l = \max \{a_{ii}:\ i =1, \ldots , n\}$ and $m = \max \{a_{ij}:\ i,j =1, \ldots , n;\, i\not = j\}$. As before denote by $M_{\overline{N}}$ the adjacency matrix of its complement. By definition $M_N + M_{\overline{N}}$ has at the diagonal entries 2l and m elsewhere.

(i) Suppose N is regular of valency v. If $M_{\overline{N}} = [b_{ij}]$ then for $i,j = 1, \ldots , n$, we have: $b_{ii} = 2l - a_{ii}$ and if $i\not =j$ then $b_{ij} = m - a_{ij}$. It follows that for all i we have that $\sum _{j=1}^n b_{ij} = 2l - a_{ii} + \sum _{j\not =i} (m - a_{ij}) = 2l + (n-1) m - \sum _{j=1}^n a_{ij}= 2l + (n-1) m - v$. That is, the complement network $\overline{N}$ is regular of valency $2l + (n-1) m - v$.

(ii) A polydiagonal $\varDelta$ in $\mathrm{\mathbf R}^n$ represents a synchrony subspace of N (resp. $\overline{N}$) if and only if it is left invariant under $M_N$ (resp. $M_{\overline{N}}$). Now the matrix $M_N + M_{\overline{N}}$ commutes with all $n \times n$ permutation matrices and so leaves invariant any polydiagonal. It follows then that a polydiagonal $\varDelta$ is left invariant under $M_N$ if and only if it is left invariant under $M_{\overline{N}}$. That is, $\varDelta$ represents a synchrony space for N if and only if it represents a synchrony space for $\overline{N}$.

(iii) As the matrix $M_N + M_{\overline{N}}$ commutes with all $n \times n$ permutation matrices it follows then that a permutation matrix commutes with $M_N$ if and only if it commutes with $M_{\overline{N}}$.   $\square$

We can generalize the above definition to homogeneous networks. Let N be an n-cell homogeneous network with k types of edges. Denote by $M^1_N, \ldots , M^k_N$ the k adjacency matrices of N, one for each edge type. It follows that N has k regular n-cell subnetworks, each with adjacency matrix $M_N^i$. Denote those by $N_1, \ldots , N_k$ and take $\overline{N}_1, \ldots , \overline{N}_k$ the corresponding complement networks. Then we can define the complement network $\overline{N}$ of N as the network with adjacency matrices $M_{\overline{N}_1}, \ldots , M_{\overline{N}_k}$.

Example 12

In Fig. 12 we show an homogeneous five-cell network at the left and its complement at the right.

Fig. 12

An homogeneous five-cell network at the left and its complement at the right

Trivially, we have the following:

Corollary 1

(i) The complement network of an homogeneous network is homogeneous.

(ii) An identical-cell network and its complement have the same lattice of synchrony subspaces.

(iii) An identical-cell network and its complement have the same group of symmetries.

Remark 1

(i) Note that, in case an n-cell network N is symmetric under a nontrivial finite group $\varGamma \subseteq \mathbf{S}_n$, the coupled cell systems associated with the network N and its complement are $\varGamma$-symmetric. It follows then that it can happen that the corresponding sets of dynamics supported by N and its complement are directly related, in the situations where the linear vector space of smooth $\varGamma$-symmetric vector fields coincide with both linear spaces of smooth vector fields with structure consistent with N and its complement, respectively.

(ii) Note that, in general, the fact that two coupled cell systems associated with N and $\overline{N}$, taking the same cell phase spaces, have the same set of synchrony subspaces, does not imply that the dynamics are closely related.