1 Introduction

Synchronization phenomenon draws attention of scientists in different disciplines of science, e.g. biology, social science, engineering, physics. Word “synchronization” has Greek origins and is combined of two parts: syn—common and chronos—time, which together mean happening at the same time. Synchronization may be defined as adjustments of rhythms of oscillating objects due to their weak interaction (Pikovsky et al. 2003).

Dutch scientist Christiaan Huygens was a pioneer of research in the field of synchronization, when back in the 17th century he observed synchronization of two pendula hanging on a common support (Huygens 1673). In the 19th century Sir John William Strutt (Lord Rayleigh) described synchronization in organ pipes (Rayleigh 1896). Pipes with the same pitch, placed side by side cause the sound to quench. Beginning of the 20th century brought observation of synchronization in electric engineering, when Eccles and Vincent (1920) discovered synchronization property of triode generator. The experiment they proposed proved that coupling generator forces common frequency of system vibration (current frequency of single generator depends on electric properties circuit elements). This idea was later developed by Appleton (1922), van der Pol (1927).

In the second half of the 20th century the synchronization phenomenon was reported in biological systems (Mirollo and Strogatz 1990; Winfree 1967). John and Elisabeth Buck investigated the synchronization phenomenon among fireflies is south-east Asia (Buck and Buck 1968), where males emit synchronous light flashes to attract female during the mating season. Phenomenon of swarm behaviour in groups of animals (e.g. fish school, flock of birds) is addressed in Heppner and Grenander (1990), Reynolds (1987). Existence of synchronization is found in pacemakers cells (Jalife 1984; Michaels et al. 1987), adjustments of menstrual cycle among women (Graham and McGrew 1980), rhythmic applause in concert halls (Néda et al. 2000). An example of synchronization in civil engineering is the case of the Millennium Bridge in London. The just opened footbridge started to vibrate unexpectedly after reaching a threshold number of pedestrian. The lateral forces exerted by pedestrians induced the bridge vibrations, which forced the walkers to move in synchronized step, which additionally amplify the lateral oscillations of the bridge (Dallard et al. 2001a, b; Eckhardt et al. 2007; Lenci and Marcheggiani 2012; Strogatz et al. 2005).

Friction is an ubiquitous force in mechanics, responsible for the resistance of contacting surfaces to relative motion. One can distinguish two types of friction: dry friction—when two solid surfaces are in contact and viscous friction—when the contact occurs through a layer of fluid (e.g. lubricant). Friction dissipates the energy of contacting interfaces into heat and can be the source of self-excited vibrations. These can be heard as squeal sound in various devices (e.g. breaks, machining tools, chalk on blackboard, string and bow in violin) (Ghazaly et al. 2013; Patitsas 2010; Warmiński et al. 2003). Proper understanding of friction phenomenon is crucial in control engineering (Gogoussis and Donath 1987; Saha et al. 2010).

The word “friction” is of Latin origin—fricare. One of the first scholars studying the properties of friction was da Vinci (1518), who formulated two theories. He reported that friction is directly proportional to the normal load applied on the friction interface. Additionally he stated that friction is independent from the apparent contact area (Dowson 1979; Hutchings 2016; Wojewoda 2008). Works of da Vinci were unpublished until they had been rediscovered by Amontons (1669) and today are now known as Amontons’ laws of friction. Euler (1750, 1761) distinguished static and kinetic friction. He also found the relation between inclination angle of inclined plane and friction coefficient \(\mu = \tan {\alpha }\) (Meyer et al. 1998). French physicist Charles Coulomb, further developed Amontons’ ideas (Coulomb 1821). He concluded that kinetic friction is independent of the relative velocity between contacting surface, which is known as Coulomb’s law of friction. A basic friction model is named after him (Coulomb friction model). However, the Coulomb model despite robustness in simple case fails in more complex applications. In the beginning of the 20th century German engineer Stribeck (Stribeck 1902) investigated the non-linearity between the friction force and relative velocity, which is known as Stribeck effect. The change between static and kinetic friction is not gradually, but follows non-linear dependency called Stribeck curve. Should the relative velocity between surface of contact be small, the friction force smoothly decrease from the static friction level, converging at kinetic friction level. The difference between static and kinetic friction in systems with energy source leads to self-excited vibration of the investigated mass.

Nowadays a variety of friction models has been proposed, which can be divided into two groups: static models (Armstrong-Helouvry 1991; Bo and Pavelescu 1982; Hess and Soom 1990; Popp and Stelter 1990) and dynamical (Al-Bender et al. 2004; de Wit et al. 1995; Dahl 1968; Stefański et al. 2003; Wojewoda et al. 2008), where friction depends on many variables. The dynamical models have even internal states described by ordinary differential equations.

In this chapter we deal with the synchronization properties and synchronization properties of coupled dry friction oscillators. The research presented in this chapter is a continuation of author’s previous research in Marszal (2017), Marszal et al. (2016), Marszal and Stefański (2017). The chapter is organized as follows. Section 2 presents theoretical background in the field of synchronization. Section 3 introduces the mathematical model and the concept of self-excited vibrations in single friction oscillator. In Sect. 4 friction oscillators are coupled forming oscillator networks. Section 5 discusses the result of numerical simulations. Finally conclusions and possible future development are shown in Sect. 6.

2 Synchronization

Let us consider a dynamical system, consisting of N oscillators, which can be described using following matrix-form equation (Stefański 2009), where \(\mathbf {x} = \left( x_1,\ldots ,x_N \right) \in \mathfrak {R}^N\) is a state vector and \(\mathbf {F\left( x\right) }=\left( f_1\left( x_1\right) ,..,f_N\left( x_N\right) \right) \) is a function describing the local dynamics of the system, which is independent of the coupling.

$$\begin{aligned} \dot{\mathbf {x}} = \mathbf {F}(\mathbf {x}) + \sigma ( \mathbf {G} \otimes \mathbf {H} ) \mathbf {x}, \end{aligned}$$
(1)

The second term in (1) describes the coupling properties. \(\mathbf {G}\) is a connectivity matrix, \(\mathbf {H}: \mathfrak {R}^N \rightarrow \mathfrak {R}^N\) linking functions, \(\mathbf {H}\) a linking matrix, \(\sigma \) coupling coefficient, \(\otimes \) denotes the Kronecker product of two matrices. For the general case the properties of \(\mathbf {G}\) and \(\mathbf {H}\) matrices can be arbitrary.

2.1 Types of Synchronization

Synchronization is a complex phenomenon. For the case of this chapter let us limit our consideration to few types of synchronization, namely, complete synchronization, imperfect complete synchronization and cluster synchronization.

Let us restrict the area of considerations to a network of identical oscillators \(\mathbf {F\!\left( x\right) }\) and linking functions \(\mathbf {H}\). In such a system it is possible to obtain complete synchronization (CS), called also full synchronization. According to Pecora and Carroll (1990) complete synchronization can be observed when two trajectories converge to the same value and later hold that conditions. Stefański (2009) proposes following definition of complete synchronization.

Definition 1

The complete synchronization of two dynamical systems represented with their phase plane trajectories \(\mathbf {x}\!\left( t\right) \) and \(\mathbf {y}\!\left( t\right) \), respectively, takes place when for all \(t>0\), the following relation is fulfilled:

$$\begin{aligned} \lim _{t \rightarrow \infty } \left\| \mathbf {x}\!\left( t\right) - \mathbf {y}\!\left( t\right) \right\| = 0\text {.} \end{aligned}$$
(2)

In practical applications it may be difficult to have identical oscillator nodes in network. Should there be a mismatch between oscillators or coupling properties, differences between their respective trajectories converge to zero with some small tolerance \(\varepsilon \). Such a situation is called imperfect complete synchronization (ICS). Stefański (2009) defines ICS as follows.

Definition 2

The imperfect complete synchronization of two dynamical systems represented with their phase plane trajectories \(\mathbf {x}(t)\) and \(\mathbf {y}(t)\), respectively, occurs when for all \(t >0\), the following inequality is fulfilled:

$$\begin{aligned} \lim _{t \rightarrow \infty } \left\| \mathbf {x}\!\left( t\right) - \mathbf {y}\!\left( t\right) \right\| < \varepsilon \text {,} \end{aligned}$$
(3)

where \(\varepsilon \) is a small parameter.

Supposing the system consists of \(N >2\) identical oscillators one may distinguish two or more subsets for which the particular oscillators are in sync with each other and out of sync with the members of the other subset. Subsets of synchronized oscillators are called clusters. It is important to mention that we can talk about cluster synchronization when whole system is not in complete synchronization. The motion of different cluster may be uncorrelated or one can observe a shift phase between them. Existence of clusters is connected with the existence and stability of synchronization manifold (Perlikowski 2007). The topic of clusters can be found in literature in Belykh et al. (2000, 2001), Dahms et al. (2012), Kaneko (1990), Wu et al. (2009), Yanchuk et al. (2001).

2.2 Synchronous State Stability

A power mathematical tool used in assessing the stability of the synchronous state is the concept of master stability function (MSF) introduced by Pecora and Carroll (1998). Master stability function enables to divide the problem of the synchronous state stability into two parts: (i) the topological part, where we need to calculate the eigenvalues of the connectivity matrix, and (ii) local dynamic part, where one need to calculate Lyapunov exponents of variational equation. The classic approach to estimate the MSF is to calculate transversal Lyapunov exponents (TLE) of the Eq. (7) derived below. Let us begin with obtaining variational equation of Eq. (1):

$$\begin{aligned} {\dot{\mathbf {\xi }}} = \left[ \mathbf {1_N} \otimes D\mathbf {F} + \sigma \mathbf {G} \otimes D\mathbf {H}\right] \mathbf {\xi }, \end{aligned}$$
(4)

where \(\xi _i\) is the variation of the ith node, \(\xi = (\xi _1, \xi _2, ... \xi _N)\) is variation vector, \(D\mathbf {F}\) is the Jacobian of any node, \(D\mathbf {H}\) is the Jacobian of the linking function. Diagonalization of Eq. (4) yields to uncoupling the variational Eq. (4) into N block having a form of:

$$\begin{aligned} \dot{\xi }_k = \left[ D\mathbf {F} + \sigma \gamma _kD\mathbf {H}\right] \xi _k, \end{aligned}$$
(5)

where \(\gamma _k\) is the kth eigenvalue of the \(\mathbf {G}\), \(i=0,1,2,...,N-1\), \(\xi _k\) is transverse mode of perturbation from the synchronous state. In case of \(k=0\) eigenvalue is \(\gamma _0=0\), and consequently Eq. (5) is reduced to

$$\begin{aligned} \dot{\xi }_0 = D\mathbf {f}\xi _0, \end{aligned}$$
(6)

which is associated with the longitudinal direction located within the synchronization manifold. The other kth eigenvalues correspond to transverse eigenvectors (Pecora and Carroll 1998). In MSF concept the tendency to synchronization is a function of eigenvalues \(\gamma _k\). Let us substitute \(\sigma \gamma = \alpha + i\beta \) in Eq. (5), where \(\alpha \) and \(\beta \) are respective real and imaginary part of eigenvalues.

$$\begin{aligned} {\dot{\mathbf {\xi }}} = \left[ D\mathbf {F} + \left( \alpha + i\beta \right) D\mathbf {H}\right] \mathbf {\xi }, \end{aligned}$$
(7)

where \(\xi \) is an arbitrary transverse mode.

Condition for the existence of invariant synchronization manifold is the zero row sum connectivity matrix \(\mathbf {G}\) (Pecora and Carroll 1998). All the real parts of eigenvalues, which correspond to transversal modes, are negative (\(\mathrm {Re}(\gamma _{k \ne 0}) < 0\)). The spectrum of eigenvalues has the descending form, i.e., \(\gamma _0 \ge \gamma _1 \ge ... \ge \gamma _{N-1}\). In general case, (Pecora and Carroll 1998) defines MSF as the largest transversal Lyapunov exponent \(\lambda _T\) surface, computed basing on Eq. (7), on a complex numbers plane \((\alpha , \beta )\). Should the interaction between the nodes be mutual (e.g. mechanical systems), then the eigenvalues have only real part and then MSF is represented only by a curve describing the largest TLE as a function of real number \(\alpha \), defined as

$$\begin{aligned} \alpha = \sigma \gamma . \end{aligned}$$
(8)
Fig. 1
figure 1

Examples of the MSF with spectrum of eigenvalue of connectivity matrix for cases of potential stable (a) and unstable (b) complete synchronization state of all network oscillators

Full size image

The synchronous state of dynamical system is stable when all eigenmodes of the discrete eigenvalue spectrum \(\sigma \gamma _k\) lay in ranges of the largest negative TLE (see Fig. 1a). Supposing even only one eigenvalue is in the range, where \(\lambda _T > 0\) (see Fig. 1b), the global synchronization is unstable, however, cluster synchronization is still possible.

The method mentioned in previous section is robust for time continuous systems, given by smooth equations, where the computation of TLE is relatively easy. However, when dealing with non-smooth dynamical systems, such as dry friction oscillators, the computation of TLE requires special care and algorithms. In such a case, techniques called three-oscillator universal probe (Fink et al. 2000) and two-oscillator probe (Wu 2001) come to our rescue. Oscillator probe is based on estimating the MSF on the complex plane by direct detection of the complete synchronization in numerical calculations or in the experiment. The methodology is simple, but yet efficient. When calculating MSF in three-oscillator probe for system containing N oscillators, one initially investigates the reference probe of three oscillators. The area on the complex plane \((\alpha , \beta )\) where the complete synchronization or imperfect complete synchronization occurs is the equivalent of the area of negative transversal Lyapunov exponents. The two-oscillator probe can be applied for mechanical systems, where due to mutual interaction between the nodes, the eigenvalues of the connectivity matrix \(\mathbf {G}\) are real and the MSF is reduced to a curve, which is also the case for real only eigenvalues when using TLE as MSF.

Let us consider system of \(N=2\) coupled oscillators, given by Eq. (1), with connectivity matrix \(\mathbf {G}\):

$$\begin{aligned} \mathbf {G} = \begin{pmatrix} -c &{} c \\ c &{} -c \\ \end{pmatrix}, \end{aligned}$$
(9)

where c is the real coupling factor. One can formulate following variational equation of the considered system.

$$\begin{aligned} \begin{pmatrix} \dot{\xi }_1 \\ \dot{\xi }_2 \\ \end{pmatrix} = \left[ \mathbf {I_2} \otimes D\mathbf {f} + \sigma \begin{pmatrix} -c &{} c \\ c &{} -c \\ \end{pmatrix} \otimes D\mathbf {H} \right] \begin{pmatrix} {\xi }_1 \\ {\xi }_2 \\ \end{pmatrix}, \end{aligned}$$
(10)

with real eigenvalues \(\gamma _0=0\), \(\gamma _1=-2c\). This yields to generic variational equation for MSF determination for the two-oscillator probe system

$$\begin{aligned} \dot{\xi } = \left( D\mathbf {f} - 2\sigma c D\mathbf {H} \right) \xi . \end{aligned}$$
(11)
Fig. 2
figure 2

Equivalence of the MSF (a) and two-oscillator probe (b)

Full size image

If the all non-zero eigenvalues of the connectivity matrix of the system of N oscillators are in the surface or range of complete (imperfect complete) synchronization for the reference probe, then the complete synchronization (imperfect complete synchronization) is possible for the the system in question. When comparing Eq. (11) with Eq. (7) one can notice that \(\alpha = 2\sigma c\). Hence, the multiplier 2 has to be taken under consideration when the MSF (e.g. from Fig. 1a) is replaced by two oscillators probe as shown in Fig. 2.

In order to estimate the MSF using two-oscillator probe, it is necessary to couple two oscillators with real coupling and perform numerical or experimental determination of synchronous ranges. The synchronous ranges can be indicated by average synchronization error for two-oscillator probe \(\langle e_{II} \rangle = 0\) and are equivalents of stable synchronous region of MSF using the largest TLE. We can project this representative two-oscillator probe for any number of coupled oscillators with arbitrary structure of connection between them via eigenvalues of the connectivity matrix \(\mathbf {G}\) (Fink et al. 2000; Marszal and Stefański 2017; Pecora and Carroll 1998; Stefański 2009; Wu 2001).

One can distinguish three different regimes of synchronous intervals in the MSF \(\langle e_{II} \rangle \left( \alpha \right) \) analysis: (i) bottom-limited \((\alpha _1, \infty )\), (ii) upper-limited \((\alpha _1=0, \alpha _2 > 0\) but of finite value) and (iii) double-limited (\(\alpha _1, \alpha _2 > 0\), but of finite value). Values of \(\alpha _1\) and \(\alpha _2\) denote upper and lower ends (Fig. 3) of the synchronous range, respectively (Stefański 2009; Stefański et al. 2007). In this chapter let us focus on the second and third cases. In the double-limited case, two transverse eigenmodes have influence on the synchronization thresholds, i.e., the longest spatial-frequency mode, which corresponds to the largest eigenvalue \(\gamma _1\), and the shortest spatial frequency, which corresponds to the smallest eigenvalue \(\gamma _{N-1}\). They determine the size of the synchronous state interval. The loss of stability can be caused by two desynchronization bifurcations. Decrease of \(\sigma \) triggers a long-wavelength bifurcation, as the longest wavelength mode \(\xi _1\) becomes unstable. Contrary, the increase of \(\sigma \) may lead to short-wavelength bifurcation, because the shortest wavelength mode \(\xi _{N-1}\) becomes unstable (Marszal and Stefański 2017; Stefański et al. 2007). One can formulate condition for the existence of the synchronous interval as

$$\begin{aligned} \frac{\gamma _{N-1}}{\gamma _1} < \frac{\alpha _2}{\alpha _1}, \end{aligned}$$
(12)

which implies the existence of the maximum number of oscillators, for which the investigated system can be in CS. The increase of N follows the increase of \(\gamma _{N-1}/\gamma _1\) ratio. Hence, the inequality in (12) cannot be fulfilled (Barahona and Pecora 2002; Nishikawa et al. 2003; Pecora et al. 2000; Pecora 1998). The discussed case of double limited synchronous interval is depicted in the Fig. 3. For the Fig. 3a the condition in (12) is fulfilled and synchronous intervals overlap with cross-hatched area marking the synchronous range \((\sigma _1,\sigma _2)\). Contrary, in the Fig. 3b the synchronous intervals do not overlap and there is no synchronous range for network of N oscillators (Marszal and Stefański 2017; Stefański 2009). In case of upper-limited synchronous interval the synchronization regions depend on the smallest eigenvalue \(\gamma _{N-1}\). The increase of N forces to narrow the synchronization interval towards the origin of the coordinates system.

As an additional effect of double-limited synchronous interval, the phenomenon of the so called ragged synchronizability can be observed, i.e., alternately occurring synchronous and desynchronous windows (Stefański et al. 2007) (e.g. Fig. 3a).

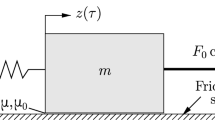
3 Single Self-excited Friction Oscillator

Consider a single, classic, dry friction, self-excited oscillator, depicted in Fig. 4. The system consists of a drive—conveyor belt, elastic element—spring and moving oscillating mass with a frictional interface. The equation of motion of the system can be formulated as follows:

$$\begin{aligned} m\frac{\mathrm {d^2} x }{\mathrm {d} t^2 } = F_Nf\left( v_r\right) -kx, \end{aligned}$$
(13)

where: m—mass of the oscillator x—displacement of the oscillator, k—stiffness constant, \(v_b\)—velocity of the belt, \(v_r\)—relative velocity between the contacting surfaces \(\left( v_r = v_b - \frac{\mathrm {d}x}{\mathrm {d}t}\right) \), \(F_N\)—normal load (the weight of oscillator is included in \(F_N\)), \(f(v_r)\)—function describing friction characteristics.

Fig. 3
figure 3

Examples of double-limited synchronous intervals: a synchronous ranges of shortest and longest frequency modes are partly overlapping, yielding to stable synchronous interval \((\sigma _1,\sigma _2\)); b synchronous ranges of both modes are disconnected—CS is not possible. Gray corresponds to desynchronous regions

Full size image

Let us non-dimensionalise the Eq. (13) by applying \(\omega _0 = \sqrt{\frac{k}{m}}\), non-dimensional time \(\tau = \omega _0t\) and characteristic constant \(x_0 = \frac{g}{\omega _0^2}\), which results in

$$\begin{aligned} \ddot{\chi } = \epsilon f(\vartheta _r) -\chi . \end{aligned}$$
(14)

The non-dimensional variables are formulated as follows: \(\epsilon =\frac{F_N}{mg}\)—load coefficient, \(\vartheta _{b} = \frac{v_{b}}{x_0\omega _0}\)—non-dimensional velocity of the belt, \(\vartheta _{r} = \vartheta _{b} - \dot{\chi }\)—non-dimensional relative velocity between contacting surfaces, \(\chi = \frac{x}{x_0}\)—non-dimensional displacement. The overdots stand for the respective derivatives with respect to \(\tau \). The relationships between dimensional and non-dimensional displacement and its derivatives is given by: \(\frac{\mathrm {d^2} x}{\mathrm {d} t^2 } = x_0\omega _0^2 \ddot{\chi }\), \(\frac{\mathrm {d}x}{\mathrm {d}t} = x_0\omega _0\dot{\chi }\).

Stribeck friction model with the exponential non-linearity is applied as the basis for friction modelling in this work. The Stribeck friction model with the exponential non-linearity is given by formula:

$$\begin{aligned} f(\vartheta _r) = \left( \mu _k + \left( \mu _s - \mu _k \right) e^{-a \left| \vartheta _r \right| } \right) \mathrm {sgn} \vartheta _r, \end{aligned}$$
(15)

where \(\mu _s\)—static friction coefficient, \(\mu _k\)—kinetic friction coefficient, a is constant defining the shape of the friction—relative velocity curve. The friction force f as a function of relative velocity \(\vartheta _r\) based on the aforementioned model is depicted in the Fig. 5. Note the negative slope of friction force—relative velocity curve, which is essential for the occurrence of self-excited vibrations (Ding 2010).

Figure 6 illustrates a limit-cycle to which all +. The segment of trajectory with horizontal line corresponds to the sticking phase when \(\vartheta _r=0\). The mass moves along with the belt and accumulates the potential energy. The value of friction force adjust itself to maintain the equilibrium with the spring force. When the maximum value of friction force is reached, the friction force cannot balance the spring and the mass begins to slide. Friction is then responsible for the dissipation of energy into heat. Eventually, the velocity of the mass decreases to the level of the velocity of the belt and the mass sticks with it. Such kind of motion form a sawtooth wave (see Fig. 8 with grey regions corresponding to stick phase). Hence, the sound of objects subjected to stick-slip phenomenon is not pleasant to our ears. In Fig. 7 a phase diagram with stick-slip limit cycle is depicted.

Fig. 4
figure 4

Single stick-slip dry friction oscillator

Full size image
Fig. 5
figure 5

Friction force f as a function of relative velocity \(\vartheta _r\)

Full size image
Fig. 6
figure 6

Phase portrait of single friction oscillator with self-excited stick-slip vibrations. Multiple trajectories approach the stick-slip limit cycle. System parameters: \(\vartheta _b = 0.1\), \(\mu _s = 0.3\), \(\mu _k = 0.15\), \(a=2.5\), \(\epsilon =2\). (Marszal 2017)

Full size image
Fig. 7
figure 7

Phase diagram of single self-excited friction oscillator. System parameters: \(\vartheta _b = 0.1\), \(\mu _s = 0.3\), \(\mu _k = 0.15\), \(a=2.5\), \(\epsilon =2\)

Full size image
Fig. 8
figure 8

Time diagram of single self-excited friction oscillator: a position of the oscillator, b velocity of the oscillator. Gray regions correspond to stick phase. System parameters: \(\vartheta _b = 0.1\), \(\mu _s = 0.3\), \(\mu _k = 0.15\), \(a=2.5\), \(\epsilon =2\)

Full size image
Fig. 9
figure 9

Array of coupled N stick-slip oscillators

Full size image
Fig. 10
figure 10

Different connection topologies for network of N oscillators: a open ring b closed ring

Full size image
Fig. 11
figure 11

Synchronization regions for open ring of N oscillators in two-parameter space (\(\sigma \) versus \(\omega \)), \(\epsilon =1\), on sides of scheme of observed cluster layouts: a \(N=3\), b \(N=4\), c \(N=5\), d \(N=6\)

Full size image
Fig. 12
figure 12

Synchronization regions for open ring of N oscillators in two-parameter space (\(\sigma \) versus \(\omega \)), \(\epsilon =1\), on sides of scheme of observed cluster layouts: a \(N=3\), b \(N=4\), c \(N=5\), d \(N=6\)

Full size image
Fig. 13
figure 13

MSF \( \langle e_{II} \rangle (\alpha )\) projected onto respective average synchronization errors \(\langle e_{3} \rangle \), \(\langle e_{1,3} \rangle \) for N coupled oscillators via eigenvalues of connectivity matrix \(\mathbf {G}_3\). \(N=3\), \(\omega =1.6\), \(\epsilon =1.5\) initial conditions \(\mathbf {\chi } = [0.2913, 0, 0.2945, 0, 0.2922, 0]^T\)

Full size image
Table 1 Non-zero eigenvalues and corresponding eigenvectors for the connectivity matrices \(\mathbf {G}_N\) for open ring networks.
Full size table
Fig. 14
figure 14

MSF \( \langle e_{II} \rangle (\alpha )\) projected onto average synchronization error between 1st and 4th oscillator \( \langle e_{1,4} \rangle \) (dashed line) and average global synchronization error \(\langle e_{IV} \rangle \) (solid line) for three coupled oscillators via eigenvalues of connectivity matrix \(\mathbf {G_4}\) for excitation angular frequency \(\omega = 1.4\). Initial conditions for each value of \(\sigma \): \(\mathbf {\chi _0} = [0.2913, 0, 0.2945, 0, 0.2922, 0]^T\)

Full size image
Fig. 15
figure 15

Synchronization regions for open ring of N oscillators in two-parameter space (\(\sigma \) versus \(\omega \)), on sides of scheme of observed cluster layouts: a \(N=4\), b \(N=6\), c \(N=8\), d \(N=9\)

Full size image
Fig. 16
figure 16

Synchronization regions for closed ring of N oscillators in two-parameter space (\(\sigma \) versus \(\omega \)), on sides of scheme of observed cluster layouts: a \(N=4\), b \(N=6\), c \(N=8\), d \(N=9\)

Full size image

The presented, 1-DOF system, can be treated as a toy model for more complicated systems used in engineering application, e.g. disc brake (Wei et al. 2016). Here mass corresponds to brake pad, belt—to disc of the brake, while spring—to the stiffness of the system, which is subjected to external excitation (Popp et al. 1995).

4 Oscillators Network

Let us now consider an array of N identical oscillators described above, which are coupled using linear springs of stiffness \(k_C\), as shown in the Fig. 9. Additional excitation \(u\cos {\omega \tau }\) is applied to each oscillator. The equation of motion for the coupled system can be written in matrix form, where the \(\sigma = {k_C}/{k}\) stands for the coupling coefficient and determines the strength of the coupling:

$$\begin{aligned} \begin{Bmatrix} \ddot{\chi }_1 \\ \vdots \\ \ddot{\chi }_N \end{Bmatrix} = - \begin{Bmatrix} {\chi _1} \\ \vdots \\ \chi _N \end{Bmatrix} + \sigma \varvec{G}_N \begin{Bmatrix} {\chi _1} \\ \vdots \\ \chi _N \end{Bmatrix} + \begin{Bmatrix} \epsilon f\left( \vartheta _{r_1}\right) + u\cos {\omega \tau } \\ \vdots \\ \epsilon f\left( \vartheta _{r_N}\right) + u\cos {\omega \tau } \end{Bmatrix}. \end{aligned}$$
(16)

Matrix \(\mathbf {G_N}\) is connectivity matrix and represents the connection topology of the network. In this work, two distinct topologies are considered, namely open and close ring of oscillators connected in nearest neighbour fashion. The scheme of the topologies is depicted in the Fig. 10. The connectivity matrices for both topologies are presented by Eq. (17) (\(\mathbf {G_{N_O}}\)—open ring) and Eq. (18) (\(\mathbf {G_{N_C}}\)—closed ring) respectively.

$$\begin{aligned} \varvec{G_{N_{O}}} = \begin{pmatrix} -1 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 0 \\ 1 &{} -2 &{} 1 &{} \ddots &{} \cdots &{} 0 \\ 0 &{} 1 &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} 1 &{} 0 \\ 0 &{} \cdots &{} \ddots &{} 1 &{} -2 &{} 1 \\ 0 &{} 0 &{} \cdots &{} 0 &{} 1 &{} -1 \end{pmatrix}, \end{aligned}$$
(17)
$$\begin{aligned} \varvec{G_{N_{C}}} = \begin{pmatrix} -2 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 1 \\ 1 &{} -2 &{} 1 &{} \ddots &{} \cdots &{} 0 \\ 0 &{} 1 &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} 1 &{} 0 \\ 0 &{} \cdots &{} \ddots &{} 1 &{} -2 &{} 1 \\ 1 &{} 0 &{} \cdots &{} 0 &{} 1 &{} -2 \end{pmatrix}. \end{aligned}$$
(18)

Note that for both matrices there are zero sum rows, which is caused by mutual interaction in mechanical systems. The eigenvalues of the connectivity matrices are used later in the master stability function to determine the synchronization thresholds.

5 Results

In this Section we present the results of numerical studies, based on the numerical model described in Sects. 3 and  4. Additionally, we present the usage of master stability function and two-oscillator probe for determining the synchronization thresholds.

The numerical simulations are based on author’s own program written in C++ using on Boost Odeint library (Ahnert and Mulansky 2011) as numerical engine. Following non-dimensional parameters are used in simulations: \(\vartheta = 0.1\), \(\mu _s = 0.35\), \(\mu _k = 0.2\), \(a=2.5\), \(u=0.1\). If different values are used, information is placed in figure caption or legend respectively. A transient time equal to 1000 excitation periods (\(\varDelta \tau _t = 1000 \cdot 2 \pi / \omega \)) is applied, which is followed by measurement of average synchronization error for time interval corresponding to 200 excitation periods. The investigated systems are started from the initial conditions, when the complete synchronization is slightly perturbed. Should the synchronous state be stable, the trajectories return to synchronous state after time \(\varDelta \tau _t\).

We perform a study of parameters in (\(\sigma , \omega \)) two-dimensional parameter space with goal to detect complete and cluster synchronization regions in open and closed ring connection topology, for different values of the network size N. Based on previous studies (Marszal et al. 2016; Marszal and Stefański 2017), we choose the following ranges of parameters: coupling coefficient \(\sigma \in [0,1]\) and angular frequency of excitation \(\omega \in [1,2]\). The parameter space is discretised into grid with grid element size \(\varDelta \sigma = \varDelta \omega = 0.01\), giving 10 201 elements in total. For each element of the grid average global e (19) and cluster \(e_{i,j}\) (20) synchronization errors are computed. Finally a type of synchronization is classified according to definitions in Sect. 2.1. If the respective synchronization error is bellow \(10^{-3}\), element of the grid is classified as synchronized.

$$\begin{aligned} e = \sum ^N_{i=2} \sqrt{\left( \chi _1 - \chi _i\right) ^2 + \left( \dot{\chi }_1 -\dot{\chi }_i \right) ^2 } \end{aligned}$$
(19)
$$\begin{aligned} e_{i,j}= \sqrt{\left( \chi _i - \chi _j\right) ^2 + \left( \dot{\chi }_i -\dot{\chi }_j \right) ^2 }. \end{aligned}$$
(20)

In Figs. 11 and 12 results of the parameter study for the open ring topology are presented. The systems in question are checked for two different values of normal load coefficient: \(\epsilon =1\) (Fig. 15), \(\epsilon =1.5\) (Fig. 12). Black colour depicts the complete synchronization region, while the yellow lack of synchronization. The other colours correspond to different cluster synchronization layouts. The complete synchronization region is larger for lower values of the normal load coefficient, which yields to lower friction force between the contacting interfaces. Scheme of cluster layouts are placed on side of respective diagrams. Note that for the case of (\(\epsilon =1\), \(N=6\)) three cluster layouts are observed (Fig. 11d). For other systems (Fig. 11a–c) only one cluster layout is observed. In all cases the complete synchronization occurs rather for weak coupling. The increase of coupling strength destroys the complete synchronization, however cluster synchronization regions emerges.

Analysis of the eigenvectors of respective eigenvalues enables us to explain the shapes of the clusters (Perlikowski et al. 2010; Yanchuk et al. 2001). Consider the case of three oscillators depicted in one parameter space in the Fig. 13. Here we have following values of eigenvalues: \(\gamma _{0(3)}=0\), \(\gamma _{1(3)} = -1\), \(\gamma _{2(3)} =-3\); together with corresponding eigenvectors: \(\mathbf {v}_{0(3)}=[1,1,1]^T\), \(\mathbf {v}_{1(3)} = [-1,0,1]^T\), \(\mathbf {v}_{2(3)} = [1,-2,1]^T\). The desynchronization process from the complete synchronization state is governed by the \(\gamma _{2(3)}\). For this particular eigenvalues the first and the third element of the eigenvector \(\mathbf {v}_2\) are equal, leading to the existence of cluster consisting of the first and the third oscillator. The other eigenvector—\(\mathbf {v}_{1(3)}\) does not have at least two equal elements, hence it cannot be responsible for the formation of cluster. The eigenvector \(\mathbf {v}_{0(3)}\) based on \(\gamma _{0(3)}\) corresponds to the direction along synchronization manifold (the global CS state), as all its elements are equal. Table 1 lists non-zero eigenvalues and their eigenvectors for all investigated networks with open ring topology. Note that \(\gamma _{0(N)}=0\) and \(\mathbf {v}_{0(N)}=[1,...,1]^T\). In the cases of \(N=3,4,5\) only one eigenvector pattern can be responsible for the creation of clusters. Thus only single cluster configuration can be observed.

More detailed analysis of global (CS) and cluster synchronization thresholds is performed for certain selection of \(\omega \), including verification of the obtained results by means of MSF (see Figs. 13, 14). The MSF is defined as average synchronization error for two-oscillator probe \( \langle e_{II} \rangle (\alpha )\) as a function of real number \(\alpha \) (see Eq. (8)). Next, MSF \( \langle e_{II} \rangle (\alpha )\) is projected via eigenvalues of connectivity matrix \(\mathbf {G}_{N}\) onto bifurcation diagrams of average synchronization error for networks consisting of N oscillators with \(\sigma \) as a bifurcation parameter. The complete synchronization for network of N oscillators occurs, provided all eigenvalues spectrum of connectivity matrix \(\mathbf {G}_{N}\) lies within zero \(\langle e_{II}(\alpha ) \rangle \) function. The areas of zero MSF within the eigenvalues spectrum, as well as complete synchronization regions in networks of N oscillators are marked with grey colour respectively. The method described above is robust for predicting the global CS thresholds and along with the analysis of eigenvectors can be used to explain the cluster synchronizability. However, due to additional coupling factors (i.e., excitation, friction or coexistence of the system attractors) the MSF method indicates only the tendencies of the oscillators to synchronize and might be not always verified in given network configuration.

For the case of three oscillators \(\epsilon = 1.5, N=3\), \(\omega =1.6\) (Fig. 13) the CS region is in range \(\sigma \in [0.12, 0.27]\). It is worth mentioning that the first and last oscillator in the network are in cluster synchronization for almost all investigated range of \(\sigma \). Similar behaviour can be seen in Fig. 12a, marked as red region, wherein cluster synchronization occupies large area of the investigated parameter space. For the case of four oscillators (see Fig. 14) with \(\omega =1.4\), \(\epsilon =1\) CS region is located for \(\sigma \in [0, 0.21]\).

In the presented systems it is possible to observe the so called ragged synchronizability phenomenon (Stefański et al. 2007). In Fig. 13 one can observe global ragged synchronizability, where all oscillators in the network are in synchronous or desynchronous state. One can also find for that case, cluster ragged synchronizability, i.e., synchronous and desynchronous regions in clusters.

Similar study as for open ring networks is performed to closed ring network topology in Figs. 15 (\(\epsilon =1\)) and 16 (\(\epsilon =1.5\)). Table 2 lists non-zero eigenvalues and their eigenvectors for all investigated networks with closed ring topology. Again the parameter space is checked for global and cluster synchronization regions for different length of identical oscillators. The systems are modelled according to Eq. (16) with \(\mathbf {G}_{N_C}\) from Eq. (18). The obtained results for different network sizes \((N=4,6,8,9)\) are depicted in the Figs. 15 and 16. The areas of complete synchronization occurs also for low values of coupling. However, in the case of closed ring topology the variety of cluster configuration is richer. This can be explained by the symmetry of the system, which aids the cluster formation.

6 Conclusion

Let us summarize this chapter, which is devoted to the analysis of synchronization properties in dynamical systems with dry friction.

Table 2 Non-zero eigenvalues and corresponding eigenvectors for the connectivity matrices \(\mathbf {G}_N\) for closed ring networks.
Full size table

We have performed a parameter study of complete and cluster synchronization properties in two-parameter space (coupling coefficient versus angular frequency of excitation). Numerical investigations involve two different network topologies, i.e., open ring and closed ring. Oscillators are connected in nearest neighbour fashion. The goal was to find synchronization thresholds in various networks of oscillators. The used methodology is based on master stability function. However, MSF is not estimated in a traditional way by TLE but by means of more direct approach, namely, two-oscillator probe.

One needs to bear in mind that MSF describes tendencies of the system to synchronize. It cannot be treated as the final condition for the synchronization. The oscillators in question are coupled also by common excitation and the friction force itself, which may contribute also to the synchronizability of the system. Velocity of the conveyor belt, which is equal for all oscillators as well as the same friction model, provide identity of the parameters, which is necessary condition for the occurrence of CS. Moreover, the common harmonic excitation correlates in time with the driving components of all oscillators and as a consequence facilitates the synchronization.

On the contrary, important factor leading to the desynchronization or appearance of cluster is the coexistence of attractors, which is characteristic and often encountered for the systems with friction and impact oscillators. Coexistence of attractors is a property of non-linear systems, which can occur also in smooth, time-continuous dynamical systems. Therefore, the MSF concept and eigenvectors analysis can be treated only as a tool for estimating the overall, global predisposition of the system of coupled oscillators to synchronize or to cluster. This may explain fact, that for some configuration in closed ring topology, some of the cluster layouts cannot be explained by the eigenvectors or eigenvalues interpretation. The results presented in this chapter also show ragged synchronization phenomenon (i.e., complete synchronization windows).

In general, the synchronization stability criterion given by the MSF does not provide for proper detection of global network synchronization state even in the case of smooth systems described by continuous differential equations. The more this problem occurs in non-smooth systems where the structure of attractors coexistence and their basins of attraction is usually more complex than in smooth systems. Hence, on the basis of our research, we can conclude that for non-smooth dynamical systems the MSF estimated with two oscillators probe can be even more effective than one calculated with use of the TLE, because then we can be sure that the synchronous region was really detected and it is not only a projection of an interval of the negative TLE. Additionally, the numerical results show that the phenomenon of ragged synchronizability concerns also the cluster synchronization case.

Based on the results of the chapter, further research can be conducted in following directions. The first research proposal is to consider the presented model in the framework of earthquake modelling as a version of Burridge-Knopoff model (Burridge and Knopoff 1967). This requires changing the system parameters, as in earthquake modelling transition from static to dynamic behaviour is a crucial property. It is also possible to analyse the presented model in the framework of the so called snaking phenomenon (Papangelo et al. 2017). Another direction of research may concern experimental investigation of the proposed model. This would involve designing and assembling experimental stand with all necessary measurement equipment, which would enable to verify experimentally the synchronizability of the system in question.