Keywords

1 Introduction

Information authentication is an indispensable part of today’s computer and communication systems. Gilbert et al. [14] considered codes that detect “deception” to provide protection against message tampering. A Message Authentication Code (MAC) is a symmetric key cryptographic primitive that consists of a pair of algorithms: a tag generation algorithm TAG that generates a short string called tag that is appended to the message, and a verification algorithm VER that takes a message and an appended tag, and accepts or rejects the message. Message Authentication Codes (MAC) when the adversary has unlimited computational power, were first modelled and analyzed by Simmons [27] as a two-party zero-sum game. Security of MAC when the adversary is computationally bounded has also been formalized using a two-party zero-sum game that allows the adversary to have a learning phase (by querying authentication and verification oracles), before constructing the forgery. Efficient constructions of MAC with provable security have been proposed using block ciphers [6] and hash functions [5]. In all these works, messages are assumed to have equal values for the adversary and the communicants, and the adversary is considered successful with any forgery that passes the verification test.

In practice however, messages have different values for the adversary and the communicants, and the impact of a successful forgery will depend on the information that they carry: forging a $1,000 transaction will be much more desirable for the adversary than forging a $1 one! Similarly, in an industrial control system that uses information communication in the daily operation of the system, a control message that causes the system to shut down is far more valuable, than a simple regular status update message.

An authentication system that provides the same protection for all messages, must either choose security parameters of the system for the protection of the most high-valued messages in the system, or accept higher risks for the more important messages.

Cryptographic authentication has two types of cost: the computation cost of generation and verification of MAC, and the extra communication cost of transmitting and receiving the appended tag. These costs could become significant for small devices that must minimize their energy and power consumption, and carefully plan their resources [31]. In the fast growing Internet of Things (IoT), the bulk of messages that are sent between devices are short status update and control messages that must be authenticated, and optimizing the cost becomes highly desirable [26]. In [22], in the context of securing IoT and in particular machine-type communication, the author noted that:

“They generally have low data rate requirements, periodic data traffic arrivals, limited hardware and signal processing capabilities, limited storage memory, compact form factors, and significant energy constraints [20] As an example, a battery life of ten years at a quarter of the cost of wideband LTE-A devices is one of the objectives of the Release 13 LTE-A MTC standardization effort [21].”

Our objective is to optimize the cost of message authentication to be commensurate with the value of information that the message carries.

Our work. We depart from the traditional two-party zero-sum game model of security of MAC, and consider the problem of using an ideal MAC for protecting messages that have different values. To adjust the protection level of messages, we will use variable tag lengths for the ideal MAC: the MAC guarantees that when the tag length is \(\tau \), the adversary’s success chance of a forgery is \(2^{-\tau }\). This implicitly assumes that the key length is at least the size of the tag length. Ideal MACs can be closely approximated with existing MAC algorithms in information theoretic and computational security.

We model the problem as a game between two rational players, a system designer that includes the sender and the receiver, and an adversary. The game is an infinite general-sum extensive form game with perfect information. We consider the following setting: there is a message source with \(\ell \) messages and a publicly known probability distribution; time is divided into intervals; in each interval the source generates a message according to the known distribution. We also allow intervals without any message (empty message). This is similar to the model considered by Simmons [27] and a natural model for many message sources including messages that are generated in an industrial control system.

The cost of a successful forgery for the system designer includes the operational cost of the cryptographic protection that they use, and the loss incurred because of the particular forgery. The adversary’s gain will also depend on the particular forgery and the information that the forged message carry.The game proceeds as follows.

There is a publicly known ideal MAC. First, the system designer chooses a vector \(T=(\tau _i) \in \mathbb {N}^{\ell \,+\,1}\) of authentication tag lengths, one for each message, and makes the vector public. We assume the empty message will also receive a tag. Next, a message \(\mathbf{m}_i\) appears in the system (e.g. a message appearing in an industrial plant). The designer computes a tag of length \(\tau _i\), appends it to the message, and sends it. Finally, the adversary sees the message and decides how to replace it with another message, including the empty message. The latter is equivalent to removing the message from the channel and had not been considered in traditional MAC systems.We derive expressions that capture the cost and the gain of the designer and the adversary, and by analyzing the strategies of the two, show how to find a Nash equilibrium of the game and determine the optimal tag lengths for messages. Our work makes the following contributions.

  1. (1)

    It introduces a novel approach to security analysis of cryptographic message authentication that takes into account the value of information that messages carry as well as the cost of using cryptographic protection,and provides an optimal fine-grained protection mechanism using a secure MAC algorithm that supports different tag lengths. The model can realistically capture a variety of costs and rewards for players. The integrity attacks include traditional message forgeries (i.e. message injection and substitution) as well as message deletion (jamming) attack.

  2. (2)

    We present a sound method of finding optimal (Nash equilibrium) strategies using backward induction argument.The method, however, requires solving an exponential (in the number of messages) number of non-linear integer optimization problems.

  3. (3)

    Using a transformation from the vertex cover problem, we show that computing optimal vector of tag lengths, is NP-hard.

  4. (4)

    We present an equivalent formulation of the problem in the form of a mixed integer linear program (MILP) that proves that the decision version of our problem is NP-complete. The MILP formulation provides an attractive approach which allows us to use an off-the-shelf solver to find a solution to a concrete instance of the problem. We apply our formulation and MILP approach to the analysis of message authentication in an industrial control system for oil pipes.

Paper organization. In Sect. 2 we provide preliminary background and describe the proposed game of message authentication. Section 3 is the analysis of the game and finding a Nash equilibrium using backward induction. Sections 3.2 and 4 give computational complexity of the game and the formulation of finding the Nash equilibrium as a solution to an MILP. In Sect. 5 we discuss related works. Section 6 concludes the paper and suggests directions for future work.

2 An Economic Model for Information Authentication

In the following we recall the security definition of MAC that is relevant to our work, and then describe our game model. Game theoretic definitions and concepts follow [23].

A Message authentication code MAC is a symmetric key cryptographic primitive for providing message integrity. A MAC consists of a pair of algorithms (TAG, VER). The TAG algorithm takes two inputs, a shared secret key k, and a message \(\mathbf{m}\), and generates a tag \(t= TAG_k(\mathbf{m})\) that is appended to the message, resulting in a tagged message. The VER algorithm takes a pair of inputs, a key k and a tagged pair \((\mathbf{m}',t')\), and outputs \( VER_k(\mathbf{m}',t') =T\) to indicate that the tagged pair is valid and message is accepted as authentic, and \( VER_k(\mathbf{m}',t') =F\) to denote detection of a forgery. Correctness of the MAC requires that \(VER_k(\mathbf{m}, TAG_k(\mathbf{m}))= T\).

A MAC is \(({\varepsilon }, u) \)-secure if an adversary who has a learning phase during which they can query u tagged messages from an authentication oracle cannot successfully forge a message with probability better than \({\varepsilon }\). (One can also allow access to verification oracle.) An u-time ideal MAC is a \((2^{-\tau }, u)\)-secure MAC, where \(\tau \) is the length of the tag in bits. A vlMAC  family in this paper is a family of \((2^{-\tau }, u)\)-secure MAC for \(\tau \in \mathbb {N}\), where \( {\mathbb N} = \{0\} \cup {\mathbb Z}^+\) denotes the set of non-negative integers. We use \(u=1\). This means that the MAC can detect with a high probability, forged messages that are injected into the system, or the substitution of a message with a forged one. Our game theoretic model also considers the cost of dropping a message. To prevent message replay, one needs to consider additional mechanisms such as counters, or ensure that each message includes extra redundancy to make each message unique. This will not affect our analysis.

Game setting. Let \(I_{\varepsilon }= \{{\varepsilon },1, \cdots \ell \}\) denote the set of indexes of possible messages, including the empty message, and let \(I= \{1, \cdots \ell \}\), denote the set of indexes of non-empty messages.

  • A sender S wants to send messages to a receiver R over a channel that is controlled by an adversary, Eve.Eve can either inject a message into the channel, delete (jam), or modify the message that is sent by S. S and R together form a system designer player.

  • Time is divided into intervals. A message source \({\mathscr {M}}=\{ \mathbf{m}_1,\cdots \mathbf{m}_\ell \}\) generates messages independent of the sender and the receiver. In each time interval a message \(\mathbf{m}_i, i\in I_{\varepsilon }\), may appear at the sender terminal that must be sent to the receiver.Let \({\mathscr {M}}_{\varepsilon }= \{\mathbf{m}_i, i\in I_{\varepsilon }\}\) denote the set of messages in the system (e.g. an industrial control system), and \(\mathbf{m}_{\varepsilon }\) be a special message denoting “no-message" appearing in the interval. We assume messages from \({\mathscr {M}_{\varepsilon }}\) appear with a publicly known probability distribution \((p_{\varepsilon }, p_1,\cdots p_\ell ) \), and \(p_i= \Pr (\mathbf{m}_i)\) is the probability of \(\mathbf{m}_i\) appearing in the system, and \(p_{\varepsilon }= \Pr (\mathbf{m}_{\varepsilon })\) is the probability that no message appears in a time interval. Messages have different lengths. We will also use \(m_i\) to denote the length of the message \(\mathbf{m}_i\).

  • Messages have different “values” for the system designer and the adversary. If Eve succeeds in changing \(\mathbf{m}_i\) to \(\mathbf{m}_j\), where \(i,j\in I_{\varepsilon }\), their gain will be \(g_{i,j}\). The impact of a successful forgery on the system designer’s operation is measured by a cost function \(c'_{i,j}\)Footnote 1 that reflects the economic cost of successful message substitution for the system designer. Note that \(i={\varepsilon }\) corresponds to message injection and \(j={\varepsilon }\) is message deletion (jamming, dropping) by the adversary. We also consider the cost \(d_i\) of a detected forgery attempt on \(\mathbf{m}_i\). This captures the cost of, for example, request for retransmission or using alternative channels for retransmission. We assume \(g_{i,j}\) and \(c'_{i,j}, i,j\in I_{\varepsilon }\), are non-negative and public.

  • The total cost of the system designer when a forgery occurs, includes the economic impact of an undetected forgery, the cost associated with detected forgeries, and the investment to provide the required computation for MAC generation and verification, and the communication cost of sending and receiving messages with the appended tag. We assume that the operational cost of the MAC system is proportional to the length of the authenticated message (i.e. message appended with the tag). This is reasonable for small devices in an IoT setting and can be replaced by other functions to reflect other settings. We use \(\alpha _t\) and \(\alpha _r\) to denote the (per bit) operational cost of the cryptographic MAC for the sender and the receiver, respectively.

  • The system designer uses a vlMAC  to provide authentication for messages. Security of MAC guarantees that a tagged message \((\mathbf{m}, t)\) can be forged with probability \(2^{-\tau }\), where \(\tau \) is the length of the tag t. We use \( T= (\tau _{\varepsilon }, \tau _1,\cdots \tau _\ell )\in {\mathbb N}^{\ell \,+\,1}\) to denote the vector of tag lengths for messages \(\mathbf{m}_{\varepsilon }, \mathbf{m}_1\cdots \mathbf{m}_\ell \).

2.1 Game Structure

We model the interaction between the two players (the system designer and the adversary) in the above scenario when messages are generated by an external source, using a perfect information extensive form game with chance moves. We assume a secure key has been shared between the sender and the receiver.

Fig. 1.
figure 1

A sketch of the game tree \(\varTheta \) that represents the message authentication game. The circles labeled by 1, 2 and c, represent the points in the game that the players 1, 2, or the chance player, must take action. The labels on the edges denote the actions taken by the player associated with the circle that is at the higher end of the edge. The leaves of the tree are labelled by the payoffs of the two players.

Full size image

The game \(\varGamma _{auth} = \langle N,H, P, f_c, (u_i) \rangle \) is defined by the set of players N, the set of histories H, a player function P, a fixed distribution for chance moves \(f_c\), and the utility functions \((u_i), i=1,2\). A tree representation of the game is given in Fig. 1.

A history is a list of actions by players corresponding to a path from the root of the game tree to a node in the tree. The length of a history is the number of elements in the list. The set of histories H is given by:

$$\begin{aligned} H= \{\emptyset , \{T\in&{\mathbb N}^{\ell \,+\,1}\}, \{(T, \mathbf{m}_i)\in {\mathbb N}^{\ell \,+\,1} \times {\mathscr {M}}_{\varepsilon }\},&\{(T, \mathbf{m}_i, \mathbf{m}_j)\in {\mathbb N}^{\ell \,+\,1}\times {\mathscr {M}}_{\varepsilon }\times {\mathscr {M}}_{\varepsilon }\}\}. \end{aligned}$$

At a history T of length one, the system designer has chosen a tag length vector \(T=(\tau _i)_{i\in I_{\varepsilon }}\); at a history \((T, \mathbf{m}_i)\) of length 2, the system designer has chosen T and the chance move has selected \(\mathbf{m}_i\); finally at a terminal history \((T, \mathbf{m}_i, \mathbf{m}_j)\) of length 3, a length 2 history \((T, \mathbf{m}_i)\) has been followed by player 2’s choice of the forged message \(\mathbf{m}_j \in \mathscr {M}_{\varepsilon }\). A player function P takes a non-terminal history \(h\in H\setminus Z\), and outputs a player in N. The set of actions available to a player at history h is denoted by \(A(h)= \{a: (h, a)\in H\}\). For all chance nodes \(h=T\in N^{\ell +1}\), \(f_c(\mathbf{m}_i|h) = p( \mathbf{m}_i) \) is an independent probability distribution on possible moves \(A(h)= \mathscr {M}_{\varepsilon }\), at h.

Let Kronecker delta \({\delta _{i,j}}\) be defined as, \({\delta _{i,j}}= 0\) if \(j\ne i\), and \({\delta _{i,j}}= 1\), otherwise. For a tag length vector \(T= (\tau _{\varepsilon }, \tau _1\cdots \tau _\ell )\), the chance move \(\mathbf{m}_i\), and Eve’s move \(\mathbf{m}_j\), where \(i,j \in I_{\varepsilon }= \{{\varepsilon }, 1,\cdots \ell \}\), the players’ utilities are,

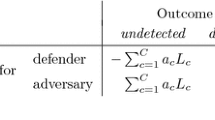
$$\begin{aligned} u_1 (T, \mathbf{m}_i, \mathbf{m}_j)= & {} \alpha _t(m_i+\tau _i) + \alpha _r(m_j+\tau _j) + c'_{i,j} 2^{-\tau _j} +d_i (1-2^{-\tau _j})(1-\delta _{i,j}),\\ u_2(T, \mathbf{m}_i, \mathbf{m}_j)= & {} g_{i,j} 2^{-\tau _j (1- {\delta _{i,j}})}. \end{aligned}$$

The utility \(u_1 (T, \mathbf{m}_i, \mathbf{m}_j)\) consists of, (i) \(\alpha _t(m_i+\tau _i)\), the sender’s cost of sending the tagged message \((\mathbf{m}_i, t_i)\), (ii) \(\alpha _r(m_j+\tau _j)\), the receiver’s cost of receiving a tagged message \((\mathbf{m}_j, t_j)\), (iii) \(c'_{i,j} 2^{-\tau _j}\), the economic cost of accepting a fraudulent message \(\mathbf{m}_j\) in place of the original message \(\mathbf{m}_i\), and (iv) \(d_i (1-2^{-\tau _j})(1-\delta _{i,j})\), the economic cost of detection of a forgery in the organization. The utility \( u_2 (T, \mathbf{m}_i, \mathbf{m}_j) \) of player 2, is their expected gain that is realized by the successful replacement of \(\mathbf{m}_i\) by \(\mathbf{m}_j\). We use,

$$\begin{aligned} u_1 (T, \mathbf{m}_i, \mathbf{m}_j)= & {} \alpha _t(m_i+\tau _i) + \alpha _r(m_j+\tau _j) + c'_{i,j} 2^{-\tau _j}+d_i (1-2^{-\tau _j})(1-\delta _{i,j}) \end{aligned}$$
(1)
$$\begin{aligned}= & {} \alpha _t(m_i+\tau _i) + \alpha _r(m_j+\tau _j) + c_{i,j}2^{-\tau _j} +d_i(1-\delta _{i,j}), \end{aligned}$$
(2)

where \(c_{i,j} = c'_{i,j} - d_i (1-\delta _{i,j}) \), effectively combining the cost of an undetected forgery and a detected forgery.

Assumptions: We assume the cost and gain parameters are known to the system designers. Real world applications of game theory in physical security suggest that these values can be reliably estimated [28]. Although exact values may be hard (or impossible) to find, system designers can use risk analysis methods to categorize messages into types, and attach a value to each type. Small errors in estimates of system designer’s costs cannot lead to large errors in the proposed solutions. This might happen due to errors in attacker’s gain estimates, however, overestimating attacker’s gains for more harmful substitutions increases robustness for the final solution. If the analysis reveals that there is a substantial uncertainty about the motivations of the attackers, the model can be extended to a Bayesian game [20], or a game with interval uncertainly [19]. These are possible future extensions of this work. The case study in the full version of this paper shows how these costs can be meaningfully estimated.

To simplify the analysis of the game, we assume \(g_{i,j}\) and \(c_{i,j}\) are non-negative. In practice one may use negative values. For example including decoy messages that serve to detect forgeries could result in communicants’ cost to be negative. We also assume \(c_{i,i}=0\) and \(c'_{i,j} \ge d_i \). The former implies that not changing a message incurs zero cost to the designer, and the latter implies that cost of undetected change of a message to the designer is higher than that of a detected change, resulting in \(c_{i,j} = c'_{i,j} - d_i (1-\delta _{i,j}) \ge 0\). This is a reasonable assumption for all sufficiently valuable messages in the system. We however allow \(g_{i,i}\) to be non-zero (we refer to this as no-change substitution), indicating it may be beneficial for the adversary not to change the sent message. These assumptions capture many scenarios in practice and are used in our analysis. Our approach can be used with other assumptions that model specific application scenarios.

2.2 Players’ Strategies

A player i’s strategy is a tuple that specifies their choices at all histories where \(P(h)=i\). Player 1 is associated with \(h=\emptyset \) and their strategy \(s_1=T \in \mathbb {N}^{\ell \,+\,1}\) specifies the choice of the tag length vector T. The set of player 1 strategies is an infinite set that is denoted by .

The choice nodes of player 2 are at histories of length 2 and are of the form \(h=(T, \mathbf{m}_i)\). A player 2 strategy \(s_2\) will choose a substitution message for all such histories. Let denote the set of player 2’s strategies. Histories of length 2 start with the choice node of player 1, and so player 2 at a history of length 2 knows the tag lengths that will be used by player 1. A strategy in determines the substitution message that will be used for every possible player 1 strategy, and every choice of the chance move. Thus is also an infinite set. We however introduce basic strategies that are from a finite set, and are used to partition and construct a finite (although very costly) algorithm for finding a Nash equilibrium.

Basic strategies of player 2: A basic strategy of player 2, denoted by \(s_2^b \), is a function \(s_2^b: \mathscr {M}_{\varepsilon }\rightarrow \mathscr {M}_{\varepsilon }\) that specifies the choices (substitution message) of player 2 at all histories \(h(T, \mathbf{m}_i), i\in I_{\varepsilon }\). For each message, player 2 has \(\ell +1\) possible actions, including replacing the message with \(\mathbf{m}_{\varepsilon }\), and keeping the message unchanged. Thus the number of basic strategies is . A basic strategy is represented by a vector \( (\mathbf{m}_{j_{\varepsilon }}, \mathbf{m}_{j_1} \cdots \mathbf{m}_{j_\ell }) , \mathbf{m}_{j_i}\in \mathscr {M}_{\varepsilon }\), or equivalently, by \( ( {j_{\varepsilon }}, {j_1} \cdots {j_\ell }) , j_i\in I_{\varepsilon }\). Note that a basic strategy can be used with any of the player 1’s strategies, and does not depend on the tag lengths. The set of player 2’s basic strategies is denoted by .

A player 2’s strategy \(s_2\) is an infinite vector of player 2’s actions at all histories of length 2, \((s_2(T,\mathbf{m}_i), T\in \mathbb {N}^{\ell \,+\,1}, i \in I_{\varepsilon })\), where player 1’s action (their strategy) and the chance player’s action have been specified. The set of actions \((s_2(T,\mathbf{m}_i), i \in I_{\varepsilon })\) for a fixed T, corresponds to a basic strategy of player 2, denoted by \(s_2^b(T)\). Thus \(s_2\) can be written as an infinite vector . The set of basic strategies of player 2 is finite. The above discussion is summarized in the following proposition.

Proposition 1

The sets and are infinite. The number of player 2’s basic strategies is \((\ell +1)^{\ell +1}\).

System designer’s cost: The expected cost of player 1 for a strategy profile , is given by:

$$\begin{aligned} C_{s_1,s_2}= \sum _{i \in I_{\varepsilon }} p_i [ \alpha _t (m_i +\tau _i) + \alpha _r(m_{j_i} +\tau _{j_i}) + c_{i,j_i} 2^{- \tau _{j_i}} +d_i(1- \delta _{i,j} ) ]. \end{aligned}$$
(3)

That is, the cost of player 1 for strategy \(s_1=T\) will only depend on the basic strategy \(s_2^b(T)\) that follows \(s_1=T\).

3 Finding a Nash Equilibrium Using Backward Induction

The authentication game above is an infinite game: both players’ strategy sets are infinite and a player 2 strategy is an infinite vector. This prohibits direct use of backward induction and finding a subgame perfect equilibrium. We however show how to use backward induction to partition the infinite strategy set into finite number of partitions, and find a Nash equilibrium for the game by solving a finite number of constrained non-linear integer optimization problems.

Backward induction: We decompose the tree representation of the game \(\varTheta \) into subtrees, \(\varTheta (T)\), one for each \(T\in \mathbb {N}^{\ell +1}\). The subtree \(\varTheta (T)\) has the same root as \(\varTheta \), starts with player 1 strategy T and includes all subsequent actions of chance node and player 2. We can use backward induction for \(\varTheta (T)\) to determine the expected cost of player 1 for a strategy \(s^b(T)\): start from terminal histories of the tree; the first backward step will arrive at a history \(h=(T,\mathbf{m}_i)\) which is a choice node for player 2. A tuple of all such choices for all messages \(\mathbf{m}_i, i\in I_{\varepsilon }\), is a basic strategy \(s_2^b(T)\) . The second backward step reaches the choice node of a chance move. Here the choice is external to the game and is given by a distribution on \(\mathscr {M}_{\varepsilon }\). The third backward step reaches player 1’s choice node. At this node, the cost of player 1 for \(s_2^b(T)\) that was selected at step 1 of backward induction by player 2, is given by (3). We would like to choose the optimal strategy T for player 1 which minimizes their cost over all choices of player 2. However, there are infinitely many T and the corresponding \(\varTheta (T)\), and for each one needs to consider \((\ell +1)^{\ell +1}\) basic strategies. We make the following crucial observation that allows us to find a Nash equilibrium of the game in finite number of steps.

The set can be partitioned into \((\ell +1)^{\ell +1}\) parts, one for each player 2 basic strategy, such that for all player 1 strategies in the partition associated with \(s_2^b\), player 2’s best response (maximizing player 2’s expected gain), is \(s_2^b\).One can then find the best choice of player 1 (T that minimizes their expected cost) for each partition. The final step is finding the \(s_2^b\) that corresponds to the least expected cost for player 1 over all More details follow.

Backward induction for \(\varTheta (T)\): The backward induction steps for \(\varTheta (T)\) are as follows.

S1: At a terminal history \(h =(T,\mathbf{m}_i, \mathbf{m}_j)\), the utilities are,

$$\begin{aligned} (u_1,u_2) = ( [ \alpha _t(m_i+\tau _i) + \alpha _r(m_j+\tau _j) + c_{i,j} 2^{-\tau _j} +d_i (1-\delta _{i,j})], [g_{i,j} 2^{-\tau _j (1- \delta (i,j) )} ] ). \end{aligned}$$

In the first backward step in \(\varTheta (T)\), the best utilities of player 2 at histories \(h =(T, \mathbf{m}_i) \in H_2,\) \(\mathbf{m}_i \in \mathscr {M}_{\varepsilon }\), are found by choosing messages \(\mathbf{m}_{j_i}\) that maximize player 2 payoffs, where

$$\begin{aligned} s_2(T, \mathbf{m}_i) = \mathbf{m}_{j_i} \hbox { if, } \qquad g_{i,j_i} 2^{-\tau _{j_i}(1-\delta _{i,j_i})} \ge g_{i, u} 2^{-\tau _u(1-\delta _{i,u})}, \forall u\in I_{\varepsilon }\setminus \{j_i\}. \end{aligned}$$
(4)

The inequalities in (4) ensure that choosing \(\mathbf{m}_{j_i}\) will have at least the same gain as any other \(\mathbf{m}_u\), different from \(\mathbf{m}_{j_i}\). The tuple of optimal choices of player 2 for all \(\mathbf{m}\in \mathscr {M}_{\varepsilon }\), determines the (optimal) basic strategy \(s_2^{b*}(T)\) of player 2.

S2: At history \(h= (T)\), we have \(P(h)=c\) and the optimal utility of player 1 is \( C_{s_1,s_2^{b*}(T)}\), given by the expression (3), when \(s_2^b(T)= s^{b*}_2(T)\), found in step S1.

S3: At history \(h= \emptyset \), player 1 has to select the best \(s_1=T\) by minimizing the expected cost over all choices of \(s_1\).

Let \({\mathscr {T}}(s^b_2) \subset {\mathbb N}^{\ell +1}\) be the set of player 1 strategies for which \(s^{b}_2\) is player 2’s optimal strategy at the first step of backward induction, S1. The following proposition follows from step S1.

Proposition 2

A basic strategy \(s^b_2= (j_{\varepsilon }, j_1\cdots j_\ell )\) is optimal for all subtrees \(\varTheta (T)\) where \(T=(\tau _{\varepsilon }, \tau _1, \cdots \tau _\ell )\), that satisfy the following:

$$\begin{aligned} g_{i,j_i} 2^{-\tau _{j_i}(1-\delta _{i,j_i})} \ge g_{i, u} 2^{-\tau _u(1-\delta _{i,u})}, \forall u\in I_{\varepsilon }\setminus \{j_i\}, i\in I_{\varepsilon } \end{aligned}$$
(5)

Moreover, and for any two strategies Thus, the sets \({\mathscr {T}}(s^b_2) \) partition the set with overlaps only due to attacker’s indifference.

The proof is in the full version of the paper. Using this lemma we prove the following theorem.

Theorem 1

A Nash equilibrium for \(\varGamma _{auth}\), and the associated optimal strategies \((T^*, s_2^{b*}(T^*))\), can be found by solving the following optimization problem,

The tag length vector \(T^*\) gives the minimal cost \(C^*\) over all strategies .

The proof is in the full version of the paper.

3.1 Tie Breaking of Indifferent Attacker

In general, there may be multiple Nash equilibria in the game. The algorithm above soundly finds the one that optimizes the expected payoff of the defender. When there is equality in (5), that is player 2 has more than one best choice, a player 1 strategy may belong to multiple partitions \({\mathscr {T}}(s_2^b)\).Since the approach in Theorem 1 select the partition achieving the mimimum cost, if the same strategy is optimal in multiple partitions, it selects the partition which is most favourable for player 1. As a result, it resolves the tie in favour of player 1.

To avoid this unrealistic assumption, we further restrict the sets \({\mathscr {T}}(s_2^b)\) so that they include only the player 1 strategies for which \(s_2^b\) is the worst possible best response of the attacker. In order to do this, we add additional constraints to the definition of \({\mathscr {T}}(s_2^b)\) in Proposition 2. The constraints request that the system designer’s cost be maximized by the substitution of \(\mathbf{m}_i\) by \(\mathbf{m}_{j_i}\) if there are other alternative messages \(\mathbf{m}_u\) that ensure the same gain to the attacker:

$$\begin{aligned}&\text {if} g_{i, j_i} 2^{- \tau _{j_i} (1-\delta _{i, j_i})}= g_{i,u} 2^{- \tau _{u}(1-\delta _{i, u})} \text{ then } \nonumber \\&\alpha _r(m_{j_i}+\tau _{j_i} ) + c_{i, j_i} 2^{- \tau _{j_i} (1-\delta _{i, j_i})}+ d_i(1-\delta _{i,j_i}) \ge \qquad \nonumber \\&\qquad \alpha _r(m_{u}+\tau _{u}) +c_{i,u} 2^{- \tau _{u}(1-\delta _{i, u})} + d_i(1-\delta _{i,u}),\;\; \forall u \in I_{\varepsilon }\setminus \{j_i\}. \end{aligned}$$
(6)

Denote these further restricted sets by \({\mathscr {T}}'(s_2^b)\). They still cover the whole strategy space of player 1. Moreover, the overlaps of the sets are formed only by the strategies that make both players indifferent. Computing solution as suggested in Theorem 1 with sets \({\mathscr {T}}'(s_2^b)\) produces the robust solution that assumes that the attacker breaks ties against the system designer if he is indifferent among multiple substitutions.

3.2 Computational Complexity

The solution to the above game requires solving exponentially many optimization problems. It is not likely that there is a substantially simpler method to solve the game, since we further show that solving the Message Authentication Game is NP-hard.

Theorem 2

Computing the optimal strategy for the system designer in the Message Authentication Game is NP-hard. This can be shown even if all messages have unit length (\(m_i=1\)), occur with uniform probability without empty interval (\(p_i=\frac{1}{|\mathscr {M}|}\)), detection cost is zero, \((d_i=0)\), and regardless of the tie breaking rule.

The proof is by reducing the NP-complete Vertex (or Node) Cover problem [17] to the problem of finding an optimal solution to the authentication game \(\varGamma _{auth}\). Messages correspond to vertices and edges of the graph. Utilities ensure that the optimal solution for \(\varGamma _{auth}\) attaches tags only to messages that correspond to vertices, and a non-zero tag for a message means that the vertex is in subset S. The basic building block of the reduction is an “edge gadget”,which ensures high cost if none of its incident vertices is selected (receive a non-zero tag), and lower cost if one or both of its incident vertices are selected (receive a non-zero tag).The complete proof is in the full version of the paper.

4 MILP Formulation of the Game

The solution provided by Theorem 1 is extremely costly. In this section we reformulate the optimization problem in Theorem 1 to improve efficiency of computation and be able to use standard highly optimized solvers. We show a transformation of this optimization problem to a single Mixed Integer Linear Program (MILP) that is polynomial in the size of the problem definition, which in turn is polynomial in the number of messages.

Theorem 1 states that the solution to the game of authentication, is the solution to the following optimization problem:

$$\begin{aligned}&\min _{(j_\epsilon \dots j_l)\in S^b_2} \min _{(\tau _\epsilon \dots \tau _l)\in \mathbb {N}^{l+1}} \sum _{i\in I_\epsilon } p_i \left[ \alpha _t (m_i + \tau _i) + \alpha _r(m_{j_i} + \tau _{j_i}) + c_{i,j_i}2^{-\tau _{j_i}} +d_i(1-\delta _{i,j}) \right] , \qquad \\&\text {subject to} \qquad g_{i,j_i}2^{-\tau _{j_i}(1-\delta _{i,j_i})} \ge g_{i,u}2^{-\tau _{u}(1-\delta _{i,u})} \;\forall i\in I_\epsilon , u\in I_\epsilon \setminus \{j_i\}. \end{aligned}$$

The problem is structurally similar to finding strong Stackelberg equilibrium in Bayesian gamesFootnote 2, which is also an NP-hard problem [8]. The proposed game model is a Stackelberg game because first the system designer selects and commits to a vector of tag lengths, and then the attacker observes this commitment and plays their best response. The similarity to the Bayesian games is that there is a set of messages (corresponding to player types) generated with a fixed probability distribution. For each of these messages, the defender performs their actions with a distinct set of payoffs. Using these observations, we derive a MILP for the Authentication Game that is similar to DOBSS [24], the MILP formulation for computing mixed Stackelberg equilibria in Bayesian games. The main differences from the Stackelberg games studied in literature is the discrete combinatorial structure of the commitment and the exponential form of the utility functions. Since our problem is NP-hard, transformation of the problem to a well studied NP-complete problem (such as MILP) and using an existing solver is generally the most efficient solution technique.

MILP is an optimization problem that can be described as the optimization of a linear function, subject to a set of linear constraints, where the variables can have real or integer domains. There are two kinds of issues that need to be resolved to transform the above optimization problem to MILP: (1) The objective function and the constraints are not linear and, (2) the set of basic strategies of player 2, , is exponentially large and in the formulation above, a set of constraints for each of these strategies is considered. We start with linearization of the non-linear terms.

4.1 Objective Linearization

The objective function is the minimization of a number of positive terms, some of which are exponential. Since \(c_{ij_i}\) is non-negative, we can replace the exponential terms \(2^{-\tau _{j_i}}\), with new variables \(e_{j_i}\), and lower bound the new variables by linear constraints so that the approximation is exact for all meaningful integer values of \(\tau _{j_i}\). Increasing the length of \(\tau _j\) increases the protection of the system for that message. Increasing the length by one bit from k to \(k+1\), reduces the cost of replacing \(m_i\) by \(m_j\) by \(c_{ij}(2^{-k} -2^{-(k+1)})\). It also has a cost \(\alpha _t\) for transmitting, and \(\alpha _r\) for receiving. It does not change the cost related to \(d_i\). If the saving in damage incurred by successful forgery is less than the extra cost of sending and receiving, extending the tag length is not meaningful. Denote \(\tau ^{max}_j\) the maximal meaningful value of \(\tau _j\). The additional bit in a tag is not worth its cost, if

$$\begin{aligned} \alpha _t+\alpha _r \ge \max _{i\in I_\epsilon } c_{ij}\left( 2^{-\tau ^{max}_j}-2^{-(\tau ^{max}_j\,+\,1)}\right) \Rightarrow \tau ^{max}_j \ge \max _{i\in I_\epsilon } \log (\frac{c_{ij}}{\alpha _t+\alpha _r}) - 1. \end{aligned}$$
(7)

A second reason why the defender may want to increase the tag length, is to prevent dropping of some other message that the attacker wants to substitute with \(m_j\). This is not worthwhile if the cost of sending and receiving the tags is more than the cost of the dropped message:

$$\tau _j^{max}(\alpha _t+\alpha _r) \ge \max _{i\in I_\epsilon } d_i \Rightarrow \tau _j^{max} \ge \frac{\max _{i\in I_\epsilon } d_i}{(\alpha _t+\alpha _r)}.$$

If we set \(\tau _j^{max}\) to the maximum of the two values above, the linearized objective will be:

$$\begin{aligned} \min _{(j_\epsilon \dots j_l)\in S^b_2} \min _{(\tau _\epsilon \dots \tau _l)\in \mathbb {N}^l} \sum _{i\in I_\epsilon } p_i \left[ \alpha _t (m_i + \tau _i) + \alpha _r(m_{j_i} + \tau _{j_i}) + c_{i,j_i}e_{j_i} +d_i(1-\delta _{i,j} )\right] \quad \end{aligned}$$
(8)

with the additional constraints:

$$\begin{aligned} e_j \ge -2^{-(k+1)}(\tau _j \,-\, k) + 2^{-k} \;\; \forall j\in I; \; k\in 0,1,\dots ,(\tau ^{max}_j\,+\,1). \end{aligned}$$

Note that this linearization does not introduce any error.Variables \(\tau _j\) can have only integer values, and the approximation by the linear functions is exact for all meaningful integer values for these variables.

4.2 Best Response Constraints Linearization

The constraints in the original problem also contain exponentials, but they can be linearized by taking the logarithm of both sides. They are equivalent to:

$$\begin{aligned} log(g_{i,j_i}) - \tau _{j_i}(1-\delta _{i,j_i}) \ge log(g_{i,u}) - \tau _{u}(1-\delta _{i,u}) \forall i\in I_\epsilon , u\in I_\epsilon \setminus \{j_i\}. \end{aligned}$$
(9)

The only problem with these constraints can occur if \(g_{i,j_i}\) or \(g_{i,u}\), is zero. In that case, the logarithm is minus infinity. If \(g_{i,u}\) is zero and \(g_{i,j_i}\) is non-zero, we can omit the constraint since it would always be satisfied. If \(g_{i,u}\) is non-zero and \(g_{i,j_i}\) is zero, the constraint would never be satisfied. Therefore \(j_i\) can be prevented from reaching the value that would cause this situation. Finally, if both values are zero, looking back at the constraint before taking the logarithm reveals the constraint is trivially satisfied and can be omitted.

If an application requires \(g_{ij}\) to be negative, it does not change the solution substantially. If for some i, there are both positive and negative \(g_{ij}\), the attacker will never attempt to make the exchange with the negative gain and we can set their gains to 0. If for some message all substitutions cause negative gain, we can reverse the constraint and perform the same linearization.

4.3 Compact Representation of the Attacker’s Strategy

After the linearization steps above, we have to find the minimum of exponentially many linear optimization problems, i.e., one for each attacker’s basic strategy. We further combine all the optimization problems to a single minimization to allow a solver, such as IBM CPLEXFootnote 3, to automatically formulate problem relaxations and prune the space of possible attacker’s strategies.

For clarity of exposition, we first describe a more intuitive formulation of the problem with quadratic terms and then further linearize it. In order to represent the attacker’s strategies, we define a set of new binary variables \(a_{ij} \in \{0,1\}\). The semantics of \(a_{ij}=1\) is that the attacker replaces message \(m_i\) with message \(m_j\). To ensure that each message can be replaced by only one other message, we require:

$$\begin{aligned} \sum _{j \in I_\epsilon } a_{ij}=1\;\; \forall i \in I_\epsilon . \end{aligned}$$

We combine all the optimization problems by activating only the best response constraints relevant to specific selection of the attacker’s strategy using the standard “big M” notation. The big M method is used to activate or deactivate specific constraints in integer programs, dependent on the value of a binary variable. The quadratic formulation of the original problem is:

$$\begin{aligned}&\min \sum _{i\in I_\epsilon } p_i \left[ \alpha _t (m_i + \tau _i) + \sum _{j\in I_\epsilon } a_{ij}(\alpha _r(m_{j} + \tau _{j}) + c_{i,j}e_{j} + d_i(1-\delta _{i,j}))\right] \end{aligned}$$
(10)
$$\begin{aligned}&e_j \ge -2^{-(k+1)}(\tau _j - k) + 2^{-k},\;\; \forall j\in I; \; k\in 0,\dots , (\tau _j^{max}+1 ) \end{aligned}$$
(11)
$$\begin{aligned}&(1-a_{ij}) M + log(\frac{g_{i,j}}{g_{i,u}}) - \tau _{j}(1-\delta _{i,j}) \ge - \tau _{u}(1-\delta _{i,u}), \nonumber \\&\quad \qquad \qquad \qquad \qquad \qquad \forall i,j\in I_\epsilon , u\in I_\epsilon \setminus \{j\} : g_{i,u}>0 \end{aligned}$$
(12)
$$\begin{aligned}&\sum _{j \in I_\epsilon } a_{ij}=1\;\; \forall i \in I_\epsilon \end{aligned}$$
(13)
$$\begin{aligned}&a_{ij} \in \{0,1\}; \tau _j \in \mathbb {N}; e_i \ge 0 \end{aligned}$$
(14)

The objective function of this optimization problem is the Eq. (8), rewritten using the binary variables \(a_{ij}\). Instead of adding directly the contribution of switching a message i to \(j_i\), it adds the contribution of switching to all alternative messages multiplied by the indicator \(a_{ij}\), which is zero with the exception of \(a_{ij_i}\). Constraints (11) are from the linearization of the exponentials in the objective. Constraints (12) are the linearization of the best response with an additional term \((1-a_{ij})M\). Here M is a sufficiently large (possibly always different) number, so that with \(a_{ij}=0\) the constraint does not restrict any meaningful assignment of variables in the constraint. As a result, the constraint is effective only in case of \(a_{ij}=1\). Each feasible assignment of variables \(a_{ij}\) encodes one of the exponential number of minimization problems that we started with. The indicators in the objective (10) set up the right objective function from Theorem 1 and the indicators in constraints (12) choose the right subset of constraints that is valid for that subproblem.

In order to be able to use any standard MILP solver, we further linearize the quadratic objective function. Since \(a_{ij}\) are binary, the quadratic terms can be rewritten using the “big M” notation with the same meaning as above. Instead of multiplication, they are interpreted more like “if \(a_{ij}=1\) then \(a_{ij}\cdot \tau _j=\tau _j\) else \(a_{ij}\cdot \tau _j=0\)”. For each possible term \(a_{ij}\cdot \tau _j\) we define a new variable \(a\tau _{ij}\), for each possible term \(a_{ij}\cdot e_j\), we define a new variable \(ae_{ij}\) and we constrain these new variables to be larger or equal to the original variables only in case of \(a_{ij}=1\). This way the minimization of the objective, in which these variables are present in positive terms, ensures that the new variables will reach their lower bounds.

$$\begin{aligned} \min \sum _{i\in I_\epsilon } p_i \left[ \alpha _t (m_i + \tau _i) + \sum _{j\in I_\epsilon } (\alpha _r(m_{j} + a\tau _{ij}) + c_{i,j}ae_{ij} +d_i(1-\delta _{i,j})a_{ij}))\right] \nonumber \\ \text {constraints} (11)-(14) \end{aligned}$$
(15)
$$\begin{aligned} a\tau _{ij} + (1-a_{ij})M \ge \tau _j \;\; \forall i,j \in I_\epsilon \end{aligned}$$
(16)
$$\begin{aligned} ae_{ij} + (1-a_{ij})M \ge e_j \;\; \forall i,j \in I_\epsilon \end{aligned}$$
(17)
$$\begin{aligned} ae_{ij} \ge 0; \; a\tau _{ij} \ge 0 \;\; \forall i,j \in I_\epsilon \end{aligned}$$
(18)
$$ \begin{aligned} a_{ij}=0\;\; \forall i,j \in I_\epsilon : g_{ij}=0 ~ \& ~ \exists u \in I_\epsilon \; g_{i,u}>0 \end{aligned}$$
(19)

The problem formulation in (15–19) is an MILP, which can be solved by any standard solver. If we require the empty message not to have a tag, we can add the constraint \(\tau _\epsilon =0\). The algorithm above computes the optimistic Nash equilibrium assuming that the attacker will break ties in favour of the defender. However, the discrete nature of the defender’s commitment allows for a MILP formulation of the pessimistic variant as well. We need to incorporate the constraints (6) in to the program.

4.4 Examples

We apply the above solution method to two cases. First we consider an example of a small message space to show how using differentiated tag lengths reduces the designers’ cost, and then model a real life message space to show that the problem can be solved for realistic cases using off-the-shelf software.

A 3-message authentication system. The goal of this example is to show the effectiveness of the proposed variable length tags compared to fixed-length tags. We consider a three message space and use Table 1 to specify the complete set of parameters, \(m_i\) (message length), \(c_{ij}\), \(g_{ij}\) (cost and gain of substitution of message i with message j), \(\alpha _t = \alpha _r = 0.1\) ( transmission and reception costs per bit), \(p_i=\frac{1}{4}\) (message distribution including empty message), and \(d_i=0\) (detection cost). The system parameters are such that the adversary must break a tie between a number of choices (when \(\mathbf{m}_{\varepsilon }\) appears, injecting any of the messages \(\mathbf{m}_i, i=1,2,3\) has the same gain 2). We consider two cases: the adversary breaks the tie against the defender, and the case that the adversary is only concerned about their own gain and breaks ties in favour of the defender. The resulting two sets of tags are shown by \(\tau _i^-\) and \(\tau _i^+\), respectively. We also consider the heuristic maximum tag lengths \(\tau _i^{max}\) defined by expression (6) for each message, that effectively show the highest protection that is “worth” offering to a message. The designers’ cost for these cases is given by \(u_1(x,y)\) values where x is the designers’ strategy given by the set of tags, and y is the best response strategy for the attacker. The small table on the righthand side of Table 1 gives player 1 utility \(u_1(x,y)\), when the tag length is the same (it can be 0,1,2 or 3) for all messages, and tie breaking is in favour or against the designer, as described above. It can be seen that: if the attacker breaks ties against the defender, tags (\(\tau _i^-\)), they will have expected cost 0.96; if the attacker breaks ties in favour of the defender (indifferent attacker), the optimal tag of all non-empty messages is one bit (\(\tau _i^+\)), and the expected cost of the defender is 0.9. In both cases the attacker prefers to replace the empty message with message 3 and drop the other messages (\(j_i\)). The defender’s cost in these cases are substantially lower than using the best fixed length (leading to costs 1.38 and 2.05), or using the heuristic tag lengths \(\tau _i^{max}\).

Table 1. (left table) Example with 3 messages, assuming \(\alpha _t = \alpha _r = 0.1\), \(d_i=0\) and \(p_i=\frac{1}{4}\). Breaking ties in favour of the defender is indicated by \(+\) and against the defender by −. (right table) Defender’s objective values with different tag length vectors. \(\tau \) without indices indicates constant length tags.
Full size table

A case study. In the full version of the paper we also present the case of protecting messages in an industrial control system used for oil pipeline management, using our proposed approach. We consider a system with 23 message types and the empty message, and show how to estimate meaningful values for players’ cost, gain and utilities for the forgeries. We compare the proposed game-theoretic solution with a simple heuristic that protects each message with the heuristic tag lengths (\(\tau ^{max}_j\)), as defined in Sect. 4. A single fixed tag length for all messages would lead to higher cost than this heuristic. The analysis shows that when the tags on empty messages are not allowed, the proposed method allows reducing the combined expected cost of the system designer for sending the tagged messages, successful, and unsuccessful attacks by 26% compared to the heuristic. When tags are added to the empty message, the cost is reduced by 33%.

Fig. 2.
figure 2

Computation time required to solve random instances of the games with and without tags on the empty message using for the optimistic and pessimistic equilibrium.

Full size image

Scalability. Figure 2 presents the runtime of solving games assuming that messages are uniformly distributed, with random game parameters \(m_i \in 1\dots 20,\) \(c_{ij}\in [0,100], g_{ij}\in [0,100], d_i\in [0,100], \alpha _r\in [0,1], \alpha _t\in [0,1]\), using CPLEX 12.6 on a standard laptop with dual core 2.8 GHz Intel i7 CPU. The solid lines are for the algorithm assuming breaking ties in favour of player 1 and the dashed lines are for the algorithm assuming breaking ties against player 1. Black lines shows the results when the empty message is not tagged, and the gray line shows the results when empty message is tagged. The points represent means of 20 different instances of the given size, the error bars represent the maximum and minimum computation time out of the 20 instances for the case with no tag on the empty message and breaking ties against the first player. All problems with 10 messages can be solved in a fraction of second and the most complex problems with 35 messages take on average 100 s.

5 Related Works

In the game-theoretic definition of security [18] for cryptographic protocols, security is defined as a two-party zero-sum game between a challenger and an adversary who can corrupt a subset of parties, and/or (partially) control communication among them.

Rational cryptography is a more recent line of research [1, 3, 11, 15, 16, 21, 25], that assumes protocol participants are “rational” and have well defined preferences, acting in the system in accordance with these preferences.Rational cryptography has resulted in overcoming some impossibility results [3, 15] and providing better efficiency [4]. Garay et al. [13] modelled security of a cryptographic protocol as a two-party zero-sum extensive game with perfect information and observable actions between the protocol designer and the attacker. We also use the same two types of participants in our game definition but use a completely different game. The notion of “cost” in all previous works is in terms of the amount of computation and/or communication. We however consider also the economic cost (and benefit) of using cryptosystems in practice. Game theoretic modelling ofauthentication codes is due to Simmons [27] who used two-party zero-sum games with adversary’s action being message injection and substitution. The idea of variable length authentication was first proposed in [10]. Using economics to decide the length of the MAC was proposed in [9].

Using games to model economics of information security and privacy scenarios has been an active area of research [7, 12, 30].The game FLIPIT is motivated by the Advanced Persistent Threats in computer systems, and models the behaviour of an attacker and a defender who both want to control a resource such as a cryptographic key [29]. Here the “benefit” of a player is defined as “the fraction of time the player controls the resource minus the average move cost”, and the goal of each player is to maximize their benefit. A comprehensive resource list is maintained at [2].

6 Concluding Remarks and Future Directions

Game theory provides a powerful framework to model economic cost and benefit of cryptographic systems in real life settings. Our work shows the usefulness of such analysis and insight that can be gained in the case of cryptographic authentication. The example of a three message space in Sect. 4.4 shows how using differentiated tag lengths can reduce the total cost of the designer, comparing the optimal cost to cases that the tag length is constant.

In economic models, one needs estimates of the system parameters and players’ gain and cost values. In our model this can be achieved using risk analysis that takes into account probability of attack in a time interval and the impact of the attack. The cost function of the designer combines the cost of the successful forgery, which is the risk of the forgery to the operation of the organization, with the communication cost of one bit. This latter cost must be estimated by taking onto account factors such as frequency of messages, life time of the battery and the operational requirements of the system.

The estimation of system parameters is feasible when the message set is small (e.g. control messages in an IoT setting), or messages are highly structured and can be grouped into well defined classes.

Our work provides a starting point for this line of investigations. We focussed on the basic authentication problem and showed finding Nash equilibrium is NP hard. More complex version of the problem, for example considering forgery after observation of t tagged messages or using other cost functions for communication, could be modelled and analyzed in a similar way. One can also consider confidentiality where different messages, or different parts of messages, require different levels of security, and optimize the cryptographic budget of the system to ensure the best possible protection.