Abstract
Lightweight cryptography is a topic of growing importance, with the goal to secure the communication of low-end devices that are not powerful enough to use conventional cryptography. There have been many recent proposals of lightweight block ciphers, but comparatively few results on lightweight Message Authentication Codes (MACs).
Therefore, this paper focuses on lightweight MACs. We review some existing constructions, and revisit the choices made in mainstream MACs with a focus on lightweight cryptography. We consider MACs based on universal hash functions, because they offer information theoretic security, can be implemented efficiently and are widely used in conventional cryptography. However, many constructions used in practice (such as GMAC or Poly1305-AES) follow the Wegman-Carter-Shoup construction, which is only secure up to \(2^{64}\) queries with a 128-bit state.
We point out that there are simple solutions to reach security beyond the birthday bound, and we propose a concrete instantiation, \(\mathsf {MAC611}\), reaching 61-bit security with a 61-bit universal hash function. We wrote an optimized implementation on two ARM micro-controllers, and we obtain very good performances on the Cortex-M4, at only 3.7 c/B for long messages, and less than one thousand cycles for short messages.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Lightweight cryptography
- Micro-controller
- MAC
- Almost universal hash functions
- Beyond-birthday-bound security
1 Introduction
Message Authentication Codes (MACs) are important cryptographic primitives, used to authenticate messages. A MAC is a short tag computed by the sender from the message and a key, and verified by the receiver with the same key.
In this paper, we focus on MAC algorithms for constrained environments. This is a field of growing importance, due to the increasing number of small communicating objects, such as contactless smart cards, wireless sensors, mobile phones, and Internet of Thing devices. In particular, we have seen that many of these devices use weak cryptography (e.g. MIFARE Crypto-1, KeeLoq), due to hardware limitations. To solve this issue, the academic community has designed new algorithms for constrained environments, creating the field of lightweight cryptography. There is now a large number of block ciphers optimized for constrained environments and some of them have been standardized (PRESENT [9] in ISO/IEC 29192, HIGHT [19] in ISO/IEC 18033-3, KASUMI in UMTS). Recently, the NIST has started a standardization effort for lightweight cryptographyFootnote 1, which shows that the field is gaining importance. However, there are still few options for modes of operation for these lightweight block ciphers and lightweight MACs; a recent survey [5] lists 117 lightweight cryptographic algorithms, including just 3 MACs.
MAC Constructions. MAC algorithms can be built in many different ways: from block ciphers (CBC-MAC [15], OMAC, PMAC), from hash functions (HMAC), or from scratch like Pelican MAC, or Chaskey. These constructions are deterministic, which makes them vulnerable against a generic forgery attack using collisions in the internal state, due to Preneel and van Oorschot [29]. Therefore, they only achieve security up to the birthday bound, i.e. when the amount of data authenticated with a single key is bounded by \(2^{n/2}\), with n the state size.
When using a lightweight block cipher with a blocksize of \(n = 64\) bits, this is typically insufficient. One way to increase the security is to use a larger internal state. Indeed, several modes have been proposed recently using a 2n-bit internal state with an n-bit block cipher (e.g. \({\texttt {SUM-ECBC}}\) [34], \({\texttt {3kf9}}\) [35], \({\texttt {PMAC+}}\) [13]).
Another way to avoid Preneel and van Oorschot’s attack is to make the MAC not deterministic, using a nonce, a unique value provided by the user (in practice, the nonce is usually a counter). An important example of nonce-based MAC is the Wegman-Carter construction [33] which authenticates a message M using a nonce N as:
with H a family of XOR universal hash functions, and F a PRF. This construction is widely deployed in schemes such as GMAC [24] and Poly1305 [3].
Lightweight MACs. While MACs seem to be an important primitive for lightweight cryptography, few constructions have been optimized for constrained environments. Notable exceptions are the ARX based Chaskey [27] and SipHash [1]. Chaskey is optimized for 32-bit micro-controllers with very good software performances, while SipHash targets 64-bit processors but should also have good performances on micro-controllers. TuLP [18] is another lightweight dedicated MAC, based on the PRESENT round function. It uses a small 64-bit state, but suffers from collision issues after \(2^{32}\) blocks of data.
Another recent proposal is LightMAC [23], a mode for block-cipher-based MAC with a security bound independent of the message length, making it more usable with a small block size (but the security is still limited to \(2^{n/2}\) queries). Lightweight hash functions such as QUARK [2] or SPONGENT [8] can also be used to build a MAC (e.g. using HMAC), but using a dedicated MAC is typically more efficient (in particular, hash functions require a larger internal state).
Our Results. In this paper we study the design of lightweight MACs, optimized for software implementation on micro-controllers. To improve performance, we use a small state size of n bits for the bulk of the computation, with a nonce-based MAC to reach a security of \(2^n\). We focus on constructions based on universal hash functions in the style of Wegman and Carter. Universal hash functions only require statistical security, rather than computational security, which usually makes them cheaper to implement.
We note that practical MACs based on universal hash functions such as GMAC and Poly1305-AES only have security up to \(2^{n/2}\) queries (the birthday bound) but simple tweaks can increase the security to \(2^n\) queries. Additionnally, we improve the security proofs of some composition results in case some components are permutations, which improves in particular the security proof of a proposal by Minematsu and Tsunoo [26] using a reduced block cipher.
We then design a concrete instantiation, \(\mathsf {MAC611}\). We use a small state of roughly 64 bits with a beyond-birthday-secure mode, which allows for a faster primitive than GMAC and Poly1305-AES, with a similar data limit of roughly \(2^{64}\) queries. Moreover, our construction can tolerate some repetition of nonces, while GMAC and Poly1305-AES fail catastrophically in this case. Nonce-misuse resistance is particularly relevant for lightweight cryptography, because the state of a device can sometimes be reset by an adversary.
\(\mathsf {MAC611}\) requires one block cipher call for the setup, just one multiplication (\(\bmod 2^{61}-1\)) per message block, and one block cipher for the finalization, making it efficient both for short and long messages. Finally, we have implemented \(\mathsf {MAC611}\) on two Cortex-M micro-controllers to compare the performance with other MAC algorithms. Our results show that \(\mathsf {MAC611}\) is extremely efficient (Table 2), making it a promising construction for micro-controllers.
Organization of the Paper. We first review the previous literature on MAC constructions from universal hash functions in Sect. 2, and concrete constructions of universal hash functions in Sect. 3. In Sect. 4, we show that the security proof of some composition results can be improved when the underlying components are permutations. In Sect. 5, we set to build a MAC function optimized for micro-controllers. We compare the existing choices for implementing a universal hash function and turning it into a MAC, and propose a concrete construction based on polynomial evaluation in a small field in Sect. 6.
2 MAC Constructions from Universal Hash Functions
Universal hash functions were introduced by Carter and Wegman in 1977 [10] and are now used in many MAC constructions and security proofs. The idea is to hash the message then encrypt the result. The original encryption was a one-time-pad, which was then replaced by a counter-mode encryption. Such constructions are used in GMAC, the authentication part of GCM [24], and in Poly1305 [3], two of the most widely used schemes in TLS today. Many constructions exist to build efficient universal hash functions, and turn them into secure MACs. We sum up the main ones in the following.
2.1 Universal Hash Functions
There are several related definitions of universal and almost universal hash functions. In general a (almost) universal hash function H is a family of functions (denoted as \(h \in H\), or \(H_k \in H\) to emphasize the key) such that a fixed pair of inputs has a low collision probability for a randomly chosen element of the family. In the following, we denote the cardinality of set H as  . We define almost universal hash functions as:
. We define almost universal hash functions as:
Definition 1
(\(\varepsilon \hbox {-}\mathbf {AU}\)). A family \(H: A \rightarrow B\) is \(\varepsilon \)-almost universal if:

To handle any output difference rather than only collisions, one can use almost XOR universal hash functions:
Definition 2
(\(\varepsilon \hbox {-}\mathbf {AXU}\)). A family \(H: A \rightarrow B\) is \(\varepsilon \)-almost XOR universal if:

If H is \(\varepsilon \hbox {-AXU}\), it is also \(\varepsilon \hbox {-AU}\), and we can further define an \(\varepsilon \hbox {-AU}\) family \(G: A\times B \rightarrow B\) as follows:

Definition 3
(\(\varepsilon \hbox {-}\mathbf {ASU}\)). A family \(H: A \rightarrow B\) is \(\varepsilon \)-almost strongly universal if:

If \(H: A \rightarrow B\) is \(\varepsilon \hbox {-ASU}\) then H is also \(\varepsilon \hbox {-AU}\).
2.2 MAC Algorithms
The security of a MAC algorithm is defined as an upper bound on the success probability of an adversary that tries to forge a valid tag. Formally, we consider an adversary \(\mathcal {A}\) with oracle access to the MAC algorithm F; the adversary must output a message and tag pair, and succeeds if the message has not been queried to the oracle, and the tag is valid. Many constructions have been proposed to build a MAC out of a (almost) universal hash function. In the following bounds, we denote the output size of the universal hash function and the tag size as n.
Wegman-Carter. The seminal work by Wegman and Carter [33] introduced the following MAC, using an \(\varepsilon \hbox {-AXU}\) family of hash functions H and a PRF F. If nonces are unique, this construction reaches n-bit security:
Wegman-Carter-Shoup. In many concrete instantiations (GMAC [24], Poly1305-AES [3]), the PRF is instantiated with a block cipher E, following the Wegman-Carter-Shoup construction [31]. The security can be analyzed using the PRF-PRP switching lemma (\(\mathbf {Adv}_{E}^{\text {PRF}} \le \mathbf {Adv}_E^{\text {PRP}} + \tfrac{q^2}{2^n}\)), but this adds a birthday term \(q^2/2^n\) to the bound:
The proof can be improved by looking directly at the MAC security (instead of the PRF security) [4, 31], but it is still limited by the birthday bound. Indeed, there is a forgery attack with roughly \(\sqrt{n} 2^{n/2}\) short queries [21, 22, 28].
Therefore the use of the nonce in WCS fails to increase the security compared to a deterministic MAC, but makes the construction more fragile (nonce repetion can leak the hash key).
Hash and PRF: F ( H ( M )). Alternatively, the hash and PRF construction builds a deterministic MAC from an \(\varepsilon \hbox {-AU}\) family H. It is analyzed in [7]:
WMAC:  . Some constructions allow to combine the n-bit security with nonces, and the birthday security when nonces are repeated. In particular, if a 2n-bit PRF is available, one can use the construction introduced by UMAC [7] and later analyzed as WMAC [6] with an \(\varepsilon \hbox {-AU}\) function. This construction was analyzed in [7] assuming that the nonces are always distinct:
. Some constructions allow to combine the n-bit security with nonces, and the birthday security when nonces are repeated. In particular, if a 2n-bit PRF is available, one can use the construction introduced by UMAC [7] and later analyzed as WMAC [6] with an \(\varepsilon \hbox {-AU}\) function. This construction was analyzed in [7] assuming that the nonces are always distinct:

EWCDM. Cogliati and Seurin have recently proposed a construction with similar security using only an n-bit block cipher and an \(\varepsilon \hbox {-AXU}\) function [11]. A later work by Mennink and Neves [25] proved security up to \(2^n\):
3 Construction of Universal Hash Functions
We now review previous results on the construction of universal hash functions.
3.1 Constructions for Short Messages
Some crucial AU/AXU families use multiplication by a secret key in a field \(\mathbb {F}\):


Polynomial Hashing [14]. In order to hash a long message with a single key, these constructions can be generalized to polynomial hashing. The input message is interpreted as a polynomial, and evaluated on the secret key:

The family H with messages of length \(\ell \) is \(\ell \varepsilon \hbox {-AXU}\). Practical MACs like GMAC and Poly1305 use this construction with different choices of the field \(\mathbb {F}\).
Using Reduced Block Ciphers [26]. Instead of multiplications, one can use reduced block ciphers. For instance, the exact MEDP of 4-round AES from [20] shows that it is \(\varepsilon \hbox {-AXU}\) with \(\varepsilon \approx 1.18 \cdot 2^{-110}\) (if the round keys are independent).

This construction has been used by Minematsu and Tsunoo to build an AES-based MAC faster than CBC-MAC [26].
3.2 Composition and Extension
To accept long messages, composition and domain extension can be used. We will focus here on the composition of (almost) universal hash functions.
Composition [32]. Let \(H_1: A \rightarrow B\) and \(H_2: B \rightarrow C\). Consider \(G: A \rightarrow C\) as:

We have the following results:
-
If \(H_1\) is \(\varepsilon _1\hbox {-AU}\) and \(H_2\) is \(\varepsilon _2\hbox {-AU}\), then G is \(\varepsilon \hbox {-AU}\), with \(\varepsilon = \varepsilon _1+\varepsilon _2-\varepsilon _1\varepsilon _2\).
-
If \(H_1\) is \(\varepsilon _1\hbox {-AU}\) and \(H_2\) is \(\varepsilon _2\hbox {-ASU}\), then G is \(\varepsilon \hbox {-ASU}\), with \(\varepsilon = \varepsilon _1+\varepsilon _2-\varepsilon _1\varepsilon _2\).
-
If \(H_1\) is \(\varepsilon _1\hbox {-AU}\) and \(H_2\) is \(\varepsilon _2\hbox {-AXU}\), then G is \(\varepsilon \hbox {-AXU}\), with \(\varepsilon = \varepsilon _1+\varepsilon _2-\varepsilon _1\varepsilon _2\).
If \(H_1\) and \(H_2\) are compressive, their composition G will compress incrementally. The last two results can be used to compose an efficient \(\varepsilon \hbox {-AU}\) function and a stronger \(\varepsilon \hbox {-AXU}\) or \(\varepsilon \hbox {-ASU}\), to build an efficient \(\varepsilon \hbox {-AXU}\) or \(\varepsilon \hbox {-ASU}\) function.
Domain Extension by Composition. Building an AU family with arbitrary input domain from a fixed-length compressing AU family can be done in a Merkle-Damgård style:
Let \(H_1: A_1 \rightarrow B_1\) and \(H_2: A_2 \times B_1 \rightarrow B_2\) be \(\varepsilon _1\hbox {-AU}\) and \(\varepsilon _2\hbox {-AU}\), respectively. We define the iteration of \(H_1\) and \(H_2\), \(H: A_1 \times A_2 \rightarrow B_2\) as follows:

Using the previous results, we can prove that H is \(\varepsilon \hbox {-AU}\) with \(\varepsilon = \varepsilon _1 + \varepsilon _2 - \varepsilon _1\varepsilon _2 \le \varepsilon _1+ \varepsilon _2\) because it is the composition of \(H_1'\) and \(H_2\), where \(H_1'\) is also \(\varepsilon _1\hbox {-AU}\):

Moreover, if \(H_2\) is \(\varepsilon _2\hbox {-AXU}\) (resp. \(\varepsilon _2\hbox {-ASU}\)), then H is also \(\varepsilon \hbox {-AXU}\) (resp. \(\varepsilon \hbox {-ASU}\)).
This result can easily be extended to the iteration of three or more functions. In particular, it can be used to iterate a single \(\varepsilon \hbox {-AU}\) function \(H: B \times A \rightarrow B\), to build the \(\ell \)-th iterate \(H^\ell : B \times A^\ell \rightarrow B\) with \(\ell \) independent keys; \(H^\ell \) is \(\ell \varepsilon \hbox {-AU}\). In particular, this construction is used in [26].
4 Improved Bounds with Permutations
We can improve the security bound of the iteration of two AU hash functions (following the construction of Sect. 3.2) in the special case where the second function is a permutation when the first input is fixed.
We show that with this extra condition, the iteration of two \(\varepsilon \hbox {-AU}\) functions is \(\varepsilon \hbox {-AU}\), while it is only \(\varepsilon '\hbox {-AU}\) with \(\varepsilon ' = 2\varepsilon - \varepsilon ^2\) in general.
Theorem 1
Let \(H_1: A_1 \rightarrow B_1\) be \(\varepsilon _1\hbox {-AU}\) and \(H_2: A_2\times B_1 \rightarrow B_2\).
Consider \(G: A_1\times A_2\rightarrow B_2\) defined as

If \(x\mapsto h_2(m,x)\) is a permutation for all \(h_2 \in H_2\) and all \(m\in A_2\), then:
-
If \(H_2\) is \(\varepsilon _2\hbox {-AU}\), then G is \(\max \{\varepsilon _1,\varepsilon _2\}\hbox {-AU}\),
-
If \(H_2\) is \(\varepsilon _2\hbox {-AXU}\), then G is \(\max \{\varepsilon _1,\varepsilon _2\}\hbox {-AXU}\),
-
If \(H_2\) is \(\varepsilon _2\hbox {-ASU}\), then G is \(\max \{\varepsilon _1,\varepsilon _2\}\hbox {-ASU}\).
In particular, we can improve the security bound of PC-MAC from Minematsu and Tsunoo [26]. PC-MAC repeats d iterations of reduced-round AES with independent keys (typically, \(d=15\)), with a security bound of:
with q queries of maximum length \(\rho \), and c is roughly equal to a small constant times d. With our results, we can replace the term \(d\varepsilon _{dp}\) by \(\varepsilon _{dp}\):
Proof
-
Case 1: \(AU \Rightarrow AU\). We denote \(N = \#\{(h_1,h_2)\in H_1\times H_2 \;:\; h_2(m_2,h_1(m_1)) = h_2(m_2',h_1(m_1'))\}\) for a fixed message pair
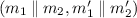 . We want to prove that: \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).
. We want to prove that: \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).If \(m_2=m_2'\) (and thus \(m_1\ne m_1'\)), we write:
$$\begin{aligned} N&= \sum _{h_2\in H_2}\#\{h_1\in H_1 \;:\; h_2(m_2,h_1(m_1)) = h_2(m_2,h_1(m_1'))\} \\&= \sum _{h_2\in H_2}\#\{h_1\in H_1 \;:\; h_1(m_1) = h_1(m_1')\} \quad \text {since } x\mapsto h_2(m_2,x) \text { is a permutation}\\&\le \sum _{h_2\in H_2}\varepsilon _1\times |H_1| = \varepsilon _1\times |H_1|\times |H_2|. \end{aligned}$$If \(m_2\ne m_2'\), we write:
$$\begin{aligned} N&= \sum _{h_1\in H_1}\#\{h_2\in H_2 \;:\; h_2(m_2,h_1(m_1)) = h_2(m_2',h_1(m_1'))\} \\&\le \sum _{h_1\in H_1}\varepsilon _2\times |H_2| = \varepsilon _2\times |H_1|\times |H_2|. \end{aligned}$$We used that \(h_1(m_1)\) and \(h_1(m_1')\) are fixed values for eached fixed \(h_1\) and \(m_2\ne m_2'\).
In the end, we get that G is \(\max \{\varepsilon _1,\varepsilon _2\}\)-AU.
-
Case 2: \(AXU \Rightarrow AXU\). We denote \(N = \#\{(h_1,h_2)\in H_1\times H_2 \;:\; h_2(m_2,h_1(m_1)) \oplus h_2(m_2',h_1(m_1')) = d\}\) for a fixed message pair
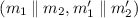 and a fixed \(d\in B_2\). We want to prove that \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).
and a fixed \(d\in B_2\). We want to prove that \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).The complicated case is collision (\(d=0\)), because collision can either occur in \(h_1\) or in \(h_2\). Using the AU case, we get that when \(d=0\), \(N \le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).
Otherwise, \(d\ne 0\). Therefore \((m_2,h_1(m_1))\ne (m_2',h_1(m_1'))\), and we simply write:
$$\begin{aligned} N&= \sum _{h_1\in H_1}\#\{h_2\in H_2 \;:\; h_2(m_2,h_1(m_1)) \oplus h_2(m_2',h_1(m_1')) = d\} \\&\le \sum _{h_1\in H_1}\varepsilon _2\times |H_2| = \varepsilon _2\times |H_1|\times |H_2|. \end{aligned}$$ -
Case 3: \(ASU \Rightarrow ASU\). First, we have to show that H is balanced. For fixed messages \(m_1, m_2\), and a fixed \(y \in B_2\), we have:
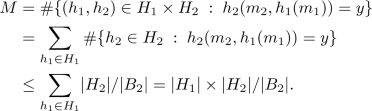
We denote \(N = \#\{(h_1,h_2)\in H_1\times H_2 \;:\; h_2(m_2,h_1(m_1)) = y,\, h_2(m_2',h_1(m_1')) = y'\}\) for a fixed message pair
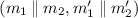 and fixed \(y, y' \in B_2\). We want to prove that \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).
and fixed \(y, y' \in B_2\). We want to prove that \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).Similarly to the AXU proof, the complicated case is collision (\(y=y'\)), because collision can either occur in \(h_1\) or in \(h_2\). Using the AU case, we get that when \(y=y'\), \(N\le \max \{\varepsilon _1,\varepsilon _2\}\times |H_1|\times |H_2|\).
Otherwise, \(y\ne y'\). Therefore \((m_2,h_1(m_1))\ne (m_2',h_1(m_1'))\), and we simply write:
$$\begin{aligned} N&= \#\{(h_1,h_2)\in H_1\times H_2 \;:\; h_2(m_2,h_1(m_1)) = y,\, h_2(m_2',h_1(m_1')) = y'\} \\&= \sum _{h_1\in H_1}\#\{h_2\in H_2 \;:\; h_2(m_2,h_1(m_1)) = y,\, h_2(m_2',h_1(m_1')) = y'\} \\&\le \sum _{h_1\in H_1}\varepsilon _2\times |H_2| = \varepsilon _2\times |H_1|\times |H_2|. \end{aligned}$$Again, we use that, for fixed \(h_1\), \(h_1(m_1)\) and \(h_1(m_1')\) are fixed values. \(\square \)
5 Instantiating a Lightweight MAC
We now consider the construction of a lightweight MAC with a small state, in order to reach good performance on 32-bit micro-controllers. Following Sect. 2, we use the WMAC construction  with a 61-bit universal hash function, and a 128-bit block cipherFootnote 2, in order to reach a data limit of \(2^{61}\) queries. The main downside of WMAC compared to Wegman-Carter is that the block cipher cannot be evaluated in parallel with the hash function, but this hardly matters for micro-controller implementations.
with a 61-bit universal hash function, and a 128-bit block cipherFootnote 2, in order to reach a data limit of \(2^{61}\) queries. The main downside of WMAC compared to Wegman-Carter is that the block cipher cannot be evaluated in parallel with the hash function, but this hardly matters for micro-controller implementations.
An important part of this work consists in the implementation and optimization of our algorithm, \(\mathsf {MAC611}\), on two 32-bit micro-controllers.
We ran benchmarks to explore design choices and compare with existing MACs. We used two micro-controllers: an FRDM-KL46Z board with a Cortex-M0+ micro-controller and an FRDM-K64F board with a Cortex-M4 micro-controller. The Cortex-M0+ is very limited, while the Cortex-M4 is slightly more powerful, with more RAM, and more instructions.
5.1 Choice of Universal Hash Function: \(\mathsf {XPoly}\)
We focus on AU families based on field arithmetics, which offer trade-offs between key size and security. Over a field \(\mathbb {F}\), the two main options are:
-
Polynomial hashing [14]: \(H_k: m_1, \ldots m_{\ell } \mapsto \sum _{i=1}^{\ell } m_{i} \times k^{\ell +1-i}\)
\(H_k\) is an \(\ell \varepsilon \hbox {-AXU}\) family using a single field element as key, with \(\varepsilon = 1/|\mathbb {F}|\).
-
Dot product [16]: \(H_{k_1, \ldots k_\ell }: m_1, \ldots m_{\ell } \mapsto \sum _{i=1}^{\ell } m_i \times k_i\)
\(H_{k_1, \ldots k_\ell }\) is an \(\varepsilon \hbox {-AXU}\) family using \(\ell \) field elements as key, with \(\varepsilon = 1/|\mathbb {F}|\).
In particular, the factor \(\ell \) in the security of polynomial hashing leads to a class of weak keys for GMAC [30].
To balance security and key size, we propose two constructions using polynomial hashing, with independent subkeys \(k_i\) for every chunk of \(\lambda \) blocks of message. We denote P[m] the polynomial whose coefficients are given by message m. The function is typically evaluated using Horner’s rule, with a single multiplication and addition per message block:
Sum of Polynomials. One option is to sum independent polynomials:
Since the polynomial hashes are \(\lambda \varepsilon \hbox {-AXU}\), this construction is also a \(\lambda \varepsilon \hbox {-AXU}\) family, using the analysis of [10, Proposition 8].
Composition of Polynomials. Alternatively, we can build a \(\lambda \varepsilon \hbox {-AU}\) family with the composition result of Theorem 1, using \(\lambda \varepsilon \hbox {-AU}\) functions defined from polynomial hashing: \(H_i : m_1, \ldots m_{\ell }, m_{\ell +1} \mapsto P[m_1, \ldots m_{\ell }](k_i) \oplus m_{\ell +1}\):

We still implement the construction with Horner’s rule, changing the subkey every \(\lambda \) blocks (see Fig. 1). The composition has a smaller state than the sum of polynomials, therefore we use composition for our design.
The parameter \(\lambda \) offers a trade-off between security and key length. The key length is linear in the message size, but we can use a PRF to stretch a master key into sub-keys for each chunk, with \(k_i = F_k(i)\). If \(\lambda \) is not too small, the time taken to derive the keys can be kept small.
For a practical MAC, we need a universal hash function family that can process messages of different lengths. To achieve this, we first pad the message with zeroes to a full block, we append a block with an encoding of the message length (the number of bytes), and we process the padded message through XPoly1. We denote this construction as \(\mathsf {XPoly}\):  ; this family is \(2\lambda \varepsilon \hbox {-AU}\), with \(\varepsilon =1/|\mathbb {F}|\).
; this family is \(2\lambda \varepsilon \hbox {-AU}\), with \(\varepsilon =1/|\mathbb {F}|\).
5.2 Choice of Field and Multiplication
We now have to choose a field to define our universal hash function. This is an important choice because the field multiplication is the main operation in \(\mathsf {XPoly}\). There are two kinds of fields that can be used for efficient implementations: fields \(\mathbb {F}_p\) defined modulo a prime number p close to \(2^{64}\) or \(2^{128}\) (as used in Poly1305), and binary fields such as \(\mathbb {F}_{2^{64}}\) and \(\mathbb {F}_{2^{128}}\) (like GMAC).
Table-Based Implementations. Since the multiplication by a fixed key is a linear operation, it can be implemented using precomputed tables. For instance, if we precompute \(\mu _i = 2^i \times k\) for \(0 \le i < n\), we can decompose an element \(x \in \mathbb {F}\) as \(x=\sum _{0 \le i < n} x_i \times 2^i\) (where \(x_i\) is just the i-th bit of x), and use:
In particular, in a binary field, the sum is just an XOR. More generally, we can precompute multiplication tables for several consecutive bits. If we divide x into t-bit chunks and precompute tables of \(2^t\) entries for each chunk, we just need n/t table accesses and \(n/t-1\) sums to evaluate the product \(x \times k\).
Benchmarks. We wrote table-based implementations of multiplication in a binary field in C and assembly, using several chunk sizes (1 bit, 4 bits, and 8 bits), and we give benchmarks results in Table 1. Note that we could not implement multiplication in \(\mathbb {F}_{2^{128}}\) with 8-bit chunks on the Cortex-M0+ because the tables do not fit in the RAM of this small micro-controller.
For reference, we also benchmarked the OpenSSL implementations of GMAC (multiplication in \(\mathbb {F}_{2^{128}}\)), which includes ARM assembly that can run on the Cortex-M4 (but not on the Cortex-M0+). It uses a single table with chunks of 4 bits (256 bytes of memory).
As expected, our benchmarks show that multiplication in a small field is more efficient (the cost of the multiplication is quadratic), and table-based implementation can be quite fast on micro-controllers, using some memory for the tables. In particular, multiplication over \(\mathbb {F}_{2^{64}}\) using 4-bit or 8-bit chunks is competitive with Chaskey.
Using the Multiplier. Alternatively, multiplication in fields defined modulo a prime can be implemented efficiently using the integer multiplier of the processor. This is useful for servers using different keys with several clients, since accessing tables would often incur cache misses [3].
To evaluate the speed of prime field multiplication, we benchmarked the OpenSSL implementations of Poly1305 (multiplication in \(\mathbb {F}_{2^{130}-5}\)), which uses assembly on the Cortex-M4, and C code on the Cortex-M0+. On the Cortex-M4, this is much faster than a table based multiplication, with just 5 c/B. Indeed, the Cortex-M4 has a fast multiplier and a well written implementation of the multiplication in a prime field can be very fast (but bad implementations can be much slower...).

Since prime field multiplications can also be implemented with tables if needed, we decided to use a prime field for our construction. We wrote optimized assembly implementations of the multiplication in \(\mathbb {F}_{2^{61}-1}\) (because we target the 64-bit security level). As detailed in Sect. 6.1, we achieved very good results, with just 3.7 c/B on the Cortex-M4 and 19 c/B on the Cortex-M0+ (without using any tables). Therefore, we use the field \(\mathbb {F}_{2^{61}-1}\) for our construction.
6 A Concrete Instantiation: \(\mathsf {MAC611}\)
We can now define a concrete MAC construction based on our analysis, and compare its performance with other MAC constructions. As explained above, we use the \(\mathsf {XPoly}\) universal hash function with \(\lambda = 1024\) over the field \(\mathbb {F}_{2^{61}-1}\). Since the field has less than \(2^{64}\) elements, we cut the message into blocks \(m_i\) of 56 bits (i.e. 7 bytes).
For the finalization of the MAC construction, we considered various choices for the PRF, and we decided to use Noekeon [12], a 128-bit block cipher with very efficient implementations on micro-controllers. Therefore, we use the construction  from WMAC: we concatenate the 64-bit hash and a 64-bit nonce, encrypt them, and truncate the output to 64 bits (we denote the first 64 bits of variable a by T64(a)). We also use Noekeon to derive the subkeys used in \(\mathsf {XPoly}\) from the block-cipher key, by encrypting a counter and truncating then reducing the output modulo \(2^{61}-1\):
from WMAC: we concatenate the 64-bit hash and a 64-bit nonce, encrypt them, and truncate the output to 64 bits (we denote the first 64 bits of variable a by T64(a)). We also use Noekeon to derive the subkeys used in \(\mathsf {XPoly}\) from the block-cipher key, by encrypting a counter and truncating then reducing the output modulo \(2^{61}-1\):  .
.
Since the output of \(\mathsf {XPoly}\) is a field element, we take the representative h between 0 and \(2^{61}-2\), and we compute the MAC as  . This ensures a domain separation between the block-cipher calls for the key-derivation and for the finalization.
. This ensures a domain separation between the block-cipher calls for the key-derivation and for the finalization.
6.1 Implementation Details
The choice of the field allows for very efficient implementations on processors or micro-controllers with a fast integer multiplier, but table-based implementations are also possible when there is no multiplier or a very slow one. More precisely, elements of the field are stored as an unsigned 64-bit integer, and the field operations are implemented as followsFootnote 3:
-
Modular reduction can be implemented very efficiently, by just computing (x>>61) + (x&0x1fffffffffffffff) (in C notation). This is a partial reduction with output between 0 and \(2^{61}+6\) (for x a 64-bit unsigned integer), but this range is small enough to reuse the output for further operations.
-
Modular addition is implemented with an integer addition. A modular reduction is rarely needed, since the result of the addition is usually smaller than \(2^{64}\) (in the easiest case, we add a partially reduced operand in \([0, 2^{61}+6]\) and a message block in \([0, 2^{56}-1]\), so that the output fits in 62 bits).
-
Modular multiplication is implemented with an integer multiplication (with roughly 64-bit inputs and 128-bit output) followed by a modular reduction. We suggest implementation strategies for several micro-controllers.
On Cortex-M4 (armv7-M) we can multiply two 32-bit inputs and get a 64-bit product in a single cycle. The 64-bit multiplication uses 4 such multiplications and few additions. The full multiplication (including a partial reduction) takes just 14 cycles. The output range is slightly larger than the input range, so we need a reduction after a few multiplications.
On Cortex-M0+ (armv6-M) we can only get a 32-bit product from the multiplication of two 32-bit inputs. Therefore, a naive implementation takes 16 multiplication instructions. Instead, we implement a 32-bit multiplication with 64-bit output using 4 multiplication instructions, and use Karatsuba’s algorithm to implement a 62-bit multiplication (with 124-bit output) using three 32-bit multiplications (we first write the input in base \(2^{31}\) to avoid overflow when adding two values). The full multiplication (including a partial reduction) takes around 100 cycles on our Cortex-M0+, with a single cycle multiplier.
Finally, some Cortex-M0+ take 32 cycles for a 32-bit product. It is then quicker to use a table-based implementation (with table entries between 0 and \(2^{61}-1\), we can add eight values without overflow). This implementation takes around 100 cycles on our Cortex-M0+, but requires 16 MB of memory.
Benchmarks Results. Table 2 shows benchmark results of \(\mathsf {MAC611}\) with various message lengths, and a comparison with other primitives. For comparison, we use several standard MACs from OpenSSL, with Noekeon as the underlying block cipher: Poly1305, GMAC (as a part of GCM), and CBC-MAC (as a part of CCM). On the Cortex-M4, this includes optimized assembly code for Poly1305, GMAC and Noekeon. For Chaskey, we use the reference C implementation on the Cortex-M4, and an assembly implementation from B. HaaseFootnote 4 optimized for the Cortex-M0+.
\(\mathsf {MAC611}\) is faster that all the primitives tested on the Cortex-M4, with less than one thousand cycles for short messages, and only 3.7 c/B for long messages. On the Cortex-M0+, Chaskey is the fastest with 14 c/B, but \(\mathsf {MAC611}\) is a close second with 19 c/B. \(\mathsf {MAC611}\) is also faster than Wegman-Carter MACs GMAC and Poly1305 thanks to the use of a smaller field.
When a crypto accelerator is available, standard based constructions such as AES-CBC-MAC or GMAC could be faster, but given the very good performance of \(\mathsf {MAC611}\), this is not always the case. For instance, presentation slides of the ST32L4Footnote 5, a Cortex-M4 with a crypto core, show that it takes 67 cycles per block for GMAC (4.2 c/B), and 206 cycles per block for AES-CBC-MAC (12.9 c/B).
We compare the security of the primitives in Sect. 6.3.
6.2 Choice of the Parameter \(\lambda \)
We used the benchmark results in Table 1 to choose a value of the parameter \(\lambda \), such that the subkey derivation and the construction of the multiplication tables (in case of a table-based implementation) have a limited impact on performance. In a 64-bit field, the time spent building the tables corresponds to roughly 500 multiplications in the worst case. Therefore, we chose \(\lambda =1024\), so that the key derivation is amortized over 1024 blocks for long messages. For short messages, we precompute the key \(k_1\) (and the corresponding table if needed), so that rekeying is not needed for messages smaller than \(\lambda \) blocks (i.e. 8 kB).
In terms of security, the next section shows that the impact of \(\lambda \) is quite limited: the advantage of an attacker with negligible data increases by a factor \(\lambda \), but when the attacker uses a large amount of data (which is necessary to reach a higher success probability), the advantage does not increase with \(\lambda \).
6.3 Security Bounds
Let us derive the security of \(\mathsf {MAC611}\). Denote \(n=64\) the output size, q the number of queries, and \(\rho \) the maximum query length. For the finalization and subkey derivation, we use a truncated block cipher with 128-bit input and 64-bit output \(E' : x\in \{0,1\}^{2n}\mapsto T64(E(x))\). Therefore, there are better security bounds than the PRP-PRF switching lemma: we can use the analysis of [17, Eq. (2.5)], with \(\mathbf {Adv}_{E'}^{\text {PRF}}(q) \le \mathbf {Adv}_{E}^{\text {PRP}}(q) + \tfrac{q}{2^{3n/2}}\,.\)
Consider first \(\mathsf {MAC611} ^\$\), defined with uniform independent subkeys in \(\mathbb {F}_{2^{61}-1}\). From the previous results, \(\mathsf {XPoly}\) is \(\tfrac{2\lambda }{|\mathbb {F}|}\)-AU. When the nonces are unique, the security proof from WMAC gives: \( \mathbf {Adv}_{\mathsf {MAC611} ^\$}^{\text {MAC}}(q) \le \mathbf {Adv}_{E'}^{\text {PRF}}(q) + \tfrac{2\lambda }{|\mathbb {F}|} + \tfrac{1}{2^n}\).
We now consider the actual \(\mathsf {MAC611}\), i.e. with subkeys  , \(1\le i\le \tfrac{\rho }{\lambda }\). The modular reduction to \(\mathbb {F}_{2^{61}-1}\) introduces a small bias: \(\delta = \frac{1}{2} \sum \left| p_i - \frac{1}{2^{61}-1}\right| = \frac{1}{2} \cdot 8 \cdot \frac{1}{2^{61}-1} \approx 2^{-62}.\) Therefore:
, \(1\le i\le \tfrac{\rho }{\lambda }\). The modular reduction to \(\mathbb {F}_{2^{61}-1}\) introduces a small bias: \(\delta = \frac{1}{2} \sum \left| p_i - \frac{1}{2^{61}-1}\right| = \frac{1}{2} \cdot 8 \cdot \frac{1}{2^{61}-1} \approx 2^{-62}.\) Therefore:
In particular, the maximum advantage of a nonce-respecting adversary is roughly \(2^{-n/2} = 2^{-32}\), even with \(q = 2^{64}\) queries of \(\rho = 2^{64}\) blocks. In Appendix A, we compare this bound with the security of Wegman-Carter-Shoup constructions such as GMAC. If the nonces are reused, the analysis of Hash-then-PRF gives:
Security Level. Comparing the security of \(\mathsf {MAC611}\), GMAC, CBC-MAC, Poly1305-AES and Chaskey is difficult, because security cannot be reduced to a single number. As a rough comparison, we can say that all these algorithms have a security level of (roughly) 64 bits, because they are broken by a forgery attack with about \(2^{64}\) time and data. On the other hand, Chacha20-Poly1305 offers a significantly higher security than the previous algorithms, because it uses the one-time MAC construction (it is secure up to \(2^{106}\) operations).
More precisely, the success rate of an attacker depends on the number of queries q and the maximum query length \(\rho \), as shown in Appendix A. While all these algorithms are secure up to roughly \(2^{64}\) queries, the success rate of an attacker with a small amount of data is higher against \(\mathsf {MAC611}\) than against the other constructions, due to the small state size.
These bounds also depend on how the algorithm is used: on the one hand the security of GMAC, CBC-MAC, Poly1305-AES and Chaskey increases if rekeying is consistently used, but on the other hand the security of GMAC and Poly1305-AES is completely lost if nonces are misused.
Conclusion
In this work we revisit MAC algorithms based on universal hash functions in the context of lightweight cryptography. We give improved results on the composition of universal hash functions, and design a concrete MAC, \(\mathsf {MAC611}\). Our construction uses a universal hash function on 61 bits, combined with the WMAC construction to obtain security up to roughly \(2^{61}\) operations.
We demonstrate the good performance of this construction with fast micro-controller implementations using the on-board multiplier. On a Cortex-M4 micro-controller, we need less than one thousand cycles for small messages, and only 3.7 cycles per byte for long messages. This is significantly faster than alternative constructions like Chaskey, GMAC, CBC-MAC, or Poly1305.
Notes
- 1.
- 2.
Unfortunately, we did not find a good 64-bit block cipher with an efficient implementation on micro-controllers to use in EWCDM.
- 3.
The code is available at: https://github.com/Cryptosaurus/MAC611.
- 4.
- 5.
References
Aumasson, J.-P., Bernstein, D.J.: SipHash: a fast short-input PRF. In: Galbraith, S., Nandi, M. (eds.) INDOCRYPT 2012. LNCS, vol. 7668, pp. 489–508. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34931-7_28
Aumasson, J.P., Henzen, L., Meier, W., Naya-Plasencia, M.: Quark: a lightweight hash. J. Cryptol. 26(2), 313–339 (2013)
Bernstein, D.J.: The Poly1305-AES message-authentication code. In: Gilbert, H., Handschuh, H. (eds.) FSE 2005. LNCS, vol. 3557, pp. 32–49. Springer, Heidelberg (2005). https://doi.org/10.1007/11502760_3
Bernstein, D.J.: Stronger security bounds for Wegman-Carter-Shoup authenticators. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 164–180. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_10
Biryukov, A., Perrin, L.: State of the art in lightweight symmetric cryptography. Cryptology ePrint Archive, Report 2017/511 (2017). http://eprint.iacr.org/2017/511
Black, J., Cochran, M.: MAC reforgeability. In: Dunkelman, O. (ed.) FSE 2009. LNCS, vol. 5665, pp. 345–362. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03317-9_21
Black, J., Halevi, S., Krawczyk, H., Krovetz, T., Rogaway, P.: UMAC: fast and secure message authentication. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 216–233. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_14
Bogdanov, A., Knežević, M., Leander, G., Toz, D., Varıcı, K., Verbauwhede, I.: spongent: a lightweight hash function. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 312–325. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23951-9_21
Bogdanov, A., et al.: PRESENT: an ultra-lightweight block cipher. In: Paillier, P., Verbauwhede, I. (eds.) CHES 2007. LNCS, vol. 4727, pp. 450–466. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74735-2_31
Carter, J.L., Wegman, M.N.: Universal classes of hash functions. In: Proceedings of the Ninth Annual ACM Symposium on Theory of Computing, pp. 106–112. ACM (1977)
Cogliati, B., Seurin, Y.: EWCDM: an efficient, beyond-birthday secure, nonce-misuse resistant MAC. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 121–149. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_5
Daemen, J., Peeters, M., Van Assche, G., Rijmen, V.: Nessie proposal: NOEKEON. In: First Open NESSIE Workshop (2000)
Datta, N., Dutta, A., Nandi, M., Paul, G., Zhang, L.: Single key variant of PMAC\_Plus. IACR Trans. Symm. Cryptol. 2017(4), 268–305 (2017)
Dietzfelbinger, M., Gil, J., Matias, Y., Pippenger, N.: Polynomial hash functions are reliable. In: Kuich, W. (ed.) ICALP 1992. LNCS, vol. 623, pp. 235–246. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55719-9_77
Computer data authentication: National Bureau of Standards, NIST FIPS PUB 113. U.S, Department of Commerce (1985)
Gilbert, E.N., MacWilliams, F.J., Sloane, N.J.: Codes which detect deception. Bell Labs Tech. J. 53(3), 405–424 (1974)
Gilboa, S., Gueron, S., Morris, B.: How many queries are needed to distinguish a truncated random permutation from a random function? J. Cryptol. 31(1), 162–171 (2018)
Gong, Z., Hartel, P.H., Nikova, S., Tang, S., Zhu, B.: Tulp: a family of lightweight message authentication codes for body sensor networks. J. Comput. Sci. Technol. 29(1), 53–68 (2014)
Hong, D., et al.: HIGHT: a new block cipher suitable for low-resource device. In: Goubin, L., Matsui, M. (eds.) CHES 2006. LNCS, vol. 4249, pp. 46–59. Springer, Heidelberg (2006). https://doi.org/10.1007/11894063_4
Keliher, L., Sui, J.: Exact maximum expected differential and linear probability for two-round advanced encryption standard. IET Inf. Secur. 1(2), 53–57 (2007)
Leurent, G., Sibleyras, F.: The missing difference problem, and its applications to counter mode encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 745–770. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_24
Luykx, A., Preneel, B.: Optimal forgeries against polynomial-based MACs and GCM. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 445–467. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_17
Luykx, A., Preneel, B., Tischhauser, E., Yasuda, K.: A MAC mode for lightweight block ciphers. In: Peyrin, T. (ed.) FSE 2016. LNCS, vol. 9783, pp. 43–59. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52993-5_3
McGrew, D.A., Viega, J.: The security and performance of the Galois/counter mode (GCM) of operation. In: Canteaut, A., Viswanathan, K. (eds.) INDOCRYPT 2004. LNCS, vol. 3348, pp. 343–355. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30556-9_27
Mennink, B., Neves, S.: Encrypted Davies-Meyer and its dual: towards optimal security using mirror theory. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 556–583. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_19
Minematsu, K., Tsunoo, Y.: Provably secure MACs from differentially-uniform permutations and AES-based implementations. In: Robshaw, M. (ed.) FSE 2006. LNCS, vol. 4047, pp. 226–241. Springer, Heidelberg (2006). https://doi.org/10.1007/11799313_15
Mouha, N., Mennink, B., Van Herrewege, A., Watanabe, D., Preneel, B., Verbauwhede, I.: Chaskey: an efficient MAC algorithm for 32-bit microcontrollers. In: Joux, A., Youssef, A. (eds.) SAC 2014. LNCS, vol. 8781, pp. 306–323. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-13051-4_19
Nandi, M.: Bernstein bound on WCS is tight. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 213–238. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_8
Preneel, B., van Oorschot, P.C.: MDx-MAC and building fast MACs from hash functions. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 1–14. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_1
Procter, G., Cid, C.: On weak keys and forgery attacks against polynomial-based MAC schemes. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 287–304. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43933-3_15
Shoup, V.: On fast and provably secure message authentication based on universal hashing. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 313–328. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_24
Stinson, D.R.: Universal hashing and authentication codes. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 74–85. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_5
Wegman, M.N., Carter, L.: New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 22, 265–279 (1981)
Yasuda, K.: The sum of CBC MACs is a secure PRF. In: Pieprzyk, J. (ed.) CT-RSA 2010. LNCS, vol. 5985, pp. 366–381. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11925-5_25
Zhang, L., Wu, W., Sui, H., Wang, P.: 3kf9: enhancing 3GPP-MAC beyond the birthday bound. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 296–312. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_19
Acknowledgments
The work of Sébastien Duval has been funded in parts by the European Commission through the H2020 project 731591 (acronym REASSURE).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Comparison of Security Bounds
A Comparison of Security Bounds
We can compare the maximum advantage of an adversary against \(\mathsf {MAC611}\), GMAC, CBC-MAC, Chakey, and LightMAC [23], as a function of the number of queries, for various query lengths. We have the following bounds:
The bounds for Poly1305-AES are essentially the same as for GMAC. Note that the bound for Chaskey involves the time t of the attacker; in the following we assume that the time and data of the attacker are the same, i.e. \(t=q\rho \).
We compare all the bounds in Fig. 2.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Duval, S., Leurent, G. (2020). Lightweight MACs from Universal Hash Functions. In: Belaïd, S., Güneysu, T. (eds) Smart Card Research and Advanced Applications. CARDIS 2019. Lecture Notes in Computer Science(), vol 11833. Springer, Cham. https://doi.org/10.1007/978-3-030-42068-0_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-42068-0_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-42067-3
Online ISBN: 978-3-030-42068-0
eBook Packages: Computer ScienceComputer Science (R0)





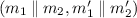 . We want to prove that:
. We want to prove that: 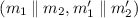 and a fixed
and a fixed 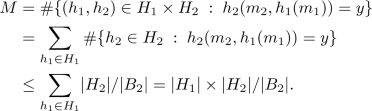
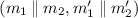 and fixed
and fixed 
