Dynamic Relationship Building: Exploitation Versus Exploration on a Social Network

Abstract

Interpersonal relations facilitate information flow and give rise to positional advantage of individuals in a social network. We ask the question: How would an individual build relations with members of a dynamic social network in order to arrive at a central position in the network? We formalize this question using the dynamic network building problem. Two strategies stand out to solve this problem: The first directs the individual to exploit their social proximity by linking to nodes that are close-by, while the second tries its best to explore distant regions of the network. We evaluate and contrast these two strategies with respect to edge- and distance-based cost metrics, as well as other structural properties such as embeddedness and clustering coefficient. Experiments are performed on models of dynamic random graphs and real-world data sets. We then discuss and test ways that combine these two strategies.

1 Introduction

The network of social relations entails important properties of individuals. Take, as an example, the structural construct of centrality [33]. Much has been revealed about the correlation between centrality and social statues [9, 10, 23, 25]. By occupying a more central position in the social network, an individual may exercise more control over the flow of information, accessing diverse knowledge and skills, and hence gaining a higher positional advantage [38]. Exploiting this principle, individuals may cultivate relationships with others towards improving their social statues [11]. One famous example is the House of Medici, who rose to prominence in 15th century Florence through intermarriage with other noble families [35]. Another example is Moscows growing statues in 12–13th century Russia thanks to trade relationships with other towns [36]. A third example is the case of Paul Revere who successfully raised a militia during the American Revolution by strategically creating social ties [38].

Imagine that an individual tries to embed herself at the center of a social network through forming new ties. From a structural perspective, this individual needs to choose a set of members to build links with. Here we put aside issues such as attitude, personality, and individual preferences, and focus on a structural perspective of network building. To this end, the individual may adopt an exploitative or an exploratory strategy: The former ensures that the individual exploits existing interpersonal ties and links to those that share a common social proximity; On the contrary, the latter allows the individual to explore far and bridge diverse parts of the network. A natural question arises as to which strategy is more suitable. Moreover, social networks in real life are rarely static, but rather, they constantly evolve with time. Thus the question has an extra layer of complexity: How to incrementally build relationships in a network to gain positional advantage while the network is evolving?

To attempt this question, we should settle several issues: Firstly, we need a notion that reasonably reflects positional advantage; here centrality metrics may be of use. Secondly, relation building costs time and effort; one needs to quantify such costs. Thirdly, one needs models on how a social network evolves.

Contribution. We list the main contributions of the paper:

• 1. In this paper, we propose the problem of dynamic network building (DNB). The input to the problem consists of a connected graph G that undergoes a sequence of updates. The problem asks for a plan that builds edges incrementally between a node v and other nodes so that v gains centrality as G evolves. (See Sect. 2).

• 2. To solve this problem, we define exploitative and exploratory strategies and present heuristics to realize each strategy. (See Sect. 3).

• 3. We compare the heuristics over various evolution models of social networks and real-world networks. Exploration often builds less number of new links, while the exploitative strategy produces better results when other factors, such as distance and embeddedness is considered (See Sect. 4).

• 4. Lastly, we propose and evaluate ways that combine the exploitative and exploratory strategies (See Sect. 5).

This work is meaningful in the following ways: Firstly, the process of socialization has been studied intensively in social sciences [21, 28, 32]. Through formalizing and analyzing mechanisms of network building with respect to distance, embeddedness and clustering, the work quantitatively reveals fundamental insights in this otherwise rather qualitative problem domain. Secondly, the exploration-exploitation tradeoff has been a recurring theme in artificial intelligence and management science [2, 6, 34]. This work discovers an instance of this tradeoff in the context of social networks. Thirdly, the work opens the door to many novel applications from engineering information channels on career-based online social networks to enhancing workplace communication and collaboration through enterprise management systems.

Related Works. The establishment of interpersonal ties has been a major problem in social network analysis. Granovetter’s pioneering work contrasts ties having high embeddedness (strong ties) with ties that bridge two otherwise disjoint social circles (weak ties); while embeddedness reflects important dimensions such as trust, commitment and solidarity [18], bridges are important to the exchange of knowledge and ideas [16]. We extends this discussion to study strategies for building different types of ties. Network building (NB) has been studied in [29,30,31]; The problem studied in this paper has crucial differences to these works: (a) While NB only operates on static networks, here we focus on evolving networks, which demand the node to be strategic towards future changes. (b) While NB focuses on smallest eccentricity, DNB aims for optimal rank on centrality. (c) DNB considers costs incurred from the distance between the two nodes when forming an edge. A large literature on strategic network formation explains tie establishment between rational agents using game theory; these works do not consider stochastic models of network evolution [20]. The general view that interpersonal ties bring social support and cohesion has been discussed in [24, 26]. Lastly, exploratory-exploitative strategies discussed in this paper parallel the two modes of network formation in [21]; there, “meeting strangers” means exploratory encounters in the network, and “meeting friends-of-friends” means exploiting existing social circles.

2 The Dynamic Network Building Problem

Following standard convention, we view a social network as a graph $G=(V,E)$ where V is a set of nodes and E is a set of undirected edges on V of the form uv where $u\ne v\in V$. Here the undirected edges are abstracted models of channels of information or transactions. The set $\varGamma (u)=\{v\mid uv\in E\}$ denotes the neighborhood of u, consisting of all nodes that are adjacent to u. A path (of length k) is a sequence of nodes $u_0,u_1,\ldots ,u_k$ where $u_iu_{i+1}\in E$ for any $0\le i<k$. The (geodesic) distance between u and v, denoted by $\mathsf {dist}_G(u,v)$, is the length of a shortest path between u and v. We omit the subscript G writing simply $\mathsf {dist}(u,v)$ when the underlying graph is clear. We also need the following formalism:

• For a node $s\in V$ and $v\ne s$, denote by $G\oplus _s v$ the expanded network $(V\cup \{v\},E\cup \{sv\})$ obtained by adding sv to G.

• We assume that the social network G evolves by some (discrete-time) stochastic mechanism, which we define below:

Definition 1

An evolution mechanism M is a function that maps a social network G to a probability distribution of social networks M(G). Starting at G, the network evolves to a sample outcome of M(G) in the next time step.

Imagine v is a node who wants to build relationships in G; Let’s call v the newcomer in this paper. We assume that (1) v is a node with few connections in G; (2) v may create edges from itself to nodes in V by paying costs (see below); and (3) v has no knowledge regarding how G may evolve.

Abstractly, one can view the interactions between v and the social network G as a two-player game: v is one player; the other player represents the evolution mechanism of the network. At each round, v creates an edge with a node in G (keeping all existing edges). For simplicity, we assume each round allows v to create at most one new edge. One may easily generalize this setting to allow v to create several edges in a single round. The evolution mechanism then modifies the updated network. Through multiple rounds, v aims to get increasingly integrated into the network. Note that we assume that v functions independently from the evolution mechanism to highlight that v builds edges without prior knowledge of the network evolution mechanism.

Definition 2

An ($\ell$-round) network building (NB) process between v and G consists of a sequence of networks $G_0=(V_0,E_0), G_1=(V_1,E_1), \ldots , G_\ell =(V_\ell ,E_\ell )$ and a sequence of nodes $s_0\in V_0, s_1\in V_1, \ldots , s_{\ell -1}\in V_{\ell -1}$ such that $G_0=G$ and each network $G_{i+1}$ is a sample output of $M(G_i\oplus _{s_i} v)$.

Definition 3

An NB strategy is a function $\varphi$ that outputs a node $\varphi (G)$ in a given network G. Any NB process $(G_0,\ldots ,G_{\ell }, s_0,\ldots , s_{\ell -1})$ is said to be consistent with strategy $\varphi$ if $\forall 0\le i<\ell :s_i=\varphi (G_i)$.

Closeness centrality amounts to an important index of social capital that captures a node’s ease in accessing information, social support and other resources [1, 13, 37]. Thus we use closeness centrality here to indicate the positional advantage of nodes. For any connected $G=(V,E)$ and $v\in V$, define

$$ C_{\mathsf {Cls}}(v)=\frac{|V|-1}{\sum _{u\in V\setminus \{v\}} \mathsf {dist}(u,v)}. $$

A higher value of $C_{\mathsf {Cls}}(v)$ implies that v is in general closer to other nodes, thus it occupies a better network position. The $\mathsf {Cls}$-rank of v is the percentage of nodes whose closeness centrality are higher or equal to $C_{\mathsf {Cls}}(v)$:

$$ \mathsf {rank}_{\mathsf {Cls}}(v)=|\left\{ u\in V\mid C_{\mathsf {Cls}}(u)\ge C_{\mathsf {Cls}}(v)\right\} |/|V|. $$

We assume that the goal of v is to gain a higher closeness centrality (or a low $\mathsf {rank}_\mathsf {Cls}$). One way to achieve this is to build a tie between v and all nodes in the network. However, establishing new relationships requires time, efforts and resources. To identify realistic solutions, one needs to define costs of relationship building. Here we consider temporal and establishment costs. Temporal cost is the number of rounds in the NB process and coincides with the number of edges created for v. The proximity principle states that ties are generally more difficult to establish between nodes that are further apart (e.g. reciprocal of distance is a score for link prediction [27]). We thus define establishment cost as the sum of distance between v and its linked nodes (prior to edge creation).

Definition 4

Let $(G_0,G_1,\ldots ,G_{\ell }, s_0,s_1,\ldots , s_{\ell -1})$ be an NB process. We define the following costs:

• 1. The temporal cost is $\ell$.

• 2. The establishment cost is $\sum _{i=1}^{\ell -1} \sum _{u\in S_i} \mathsf {dist}_{G_i}(v,u)$.

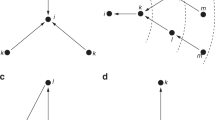
We are now ready to present the dynamic network building (DNB) problem: Given a connected social network G and newcomer v, the problem asks for an NB strategy $\varphi$ such that any NB process consistent with $\varphi$ will have high $C_\mathsf {Cls}(v)$ (or small $\mathsf {rank}_\mathsf {Cls}(v)$) value, and low temporal and and establishment costs. Note that due to restriction to unary NB strategies, the temporal cost coincides with the number of edges added to the newcomer v. Figure 1 displays a simple example where the graph evolves with the dynamic $\mathsf {BA}$ mechanism (see below); the newcomer gains a high centrality in three rounds.

Fig. 1.

A newcomer adds one edge at each round and achieves high centrality after 3 rounds, while the network is evolving.

The DNB problem differs from building relations in a static networks, which has been discussed in [29,30,31]: (1) As the network evolves, the NB process may last indefinitely where v tries to improves and maintains its centrality; (2) Network evolution forces v to balance between current knowledge with future predicted outcome. For example, linking to a central node will improve v’s centrality quickly, but also incurs a high cost; on the other hand, linking to a low-centrality node may seem undesirable in the current network, but this link may improve the newcomer’s centrality in the future. In this way, the evolution mechanism significantly impacts the newcomer’s strategy.

3 Exploratory and Exploitative Strategies

Exploitative Strategy. This strategy utilizes existing social proximity of the node v and searches for the most promising node that lies within a pre-defined distance from v. Fix as parameter a centrality index $C_*:V\rightarrow \mathbb {R}$ for nodes. Let $d\ge 2$ be a proximity threshold. When creating an edge, the strategy traverses through nodes with distance $\le d$ from v, and picks a node found with maximum $C_*$ value. Procedure 1 defines one round of the exploitative strategy. For the choice of $C_*$, we use standard centrality metrics that reflect aspects of social capital. The variety of centrality metrics below allow us to examine different potential heuristics, which may not always correlate [7].

• 1. Degree: $C_{\mathsf {Deg}}(u)=\{w\mid uw\in E\}$.

• 2. Betweenness: $C_{\mathsf {Btw}}(u)=\sum _{s\ne u\ne t\in V} |P_{st}(u)|/|P_{st}|$ where $P_{st}$ is the set of shortest paths between s and t, $P_{st}(u)\subseteq P_{st}$ is those shortest paths that contain u.

• 3. Closeness: $C_{\mathsf {Cls}}(u)$.

We denote using $\mathsf {L}d$-$\mathsf {Deg}$, $\mathsf {L}d$-$\mathsf {Btw}$ and $\mathsf {L}d$-$\mathsf {Cls}$ the local heuristics with centrality $C_\mathsf {Deg}$, $C_\mathsf {Btw}$, $C_\mathsf {Cls}$, resp. When $d=2$, the newcomer always links to a “friend-of-friends”, a strategy studied in [21].

Exploratory Strategy. This strategy explores beyond the social proximity of v and links v with promising nodes in potentially distant parts of the network: The strategy takes a centrality index $C_*:V\rightarrow \mathbb {R}$ and a distance threshold $\gamma \in \mathbb {N}$ as parameters. Call all nodes within distance $\gamma$ from v covered; at each round, the strategy will pick an uncovered node that has maximum $C_*\text {-value}$. Procedure 2 describes a single round of this strategy. We use $\mathsf {G}\gamma$-$\mathsf {Deg}$, $\mathsf {G}\gamma$-$\mathsf {Btw}$ and $\mathsf {G}\gamma$-$\mathsf {Cls}$ to denote the exploratory heuristic that use $C_\mathsf {Deg}, C_\mathsf {Btw}$ and $C_\mathsf {Cls}$, respectively.

Since exploration creates edges to nodes that may be far away from v, this strategy by definition bridges different parts of the network more quickly than exploitation. Indeed, this can be verified using a simple example: Fix a large natural number n. Consider the path graph $L_{2n+1}$ with $2n+1$ nodes (with nodes $v_1,v_2,\ldots ,v_{2n+1}$ and edges $v_1v_2,v_2v_3,\ldots ,v_{2n}v_{2n+1}$). Say $v_{1}$ is the newcomer. Assuming the network is static, $\mathsf {G}2$-$\mathsf {Cls}$ builds O(1) edges from $v_1$ (e.g. to $v_{n+1},v_{n-2},v_{n+2}$) and gives $v_1$ the highest closeness centrality. On the contrary, the exploitative strategy will create $\Omega (n)$ new edges to have the highest closeness centrality. In the next section, we compare the two strategies above through experiments on standard network evolution mechanisms and real-world data.

4 Contrasting Exploitative and Exploratory Strategies

4.1 Network Evolution Mechanisms

We consider three standard network formation models. Originally, each of these model were used to generated static networks. Here we extend them so that they entail mechanisms for network generation and evolution.

(a) Dynamic $\mathsf {ER}$ Model. The Erdös-Renyi ($\mathsf {ER}$) random graph model adds edges between nodes as Bernoulli random variables with probability p. The degree distribution in the resulting graph thus follows a binomial distribution $B(n-1,p)$ [8]. We extend the model to a death-birth evolution model: Start from an $\mathsf {ER}$ random graph and introduce parameter $r\in [0,1]$. At each round, first remove a randomly chosen set of nodes of size rn (i.e., death); then, add rn new nodes and link them with nodes in the graph with probability p (i.e., birth). It is clear that the operation preserves the binomial degree distribution $B(n-1,p)$.

(b) Dynamic $\mathsf {BA}$ Model. The Barabási-Albert model generates scale-free networks through a preferential attachment mechanism [4]. To define an evolving network model, we follow Barabási’s dynamic extension. The key ideas include growth, link establishment and node deletion [3]. (a) Growth takes a rate $g\in [0,1]$ and adds gn new nodes; adds m edges from each new node to an existing node with probability $k_i/\sum _{v_j\in V} k_j$ where $k_j$ is the degree of $v_j$, $\forall v_j\in V$. (b) Link establishment takes a parameter $\lambda \in [0,1]$; selects $\lambda n$ pairs of nodes in the current graph and randomly creates edges between these pairs; the probability of creating edge $v_iv_j$ is proportional to $k_ik_j$. (c) Node deletion takes a rate $d\in [0,1]$; picks dn nodes, and remove each of them (say, $v_i$) with probability $\frac{1/k_i}{\sum _j 1/k_j}$.

(c) Dynamic $\mathsf {WS}$-Model. The Watts-Strogatz model starts from a regular lattice, and performs random edge rewirings (with probability $\beta$) to obtain small-world networks, which have high levels of clustering and low average path length [39]. We extend the process to an evolution mechanism: after initialization, the network evolves in each round by rewiring those previously-rewired edges to a random node. This dynamic network preserves the small-world property.

Table 1 summarizes the parameters used in our experiments. We choose these values either because they are standard choices used by others (e.g. $m=2$ for dynamic $\mathsf {BA}$ [4]), or they ensure a gradual and smooth change at each round (e.g. for dynamic $\mathsf {ER}$ and $\mathsf {WS}$ models).

Table 1. Parameters for evolving network models.

Experiment 1 (Costs). Through simulating DNB processes, we compare the temporal and establishment costs between the exploitative and exploratory strategies. DNB processes are generated by applying the heuristics in conjunction with the $\mathsf {ER},\mathsf {BA}$ and $\mathsf {WS}$ models. As a DNB process may have indefinite length, we need a termination condition to specify when the simulation stops. A natural method is to set a (high) threshold on centrality $C_\mathsf {Cls}(v)$, or set a (small) threshold on $\mathsf {rank}_\mathsf {Cls}(v)$, such that the process terminates once the threshold is met. There are problems with this approach: (1) It is difficult to determine a desired $C_\mathsf {Cls}(v)$ that facilitates fair comparisons across all evolving models. (2) In certain cases (e.g. $\mathsf {WS}$ model), closeness centrality of nodes are distributed within a small range; Hence, a node with low centrality may still have a small $\mathsf {rank}_\mathsf {Cls}$. These concerns motivate us to set a termination condition based on the ratio $g(v)=C_\mathsf {Cls}(v)/\mathsf {rank}_\mathsf {Cls}(v)$; we introduce a threshold $\zeta$ such that the process terminates at the first round when $g(v)\ge \zeta$ is satisfied.

We generate 10 networks of each size $n=100,200,500,1000$ using any network models above. We compare the exploitative with the exploratory strategies by running $\mathsf {L}2$-$*$, $\mathsf {L}3$-$*$ and $\mathsf {G}2$-$*$ heuristic on each graph. Note that $\mathsf {L}2$-$*$ only links v to her “friends-of-friends” which amounts to the most “local” exploitative strategy; $\mathsf {L}3$-$*$ reaches beyond this local proximity and results in a different performance (see below); $\mathsf {G}2$-$*$ is an exploratory strategy which tries its to link v to nodes outside of her local proximity. We do not include results for $\mathsf {G}3$-$*$ as they are very similar to $\mathsf {G}2$-$*$. For any generated graph G and heuristic, we do the following: (1) Build an edge between the newcomer v and a randomly chosen node in G. (Here we run the same experiment while linking v with initial nodes of different $\mathsf {Cls}$-rank (10%–90%). The resulting temporal and establishment costs are very similar. This shows that the rank of the initial node does not significantly affect the performance of the strategies.) (2) Apply the heuristic to the evolution mechanism (corresponding to the network formation model) to generate 100 DNB processes; the threshold $\zeta$ is 33. Here, the value $\zeta =33$ reflects the fact that the desired $C_\mathsf {Cls}(v)\approx 1/3$ and $\mathsf {rank}_\mathsf {Cls}(v) \approx 1\%$. Other outcomes with $g(v)=33$ that have either considerably lower centrality and $\mathsf {Cls}$-rank, or considerably higher centrality and $\mathsf {Cls}$-rank (e.g. $(C_\mathsf {Cls}(v), \mathsf {rank}_\mathsf {Cls}(v))$ is $(1/6,0.5\%)$ or $(1,3\%)$) have been empirically shown to be unlikely. (3) After the DNB process terminates, measure the resulting temporal and establishment costs. (4) Finally, record the average costs among all DNB processes of the same evolving network model, initial network size, and heuristic.

Fig. 2.

Average temporal and establishment costs of simulated DNB processes by different heuristics on networks of different sizes.

A few facts stand out from the results in Fig. 2: (i) Temporal costs are mostly below 10, suggesting that a small number of edges are built by the strategies, even when the size of the network becomes 1000. (ii) For $\mathsf {ER}$ and $\mathsf {WS}$, exploration results in a lower temporal cost compared to the exploitation. (iii) For the scale-free model $\mathsf {BA}$, the number of edges built decreases as n increases. This may be due to the expanding nature of the dynamic $\mathsf {BA}$ model and the skewed degree distribution. As a result, exploitation creates less or similar numbers of edges than exploration. (iv) In general, exploration results in a much higher establishment costs. This is easy to understand: the strategy links to distant nodes from v. The $\mathsf {L}3$ heuristics builds less edges than $\mathsf {L}2$ due to the ability to traverse to a wider part of the graph. (v) The effects of the centrality metrics $C_*$ vary with graph models: For $\mathsf {ER}$, closeness centrality is in general preferred, while for $\mathsf {BA}$, degree centrality is slightly more preferred. For $\mathsf {WS}$, $C_\mathsf {Btw}$ is better for exploration, while $C_\mathsf {Cls}$ is better for exploitation as the graph becomes large.

We then plot v’s $\mathsf {Cls}$-rank as new edges are created during the DNB process; See Fig. 3. $\mathsf {rank}_\mathsf {Cls}(v)$ reaches ${<}1\%$ after 10 rounds under all heuristics. $\mathsf {G}2$ improves $\mathsf {Cls}$-rank faster than $\mathsf {L}2$ heuristics. This is most evident for $\mathsf {L}2$-$\mathsf {Deg}$ and $\mathsf {L}2$-$\mathsf {Cls}$ in $\mathsf {WS}$-graphs: the high level of clustering may make it hard for exploitation to get out of a dense cluster, but clustering does not seem to pose a problem for $\mathsf {L}2$-$\mathsf {Btw}$.

Fig. 3.

Changes to $\mathsf {rank}_\mathsf {Cls}(v)$ (solid lines) and the establishment costs (dashed lines) during 10 rounds of the DNB process. The network starts with 1000 nodes and v initially connects to a node with the lowest centrality.

Experiment 2 (Embeddedness and clustering). Experiment 1 implies that, to some extend, exploitation and exploration perform on par with each other from a centrality perspective. In building relationship, trust, tie strength and role integrity are other important dimensions not captured by centrality alone [17]. These notions are closely affected by two concepts:

• 1. Embeddedness in a social network refers to the degree to which an individual is constrained by social relationships and is often viewed as a platform for trust [18]. The embeddedness of an edge between x, y is defined as the size of their shared neighborhoods $D(x)\cap D(y)$ [12]. We define $\mathsf {embed}(v)$ as a normalized sum of embeddedness:

  $$\mathsf {embed}(v) = \frac{\sum _{vu\in E}|\{w\in V\mid wu,wv\in E\}|}{(|V|-1)(|V|-2)}.$$

  Note that the highest $\mathsf {embed}(v)$ is 1 when v is a node in a complete graph.

• 2. Clustering coefficient of a node measures the probability of two randomly chosen friends of the node are also friends and relates to the self-identify of individuals [5]:

  $$\mathsf {cc}(v)= \frac{2\cdot |\{uw\in E\mid uv\in E, vw\in E\}|}{\deg (v)(\deg (v)-1)}.$$

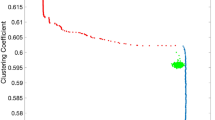
We measure $\mathsf {embed}(v)$ and $\mathsf {cc}(v)$ during DNB processes; See Fig. 4. Remarkably, $\mathsf {embed}(v)$ increases drastically with exploitation, while staying close to 0 with exploration. The clustering coefficient $\mathsf {cc}(v)$ also stays close to 0 with exploration, while with exploitation, it quickly rises to a very high level in the first few rounds, and drops down to below 0.1 after 10–15 rounds. This highlights the newcomer’s ability to cut across different clusters. Overall, this experiment demonstrates the crucial difference between the strategies: while both strategies improve v’s closeness centrality, exploitation enables a higher embeddedness and clustering coefficient which positively correlates with tie strength and trusts on its social relations.

Fig. 4.

Changes to v’s embeddedness and $\mathsf {cc}$ as edges are added to v. The network starts with 1000 nodes where v is connected to a node with the lowest centrality.

4.2 Real-World Evolving Networks

We next take real-world evolving network data as case studies.

Experiment 3 (Contact networks). We take two evolving physical contact networks: The first data set records face-to-face contacts among roughly 110 attendees of ACM Hypertext 2009 conference during a 2.5-day period [19]. The second records contacts among roughly 100 employees in a French workplace June 24 to July 3, 2013 [14]. In both data sets, contacts are updated every 20 seconds. We ask the question: If a newcomer attends the conference, or joins the workplace, how does she utilize face-to-face contacts to reach a central position of the network?

We simulate DNB processes on the accumulated network, i.e., networks constructed by accumulating edges in previous times, using the $\mathsf {G}2$ and $\mathsf {L}2$ heuristics. For the first data set, an edge is built every 15 min, and for the second data set, an edge is built very hour. Figure 5 plots the changes on the newcomer’s $\mathsf {Cls}$-rank. All heuristics have similar results in terms of improving the $\mathsf {Cls}$-rank as time progresses. As the networks are relatively small and edges are accumulated, the heuristics somehow fail to improve newcomer’s rank in the last three days of the second network beyond 20%. The exploitative strategy, however, gives much smaller establishment costs. On the other hand, exploitation leads to considerably higher embeddedness and clustering coefficient than exploration.

Fig. 5.

The $\mathsf {Cls}$-rank and establishment cost resulted from running the heuristics on (a) ACM Hypertext 2009 contact network; (b) French workplace contact network.

5 Balancing Exploitation with Exploration with UBC

As demonstrated above, exploration usually brings faster improvement to the newcomer v’s centrality, while exploitation by definition incurs less establishment cost. The trade-off between the two strategies is further complicated by the evolving nature of the network (e.g. exploitation exhibits lower temporal costs than exploration in general on scale-free networks). As in many scenarios of reinforcement learning, to obtain an optimal solution one needs to strike a balance between exploitation and exploration. In this section, we adopt upper confidence bound (UBC), a well-known reinforcement learning method for resolving the exploitation-exploration dilemma to build relations by integrating the two strategies.

We adapt the $\mathsf {UCB1}$ algorithm proposed in [2] which has a guaranteed logarithm regret uniformly over the number of rounds. Here, exploitative and exploratory strategies are regarded as two actions, 0 and 1, respectively and dynamic network building is viewed as a 2-armed bandit problem. In each round of the DNB process, v evaluates plausible $\mathsf {Cls}$-rank achieved through performing each action $i\in \{0,1\}$ using past experience, and then selects the strategy that seems to be the best. To estimate the plausible mean $\mathsf {Cls}$-rank of a strategy, we introduce the following notations: Let $(G_0,G_1,\ldots ,G_{t}, s_0,s_1,\ldots , s_{t-1})$ be a t-round DNB process. For $m<\ell$, we use $\mathsf {rank}(m)$ to denote the $\mathsf {Cls}$-rank of v in the graph $G_{m+1}$. The estimate on the expected $\mathsf {Cls}$-rank resulted by choosing action $i\in \{0,1\}$ at round $\ell +1$ is defined by

$$\begin{aligned} \Upsilon (i)=\underbrace{\frac{\sum _{j=1}^{n_i}\mathsf {rank}(r_{ij}-1)-\mathsf {rank}(r_{ij})}{n_i}}_{average\,function}\quad +\underbrace{\sqrt{\frac{2\ln t}{n_i}}}_{padding\,function} \end{aligned}$$

(1)

where t is the number of rounds passed, $n_i$ is the times that strategy i is selected, $r_{ij}$ is the jth round that action i is selected. We use the difference of v’s $\mathsf {Cls}$-rank between two contiguous rounds to define the reward that v receives after each round. Then $Average\,function$ denotes average reward that v has got so far by choosing action i. $Padding\,function$ denotes an estimated uncertainty on i; the more times that i is selected, the less uncertainty it has.

At the beginning of a DNB process, we apply exploration and exploitation in the first and the second round, resp. Then, in subsequent rounds, we select the strategy that achieves the highest $\Upsilon (i)$ value (as (1)). See Procedure 3, which we call $\mathsf {DNB\_UCB}$. Note that the algorithm again requires fixing a centrality measure $C_*$ and a distance threshold $\gamma \in \mathbb {N}$ as parameters as for $\mathsf {L}$ and $\mathsf {G}$ heuristics.

We implement the algorithm and evaluate its performance over dynamic network models. At the beginning, all networks have 1000 nodes, and the parameters used by the evolution mechanisms are the same as in Sect. 4. Figure 6 plots the change in $\mathsf {Cls}$-rank as well as the resulting establishment costs after running both the pure (exploratory or exploitative) strategies, and the mixed strategy during a fixed number of rounds. In all three types of random networks, the speed that $\mathsf {DNB\_UCB}$ improves $\mathsf {Cls}$-rank sits between the exploitative and exploratory strategies. The improvement is most evident in $\mathsf {WS}$ where $\mathsf {DNB\_UCB}$ performs similarly well to exploration. On the other hand, $\mathsf {DNB\_UCB}$ also results in a significant reduction of the establishment costs than exploratory strategy.

Fig. 6.

The $\mathsf {Cls}$-rank and establishment cost resulted from running the pure and mixed strategies on the dynamic $\mathsf {BA}$, $\mathsf {WS}$ and $\mathsf {ER}$ networks. The speed that $\mathsf {DNB\_UCB}$ improves $\mathsf {Cls}$-rank sits between the exploitative and exploratory strategies. On the other hand, $\mathsf {DNB\_UCB}$ significantly reduces the establishment costs than exploration alone.

6 Conclusion and Future Work

The paper proposes dynamic network building problem and concentrates on exploratory-exploitative strategies and their combinations. The focus is on introducing the algorithmic framework: Many methods exist for the multi-armed bandit problem; A natural future work is to compare these methods with $\mathsf {DNB\_UCB}$. Furthermore, despite closeness centrality’s importance in capturing social support and access to resources, other measures of social capital, e.g. betweenness, eigenvector centrality, can be used as a goal for the newcomer v as well.

Other future works that we will consider include: (1) designing strategies that build relations while respecting bounded capacity of individuals, i.e., v has only a bounded number of links so severing ties may be needed. (2) investigating network building on attributed networks where pairs of nodes have different likelihood of being connected due to features such as personality, common interests, etc. (3) Studying information diffusion and influence maximization through network building. (4) A crucial future work is on applications of the presented framework. In particular, the work develops a foundation of new functionality on the Web that engineers optimal links among OSN users to enhance communication and capability. Here, a possible scenario is to recommend information agencies to a user on a career-based OSN to boost their access to resources and enhance career-prospect. Another possible scenario is to provide social support to those that are in need through social network building [40].