Keywords

1 Introduction

We will consider two classes of (nonlocal) evolution equations and study the associated traveling wave problems in parallel: On the one hand, we consider scalar conservation laws with (nonlocal) diffusive-dispersive regularization

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {} f(u) = \varepsilon \mathscr {L}_1[u] + \delta \partial _{x} {} \mathscr {L}_2[u] \ , \quad t>0 \ ,\quad x\in \mathbb {R}\ , \end{aligned}$$
(1)

for some nonlinear function \(f:\mathbb {R}\rightarrow \mathbb {R}\), Lévy operators \(\mathscr {L}_1\) and \(\mathscr {L}_2\), as well as constants \(\varepsilon ,\delta \in \mathbb {R}\). The Fourier multiplier operators \(\mathscr {L}_1\) and \(\partial _{x} {} \mathscr {L}_2\) model diffusion and dispersion, respectively. On the other hand, we consider scalar reaction-diffusion equations

$$\begin{aligned} \partial _{t} {u} = \sigma \mathscr {L}_3[u] + r(u) \ , \quad t>0 \ ,\quad x\in \mathbb {R}\ , \end{aligned}$$
(2)

for some positive constant \(\sigma \), as well as a nonlinear function \(r:\mathbb {R}\rightarrow \mathbb {R}\) and a Lévy operator \(\mathscr {L}_3\) modeling reaction and diffusion, respectively.

Definition 1

A traveling wave solution (TWS) of an evolution equation–such as (1) and (2)–is a solution \(u(x,t)=\bar{u}(\xi )\) whose profile \(\bar{u}\) depends on \(\xi :=x-ct\) for some wave speed \(c\). Moreover, the profile \(\bar{u}\in C^2(\mathbb {R})\) is assumed to approach distinct endstates \(u_\pm \) such that

$$\begin{aligned} \lim _{\xi \rightarrow \pm \infty } \bar{u}(\xi ) =u_\pm \ , \qquad \lim _{\xi \rightarrow \pm \infty } \bar{u}^{(n)}(\xi ) =0 \quad \text {with n=1,2.} \end{aligned}$$
(3)

Such a TWS is also known as a front in the literature. A TWS \((\bar{u},c)\) is called monotone, if its profile \(\bar{u}\) is a monotone function.

Definition 2

The traveling wave problem (TWP) associated to an evolution equation is to study for some distinct endstates \(u_\pm \) the existence of a TWS \((\bar{u},c)\) in the sense of Definition 1.

We want to identify classes of evolutions equations of type (1) and (2), which lead to the same TWP. This connection is especially useful, if the TWP is not studied directly, but the existence of a TWS is proven using one of the evolution equations instead. A classical example of (1) is a scalar conservation law with local diffusive-dispersive regularization

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {} f(u) = \varepsilon \partial ^{2}_{x} {u} +\delta \partial ^{3}_{x} {u} \ , \quad t>0 \ ,\quad x\in \mathbb {R}\ , \end{aligned}$$
(4)

for some nonlinear function \(f:\mathbb {R}\rightarrow \mathbb {R}\) and some constants \(\varepsilon >0\) and \(\delta \in \mathbb {R}\). Equation (4) with Burgers flux \(f(u)=u^2\) is known as Korteweg-de Vries-Burgers (KdVB) equation; hence we refer to Eq. (4) with general f as generalized KdVB equation and Eq. (1) as nonlocal generalized KdVB equation. A TWS \((\bar{u},c)\) satisfies the traveling wave equation (TWE)

$$\begin{aligned} -c \bar{u}' + f'(\bar{u})\ \bar{u}' = \varepsilon \bar{u}'' + \delta \bar{u}''' \ , \quad \xi \in \mathbb {R}\ , \end{aligned}$$
(5)

or integrating on \((-\infty ,\xi ]\) and using (3),

$$\begin{aligned} h(\bar{u}) := f(\bar{u}) -c \bar{u}-(f(u_-) -c \ u_-) = \varepsilon \bar{u}' + \delta \bar{u}'' \ , \quad \xi \in \mathbb {R}\ . \end{aligned}$$
(6)

However, the TW ansatz \(v(x,t)=\bar{u}(x -\varepsilon t)\) for the scalar reaction-diffusion equation

$$\begin{aligned} \partial _{t} {v} = -h(v) +\delta \partial ^{2}_{x} {v} \ , \quad t>0 \ , \quad x\in \mathbb {R}\ , \end{aligned}$$
(7)

leads to the same TWE (6) except for a different interpretation of the parameters. The traveling wave speeds in the TWP of (4) and (7) are \(c\) and \(\varepsilon \), respectively. For fixed parameters \(c\), \(\varepsilon \), and \(\delta \), the existence of a traveling wave profile \(\bar{u}\) satisfying (3) and (6) reduces to the existence of a heteroclinic orbit for this ODE. This is an example, where the existence of TWS is studied directly via the TWE.

An example, where the TWE is not studied directly, is the TWP for a nonlocal KdVB equation (1) with \(\mathscr {L}_1[u] =\partial ^{2}_{x} {u}\) and \(\mathscr {L}_2[u] = \phi _\varepsilon *u - u\) for some even non-negative function \(\phi \in L^1(\mathbb {R})\) with compact support and unit mass, where \(\phi _\varepsilon (\cdot ) := \phi (\cdot /\varepsilon ) / \varepsilon \) with \(\varepsilon >0\). It has been derived as a model for phase transitions with long range interactions close to the surface, which supports planar TWS associated to undercompressive shocks of (B.1), see [52]. In particular, the TWP for a cubic flux function \(f(u)=u^3\) is related to the TWP for a reaction-diffusion equation (2) with \(\mathscr {L}_3[u] = \mathscr {L}_2[u]\). The existence of TWS for this reaction-diffusion equation has been proven via a homotopy of (2) to a classical reaction-diffusion model (7), see [14].

Outline. In Sect. 2 we collect background material on Lévy operators \(\mathscr {L}\), which will model diffusion in our nonlocal evolution equations. Special emphasize is given to convolution operators and Riesz–Feller operators. In Sect. 3 we review the classical results on the TWP for reaction-diffusion equations (7) and generalized Korteweg-de Vries-Burgers equation (4). We study their relationship in detail, especially the classification of function h(u), which will be used again in Sect. 4. In Sect. 4, first we review the results on TWP for nonlocal reaction-diffusion equations (2) with operators \(\mathscr {L}_3\) of convolution type and Riesz–Feller type, respectively. Finally, we study the example of nonlocal generalized Korteweg-de Vries-Burgers equation (1) with \(\mathscr {L}_1[u] = \mathscr {D}^{1/3}_{+} u\) and \(\mathscr {L}_2[u] =\partial ^{2}_{x} {u}\) modeling a shallow water flow [44], and Fowler’s equation

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {} u^2= \partial ^{2}_{x} {} u -\partial _{x} {} \mathscr {D}^{1/3}_{+} u \ , \quad t>0 \ , \quad x\in \mathbb {R}\ , \end{aligned}$$
(8)

modeling dune formation [36], where \(\mathscr {D}^{\alpha }_{+}\) is a Caputo derivative. In the Appendix, we collect background material on Caputo derivatives \(\mathscr {D}^\alpha _{+}\) and the shock wave theory for scalar conservation laws, which will explain the importance of the TWP for KdVB equations.

Scalar conservation laws with fractional Laplacian are another example of equation (1) with \(\mathscr {L}_1[u] = -(-\partial ^{2}_{x} {})^{\alpha /2}\ u\), \(0<\alpha <2\), and \(\mathscr {L}_2[u] \equiv 0\). However, its traveling wave problem can not be related to a nonlocal reaction-diffusion problem like our examples. Therefore, instead of discussing its traveling wave problem, we refer the interested reader to the literature [7, 8, 10, 15, 23, 26, 30,31,32,33, 43] and references therein.

Notations. We use the conventions in probability theory, and define the Fourier transform \(\mathscr {F}\) and its inverse \(\mathscr {F}^{-1}\) for \(g\in L^1(\mathbb {R})\) and \(x,k\in \mathbb {R}\) as

$$ \mathscr {F}[g](k) := \int _{\mathbb {R}} \; { {\text {e}}^{+{\text {i}}kx} g(x)} \; \,{\text {d}}\!x\, \ ; \qquad \mathscr {F}^{-1}[g](x) := \tfrac{1}{2\pi } \int _{\mathbb {R}} \; { {\text {e}}^{-{\text {i}}kx} g(k)} \; \,{\text {d}}\!k\, \ . $$

In the following, \(\mathscr {F}\) and \(\mathscr {F}^{-1}\) will denote also their respective extensions to \(L^2(\mathbb {R})\).

2 Lévy Operators

A Lévy process is a stochastic process with independent and stationary increments which is continuous in probability [12, 40, 53]. Therefore a Lévy process is characterized by its transition probabilities p(t, x), which evolve according to an evolution equation

$$\begin{aligned} \partial _{t} {p} = \mathscr {L}p \end{aligned}$$
(9)

for some operator \(\mathscr {L}\), also called a Lévy operator. First, we define Lévy operators on the function spaces \(C_0(\mathbb {R}) :=\{ f\in C(\mathbb {R}) \,|\, \lim _{|x|\rightarrow \infty } f(x)=0 \}\) and \(C^2_0(\mathbb {R}) :=\{ f,f',f'' \in C_0(\mathbb {R})\}\).

Definition 3

The family of Lévy operators in one spatial dimension consists of operators \(\mathscr {L}\) defined for \(f\in C^2_0(\mathbb {R})\) as

$$\begin{aligned} \mathscr {L}f(x) = \tfrac{1}{2} A f''(x) + \gamma \ f'(x) + \int _{\mathbb {R}} \; { \big ( f(x+y) - f(x) - y\ f'(x) 1_{(-1,1)}(y) \big ) } \; {\nu ( \,{\text {d}}\!y)}\, \end{aligned}$$
(10)

for some constants \(A\ge 0\) and \(\gamma \in \mathbb {R}\), and a measure \(\nu \) on \(\mathbb {R}\) satisfying

$$\begin{aligned} \nu (\{0\}) = 0 \quad \text {and} \quad \int _{\mathbb {R}} \; { \min (1,|y|^2)} \; {\nu (\,{\text {d}}\!y)}\, < \infty \,. \end{aligned}$$

Remark 1

The function \(f(x+y) - f(x) - y\ f'(x) 1_{(-1,1)}(y)\) is integrable with respect to \(\nu \), because it is bounded outside of any neighborhood of 0 and

$$ f(x+y) - f(x) - y\ f'(x) 1_{(-1,1)}(y) = O(|y|^2) \quad \text {as} \quad |y|\rightarrow 0 $$

for fixed x. The indicator function \(c(y) =1_{(-1,1)}(y)\) is only one possible choice to obtain an integrable integrand. More generally, let c(y) be a bounded measurable function from \(\mathbb {R}\) to \(\mathbb {R}\) satisfying \(c(y) = 1+o(|y|)\) as \(|y|\rightarrow 0\), and \(c(y) = O(1/|y|)\) as \(|y|\rightarrow \infty \). Then (10) is rewritten as

$$\begin{aligned} \mathscr {L}f(x) = \tfrac{1}{2} A f''(x) + \gamma _c\ f'(x) + \int _{\mathbb {R}} \; { \big ( f(x+y) - f(x) - y\ f'(x) c(y) \big ) } \; {\nu ( \,{\text {d}}\!y)}\, \ , \end{aligned}$$
(11)

with \(\gamma _c = \gamma + \int _{\mathbb {R}} \; { y\ (c(y)-1_{(-1,1)}(y)) } \; {\nu (\,{\text {d}}\!y)}\,\).

Alternative choices for c:

  1. (c 0)

    If a Lévy measure \(\nu \) satisfies \(\int _{|y|< 1} \; { |y|} \; {\nu (\,{\text {d}}\!y)}\, < \infty \) then \(c\equiv 0\) is admissible.

  2. (c 1)

    If a Lévy measure \(\nu \) satisfies \(\int _{|y|> 1} \; { |y|} \; {\nu (\,{\text {d}}\!y)}\, < \infty \) then \(c\equiv 1\) is admissible.

We note that A and \(\nu \) are invariant no matter what function c we choose.

Examples

  1. (a)

    The Lévy operators

    $$\begin{aligned} \mathscr {L}f = \int _{\mathbb {R}} \; { \big ( f(x+y) - f(x) \big ) } \; {\nu ( \,{\text {d}}\!y)}\, \end{aligned}$$
    (12)

    are infinitesimal generators associated to a compound Poisson process with finite Lévy measure \(\nu \) satisfying (c 0). The special case of \(\nu (\,{\text {d}}\!y) = \phi (-y) \,{\text {d}}\!y\) for some function \(\phi \in L^1(\mathbb {R})\) yields

    $$\begin{aligned} \mathscr {L}f (x) = \int _{\mathbb {R}} \; { \big ( f(x+y) - f(x) \big ) } \; {\phi (-y) \,{\text {d}}\!y}\, = \left( \phi *f - \int _{\mathbb {R}} \; {\phi } \; \,{\text {d}}\!y\,\ f\right) (x) \ . \end{aligned}$$
    (13)
  2. (b)

    Riesz–Feller operators. The Riesz–Feller operators of order \(a\) and asymmetry \(\theta \) are defined as Fourier multiplier operators

    $$\begin{aligned} \mathscr {F}[D^{a}_{\theta }f](k) = \psi ^{a}_{\theta }(k)\ \mathscr {F}[f] (k) \ ,\qquad k\in \mathbb {R}\ , \end{aligned}$$
    (14)

    with symbol \(\psi ^{a}_{\theta }(k) = -|k|^{a} \exp \left[ {\text {i}}\ {{\mathrm{sgn}}}(k)\ \theta \pi /2 \right] \) such that \((a,\theta ) \in \mathfrak {D}_{a,\theta }\) and

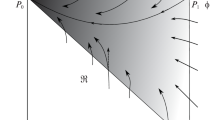
    $$\begin{aligned} \mathfrak {D}_{a,\theta }:= \{\, { (a,\theta )\in \mathbb {R}^2 } \,|\, { 0<a\le 2 \ , \quad |\theta | \le \min \{a, 2-a\} } \,\}\ , \end{aligned}$$

    see also (Fig. 1)

    Special cases of Riesz–Feller operators are

    • Fractional Laplacians \(-(-\varDelta )^{a/2}\) on \(\mathbb {R}\) with Fourier symbol \(-|k|^{a}\) for \(0<a\le ~2\). In particular, fractional Laplacians are the only symmetric Riesz–Feller operators with \(-(-\varDelta )^{a/2} = D^{a}_{0}\) and \(\theta \equiv 0\).

    • Caputo derivatives \(-\mathscr {D}^\alpha _{+}\) with \(0<\alpha <1\) are Riesz–Feller operators with \(a=\alpha \) and \(\theta =-\alpha \), such that \(-\mathscr {D}^\alpha _{+} =D^{\alpha }_{-\alpha }\), see also Sect. A.

    • Derivatives of Caputo derivatives \(\partial _{x} {} \mathscr {D}^\alpha _{+}\) with \(0<\alpha <1\) are Riesz–Feller operators with \(a=1+\alpha \) and \(\theta =1-\alpha \), such that \(\partial _{x} {} \mathscr {D}^\alpha _{+} =D^{1+\alpha }_{1-\alpha }\).

Fig. 1
figure 1

The family of Fourier multipliers \(\psi ^{a}_{\theta }(k) = -|k|^{a} \exp \big [{\text {i}}{{\mathrm{sgn}}}(k) \theta \pi /2)\big ]\) has two parameters \(a\) and \(\theta \). Some Fourier multiplier operators \(\mathscr {F}[Tf](k) = \psi ^{a}_{\theta }(k)\ \mathscr {F}[f](k)\) are inserted in the parameter space \((a,\theta )\): partial derivatives and Caputo derivatives \(\mathscr {D}^\alpha _{+}\) with \(0<\alpha <1\). The Riesz–Feller operators \(D^{a}_{\theta }\) are those operators with parameters \((a,\theta )\in \mathfrak {D}_{a,\theta }\). The set \(\mathfrak {D}_{a,\theta }\) is also called Feller-Takayasu diamond and depicted as a shaded region, see also [47]

Full size image

Next we consider the Cauchy problem

$$\begin{aligned} \partial _{t} {u}(x,t) = D^{a}_{\theta }{} [u(\cdot ,t)](x) \ , \quad u(x,0) =u_0(x)\ , \end{aligned}$$
(15)

for \((x,t)\in \mathbb {R}\times (0,\infty )\) and initial datum \(u_0\).

Proposition 1

For \((a,\theta )\in \mathfrak {D}_{a,\theta }\) with \(\theta \ne \pm 1\) and \(1\le p<\infty \), the Riesz–Feller operator \(D^{a}_{\theta }\) generates a strongly continuous \(L^p\)-semigroup

$$ S_t: L^p(\mathbb {R}) \rightarrow L^p(\mathbb {R})\ , \quad u_0 \mapsto S_t u_0 = G^{a}_{\theta }(\cdot ,t)*u_0 \ , $$

with heat kernel \(G^{a}_{\theta }(x,t) =\mathscr {F}^{-1}[\exp (t\ \psi ^{a}_{\theta }(\cdot ))](x)\). In particular, \(G^{a}_{\theta }(x,t)\) is the probability measure of a Lévy strictly \(a\)-stable distribution.

The proof of this proposition for a subclass \(1<\alpha \le 2\) in [6, Proposition 2.2] can be extended to cover all cases \((a,\theta )\in \mathfrak {D}_{a,\theta }\) with \(\theta \ne \pm 1\). For \((a,\theta )\in \{(1,1),(1,-1)\}\), the probability measure \(G^{a}_{\theta }\) is a delta distribution, e.g. \(G^1_1(x,t) = \delta _{x+t}\) and \(G^1_{-1}(x,t) = \delta _{x-t}\), and is called trivial [53, Definition 13.6]. However, we are interested in non-trivial probability measures \(G^{a}_{\theta }\) for

$$\begin{aligned} (a,\theta )\in \mathfrak {D}_{a,\theta }^{\diamond }:=\{\, {(a,\theta )\in \mathfrak {D}_{a,\theta }} \,|\, { |\theta |<1} \,\} \ , \end{aligned}$$

such that \(\mathfrak {D}_{a,\theta }= \mathfrak {D}_{a,\theta }^{\diamond }\cup \{(1,1), \ (1,-1)\}\). Note, nonlocal Riesz–Feller \(D^{a}_{\theta }\) operators are those with parameters

$$\begin{aligned} (a,\theta )\in \mathfrak {D}_{a,\theta }^\bullet :=\{\, {(a,\theta )\in \mathfrak {D}_{a,\theta }} \,|\, {0<a< 2 \ , \quad |\theta |<1} \,\}, \end{aligned}$$

such that \(\mathfrak {D}_{a,\theta }^{\diamond }=\mathfrak {D}_{a,\theta }^\bullet \cup \{(2,0)\}\).

Proposition 2

([6, Lemma 2.1]) For \((a,\theta )\in \mathfrak {D}_{a,\theta }^{\diamond }\) the probability measure \(G^{a}_{\theta }\) is absolutely continuous with respect to the Lebesgue measure and possesses a probability density which will be denoted again by \(G^{a}_{\theta }\). For all \((x,t)\in \mathbb {R}\times (0,\infty )\) the following properties hold;

  1. (a)

    \(G^{a}_{\theta }(x,t)\ge 0\). If \(\theta \ne \pm a\) then \(G^{a}_{\theta }(x,t)> 0\);

  2. (b)

    \(\Vert G^{a}_{\theta }(\cdot ,t)\Vert _{L^1(\mathbb {R})}=1\);

  3. (c)

    \(G^{a}_{\theta }(x,t)=t^{-1/a} G^{a}_{\theta }(x t^{-1/a},1)\);

  4. (d)

    \(G^{a}_{\theta }(\cdot ,s)*G^{a}_{\theta }(\cdot ,t) = G^{a}_{\theta }(\cdot ,s+t)\) for all \(s,t\in (0,\infty )\);

  5. (e)

    \(G^{a}_{\theta }\in C^\infty _0(\mathbb {R}\times (0,\infty ))\).

The Lévy measure \(\nu \) of a Riesz–Feller operator \(D^{a}_{\theta }\) with \((a,\theta )\in \mathfrak {D}_{a,\theta }^\bullet \) is absolutely continuous with respect to Lebesgue measure and satisfies

$$\begin{aligned} \nu (\,{\text {d}}\!y) = {\left\{ \begin{array}{ll} c_-(\theta ) y^{-1-a}\ \,{\text {d}}\!y &{} \text {on } (0,\infty )\ , \\ c_+(\theta ) |y|^{-1-a}\ \,{\text {d}}\!y &{} \text {on } (-\infty ,0)\ , \end{array}\right. } \end{aligned}$$
(16)

with \(c_\pm (\theta )= \varGamma (1+a) \sin ( (a\pm \theta ) \pi /2 ) /\pi \), see [47, 54].

To study a TWP for evolution equations involving Riesz–Feller operators, it is necessary to extend the Riesz–Feller operators to \(C^2_b(\mathbb {R})\). Their singular integral representations (10) may be used to accomplish this task.

Theorem 1

([6]) If \((a,\theta )\in \mathfrak {D}_{a,\theta }^\bullet \) with \(a\ne 1\), then for all \(f\in \mathscr {S}(\mathbb {R})\) and \(x\in \mathbb {R}\)

$$\begin{aligned} D^{a}_{\theta }f(x) =&\frac{c_+(\theta ) - c_-(\theta )}{1-a} f'(x) \nonumber \\&+ c_+(\theta ) \int _{0}^{\infty } \; { \frac{f(x+y)-f(x)-f'(x)\,y 1_{(-1,1)}(y)}{y^{1+a}} } \; \,{\text {d}}\!y\, \\&+ c_-(\theta ) \int _{0}^{\infty } \; { \frac{f(x-y)-f(x)+f'(x)\,y 1_{(-1,1)}(y)}{y^{1+a}} } \; \,{\text {d}}\!y\, \nonumber \end{aligned}$$
(17)

with \(c_\pm (\theta )= \varGamma (1+a) \sin ( (a\pm \theta ) \pi /2 ) /\pi \). Alternative representations are

  • If \(0<a<1\), then

    $$ D^{a}_{\theta }f(x) = c_+(\theta ) \int _{0}^{\infty } \; { \frac{f(x+y)-f(x)}{y^{1+a}} } \; \,{\text {d}}\!y\, + c_-(\theta ) \int _{0}^{\infty } \; { \frac{f(x-y)-f(x)}{y^{1+a}} } \; \,{\text {d}}\!y\, \,. $$

  • If \(1<a<2\), then

    $$\begin{aligned} D^{a}_{\theta }f(x) =\,&c_+(\theta ) \int _{0}^{\infty } \; { \frac{f(x+y)-f(x)-f'(x)\,y}{y^{1+a}} } \; \,{\text {d}}\!y\, \nonumber \\&+\,c_-(\theta ) \int _{0}^{\infty } \; { \frac{f(x-y)-f(x)+f'(x)\,y}{y^{1+a}} } \; \,{\text {d}}\!y\, \,. \end{aligned}$$
    (18)

These representations allow to extend Riesz–Feller operators \(D^{a}_{\theta }\) to \(C^2_b(\mathbb {R})\) such that \(D^{a}_{\theta }C^2_b(\mathbb {R})\subset C_b(\mathbb {R})\). For example, one can show

Proposition 3

([6, Proposition 2.4]) For \((a,\theta )\in \mathfrak {D}_{a,\theta }\) with \(1<a<2\), the integral representation (18) of \(D^{a}_{\theta }\) is well-defined for functions \(f\in C^2_b(\mathbb {R})\) with

$$\begin{aligned} \sup _{x\in \mathbb {R}} |D^{a}_{\theta }f(x)| \le \mathscr {K}\Vert {f''}\Vert _{C_b(\mathbb {R})} \frac{M^{2-a}}{2-a} + 4 \mathscr {K}\Vert f'\Vert _{C_b(\mathbb {R})} \frac{M^{1-a}}{a-1} < \infty \end{aligned}$$
(19)

for some positive constants M and \(\mathscr {K}=\frac{\varGamma (1+a)}{\pi } | \sin ( (a+\theta ) \frac{\pi }{2} ) + \sin ( (a-\theta ) \frac{\pi }{2} ) |\).

Estimate (19) is a key estimate, which is used to adapt Chen’s approach [24] to the TWP for nonlocal reaction-diffusion equations with Riesz–Feller operators [6].

3 TWP for Classical Evolution Equations

In this section we review the importance of the TWP for reaction-diffusion equations and scalar conservation laws with higher-order regularizations, respectively.

3.1 Reaction-Diffusion Equations

A scalar reaction-diffusion equation is a partial differential equation

$$\begin{aligned} \partial _{t} {u} = \sigma \partial ^{2}_{x} {u} + r(u) \ , \quad t>0 \ ,\quad x\in \mathbb {R}\ , \end{aligned}$$
(20)

for some positive constant \(\sigma >0\), as well as a nonlinear function \(r:\mathbb {R}\rightarrow \mathbb {R}\) and second-order derivative \(\partial ^{2}_{x} {u}\) modeling reaction and diffusion, respectively. The TWP for given endstates \(u_\pm \) is to study the existence of a TWS \((\bar{u},c)\) for (20) in the sense of Definition 1. If the profile \(\bar{u}\in C^2(\mathbb {R})\) is bounded, then it satisfies \(\lim _{\xi \rightarrow \pm \infty } \bar{u}^{(n)}(\xi ) =0\) for \(n=1,2\). A TWS \((\bar{u},c)\) satisfies the TWE

$$\begin{aligned} -c \bar{u}' = r(\bar{u}) + \sigma \bar{u}'' \ , \quad \xi \in \mathbb {R}\ . \end{aligned}$$
(21)

Phase plane analysis. A traveling wave profile \(\bar{u}\) is a heteroclinic orbit of the TWE (21) connecting the endstates \(u_\pm \). To identify necessary conditions on the existence of TWS, TWE (21) is written as a system of first-order ODEs for u, \(v:=u'\):

$$\begin{aligned} \frac{\,{\text {d}}\!}{\,{\text {d}}\!\xi } \left( {\begin{array}{c}u\\ v\end{array}}\right) = \left( {\begin{array}{c}v\\ (-r(u) -cv)/\sigma \end{array}}\right) =: F(u,v) \ , \quad \xi \in \mathbb {R}\ . \end{aligned}$$
(22)

First, an endstate \((u_s,v_s)\) of a heteroclinic orbit has to be a stationary state of F, i.e. \(F(u_s,v_s)=0\), which implies \(v_s\equiv 0\) and \(r(u_s) =0\). Second, \((u_-,0)\) has to be an unstable stationary state of (22) and \((u_+,0)\) either a saddle or a stable node of (22). As long as a stationary state \((u_s,v_s)\) is hyperbolic, i.e. the linearization of F at \((u_s,v_s)\) has only eigenvalues \(\lambda \) with non-zero real part, the stability of \((u_s,v_s)\) is determined by these eigenvalues. The linearization of F at \((u_s,v_s)\) is

$$\begin{aligned} {\text {D}}\!F(u_s,v_s) = \begin{pmatrix} 0 &{} 1 \\ -r'(u_s)/\sigma &{} -c/\sigma \end{pmatrix} \ . \end{aligned}$$
(23)

Eigenvalues \(\lambda _\pm \) of the Jacobian \({\text {D}}\!F(u_s,v_s)\) satisfy the characteristic equation \(\lambda ^2 + \lambda c/\sigma +r'(u_s)/\sigma =0\). Moreover, \(\lambda _- + \lambda _+ = -c/\sigma \) and \(\lambda _- \lambda _+ = r'(u_s)/\sigma \). The eigenvalues \(\lambda _\pm \) of the Jacobian \({\text {D}}\!F(u_s,v_s)\) are

$$\begin{aligned} \lambda _\pm = -\frac{c}{2\sigma } \pm \sqrt{ \frac{c^2}{4\sigma ^2} - \frac{r'(u_s)}{\sigma }} = \frac{-c\pm \sqrt{ c^2 - 4\sigma r'(u_s)}}{2\sigma } \ . \end{aligned}$$
(24)

Thus \(r'(u_s)<0\) ensures that \((u_s,0)\) is a saddle point, i.e. with one positive and one negative eigenvalue.

Balance of potential. The potential R (of the reaction term r) is defined as \(R(u) :=\int _{0}^{u} \; { r(\upsilon )} \; \,{\text {d}}\!\upsilon \,\). The potentials of the endstates \(u_\pm \) are called balanced if \(R(u_+)=R(u_-)\) and unbalanced otherwise. A formal computation reveals a connection between the sign of \(c\) and the balance of the potential R(u): Multiplying TWE (21) with \(\bar{u}'\), integrating on \(\mathbb {R}\) and using (3), yields

$$\begin{aligned} -c\Vert \bar{u}'\Vert _{L^2}^2 = \int _{u_-}^{u_+} \; { r(\upsilon )} \; \,{\text {d}}\!\upsilon \, = R(u_+) -R(u_-) \ , \end{aligned}$$
(25)

since \(\int _{\mathbb {R}} \; { \bar{u}'' \bar{u}'} \; \,{\text {d}}\!\xi \, = 0\) due to (3). Thus \(-{{\mathrm{sgn}}}c= {{\mathrm{sgn}}}(R(u_+) -R(u_-))\). In case of a balanced potential the wave speed \(c\) is zero, hence the TWS is stationary.

Definition 4

Assume \(u_->u_+\). A function \(r\in C^1(\mathbb {R})\) with \(r(u_\pm )=0\) is

  • monostable if \(r'(u_-)<0\), \(r'(u_+)>0\) and \(r(u)>0\) for \(u\in (u_+,u_-)\).

  • bistable if \(r'(u_\pm )<0\) and

    $$ \exists u_*\in (u_+,u_-) \ : \ r(u) {\left\{ \begin{array}{ll} <0 &{} \text {for } u\in (u_+,u_*) \ , \\ >0 &{} \text {for } u\in (u_*,u_-) \ . \end{array}\right. } $$

  • unstable if \(r'(u_\pm )>0\).

We chose a very narrow definition compared to [56]. Moreover, in most applications of reaction-diffusion equations a quantity u models a density of a substance/population. In these situations only nonnegative states \(u_\pm \) and functions u are of interest.

If a TWS \((\bar{u},c)\) exists, then a closer inspection of the eigenvalues (24) at \((u_+,0)\) indicates the geometry of the profile \(\bar{u}\) for large \(\xi \):

$$ c^2 - 4\sigma r'(u_+) {\left\{ \begin{array}{ll} \ge 0 &{} \text {TWS with monotone decreasing profile }~\bar{u}\,\text { for large }\,\xi ; \\ < 0 &{} \text {TWS with oscillating profile }~\bar{u}\,\text { for large }\,\xi . \end{array}\right. } $$

Proposition 4

([56, Sect. 2.2]) Assume \(\sigma >0\) and \(u_->u_+\).

  • If r is monostable, then there exists a positive constant \(c_*\) such that for all \(c\ge c_*\) there exists a monotone TWS \((\bar{u},c)\) of (20) in the sense of Definition 1. For \(c<c_*\) no such monotone TWS exists (however oscillatory TWS may exist).

  • If r is bistable, then there exists an (up to translations) unique monotone TWS \((\bar{u},c)\) of (20) in the sense of Definition 1.

  • If r is unstable, then there does not exist a monotone TWS \((\bar{u},c)\) of (20).

3.2 Korteweg-de Vries-Burgers Equation (KdVB)

A generalized KdVB equation is a scalar partial differential equation

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {} f(u) = \varepsilon \partial ^{2}_{x} {u} + \delta \partial ^{3}_{x} {u}, \quad x\in \mathbb {R}, \quad t>0, \end{aligned}$$
(26)

for some flux function \(f:\mathbb {R}\rightarrow \mathbb {R}\) as well as constants \(\varepsilon >0\) and \(\delta \in \mathbb {R}\). The TWP for given endstates \(u_\pm \) is to study the existence of a TWS \((\bar{u},c)\) for (26) in the sense of Definition 1. The importance of the TWP for KdVB equations in the shock wave theory of (scalar) hyperbolic conservation laws is discussed in Sect. B. A TWS \((\bar{u},c)\) satisfies the TWE

$$\begin{aligned} -c \bar{u}' + f'(\bar{u})\ \bar{u}' = \varepsilon \bar{u}'' + \delta \bar{u}''' \ , \quad \xi \in \mathbb {R}\ , \end{aligned}$$
(27)

or integrating on \((-\infty ,\xi ]\) and using (3),

$$\begin{aligned} h(\bar{u}) := f(\bar{u}) -c \bar{u}-(f(u_-) -c \ u_-) = \varepsilon \bar{u}' + \delta \bar{u}'' \ , \quad \xi \in \mathbb {R}\ . \end{aligned}$$
(28)

Connection with reaction-diffusion equation. A TWS \(u(x,t)=\bar{u}(x-c t)\) of a generalized Korteweg-de Vries-Burgers equation (26) satisfies TWE (28). Thus \(v(x,t)=\bar{u}(x-\varepsilon t)\) is a TWS \((\bar{u},\varepsilon )\) of the reaction-diffusion equation

$$\begin{aligned} \partial _{t} {v} = -h(v) + \delta \partial ^{2}_{x} {v}\ , \quad x\in \mathbb {R}\ , \quad t>0\ . \end{aligned}$$
(29)

Phase plane analysis. Following the analysis of TWE (21) for a reaction-diffusion equation (20) with \(r(u)=-h(u)\) and \(\sigma =\delta \), necessary conditions on the parameters can be identified. First, a TWE is rewritten as a system of first-order ODEs with vector field F. Then the condition on stationary states implies that endstates \(u_\pm \) and wave speed c have to satisfy

$$\begin{aligned} f(u_+)-f(u_-) = c(u_+- u_-) \ . \end{aligned}$$
(30)

This condition is known in shock wave theory as Rankine–Hugoniot condition (B.4) on the shock triple \((u_-,u_+;c)\). The (nonlinear) stability of hyperbolic stationary states \((u_s,v_s)\) of F is determined by the eigenvalues

$$\begin{aligned} \lambda _\pm = -\frac{1}{2} \frac{\varepsilon }{\delta }\pm \frac{\sqrt{ \varepsilon ^2 + 4 \delta h'(u_s)}}{2 |\delta |} \end{aligned}$$
(31)

of the Jacobian \({\text {D}}\!F(u_s,v_s)\). If \(\varepsilon ,\delta >0\), then \((u_+,0)\) is always either a saddle or stable node, and \(h'(u_-)=f'(u_-)-c>0\) ensures that \((u_-,0)\) is unstable. For example, Lax’ entropy condition (B.5), i.e. \(f'(u_+)<c<f'(u_-)\), implies the latter condition.

Convex Flux Functions

Theorem 2

Suppose \(f\in C^2(\mathbb {R})\) is a strictly convex function. Let \(\varepsilon \), \(\delta \) be positive and let \((u_-,u_+;c)\) satisfy the Rankine–Hugoniot condition (B.4) and the entropy condition (B.5), i.e. \(u_->u_+\). Then, there exists an (up to translations) unique TWS \((\bar{u},c)\) of (26) in the sense of Definition 1.

Proof

We consider the associated reaction-diffusion equation (29), i.e. \(\partial _{t} {u} = r(u) +\delta \partial ^{2}_{x} {u}\) with \(r(u)=-h(u)\). Due to (B.4) and (B.5), r(u) is monostable in the sense of Definition 4. Moreover, function r is strictly concave, since \(r''(u)=-f''(u)\) and \(f\in C^2(\mathbb {R})\) is strictly convex. In fact, \((u_\pm ,0)\) are the only stationary points of system (22), where \((u_-,0)\) is a saddle point and \((u_+,0)\) is a stable node. Thus, for all wave speeds \(\varepsilon \) there exists a TWS \((\bar{u},\varepsilon )\) – with possibly oscillatory profile \(\bar{u}\) – of reaction-diffusion equation (29). Moreover, \((\bar{u},c)\) is a TWS of (26), due to (27)–(29).    \(\square \)

The TWP for KdVB equations (26) with Burgers’ flux \(f(u) =u^2\) has been investigated in [16]. The sign of \(\delta \) in (26) is irrelevant, since it can be changed by a transformation \(\tilde{x}=-x\) and \(\tilde{u}(\tilde{x},t)=-u(x,t)\), see also [41]. First, the results in Theorem 2 on the existence of TWS and geometry of its profiles are proven. More importantly, the authors investigate the convergence of profiles \(\bar{u}(\xi ;\varepsilon ,\delta )\) in the limits \(\varepsilon \rightarrow 0\), \(\delta \rightarrow 0\), as well as \(\varepsilon \) and \(\delta \) tending to zero simultaneously. Assuming that the ratio \(\delta /\varepsilon ^2\) remains bounded, they show that the TWS converge to the classical Lax shocks for this vanishing diffusive-dispersive regularization [16].

Concave-Convex Flux Functions

Definition 5

([45]) A function \(f\in C^3(\mathbb {R})\) is called concave-convex if

$$\begin{aligned} u f''(u)> 0 \quad \forall u\ne 0 \ , \quad f'''(0)\ne 0 \ , \quad \lim _{u\rightarrow \pm \infty } f'(u) = +\infty \ . \end{aligned}$$
(32)

Here the single inflection point is shifted without loss of generality to the origin. We consider a cubic flux function \(f(u)=u^3\) as the prototypical concave-convex flux function with a single inflection point, see [39, 45].

Proposition 5

([38, 41]) Suppose \(f(u) =u^3\) and \(\varepsilon >0\).

  1. (a)

    If \(\delta \le 0\) then a TWS \((\bar{u},c)\) of (26) exists if and only if \((u_-,u_+;c)\) satisfy the Rankine–Hugoniot condition (B.4) and the entropy condition (B.5).

  2. (b)

    If \(\delta > 0\) then a TWS \((\bar{u},c)\) of (26) exists for \(u_->0\) if and only if \(u_+\in S(u_-)\) with

    $$\begin{aligned} S(u_-) = {\left\{ \begin{array}{ll} [-\frac{u_-}{2} , u_-) &{} \,\text { if }\, u_-\le 2\beta \ , \\ \{ -u_-+ \beta \} \cup [-\beta , u_-) &{} \,\text { if }\, u_-> 2\beta \ , \end{array}\right. } \end{aligned}$$
    (33)

    where the coefficient \(\beta \) is given by \(\beta =\tfrac{\sqrt{2}}{3}\tfrac{\varepsilon }{\sqrt{\delta }}\).

Proof

Following the discussion from (26)–(29), we consider the associated reaction-diffusion equation (29), i.e. \(\partial _{t} {u} = r(u) + \delta \partial ^{2}_{x} {u}\) with \(r(u)=-h(u)\). From this point of view, we need to classify the reaction term \(r(u)=-h(u)\): Whereas \(r(u_-)=0\) by definition, \(r(u_+)=0\) if and only if \((u_-,u_+;c)\) satisfies the Rankine–Hugoniot condition (B.4). The Rankine–Hugoniot condition implies \(c=u_+^2+u_+\ u_-+u_-^2\). Hence, the reaction term r(u) has a factorization

$$\begin{aligned} r(u) = -(u^3-u_-^3-c(u-u_-)) = -(u-u_-)\ (u-u_+)\ (u+u_++u_-) \end{aligned}$$
(34)
Fig. 2
figure 2

Classification of the cubic reaction function \(r(u)=-h(u)\) in (34) depending on its roots \(u_-\), \(u_+\) and \(u_*=-u_--u_+\) according to Definition 4

Full size image

Thus, r(u) is a cubic polynomial with three roots \(u_1 \le u_2 \le u_3\), such that \(r(u) = -(u-u_1) (u-u_2) (u-u_3)\). In case of distinct roots \(u_1< u_2 < u_3\) we deduce \(r'(u_1)<0\), \(r'(u_2)>0\) and \(r'(u_3)<0\). The ordering of the roots \(u_\pm \) and \(u_*=-u_--u_+\) depending on \(u_\pm \) is visualized in Fig. 2. Next, we will discuss the results in Proposition 5(b) (for \(u_->0\) and \(\delta >0\)) via results on the existence of TWS for a reaction-diffusion equation (29).

  1. 1.

    For \(u_+<u_*<u_-\), function r(u) is bistable, see also Fig. 2. Due to Proposition 4, there exists an (up to translations) unique TWS \((\bar{u},\varepsilon )\) with possibly negative wave speed. Under our assumption that the wave speed \(\varepsilon \) is positive, relation (25) yields the restriction \(-u_+>u_-\). In fact, for \(u_-> 2\beta \) and \(u_+=-u_-+\beta \) there exists a TWS \((\bar{u},\varepsilon )\) for reaction-diffusion equation (29), see [41, Theorem 3.4]. The function r is bistable with \(u_*=-u_--u_+=-\beta \), hence \(f'(u_\pm )>c\). This violates Lax’ entropy condition (B.5) and is known in the shock wave theory as a slow undercompressive shock [45].

  2. 2.

    For \(u_*<u_+<u_-\), function r(u) is monostable, see Fig. 2. Due to Proposition 4, there exists a critical wave speed \(c_*\), such that monotone TWS \((\bar{u},\varepsilon )\) for (29) exist for all \(\varepsilon \ge c_*\). However, not all endstates \((u_-,u_+)\) in the subset defined by \(u_*<u_+<u_-\) admit a TWS \((\bar{u},c)\), see (33) and Fig. 3b. The TWS \((\bar{u},c)\) associated to non-classical shocks appear again, with reversed roles for the roots \(u_+\) and \(u_*\): For \(u_-> 2\beta \) and \(u_+= -\beta \), there exists a TWS \((\bar{u},\varepsilon )\) for reaction-diffusion equation (29), see [41, Theorem 3.4]. These TWS form a horizontal halfline in Fig. 3b and divides the set defined by \(u_*<u_+<u_-\) into two subsets. In particular, TWS exist only for endstates \((u_-,u_+)\) in the subset above this halfline.

  3. 3.

    For \(u_+\,{<}\,u_-<u_*\), function \(r(u)\,{=}\,-h(u)\) satisfies \(r(u)\,{<}\,0\) for all \(u\in (u_+,u_-)\), see also Fig. 2. Thus the necessary condition (25) can not be fulfilled for positive \(c=\varepsilon \), hence there exists no TWS \((\bar{u},\varepsilon )\) for the reaction-diffusion equation.

  4. 4.

    For \(u_*<u_-<u_+\), function r(u) is monostable with reversed roles of the endstates \(u_\pm \), see Fig. 2. Due to Proposition 4, there exists a TWS \((\bar{u},\varepsilon )\) however satisfying \(\lim _{\xi \rightarrow \mp \infty } \bar{u}(\xi ) = u_\pm \).

If \(\delta =0\), then equation (26) is a viscous conservation law, and its TWE (28) is a simple ODE \(-\varepsilon \bar{u}' = r(\bar{u})\) with \(r(u)=-h(u)\). Thus a heteroclinic orbit exists only for monostable r(u), i.e. if the unstable node \(u_-\) and the stable node \(u_+\) are not separated by any other root of r.

If \(\delta <0\), then we rewrite TWE (28) as \(\varepsilon \bar{u}' = h(u) + |\delta | \bar{u}''\). It is associated to a reaction-diffusion equation \(\partial _{t} {u} = h(u) + |\delta |\partial ^{2}_{x} {u}\) via a TWS ansatz \(u(x,t) = \bar{u}(x-(-\varepsilon ) t)\); note the change of sign for the wave speed. If \(u_+<u_*<u_-\) then h(u) is an unstable reaction function. Thus there exists no TWS \((\bar{u},-\varepsilon )\) according to Proposition 4. If \(u_*<u_+<u_-\) then function \(h(u)=-r(u)\) satisfies \(h(u)<0\) for all \(u\in (u_+,u_-)\), see also Fig. 2. The necessary condition (25) is still fine, since also the sign of the wave speed changed. In contrast to the case \(\delta >0\), there exists no TWS connecting \(u_-\) with \(u_*\), which would indicate a bifurcation. Thus, the existence of TWS for all pairs \((u_-,u_+)\) in the subset defined by \(u_*<u_+<u_-\) can be proven. The TWP for other pairs \((u_-,u_+)\) is discussed similarly.    \(\square \)

Fig. 3
figure 3

a Classification of reaction function r in (34) depending on its roots \(u_-\), \(u_+\) and \(u_*=-u_--u_+\) according to Definition 4; b Endstates \(u_\pm \) in the shaded region and on the thick line can be connected by TWS of the cubic KdVB equation; TWS in the shaded region and on the thick line are associated to classical and non-classical shocks of \(\partial _{t} {u}+\partial _{x} {u^3} = 0\), respectively. For a classical shock the shock triple satisfies Lax’ entropy condition \(f'(u_-)>c>f'(u_+)\); i.e. characteristics in the Riemann problem meet at the shock. In contrast, the non-classical shocks are of slow undercompressive type, i.e. characteristics in the Riemann problem cross the shock

Full size image

4 TWP for Nonlocal Evolution Equations

4.1 Reaction-Diffusion Equations

The first example of a reaction-diffusion equation with nonlocal diffusion is the integro-differential equation

$$\begin{aligned} \partial _{t} {u} = J *u - u + r(u) \ , \quad t>0 \ , \quad x\in \mathbb {R}\ , \end{aligned}$$
(35)

for some even, non-negative function J with mass one, i.e. for all \(x\in \mathbb {R}\)

$$\begin{aligned} J\in C(\mathbb {R})\ , \quad J\ge 0\ , \quad J(x)=J(-x)\ , \quad \int _{\mathbb {R}} \; { J(y)} \; \,{\text {d}}\!y\,=1 \ , \end{aligned}$$
(36)

and some function r. The operator \(\mathscr {L}[u] = J*u -u\) is a Lévy operator, see (13), which models nonlocal diffusion. It is the infinitesimal generator of a compound Poisson stochastic process, which is a pure jump process.

The TWP for given endstates \(u_\pm \) is to study the existence of a TWS \((\bar{u},c)\) for (35) in the sense of Definition 1. Such a TWS \((\bar{u},c)\) satisfies the TWE \(-c\bar{u}' = J *\bar{u}- \bar{u}+ r(\bar{u})\) for \(\xi \in \mathbb {R}\). Next, we recall some results on the TWP for (35), which will depend crucially on the type of reaction function r and the tail behavior of a kernel function J. We will present the existence of TWS with monotone decreasing profiles \(\bar{u}\), which will follow from the cited literature after a suitable transformation.

Proposition 6

((monostable [27]), (bistable [14, 24])) Suppose \(u_->u_+\) and consider reaction functions r in the sense of Definition 4. Suppose \(J\in W^{1,1}(\mathbb {R})\) and its continuous representative satisfies (36).

  • If r is monostable and there exists \(\lambda >0\) such that \(\int _{\mathbb {R}} \; {J(y)\ \exp (\lambda y)} \; \,{\text {d}}\!y\, < \infty \) then there exists a positive constant \(c_*\) such that for all \(c\ge c_*\) there exists a monotone TWS \((\bar{u},c)\) of (35). For \(c<c_*\) no such monotone TWS exists.

  • If r is bistable and \(\int _{\mathbb {R}} \; {|y| J(y)} \; \,{\text {d}}\!y\,<\infty \), then there exists an (up to translations) unique monotone TWS \((\bar{u},c)\) of (35).

For monostable reaction functions, the tail behavior of kernel function J is very important. There exist kernel functions J, such that TWS exist only for bistable – but not for monostable – reaction functions r, see [58]. The prime example are kernel functions J which decay more slowly than any exponentially decaying function as \(|x|\rightarrow \infty \) in the sense that \(J(x)\exp (\eta |x|) \rightarrow \infty \) as \(|x|\rightarrow \infty \) for all \(\eta >0\).

For reaction-diffusion equations of bistable type, Chen established a unified approach [24] to prove the existence, uniqueness and asymptotic stability with exponential decay of traveling wave solutions. The results are established for a subclass of nonlinear nonlocal evolution equations

$$\begin{aligned} \partial _{t} {u} (x,t) = \mathscr {A}[u(\cdot ,t)](x) \quad \text { for }\, (x,t)\in \mathbb {R}\times (0,T]\ , \end{aligned}$$

where the nonlinear operator \(\mathscr {A}\) is assumed to

  1. (a)

    be independent of t;

  2. (b)

    generate a \(L^\infty \) semigroup;

  3. (c)

    be translational invariant, i.e. \(\mathscr {A}\) satisfies for all \(u\in {{\mathrm{dom}}}\mathscr {A}\) the identity

    $$\begin{aligned} \mathscr {A}[u(\cdot +h)](x) = \mathscr {A}[u(\cdot )](x+h)\quad \forall x\ ,h \in \mathbb {R}\,. \end{aligned}$$

    Consequently, there exists a function \(r:\mathbb {R}\rightarrow \mathbb {R}\) which is defined by \(\mathscr {A}[\upsilon \mathbf 1]=r(\upsilon )\mathbf 1\) for \(\upsilon \in \mathbb {R}\) and the constant function \(\mathbf 1:\mathbb {R}\rightarrow \mathbb {R}\), \(x\mapsto 1\). This function r is assumed to be bistable in the sense of Definition 4;

  4. (d)

    satisfy a comparison principle: If \(\partial _{t} {u}\ge \mathscr {A}[u]\), \(\partial _{t} {v}\le \mathscr {A}[v]\) and \(u(\cdot ,0)\gneq v(\cdot ,0)\), then \(u(\cdot ,t)>v(\cdot ,t)\) for all \(t>0\).

Chen’s approach relies on the comparison principle and the construction of sub- and supersolutions for any given traveling wave solution. Importantly, the method does not depend on the balance of the potential. More quantitative versions of the assumptions on \(\mathscr {A}\) are needed in the proofs. Finally integro-differential evolution equations

$$\begin{aligned} \partial _{t} {u} = \varepsilon \partial ^{2}_{x} {u} + G(u,J_1*S^1(u),\ldots ,J_n*S^n(u)) \end{aligned}$$
(37)

are considered for some diffusion constant \(\varepsilon \ge 0\), smooth functions G and \(S^k\), and kernel functions \(J_k\in C^1(\mathbb {R})\cap W^{1,1}(\mathbb {R})\) satisfying (36) where \(k=1,\ldots ,n\). Additional assumptions on the model parameters guarantee that (37) can be interpreted as a reaction-diffusion equation with bistable reaction function including Eqs. (20) and (35) as special cases.

Another example of reaction-diffusion equations with nonlocal diffusion are the integro-differential equations

$$\begin{aligned} \partial _{t} {u} = D^{a}_{\theta }u + r(u) \ , \quad t>0 \ , \quad x\in \mathbb {R}\ , \end{aligned}$$
(38)

for a (particle) density \(u=u(x,t)\), some function \(r=r(u)\), and a Riesz–Feller operator \(D^{a}_{\theta }\) with \((a, \theta )\in \mathfrak {D}_{a,\theta }\). The nonlocal Riesz–Feller operators are models for superdiffusion, where from a probabilistic view point a cloud of particle is assumed to spread faster than by following Brownian motion. Integro-differential equation (38) can be derived as a macroscopic equation for a particle density in the limit of modified Continuous Time Random Walk (CTRW), see [48]. In the applied sciences, Eq. (38) has found many applications, see [54, 57] for extensive reviews on modeling, formal analysis and numerical simulations.

The TWP for given endstates \(u_\pm \) is to study the existence of a TWS \((\bar{u},c)\) for (38) in the sense of Definition 1. Such a TWS \((\bar{u},c)\) satisfies the TWE

$$\begin{aligned} -c\bar{u}' = D^{a}_{\theta }\bar{u}+ r(\bar{u}) \ , \quad \xi \in \mathbb {R}\ . \end{aligned}$$
(39)

First we collect mathematical rigorous results about the TWP associated to (38) in case of the fractional Laplacian \(D^{a}_{0} = -(-\varDelta )^{a/2}\) for \(a\in (0,2)\), i.e. a Riesz–Feller operator \(D^{a}_{\theta }\) with \(\theta =0\).

Proposition 7

((monostable [17, 18, 34]), (bistable [19,20,21, 25, 37, 50])) Suppose \(u_->u_+\). Consider the TWP for reaction-diffusion equation (38) with functions r in the sense of Definition 4 and fractional Laplacian \(D^{a}_{0}\), i.e. symmetric Riesz–Feller operators \(D^{a}_{\theta }\) with \(0<a<2\) and \(\theta =0\).

  • If r is monostable then there does not exist any TWS \((\bar{u},c)\) of (38).

  • If r is bistable then there exists an (up to translations) unique monotone TWS \((\bar{u},c)\) of (38).

For monostable reaction functions, Cabré and Roquejoffre prove that a front moves exponentially in time [17, 18]. They note that the genuine algebraic decay of the heat kernels \(G^{a}_{0}\) associated to fractional Laplacians is essential to prove the result, which implies that no TWS with constant wave speed can exist. Engler [34] considered the TWP for (38) for a different class of monostable reaction functions r and non-extremal Riesz–Feller operators \(D^{a}_{\theta }\) with \((a,\theta )\in \mathfrak {D}_{a,\theta }^{+}\) and \(\mathfrak {D}_{a,\theta }^{+}:= \{\, {(a,\theta )\in \mathfrak {D}_{a,\theta }} \,|\, { |\theta |<\min \{a, 2-a\} } \,\}\). Again the associated heat kernels \(G^{a}_{\theta }(x,t)\) with \((a,\theta )\in \mathfrak {D}_{a,\theta }^{+}\) decay algebraically in the limits \(x\rightarrow \pm \infty \), see [47].

To our knowledge, we established the first result [6] on existence, uniqueness (up to translations) and stability of traveling wave solutions of (38) with Riesz–Feller operators \(D^{a}_{\theta }\) for \((a,\theta )\in \mathfrak {D}_{a,\theta }\) with \(1<a< 2\) and bistable functions r. We present our results for monotone decreasing profiles, which can be inferred from our original result after a suitable transformation.

Theorem 3

([6]) Suppose \(u_->u_+\), \((a,\theta )\in \mathfrak {D}_{a,\theta }\) with \(1<a< 2\), and \(r\in C^\infty (\mathbb {R})\) is a bistable reaction function. Then there exists an (up to translations) unique monotone decreasing TWS \((\bar{u},c)\) of (38) in the sense of Definition 1.

The technical details of the proof are contained in [6], whereas in [5] we give a concise overview of the proof strategy and visualize the results also numerically. In a forthcoming article [4], we extend the results to all non-trivial Riesz–Feller operators \(D^{a}_{\theta }\) with \((a,\theta )\in \mathfrak {D}_{a,\theta }^{\diamond }\). The smoothness assumption on r is convenient, but not essential. To prove Theorem 3, we follow – up to some modifications – the approach of Chen [24]. It relies on a strict comparison principle and the construction of sub- and supersolutions for any given TWS. His quantitative assumptions on operator \(\mathscr {A}\) are too strict, such that his results are not directly applicable. A modification allows to cover the TWP for (38) for all Riesz–Feller operators \(D^{a}_{\theta }\) with \(1<a< 2\) also for non-zero \(\theta \), and all bistable functions r regardless of the balance of the potential.

Next, we quickly review different methods to study the TWP of reaction-diffusion equation (38) with bistable function r and fractional Laplacian. In case of a classical reaction-diffusion equation (20), the existence of a TWS can be studied via phase-plane analysis [13, 35]. This method has no obvious generalization to our TWP for (38), since its traveling wave equation (39) is an integro-differential equation. The variational approach has been focused – so far – on symmetric diffusion operators such as fractional Laplacians and on balanced potentials, hence covering only stationary traveling waves [50]. Independently, the same results are achieved in [19,20,21] by relating the stationary TWE (39)\(_{\theta =0, c=0}\) via [22] to a boundary value problem for a nonlinear partial differential equation. The homotopy to a simpler TWP has been used to prove the existence of TWS in case of (35), and (38)\(_{\theta =0}\) with unbalanced potential [37].

Chmaj [25] also considers the TWP for (38)\(_{\theta =0}\) with general bistable functions r. He approximates a given fractional Laplacian by a family of operators \(J_\varepsilon *u - (\int J_\varepsilon )u\) such that \(\lim _{\varepsilon \rightarrow 0} J_\varepsilon *u - (\int J_\varepsilon ) u = D^{a}_{0}u\) in an appropriate sense. This allows him to obtain a TWS of (38)\(_{\theta =0}\) with general bistable function r as the limit of the TWS \(u_\varepsilon \) of (35) associated to \((J_\varepsilon )_{\varepsilon \ge 0}\). It might be possible to modify Chmaj’s approach to study reaction-diffusion equation (38) with asymmetric Riesz–Feller operators. This would give an alternative existence proof for TWS in Theorem 3. However, Chen’s approach allows to establish uniqueness (up to translations) and stability of TWS as well.

4.2 Nonlocal Korteweg-de Vries-Burgers Equation

First we consider the integro-differential equation in multi-dimensions \(d\ge 1\)

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {f(u)} = \varepsilon \varDelta _x u + \gamma \varepsilon ^2 \sum _{j=1}^d \big ( \phi _\varepsilon *\partial _{x_j} {u} -\partial _{x_j} {u}\big )\ , \quad x\in \mathbb {R}^d \ , \quad t>0 \ , \end{aligned}$$
(40)

for parameters \(\varepsilon >0\), \(\gamma \in \mathbb {R}\), a smooth even non-negative function \(\phi \) with compact support and unit mass, i.e. \(\int _{\mathbb {R}^d} \; {\phi (x)} \; \,{\text {d}}\!x\,=1\), and the rescaled kernel function \(\phi _\varepsilon (x) = \phi (x/\varepsilon ) / \varepsilon ^d\). It has been derived as a model for phase transitions with long range interactions close to the surface, which supports planar TWS associated to undercompressive shocks of (B.1), see [52]. A planar TWS \((\bar{u},c)\) is a solution \(u(x,t)=\bar{u}(x-ct e)\) for some fixed vector \(e\in \mathbb {R}^d\), such that the profile is transported in direction e. The existence of planar TWS is proven by reducing the problem to a one-dimensional TWP for (40)\(_{d=1}\), identifying the associated reaction-diffusion equation (35) and using results in Proposition 6. For cubic flux function \(u^3\), the existence of planar TWS associated to undercompressive shocks of (B.1) is established. Moreover, the well-posedness of its Cauchy problem and the convergence of solutions \(u^\varepsilon \) as \(\varepsilon \searrow 0\) have been studied [52].

Another example is the fractal Korteweg-de Vries-Burgers equation

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {f(u)} = \varepsilon \partial _{x} {} \mathscr {D}^{\alpha }_{+}u + \delta \partial ^{3}_{x} {u}, \quad x\in \mathbb {R}, \quad t>0, \end{aligned}$$
(41)

for some \(\varepsilon >0\) and \(\delta \in \mathbb {R}\).

Equation (41) with \(\alpha =1/3\) has been derived as a model for shallow water flows, by performing formal asymptotic expansions associated to the triple-deck (boundary layer) theory in fluid mechanics, e.g. see [44, 55]. In particular, the situations of one-layer and two-layer shallow water flows have been considered, which yield a quadratic (one layer) and cubic flux function (two layer), respectively. In the monograph [49], similar models are considered and the well-posedness of the initial value problem and possible wave-breaking are studied.

The TWP for given endstates \(u_\pm \) is to study the existence of a TWS \((\bar{u},c)\) for (41) in the sense of Definition 1. Such a TWS \((\bar{u},c)\) satisfies the TWE

$$\begin{aligned} h(\bar{u}) := f(\bar{u}) - f(u_-) - c(\bar{u}-u_-) = \varepsilon \mathscr {D}^{\alpha }_{+}\bar{u}+ \delta \bar{u}'' \ . \end{aligned}$$
(42)

We obtain a necessary condition for the existence of TWS – see also (25) – by multiplying the TWE with \(\bar{u}'\) and integrating on \(\mathbb {R}\),

$$\begin{aligned} \int _{u_-}^{u_+} \; { h(u) } \; \,{\text {d}}\!u\, = \varepsilon \int _{-\infty }^{\infty } \; { \bar{u}'\ \mathscr {D}^{\alpha }_{+}\bar{u}(\xi ) } \; \,{\text {d}}\!\xi \, \ge 0 \ , \end{aligned}$$
(43)

where the last inequality follows from (A.1).

Connection with reaction-diffusion equation. If a TWS \((\bar{u},c)\) for (41) exists, then \(u(x,t)=\bar{u}(x)\) is a stationary TWS \((\bar{u},0)\) of the evolution equation

$$\begin{aligned} \partial _{t} {u} = -\varepsilon \mathscr {D}^{\alpha }_{+}u -\delta \partial ^{2}_{x} {u} +h(u), \quad x\in \mathbb {R}, \quad t>0. \end{aligned}$$
(44)

To interpret Eq. (44) as a reaction-diffusion equation, we need to verify that \(-\varepsilon \mathscr {D}^{\alpha }_{+}u -\delta \partial ^{2}_{x} {u}\) is a diffusion operator, e.g. that \(-\varepsilon \mathscr {D}^{\alpha }_{+}u -\delta \partial ^{2}_{x} {u}\) generates a positivity preserving semigroup.

Lemma 1

Suppose \(0<\alpha <1\) and \(\gamma _1,\gamma _2 \in \mathbb {R}\). The operator \(\gamma _1 \mathscr {D}^{\alpha }_{+}u + \gamma _2 \partial ^{2}_{x} {u}\) is a Lévy operator if and only if \(\gamma _1\le 0\) and \(\gamma _2\ge 0\). Moreover, the associated heat kernel is strictly positive if and only if \(\gamma _2>0\).

Proof

For \(\alpha \in (0,1)\), the operator \(-\mathscr {D}^{\alpha }_{+}\) is a Riesz–Feller operator \(D^{\alpha }_{-\alpha }\) and generates a positivity preserving convolution semigroup with a Lévy stable probability distribution \(G^{\alpha }_{-\alpha }\) as its kernel. The probability distribution is absolutely continuous with respect to Lebesgue measure and its density has support on a half-line [47]. For example the kernel associated to \(-\mathscr {D}^{1/2}\) is the Lévy–Smirnov distribution. Thus, for \(\gamma _1\le 0\) and \(\gamma _2\ge 0\), the operator \(\gamma _1 \mathscr {D}^{\alpha }_{+}u + \gamma _2 \partial ^{2}_{x} {u}\) is a Lévy operator, because it is a linear combination of Lévy operators. Using the notation for Fourier symbols of Riesz–Feller operators, the partial Fourier transform of equation

$$\begin{aligned} \partial _{t} {u} = -|\gamma _1| \mathscr {D}^{\alpha }[u] + \gamma _2 \partial ^{2}_{x} {u} \end{aligned}$$

is given by \(\partial _{t} {} \mathscr {F}[u](k) = ( |\gamma _1| \psi ^\alpha _{-\alpha }(k) - \gamma _2 k^2 ) \mathscr {F}[u](k)\). Therefore, the operator generates a convolution semigroup with heat kernel

$$ \mathscr {F}^{-1}[\exp \{( |\gamma _1| \psi ^\alpha _{-\alpha }(k) - \gamma _2 k^2 )\ t\}] (x) = G^{\alpha }_{-\alpha } (\cdot ,|\gamma _1| t) *G^{2}_{0} (\cdot ,\gamma _2 t) \ (x) \ , $$

which is the convolution of two probability densities. The kernel is positive on \(\mathbb {R}\) since probability densities are non-negative on \(\mathbb {R}\) and the normal distribution \(G^{2}_{0}\) is positive on \(\mathbb {R}\) for positive \(\gamma _2 t\).

The operator \(\mathscr {D}^{\alpha }_{+}\) for \(\alpha \in (0,1)\) is not a Riesz–Feller operator, see Fig. 1, and it generates a semigroup which is not positivity preserving. Therefore, this operator and any linear combination with it for \(\gamma _1>0\) is not a Lévy operator.    \(\square \)

Convex Flux Functions

Proposition 8

Consider (41) with \(0<\alpha <1\), \(\delta \in \mathbb {R}\) and strictly convex flux function \(f\in C^3(\mathbb {R})\). For a shock triple \((u_-,u_+;c)\) satisfying the Rankine–Hugoniot condition (B.4), a non-constant TWS \((\bar{u},c)\) can exist if and only if Lax’ entropy condition (B.5) is fulfilled, i.e. \(u_->u_+\).

Proof

The Rankine–Hugoniot condition (B.4) ensures that h(u) in (42) has exactly two roots \(u_\pm \). If Lax’ entropy condition (B.5) is fulfilled, then \(u_->u_+\) and \(-h(u)\) is monostable in the sense of Definition 4. Thus, the necessary condition (43) is satisfied. If \(u_-=u_+\) then (43) implies that \(\bar{u}\) is a constant function satisfying \(\bar{u}\equiv u_\pm \). If \(u_-<u_+\) then \(-h(u)\) is monostable in the sense of Definition 4 with reversed roles of \(u_\pm \). Thus, the necessary condition (43) is not satisfied.    \(\square \)

Next, we recall some existence result which have been obtained by directly studying the TWE. In an Addendum [28], we removed an initial assumption on the solvability of the linearized TWE.

Theorem 4

([3]) Consider (41) with \(\delta =0\) and convex flux function f(u). For a shock triple \((u_-,u_+;c)\) satisfying (B.4) and (B.5), there exists a monotone TWS of (41) in the sense of Definition 1, whose profile \(\bar{u}\in C^1_b(\mathbb {R})\) is unique (up to translations) among all functions \(u\in u_-+ H^2(-\infty ,0) \cap C^1_b(\mathbb {R})\).

This positive existence result is consistent with the negative existence result in Proposition 7 and Engler [34] for (38) with non-extremal Riesz–Feller operators \(D^{a}_{\theta }\) for \((a,\theta )\in \mathfrak {D}_{a,\theta }^{+}\). The reason is that \(-\mathscr {D}^{\alpha }_{+}\) for \(0<\alpha <1\) is the generator of a convolution semigroup with a one-sided strictly stable probability density function as its heat kernel; in contrast to heat kernels with genuine algebraic decay [17, 18, 34].

Theorem 5

([2]) Consider (41) with flux function \(f(u) =u^2/2\). For a shock triple \((u_-,u_+;c)\) satisfying (B.4) and (B.5), there exists a TWS of (41) in the sense of Definition 1, whose profile \(\bar{u}\) is unique (up to translations) among all functions \(u\in u_-+ H^4(-\infty ,0) \cap C^3_b(\mathbb {R})\).

If dispersion dominates diffusion then the profile of a TWS \((\bar{u},c)\) will be oscillatory in the limit \(\xi \rightarrow \infty \). For a classical KdVB equation this geometry of profiles depends on the ratio \(\varepsilon ^2/\delta \) and the threshold can be determined explicitly.

Concave-convex flux functions. We consider a cubic flux function \(f(u)=u^3\) as the prototypical concave-convex flux function. Again the necessary condition (43) and the classification of function \(h(u)=-r(u)\) in Fig. 2 can be used to identify non-admissible shock triples \((u_-,u_+;c)\) for the TWP of (41).

We conjecture that a statement analogous to Proposition 5 holds true. Of special interest is again the occurrence of TWS \((\bar{u},c)\) associated to non-classical shocks, which are only expected in case of (41) with \(\varepsilon >0\) and \(\delta >0\).

Proposition 9

Suppose \(f(u) =u^3\) and \(\varepsilon >0\).

  1. 1.

    If \(\delta \le 0\) then a TWS \((\bar{u},c)\) of (41) exists if and only if \((u_-,u_+;c)\) satisfy the Rankine–Hugoniot condition (B.4) and the entropy condition (B.5).

  2. 2.

    Conjecture: If \(\delta > 0\) then a TWS \((\bar{u},c)\) of (41) exists for \(u_->0\) if and only if \(u_+\in S(u_-)\) for some set \(S(u_-)\) similar to (33).

Proof

(Sketch of proof) If \(\delta =0\), then Eq. (41) is a viscous conservation law, and its TWE (42) is a fractional differential equation \(\varepsilon \mathscr {D}^{\alpha }_{+}\bar{u}= h(\bar{u})\). Thus a heteroclinic orbit exists only for monostable \(-h(u)\), i.e. if the unstable node \(u_-\) and the stable node \(u_+\) are not separated by any other root of h. This follows from Theorem 4 and its proof in [3, 28].

If \(\delta <0\), then the TWE (42) is associated to a reaction-diffusion equation (44) via a stationary TWS ansatz \(u(x,t) = \bar{u}(x)\). First we note that a stronger version of the necessary condition (43) is available

$$\begin{aligned} \int _{-\infty }^{\xi } \; { h(\bar{u}) \bar{u}' (y) } \; \,{\text {d}}\!y\, = \varepsilon \int _{-\infty }^{\xi } \; { \bar{u}'\ \mathscr {D}^{\alpha }_{+}\bar{u}(y) } \; \,{\text {d}}\!y\, \ge 0 \ , \quad \forall \xi \in \mathbb {R}\ , \end{aligned}$$
(45)

see [2]. If \(u_+<u_*<u_-\) then h(u) is an unstable reaction function, see Fig. 2. Thus there exists no TWS in the sense of Definition 1 satisfying the necessary condition (45). If \(u_*<u_+<u_-\) then function \(-h(u)\) is monostable in the sense of Definition 4 and the necessary condition (43) can be satisfied. The existence of a TWS \((\bar{u},c)\) can be proven by following the analysis in [2, 28]. The TWP for other pairs \((u_-,u_+)\) is discussed similarly.

If \(\delta >0\) then the occurrence of TWS \((\bar{u},c)\) associated to non-classical shocks is possible. Unlike in our previous examples, the associated evolution Eq. (44) is not a reaction-diffusion equation, since \(-\varepsilon \mathscr {D}^{\alpha }_{+}\bar{u}-\delta \bar{u}''\) is not a Lévy operator. Especially, the results on existence of TWS for reaction-diffusion equations with bistable reaction function can not be used to prove the existence of TWS \((\bar{u},c)\) associated to undercompressive shocks. Instead, we investigate the TWP directly [1], extending the analysis in [2, 28] for Burgers’ flux to the cubic flux function \(f(u)=u^3\).    \(\square \)

4.3 Fowler’s Equation

Fowler’s equation (8) for dune formation is a special case of the evolution equation

$$\begin{aligned} \partial _{t} {u} + \partial _{x} {f(u)} = \delta \partial ^{2}_{x} {} u -\varepsilon \partial _{x} {} \mathscr {D}^{\alpha }_{+}u \ , \quad t>0 \ , \quad x\in \mathbb {R}\ , \end{aligned}$$
(46)

with \(0<\alpha <1\), positive constant \(\varepsilon ,\delta >0\) and flux function f. Here the fractional derivative appears with the negative sign, but this instability is regularized by the second order derivative. The initial value problem for (8) is well-posed in \(L^2\) [9]. However, it does not support a maximum principle, which is intuitive in the context of the application due to underlying erosions [9]. The existence of TWS of (8) – without assumptions (3) on the far-field behavior – has been proven [11].

For given endstates \(u_\pm \), the TWP for (46) is to study the existence of a TWS \((\bar{u},c)\) for (46) in the sense of Definition 1. Such a TWS \((\bar{u},c)\) satisfies the TWE

$$\begin{aligned} h(\bar{u}) := f(\bar{u}) - f(u_-) - c(\bar{u}-u_-) = \delta \bar{u}' - \varepsilon \mathscr {D}^{\alpha }_{+}\bar{u}\ , \quad \xi \in \mathbb {R}\ . \end{aligned}$$
(47)

For \(\delta =0\), the TWE reduces to a fractional differential equation \(\varepsilon \mathscr {D}^{\alpha }_{+}\bar{u}= -h(\bar{u})\), which has been analyzed in [3, 28] for monostable functions \(-h(u)\).

Equation (47) is also the TWE for a TWS \((\bar{u},\delta )\) of an evolution equation

$$\begin{aligned} \partial _{t} {u} = -\varepsilon \mathscr {D}^{\alpha }_{+}u - h(u), \quad x\in \mathbb {R}, \quad t>0. \end{aligned}$$
(48)

For \(\varepsilon >0\), the operator is \(-\varepsilon \mathscr {D}^{\alpha }_{+}\bar{u}\) is a Riesz–Feller operator \(\varepsilon D^{\alpha }_{-\alpha }\) whose heat kernel \(G^{\alpha }_{-\alpha }\) has only support on a halfline. For a shock triple \((u_-,u_+;c)\) satisfying the Rankine–Hugoniot condition (B.4), at least \(h(u_\pm )=0\) holds. Under these assumptions, Eq. (48) is a reaction-diffusion equation with a Riesz–Feller operator modeling diffusion.

The abstract method in [11] does not provide any information on the far-field behavior. Thus, assume the existence of a TWS \((\bar{u},c)\) in the sense of Definition 1, for some shock triple \((u_-,u_+;c)\) satisfying the Rankine–Hugoniot condition (B.4). Again, a necessary condition is obtained by multiplying TWE (47) with \(\bar{u}'\) and integrating on \(\mathbb {R}\); hence,

$$\begin{aligned} \int _{u_-}^{u_+} \; {h(u)} \; \,{\text {d}}\!u\, = \int _{\mathbb {R}} \; {(\bar{u}')^2} \; \,{\text {d}}\!\xi \, - \int _{\mathbb {R}} \; {\bar{u}' \mathscr {D}^{\alpha }_{+}\bar{u}} \; \,{\text {d}}\!\xi \, \ . \end{aligned}$$
(49)

The sign of the right hand side is not pre-determined since each integral is non-negative, see also (A.1).

For a cubic flux function \(f(u)=u^3\) and a shock triple \((u_-,u_+;c)\) satisfying the Rankine–Hugoniot condition (B.4), we deduce a bistable reaction function \(r(u)=-h(u)\) as long as \(u_+<-u_+-u_-<u_-\) see Fig. 2. However, since the heat kernel has only support on a halfline, we can not obtain a strict comparison principle as needed in Chen’s approach [4, 6, 24].