Traveling Wave Solutions for Nonlinear Reaction-Diffusion Equations as Dynamical Systems Problems

Abstract

In this paper we present a review of the traveling wave solutions (tws) analysis associated with different families of nonlinear reaction-diffusion equations. Here we emphazis the method of dynamical systems approach where searching conditions for the existence of tws satisfying appropriate boundary conditions in the full partial differential equations (PDE), it is equivalent to looking for conditions for the existence of heteroclinic (or homoclinic) trajectories of a nonlinear autonomous ordinary differential (ODE) system. The reaction-diffusion equations we consider cover a wide range. From those with constant diffusion coefficient, $D>0$ with nonlinear reactive part like Fisher-KPP equation and FitzHugh-Nagumo system, to those where a nonlinear density-dependent diffusion coefficient, $D(u)$ is introduced whose properties makes the corresponding PDE a degenerate one at the point where $D$ vanishes. In addition of presenting a sketch of the proof of theorems which give sufficient conditions for the existence of tws we include a number of numerical simulations of the phase space of the ODE system with the aim of showing the different types of heteroclinic (or homoclinic) trajectories which give us the tws for the corresponding PDE.

1 INTRODUCTION

A wide range of phenomena in nature exhibit wave behaviour, for example in physics there are the well known acoustic, electromagnetic and sea waves; in chemical, physiological and biological systems there are several examples of wave like phenomena. One approach to model such wave behaviour is in terms of so the called reaction-diffusion-equations.

For many years it was thought that in homogeneous chemical reactions carried out at constant temperature, the appearance of temporal oscillations of the concentration of the reactants could not occur. However, in 1920, Alfred Lotka proposed an autocatalytic model of reaction exhibiting temporal oscillations. Moreover, in the early 1950s, Belousov, a Russian biophysicist, found oscillations in the colour and electrochemical potential of a mixture of citric acid, cerium and bromate in sulphiric acid.

Since these pioneering works, much experimental and theoretical research have been carried out on kinetic chemistry to show and to explain not only temporal or spatial wave patterns, but also spatio-temporal wave patterns observed in different types of chemical reactions. Perhaps the most impressive wave behaviour is chemistry is exhibited by the so called Belouzov–Zhabotinsky reaction. The complex wave behaviour of this reaction include changing coloured bands, simple and multi-armed rotating spirals in two-dimensional films and scroll waves and helicoidal twisted chemical scrolls in three dimensions.

Several living systems also exhibit similar wave behaviours to those observed in chemistry. For example, the chemotactic aggregation phenomena in the cellular slime model of Dyctyostelium discoideum show aggregative spiral patterns towards those places where a chemoatractant is delivereded. Some dynamical features of the Belousov–Zhabotinsky reaction suggest analogues for behaviour in heart muscle, particularly in fibrillation state.

Other types of waves have also been observed in autocatalytic and isothermal chemical reactions, such as those in which the substances propagate in space at constant speed in such a way that the concentration does not change its profile as time increases. These are the so called traveling waves.

Traveling waves have been successfully used in physiology to describe nerve action potential conduction through the axon of neurons. Based in some delicate and systematic experiments carried out in squid axon, Hodgkin and Huxley developed a theory to explain the above phenomenon. Their model consists of a system of four nonlinear differential equations: one of reaction-diffusion type and three ordinary differential equations. Their analysis predict the existence of two pulses, which have been observed experimentally. Since the Hodgkin–Huxley is not easy to analyse, several simplifications have been proposed to reduce the number and the form of their equations. Two of them were developed by Nagumo and FitzHugh.

Traveling wave behaviour has also been observed in ecology. As a way of example, we have the wave of invasion of grey squirrels in Britain during the first half of last century and the epizootic wave of rabies among foxes in England.

The above examples show a wide range of traveling wave behaviours in different systems. The first mention of traveling waves in biological and chemical sciences occurs in the work of Luther in 1906. To describe a nerve conduction problem, he draws an analogy between these phenomena and a crystallization process. Three decades later, in two separate papers, Fisher and Kolmogoroff et al. who were studying the spread of an advantageous gene in a population living in a one-dimensional habitat, began a mathematical approach to analyse the existence of tws in reaction-diffusion models with constant diffusion coefficient. In fact, the main ideas of Kolmogoroff et al.’s work are still used today. Since their seminal investigations, much work have been undertaken to extend this analysis to more general reaction-diffusion equations, particularly in cases in which the diffusion term is nonlinear.

From a mathematical perspective, a wide range of methods and approaches have been introduced with the aim of investigating the existence of tws of different nonlinear reaction-diffusion models. One approach, which has been widely and successfully used, is that of dynamical systems. In this, searching for the conditions for the existence of tws in the nonlinear reaction-diffusion equations, is restated as a dynamical system problem consisting in looking for conditions for the existence of heteroclinic trajectories connecting pairs of equilibrium points of an autonomous nonlinear ODE system. This system comes from writing down the reaction-diffusion equations in the traveling wave coordinates. Even within the dynamical approach, several tools have been used for that purpose. These range from those of topological perspective as the Conley index or isolate blocks to those more visual and transparent as shooting arguments, including bifurcation analysis and perturbation methods.

In this paper, we present an overview of the existence of tws analysis for different nonlinear reaction-diffusion equations. This review covers a wide range of the above-mentioned equations: from those with constant diffusion coefficients and nonlinear reactive part to those which have density-dependent diffusion coefficient and nonlinear reactive part as well. The contents of this paper is organized as follows. In Section 2 we begin our review by presenting a sketch of the tws analysis for classical one-dimensional nonlinear reaction-diffusion equations. The origin of these is quite diverse, ranging from the propagation of and advantageous gene within a population to the voltage propagation along the neural axon. In Section 3 we introduce other nonlinearity into the equations by considering density-dependet diffusion coefficient giving rise to nonlinear degenerate reaction-diffusion equations. Here, we also present a summarized version of the tws analysis for two families of PDE of this type. In all the above-mentioned cases, in addition to presenting an abbreviated version of the analysis, we included a number of numerical simulations with the aim to illustrate the results. Those are organized as examples. The paper ends in section 4 where we present some concluding remarks and some perspectives for future studies which we consider are worth of investigating.

2 CLASSICAL REACTION-DIFFUSION EQUATIONS

This section is devoted to sketch the proof of existence of tws for classical reaction-diffusion-equations which have constant diffusion coefficient and nonlinear different reactive or kinetic part. Just for completeness prior to do so, we present a schematic derivation of the reaction-diffusion equations.

2.1 A Sketched Derivation

Reaction-diffusion equations is a suitable mathematical frame of work for modelling and describing a wide range of wave behaviours in living and non-living systems. In these lines, we present just a quick view of the derivation of such equations. There exist two main approaches for the derivation of reaction-diffusion equations: random walks and continuum media. In the later, two fundamental laws are used. Namely:

• 1. The conservation mass law. Here, denoting by $u(\vec{r},t)$ the concentration at the point $\vec{r}\in\Omega\subset{\mathbb{R}}^{3}$ at time $t$, of a diffusing substance. For the a strict diffusive process the conservation mass law reads as

  $$\frac{\partial u}{\partial t}=-\nabla\cdot\vec{J},$$

  (1)

  where $\vec{J}$ is the flow of the substance in such a way that its norm, $||\vec{J}||$, measures the amount of substance crossing a unitary area in a time unit in the normal exterior (to the boundary $\partial\Omega$) direction.

• 2. A law for the flow. In the conservation mass law (1), the explicit expression for the flow $\vec{J}$ could be quite different giving rise to different diffusion equations. The simplest form for $\vec{J}$ comes from the Fick’s law according which the flow is in the opposite direction of the gradient of the substance concentration. In such a case

  $$\vec{J}=-D\nabla u,$$

  (2)

  where $D>0$ is the diffusivity of the substance and the operator $\nabla$ acts only on the spatial coordinates. Once we substitute (2) into (1), we obtain the partial differential equation for just the diffusive process

  $$\frac{\partial u}{\partial t}=D\sum_{i=1}^{3}\frac{\partial^{2}u}{\partial x_{i}^{2}}.$$

  (3)

  In case the substance takes part of a kinetic process whose instantaneous rate depends on the concentration $u$ given by the function $f(u;\mu)$, where $\mu$ is a kinetic parameter, then we have the following reaction-diffusion equation for $u$

  $$\frac{\partial u}{\partial t}=D\sum_{i=1}^{3}\frac{\partial^{2}u}{\partial x_{i}^{2}}+f(u;\mu),$$

  (4)

  where the explicit form of $f$ depends on the specific kinetics is taking place.

In case of $n$ reactants which diffuse and react together, the Eq. (4) is transformed in a reaction-diffusion equations system for the concentrations vector $\vec{U}=(u_{1},u_{2},\cdots,u_{n})$ and the diffusion coefficient $D$ becomes the positive diagonal matrix, $\mathcal{D}=diag\,(D_{1},D_{2},\cdots,D_{n})$, where $D_{i}$ for $i=1,2,\cdots,n$ is the diffusivity of the $i$th reactant. Once we add the initial and the boundary conditions, the mathematical problem is completed.

In other side it is documented in the scientific literature the existence of processes or phenomena in which the diffusivity, $D$, appearing in (2) is not constant any more. In certain cases such a coefficient is a density-dependent function. The consequence of this is that the corresponding diffusive part in (3), becomes nonlinear. This nonlinearity in addition to other nonlinearity coming from the function $f$, makes the corresponding PDE highly nonlinear. As a way of example we have the one-dimensional nonlinear reaction-diffusion equation

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[D(u)\frac{\partial u}{\partial x}\right]+f(u;\mu),$$

(5)

where typically $D:[0,1]\rightarrow\mathbb{R}$ with $D(0)=0$ and $D(u)>0$ $\forall\;u\in(0,1]$. For appropriate kinetic part $f$ the above equation describes the spatio-temporal dynamics of a population whose capacity for diffusing over the one-dimensional space, depends on the local population density. Since $D(0)=0$ and $D(u)>0$ $\forall\,u\in(0,1]$ the Eq. (5) degenerates at $u=0$ into an ODE and is of parabolic type for $u\in(0,1]$. As we will see in Section 3, the degeneracy has both mathematical and interpretative important consequences.

2.2 Fisher-KPP Equation

In 1937 the British statistician and genetician Ronald Aylmer Fisher (see [9]) when he was working at Rothamsted Experimental Station (focused on agriculture) he was interested in the description of the way in which an advantageous gene $A$, is propagated within a population which is living in an infinite one-dimensional space. For this aim, he introduced as state variable the probability, $u(x,t)$, that the gen $A$ is at point $x$ at time $t$. Fisher derived the partial differential equation (PDE) which is satisfied by $u$:

$$\frac{\partial u}{\partial t}=D\frac{\partial^{2}u}{\partial x^{2}}+ru(1-u),\quad-\infty<x<+\infty,\quad t>0,$$

(6)

where $D>0$ is the diffusivity. The above PDE has two stationary and homogeneous solutions: $\tilde{u}_{0}(x,t)\equiv 0$ and $\tilde{u}_{1}(x,t)\equiv 1$. By using a series of plausible reasoning, he was able of providing a condition on the propagation speed, $c>0$, for the existence of a wave, $u(x,t)=\phi(x-ct)\equiv\phi(\xi)$ of the advantageous gene connecting the states $\tilde{u}_{1}(x,t)\equiv 1$ with $\tilde{u}_{0}(x,t)\equiv 0$. In fact, he found the minimal speed, $c^{*}=2\sqrt{Dr}$, such that for each $c\geq c^{*}$ Eq. (6) has a monotone decreasing tws satisfying

• 1. $0<\phi(\xi)<1,\;\forall\;\xi\in(-\infty,+\infty)$, $\lim_{\xi\rightarrow-\infty}\phi(\xi)=1$, $\lim_{\xi\rightarrow+\infty}\phi(\xi)=0$,

• 2. $\phi^{\prime}(\xi)<0,\forall\,\xi\in(-\infty,+\infty)$, $\lim_{\xi\rightarrow-\infty}\phi^{\prime}(\xi)=\lim_{\xi\rightarrow-\infty}\phi^{\prime}(\xi)=0$.

Also in 1937 independently from Fisher, the Russian mathematicians Kolmogoroff, Petrovsky and Piskounov (see [12]) studied a more general nonlinear reaction-diffusion equation with the same aim as that of Fisher. The equation these authors studied is

$$\frac{\partial u}{\partial t}=\frac{\partial^{2}u}{\partial x^{2}}+f(u),$$

(7)

where $f$ satisfies

• 1. $f:[0,1]\rightarrow\mathbb{R}$ with $f(0)=f(1)=0$, $f(u)>0\,\forall\,u\in(0,1)$,

• 2. $f\in C^{1}_{[0,1]}$ with $f^{\prime}(0)>0$ and $f^{\prime}(1)<0$.

Kolmogoroff et al. approached the problem in a rigorous and formal way. Indeed, their paper contains a series of analytical results for supporting the existence of monotonic decreasing tws of front type for Eq. (7). What we present here is a modern and resumed version.

Setting $\nu=sup\left[\frac{f(u)}{u}\right]$, where the suppremum is taken on the interval $(0,1)$ the following theorem can be proven.

Theorem 1 (cited from [3]). If the function $f$ satisfies the above conditions then for each $c$ Eq. (7) possesses a monotonic decreasing tws $u(x,t)=\phi(x-ct)\equiv\phi(\xi)$ satisfying

• 1. $\lim_{\xi\rightarrow-\infty}\phi(\xi)=1$, $\lim_{\xi\rightarrow+\infty}\phi(\xi)=0$, $0<\phi(\xi)<1$, $\forall\,\xi\in(-\infty,+\infty),$

• 2. $\lim_{\xi\rightarrow-\infty}\phi^{\prime}(\xi)=\lim_{\xi\rightarrow+\infty}\phi^{\prime}(\xi)=0$, $\phi^{\prime}(\xi)<0$, $\forall\,\xi\in(-\infty,+\infty)$

if and only if $c\geq c^{*}$ , where $2\sqrt{f^{\prime}(0)}\leq c^{*}\leq 2\sqrt{\nu}$ .

Sketch of the proof. This is based on the restatement of the original traveling wave solution problem satisfying the appropriate boundary value conditions in the PDE (7) into a dynamical problem consisting in searching the values of the speed $c$ for wich the two-dimensional nonlinear autonomous ODE system

$$\phi^{\prime}=v,$$

$$v^{\prime}=-cv-f(\phi)$$

(8)

has heteroclinic trajectories connecting (exactly in this order) the equilibrium points $P_{1}=(1,0)$ and $P_{0}=(0,0)$. By a straightforward linear analysis it can be seen $P_{0}$ is locally asymptotically stable equilibrium: of focus type for $c^{2}<4f^{\prime}(0)$ and of node type for $c^{2}\geq 4f^{\prime}(0)$. In the focus case, the oscillations around $P_{0}$, implies $\phi(\xi)$ take negative values which are not realistic from interpretative point of view. Because of this, these values of $c$ are not considered hereafter. The linear local analysis indicates $P_{1}$ is a saddle point for all $c>0$. The left branch of the one-dimensional unstable manifold, $W^{u}_{c}(P_{1})$, of (8) at $P_{1}$ enters the region

$$\mathcal{R}=\left\{(\phi,v)|0<\phi<1,-\infty<v<0\right\}.$$

Moreover, given that the system (8) has no closed trajectories on the phase plane (this follows by using the Negative Bendixon criterium), the restriction of the vector field which defines the system (8) on $(0,1)$ and on $(1,v)$ with $v<0$ gives vectors pointing inwards the region $\mathcal{R}$. In addition value of the slope $m$ of the segment $P_{0}Q$ can be chosen in such a way that the side $P_{0}Q$ of the triangle $P_{0}P_{1}QP_{0}$ shown in the Fig. 1, is a positive invariant set of the system (8). Indeed, this happens whenever $c>0$ satisfies $c\geq 2\sqrt{\nu}$, then by using the Poincaré–Bendixson Theorem (see [11]), the corresponding trajectories $W^{u}_{c}(P_{1})$ must end at $P_{0}$ as $\xi\rightarrow+\infty$.

Fig. 1

The segment $P_{0}Q$ can be choosen in such a way triangle $P_{0}P_{1}QP_{0}$ is a positive invariant set of (8). This happens for $c\geq 2\sqrt{\nu}$. See the text for details.

Let us denote by $(\phi_{c}(\xi),v_{c}(\xi))$ the parametric representation of $W^{u}_{c}(P_{1})$ corresponding to $c>0$ such that $c\geq 2\sqrt{\nu}$. Such a continuum set of trajectories satisfy:

• 1. $\lim_{\xi\rightarrow-\infty}(\phi_{c}(\xi),v_{c}(\xi))=(1,0)$, $\lim_{\xi\rightarrow+\infty}(\phi_{c}(\xi),v_{c}(\xi))=(0,0)$,

• 2. $0<\phi_{c}(\xi)<1\,\forall\,\xi\in(-\infty,+\infty)$, $v(\xi)<0\,\forall\;\xi\in(-\infty,+\infty)$.

It follows that Eq. (7) has a continuum of tws $\phi_{c}(\xi)$ satisfying the required boundary conditions.

Example 1. With the aim of illustrating the results presented so far we take $f(u)=u(1-u)$ from which $f^{\prime}(0)=\nu=1$ and $c^{*}=2$ is the minimum value of the speed $c$ for which the corresponding PDE (7) has a monotonic decreasing tws. Indeed, for each $c\geq 2$ the PDE $u_{t}=u_{xx}+u(1-u)$ has a monotonic decreasing tws satisfying the above mentioned boundary conditions. Figure 2(a) shows the phase portrait of the corresponding ODE system where the saddle-node heteroclinic trajectory is illustrated; meanwhile Fig. 2(b) shows the $\phi_{c^{*}}(\xi)$ component of such a trajectory.

Fig. 2

(a) Phase portrait of system (8) for $f(u)=u(1-u)$ with $c=2$ exhibiting the saddle-node heteroclinic trajectory. (b) A monotone decreasing tws for Eq. (7) physically realistic.

Remark 1. The tws $\phi(x-c^{*}t)$ of (7) corresponding to the minimal speed, acts as an attractor for the solutions of (7) corresponding to compact supported initial conditions.

2.3 Hodgkin–Huxley Model and Two Reductions

The Hodgkin–Huxley mathematical model for describing the propagation of nerve impulses through the neuron axon was derived after a series of experiments carried out on the axon of the giant squid. The first great step in this process consisted of drawing an analogy between the refractary property of the axon membrane to the flux of the different types of ions (mainly of sodium, potasium) through it and three resistences in a $RLC$ electrical circuit. Then, by assuming that the axon has a one-dimensional structure and denoting by $u(x,t)$ the membrane potential at point $x$ at time $t$, using the laws for electrical circuits and using the appropriate scaling state variables, they proposed

$$\frac{\partial u}{\partial t}=\frac{\partial^{2}u}{\partial x^{2}}+I_{i},$$

(9)

$I_{i}=I_{Na}+I_{K}+I_{L}+I_{ap},$ where each one of the currents, $I_{i}$, were characterized by introducing the so-called gate variables $m,n$ and $h$ in such a way that

$$I_{i}=g_{Na}m^{3}h(u-u_{Na})+g_{K}n^{4}(u-u_{K})+g_{L}(u-u_{L}).$$

Here $g_{(\cdot)}$ are conductances and $u_{(\cdot)}$ are the equilibrium potential of each one of the three types of ions. The gate variables satisfy the ODE system

$$\dot{n}=\alpha_{n}(1-n)-\beta_{n}(u)n,$$

$$\dot{m}=\alpha_{m}(1-m)-\beta_{m}(u)m,$$

$$\dot{h}=\alpha_{h}(1-h)-\beta_{h}(u)h,$$

(10)

where the functions $\alpha_{(\cdot)}$ and $\beta_{(\cdot)}$ were empirically determined as

$$\alpha_{n}(u)=0.01(u+10)\exp\left\{1-\left(\frac{u+10}{10}\right)\right\},$$

$$\alpha_{m}(u)=0.1(u+25)\exp\left\{1-\left(\frac{u+25}{10}\right)\right\},$$

$$\alpha_{h}(u)=0.01\exp(u/20),\quad\beta_{n}(u)=0.125\exp(u/80),$$

$$\beta_{m}(u)=4.0\exp(u/18),\quad\beta_{h}(u)=\exp\left\{-1-\left(\frac{u+30}{10}\right)\right\}.$$

By noting that the time scale variation of the gate variables is quite different, it was possible to produce a remarkable simplification of the original Hodgkin–Huxley model. Indeed, the variable $m$ is much more quiker than the others. Because of this we can consider that $m$ atains its equilibrium quicker than the others do. By using these reasonings, independently FitzHugh and Nagumo arrived to a two-variables mathematical model which takes the form

$$\frac{\partial u}{\partial t}=\frac{\partial^{2}u}{\partial x^{2}}+f(u)-w+I_{ap},\quad\frac{\partial w}{\partial t}=bu-\gamma w,$$

(11)

where $f(u)=u(1-u)(u-\alpha)$ with $0<\alpha<1$, $I_{ap}$ is an external supplied current, $b$ and $\gamma$ are positive constants. In system (11) the state variable $w$ contains the behaviour of the gate variables.

2.4 FitzHugh–Nagumo System, the One-Dimensional Case

Here by setting $I_{ap}=0$, we consider the reaction-diffusion system

$$\frac{\partial u}{\partial t}=\frac{\partial^{2}u}{\partial x^{2}}+f(u)-w,\quad\frac{\partial w}{\partial t}=bu-\gamma w,$$

(12)

where $f(u)=u(1-u)(u-\alpha)$ with $0<\alpha<1$. By setting $u(x,t)=\phi(x-ct)$ and $w(x,t)=\psi(x-ct)$ the following boundary conditions are required

$$\lim_{\xi\rightarrow-\infty}(\phi(\xi),\psi(\xi))=(0,0)\quad\textrm{and}\quad\lim_{\xi\rightarrow+\infty}(\phi(\xi),\psi(\xi))=(0,0),$$

(13)

whose interpretation is: the system comes from the unique steady state (its existence guaranteed by choosing the appropriate parameter values which will be given below) and asymptotically, gets back to such state. By sustituting $\phi(\xi)$ and $\psi(\xi)$ into (12), we obtain

$$-c\phi^{\prime}=\phi^{\prime\prime}+f(\phi)-\psi,\quad-c\psi^{\prime}=b\phi-\gamma\psi,$$

(14)

which, introducing $v=\phi^{\prime}$ is equivalent to the following nonlinear ODE system

$$\phi^{\prime}=v,\quad v^{\prime}=-cv-f(\phi)+\psi,\quad\psi^{\prime}=\frac{1}{c}[\gamma\psi-b\phi].$$

(15)

The nullclines of this system are $v=0,\psi_{1}(\phi)=f(\phi)$ and $\psi_{2}(\phi)=\frac{b}{\gamma}\phi$. In order to guarantee the system (15) has just one equilibrium at the origin of the three-dimensional coordinates, the parameters $\alpha,b$ and $\gamma$ must be choosen in such a way that

$$\frac{b}{\gamma}>\phi^{\prime}(\phi^{*})\Longrightarrow\frac{b}{\gamma}>\left(\frac{1-\alpha}{2}\right)^{2},$$

where $\phi^{*}=(1+\alpha)/2$ is the value of $\phi$ for which the two roots, $\phi_{1},\phi_{2}$, of $(1-\phi)(\phi-\alpha)-b/\gamma=0$ coincide. In turn, this happens if and only if $(1+\alpha)^{2}=4\left(\alpha+\frac{b}{\gamma}\right)$.

Denoting by $\vec{F}$ the vector field which defines the system (15), the Jacobian matrix of $\vec{F}$ at the origin is

$$J[\vec{F}]_{\vec{0}}=\left[\begin{matrix}0&1&0\\ -f^{\prime}(0)&-c&1\\ -b/c&0&\gamma/c\end{matrix}\right],$$

whose characteristic polynomial is

$$\mathcal{P}(\lambda)=\lambda^{3}+\left(\frac{c^{2}-\gamma}{c}\right)\lambda^{2}-(\gamma+a)\lambda+\left(\frac{b+a\gamma}{c}\right).$$

By using the Descartes rulle we have that $\mathcal{P}$: has two roots, $\lambda_{1},\lambda_{2}$, which have negative real part and the third root, $\lambda_{3}$, is positive. In case the three roots are real, two of them must be negative and the third one must be positive. By using the invariant manifold theorem (see [2]) it follows that the system (15) has

• A two dimensional asympotically stable manifold, $W^{s}(\vec{0})$, which locally is the plane sppaned by the eigenvectors associated with the eigenvalues $\lambda_{1}$ and $\lambda_{2}$,

• An one-dimensional unstable manifold, $W^{u}(\vec{0})$, which is transversal to $W^{s}(\vec{0})$ at $\vec{0}$ and locally is the straight line generated by the eigenvector corresponding to the eigenvalue $\lambda_{3}$.

Let us denote by $W^{u}_{-}(\vec{0})$ and $W^{u}_{+}(\vec{0})$ the negative and the positive branches of $W^{u}(\vec{0})$, respectively. It is proven that $\lim_{\xi\rightarrow+\infty}||W^{u}_{-}(\vec{0})||=\infty$. Because of this, the candidate to being the trajectory of the system (15) satisfying the above mentioned boundary conditions is $W^{u}_{+}(\vec{0})$. Therefore we must study the behaviour of this branch of the unstable manifold as the parameters change. In particular, we are interested in searching the existence of values of $c$ for which

• $W^{u}_{+}(\vec{0})$ must be bounded for all $\xi\in(-\infty,+\infty)$,

• $\lim_{\xi\rightarrow-\infty}\left\{W^{u}_{+}(\vec{0})\right\}=(0,0,0)$ and $\lim_{\xi\rightarrow+\infty}\left\{W^{u}_{+}(\vec{0})\right\}=(0,0,0)$,

which in turn means that $W^{u}_{+}(\vec{0})$ should b e a homoclinic trajectory of the system (15). By using different approaches the above mentioned investigations already have been done (see for instance [10]). Those have shown the system (15) has

• 1. A simple homoclinic trajectory, $(\phi(\xi),v(\xi),\psi(\xi))$, whose first component, $\phi(\xi)$, defines a traveling simple pulse representing the membrane potential,

• 2. A sort of double homoclinic trajectory whose first component, $\phi(\xi)$, corresponds to a traveling train composed by two pulses. The phrase ‘‘A sort of’’ makes sense since strictly speaking is not a double homoclinic trajectory. The trajectory does not land at the origin twice, but it does so at the second try instead.

In fact, the system (15) also exhibits a sort of multiple homoclinic trajectories which correspond to a traveling train composed by multiple pulses. The detailed analysis can be seen elsewhere (see [10]).

Example 2. Here we restrict ourselves just by showing a couple of numerical simulations which give us the phase space of the system (15) when $f(u)$ is a Heaviside function. These can be seen in Figs. 3 and 4.

Fig. 3

(a) A simple homoclinic trajectory of the system (15). (b) Graph of the first component, $\phi(\xi)$, of the homoclinic trajectory in (a) which defines is a traveling simple pulse. Here we choosed $f(u)$ as the Heaviside function.

Fig. 4

(a) A double homoclinic trajectory of the system (15). (b)The graph of the first component, $\phi(\xi)$, of the ‘‘double homoclinic trajectory’’ in (a) which defines a traveling train compoused by two pulses.

2.5 FitzHugh–Nagumo System, a Two-Dimensional Case

For introducing the two-dimensional FitzHugh–Nagumo model, let us define the annular region

$$\mathcal{A}_{R}=\left\{(r,\theta)|R<r<1,\theta\in(-\pi,+\pi)\right\}.$$

The mathematical model we consider here is

$$\frac{\partial u}{\partial t}=D\nabla^{2}u+f(u)-w+I_{ap},\quad\frac{\partial w}{\partial t}=bu-\gamma w,$$

(16)

for all $(r,\theta,t)\in\mathcal{A}_{R}\times[0,+\infty)$ where $b,\gamma$ and $D$ are positive constants and the Laplacian operator is written in polar coordinates as

$$\nabla^{2}u=\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial u}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial^{2}u}{\partial\theta^{2}},$$

and typically $f(u)=u(1-u)(u-\alpha)$ with $0<\alpha<1$. Depending upon $I_{ap}$ let us assume the system (16) has a stationary and homogeneous positive state $(\hat{u}(I_{ap}),\hat{w}(I_{ap}))$.

For completing the mathematical problem we are interested in, we add the boundary conditions

$$\frac{\partial u}{\partial r}(R,\theta,t)=\frac{\partial u}{\partial r}(1,\theta,t)=0,\quad\theta\in[-\pi,+\pi],\quad t>0.$$

(17)

We require that both $u$ and $w$ must be $2\pi$-periodic in $\theta$. For given $R,D$ and $I_{ap}$, we look for conditions for the existence of rotating traveling waves as solutions of the problem (16), (17). By these we mean

$$u(r,\theta)=\phi(r,\theta-ct)\quad\textrm{and}\quad w(r,\theta)=\psi(r,\theta-ct),$$

(18)

where $c>0$ is the rotating speed. By substituting (18) into (16) we obtain

$$D\nabla^{2}\phi+c\phi^{\prime}+f(\phi)-\psi+I_{ap}=0,$$

$$c\psi^{\prime}+b\phi-\gamma\psi=0,$$

(19)

where the symbol ${}^{\prime}$ on $\phi$ and $\psi$ denotes the derivative with respect $\xi=\theta-ct$. For $R,D$ and $I_{ap}$ we look for positive values of $c$ such that the pair $(\phi(r,\xi),\psi(r,\xi))$ must be solution of (16), (17).

In short the rotatory solutions of (16) emerge from a Hopf bifurcation of the homogeneous and stationary solution, $(\hat{u}(I_{ap}),\hat{w}(I_{ap}))$, we assumed to exists. Here, we just sketch the analysis, full details can be seen in the reference [1].

The first step is to linearize (19) around $(\hat{u}(I_{ap}),\hat{v}(I_{ap}))$. Thus, let us write

$$\phi(r,\xi)=\hat{u}(I_{ap})+\nu_{1}(r,\xi),$$

$$\psi(r,\xi)=\hat{v}(I_{ap})+\nu_{2}(r,\xi).$$

Substituting these expresions into (19) and retainig the just the linear terms, we obtain that $\nu_{1}(r,\xi)$ and $\nu_{2}(r,\xi)$ must satisfy

$$D\nabla^{2}\nu_{1}+c\frac{\partial\nu_{1}}{\partial\xi}+f^{\prime}(\hat{u}(I_{ap}))\nu_{1}-\nu_{2}=0,$$

$$c\frac{\partial\nu_{2}}{\partial\xi}+b\nu_{1}-\gamma\nu_{2}=0.$$

(20)

We propose $\nu_{1}(r,\xi)=a_{1}(r)e^{im\xi},$ $\nu_{2}(r,\xi)=a_{2}(r)e^{im\xi}$ as solution of the system (20). Then

$$-D\mathcal{L}_{m}(a_{1}(r))+f^{\prime}(\hat{u}(I_{ap}))a_{1}(r)-a_{2}(r)=-imca_{1}(r),$$

$$ba_{1}(r)-\gamma a_{2}(r)=-imca_{2}(r),$$

(21)

where

$$\mathcal{L}_{m}(a_{1}(r))=-\frac{1}{r}\frac{d}{dr}\left[r\frac{da_{1}}{dr}\right]+\frac{m^{2}}{r^{2}}a_{1},\quad\textrm{with}\quad r\in(R,1),$$

(22)

$a_{1}^{\prime}(R)=a_{2}^{\prime}(R)=0$. From the second equation in (21)

$$a_{2}(r)=\frac{ba_{1}(r)}{b(\gamma-imc)}$$

then we obtain the following Sturm–Liouville problem

$$\mathcal{L}_{m}(a_{1}(r))=\lambda a_{1}(r),$$

(23)

where $\lambda=D^{-1}(imc-b(\gamma-imc))^{-1}+f^{\prime}(\hat{u}(I_{ap})).$ By the classical Sturm–Liouville theory we have that for each positive integer $m$ the problem (23) has an infinite number of eigenvalue, $\lambda_{mn}$, with $n=1.2,\cdots$. The set of eigenvalues are ordered as follows $0<\lambda_{m1}<\lambda_{m2}<...<\lambda_{mn}<\cdots$ and all of them depend on $R$. Let us introduce the following notation $\vec{b}=(a_{1}(R),a_{2}(R))^{T}$, where $T$ means transpose and

$$S_{mn}(R,I_{ap})=\left[\begin{matrix}-\lambda_{mn}(R)D+f^{\prime}(\hat{u}(I_{ap}))&-1\\ b&-\gamma\end{matrix}\right],$$

whose

$$tr\,S_{mn}(I_{ap})=-\lambda_{mn}(R)D+f^{\prime}(\hat{u}(I_{ap}))-\gamma$$

and

$$det\;S_{mn}(I_{ap})=-\gamma[-\lambda_{mn}(R)D+f^{\prime}(\hat{u}(I_{ap}))]+b.$$

By choosing $I_{ap}$ as bifurcation parameter, there exists a critical value of $I_{ap}$ for which $S_{mn}(I_{ap})$ has purelly imaginary eigenvalues. Moreover a Hopf-bifurcation occurs from which rotatory tws emerge. Full details can be seen in [1] and [4].

Example 3. Figure 5 contains a panel of numerical simulations which shows the temporal evolution of rotatory traveling waves of the system (16) corresponding to and homogeneous Neumann boundary conditions. As it can be seen in Fig. 5 the rotatory waves rotate in clockwise sense. One remarkable feature of these waves is that the front and the back evolve in such a way that both of them do so in such a way they look like branches of spirals and the excited area (the red one) changes in size as the running time increases.

Fig. 5

This panel shows the $u$ component of the rotating tws for the FitzHugh–Nagumo model (16) at different running times. The color code is as follows: Red color indicates high $u$ concentration and blue means low $u$ concentration. The snapshoots were taken each twenty running time units.

3 NONLINEAR DEGENERATE REACTION-DIFFUSION EQUATIONS

The nonlinearity of the PDE’s presented so far comes from the reactive part. In this section we are going to introduce another source of nonlinearty: this comes from the nonlinear Fickian law for the flow. Actually along this section we are going to consider density dependent diffusion coefficients, $D(u)$, which vanish at certain point of its domain (typically at $u=0$) and positive for $u>0$. Thus, we will consider two families of such nonlinear degenerate reaction-diffusion equations which generalize the previously studied equations.

3.1 The Degenerate Fisher-KPP Equation

Here we consider the so-called degenerate Fisher-KPP equation

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[D(u)\frac{\partial u}{\partial x}\right]+f(u),\quad-\infty<x<+\infty,\quad t>0,$$

(24)

where $f$ and $D$ satisfy

• 1. $f:[0,1]\rightarrow\mathbb{R}$ with $f(0)=f(1)=0$, $f(u)>0$ $\forall\,u\in(0,1)$,

• 2. $f\in C^{2}_{[0,1]}$ with $f^{\prime}(0)>0$ and $f^{\prime}(1)<0$,

• 3. $D:[0,1]\rightarrow\mathbb{R}$ with $D(0)=0$, $D(u)>0$ $\forall\,u\in(0,1]$,

• 4. $D\in C^{2}_{[0,1]}$ with $D^{\prime}(u)>0$ and $D^{\prime\prime}(u)\neq 0$, $\forall\,u\in[0,1].$

Since $D(0)=0$, Eq. (24) is degenerate at $u=0$ and of parabolic type for $u>0$. Let us introduce the following definition.

Definition 1. If there exists a value $c^{*}>0$ of the speed $c$, and a value $\xi^{*}\in(-\infty,+\infty)$ of $\xi$ such that $u(x,t)=\phi(x-c^{*}t)$ satisfies:

• 1. $D(\phi)\phi^{\prime\prime}+c^{*}\phi^{\prime}+D^{\prime}(\phi)[\phi^{\prime}]^{2}+f(\phi)=0$ $\forall\,\xi\in(-\infty,\xi^{*})$,

• 2. $\phi(-\infty)=1$, $\phi(\xi^{*-})=\phi(\xi^{*+})=0$ and $\phi(\xi)=0$ $\forall\,\xi\in(\xi^{*},+\infty)$,

• 3. $\phi^{\prime}(\xi^{*-})=-\frac{c^{*}}{D^{\prime}(0)}$, $\phi^{\prime}(\xi^{*+})=0$ and $\phi^{\prime}(\xi)<0$ $\forall\,\xi\in(-\infty,\xi^{*})$

then the function $u(x,t)=\phi(x-c^{*}t)$ is called a travelling wave solution of sharp type for (24).

Because of the features of the function $f$, the Eq. (24) has two stationary and homogeneous solutions: $\tilde{u}_{0}(x,t)\equiv 0$ and $\tilde{u}_{1}(x,t)\equiv 1$.

In this case the following theorem can be proven.

Theorem 2 (adapted from [18]). Whenever the functions $D$ and $f$ satisfy the conditions 1–4, there exists a unique positive value, $c^{*}$, of $c$ such that the Eq. (24) has

• 1. No tws for $0<c^{*}<c$ ,

• 2. A unique tws of sharp type for $c=c^{*}$ ,

• 3. A monotonic tws of front type for each $c>c^{*}$ connecting the stationary and homogeneous states $\tilde{u}_{1}(x,t)\equiv 1$ and $\tilde{u}_{0}(x,t)\equiv 0$ .

Sketch of the proof. By setting $u(x,t)=\phi(x-ct)\equiv\phi(\xi)$ and substituting this anzats into the PDE (24) we obtain $\phi(\xi)$ must satisfy

$$-c\phi^{\prime}=D(\phi)\phi^{\prime\prime}+D^{\prime}(\phi)[\phi^{\prime}]^{2}+f(\phi),\quad\forall\;\xi\in(-\infty,+\infty),$$

(25)

which by introducing $v=\phi^{\prime}$ it can be written as the singular (at $\phi=0$) ODE system

$$\phi^{\prime}=v,$$

$$D(\phi)v^{\prime}=-cv-D^{\prime}(\phi)v^{2}-f(\phi).$$

(26)

The singularity of this system comes from the degeneracy (at $u=0$) of Eq. (24). By means of a reparameterization of the trajectories of (26), such a singularity can be removed. Indeed by introducing $\tau$ such that for $D(u)>0$

$$\frac{d\tau}{d\xi}=\frac{1}{D(\phi(\xi))}$$

(27)

and setting

$$\phi(\xi)=\phi(\tau(\xi))\quad\textrm{and}\quad v(\xi)=v(\tau(\xi)),$$

(28)

the ODE system (26) can be written as

$$\dot{\phi}=D(\phi)v\equiv F_{1}(\phi,v),$$

$$\dot{v}=-cv-D^{\prime}(\phi)v^{2}-f(\phi)\equiv F_{2}(\phi,v),$$

(29)

where the dot on $\phi$ and $v$ denotes derivative with respect $\tau$. We successfully have removed the singularity of the system (26). Note that the ODE systems (26) and (29) are topologically equivalent in the positive half plane $\left\{(\phi,v)|\phi>0,\;-\infty<v<+\infty\right\}$.

For the stated conditions on $D$ and $f$ system (29) has three equilibrium points: $P_{0}=(0,0),P_{1}=(1,0)$ and $P_{c}=(0,-c/D^{\prime}(0))$. The local linear analysis of (29) gives: $P_{1}$ and $P_{c}$ are saddle points for all positive values of $c$; meanwhile $P_{0}$ is a non-hyperbolic point and then a nonlinear local analysis of (29) around $P_{0}$ is required. This gives $P_{0}$ is a non-hyperbolic saddle-node having an one-dimensional stable centre manifold which can be approximated with any degree of accuracy (see [5]). Actually the proof of Theorem 2 is based in the corresponding proof of the following lemma.

Lemma 1 (cited from [18]). Whenever the functions $D$ and $f$ satisfy the stated previous conditions, there exists a unique positive value, $c^{*}>0$, of $c$ such that the ODE system (29) has

• 1. Not heteroclinic trajectories for $0<c<c^{*}$ ,

• 2. A unique heteroclinic trajectory connecting (exactly in this order) the equilibrium $P_{1}$ and $P_{c^{*}}$ for $c=c^{*}$ ,

• 3. A continuum of heteroclinic trajectories connecting (exactly in this order) the equilibrium $P_{1}$ and $P_{0}$ .

For the proof of this lemma the following points are key ones:

• 1. The left branch of the unstable manifold, $W_{c}^{u}(P_{1})$, of the system (29) at the equilibium $P_{1}$ enters the region ${\mathcal{R}}:\left\{(\phi,v)|0<\phi<1,\,-\infty<v<0\right\}$.

• 2. The angle $\theta(\phi,v;c)$ formed by the vector field $(F_{1}(\phi,v),F_{2}(\phi,v))$ which defines the system (29) with the positive $\phi$ horizontal axis is a decreasing function of $c$ within the region $\mathcal{R}$.

• 3. Looking at the behavoiur of the nontrivial branches of the vertical null-clines

  $$V_{1}(\phi)=\frac{-c+\sqrt{c^{2}-4D^{\prime}(\phi)f(\phi)}}{2D^{\prime}(\phi)}\quad\textrm{and}\quad V_{2}(\phi)=\frac{-c-\sqrt{c^{2}-4D^{\prime}(\phi)f(\phi)}}{2D^{\prime}(\phi)}$$

  of the system (29) as $c>0$ changes.

• 4. The usage of shooting arguments (see [21]) allows to choose $c$ in such a way that $W_{c}^{u}(P_{1})$ goes to $(0,-\infty)$ for $0<c<c^{*}$ or ends: at $P_{c^{*}}$ for $c=c^{*}$ and at $P_{0}$ for all each $c>c^{*}$.

Full details can be seen in the reference [18]. $\Diamond$

Let us denote by $(\phi_{c^{*}}(\tau),v_{c^{*}}(\tau))$ the parametric representation of the saddle-saddle heteroclinic trajectory connecting $P_{1}$ with $P_{c^{*}}$ mentioned in Lemma 1. According with Definition 1 the first component, $\phi_{c^{*}}(\tau)$, of such a trajectory defines the sharp tws of (24); meanwhile for each $c>c^{*}$, let us denote by $(\phi_{c}(\tau),v_{c}(\tau))$ the continuum of heteroclinic trajectories connecting $P_{1}$ with $P_{0}$ mentioned in item 3 of Lemma 1. It is clear that for each $c>c^{*}$, $\phi_{c}(\tau)$ defines a monotonic decreasing tws of front type for Eq. (24).

The following example illustrates the results presented in this subsection for specific selected functions $D(u)$ and $f(u)$ having the above mentioned features.

Example 4. By choosing $D(u)=u$ and $f(u)=u(1-u)$ we have the degenerate PDE

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[u\frac{\partial u}{\partial x}\right]+u(1-u)$$

then the desingularizated ODE system (29) takes the form

$$\dot{\phi}=\phi v,$$

$$\dot{v}=-cv-v^{2}-\phi(1-\phi)$$

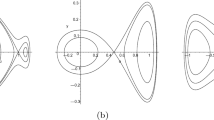
whose equilibrium points are: $P_{0}=(0,0),\;P_{1}=(1,0)$ and $P_{c}=(0,-c)$. Here, by using a straightforward procedure, an exact evaluation of the critical value, $c^{*}$, of $c$ mentioned in the Theorem 1, can be obtained resulting in $c^{*}=1/\sqrt{2}$. Figure 6 shows a panel of the relevant phase portraits the above ODE system for different values of $c$. For completeness, we drawn the phase portrait on the Poincaré disk. The numerics contained in Fig. 6 give us the whole dynamics of the system (29) on the plane. As it can be seen the ODE system has a rich dynamics particularly the existence of six equilibria at infinity which appear on the boundary of the disk. In addition, such simulations show us a nice symmetry of the phase portrait.

Fig. 6

Phase portrait of the ODE system (29) for $D(u)=u$ and $f(u)=u(1-u)$ and different values of $c$. Here $c^{*}=1/\sqrt{2}$.

Associated with each heteroclinic trajectory shown in Fig. 6, we have two different tws solutions for the above mentioned degenerate PDE. These are shown in Fig. 7.

By considering compact supported initial condition we numerically solved the corresponding degenerate PDE we also numerically evaluated the critial speed $c^{*}$. The obtained numerical evaluation of $c^{*}$ nicely matches with that for which the ODE system (29) has the unique saddle-saddle heteroclinic trajectory. The detalied analysis, other numerical simulations showing the relevant phase spaces for other illustrative examples, can be found in references [18] and [19].

Fig. 7

Different tws for the degenerate PDE with $D(u)=u$ and $f(u)=u(1-u)$. (a) The sharp tws for $c*=1/\sqrt{2}$. (b) A monotonic decreasing and smooth front for each $c>1/\sqrt{2}$.

Remark 2. Because of the existence of a saddle-saddle heteroclinic trajectory for (29), this system is not structurally stable (see [8]). In particular, a slight change on the $c$ values around $c^{*}$ drastically changes the structure of the dynamics of (29).

By considering functions with compact support on the one-dimensional space as initial conditions, the corresponding numerical solution of the full PDE (24) for specific examples nicely evolves to the sharp tws of such an equation which in addition, in good agreement with the saddle-saddle heteroclinic trajectory of the system (29). In [18] the reader can find a series of numerical simulations on both the phase portrait of particular systems of the form (29) showing the relevant dynamical behaviour contained in Lemma 1 and on the full PDE equation as well.

Remark 3. Note that the sharp tws of the PDE (24) whose sufficient conditions for its existence are stated in Theorem 2, has discontinuous derivative at finite value of $\xi$. Because of this, such a solution is not a classical (or strong) solution of (24). Actually, by introducing an appropriate sense of weak solution such sharp solution is of that type. For instance, the authors in [Depablo], the authors introduced a weak solution sense for a porous media PDE. In their sense our tws of sharp type can be included.

3.2 An Approximation to a Sharp Traveling Wave

In [17] the authors, by noting that the path of the saddle$(P_{1}=(1,0))$–saddle$(P_{c^{*}}=(0,-c^{*}))$ heteroclinic trajectory of the ODE system

$$\dot{\phi}=\phi v,$$

$$\dot{v}=-cv-v^{2}-\phi(1-\phi)),$$

(30)

which becomes from the nonlinear degenerate PDE

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[u\frac{\partial u}{\partial x}\right]+u(1-u),$$

(31)

once it is written in the traveling wave coordinates and the singularity (at $u=0$) has been removed, is the straight line

$$v_{0}(\phi)=\frac{1}{\sqrt{2}}(\phi-1),$$

occurring for $c^{*}=1/\sqrt{2}$, used a singular perturbation method to approximate the corresponding path of the saddle$(P_{1}=(1,0))$–saddle$(P_{c^{*}}=(0,-c^{*}))$ heteroclinic trajectory of the ODE system

$$\dot{\phi}=(\phi+\varepsilon\phi^{2})v,$$

$$\dot{v}=-cv-(1+2\varepsilon\phi)v^{2}-\phi(1-\phi),$$

(32)

where $0\leq\varepsilon<<1$, which comes from the degenerate PDE equation

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[(u+\varepsilon u^{2})\frac{\partial u}{\partial x}\right]+u(1-u)$$

(33)

once this is written in the traveling wave coordinates. Thus, by proposing

$$v(\phi;\varepsilon)=v_{0}(\phi)+v_{1}(\phi)\varepsilon\quad\textrm{and}\quad c(\varepsilon)=\frac{1}{\sqrt{2}}+c_{1}\varepsilon,$$

where $v_{1}(\phi)$ and $c_{1}$ are unknown, up to first order approximation (in terms of $\varepsilon$) for the path of the saddle$(P_{1}=(1,0))$-saddle$(P_{c^{*}}=(0,-c^{*}))$ heteroclinic trajectory of system (32) and the speed, respectively. These authors found

$$v(\phi;\varepsilon)=\frac{1}{\sqrt{2}}(\phi-1)\left[1+\frac{(1-3\phi)}{5}\varepsilon\right]\quad\textrm{and}\quad c(\varepsilon)=\frac{1}{\sqrt{2}}+\frac{1}{5\sqrt{2}}\varepsilon,$$

from which an approximation for the sharp tws of (33) can be obtained. Full details can be seen in the reference [17].

3.3 The Degenerate Nagumo Equation

In this subsection we briefly review the existence of tws for the degenerate (at $u=0$) nonlinear reaction-diffusion equation

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[D(u)\frac{\partial u}{\partial x}\right]+f(u),\quad-\infty<x<+\infty,\quad t>0,$$

(34)

where for $\alpha\in(0,1)$, $f$ and $D$ satisfy

• 1. $f:[0,1]\rightarrow\mathbb{R}$ with $f(0)=f(\alpha)=f(1)=0$, $f(u)<0$ $\forall\,u\in(0,\alpha)$, $f(u)>0$ $\forall\,u\in(\alpha,1)$,

• 2. $f\in C^{2}_{[0,1]}$ with $f^{\prime}(0)<0$, $f^{\prime}(\alpha)>0$ and $f^{\prime}(1)<0$,

• 3. $D:[0,1]\rightarrow\mathbb{R}$ with $D(0)=0$, $D(u)>0$ $\forall\,u\in(0,1]$,

• 4. $D\in C^{2}_{[0,1]}$ with $D^{\prime}(u)$ and $D^{\prime\prime}(u)$ strictly positive $\forall\,u\in[0,1]$.

A typical kinetic term $f$ satisfying the above conditions is $f(u)=u(1-u)(u-\alpha)$ which has relevant ecological and physiological interpretations. In the first case $u$ denotes the population density and such a reactive part describes the so called Alee effect characterized by the existence of a threshold $\alpha$ such that bellow this amount the population density diminishes tending to the extinction and above that, the population density increases. For the second interpretation $u$ denotes the membrane potential.

Note the Eq. (34) has three homogeneous and stationary solutions: $\tilde{u}_{0}(x,t)\equiv 0$, $\tilde{u}_{\alpha}(x,t)\equiv\alpha$ and $\tilde{u}_{1}(x,t)\equiv 1$ which have the following interpretation: $\tilde{u}_{0}(x,t)$ is the steady state, $\tilde{u}_{\alpha}(x,t)$ is the threshold and $\tilde{u}_{1}(x,t)$ is the excited state, respectively. As we will see, due to the existence of these three solutions, the tws problem for (34), is richer than the corresponding for the degenerate Fisher-KPP equation.

Let us introduce the function $\mathcal{D}:[0,1]\rightarrow\mathbb{R}$ defined as

$$\mathcal{D}(\phi)=\int\limits_{0}^{\phi}D(s)f(s)ds.$$

For the degenerate Nagumo equation the following theorem can be proven.

Theorem 3 (cited from [20]). If the functions $D$ and $f$ satisfy the conditions 1–4 previously stated, then there exists a unique value, $c^{*}>0$, of the speed $c$ such that the Eq. (34)

• 1. has for $c=0$ : a) an isolated pulse based at $P_{0}$ if $\mathcal{D}(1)>0$ ; b) an isolated pulse based at $P_{1}$ if $\mathcal{D}(1)<0$ ; c) two stationary monotonic fronts: one connecting the states $0$ to $1$ and the other connecting $1$ to $0$ if $\mathcal{D}(1)=0$ ,

• 2. has an oscillatory front from $0$ to $\alpha$ and another from $1$ to $\alpha$ for each $c$ such that $0<c<c^{*}<\sqrt{4D(\alpha)f^{\prime}(\alpha)},$

• 3. has a unique traveling wave solution of sharp type from $1$ to $0$ for the critical value, $c^{*}$ , of the speed $c$ . For this value of $c$ there exists an oscillatory traveling wave from $0$ to $\alpha$ ,

• 4. does not possess tws connecting the homogeneous and stationary steady states: i) $\tilde{u}_{1}(x,t)\equiv 1$ and $\tilde{u}_{0}(x,t)\equiv 0$ for $\mathcal{D}(1)\leq 0$ and $c>0$ ii) $\tilde{u}_{0}(x,t)\equiv 0$ and $\tilde{u}_{1}(x,t)\equiv 1$ for $\mathcal{D}(1)>0$ ,

• 5. has two oscillatory traveling fronts for $c^{*}<c<\sqrt{4D(\alpha)f^{\prime}(\alpha)}$ : one from $0$ to $\alpha$ and another from $1$ to $\alpha$ ,

• 6. has monotonic decreasing front from $1$ to $\alpha$ for each $c$ such that $c\geq\sqrt{4D(\alpha)f^{\prime}(\alpha)}$ . For the same values of $c$ it has monotonic increasing front from $0$ to $\alpha$ .

Sketch of the proof. In spite of this case has its own characteristics, the general scheme for proving this theorem it follows similar steps as those for the proof of Theorem 2. In fact, once we substitute $u(x,t)=\phi(x-ct)\equiv\phi(\xi)$ into (34) a nonlinear second order equation is obtained for $\phi$ which by defining $v=\phi^{\prime}$, is equivalent to a singular (at $\phi=0)$ nonlinear ODE autonomous system. The singularity can be removed in the same fashion as in Theorem 2 resulting in the nonsingular ODE system

$$\dot{\phi}=D(\phi)v\equiv F_{1}(\phi,v),$$

$$\dot{v}=-cv-D^{\prime}(\phi)v^{2}-f(\phi)\equiv F_{2}(\phi,v).$$

(35)

Because of the features of $f$, this system has four equilibrium points: $P_{0}=(0,0)$, $P_{\alpha}=(\alpha,0)$, $P_{1}=(1,0)$ and $P_{c}=(0,-c/D^{\prime}(0))$. From the linear local analysis of the system (35) around each equilibrium it follows: $P_{0}$ is a nonhyperbolic point, $P_{1}$ and $P_{c}$ are saddle points for all $c\geq 0$ and $P_{\alpha}$: is a center for $c=0$ and an asymptotically stable of focus type for $c>0$ such that $c^{2}<4D(\alpha)f^{\prime}(\alpha)$ and of node type for $c>0$ such that $c^{2}\geq 4D(\alpha)f^{\prime}(\alpha)$. The nonlinear local analysis around $P_{0}$ indicates this point is a nonhyperbolic point of saddle-node type.

The global dynamics of the system (35) strongly depends on $c>0$ and on $\mathcal{D}(1)$ as well.

Let us denote by $W_{c}^{u}(P_{1})$ and $W^{s}_{c}(P_{c})$ the left branch of the unstable manifold of the system (35) at $P_{1}$ and the right branch of the stable manifold of (35) at $P_{c}$, respectively.

The item 1 of the Theorem 3 it follows by noting that for $c=0$ the system (35) can be transformed into a hamiltonian-like system. Indeed its hamiltonian is

$$H(\phi,v)=\frac{1}{2}[D(\phi)v]^{2}+\int\limits_{0}^{\phi}D(w)f(w)dw$$

whose level curves parametrized give us the trajectories of the system (35). Actually those depend on the sign of $\mathcal{D}(1)$ as follows. The system (35) has

• A homoclinic trajectory based at $P_{0}$ for $\mathcal{D}(1)>0$,

• A heteroclinic cycle from $P_{0}$ to $P_{1}$ and from $P_{1}$ to $P_{0}$ for $\mathcal{D}(1)=0$,

• A homoclinic trajectory based at $P_{1}$ for $\mathcal{D}(1)<0$.

For the proof of items 2–6 of Theorem 3 here are the key points to consider

• 1. For small enough positive values of $c$ the heteroclinic cycle mentioned in the previous second item, is destroyed and

  $$\lim_{\tau\rightarrow+\infty}W_{c}^{u}(P_{1})=(0,-\infty);\quad\textrm{and}\quad\lim_{\tau\rightarrow-\infty}W^{s}_{c}(P_{c})=(0,+\infty);$$

• 2. For $c>0$ such that $c^{2}\geq\max\;\left\{4D^{\prime}(\phi)f(\phi)\right\}$, where the maximum is taken on the interval $[0,1]$ the equilibrium $P_{c}$ runs away along the negative vertical $v$ axis and

  $$\lim_{\tau\rightarrow+\infty}W_{c}^{u}(P_{1})=(0,\alpha)\quad\textrm{and}\quad\lim_{\tau\rightarrow-\infty}W^{s}_{c}(P_{c})=(+\infty,\bar{v});$$

• 3. The behaviour of the vertical null-clines of the system as $c>0$ changes

  $$V_{1}(\phi)=\frac{-c+\sqrt{c^{2}-4D^{\prime}(\phi)f(\phi)}}{2D^{\prime}(\phi)},\;V_{2}(\phi)=\frac{-c-\sqrt{c^{2}-4D^{\prime}(\phi)f(\phi)}}{2D^{\prime}(\phi)}$$

• 4. Once $W_{c}^{u}(P_{1})$ leaves the equilibrium $P_{1}$ enters the region

  $$\mathcal{R}=\left\{(\phi,v)|0<\phi<1,\;V_{2}(\phi)\leq v<0\right\};$$

• 5. Let $\theta(\phi,v;c)$ be the angle formed by the vector field which defines the system (35) at the point $(\phi,v)$ for the value $c$ and the positive horizontal $\phi$-axis. One can verify that $\theta(\phi,v;c)$ is a decreasing function as $c>0$ increases. As consequences of this and previous items:

  • There exists a unique value, $c^{*}$, of $c$ for which the system (35) has a saddle-saddle heteroclinic trajectory, $(\phi_{c^{*}}(\tau),v_{c^{*}}(\tau))$, connecting $P_{1}$ with $P_{c^{*}}$. Associated with this trajectory, actually its first component, $\phi_{c^{*}}(\tau)$, defines the unique tws solution of sharp type for (34),

  • For $c=c^{*}$ the system (35) has a heteroclinic oscilatory (around $\alpha$) trajectory connecting $P_{0}$ with $P_{\alpha}$,

  • For big enough values of $c$ the system (35) has two monotonic heteroclinic trajectories: one from $P_{0}$ to $P_{\alpha}$ and other from $P_{1}$ to $P_{\alpha}$.

We encourage the reader to see the reference [20] for further details. With this comment the sketch of the proof is finished. $\Diamond$

Example 5. By choosing $D(u)=\beta u+u^{2}$ and $f(u)=u(1-u)(u-\alpha)$ with $\beta>0$ and $\alpha\in(0,1)$ we have the following degenerate PDE

$$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left[(\beta u+u^{2})\frac{\partial u}{\partial x}\right]+u(1-u)(u-\alpha)$$

which, once is written in the traveling wave coordinates the desingularized system (35) takes the form

$$\dot{\phi}=(\beta\phi+\phi^{2})v,$$

$$\dot{v}=-cv-(\beta+2\phi)v^{2}-\phi(1-\phi)(\phi-\alpha),$$

which has the equilibria: $P_{0}=(0,0),P_{\alpha}=(\alpha,0)$ and $P_{c}=(0,-c/D^{\prime}(0))$. Figure 8 contains a panel of numerical simulations showing the phase portrait of the system (35) for different values of $c$ and the above mentioned functions $D(u)$ and $f(u)$. The simulations are in aggreement with the theoretical results. In particular, the $\phi_{c^{*}}(\tau)$ component of the saddle-saddle heteroclinic trajectory, corresponds to the sharp tws of the corresponding degenerate PDE. This is shown in Fig. 9.

With this example we conclude the main part of the paper for giving place to the conclusions and perspectives.

Fig. 8

Phase portrait of the system (35) for $D(u)=2u+u^{2}$ with and $f(u)=u(1-u)(u-\alpha)$ for different values of $c$.

Fig. 9

Traveling wave solution of sharp type for the degenerate PDE (34) for $D(u)=(\beta u+u^{2})$ and $f(u)=u(1-u)(u-\alpha)$. (a) Tws coming from the heteroclinic saddle–saddle connection of the system (35). (b) Tws coming from $P_{0}$ to $P_{\alpha}$ heteroclinic trajectory.

4 CONCLUSIONS AND PERSPECTIVES

Our presentation is not an exhaustive one, but it contains just a sample of representative equations which frequently are cited in the scientific literature. In the following points we briefly summarize the contents of this paper, we also mention some promising future perspectives on this field.

• 1. A long this paper we reviewed the tws analysis for different nonlinear reaction-diffusion equations ranging from nongenerate cases to those of degenerate type. The approach we emphazised to carried out such analysis, it consits in restating the tws problem in the full PDE into a series of dynamical system problems consisting in looking for the existence of parameter values for which there exist different types of heteroclinic trajectories for nonlinear autonomous ODE systems. Here shooting arguments play a relevant rolle (see [21]). As a consequence of the analysis, a rich variety of tws have been shown ranging from smooth fronts, sharp fronts and different pulse types.

• 2. In the sketched scenario mentioned in the previous item, the existence of tws of sharp type which comes from a saddle-saddle heteroclinic trajectory. Because such type of solutions have discontinuous derivative at certain finite point, they are not classical solutions of the corresponding degenerate PDE. The introduction of an appropriate concept of weak solution was requiered already has been introduced.

• 3. Higher order of degeneracies (as $D(0)=D^{\prime}(0)=0$) or multiple points of degeneracy within the domain of the density-dependent diffusion $D(u)$ coefficient, in recent years have been studied by a number of reserchers. See [15, 16] and [19].

• 4. It is documented in the scientific literature that the so-called direct aggregative behaviour of a population can be described by means of a single density-dependent reaction-diffusion equation where the sign of this changes. In fact, by combining signs of the diffusion coeffcient, for instance from positive to negative, we can describe diffusion and aggregation of a population. The negativeness of the diffusion coefficient involves ill posed initial and boundary value problems. In the references [14] and [22] the reader can be see some studies have been carried on these topics.

• 5. The convergence problem is other quite important problem in this field. Let us summarize what we mean by this. Let us denote by $\phi(x-c^{*}t)$ the tws of sharp type for a degenerate PDE and $\psi(x,t)$ the corresponding solution of an initial condition value problem associated with such a degenerate equation. The convergence problem is: How does the limit

  $$\lim_{t\rightarrow+\infty}|\psi(x,t)-\phi(x-c^{*}t)|$$

  behaves? For the degenerate bistable case this analysis it seems to be easier that the corresponding for the degenerate Fisher-KPP equation. For this one in [13] the authors carried out an spectral stability analysis.

• 6. The tws analysis is not straightforward when we have couple degenerate equations or models having degenerate cross dependent diffusion systems. In [23] such analysis has been developed in a simplified mathematical model arising in pattern formation Bacillus subtilis bacteria colonies. Recent developments of tws analysis have been used with the aim of elucidating the tumour cancer invasion process. For instance, in [6] the authors present a travelling wave analysis of a mathematical model proposed with the aim of describing the invasion of a cancer tumour. The model consists of two coupled PDE of reaction-diffusion type where in one of them it appears a degenerate cross-dependent diffusion coefficient. The model supports the existence of biological meaningfull tws.