Mechanical/Control Integrated Design of a Flexible Planar Rotatory Spacecraft

Abstract

This study presents an innovative method to perform integrated control/structure design of large flexible structures. The method is based on the application of structured $\mathscr {H_\infty }$ control tools which provide the framework for mechanical/control integrated design. The parametric model is built based on the TITOP modeling technique for flexible multi-body systems. The integrated design specifications are explained and applied to a flexible planar rotatory spacecraft, optimizing simultaneously the appendage lengths and masses and the control system for perturbation rejection respecting bandwidth requirements.

1 Introduction

Currently Large Space Structures (LSS) are a challenging problem in control system design because they involve large complex kinematic chains composed of rigid and flexible bodies, mostly large-sized, maximally lightened, low-damped and with closed-spaced low natural frequencies. In this case structural modes interfere the controlled bandwidth, provoking a critical Control-Structure Interaction (CSI). Therefore, LSS design is increasingly becoming subject to a close coordination among the different spacecraft sub-systems, demanding methods which tie together spacecraft structural dynamics, control laws and propulsion design. These methods are often called as Integrated Control/Structure Design (ICSD), Plant-Controller Optimization (PCO) or simply co-design (CD).

ICSD methods began being studied in the 80 s as an opposite technique to the current method of separated iterative sequences within the structural and control disciplines. The first integrated design methodologies were those in [1,2,3]. These methods were based on iterative methodologies with optimization algorithms. Lately, other methods have been proposed such as those solved by LMI (Linear Matrix Inequality) algorithms or with LQG (Linear Quadratic Gaussian) methods like in [4, 5] respectively. However, these approaches give conservative results and their applicability is restricted by problem dimension. Recently, a counterpart technique currently under development in ONERA Toulouse Research Center and ISAE-SUPAERO allows a more general approach [6]. Actually, this method is based on structured $\mathscr {H}_\infty$ synthesis algorithms developed in [7] or [8], granting structured controllers and tunable parameters optimization. This synthesis, merged with a correct plant modeling, can reveal important applications of integrated design methodologies.

To be compliant with such an ICSD approach, the plant modeling of LSS must provide a model where the structural or mechanical sizing parameters can be isolated under the general Linear Fractional Representation (LFR). That can be performed using the Two-Input Two-Output Port (TITOP) approach to build the linear dynamical model of Flexible Multi-body System (FMS) from the model of each body. The TITOP model approach was first proposed in [9], then generalized to take into account varying sizing parameters in [10, 11]. For uniform beam, an analytic model was developed in [12] where a first ICSD was presented. Augmented TITOP models for flexible body actuated with piezoelectric strip [13] involve an additional channel between the input voltage and the output piezoelectric charge, allowing any active substructure to be embedded in the whole structure. Some applications of ICSD using such a modeling technique are presented in [14, 15].

This work aims at showing the way to apply these modeling and design tools to perform the ICSD of a flexible planar rotatory spacecraft. Such a system was presented in [16] to illustrate interactions between control and structure in space engineering. The objective is to maximize the length and the tip mass of one appendage, in order to increase the spacecraft payload capacity, while minimizing the total mass of the spacecraft and meeting attitude pointing requirement in spite of external disturbances. This paper is organized as follows. First, the parametric model of the spacecraft is developed. Second the integrated control design is presented. Finally, results and discussion on advantages of using this methodology rather than single control optimization alone are detailed.

2 Flexible Rotatory Spacecraft Modeling

2.1 Spacecraft System Description

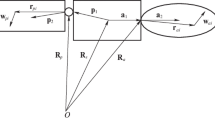
The system, considered as an academic example, is composed of a rigid main hub with four identical cantilevered flexible appendages and tip masses as shown in Fig. 1. The configuration parameters are provided in Table 1. Under normal operation, the spacecraft undergoes planar rotational maneuvers around the inertial fixed axis $\mathbf {z}$. The spacecraft body frame is attached to the center of mass of the rigid hub, and it is denoted by a right-handed triad $\mathbf {x}$, $\mathbf {y}$ and $\mathbf {z}$. The rotation about the axis $\mathbf {z}$ is denoted by the angle $\theta$ and the translational deformation of each tip by $\mathrm {w}_{tip}^i$, with superscript i denoting the beam number.

The system is actuated by three different torques. The main torque, $t_{hub}$ is provided by the main hub about the axis $\mathbf {z}$. Two additional input torques, $t_{tip,1}$ and $t_{tip,2}$, are applied at the tip masses 1–3 and 2–4 respectively. These torques can be applied purposely for control reasons or can represent environment disturbances (as it is the case in this paper). In addition, the appendage $\#\;1$ is actuated using a piezoelectric strip for active damping of vibrations.

Fig. 1

Rotatory flexible spacecraft

Table 1 Spacecraft configuration parameters

Fig. 2

Model $A_i(s)$ of a single appendage ($i=2,3,4$)

2.2 Spacecraft System Modeling

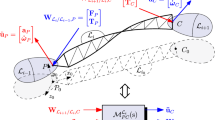
The whole spacecraft is decomposed in various sub-structures: the hub h and the 4 appendages $\mathscr {A}_i, i=1,\ldots , 4$. Each appendage is itself decomposed into a uniform beam which flexible dynamics is represented by a super-element [11] and a local mass/inertia at the tip of the beam. The TITOP (Two-Input Two-Output) model approach is used to described each sub-structure. The block diagram representation of a single appendage model is depicted in Fig. 2 where:

• $G^{\mathscr {A}_i}_{P_i,Q_i}(s)$ is the planar TITOP model of the flexible uniform beam # i (see [11] for more details): the inputs are the time-derivative of the planar twist $\ddot{q}_{P_i}$ (3 components: 2 linear accelerations and 1 angular acceleration) at point $P_i$ of the beam and the external planar wrench $F_{tip/beam,Q_i}$ (3 components: 2 forces and 1 torque) applied to the beam at point $Q_i$. The output are the wrench $F_{{\mathscr {A}_i}/h,P_i}$ applied by the appendage to the hub at point $P_i$ and the time-derivative of the twist $\ddot{q}_{Q_i}$ at point $Q_i$,

• $J_{Q_i}^{tip}(s)$ is the planar dynamical model of the tip mass and inertia:

  $$\begin{aligned} J^{tip}_{Q_i} = \begin{bmatrix} m_t&0&0 \\ 0&m_t&0 \\ 0&0&J_t \end{bmatrix} \end{aligned}$$

  (1)

• $\tau _{P_iG}$ is the kinematic models between points G and $P_i$. In the planar case:

  $$\begin{aligned} \tau _{P_1G} = \begin{bmatrix} 1&0&0 \\ 0&1&r \\ 0&0&1 \end{bmatrix} \; \; \tau _{P_2G} = \begin{bmatrix} 1&0&0 \\ 0&1&-r \\ 0&0&1 \end{bmatrix} \; \; \tau _{P_3G} = \begin{bmatrix} 1&0&-r \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \; \; \tau _{P_4G} = \begin{bmatrix} 1&0&r \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \end{aligned}$$

  (2)

• $R_i$ is the rotation matrix written as follows:

  $$\begin{aligned} R_i = \begin{bmatrix} \cos \beta _i&-\sin \beta _i&0 \\ \sin \beta _i&\cos \beta _i&0 \\ 0&0&1 \end{bmatrix}_{App \rightarrow Hub} \end{aligned}$$

  (3)

  where $\beta _i$ is the angle of the ith appendage i with $\mathbf {x}$.

For the appendage $\#\;1$, actuated with a piezoelectric strip, the extension of TITOP model described in [13] is used. The augmented model $A_1(s)$ involves an additional channel between v (input voltage) and g (output piezoelectric charge). Furthermore a radial disturbance force $f_{y,tip}$ on input and the radial acceleration $\ddot{w}_{tip}$ on output are included to shape the control problem (see Sect. 3.2). For appendage $\mathscr {A}_1$, the model is then described in Fig. 3 where $S_y=[0\;\;\;1 \;\; 0]^T$.

Fig. 3

Model $A_1(s)$ of appendage # 1 $i=1$)

The assembly of the various sub-models is described by the block diagram scheme presented in Fig. 4, where:

• $J^{Hub}_G = \begin{bmatrix} m_h&0&0 \\ 0&m_h&0 \\ 0&0&J_h \end{bmatrix}$

• $S_z=[0\;\;\;0 \;\; 1]^T$

The inputs and the outputs of the whole system mechanical model $(J_G^{sat})^{-1}(s)$ are:

• a vector w of two exogenous inputs: a disturbance $w_{\ddot{\theta }_{out}}$ on the hub angular acceleration and $f_{y,tip}$,

• a vector u of two control signals: the torque on the hub $t_{hub}$ and the piezo input voltage v,

• a vector z of two controlled outputs: the hub angular rate $\ddot{\theta }_{hub}$ and the lateral tip acceleration $\ddot{w}_{tip}$ of appendage 1,

• a vector y of 3 measurements: the hub angular rate $\dot{\theta }_{hub}$ and attitude $\theta _{hub}$ and the lateral tip acceleration $\ddot{w}_{tip}$ of appendage 1.

Fig. 4

Rotatory flexible spacecraft $(J_G^{sat})^{-1}(s)$

2.3 Spacecraft Model with Varying Parameters

The structured model $(J_G^{sat})^{-1}(s)$ of the spacecraft is quite convenient to take into account some sizing mechanical parameters or design parameters. In this application, the design parameters are the length $L_i$ and the tip mass $M_i$ of each appendage. More precisely:

$$ L_i=L(1+0.3\delta _{L_i}),\quad M_i=m_t(1+0.3\delta _{M_i}), \quad i=1,2,3,4. $$

That is to say: 30% of variations around the nominal value are allowed for each design parameters $L_i$ and $M_i$ in such a way that $\delta _{L_i}$ and $\delta _{M_i}$ are normalized to vary between $-1$ and 1. These design can be very easily isolated in the various submodels ($L_i$ in $G^{\mathscr {A}_i}_{P_i,Q_i}(s)$ and $M_i$ in $J^{tip}_{Q_i}$). Thus, using LFR for each parameters and basic LFR operations, one can easily derived the LFR of the whole spacecraft depicted in Fig. 5, also written:

$$ (J_G^{sat})^{-1}(s,\delta _{L_1},\delta _{L_2},\delta _{L_3},\delta _{L_4},\delta _{M_1},\delta _{M_2},\delta _{M_3},\delta _{M_4})=F_u((M_G^{sat})^{-1}(s),\varDelta )\;. $$

After assembly, the system has a block $\varDelta$ of $125 \times 125$ size and reads:

$$\begin{aligned}{}[\varDelta ] = \begin{bmatrix} [\delta _{L_1}]_{30\times 30}&0&0&0&0&0&0&0 \\ 0&[\delta _{M_1}]_{2\times 2}&0&0&0&0&0&0 \\ 0&0&[\delta _{L_2}]_{29\times 29}&0&0&0&0&0 \\ 0&0&0&[\delta _{M_2}]_{2\times 2}&0&0&0&0 \\ 0&0&0&0&[\delta _{L_3}]_{29\times 29}&0&0&0 \\ 0&0&0&0&0&[\delta _{M_3}]_{2\times 2}&0&0 \\ 0&0&0&0&0&0&[\delta _{L_4}]_{29\times 29}&0 \\ 0&0&0&0&0&0&0&[\delta _{M_4}]_{2\times 2} \\ \end{bmatrix} \end{aligned}$$

(4)

That is: 2 parameter occurrences for each tip mass, 29 parameter occurrences for the non-actuated appendage lengths and 30 parameter occurrences for the actuated appendage length $i=1$. The system results in a state-space system with a $\varDelta$ block of size 125$\times$125, 11 inputs, 11 outputs and 50 states.

Fig. 5

Rotatory flexible spacecraft model with varying design parameters

It should be highlighted that the ICSD of the rotatory spacecraft strongly demands a modeling technique such as the TITOP modeling technique, since the boundary conditions of the flexible beams are to be changed when varying the mass located at their tips. Thus, by using the TITOP modeling technique, the impact of mass variation in the whole system will be taken into account when ICSD is performed with structured $\mathscr {H}_\infty$ synthesis. Indeed, in the symmetric nominal parametric configuration ($\varDelta =0$), some flexible modes are uncontrollable from u. Then, the damping of these flexible modes, when excited by a disturbance (on $f_{y,tip}$, $t_{tip,1}$ or $t_{tip,3}$), is not possible. The asymmetry introduced by the ICSD will restore the controllability and will allow active damping of all the modes, as it will be seen in Sect. 4.

3 Integrated Control/Structure Design (ICSD)

3.1 General Approach

Figure 6 shows the standard multi-channel $\mathscr {H}_\infty$ synthesis problem for ICSD of a generic system G(s). The synthesis scheme is build by establishing the feedback of the augmented controller $K(s) = \mathrm {diag}(C(s),\varDelta )$ with the corresponding inputs/outputs of the nominal system G(s). Additional channels are added in order to weight the controller’s frequency response and mechanical performance index. The synthesis scheme has three different channels:

• One multidimensional channel which connects the perturbations of the system, w, to the performance outputs, z, through the weighting $W_z$.

• One multidimensional channel which connects the inputs of the control system, $y_c$, to the outputs, $u_c$, to shape the frequency-domain response of the controller C(s) (roff-off behavior for instance) through the weighting $W_C$.

• One multidimensional channel which connects the inputs $w_k$ of the mechanical performance function $f_k(\delta _i)$ block to its outputs $z_k$, through a weighting $W_k$. This function $f_k(\delta _i)$ depends directly on the design parameters variations $\delta _i$ (i.e. the various independent components of the block $\varDelta$).

Structured $\mathscr {H}_\infty$ synthesis computes the sub-optimal tuning of the free parameters of C(s) and $\varDelta$ embedded in K(s) to enforce closed-loop internal stability, $\mathscr {F}_l(G(s),K(s))$, such that:

$$ \min _{K(s)} \{ \max \{\Vert W_{k} (s)f_k(\delta _i) \Vert _\infty , \Vert W_{C}(s)C(s)\Vert _\infty \} \} $$

such that

$$\begin{aligned} \Vert W_z(s)T_{w\rightarrow z}(s)\Vert _\infty < \gamma _{perf} \end{aligned}$$

i.e., it minimizes the $\mathscr {H}_\infty$ norm between the transfer of the perturbation input w and the performance output z, $T_{w\rightarrow z}(s)$, such that it is constrained to be below $\gamma _{perf}>0$ to meet the required performances. The problem is in the form of multi-channel $\mathscr {H}_\infty$ synthesis, and it allows the set of desired properties to the augmented controller such as its internal stability [6], frequency template [17] or maximum gain values, while minimizing a mechanical performance index. In substance, the structured $\mathscr {H}_\infty$ integrated design synthesis tunes the free parameters contained in the augmented controller $K(s) = \mathrm {diag}(C(s),\varDelta _i)$ to ensure closed loop internal stability and meet normalized $\mathscr {H}_\infty$ requirements through $W_z$, $W_C$ and $W_k$.

Fig. 6

Block diagram of integrated design optimization

3.2 Application to the Rotatory Spacecraft

The augmented controller is formed by concatenating the block of tunable parameters $\varDelta$ with the real controller of the system, C(s). Since the $\varDelta$ block has been defined in Sect. 2.3, the structure of C(s) is addressed in this section.

The system needs to reject low frequency disturbances in the rigid body DOF, the system’s rotation around the hub, and can be helped by inducing active damping through the piezoelectric laminate installed on appendage 1. Thus, the control system will consist of two decentralized loops: one for the rigid body rotation of the hub, $\theta _{hub}$, and the other to damp the first appendage’s tip vibrations, $\ddot{w}_{tip_1}$.

The control of the rigid body motion is achieved with a PD (Proportional-Derivative) controller to compute the control torque provided by the reaction wheel located at the hub. The active damping controller (Active: AF) will be a simple rate feedback, integrating the first appendage’s vertical acceleration (acceleration feedback strategy). Therefore the control law is structured as follows:

$$\begin{aligned} \{u\} = [C(s)] \{ y \} = \begin{Bmatrix} t_{hub} \\ v \end{Bmatrix} = \begin{bmatrix} k_v&k_p&0 \\ 0&0&k_a/s \end{bmatrix}\begin{Bmatrix} \dot{\theta }_{hub} \\ \theta _{hub} \\ \ddot{y}_{tip_1} \end{Bmatrix} \end{aligned}$$

(5)

The proportional control gain $k_p$, the derivative control gain $k_v$ and the damping gain $k_a$, together with the tunable parameters of the $\varDelta$ block, are to be optimized with structured $\mathscr {H}_\infty$ synthesis. The values of the PD controller gains are initialized using the standard tuning assuming the spacecraft is rigid: $k_p = J_t\omega ^2$ and $k_v=1.4J_t \omega$ where $J_t$ is the total inertia and $\omega$ the wanted attitude servo-loop bandwidth ($\omega =1$ rad/s leads to: $K_p=633.33$ Nm and $k_v=231.21$ Nms).

Fig. 7

Constraint (yellow) on the hub’s dynamics (blue)

Fig. 8

Constraint (yellow) on the tip’s dynamics (blue)

As previously specified, the control of the hub rotation must be able to reject low frequency disturbance torque. The desired closed-loop dynamics for perturbation rejection are $\omega = 1$ rad/s and $\xi = 0.7$, which leads to the following weighting filter on the Acceleration Sensitivity Function ASF [6] (i.e. transfer from $w(1)=w_{\ddot{\theta }_{hub}}$ to output $z(1)=\ddot{\theta }_{hub}$ in Fig. 4):

$$\begin{aligned} W_{\ddot{\theta }_{hub}} (s)= \frac{s^2 + 1.4\omega s + \omega ^2}{s^2} = \frac{s^2 + 1.4s + 1}{s^2} \end{aligned}$$

(6)

The damping of the flexible modes is imposed by a template on the transfer between the hub’s acceleration disturbance $w(1)=w_{\ddot{\theta }_{hub}}$ and the performance output $z(2)=\ddot{w}_{tip}$. This template reads: $W_{\ddot{q}P}(s)= L/W_{\ddot{\theta }_{hub}}$ (L is the nominal length of the beam). A static filter $W_d=1/M_{tot}$ (with $M_{tot}$ the nominal total mass) is added in the transfer $f_{y,tip}\rightarrow \ddot{w}_{tip}$ to add additional damping. In Figs. 7 and 8 frequency-domain responses of the closed-loop transfers $T_{w(1)\rightarrow z(1)}$ (called hub’s dynamics) and $T_{w(1)\rightarrow z(2)}$ (called tip’s dynamics) when only the 2 gains $k_p$ and $k_v$ of the PD controller are optimized. These responses are compared with the desired frequency response imposed through the templates and $W_{\ddot{\theta }_{hub}}^{-1} (s)$ and $W_{\ddot{q}P}(s)$. It is seen that the flexible modes are badly damped and the PD controller gains have a larger value than the needed to respect the template on the ASF of the hub position $\theta _{hub}$.

Once the constraints for rigid and flexible motion have been defined, additional channels can be added to constraint the variation of structural parameters. The constraints for the maximization of the length and tip mass of appendage 1, $L_1$ and $M_1$ respectively, are implemented as follows:

$$\begin{aligned} f_{M_1}(\delta _{M_1}) = \frac{1}{1 + 0.3 \delta _{M_1} } ; \quad W_{M_1}= 0.75 \end{aligned}$$

(7)

$$\begin{aligned} f_{L_1}(\delta _{L_1}) = \frac{1}{1 + 0.3 \delta _{L_1} } ; \quad W_{L_1}= 0.75 \end{aligned}$$

(8)

where the $W_k$ values have been fixed to 0.75, a value which can never be reached with the allowed maximal variation, in order to encourage the maximum possible value for $\delta _{L_1}$ and $\delta _{M_1}$. The constraint for minimum total mass is:

$$\begin{aligned} f_{M_{total}} (\delta _{L_i},\delta _{M_i}) = L\,\rho \,t \,h \,(4+0.3\sum _{i=1}^4 \delta _{L_i}) + m_t(4+0.3\sum _{i=1}^4 \delta _{M_i}); \quad W_{M_{total}} = M_0 \end{aligned}$$

(9)

where $M_0 = 15.51$ kg is the nominal total mass of all the appendages. Equation (9) is a combination of all the structural parameters that can be varied, weighted by their impact on the system total mass (total beams mass for the lengths, total tip mass for the tip masses).

Finally, the ICSD problem can be summarized in the following way ($T_{i\rightarrow o}$ denotes the closed-loop transfer from input i to output o defined in the model of Fig. 4):

Find a stabilizing set of parameters $\Theta =\{k_v, k_p,k_a,\delta _{M_i},\delta _{L_i}\}$ such that:

$$\begin{aligned} \min _{\Theta } \{ \max \{&\Vert W_{M_1} f_{M_1}(\delta _{M_1}) \Vert _\infty , \Vert W_{L_1} f_{L_1}(\delta _{L_1}) \Vert _\infty , \\ \nonumber&\Vert W_{M_{total}} f_{M_{total}}(\delta _{L_i},\delta _{M_i}) \Vert _\infty , \Vert W_{\ddot{q}P}^{-1}(s) T_{w(1) \rightarrow z(2)}(s)\Vert _\infty , \\&\Vert W_dT_{w(2) \rightarrow z(2)}(s)\Vert _\infty \} \} \end{aligned}$$

under the constraint:

$$\begin{aligned} \Vert W_{\ddot{\theta }_{hub}}(s)T_{w(1) \rightarrow z(1)}(s)\Vert _\infty < 1.5. \end{aligned}$$

4 Results

The optimization of the controller and the structural parameters is performed using the structured $\mathscr {H}_\infty$ synthesis tool systune. The results of the ICSD solution are compared with those of a solution with control optimization alone (COA). Table 2 shows the optimized and nominal structural parameters. It can be seen that the length and tip mass of appendage 1 have been increased the maximum allowed, 30%. For appendages 2, 3 and 4 the tip masses have been minimized while the lengths have been increased almost to the maximum, with the exception of appendage 2. Appendage 3 and its opposite appendage 4 are no longer symmetric since they lengths are slightly different and the tip masses difference is around 0.15 kg. The structural optimization meets the specifications: maximization of mass and length of appendage 1 while minimizing the impact on the total system’s mass.

Table 2 Structural data before optimization (COA) and after performing ICSD to the rotatory flexible spacecraft

Figures 9 and 10 show the resulting frequency response for $T_{w(1)\rightarrow z(1)}$ and $T_{w(1)\rightarrow z(2)}$ compared with the desired templates $W_{\ddot{\theta }_{hub}}^{-1}$ and $W_{\ddot{q}P}$ after optimization. The gains of the PD controller have been adjusted to fit the frequency template and flexible modes are shifted and more damped when comparing with the response given in Figs. 7 and 8. The shift of flexible modes is a consequence of the structural optimization, since tip masses and lengths have been modified. The damping is provided by the active damping provided by the piezoelectric material controlled with an acceleration feedback control law.

Fig. 9

Constraint (yellow) on the hub’s dynamics (blue)

Fig. 10

Constraint (yellow) on the tip’s dynamics (blue)

Fig. 11

Nichols plot

Fig. 12

Bode plot

The ICSD solution enjoys the same robust performance as the COA solution for the hub position control. The Nichols diagram of the open loop $t_{hub}\rightarrow t_{com}$ response in Fig. 11 shows that the ICSD solution has satisfactory phase and gain margins (GM $=$ 20.5 dB, PM $=$ 69.1$^{\circ }$) which are as good as the COA solution (GM $=$ 13.5 dB, PM $=$ 69.1$^{\circ }$). However, this is achieved by the ICSD solution with longer appendages which are not symmetric. Indeed, the first flexible mode, located at $\omega =$ 4.4 rad/s appears to be uncontrollable in nominal configuration, corresponding to the symmetric bending of the system’s appendages. However, the ICSD solution has tuned the system to be completely asymmetric so that the first flexible mode can be governed with the hub torque as well. This is confirmed in Fig. 12, where the bode diagram of the open loop response shows that the first flexible mode appears as a resonance frequency in the ICSD solution and as an anti-resonance frequency for the COA solution.

The uncontrollability of the first symmetric bending mode at $\omega = 4.4$ rad/s is also verified in the time domain response. Figures 13 and 14 show the closed-loop response of the hub’s acceleration $\ddot{\theta }_{hub}$ and the first appendage tip’s acceleration $\ddot{y}_{tip_1}$, respectively, to an asymmetric torque disturbance at tips 1 and 3 and for both ICSD and COA solutions. This input excites the symmetric bending mode of appendages 3 and 4, which cannot be damped by the COA solution. It can be seen as well that the acceleration of the COA solution has a higher overshoot than the ICSD solution, even if the ICSD solution has higher tip mass and length. On the other hand, the ICSD solution needs two times more time for damping the tip vibrations and hub’s position oscillations.

Fig. 13

Hub acceleration $\ddot{\theta }_{hub}$

Fig. 14

Tip acceleration $\ddot{w}_{tip}$

The results show that ICSD using structured $\mathscr {H}_\infty$ synthesis can be achieved by implementing the desired specifications in $\mathscr {H}_\infty$ form. The structured $\mathscr {H}_\infty$ synthesis optimizes the controller and the structural parameters to better fit the dynamic specifications, while respecting the structural constraints imposed to the varying parameters. The same level of performance can be achieved with a modified structure, discovering new configurations which can improve control performance. The optimization process has provided an intuitive fact: the maximization of the mass of one appendage will decrease the total mass of the others. The optimization has provided a counter-intuitive fact as well: system’s asymmetry can help to increase controllability of system’s modes and to improve system’s performance. Therefore, integrated design is possible and it takes into account the issues and trade-offs of the physical system.

5 Conclusions and Perspectives

The implementation of dynamic, structural and controller specifications for the integrated control/structure design (ICSD) has been explained in this paper. The specifications for the rigid body motion are implemented weighting the Acceleration Sensitivity Function (ASF), while the flexible motion damping is achieved by projecting the rigid body motion template at different points of the Flexible Multi-body System (FMS). The structural constraints for structured optimization are implemented with additional channels which included the cost functions and weighting filters applied to the varying parameters involved in the constraints. Controller frequency shaping can be stated through a roll-off filter. The application of ICSD on a flexible planar rotatory spacecraft provided quite promising results. Further works will use the same approach to perform the ICSD of a more complex system, a flexible satellite, in the 3D case. The TITOP approach, used to obtain linear parameter varying models of flexible multi-body systems required for such a ICSD, will be extended to flexible multi-body systems with closed-loop kinematic mechanisms.