Sliding Mode Control of Power Converters with Switching Frequency Regulation

Abstract

This chapter deals with the development of a hysteresis band controller in charge of fixing the switching frequency of a sliding mode controller. The proposed control measures the switching period of the control signal and modifies the hysteresis band of the comparator in order to regulate the switching frequency of the sliding motion. The switching frequency control system is modelled and a design criterion for the control parameters is derived to guarantee closed loop stability. The technique is applied to power electronics. Specifically, DC-to-DC and DC-to-AC power converters are considered, a sliding mode controller providing robustness in the face of load disturbances and input voltage variations is designed and, finally, the stability analysis of these systems when the switching frequency is regulated is also presented. A set of numerical simulations will confirm the achievement of fixed switching frequency, robustness of the controller, and stability of the closed-loop system.

1 Introduction

Sliding mode control (SMC) constitutes a natural control tool for variable structure systems (VSS), such as power converters, which are nonlinear systems where the control inputs are inherently discontinuous functions of time. Several first order SMC applications for linear and nonlinear systems can be found in the literature [21].

In most cases SMC designs assume an infinite switching frequency of the control action in accordance with the sign of a certain function, but this entails issues when implemented in real systems. In the field of power converters, the first realistic SMC implementations are reported in [2, 22]. In these works, the sign function is replaced by a hysteresis comparator, and the control action is enforced to switch at finite frequency, but variable and system dependent [3, 4]. However, power converters require a fixed switching frequency operation since the design of their reactive components is highly dependent on the switching frequency of the system.

Several different approaches have been proposed to regulate the SMC switching frequency to a fixed value. Some of them adapt the comparator hysteresis band, adjusting its level in accordance with the system state [5, 7, 8, 10, 12, 17]. The procedure provides good results, but requires perfect knowledge of the plant, and it is not robust in the face of parametric variations. Additional sensors and/or observers can be included to get a proper adaptation of the hysteresis band amplitude but, in this case, the system reliability decreases and the cost raises.

Fixed switching frequency can also be achieved by using an external signal to force the switching instants [11, 18]. This approach needs some additional hardware on the controller and requires the switching frequency to be low enough with respect to the system time constants, otherwise the state dynamics drifts away from the ideal sliding mode and an unexpected steady-state error appears.

The Zero Averaged Dynamics (ZAD) concept was presented in [6]. The method computes a duty cycle that guarantees zero T-periodic mean value of the switching function, with T denoting the switching period. Therefore, fixed switching frequency is reached in the steady-state, and the averaged behaviour is close to the ideal sliding mode one. The ZAD strategy has been successfully implemented in [13]. The results presented therein show a good performance of the ZAD, but also point out the requirement of a fast digital processor to solve the complex calculations involved in the duty cycle computation, which in the end constitute the main drawbacks of ZAD-based SMC fixed frequency implementations.

Pulse Width Modulators (PWM) at fixed frequency have been used to implement the so-called PWM-SMC. Initially proposed in [9, 19], the method implements directly the equivalent control and obtains the switching instants comparing the equivalent control with the fixed frequency saw-tooth waveform at the PWM. The results presented in [20] show overall good performance, but it should be noted that the same solution can also be derived by calculating the duty cycle required to obtain the desired system dynamics. Moreover, some sliding mode properties, such as order reduction or robustness in the face of disturbances, could be lost.

Alternatively, a simple hysteresis band controller in charge of fixing the switching frequency of a sliding mode controller is presented in the next sections. The controller is based on a variable hysteresis band comparator which regulates the switching frequency to a desired constant value. The analysis allows to develop a large signal model for the frequency control loop, and the controller parameters design guarantees stability and asymptotic tendency to a fixed switching frequency when the system is on the sliding surface. Furthermore, in order to cover the case of tracking time-varying references, the switching frequency controller design has also been extended with the addition of a feedforward term which, once properly designed following the guidelines presented here, is able to provide the desired switching frequency in the steady state.

Fig. 16.1

Behavior of $\sigma$ within a constant amplitude boundary layer

2 Hysteresis Band Controller for Switching Frequency Regulation

Let us consider a single input single output (SISO) system, with dynamics given by

$$\begin{aligned} \dot{x} = f(x)+g(x)u,\end{aligned}$$

(16.1)

where x denotes the state vector, f(x), g(x) are smooth nonlinear functions, and $u \in \{ u^+, \, u^- \}$ is the control input. According to [3, 21], a system with the structure presented in (16.1), where a sliding motion is enforced over a switching surface $\sigma (x)=0$ in a comparator with a fixed hysteresis band value $\varDelta > 0$, see Fig. 16.1, as

$$ \begin{aligned} u=\left\{ \begin{array}{ccl} u^+ \,\, \text {if} \,\, \sigma &{}< -\varDelta , \,\, &{}\text {or} \,\, \left( |\sigma |< \varDelta \,\, \& \,\, \dot{\sigma }> 0 \right) \\ u^- \,\, \text {if} \,\, \sigma &{}> \varDelta , \,\, &{}\text {or} \,\, \left( |\sigma |< \varDelta \,\, \& \,\, \dot{\sigma } < 0 \right) \end{array} \right. \end{aligned}$$

(16.2)

produces a series of consecutive kth switching periods ($k > 0$), corresponding to

$$\begin{aligned} T_k=T_k^++T_k^-=2\varDelta \left( \rho _k^+-\rho _k^-\right) ,\end{aligned}$$

(16.3)

where $\rho ^+_k, \, \, \rho ^-_k$ are defined as the inverses of $\dot{\sigma }$ for each control input state:

$$\begin{aligned} \rho ^+_k = \frac{1}{\dot{\sigma }_{k_{u=u^+}}}, \,\, \rho ^-_k = \frac{1}{\dot{\sigma }_{k_{u=u^-}}} \end{aligned}$$

The obtaining of (16.3) relies on the assumption of piecewise linear behavior for $\sigma$, which implies that $\rho ^+_k, \, \, \rho ^-_k$ are constant during the switching interval. This is a standard hypothesis in the SMC literature [3, 21] which holds if the switching frequency is high enough with respect to the system dynamics.

Notice that the expected switching period depends on $\rho ^+_k, \, \, \rho ^-_k$, which are inversely proportional to the switching function slopes, and this implies that the switching period varies as the state vector does. This phenomenon is sometimes disadvantageous for specific systems, as happens with power converters. Hence, a solution is provided hereafter.

2.1 Control Architecture

The proposed structure, already presented in [14,15,16], includes a control loop that regulates the switching period of the control action under sliding motion, thus achieving a fixed switching frequency in the steady state. The idea is sketched in Fig. 16.2. The control loop measures each switching period of the control action and compares it with the desired switching period, $T^*$. The difference is processed by the switching frequency controller (SFC), which will update the hysteresis band value of the hysteretic comparator in such a way that $T_k \rightarrow T^*$.

Fig. 16.2

Overall controller architecture

2.2 Discrete-Time Modelling of the Control Loop

It is assumed that the hysteresis band amplitude can be updated at the beginning of each switching interval by the SFC, keeping it constant up to the next switching interval. The behavior of $\sigma$ when confined in a time-varying boundary layer is represented in Fig. 16.3. Therefore, the expression of the switching period needs to be revisited. Following an analogue procedure to the derivation of (16.3), the kth switching period in the time-varying case is now given by:

$$\begin{aligned} T_k = T_k^++T_k^- = \rho ^+_k\left( \varDelta _k+\varDelta _{k-1}\right) -2\rho ^-_k\varDelta _k = \hat{\rho }_k\varDelta _k+\left( \tilde{\rho }_k - \hat{\rho }_k \right) \varDelta _{k-1}, \end{aligned}$$

(16.4)

with

$$\begin{aligned} \hat{\rho }_k&= \rho ^+_k -2\rho ^-_k, \\ \tilde{\rho }_k&= 2\left( \rho ^+_k - \rho ^-_k\right) . \end{aligned}$$

Fig. 16.3

Behavior of $\sigma$ within a time-varying amplitude boundary layer

Let us define the switching period error as $e:=T^*-T$. Therefore, using (16.4) one easily finds out that

$$\begin{aligned} e_k-e_{k-1} = \hat{\rho }_k \left( \varDelta _{k-1}-\varDelta _k\right) + \rho ^+_{k-1} \left( \varDelta _{k-2}-\varDelta _{k-1}\right) + \left( \tilde{\rho }_{k-1} - \tilde{\rho }_k \right) \varDelta _{k-1}. \end{aligned}$$

(16.5)

Next subsections will particularize expression (16.5) in two different working conditions, namely: the regulation case and the tracking case.

2.2.1 The Regulation Case

In regulation tasks the state vector reference, $x^*$, is constant. Assuming that the amplitude of the ripple, $2\varDelta$, of $\sigma$ in the vicinity of $\sigma =0$ is small, the steady state vector can be considered also constant, and hence $x=x^*$. As a consequence, the switching function derivatives and their inverses are constant in the steady state as well. Therefore, from a certain discrete-time instant $k_0$ it results that:

$$\begin{aligned} \rho ^\pm _k=\rho \left( x^*,u^\pm \right) :=\rho ^\pm _{*}, \ \ \hat{\rho }_k:=\hat{\rho }^*, \ \ \tilde{\rho }_k:=\tilde{\rho }^*, \ \forall k \ge k_0. \end{aligned}$$

(16.6)

With these approximations, (16.5) can be simplified up to the following expression:

$$\begin{aligned} e_k-e_{k-1} = \hat{\rho }^*\left( \varDelta _{k-1}-\varDelta _k\right) +\rho ^+_*\left( \varDelta _{k-2}-\varDelta _{k-1}\right) . \end{aligned}$$

(16.7)

The control law proposed for the hysteresis band amplitude in the regulation case is of integral type and answers to the following difference equation:

$$\begin{aligned} \varDelta _k=\varDelta _{k-1}+\gamma e_{k-1},\end{aligned}$$

(16.8)

with $\gamma > 0$ denoting the integral constant. Notice that taking (16.8) to (16.7) results in the following linear homogeneous difference equation with constant coefficients:

$$\begin{aligned} e_k = \left( 1-\gamma \hat{\rho }^*\right) e_{k-1}-\gamma \rho ^+_*e_{k-2}. \end{aligned}$$

(16.9)

The stability of the zero solution of (16.9), which means $T_k \rightarrow T^*$, is studied in Sect. 16.2.3.

2.2.2 The Tracking Case

When the system tracks a time-varying reference $x^*=x^*(t)$, the time derivatives of the switching functions can not be considered constant values, i.e. $\rho ^+_k \ne \rho ^+_{k-1}$, $\rho ^-_k \ne \rho ^-_{k-1}$. Hence, when using the integral action (16.8) as SFC, the corresponding closed-loop response given by (16.5) results in:

$$\begin{aligned} e_k = \left( 1-\gamma \hat{\rho }_{k}\right) e_{k-1}-\gamma \rho ^+_{k-1} e_{k-2} + \varDelta _{k-1} \left( \tilde{\rho }_{k-1} - \tilde{\rho }_k\right) . \end{aligned}$$

(16.10)

Fig. 16.4

Switching frequency regulation control loop with feedforward action. The inherent time delay due to the switching period measurement is represented by $z^{-1}$, see [14] for details

Notice that (16.10) is non-homogeneous, and does not have $e_k = 0$ as an equilibrium solution. In order to overcome this drawback the proposal presented here adds a feedforward loop that compensates the undesirable effect of the last term of (16.10). Therefore, the new SFC structure for systems under tracking tasks is shown in Fig. 16.4 and consists of setting

$$\begin{aligned} \varDelta _k=\varPsi _k+\varOmega _k, \end{aligned}$$

(16.11)

where $\varPsi _k$ is the integral control action

$$\begin{aligned} \varPsi _k=\varPsi _{k-1}+\gamma e_{k-1},\end{aligned}$$

(16.12)

while the feedforward term $\varOmega _k$ responds to:

$$\begin{aligned} \varOmega _k= \frac{\hat{\rho }_{k-1}-\rho ^+_k}{\hat{\rho }_k}\varOmega _{k-1}+\frac{ \rho ^+_{k-1}}{\hat{\rho }_k}\varOmega _{k-2}+ \frac{\tilde{\rho }_{k-1} - \tilde{\rho }_k }{\hat{\rho }_k}\varPsi _{k-1}. \end{aligned}$$

(16.13)

Merging (16.11)–(16.13) the new closed-loop error dynamics is given by

$$\begin{aligned} e_k = \left( 1-\gamma \hat{\rho }_k\right) e_{k-1}-\gamma \rho ^+_{k-1}e_{k-2}. \end{aligned}$$

(16.14)

Now the equation of the switching period error boils down to a homogeneous time-varying discrete-time linear system recovering $e_k = 0$ as the desired equilibrium solution. Under sliding motion and in the steady state, the state vector profile $x^*(t)$ will produce time-varying values for $\rho _k$:

$$\begin{aligned} \begin{array}{l} \rho ^+_k = \rho _k\left( x^*(t),u^+\right) :=\rho ^+_{*k}, \\ \rho ^-_k = \rho _k\left( x^*(t),u^-\right) :=\rho ^-_{*k}, \\ \hat{\rho }_k = \hat{\rho }_k \left( x^*(t)\right) :=\hat{\rho }^*_k, \\ \tilde{\rho }_k = \tilde{\rho }_k \left( x^*(t)\right) :=\tilde{\rho }^*_k, \end{array} \end{aligned}$$

(16.15)

$\forall k \ge k_0$, and the preceding error equation becomes

$$\begin{aligned} e_k = \left( 1-\gamma \hat{\rho }^*_k\right) e_{k-1}-\gamma \rho ^+_{*k-1}e_{k-2}. \end{aligned}$$

(16.16)

The stability analysis of the zero solution of (16.16) is conducted in Sect. 16.2.3.

2.3 Stability Analysis and Design Criteria

The obtained results rely upon the hypotheses established in the above analysis. These can be summarized as follows:

Assumption 16.1

The control law (16.2) induces system (16.1) to evolve within a boundary layer defined by $\left| \sigma \left( x,x^*(t)\right) \right| < \varDelta$. Moreover, sliding motion exists on the switching hyperplane $\sigma \left( x,x^*(t)\right) =0$ for $\varDelta \rightarrow 0$, with $x^*(t) \in \mathbb {R}^n$ being the steady state of the ideal sliding dynamics. Finally, $\sigma \left( x,x^*(t)\right)$ shows constant time derivatives at either sides of the switching hyperplane during a complete switching period within the boundary layer.

2.3.1 The Regulation Case

Theorem 16.1

Let Assumption 16.1 be fulfilled, with $x^*$ being a constant regulation point, and let the hysteresis band amplitude, $\varDelta$, be updated according to (16.8). If the integral gain $\gamma$ is selected as

$$\begin{aligned} 0< \gamma < \min \left\{ {\left( \rho ^+_*\right) }^{-1},{\left| \rho ^-_*\right| }^{-1}\right\} , \end{aligned}$$

with $\rho ^\pm _*$ defined in (16.6), then the switching period, $T_k$, converges asymptotically to its reference value, $T^*$, in the steady state.

Proof

It follows applying Jury stability criterion to the characteristic polynomial associated to the difference equation (16.5), see [14] for details.

2.3.2 The Tracking Case

Theorem 16.2

Let Assumption 16.1 be fulfilled, with $x^*= x (t)$ being a time-varying reference signal, and let the hysteresis band amplitude, $\varDelta$, be updated according to (16.11)–(16.13). If the integral gain $\gamma$ is selected as

$$\begin{aligned} \gamma _m:=&\max \left\{ \frac{\hat{\rho }^*_{k}-\sqrt{\frac{1}{2}\left( \hat{\rho }^{*^2}_k-\rho ^{+^2}_{*k}\right) }}{\hat{\rho }^{*^2}_k+\rho ^{+^2}_{*k} }, \ \forall k \ge 0\right\} , \\ \gamma _M:=&\min \left\{ \frac{\hat{\rho }^*_{k}+\sqrt{\frac{1}{2}\left( \hat{\rho }^{*^2}_k-\rho ^{+^2}_{*k}\right) }}{\hat{\rho }^{*^2}_k+\rho ^{+^2}_{*k} }, \ \forall k \ge 0\right\} , \end{aligned}$$

with $\hat{\rho }^*_{k}$ and $\rho _{*k}^{+}$ defined in (16.15), then the switching period, $T_k$, converges asymptotically to its reference value, $T^*$, in the steady state.

Proof

It follows using a Lyapunov-based discrete time approach, see [15] for details.

3 Application to Power Electronics

In this section, the previously proposed structures for switching frequency regulation in SMC are designed for several power converters. Specifically, three different cases are considered: a SMC in a regulation task for a buck converter, a SMC in a regulation case for a boost converter, and a SMC in a tracking task for a voltage source inverter (VSI).

3.1 Output Regulation of a Linear System: The Buck Converter

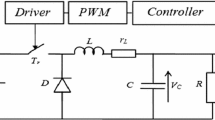
A buck converter circuit scheme is shown in Fig. 16.5, and the values of its parameters are listed in Table 16.1.

Fig. 16.5

Buck converter

The converter state space equations are:

$$\begin{aligned} C \, \frac{d \, v_c }{dt}&=i_l-\frac{v_c}{R} \\ L \, \frac{d \, i_l }{dt}&=E \, u-v_c, \end{aligned}$$

where u is the control signal and takes values in the set $\left\{ 0, 1 \right\}$. The power switches M1 and M2 work in a complementary way, remaining closed when u takes the values showed in Fig. 16.5.

Table 16.1 Buck converter parameters

3.1.1 Sliding Mode Control

Taking into account that the relative degree of the buck converter with respect to the output voltage is two, the chosen switching surface for output voltage regulation is:

$$ \sigma (v_c,i_l):=\lambda _1 e_v + \lambda _2 \dot{e}_v = 0, \quad \lambda _{1,2} > 0, $$

where ${v_c}^*$ and $e_v = {v_c}^* - v_c$ are the output voltage reference and the voltage error, respectively. The switching function derivative becomes:

$$\begin{aligned} \dot{\sigma }(v_c,i_l) = f_1 (v_c,i_l) - \frac{\lambda _2}{\textit{LC}} \, E \, u \end{aligned}$$

(16.17)

where

$$\begin{aligned} f_1 (v_c,i_l) = i_l \left( \frac{\lambda _2}{R \, C^2} - \frac{\lambda _1}{C} \right) + v_c \left( \frac{\lambda _1}{\textit{RC}} + \frac{\lambda _2}{\textit{LC}} - \frac{\lambda _2}{R^2 \, C^2} \right) . \end{aligned}$$

From (16.17), it is clear that sliding motion exists if $\frac{\lambda _2 \, E}{\textit{LC}}> f_1 > 0$. In turn, the equivalent control results in:

$$\begin{aligned} u_{eq} = \frac{\textit{LC}}{E \, \lambda _2} \, f_1 (v_c,i_l), \end{aligned}$$

and the control law that enforces a real sliding motion in the vicinity of $|\sigma (v_c,i_l)|<\varDelta$ is:

$$ u=\left\{ \begin{array}{ccl} 0 \,\, \text{ if }&{} \,\, \sigma< -\varDelta _k \,\, &{}\text{ or } \,\, \left( |\sigma |< \varDelta _k \,\, \& \,\, \dot{\sigma }> 0 \right) \\ 1 \,\, \text{ if }&{} \,\, \sigma > \varDelta _k \,\, &{}\text{ or } \,\, \left( |\sigma |< \varDelta _k \,\, \& \,\, \dot{\sigma } < 0 \right) . \end{array} \right. $$

Under sliding motion the system dynamics are governed by:

$$\begin{aligned} \frac{\mathrm{d} \, v_c }{\mathrm{d}t}&= - \frac{\lambda _1}{\lambda _2} v_c + \frac{\lambda _1}{\lambda _2} v_c^* + \dot{v}_c^* \end{aligned}$$

(16.18)

$$\begin{aligned} \frac{\mathrm{d} \, i_l }{\mathrm{d}t}&= \left( \frac{1}{\textit{RC}} - \frac{\lambda _1}{\lambda _2} \right) \left( i_l - \frac{v_c}{R} \right) , \end{aligned}$$

(16.19)

which is a linear system with equilibrium point $v_c = v_c^*, \, i_l=\frac{v_c^*}{R}$. From (16.18), (16.19) it is evident that system will be asymptotically stable if $\frac{\lambda _1}{\lambda _2} > \frac{1}{\textit{RC}}$. According to Table 16.1, the selected values for the sliding coefficients are: $\lambda _1 = 0.2$, $\lambda _2 = 1.9 \cdot 10^{-5}$, which ensures stability and delivers a good transient response.

3.1.2 Switching Frequency Regulation

In order to select $\gamma$ for the SFC, $\rho _k^+$ and $\rho _k^-$ have to be evaluated. This requires (16.17) to be particularized for the ideal steady-state sliding mode dynamics, namely ${v_c=v_c^*, i_l = \frac{v_c^*}{R}}$:

$$\begin{aligned} \dot{\sigma }(v_c^*,i_l^*)=\frac{\lambda _2}{\textit{LC}} \left( v_c^* - E \, u\right) , \end{aligned}$$

which yields

$$\begin{aligned} \rho _{*k}^{+}&= \left[ {\dot{\sigma }(v_c^*,i_l^*)_{u=u^-}} \right] ^{-1} = \frac{\textit{LC}}{\lambda _2 v_c^*}\\ \rho _{*k}^{-}&= \left[ {\dot{\sigma }(v_c^*,i_l^*)_{u=u^+}} \right] ^{-1} = \frac{\textit{LC}}{\lambda _2 \left( v_c^* - E \right) }. \end{aligned}$$

Then, with the data given in Table 1.1, one gets:

$$ \begin{matrix} v^*_c = 12V&{}\rightarrow \rho _{*k}^+ = 4.82e^{-6};\, \rho _{*k}^- = -1.61e^{-6} , \\ v^*_c = 24V&{}\rightarrow \rho _{*k}^+= 2.41e^{-6};\, \rho _{*k}^- = -2.41e^{-6} . \\ \end{matrix} $$

According to Theorem 16.1, the values of $\gamma$ within the range $\left( 0, \, 207470 \right)$ provide stability for the SFC. It should be noted that this range corresponds to 12 V at the output, corresponding to the worst case for the SFC stability. Consequently, the chosen value is $\gamma = 2 \cdot 10^4$.

3.1.3 Simulation Results

The simulations are performed using Matlab Simulink, with the data shown in Table 16.1 and with the previously selected control parameters, namely $\lambda _1 = 0.2$,   $\lambda _2 = 1.9 \cdot 10^{-5}$, and $\gamma = 2 \cdot 10^{4}$.

Figure 16.6 shows the response of the system with different initial conditions, $\varDelta _{ini}$, for the hysteresis value. From the top plots it can be seen how the system always reaches the desired steady state, $\varDelta _{ss}$, i.e. when $\varDelta _{ini} < \varDelta _{ss}$ and also when $\varDelta _{ini} > \varDelta _{ss}$. The second and third plots show the evolution of the hysteresis band and the corresponding switching period, respectively, confirming a good regulation to the desired value, $10^{-5}$ s i.e. 100 kHz, in both cases.

Fig. 16.6

Buck Converter: start-up with different initial values for $\varDelta$. From top to bottom. 1- Output voltage, $v_c$, and reference voltage, $v_c^*$. 2- Switching function $\sigma$. 3- Desired and real switching period ($T^*$, T)

Fig. 16.7

Buck Converter: output voltage response to a step-changing reference. From top to bottom. 1- Output voltage, $v_c$, and reference voltage, $v_c^*$. 2- Switching function $\sigma$. 3- Desired and real switching period ($T^*$, T)

Fig. 16.8

Buck Converter: switching period regulation. From top to bottom. 1- Output voltage, $v_c$, and reference voltage, $v_c^*$. 2- Switching function $\sigma$. 3- Desired and real switching period ($T^*$, T)

In Fig. 16.7 the system response to a variation of the voltage reference between 24 and 12 V is plotted. Besides a correct regulation of the output voltage, it is possible to confirm how, after the sliding transient, the desired switching frequency is reached in both cases.

The results shown in Fig. 16.8 correspond to the variation of the switching period reference when the value of $\gamma$ brings the system close to the unstable region. Such tests are performed in order to numerically verify the theoretical values that ensure stable behaviour of the SFC. Specifically, $\gamma$ is set to $2 \cdot 10^{5}$. In the test, the switching period reference is step varied from 14 to 12 $\upmu$s and from 10 to 12 $\upmu$s, respectively. From the results, it is clear that this value of $\gamma$ is close to the ones which would produce instability, as Theorem 16.1 claims.

3.2 Output Regulation of a Nonlinear System: The Boost Converter

A boost converter circuit scheme is shown in Fig. 16.9, and the values of its parameters are listed in Table 16.2.

Fig. 16.9

Boost converter

Table 16.2 Boost Converter Parameter

The nonlinear state space equations of the converter are:

$$\begin{aligned} L \frac{\mathrm{d} i_l}{\mathrm{d}t}&= E -v_c (1 - u) \\ C \frac{\mathrm{d} v_c}{\mathrm{d}t}&= i_l (1 - u) - \frac{v_c}{R}, \end{aligned}$$

where u is the control signal and takes values in $\left\{ 0, 1 \right\}$. The power switches M1 and M2 work in a complementary way, as in the Buck converter case.

3.2.1 Sliding Mode Control

The relative degree between the output voltage and the control input is one. However, imposing a sliding dynamics directly over the output voltage results in an unstable behaviour of the inductor current, which prevents its practical use [1]. An alternative solution in order to regulate the output voltage, $v_c$, is to consider the following switching function:

$$\begin{aligned} \sigma (v_c,i_l) := \kappa _1 e_v + \kappa _2 \int e_v \mathrm{d}t - \kappa _3 \, i_l, \quad \kappa _{1,2,3} > 0 \end{aligned}$$

where $e_v = v^*_c - v_c$.

The switching function derivative results in

$$\begin{aligned} \dot{\sigma }(v_c,i_l) = - \psi _1 (v_c,i_l) + \left( 1 - u \right) \psi _2 (v_c,i_l), \end{aligned}$$

(16.20)

where

$$\begin{aligned} \psi _1 (v_c,i_l) = \frac{\kappa _3 \, E}{L} - \frac{\kappa _1}{R \, C} v_c - \kappa _2 e_v, \quad \psi _2 (v_c,i_l) = \frac{\kappa _3}{L} v_c - \frac{\kappa _1}{C} i_l.\end{aligned}$$

(16.21)

Notice from (16.20) that sliding motion can be enforced on $\sigma (v_c,i_l)=0$ if $1> \frac{\psi _1 (v_c,i_l)}{\psi _2 (v_c,i_l)} > 0$. Using the last expression, the equivalent control is easily derived:

$$\begin{aligned} u_{eq} = \frac{\psi _2 (v_c,i_l) - \psi _1 (v_c,i_l)}{\psi _2 (v_c,i_l)}. \end{aligned}$$

(16.22)

Therefore, the equivalent system in sliding mode is:

$$\begin{aligned} L \frac{\mathrm{d} i_l}{\mathrm{d}t}&= E - v_c \frac{\psi _1 (v_c,i_l)}{\psi _2 (v_c,i_l)} \end{aligned}$$

(16.23)

$$\begin{aligned} C \frac{\mathrm{d} v_c}{\mathrm{d}t}&= i_l \frac{\psi _1 (v_c,i_l)}{\psi _2 (v_c,i_l)} - \frac{v_c}{R}, \end{aligned}$$

(16.24)

which is highly nonlinear. It is straightforward to check that $(i_l^*,v_c^*)$, with

$$\begin{aligned} i_l^*= \frac{{v_c^*}^2}{ER}, \end{aligned}$$

is an equilibrium point for this system. In the following, conditions will be obtained to guarantee local asymptotic stability of such equilibrium.

Indeed, defining the error variables $e_1 = i_l - i_l^*$, $e_2 = v_c - v_c^*$, the linearized model of the error system corresponding to (16.23), (16.24) reads as:

$$\begin{aligned} \nonumber L \frac{\mathrm{d} e_1}{\mathrm{d}t}&= - \frac{ E^2 \kappa _1 }{C v_c^*\psi _1 (v_c^*, i_l^*)} e_1 - \frac{E}{\psi _1 (v_c^*, i_l^*)} \left( \kappa _2 - \frac{2 \kappa _1}{R C} \right) e_2 \\ C \frac{\mathrm{d} e_2}{\mathrm{d}t}&= \frac{E^2 \kappa _3}{L v_c^*\psi _1 (v_c^*, i_l^*)} e_1 + \frac{1}{R\psi _1 (v_c^*, i_l^*)}\left( v_c^*\kappa _2 - \frac{2 E \kappa _3 }{L} \right) e_2, \end{aligned}$$

(16.25)

where it follows from (16.21) that

$$\begin{aligned} \psi _1 (v_c^*, i_l^*) = \frac{E \kappa _3}{L} - \frac{\kappa _1 v_c^*}{\textit{RC}}. \end{aligned}$$

The characteristic polynomial of (16.25) is given by:

$$\begin{aligned} P(\lambda ) = \lambda ^2 + \frac{1}{\psi _1 (v_c^*, i_l^*)}\left( \frac{E^2 \kappa _1}{\textit{LC}v_c^*} - \frac{\kappa _2 v_c^*}{\textit{RC}} + \frac{2 E \kappa _3}{\textit{RLC}} \right) \lambda + \frac{E^2 \kappa _2}{\textit{LC}v_c^*\psi _1 (v_c^*, i_l^*)}. \end{aligned}$$

Hence, under the current hypotheses ($\kappa _1, \, \kappa _2, \, \kappa _3 > 0$), the origin of (16.25) will be locally asymptotically if and only if

$$\begin{aligned} \frac{E v_c^*\kappa _3}{L} - \frac{\kappa _1 {v_c^*}^2}{\textit{RC}}> 0, \ \ \text{ and } \ \ \frac{E^2 \kappa _1}{L} - \frac{\kappa _2 {v_c^*}^2 }{R } + \frac{2 E v_c^*\kappa _3}{\textit{RL} } > 0. \end{aligned}$$

In this simulation case, the chosen values are: $\kappa _1 = 0.8$, $\kappa _2 = 4500$, $\kappa _3= 0.6$, which deliver a good transient response for the output voltage. Finally, using (16.20), the hysteretic control law that confines the switching function within the space region $|\sigma (v_c,i_l)|< \varDelta _k$ is:

$$ u=\left\{ \begin{array}{ccl} 0 \,\, \text{ if }&{} \,\, \sigma \cdot {{\mathrm{sign}}}\left( \psi _2\right)< -\varDelta _k \,\, &{}\text{ or } \,\, \left( |\sigma |< \varDelta _k \,\, \& \,\, \dot{\sigma }> 0 \right) \\ 1 \,\, \text{ if }&{} \,\, \sigma \cdot {{\mathrm{sign}}}\left( \psi _2\right) > \varDelta _k \,\, &{}\text{ or } \,\, \left( |\sigma |< \varDelta _k \,\, \& \,\, \dot{\sigma } < 0 \right) . \end{array} \right. $$

3.2.2 Switching Frequency Regulation

In order to select $\gamma$ for the SFC, $\rho _k^+$ and $\rho _k^-$ have to be evaluated. This requires (16.22) to be particularized for the steady state sliding mode, i.e. assuming $v_c=v_c^*$ and $i_l = \frac{{v_c ^*}^2}{R \, E}$,

$$\begin{aligned} \dot{\sigma }(v_c^{*},i_l^{*})= \psi _2 (v_c ^{*},i_l ^{*}) \left( 1 - \frac{E}{v_c ^{*}} - u \right) \end{aligned}$$

where

$$\begin{aligned} \psi _2 (v_c ^{*},i_l ^{*}) = \frac{ \kappa _3 v_c ^{*} }{L} - \frac{\kappa _1 v_c ^{*2}}{\textit{ERC}}. \end{aligned}$$

Using the data given in Table 16.2, $\psi _2 (v_c ^{*},i_l ^{*})$ results positive; therefore, the expected switching function slopes become:

$$\begin{aligned} \rho _{*k}^+&= \left[ { \dot{\sigma }(v_c^{*},i_l^{*})_{u=0}} \right] ^{-1} = \psi _2 (v_c ^{*},i_l ^{*})^{-1} \left( 1 - \frac{E}{v_c ^{*}} \right) ^{-1} \\ \rho _{*k}^-&= \left[ { \dot{\sigma }(v_c^{*},i_l^{*})_{u=1}} \right] ^{-1} = - \psi _2 (v_c ^{*},i_l ^{*})^{-1} \frac{v_c ^*}{E}. \end{aligned}$$

Replacing the values of the parameter shown in the Table 16.2 one gets:

$$ \begin{matrix} v^*_c = 36V&{}\rightarrow \rho _{*k}^+ = 1.67 \cdot 10^{-5};\, \rho _{*k}^- = -3.35 \cdot 10^{-5} ; \\ v^*_c = 48V&{}\rightarrow \rho _{*k}^+ = 1.15 \cdot 10^{-5};\, \rho _{*k}^- = -3.46 \cdot 10^{-5} ; \\ \end{matrix} $$

According to Theorem 16.1, the closed-loop system is stable for $\gamma \in (0,\, 2.89 \cdot 10^5)$. Hence, we choose $\gamma = 2 \cdot 10^{4}$.

Fig. 16.10

Boost Converter: start-up with different initial values for $\varDelta$. From top to bottom. 1- Output voltage, $v_c$, and reference voltage, $v_c^*$. 2- Switching function $\sigma$. 3- Desired and real switching period ($T^*$, T)

3.2.3 Simulation Results

The simulations are performed using Matlab Simulink with the data shown in Table 16.2 and the control parameters $\kappa _1$ =0.8, $\kappa _2$ = 4500, $\kappa _3$ = 0.6, and $\gamma = 2 \cdot 10^{4}$.

Figure 16.10 shows the response of the system with different initial conditions, $\varDelta _{ini}$, for the hysteresis value $\varDelta$. Both voltage and frequency regulation are confirmed from the results.

The simulation shown in Fig. 16.11 plots the system response when the voltage reference is step changed between 48 and 36 V (see the top plots). Once the sliding motion is recovered, the switching period reaches the desired value in around 500$\upmu$s. Notice from the mid plots of the figure how the SFC adjusts the hysteresis value in order to keep the switching period at the desired value.

The results presented in Fig. 16.12 show the switching period response when $\gamma = 2.75 \cdot 10^5$, which is close to the maximum value that guarantees stability, i.e. $\gamma = 2.88 \cdot 10^5$. The underdamped response illustrates the validity of the stability range.

Fig. 16.11

Boost Converter: step-changing output voltage reference. From top to bottom. 1- Output voltage, $v_c$, and reference voltage, $v_c^*$. 2- Switching function $\sigma$. 3- Desired and real switching period ($T^*$, T)

Fig. 16.12

Boost Converter: switching period regulation with $\gamma = 275000$. From top to bottom. 1- Output voltage, $v_c$, and reference voltage, $v_c^*$. 2- Switching function $\sigma$. 3- Desired and real switching period $T^*$, T

Fig. 16.13

Voltage source inverter structure

3.3 Output Tracking: The Voltage Source Inverter

The voltage source inverter (VSI) circuit scheme is depicted in Fig. 16.13. This circuit is commonly employed to generate a sinusoidal signal at its output and is classified as DC/AC converter.

The VSI dynamics are governed by:

$$\begin{aligned} C\frac{\mathrm{d}v_c}{\mathrm{d}t}&=-\frac{v_c}{R}+i_L, \end{aligned}$$

(16.26)

$$\begin{aligned} L\frac{\mathrm{d}i_L}{\mathrm{d}t}&=-v_c+E \, u, \end{aligned}$$

(16.27)

where $i_L$ is the inductor current, $v_c$ is the output voltage, R is the resistive load, L is the inductance, C is the capacitor and E is the input voltage. The control action u takes values in $\{ -1, 1 \}$. The power switches are represented by $M_1,M_2,M_3,$ and $M_4$. As it is shown in Fig. 16.13, $M_1$ and $M_4$ are short circuited when $u=1$, and remain open when $u=-1$, whereas $M_2$ and $M_3$ work in a complementary way. Table 16.3 presents the specific values of the converter parameters used in the simulation.

3.3.1 Sliding Mode Control

In this case, the control objective is to track a time-varying reference at the output. The signal to be tracked is defined as:

$$\begin{aligned} v_c^*(t)= A \sin \omega t. \end{aligned}$$

Since the relative degree of the output voltage with respect to the control is two, the following first order linear switching surface is used [4]:

$$\begin{aligned} \sigma \left( v_c,\dot{v}_c\right) = \phi _1 e_v + \phi _2 C \dot{e}_v=0, \quad \phi _{1,2} > 0, \end{aligned}$$

(16.28)

where $e_v = v_c^*- v_c$.

The switching function derivative becomes:

$$\begin{aligned} \dot{\sigma }\left( v_c,\dot{v}_c\right) = f_{vsi} - \frac{\phi _2 \, E}{L} u \end{aligned}$$

(16.29)

where

$$f_{vsi} = \phi _1 \dot{v}_c^* + \phi _2 C \ddot{v}_c^* + v_c \left( \frac{\phi _1}{\textit{RC}} - \frac{\phi _2}{R^2 \, C} + \frac{\phi _2}{L} \right) + i_l \left( \frac{\phi _2}{\textit{RC}} -\frac{\phi _1}{C} \right) .$$

It is clear that sliding motion exists if $\frac{\phi _2 \, E}{L} > | f_{vsi} |$. The equivalent control results in:

$$\begin{aligned} u_{eq} = \frac{L}{\phi _2 \, E} f_{vsi}. \end{aligned}$$

According to the definition of the equivalent control, the expression (16.29) can be redefined as:

$$\begin{aligned} \dot{\sigma }\left( v_c,\dot{v}_c\right) = \frac{\phi _2 \, E}{L} (u_{eq} - u) \end{aligned}$$

(16.30)

The corresponding ideal sliding behavior is given by the linear time-varying system:

$$\begin{aligned} C\frac{\mathrm{d}v_C}{\mathrm{d}t}&=-\frac{\phi _1}{\phi _2}v_C +\frac{\phi _1}{\phi _2} v_C^*+C\dot{v}_C^*, \\ L\frac{\mathrm{d}i_L}{\mathrm{d}t}&=\frac{\alpha \phi _1}{R \phi _2}v_C-\frac{\alpha \phi _1}{\phi _2}i_L+Lh(t), \end{aligned}$$

where

$$\begin{aligned} \alpha :=\frac{L}{C}\left( 1-\frac{\phi _2}{R \phi _1}\right) \quad \text{ and } \quad h(t):=\frac{\phi _1}{\phi _2} \dot{v}_C^*+C\ddot{v}_C^*. \end{aligned}$$

It is then immediate that the system is asymptotically stable if $R> \phi _2 \phi _1^{-1} > 0$. According to the VSI parameters values defined in Table 16.3, the sliding coefficients are selected as: $\phi _1 = 0.1$, and $\phi _2 = C$.

Finally, the hysteretic control law that confines $\sigma$ within a boundary layer of width $2\varDelta _k$, is:

$$ u=\left\{ \begin{array}{ccl} -1 \,\, \text{ if }&{} \,\, \sigma< -\varDelta _k \,\, &{}\text{ or } \,\, \left( |\sigma |< \varDelta _k \,\, \& \,\, \dot{\sigma }> 0 \right) \\ 1 \,\, \text{ if }&{} \,\, \sigma > \varDelta _k \,\, &{}\text{ or } \,\, \left( |\sigma |< \varDelta _k \,\, \& \,\, \dot{\sigma } < 0 \right) . \end{array} \right. $$

Fig. 16.14

VSI Converter. From top to bottom. 1- Desired output voltage, $v_c^*$. 2- Dynamic evolution of $\rho _{*k}^+$ and $\rho _{*k}^-$. 3- Groups of roots produced by the conditions given in Theorem 16.2

Table 16.3 Voltage Source Inverter parameters

3.3.2 Switching Frequency Regulation

In order to select $\gamma$ for the SFC, the values of $\rho _{*k}^+$ and $\rho _{*k}^-$ have to be evaluated. The switching function slopes can be obtained from (16.30). The equivalent control in the steady sliding motion can be derived from (16.26), (16.27) imposing that $v_c = v_c^*$.

Therefore, (16.30) becomes:

$$\begin{aligned} \dot{\sigma }\left( v_c^*,\dot{v}_c^*\right) = \phi _2 \left[ \frac{v_c^* - E u}{L} + \frac{\dot{v}_c^*}{R} + C \ddot{v}_c^* \right] , \end{aligned}$$

and $\rho _{*k}^+$ and $\rho _{*k}^-$ are finally given by:

$$\begin{aligned} \rho _{*k}^+&= \left[ {\dot{\sigma }\left( v_c^*,\dot{v}_c^*\right) _{u=-1} } \right] ^{-1} =\phi _2^{-1} \left[ \frac{v_c^* + E}{L} + \frac{\dot{v}_c^*}{R} + C \ddot{v}_c^* \right] ^{-1}\\ \rho _{*k}^-&= \left[ {\dot{\sigma }\left( v_c^*,\dot{v}_c^*\right) _{u=1} } \right] ^{-1} = \phi _2^{-1} \left[ \frac{v_c^* - E}{L} + \frac{\dot{v}_c^*}{R} + C \ddot{v}_c^* \right] ^{-1}. \end{aligned}$$

Fig. 16.15

VSI Converter. From top to bottom. 1- Desired and real output voltage $(v_c^*, \, v_c)$. 2- Inductor current, $i_l$. 3- Switching surface, $\sigma$. 4- Desired and real switching period of the control action ($T^*$, T)

Fig. 16.16

VSI Converter. From top to bottom. 1- Desired and real output voltage $(v_c^*, \, v_c)$. 2- Desired and real switching period of the control action ($T^*$, T)

According to Theorem 16.2, the previous expressions allow to select the value of $\gamma$ which ensures stability. In the top plot, Fig. 16.14 shows the desired output voltage, $v_c^*$, and the dynamic evolution of $\rho _{*k}^+, \, \rho _{*k}^-$ in the mid plot. Finally, the set of solutions of the condition stated at Theorem 16.2 for the resulting values of $\rho _{*k}^+, \, \rho _{*k}^-$ are presented in the bottom plot. With such signals, it is straightforward to find the maximum and minimum values which guarantee stability of the SFC. Specifically, the exact values that define the stability margin are $\gamma _M = 1.14 \cdot 10^5$ and $\gamma _m = 9.3\cdot 10^4$, i.e. $9.3\cdot 10^4< \gamma < 1.14 \cdot 10^5$. The chosen value for the simulations is $\gamma = 1 \cdot 10^5$.

3.3.3 Simulation Results

The simulations are performed with Matlab-Simulink. Figure 16.15 shows the response of the system under sliding motion when some variations are introduced. On the one hand, at the beginning of the simulations a fixed value for the hysteresis band is used, which leads to an expected time-varying switching period. At time instant $t=0.02$ s the proposed SFC structure is enabled. In the bottom plot in Fig. 16.15 one can observe how the switching period converges to the desired value, confirming a proper performance of the SFC. Additionally, a load transient is introduced at time $t=0.05$ s, from $R=1\,\mathrm{k}\Omega$ to $R= 10\,\Omega$. Notice how the output voltage $v_c$ tracks perfectly the desired voltage $v^*_c$ during the entire test. The use of the feedforward signal $\varOmega$ (see (16.13)) implies knowledge of $\rho ^{\pm }_k$, but when the SFC is implemented the information to calculate $\varDelta _k$ is related to the last interval measured $k-1$, since $\rho ^{\pm }_k$ is not available until the kth interval ends. Specifically, $\rho ^{\pm }_k$ are approximated by the immediately preceding values:

$$\begin{aligned} \rho ^+_{k-1}=\frac{T^+_{k-1}}{\varDelta _{k-1}+\varDelta _{k-2}}, \quad \rho ^-_{k-1}=\frac{T^-_{k-1}}{2\varDelta _{k-1}}. \end{aligned}$$

The last test, shown in Fig. 16.16, presents the switching period response when some parameters are varied, as the amplitude and frequency of the time-varying reference signal, and the desired switching frequency. An overall good performance of the system is confirmed. However, it is worthwhile commenting on the switching period oscillation that appears when the desired frequency, $\omega$, of the tracking signal is set to 200 Hz (see second plot in Fig. 16.16 at $t=0.07$ s). When the frequency signal increases, the values of $\rho ^{\pm }_k$ have a higher time variation, and the assumption of constant slopes during the switching interval is not completely fulfilled. As a consequence, the variable hysteresis band provided by the SFC does not perfectly reject the period oscillations. In the same way, notice that when the desired switching frequency is increased ($t=0.09$ s), the assumption is newly met, and the switching period recovers the desired fixed value.

4 Conclusions

Fixing the switching frequency is a key issue in sliding mode control implementations when it is applied in inherently switched systems. This chapter presented a hysteresis band controller capable of setting a constant value for the steady-state switching frequency of a sliding mode controller in regulation and tracking tasks. Problem statement, practical assumptions, stability proofs and control parameters design criteria were also provided. The proposal was numerically validated through a set of simulations in power converters such as a Buck converter, a Boost converter, and a voltage source inverter.