Higher-Order Sliding Mode Control Scheme with an Adaptation Low for Uncertain Power DC–DC Converters

Abstract

In this paper, a higher-order sliding mode controller for a power DC–DC converter is proposed. The uncertainty and disturbance are implicit to be unknown. A detailed analysis to explore the local and global stability of a Buck DC–DC converter was presented in this paper. Different control schemes were implemented to regulate the output voltage and to eliminate the high current ripples for the proposed converter, beginning with a proportional-integral-derivative compensation scheme, then a sliding mode controller, a higher-order sliding mode controller and finally an adaptation low with higher-order sliding mode controller (AHOSMC). Stability and robustness of the AHOSMC are proved by using the classical Lyapunov criterion. The sensitivity of parameters variation is analyzed, and a detailed bifurcation analysis is undertaken.

1 Introduction

High-frequency and high-power converters are necessary in DC–DC conversion (Tan et al. 2004a, b). However, increasing the switching frequency leads to significant switching losses, which can deteriorate all system efficiency. A huge step in DC–DC converter technology was taken when the DC link converter was invented (Tan et al. 2005). Stable pulse width modulation (PWM) DC–DC converters are deemed necessary. This leads to analyze the bifurcation pattern of these converters. This PWM DC–DC converter not only has to meet the characteristics demanded by the load, but also must process energy with high efficiency, high reliability, high-power density and low cost (Tan et al. 2006; Hadri Hamida et al. 2006).

The bifurcation analysis denotes for a change in the number of candidate operating conditions of a nonlinear system when a parameter is quasi-statically varied (Tse and Adams 1992; Hadri-Hamida and Allag 2009; Nayfeh and Balachandran 1995). The parameter being varied is referred to as the bifurcation parameter (bp). A nonlinear dynamical system can exhibit many different kinds of bifurcations as one or more parameters are varied.

In its simplest terms, the operation of DC–DC converter can be described as an orderly repetition of a fixed sequence of circuit topologies. The conversion function of the converter is determined by the constituent topologies and the order in which they are repeated (Middlebrook and Cuk 1997; Venkataramanan et al. 1985).

The major difficulty, in the analysis and modeling of PWM DC–DC converters, lies in the fact that the manner in which the system operates is highly nonlinear (Mazumder et al. 2001; Maity et al. 2007). To date, most analytic techniques of modeling and analysis of these converters implement linear feedback systems (Rosehart and Cañizares 1999).

In most of the above investigations, sampled data models or maps of the converters have been derived, and the bifurcation structures have been investigated with the discrete models. Using an exact formulation based on nonlinear maps (Wiggins 1990), we develop a systematic method to model PWM DC–DC converters operating with feedback control.

Here, we have investigated the behavior of the Buck PWM DC–DC converter in the instability zones to shed light on its associated bifurcation with the help of the software package MATLAB (Wang et al. 2000).

To improve the performances of the PWM DC–DC converter, a control strategy based on AHOSMC is proposed, which gives the good performance robust to disturbances as well as the fast transient responses.

The SMC is one of the popular strategies to deal with uncertain control systems (Deane and Hamill 1990). The main feature of SMC is the robustness against parameter variations and external disturbances. Various applications of SMC have been conducted, such as robotic manipulators, aircrafts, DC motors, chaotic systems, and so on (Mattavelli et al. 1993).

The reference Tsang and Chan (2008) presented a model-based cascade controller for DC–DC Buck converters. A dead band relay is introduced in the voltage loop to improve the disturbance rejection and speed of response of the Buck converter which is modified into an uncertain linear model in Tsai and Chen (2007). Then, SMC technology is adopted to suppress the input disturbance and reduce the effects from the load variation.

In Li et al. (2013), an improved SMC method for a modular multilevel high-voltage DC converter is presented. It merges the merits of the PID neural network and can solve the chattering problem that exists in conventional SMC on-line. The hysteresis modulation SMC is designed in Ramash Kumar and Jeevananthan (2012) for the inherently variable structure of the negative-output elementary boost converter by using a state-space average-based model. In Das and Mahanta (2014), the problem of driving stability for a hybrid vehicle is discussed. The vehicle stability control is addressed using HOSMC and observation techniques. Comparing these works with our work, the contribution of this paper is to apply an AHOSMC to an uncertain Buck DC–DC converter.

We first show that it is feasible to apply a PID feedback control technique to such a system that is operated in high-frequency regimes. Also, the effect of parameter perturbation on the control performance is investigated. In order to eliminate the bifurcations and stead-state error, an SMC control is also introduced to the exact feedback control law. The goal of the first-order SMC is to force the state trajectories to move along the sliding manifold. In the HOSMC, the purpose is to move the states along the switching surface and to keep its order successive time derivatives by using a suitable discontinuous control action. In the AHOSMC, the time derivative of the control input would be designed to act on the higher-order derivatives of the sliding variable (Utkin and Young 1978). Hence, the time derivative of the control would be used as the control input. The new control would be designed as a discontinuous signal, but its integral would be continuous for the eliminating of the high-frequency chattering. It is shown via simulation results that the AHOSMC has high performance both in the transient and in steady-state operations. A good control of the output voltage is obtained.

2 System Model Development

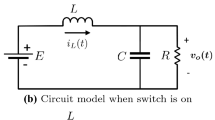
A power circuit of a high-frequency Buck DC–DC converter is introduced in Fig. 1. From the detailed analysis of the PWM Buck converter presented in Hadri-Hamida et al. (2014), we deduce the following large-signal continuous-time system:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{\bar{x}}} =\left( {\left[ {{\begin{array}{ll} {-\frac{1}{L}\left( {r_L +\frac{r_C \times R}{r_C +R}} \right) }&{} {-\frac{1}{L}\left( {\frac{R}{r_C +R}} \right) } \\ {\frac{R}{C\times \left( {r_C +R} \right) }}&{} {-\frac{1}{C\times \left( {r_C +R} \right) }} \\ \end{array} }} \right] \overline{x} + \left[ {{\begin{array}{l} {\frac{1}{L}} \\ 0 \\ \end{array} }} \right] \overline{V_e } } \right) \upalpha \\ \qquad +\left( {\left[ {{\begin{array}{ll} {-\frac{1}{L}\left( {r_L +\frac{r_C \times R}{r_C +R}} \right) }&{} {-\frac{1}{L}\left( {\frac{R}{r_C +R}} \right) } \\ {\frac{R}{C\times \left( {r_C +R} \right) }}&{} {-\frac{1}{C\times \left( {r_C +R} \right) }} \\ \end{array} }} \right] \overline{x} +\left[ {{\begin{array}{l} 0 \\ 0 \\ \end{array} }} \right] \overline{V_e } } \right) \left( {1-\upalpha } \right) \\ \overline{V_s } =\left( {\left[ {{\begin{array}{ll} {\frac{r_C \times R}{r_C +R}}&{} {\frac{R}{r_C +R}} \\ \end{array} }} \right] \upalpha +\left[ {{\begin{array}{ll} {\frac{r_C \times R}{r_C +R}}&{} {\frac{R}{r_C +R}} \\ \end{array} }} \right] \left( {1-\upalpha } \right) } \right) \bar{x} \\ \end{array}} \right. \end{aligned}$$

(1)

where $x = [i_{L}, V_\mathrm{C}]^{t}$.

3 Design of the Feedback Control

In this section, different linear and nonlinear controllers are designed for Buck DC–DC converter.

3.1 PID and SMC Controllers

Control applications of PWM DC–DC converters have been widely investigated (Mondal and Mahanta 2011; Utkin et al. 1999; Hadri Hamida et al. 2013; Dong and Tang 2014). The main objective of research and development in this field is always to find the most suitable control method to be implemented in various DC–DC converter topologies. In other words, the goal is to select a control method capable of improving the efficiency of the converter, lessening the effect of electromagnetic interference (EMI), and being less effected by component variation which is the main objective in this work. The bloc scheme in Fig. 2 gives the configuration of the DC–DC Buck converter which utilizes a controller based on a SMC law. The analysis of the PID and the SMC controllers is presented in Appendix.

Fig. 1

High-frequency buck DC–DC converter

Fig. 2

Closed-loop DC–DC buck converter with SMC

3.2 Higher-Order Sliding Mode Controller

The objective of the synthesis of a higher-order sliding mode control is to force the trajectories of the system (22) to move in a finished time on the whole sliding surfaces with a defined order r by:

$$\begin{aligned} S^{r}=\left\{ {\left. {x\in R^{n}} \right| {S=\dot{S} =\ldots \ldots =S^{r-1}=0}} \right\} \end{aligned}$$

(2)

The $r$th-order derivative of S(x) satisfies the following equation:

$$\begin{aligned} S^{r}\left( x \right) =EE\left( x \right) +QQ\,T_{R} \end{aligned}$$

(3)

where the matrices EE(x) and QQ(x) are the derivatives of the smooth functions in (29). The $r$th-order sliding mode control of system (22) with respect to the sliding variable S(x) can be expressed as Benbouzid et al. (2014):

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_i =z_{i+1} \\ \dot{z}_r =EE\left( x \right) +QQ\,\left( x \right) \,T_R \\ \end{array}} \right. \end{aligned}$$

(4)

where $1 \le \hbox {i} \le \hbox {r} - 1, \,\hbox {and}\, [\hbox {z}_{1} \hbox {z}_{2} \ldots \ldots \hbox {z}_\mathrm{r}]^\mathrm{t} = [\hbox {S}(\mathrm{x}) \dot{\mathrm{S}}(\mathrm{x}) \ldots$ $\ldots \hbox {S}^\mathrm{r-1}(\mathrm{x})]^\mathrm{t}$. By taking the first-order time derivative of (29), we obtain:

$$\begin{aligned} \ddot{S}&= \dot{E} \left( x \right) +\dot{Q} \,T_R +Q\dot{T}_{R}\nonumber \\&= EE\left( {x,T_R } \right) +Q\dot{T}_{R} \end{aligned}$$

(5)

where

$$\begin{aligned} EE&= \left( {\frac{H_{i}}{LC}-\frac{H_{i} r_{L}^{2} }{L^{2}}+\frac{H_\mathrm{v} r_{L}}{LC}} \right) i_{L} +\left( {\frac{H_\mathrm{v} }{LC}-\frac{H_{i} r_{L} }{L^{2}}} \right) V_C \\&\quad -\frac{H_{i}}{LC}I_{s} +\left( {\left( {\frac{H_{i} r_{L} }{L^{2}}-\frac{H_\mathrm{v}}{LC}} \right) V_{e}} \right) T_R. \end{aligned}$$

Finally, the new control law is given by:

$$\begin{aligned} \dot{T}_{R} =-Q^{-1} \,EE\left( x,T_{R} \right) \end{aligned}$$

(6)

3.3 Adaptive Higher-Order Sliding Mode Controller

Our objective is to design an adaptive HOSMC for use with a Buck DC–DC converter having parameter but unknown R load. With $z$ as the state variable, and from Defoort et al. (2009), the $r$th-order sliding mode control for system (22) can be written as:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_{i} =z_{i+1} +\Delta f_i \left( z,t \right) \\ \dot{z}_{r} =EE_n \left( z \right) +QQ_n \left( z \right) \,T_R +\Delta f_{r} \left( {z,t} \right) \\ \end{array}}\right. \end{aligned}$$

(7)

where $\Delta f\left( {z,t} \right) =\Delta EE\left( z \right) +\Delta QQ\left( z \right) T_{R}$, which are the uncertain parts of the matrices EE(z) and QQ(z), and $EE_n \left( z \right) , QQ_{n} \left( z \right)$are the nominal parts of matrices EE(z) and QQ(z) respectively.

Assuming $\hbox {y}_{1} = \hbox {S}(\hbox {z})\, \hbox {and}\, \hbox {y}_{2} = \dot{\mathrm{S}} (\mathrm{z})$, the system dynamics can be written as Mondal and Mahanta (2013)

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{y}_{1} =y_2 \\ \dot{y}_{2}=\Phi \left( {z,T_R } \right) +\Psi \left( z \right) v \\ \end{array}} \right. \end{aligned}$$

(8)

where $\Phi \left( {z,T_R} \right) =\dot{EE}_{n} \left( z \right) +\dot{QQ}_{n} \left( z \right) T_{R} +\dot{\Delta f} \left( {z,t} \right) , \Psi$ $\left( z \right) =QQ_n \left( z \right)$, and $v=\dot{T}_{R}$. Thus, the new control input of the system (8) to be determined becomes $v$. The sliding function for system (8) is considered as:

$$\begin{aligned} \upsigma =y_2 +K\,y_1 \end{aligned}$$

(9)

The derivative of (9) is obtained as:

$$\begin{aligned} \dot{\upsigma } =\dot{y}_{2} +K\,\dot{y}_{1} \end{aligned}$$

(10)

Now, we consider the sliding surface suggested by Defoort et al. (2009)

$$\begin{aligned} S\left( z \right) =z_{n} -z_{n} \left( 0 \right) \end{aligned}$$

(11)

where $\hbox {z}_\mathrm{n}(0)$ is the initial condition of the system. The time derivative of (11) is:

$$\begin{aligned} \dot{S} \left( z \right) =\dot{z}_{n} \,=EE_n \left( z \right) +QQ_n \left( z \right) T_{R} +\Delta f \left( z,t \right) \end{aligned}$$

(12)

and consequently:

$$\begin{aligned} \ddot{S} \left( z \right) =\dot{EE}_{n} \left( z \right) +\dot{QQ}_{n} \left( z \right) T_R +QQ_n \left( z \right) \dot{T}_{R}+\Delta \dot{f}\left( {z,t}\right) \end{aligned}$$

(13)

From Eqs. (10), (12), and (13) we can obtain:

$$\begin{aligned} \dot{\upsigma }&= \dot{EE}_{n} \left( z \right) +\dot{QQ}_{n} \left( z \right) T_{R} +QQ_{n} \left( z \right) \dot{T}_{R} +\Delta \dot{f} \left( {z,t} \right) \nonumber \\&+\,K\left( {EE_n \left( z \right) +QQ_n \left( z \right) T_{R} +\Delta f\left( {z,t} \right) } \right) \nonumber \\&= \Phi \left( {z,T_R } \right) +\Psi \left( z \right) v+K\left( \dot{z} \right) \end{aligned}$$

(14)

The control goal is to regulate the voltage source $\hbox {V}_\mathrm{C}$ and to reduce the impact of load and component variation (Zhang et al. 2015) with the elimination of the high current ripple. The new control law becomes:

$$\begin{aligned} v=-\Psi ^{-1} \left( z \right) \left\{ {\Phi \left( {z,T_R } \right) +K\left( \dot{z} \right) -\dot{\upsigma }} \right\} \end{aligned}$$

(15)

After the use of the constant plus proportional reaching law from Utkin and Young (1978), we obtain:

$$\begin{aligned} \dot{\upsigma } =-\uprho \, \upsigma -\updelta \, \hbox {sign}\left( \upsigma \right) \end{aligned}$$

(16)

Fig. 3

Frequency response analysis of the converter for $V_{e} = 18 (-), 24 (-), 40\,\hbox {V} ({\ldots })$ respectively

Fig. 4

The asymptotic behavior of a system

Fig. 5

Steady states of the closed-loop system with a PID controller for different values of $V_{e}$, ($\mathbf{1}$) Bifurcation diagram where $V_{e}$ is the bp, ($\mathbf{2}$) $i_{L}$, ($\mathbf{3}$) $V_\mathrm{C}$, ($\mathbf{4}$) state plane and (5) power spectral density of the inductor current

Fig. 6

Bifurcation diagrams. a controller gain is the bp, b $L$ is the bp, c $V_{e}$ is the bp

Fig. 7

Bifurcation diagram, $R$ is the bp. a with PID controller, b with SMC

where $\uprho \ge 0$, and $\updelta =\frac{1}{R}-\frac{1}{R_n }$. Since $\updelta$ is unknown, we replace it by its estimate $\hat{\updelta }=\frac{1}{\hat{R}}-\frac{1}{R_{n}}$, we can rewrite equation (15) in a form that suggests an adaptive scheme for the estimation of R load:

$$\begin{aligned} v=-\Psi ^{-1} \left( z \right) \left\{ {\Phi \left( {z,T_R } \right) +K\left( {\dot{z}} \right) +\,\uprho \upsigma +\,\hat{\updelta }\,sign\left( \upsigma \right) } \right\} \end{aligned}$$

(17)

We can determine by simulation the poles that give good performance. By using MATLAB Control System Toolbox, one can obtain the gain $k_{1}$. We define the adaptation error $e$ which satisfies:

$$\begin{aligned} \dot{e} =k_1 e+W_1 \Delta \updelta +W_2 \dot{\hat{\updelta }} \end{aligned}$$

(18)

where $\Delta \updelta =\frac{1}{R}-\frac{1}{\hat{R}}$ is the error estimate. The existence of the nonlinear term $W_2 \dot{\hat{\updelta }}$ suggests the use of the concept of augmented error $\upsigma$ which puts (18) in a familiar form. We introduce the signal $\upvarepsilon$ satisfying $(\dot{\upvarepsilon } =k_{1} \upvarepsilon +W_2\dot{\hat{\updelta }}, \upvarepsilon (0) =0)$ and the augmented error $\upsigma$ by ($\upsigma = \hbox {e} - \upvarepsilon )$ which satisfies $\dot{\upsigma } =k_1 \upsigma +W_1 \Delta \updelta$. We choose the candidate Lyapunov function $V=\upsigma ^{T}P\upsigma +\Delta \updelta ^{T}\Gamma \Delta \updelta$, and then, we differentiate it, we have:

$$\begin{aligned} \dot{V} =\upsigma ^{T}\left( {k_1 ^{T}P+Pk_1 } \right) \upsigma +2\Delta \updelta ^{T}\left( {W^{1T}P\upsigma \Gamma \dot{\Delta \updelta }} \right) \end{aligned}$$

(19)

In defining the parameter update law under the form $\dot{\hat{\updelta }} =-\Gamma ^{-1}W^{1T}P\upsigma$, we can guarantee that $\dot{V} =-\upsigma ^{T}Q\upsigma \le 0$ where $P=P^{T}\rangle 0$ is the solution of Lyapunov equation:

$$\begin{aligned} k_1 ^{T}P+Pk_1 =-\upvartheta \end{aligned}$$

(20)

Using a standard Lyapunov agreement, we can show that the augmented error $\upsigma \rightarrow 0 \hbox { as t} \rightarrow \infty$ and that the state $z$ and the error $\Delta \updelta$ remain bounded. Considering $\upvartheta$ as an identity matrix and $k_{1}$, then one can find the solution of Equation (19).

Fig. 8

Estimation of R load

Fig. 9

Inductor current $i_{L}$, capacitor voltage $V_\mathrm{C}$, and control law $u_{c}$. a with PID controller. Inductor current $i_{L}$, capacitor voltage $V_\mathrm{C}$, and the sliding surface S. b with SMC, c with AHOSMC

4 Simulation Results

We plot in Fig. 3 the loop gain of the closed-loop regulator system with a PID controller for different values of the input voltage. Even when the input voltage varied, the asymptotic behavior of the converter is overall stable (see Fig. 4) according to the frequency response analysis. In the other hand, in Fig. 5(1), we show the bifurcation diagram with the input voltage as a bp where the converter is not stable locally. The period-one orbit of the closed-loop system is stable. When $V_{e} = 18$ V, the period-one orbit becomes unstable and a stable period-two orbit emerges. The period-doubling bifurcation was ascertained by computing the Floquet multipliers of the map. When $V_{e} = 21$ V, the period-two orbit becomes unstable and a period 3 emerges. After the period-three bifurcation, the period-three orbit directly bifurcates into a chaotic orbit ($V_{e} > 40\hbox {V}$). Next, we present in Fig. 5(2–5) the steady-state waveforms of the closed-loop system with a PID controller applying $V_{e} = 18, 21, 24$, and 40V, respectively. The two-dimensional projections of the phase portraits on the $i_{L}-V_\mathrm{C}$ plane corresponding to these four cases are also shown (Fig. 5(4)). They demonstrate clearly the period 1, period 2, period 3, and chaotic orbits.

The power spectrum density for each of these cases is also shown (Fig. 5(5)). We note that in the case of period 1, appears in the current spectrum an harmonics series of frequency $k * f$ such as $k$ is an entire number, on the other hand, in the case of period 2, the spectrum of the current is enriched with a new series of harmonics of frequency $(k + 0.5) * f$. In period 3, another series of harmonics of frequency $(k / 3) * f$ appears in the spectrum of the current, whereas the chaos is appeared by the absence of an ordered series of harmonics.

In Fig. 6, we investigate the effect of the parameter perturbation of the Buck DC–DC converter. These parameters are, respectively, the controller gain, the inductor $L$, and the input voltage $V_{e}$.

The AHOSMC is verified by detailed using MATLAB. A PWM DC–DC model is developed to simulate a switch-on and change load transient conditions, with the control scheme in Fig. 2. In Fig. 7, we show the bifurcation diagram for the system (a) with a PID controller and (b) with an SMC, where the load resistance is the bifurcation parameter. When the load resistance is increased, inductor current decreases, the period-one solution is stable. As $R$ is increased beyond 19 $\Omega$, the period-one solution is still stable and the period of the response is not doubled (Fig. 7b). Note that the SMC eliminates the bifurcation of the system orbit. Figure 8 shows the estimation of $R$ load.

From Fig. 9a, we show that the SMC controller ensures finite-time convergence of the system states. However, the high-frequency chattering is always present. In Fig. 9b, the undesired chattering in the current and voltage signal was removed. The dynamic performance of the designed AHOSMC controller is found to be satisfactory compared with that obtained with the conventional SMC and PID controller.

5 Conclusion

In this paper, a nonlinear model was derived for a high-frequency Buck DC–DC converter. The nonlinear model was used to study the stability of this converter. Bifurcation diagrams were generated to study the total behavior of the system as one of its parameters varies.

Next, to improve the performances of our system, we have introduced a sliding mode controller. The results show that the SMC control has fast dynamic response to external disturbances than the PID control and with the SMC control the static and dynamic performances of the output voltage are much better than with the PID control. This technique of control can reduce and sometimes eliminate the effect of load and component variation (bifurcations).

Moreover, a robust model reference AHOSMC is designed in order to diminish the influence of the unknown load uncertainties and disturbances. The advantage of the adaptive HOSMC is translated by the reduction of chattering. The proposed control scheme gives satisfactory simulation results with nominal load.

It is shown through simulation results that the AHOSMC can reduce the internal oscillations, and the performance of the high-frequency Buck DC–DC converter based on AHOSMC scheme is better than the ones based on classical SMC scheme and the PID feedback control scheme.

Appendix

1.1 PID and SMC Controllers

We have introduced firstly a PID feedback controller which has the following transfer function:

$$\begin{aligned} G_\mathrm{contr} (p)=k_p \frac{1+p\cdot T_i +p^{2}\cdot T_i \cdot T_d }{p\cdot T_i } \end{aligned}$$

(21)

Then, we have presented the SMC controller. In SMC, the trajectory of the system is constrained to move or slide along a predetermined hyper plane in the state space. Such mode is completely robust and independent of parametric variations and disturbances (Utkin 1992; Song and Sun 2014). By eliminating the parasitic effect of the capacitor ($r_{C} = 0$), The system is described by the following state-space equations (Mondal and Mahanta 2013):

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x} =F\left( x \right) +G\left( {x,V_{e}} \right) T_{R} \\ y=S\left( x \right) \\ \end{array}} \right. \end{aligned}$$

(22)

where the matrices F and G are given by:

$$\begin{aligned} F\left( x \right) = \left[ {\begin{array}{l} -\frac{r_{L} }{L}i_L -\frac{1}{L}V_\mathrm{C} \\ \frac{1}{C}i_L -\frac{1}{\hbox {RC}}V_\mathrm{C} \\ \end{array}} \right] , \quad G\left( {x,V_{e} } \right) = \left[ {\begin{array}{l} \frac{V_{e} }{L} \\ 0 \\ \end{array}} \right] \end{aligned}$$

(23)

And S(x) is the measured output function known as the sliding variable. The general form of S(x) is given as follows (Utkin 1992):

$$\begin{aligned} S\left( x \right) =\left( {\frac{d}{dt}+\uplambda _x } \right) ^{r-1}e\left( x \right) \end{aligned}$$

(24)

Table 1 Parameters of the buck DC–DC converter (Hadri Hamida 2011)

It is the first convergence condition which permits dynamic system to converge toward the sliding surfaces. It is a question of formulating a positive scalar function $\hbox {V(x) }> 0$ for the system states variables which are defined by the following Lyapunov function (Utkin et al. 1999; Filippov 1964):

$$\begin{aligned}&V\left( x \right) =\frac{1}{2}S\left( x \right) ^{T}S\left( x \right) \end{aligned}$$

(25)

$$\begin{aligned}&\dot{V} \left( x \right) <0\Rightarrow S\left( x \right) ^{T}\dot{S} \left( x \right) <0 \end{aligned}$$

(26)

Now, we define

$$\begin{aligned} T_{R} \left( t \right) =\frac{1}{2}\left( {1+\hbox {sign}\left( S \right) } \right) =T_{R_{eq} } \left( t \right) +T_{R_n } \left( t \right) \end{aligned}$$

(27)

where $T_\mathrm{Req}(t)$ and $T_{Rn}(t)$ represent the equivalent control (Utkin 1992) and the nonlinear switching control and:

$$\begin{aligned} \hbox {sign} \left( S \right) = \left\{ {\begin{array}{ll} 1 &{}S\left( x \right) >0 \\ -1 &{}S\left( x \right) <0 \\ \end{array}} \right. \end{aligned}$$

The sliding surfaces are given by the following expression (Table 1):

$$\begin{aligned} S=e\left( {V_s } \right) +e\left( {i_L } \right) =V_{r\acute{e}f} -H_v V_s +i_{r\acute{e}f} -H_i i_L \end{aligned}$$

(28)

and consequently, their derivatives are given by:

$$\begin{aligned} \dot{S} =E\left( x \right) +QT_{R} \end{aligned}$$

(29)

where $x = [i_{L} \quad V_\mathrm{C}]^{ T}$,

$$\begin{aligned} E=\left( {\frac{H_{i} r_{L} }{L}-\frac{H_{\mathrm{v}}}{\mathrm{C}}} \right) i_{L} +\frac{H_{i}}{L}V_{C} +\frac{H_{\mathrm{v}}}{C}I_{s}, \end{aligned}$$

and

$$\begin{aligned} Q=-\frac{H_{i}}{L}V_{e}. \end{aligned}$$

Finally, the control law is given by:

$$\begin{aligned} T_R =-Q^{-1} E\left( x \right) +K \hbox {sign} \left( S \right) \end{aligned}$$

(30)

1.2 Parameters of the Buck DC–DC Converter

1.3 How to Plot a Bifurcation Diagram?

Let us consider the state equation:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x} =Ax+BV_e \\ x_0 \\ \end{array}} \right. \end{aligned}$$

(31)

The diagram of bifurcation of this system is defined in the following way: One represents $V_{e}$ in X-coordinate ($V_{e}$ ranging between 15 and 50 V), and we present in ordinate, the values obtained by the solution of the state equation, after a certain iteration count (400 for example). For each value of $V_{e}$, the operation is started again a great number of times by choosing each time a random value of the first term $x_{0}$ (equilibrium values). One thus obtains the bifurcation diagram of our system.