An Efficient Distributed Randomized Data Replication Algorithm in VANETs

Abstract

Motivated by message delivery in vehicular ad hoc networks, we study distributed data replication algorithms for information delivery in a special completely connected network. To improve the efficiency of data dissemination, the number of message copies that can be spread is controlled and a distributed randomized data replication algorithm is proposed. The key idea is to let the data carrier distribute the data dissemination tasks to multiple nodes to speed up the dissemination process. We show how the network converges and prove that the network can enter into a balanced status in a small number of stages. Most of the theoretical results described in this paper are to study the complexity of network convergence. Simulation results show that the proposed algorithm can disseminate data to a specific area with low delay.

C. Huang—This work is supported by the National Science Foundation of China (Nos. 61373040, 61173137), by National Science Foundation Early Career Award 0845376 and Bensten Fellowship of the University of Texas - Rio Grande Valley.

1 Introduction

Vehicular ad hoc networks (VANETs) have become an important area of research with potential applications in various domains such as safety, navigational applications, in-vehicle infotainment etc. [1]. Lots of researches have been done on safety and comfort purposes of VANETs. Efficient data dissemination is essential for such applications, which require that data can be delivered with high success rate and low delay. Data replication has been recognized as an effective approach for data dissemination in VANETs [2]. Data replication enables multiple copies of the same data carried by different nodes to be transmitted to most of the nodes in the network. Thus, useful data will be distributed to a specific area in a quick manner [3].

Moreover, as emerging large-scale ad hoc networks are characterized by the lack of centralized access to information and control, distributed coordination and consensus problems are fundamental problems in ad hoc network applications [4]. Motivated by these problems, distributed algorithms are designed, in which agents can reach consensus on a common decision or achieve a global objective collectively [5]. The problems also arise in a number of applications including information delivery in vehicular ad hoc networks. This paper focuses on the randomized average consensus problem as well as studies the data replication algorithms [6].

1.1 Primary Motivations

Dynamic data replication in distributed network systems can accelerate information spread in a specific area. However, some algorithms, such as epidemic and gossip algorithms, could cause significant network overhead by essentially passing around redundant information multiple times. The redundant messages can also cause congestion issues. Aiming at the problem, this paper proposes a data replication scheme, in which the number of message copies is bounded, to reduce unnecessary transmissions. Data replication algorithms also improve upon the convergence speed of message transmission by increasing the diversity of pairwise exchanges. As load balancing is an important goal in ad hoc networks, we hope every node in the network can carry an approximately equal number of message copies. In this way, the data delivery and network computing burden will be distributed among the nodes and communication can be managed in a very quick and efficient way.

1.2 Main Contributions

To overcome the drawbacks of the data replication algorithms, we propose two conceptions: bounded number of copies and balanced network status. In this paper, according to the network traffic density, based on graph theory, we divide the VANET topology into three types of graphs: linear graph, arbitrary graph and complete graph. In this paper, we propose a distributed randomized algorithm for one certain type of graph, complete graph. We measure the complexity of convergence by the number of communication stages in a distributed computing environment. In each stage, every node is involved in at most one message transmission. If a network can enter into a balanced status in a small number of stages, it can improve the efficiency of message passing. Following the algorithms, the paper provides mathematical analysis of the proposed randomized algorithm. It shows how the network converges.

The rest of this paper is organized as follows. Section 2 overviews the related work. Section 3 describes some definitions used in the paper. In Sect. 4, we propose a randomized algorithm for complete graph in VANET. Section 5 gives some theoretical analysis of the proposed algorithm. Section 6 presents the simulation results. Finally, Sect. 7 concludes the paper.

2 Related Work

In this section, we give an overview of the related work. First, we review on the data replication algorithms in vehicular network, then discuss existing studies about randomized average consensus problem.

As broadcast is the basic mechanism of VANET communication, flooding is the most common method in data dissemination. While it can achieve the maximum coverage and rapid data dissemination, flooding can cause broadcast storm. In epidemic routing [7], two nodes exchanged the data that they didn’t hold whenever they met. Yang et al. [8] first challenged the accuracy of the innovative assumption that is widely adopted in delay performance analysis of network-coding-based epidemic routing in delay-tolerant networks. Some algorithms delivered data packets with control on the replication rules. Balasubramanian et al. [9] proposed RAPID. RAPID explicitly calculated the effect of replication on the routing metric while considered resource constraints. To exploit constrained network capacity with data replication, Wu et al. [10] proposed a capacity-constrained replication scheme for data delivery. The authors explored the residual network capacity for data replication and designed a distributed algorithm. [11] designed the data dissemination to a desired number of receivers in VANET scheme, which was inspired by processor scheduling treating roads as processors to optimize the workload assignment.

Randomized average consensus gossiping is an asynchronous protocol where a node contacts a neighbor randomly within its connectivity radius, and exchanges a state variable to produce a computation update. Wu and Rabbat [12] proposed and analyzed a family of broadcast gossip algorithms for strongly connected directed graphs, which were guaranteed to converge to the average consensus. In [13], the authors analyzed the averaging problem under the gossip constraint for an arbitrary network graph. [14] proved that the random consensus value was the average of initial node measurements and that it could be made arbitrarily close to this value in mean squared error sense under a balanced connectivity model. Fabio and Sandro [15] allowed to reach consensus in a point which may be different from the average of the initial states. Nedic and Liu [16] proposed an algorithm for finite time distributed averaging in the case of a ring network of agents, subject to a gossip constraint on communications. Falsone et al. [17] investigated the properties of the weighted-averaging dynamic for consensus problem and established new convergence rate results related to the diameters of weakly spanning trees contained in the given graphs.

3 Definitions and Models

An $\epsilon$-balanced status (See Definition 3) will be obtained after a series of average operations. We define some concepts in this section.

When a node carries message M and it controls at most a copies of message M to be distributed over a network, it must have $a\ge 1$, and each node with nonzero value is at least one. The total number of message copies is bounded by parameter n.

We need to define the concept of potential in order to analyze the number of stages for the system to enter into a balanced status, and need the following lemma.

Definition 1

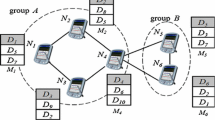
For a set of vehicles, their connected graph is an undirected graph G(V, E) such that each node represents a vehicle and an edge between two nodes indicates that the corresponding vehicles are within the distance of communication. We consider G(V, E) constructed in a high traffic density, such as a parking lot. Assume every two vehicle nodes are within each other’s communication range under such condition. G(V, E) is treated as a Complete Graph.

Definition 2

Let M be a message. Let G(V, E) be the connected graph for a set of vehicles. If each node i has a parameter $n_i$ to control the number of copies of message M that i can replicate, then G(V, E) associated with $n_i$ becomes a graph with a bounded number of message copies.

Definition 3

Let G(V, E) be a connected graph. Each node of G is assigned a nonnegative number $n_i$. The nodes of G are $\epsilon$-balanced in the corresponding bounded message graph if the following conditions are satisfied:

• Each node of G with $n_i>0$ satisfies $n_i\ge 1$.

• For every two nodes with $n_i,n_j> 0$, $|n_i-n_j|\le \epsilon$, and

• There is no edge between nodes of values $n_i$ and $n_j$ in G, respectively, such that $n_i\ge 2$ and $n_j=0$.

Definition 4

Let R be the set of real numbers and N be the set of nonnegative integers. Define the following concepts:

• A real average function A(., .) is a mapping $R\times R\rightarrow R\times R$, such that for two numbers $a\le b$, $A(a,b)=({a+b\over 2},{a+b\over 2})$ if $a+b\ge 2$, or $A(a,b)=(a,b)$ if $a+b<2$.

• An integer average function A(., .) is a mapping $N\times N\rightarrow N\times N$ such that for two numbers $a\le b$, $A(a,b)=(k,k)$ if $a+b=2k\ge 2$, $A(a,b)=(k,k+1)$ if $a+b=2k+1\ge 2$, or $A(a,b)=(a,b)$ if $a+b<2$.

• For a list $L:a_1, a_2,\cdots , a_m$ of numbers, define the potential of L to be $P(L)=a_1^2+a_2^2+\cdots +a_m^2$.

• Let A(., .) be an average function and $S_A(\langle a,b\rangle )=2(b-d)(b-c)$. Assume that $a_1,a_2,$ $\cdots ,a_n$ is a list of numbers. It is transformed into another list $a_1',a_2',\cdots , a_n'$ by a series of average operations. Define its sum of product to be $S(H)=\sum _{(a,b)\in H} S_A(a,b)=P (L)-P(L')$, where H is the set of tuples (a, b) that take average operations. It is considered as the change of the potential after taking an average operation.

Definition 5

A stage of communication is an average operation among a set of independent edges in the connected graph. Pairs of nodes in the network to exchange messages in parallel are allowed.

We use the number of stages to characterize the complexity to enter into $\epsilon$-balanced status.

4 Complete Connected Graph

We consider the case that the connected graph of a set of nodes is a complete graph, in which every two nodes are within each other’s communication rage. Our results show fast speed to achieve $\epsilon$-balanced status by applying randomized algorithms.

4.1 Distributed Randomized Algorithm for Complete Graph

In this section, we present a distributed randomized algorithm (see Algorithm 1). It is very simple and easy to implement in practice.

Assume each vehicle node has a value to indicate the data distribution task, trying to achieve a general consensus in the shortest possible time. As we know, nodes within each other’s communication range can exchange their information. In the case of complete connected graph, there might be many vehicles in one vehicle’s communication range. When the vehicle who carries message receives more than one communication requests, it chooses the vehicle with the largest gap to take average operation and computes the pairwise average, which then becomes the new value for both nodes. It will stop iterating this pairwise averaging process until the network enters into $\epsilon$-balanced status.

The analysis of our randomized algorithm uses the well-known Chernoff bounds, which are described below. All proofs of this paper are self-contained except the following famous theorems in probability theory and the existence of a polynomial time algorithm for linear programming.

Theorem 1

[18]. Let $X_1,\ldots , X_n$ be n independent random 0-1 variables, where $X_i$ takes 1 with probability $p_i$. Let $X=\sum _{i=1}^n X_i$, and $\mu =E[X]$. Then for any $\delta >0$,

• 1. $\Pr (X<(1-\delta )\mu )<e^{-{1\over 2}\mu \delta ^2}$, and

• 2. $\Pr (X>(1+\delta )\mu )<\left[ {e^{\delta }\over (1+\delta )^{(1+\delta )}}\right] ^{\mu }$.

We follow the proof of Theorem 1 to make the following versions (Theorem 2, Theorems 3, and Corollary 1) of Chernoff bounds for our algorithm analysis.

Theorem 2

Let $X_1,\ldots , X_n$ be n independent random 0-1 variables, where $X_i$ takes 1 with probability at least p for $i=1,\ldots , n$. Let $X=\sum _{i=1}^n X_i$, and $\mu =E[X]$. Then for any $\delta >0$, $\Pr (X<(1-\delta )pn)<e^{-{1\over 2}\delta ^2 pn}$.

Theorem 3

Let $X_1,\ldots , X_n$ be n independent random 0-1 variables, where $X_i$ takes 1 with probability at most p for $i=1,\ldots , n$. Let $X=\sum _{i=1}^n X_i$. Then for any $\delta >0$, $\Pr (X>(1+\delta )pn)<\left[ {e^{\delta }\over (1+\delta )^{(1+\delta )}}\right] ^{pn}$.

Define $g_1(\delta )=e^{-{1\over 2}\delta ^2}$ and $g_2(\delta )={e^{\delta }\over (1+\delta )^{(1+\delta )}}$. Define $g(\delta )=\max (g_1(\delta ),g_2(\delta ))$. We note that $g_1(\delta )$ and $g_2(\delta )$ are always strictly less than 1 for all $\delta >0$. It is trivial for $g_1(\delta )$. For $g_2(\delta )$, this can be verified by checking that the function $f(x)=(1+x)\ln (1+x)-x$ is increasing and $f(0)=0$. This is because $f'(x)=\ln (1+x)$ which is strictly greater than 0 for all $x>0$.

Corollary 1

[19]. Let $X_1,\ldots , X_n$ be n independent random 0-1 variables and $X=\sum _{i=1}^n X_i$.

• (1) If $X_i$ takes 1 with probability at most p for $i=1,\ldots , n$, then for any ${1\over 3}>\epsilon >0$, $\Pr (X>pn+\epsilon n)<e^{-{1\over 3}n\epsilon ^2}$.

• (2) If $X_i$ takes 1 with probability at least p for $i=1,\ldots , n$, then for any $\epsilon >0$, $\Pr (X<pn-\epsilon n)<e^{-{1\over 2}n\epsilon ^2}$.

5 Analysis of the Proposed Randomized Algorithm

In this section, we present a detailed analysis of the proposed randomized distributed algorithm. We will show how a list of numbers shrinks its gap after a series of random average operations.

Lemma 1

Let r(.) be a function from $S\rightarrow S$ that r(x) generates a random element in S. Assume that A and B are two subsets of S. Assume that $|A|\le |B|$, and $R(A)=\{x:x\in A, r(x)\in B\}$, $H(A)=\{r(x):x\in A, r(x)\in B\}$. Then with a probability at most

$$g(\epsilon )^{ |A||B|\over |S|}+((1-\gamma ))^{(2\gamma -1) {(1-\epsilon )\cdot {|B|\over |S|}\cdot |A|}},$$

we have

$$|H(A)|\le (1-\gamma )(1-\epsilon )\cdot {|B|\over |S|}\cdot |A|,$$

where $\gamma$ is a constant in (0, 1). Furthermore, if $|B|\ge \delta |S|$ for some fixed $\delta \in (0,1)$, then the failure probability is at most $2(1-a)^{|A|}$ for some fixed $a\in (0,1)$.

Proof

Let $m=|R(A)|$. For each element in A, with probability ${|B|\over |S|}$, it sends a request to an element in B. By Chernoff bound, we have $m< (1-\epsilon )\cdot {|B|\over |S|}\cdot |A|$ with a small probability

$$\begin{aligned} \zeta _1\le g(\epsilon )^{ |A||B|\over |S|}. \end{aligned}$$

(1)

For each $x\in A$, define r(x) to be the element that x sends.

Let $\gamma$ have $e(1-\gamma )\le 1$ and $\gamma \in (0, 1)$.

Let $n=|B|$. The probability that $|H(A)|\le (1-\gamma )m$ is

$$\begin{aligned}&\zeta _2\le {n\atopwithdelims ()(1-\gamma )m}\cdot ({(1-\gamma )m\over n})^m \end{aligned}$$

(2)

$$\begin{aligned}\le & {} {n^{(1-\gamma )m}e^{(1-\gamma )m}\over ((1-\gamma )m)^{(1-\gamma )m}}\cdot ({(1-\gamma )m\over n})^m \end{aligned}$$

(3)

$$\begin{aligned}\le & {} e^{(1-\gamma )m}({(1-\gamma )m\over n})^{\gamma m} \end{aligned}$$

(4)

$$\begin{aligned}\le & {} ({e(1-\gamma )m\over n})^{(1-\gamma )m}({(1-\gamma )m\over n})^{(2\gamma -1) m} \end{aligned}$$

(5)

$$\begin{aligned}\le & {} ({(1-\gamma )m\over n})^{(2\gamma -1) m} \end{aligned}$$

(6)

$$\begin{aligned}\le & {} ((1-\gamma ))^{(2\gamma -1) m}. \end{aligned}$$

(7)

From above analysis, the total failure probability is at most $\zeta _1+\zeta _2\le g(\epsilon )^{ |A||B|\over |S|}+((1-\gamma ))^{(2\gamma -1) {(1-\epsilon )\cdot {|B|\over |S|}\cdot |A|}}$ by inequalities (1) and (7). This proves the lemma.

Definition 6

Let $L=a_1,\cdots , a_k$ be a list of real numbers. Define $\mathrm{gap}(L)$ to be $\max _{1\le i,j\le k}|a_i-a_j|$.

Definition 7

Let $\alpha >0$, and $K=a_1,\cdots , a_k$ be a list of real numbers. Assumed K is transformed into another list $K'=a_1',\cdots , a_k'$ after a series of average operations. If $\mathrm{gap}(K')\le (1-\alpha )\mathrm{gap}(K)$, then $K'$ is called $\alpha$-shrink of K.

Definition 8

Let $c,d,\delta$ be parameters. A series of c stages is $\alpha$-successful if the gap of a list of numbers is shrinked by a factor of at least $\alpha$. The failure probability of an $\alpha$ shrink of the list is denoted by $\delta$.

Lemma 2

Let c be a parameter. All stages are partitioned into multiple groups of c stages $G_1,G_2,\cdots , G_k$. Then there are k independent 0, 1 random variables $r_i$ for each group $G_i$ such that

• 1. $\mathrm{Prob}(G_i$ is $\alpha$-successful) $\ge \mathrm{Prob}(r_i= 1)$

• 2. $\mathrm{Prob}(r_i=1)\ge 1-\delta$.

• 3. $\mathrm{Prob}($there are at least t $G_i$ to be $\alpha$-successful$)\ge \mathrm{Prob}(r_1+r_2+\cdots +r_k\ge t)$.

Proof

First, let $S_1, S_2,..., S_m \in \{1,2,\cdots , m\}$ denote the m random numbers in the range $\{1,2,\cdots , m\}$. Let $a_i \in {\{0,1\}}$ denote the status that whether a vehicle is receiving or sending requests.

Then, we have the 0,1 string $W_j=a_1S_1, a_2S_2,..., a_mS_m$, which denotes an average operation among the m vehicles.

Let $D_i=W_1...W_z$, $z=O(\log m)$. It means after $O(\log m)$ stages, the string $D_i$ will get an $\alpha$ shrink. There are $O(\log n)$ stages of $D_i$ which will get an $\alpha$ shrink.

Each $G_i$ corresponds to a random sequence $D_i$. Let T be the total number of random paths for group $G_i$.

Let $D_1, D_2,\cdots , D_T$ be an rearrangement of all the random paths such that $D_1,\cdots D_{H_{i}}$ are all $\alpha$-successful sorted by lexicographic order. In the same way, $D_{H_{i+1}+1}, \cdots , D_T$ are also sorted by lexicographic order. For each random sequence $D_i$ to be $\alpha$-successful, make it correspond to an integer in [1, T]. Assume that $G_i$ is $\alpha$-successful for $H_i$ random paths with $H_i\ge T\cdot (1-\delta )$. Without loss of generality, each $\alpha$-successful sequence corresponds to a unique integer in the range $[1, H_i]$. Then $G_i$ is $\alpha$-successful if and only if $r_i$ is an event with a random number $s_i$ in [1, T] with $s\le T\cdot (1-\delta )$.

It is proved by an induction on the number of groups k. It is trivial for the case $k=1$. Assume that it is true for k. Consider the case $k+1$. For each random sequence $D_1D_2\cdots D_k$, we consider the extension $D_1D_2\cdots D_kD$ for a random sequence D for $G_{k+1}$. The number of cases of D that $G_{k+1}$ is $\alpha$-successful for D random paths is $H_{k+1}\ge T\cdot (1-\delta )$. Then $G_{k+1}$ is $\alpha$-successful if and only if $r_{k+1}$ is an event with a random number $s_{k+1}$ in [1, T] with $s_{k+1}\le T\cdot (1-\delta )$.

6 Performance Evaluation

In this section, we first introduce the simulation environment, then present the compared algorithms, performance metrics and finally give the simulation results.

6.1 Simulation Setup

To evaluate the performance of the proposed algorithm, we have conducted extensive simulations. In simulation, the following default settings are used. Compromised to the complexity of simulations, we select a bounded 3 km*4 km regional area for our simulations. Each road segment has two lanes with the bidirectional traffic. For each simulation run, different number of vehicle nodes are involved in the message delivery. The number varies from 100 to 500. The mobility of vehicles is generated by VANET-Mobisim [20], in which the destination of each transmission is randomly selected. The coverage of V2V communications is set to be 300 m. Transmission frame duration is set as 1ms. The number of allowed maximum data copies varies from 200 to 800.

6.2 Compared Algorithms

We compare the proposed algorithm with the following data dissemination algorithms.

• Epidemic: It is flooding-based in nature, as nodes continuously replicate and transmit messages to newly discovered relays that do not possess a data copy.

• Randomized flooding or Gossiping (random-flood): Similar to epidemic routing, but a message only gets copied with some probability.

• Bounded copied in arbitrary graph (arbitrary): Vehicles randomly choose the vehicle to take average.

• Bounded copied in linear graph (linear): Vehicles randomly choose the vehicle to take average.

• Bounded copied in complete graph (randomized): A vehicle randomly selects another vehicle within its communication range and sends request. The vehicle selects the request with the largest gap among all the requests it has received.

6.3 Performance Metrics

We choose the total number of average operations as a measure of overhead and choose the dissemination delay and the actual number of vehicles reached as measures of effectiveness.

The following performance metrics will be taken into account for purpose of algorithms evaluation in the simulation experiments.

Number of stages: Average operations that characterize the complexity to enter into a balanced status among a set of nodes whose communication are based on their connected graph.

Dissemination delay: It denotes the average time between the sending and receiving times for packets received. In this paper, it indicates the time for the network to enter into a balanced status.

6.4 Simulation Results

In this section, we will evaluate the effect of the number and velocity of vehicles on the performance of different algorithms.

• (1) The effect of the number of vehicles on routing performance

Figures 1 and 2 respectively depict the number of stages and dissemination delay as the number of vehicles changes from 100 to 500. As is evident by these figures, the distributed randomized algorithm performs significantly fewer transmissions than other compared algorithms. Assume that traffic loads are low with enough network capacity, in terms of dissemination delay, as epidemic has close-to-optimal delays under these conditions, the proposed distributed randomized algorithm manages to achieve delays that are quite close to those of flooding-based schemes. Meanwhile, if traffic starts increasing, it actually outperforms all schemes in terms of delay.

• (2) Effect of different velocities on the performance of different algorithms

As the number of message copies varies from 800 to 200, Figs. 3 and 4 compare the number of communication stage and dissemination delay of all the compared algorithms.

As can be seen from Fig. 3, when the number of allowed maximum copies decreases all the way from 800 to 200, the averaging time for the network to enter into a balanced status decreases in all the compared algorithms. It is obvious that the proposed randomized algorithm consumes fewer communications than other algorithms. Figure 4 shows that proposed randomized algorithm performs better dissemination delay when there are more message copies in the network.

Fig. 1.

Stages VS. number of nodes

Fig. 2.

Delay VS. number of nodes

Fig. 3.

Stages VS. number of copies

Fig. 4.

Delay VS. number of copies

7 Conclusion

To facilitate message delivery in ad hoc networks, we study distributed data replication algorithms in a connected network. We use graph theory to describe network topology, then propose a distributed randomized data replication algorithm for complete graph. We show how the network converges after a series of random average operations. Most of the results in the paper are to study the network convergence speed. Extensive simulations show that the performance of the proposed algorithm is superior to the other approaches.