R-DRA: a replication-based distributed randomized algorithm for data dissemination in connected vehicular networks

Abstract

As data dissemination is of great importance for applications in connected vehicular networks (VANETs), we aim to facilitate the performance of data dissemination in this study. Consider strongly connected VANETs where a set of vehicular nodes exists to disseminate information. To reduce redundant transmissions and improve data dissemination delay, the number of data replicas that can be spread in the network is controlled. A replication-based distributed randomized algorithm is proposed, in which a balanced network status can be achieved after average operations among the nodes. In the algorithm, the data carrier distributes the dissemination tasks to multiple nodes to speed up the dissemination process such that the dissemination would be accelerated and consume less network resource. We evaluate the complexity of network convergence by analyzing the number of communication stages consumed when the network converges to a consensus. Theoretical analysis shows that the network can achieve balance quickly in the case of complete graph, which supports the real-time data dissemination in dense VANETs. Simulation results validate that the proposed algorithm can disseminate data to the vehicles within a specific area with high efficiency.

1 Introduction

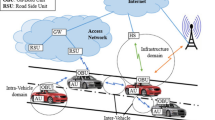
As important components of Intelligent Transportation System (ITS), vehicular networks (VANETs) are large-scale mobile ad hoc networks composed of vehicles with communication functions and roadside infrastructures, which aims to provide services for autonomous driving and fast information sharing [1, 2]. In VANETs, vehicles mainly obtain real-time road conditions and location information sent by other vehicles through wireless communication technology [3]. In this way, traffic accidents and road congestions can be effectively reduced. Meanwhile, VANETs can provide information services, such as news and entertainments, which can add fun to the boring journey.

To enhance on-road transportation safety and efficiency, efficient data dissemination that can provide high-rate communications and rapid data dissemination, is essential for applications in VANETs [4, 5]. Data replication has been recognized as an effective approach to improve data dissemination [6], which enables multiple replicas of the same data carried by different nodes to be transmitted to a number of nodes in the network. Thus, the data will be distributed to a specific area in a quick manner. A variety of distributed algorithms have been proposed based on data replication [7].

As VANETs are characterized by the lack of centralized control, distributed coordination among vehicles and averaging consensus are challenging issues in emerging applications [8]. Adapting to dynamically changing network topologies, gossip algorithm, a distributed averaging approach on the basis of iterative communications among the nodes in the network, has obtained a lot of interest due to its simplicity and effectiveness [9]. Through a series of communications, the nodes could reach consensus on a common decision or achieve the same state. Generally, this type of algorithms is evaluated by comparing their convergence speed. However, the gossip-based algorithms could waste significant network resource, such as bandwidth and energy, by transmitting redundant information multiple times. From this point of view, lots of researches have been done to improve the performance of the algorithms by accelerating their convergence speed.

1.1 Motivation

Dynamic data replication can accelerate data dissemination and decrease dissemination delay in distributed ad hoc networks. However, replication-based methods might meet some problems, such as long dissemination delay caused by network congestion in high density area, network resource wasting and scalability issues. Additionally, traditional replication-based dissemination algorithms (e.g. epidemic and gossip algorithms), could lead to high communication overhead as well as congestions and sometimes even broadcast storms by passing around redundant information. Thus the quantity of data replicas spread in the area should be controlled to address the above issues.

To achieve network consensus among the nodes, every node should carry an approximately equal number of data replicas such that the computational burden is distributed among the nodes. As a result, the progress of data dissemination could be accelerated. Accordingly, we propose a concept of network balance, and we will see that the balanced status in the network can realize distributed load balancing which can alleviate the entire network load and enhance information dissemination.

As stated above, replication-based data dissemination algorithms with high efficiency need to be developed. The number of replicas spread in the destination area should be limited to decrease redundant transmissions and dissemination delay, while a balanced network status is desired to be achieved.

1.2 Methodology and contributions

Graph theory can be used for describing the network topology. Based on traffic density, the network topology can be abstracted as three types of graphs: arbitrary, linear and complete graphs. In this study, we mainly focus on the case of complete graph. As arbitrary and linear graphs are abstracted from the scenarios of urban areas and highway, complete graph describes dense traffic scenarios, such as the scenarios where traffic congestions happen or parking lots. In complete graph, it is assumed every two vehicular nodes can communicate with each other.

This study investigates the problem of a vehicular node disseminating a message to a number of nodes in a specific area in dense VANETs, and the objective is to realize data dissemination in a target area with reduced dissemination delay and consumed resource. To achieve our goal, a distributed randomized algorithm based on data replication is proposed for data dissemination in dense scenarios. In the algorithm, the maximum number of message replicas is limited, and every vehicular node is assigned with a corresponding value that indicates the quantity of data replicas that the node can spread. Each node selects one of its neighbors to communicate and averages their values, through which the values of the nodes will be updated. Once specific average operations are taken, the values of nodes can be approximately equal to the global average in distributed mode. The convergence complexity is evaluated through calculating the consumed communication stages. Efficiency of replication-based data dissemination can be verified if the network converges in a few communication stages. Additionally, theoretical analysis is provided to validate the convergence complexity when the network achieves a balanced status. The results of complete graph could be considered as a contribution to distributed networks while complete graph cannot be fully treated as typical vehicular networks.

As a preliminary study, the conference version of our study [10] studied the problem in complete graph, in which the concept of network balance and the randomized replication-based scheme were proposed. We construct this study on the basis of [10]. In this study, to validate the effectiveness of data replication, we first present a deterministic process and derive the communication stages consumed for network consensus. As to the proposed randomized algorithm, important theorems are derived based on Lemmas 2 and 4 (these two lemmas are derived in the conference paper). The theorems show the mathematical upper bound and lower bound of the proposed randomized algorithm, which has not been fulfilled in the conference paper. Meanwhile, we compare the randomized algorithm with additional algorithms such as CCR in performance evaluation and evaluate the impact of different numbers of vehicles and data replicas on data delivery ratio of the compared algorithms.

Fully exploiting data replication to improve data dissemination, the key contributions are described as below.

• 1. We propose a replication-based distributed randomized algorithm for dense scenarios in VANETs. In the algorithms, the quantity of data copies is bounded while a balanced network status can be achieved.

• 2. We present the number of stages needed when the network achieves a balanced status in a deterministic manner. Then we derive the upper bound and lower bound of the distributed randomized algorithm. Through theoretical analysis, we show that when the network is strongly connected, the proposed randomized algorithm can achieve network consensus quickly.

• 3. We conduct simulations to evaluate the effect of the number of vehicular nodes and allowed data replicas on network convergence speed in terms of communication stages, dissemination delay and delivery ratio. Simulation results show the efficiency and rigorousness of the distributed randomized algorithm.

The rest of this paper is organized as follows. Section 2 summarizes the related work on data dissemination and average consensus problem. Section 3 describes some definitions used in data replication. In Sect. 4, we propose a distributed randomized algorithm for dense vehicular scenarios. Upper and lower bounds of the proposed algorithm are derived in Sect. 5. Section 6 evaluates the proposed algorithm. Finally, Sect. 7 concludes the paper and presents future directions.

2 Related work

In this section, we give an overview of related studies on data dissemination algorithms in VANETs, and then discuss existing works on randomized average consensus problem.

2.1 Data dissemination schemes

As the basic broadcast algorithm, flooding is a common replication-based data dissemination algorithm. Apart from the large wireless coverage, flooding is also popular for its fast dissemination speed. However, it can cause broadcast storms when there are too many data transmissions. Torres et al. [11] made improvements on the flooding scheme to deal with different network traffic densities.

Many works study how to devise efficient routing schemes in vehicular networks, thus the dissemination delay and overhead can be improved. In [12], the authors developed a routing algorithm, and the carrier could get at most a number of replicas of the packet generated based on a binary tree. However, the available network bandwidth and capacity were not considered. Considering resource constraints and replication, RAPID [13] studied the routing problem in delay tolerant networks and solved the problem by analyzing data utilities to decide on the replication strategy. Takahashi et al. [14] proposed an advanced routing mechanism. They controlled the maximum number of messages that could be replicated, depending on the distance from source to the base station within its communication range. Xing et al. [15] proposed a framework for utility maximization problem for multimedia dissemination, and obtained the closed form of the network utility. To find an optimal path for the dissemination, the authors developed a dissemination algorithm. Wu et al. [16] aimed to fully utilize the available network capacity, and presented a distributed data replication scheme. Xiang et al. [17] studied data preferences of vehicle in VANETs, quantified different classes of data preferences and designed a safety data dissemination protocol named PVCast. The authors studied multiple mix zones problems [18] and developed a clustering based communication protocol for multiple mix-zones over road networks to collect traffic information in an energy efficient way [19]. Zhao et al. [20] proposed a sender impact metric that considered both the quality and diversity of corresponding link and then developed an efficient selection mechanism for bulk data dissemination. Zhuang et al. [21] introduced a node cooperation strategy for vehicular networks to select the best relay node and provided an upper bound of the performance. The relation between content replication and RSU deployment was studied in [22], toward which a cooperative replication scheme was developed. To minimize the probability of task deadline violation, Jiang et al. [23] proposed a balanced task assignment policy that could be obtained by value iteration. Chen et al. [24] focused on data dissemination in Internet of Vehicles with social characteristic and applied the property in the design of dissemination strategies.

2.2 Average consensus problem

Gossip algorithms are widely used in modern distributed systems, with applications ranging from sensor networks and peer-to-peer networks to mobile vehicle networks and social networks [25, 26]. Boyd et al. [27] studied gossip algorithms for information exchange and computation in an arbitrarily connected network. The authors developed a distributed sub-gradient method to improve the speed of gossip algorithms and the framework they designed could be applied to analyze distribute algorithms in different scenarios. Angelia and Asuman [28] studied the consensus problem with delays by reducing it to a consensus problem in an agent system without delays, thus obtained the convergence rate results for the studied consensus problem. In [29], the authors investigated the characteristics of weighted-averaging dynamic for network consensus. Franceschelli et al. [30] proposed a novel gossip-based distributed algorithm that utilized local randomized interactions for task assignment in heterogeneous networks. Additionally, the asynchronous interactions could minimize the executing time of tasks in the network. Aysal et al. [31] proved that the random consensus value was the average of initial node measurements and that it could be made arbitrarily close to this value in mean squared error sense under a balanced connectivity model and by trading off convergence speed with accuracy of the computation. The results illuminated that the algorithm based on broadcast mechanism could reach a consensus with very low failure probability. Wu et al. [32] presented a gossip-based algorithm to study network consensus in strongly connected networks. Through analysis, they showed that the proposed algorithm could quickly reach consensus as well as reduce the consumed transmissions by omitting some agents’ states.

The first part of related work focuses on the reliability and effectiveness of data dissemination in VANETs while the second part mainly talks about the properties of network consensus and convergence rate. The goal of this study is to develop novel replication strategies to enhance dissemination performance through utilizing data replication and evaluate the convergence rate of replication-based algorithms. To achieve these purposes, we combine data replication with average network consensus in data dissemination, which has not been considered in previous works. Table 1 compares the differences of works in the literature according to whether the works study data replication and average consensus problems or not.

Table 1 Relate work comparison

3 Definitions and models

Assume a vehicular node carries a message M. The node aims to disseminate the message to a specific area, and we let parameter n denote the maximum quantity of data replicas. Let parameter $n_{i}$ represent the replicas that node i can spread, we have $n_{i}\ge 1$. Assume there are m nodes in the area, we have $\sum _{{i=1}}^{m}n_{{i}}=n$. After a number of average operations, the values of nodes could reach the global average, and we define the state as $\epsilon$-balanced network status (see Definition 4). To analyze the communication stages needed to obtain network balance, we have the following lemma and definitions.

Lemma 1

Assume that a, b, c, and dare real numbers with $a+b=c+d$. Then we have (1) $(a^{2}+b^{2})-(c^{2}+d^{2})=2(b-d)(b-c)$, and (2) $(a^{2}+b^{2})-(c^{2}+d^{2})\ge 0$if $a\le c\le d\le b$.

Proof

By the condition of the lemma, we have $b-d=c-a$ and $b-c=d-a$. Thus, $(a^{2}+b^{2})-(c^{2}+d^{2})=(b-d)(b+d)+(a-c)(a+c)=(b-d)(b+d-c-a)=2(b-d)(b-c).$ This proves (1). With (1), we can prove that (2) is also correct. $\square$

Definition 1

G(V, E) is an undirected graph to describe the network topology. In such a graph, the vertices and edges denote the vehicular nodes and the communication links among the vehicular nodes, respectively.

Definition 2

Consider dense vehicular networks, such as scenarios when road congestions happen or parking lots with many parked cars. Assume that every two vehicular nodes can exchange information with each other. According to graph theory, the network topology can be abstracted as complete graph.

Definition 3

Assume M denotes the message that would be disseminated to a specific area. G(V, E) is an undirected graph to describe the network topology. The maximum number of allowed data replicas is denoted by n. Every vehicular node is assigned with a value that indicates the number of message replicas that the node can spread in the network, such as node i with a value $n_{i}$. Therefore, G(V, E) associated with $n_{i}$ becomes a weighted graph with a bounded number of message replicas.

Definition 4

According to Definition 3, the nodes in the weighted graph are associated with corresponding nonnegative numbers. We say that an $\epsilon$-balanced status is achieved among the nodes if the following conditions are satisfied:

• All the associated values of the nodes in the weighted graph are no smaller than 1, that is, $n_{i} \ge 1$.

• For every two nodes with $n_{i},n_{j}> 0$, the values satisfy $|n_{i}-n_{j}|\le \epsilon$, where $\epsilon > 0$.

• If $n_{i}\ge 2$ and $n_{j}=0$, no edge exists between the nodes with $n_{i}$ and $n_{j}$.

Definition 5

Let R be the set of real numbers and N be the set of nonnegative integers. Define the following concepts:

• A real average function A(., .) is a mapping $R\times R\rightarrow R\times R$, such that for two numbers $a\le b$, $A(a,b)=({a+b\over 2},{a+b\over 2})$ if $a+b\ge 2$, or $A(a,b)=(a,b)$ if $a+b<2$.

• An integer average function A(., .) is a mapping $N\times N\rightarrow N\times N$ such that for two numbers $a\le b$, $A(a,b)=(k,k)$ if $a+b=2k\ge 2$, $A(a,b)=(k,k+1)$ if $a+b=2k+1\ge 2$, or $A(a,b)=(a,b)$ if $a+b<2$.

• For a list $L:a_{1}, a_{2},\ldots , a_{k}$, define the potential of L to be $P(L)=a_{1}^{2}+a_{2}^{2}+\cdots +a_{k}^{2}$.

• For an average function A(., .), define $S_{A}(\langle a,b\rangle )=2(b-d)(b-c)$, where $A(a,b)=(c,d)$. Number b is considered a bar of length b. $S_{A}(\langle a,b\rangle )$ can be considered that a small piece of length $b-d$ from the bar of length b to go down by $(b-c)$. Function $S_{A}(.)$ gives the potential change after an average operation (See Lemma 1).

• Let A(., .) be an average function. Assume that $a_{1},a_{2},$$\ldots ,a_{k}$ is a list of numbers. It is transformed into another list $a_{1}^{\prime },a_{2}^{\prime },\ldots , a_{k}^{\prime }$ by a series of average operations. Define its sum of product to be $S(H)=\sum _{(a,b)\in H} S_{A}(a,b)=P (L)-P(L^{\prime })$ (See Lemma 1), where H is the set of tuples (a, b) that take average operations to transform the first list into the second list. It is considered as the change of the potential after taking an average operation.

Through iterative average operations between the nodes, the network will converge and achieve an $\epsilon$-balanced status. To measure the network convergence rate, we calculate the number of communication stages that needed for the network to be $\epsilon$-balanced, which can also reflect the complexity of network convergence. The concept of communication stage is shown as Definition 6.

Definition 6

A stage of communication is an average operation among a set of independent edges in the connected graph. Two nodes connected by one of the independent edges can communicate. It allows those pairs of nodes to communicate and take average in parallel.

Before explaining the details of the proposed solution, a list of variables used in this paper is provided as Table 2.

Table 2 Variables used in this paper

4 Proposed solution

We consider the case that the connected graph of a set of nodes is a complete graph. A set of nodes with a complete connection has the property that every two nodes are within each other’s communication range. To facilitate data dissemination in the case of complete graph, we propose a distributed randomized algorithm that combines data replication and distributed averaging. Theoretical results show that a balanced status can be achieved within low delay when the randomized algorithm is applied.

4.1 Replication-based distributed randomized algorithm

In this section, we present a distributed randomized algorithm (see Algorithm 3). It is very simple and easy to implement in practice.

We first assume that the nodes in the network perform average operations in a deterministic manner to achieve network balance. The deterministic procedure is presented as Algorithm 1 and the initialization process is described as Algorithm 2.

After initialization by Algorithm 2, the process of the deterministic algorithm can be divided into two cases: (1) when the number of nodes with value at least two is no smaller than the number of nodes with zero, the nodes with zero would take average with the nodes with larger values, otherwise, the operations should be done the other way round; (2) When the values of all the nodes are larger than zero, select the nodes with value $n_{i}$ and $n_{m-i+1}$ to take average which can accelerate the convergence. Iterate the average operations until the network converges. Theorem 1 gives the quantity of stages consumed for network balance in a deterministic manner.

Theorem 1

Assume in the case of complete graph, the nodes perform average operations in a deterministic manner, such that after $O(\log {n\over \epsilon })$stages of real average operations, the network can reach an $\epsilon$-balanced status.

Proof

It is easy to see that there are at most $O(\log n)$ stages for Case 1. In the following part, we will give an upper bound for Case 2.

Let $n_{i}$ be the parameter value of node i. Without loss of generality, assume that $n_{1}\ge n_{2}\ge \cdots \ge n_{m}$. Let $n_{i}$ and $n_{m-i+1}$ take average.

Assume that after one stage, pair $n_{i}$ and $n_{m-i+1}$ has the largest average $d_{i}={n_{i}+n_{m-i+1}\over 2}$, and pair $n_{j}$ and $n_{m-j+1}$ has the least average $d_{j}={n_{j}+n_{m-j+1}\over 2}$. We assume that $i\not =j$.

We note that either ${n_{i}-n_{j}\over 2}\le 0$ or ${n_{m-i+1}-n_{m-j+1}\over 2}\le 0$.

$$\begin{aligned} d_{i}-d_{j}= & {} {n_{i}+n_{m-i+1}\over 2}-{n_{j}+n_{m-j+1}\over 2}\\= & {} {(n_{i}-n_{j})+\left( n_{m-i+1}-n_{m-j+1}\right) \over 2}\\\le & {} \max \left( |{n_{i}-n_{j}\over 2}|, |{n_{m-i+1}-n_{m-j+1})\over 2}|\right) \\\le & {} {n_{1}-n_{m}\over 2}. \end{aligned}$$

After t stages, each piece has at most ${n_{1}-n_{m}\over 2^{t}}$ difference among all nodes. Therefore, after $O(\log {n\over \epsilon })$ stages, it enters into an $\epsilon$-balanced status. $\square$

Theorem 1 shows the validity of data replication in complete graph. To speed up the convergence, a replication-based distributed randomized algorithm R-DRA for complete graph is proposed, which is shown as Algorithm 3.

The process of the algorithm R-DRA can be divided into three steps, which is presented as follows.

Firstly, the algorithm abstracts a graph based on network topology and then calls the initialization process. The graph becomes a weighted graph after initialization, in which the source node is assigned with a value n and others are zero. Thus we have the initial states of all the nodes.

Secondly, the node in sending state randomly selects a node, and sends a request to it. Meanwhile, the node in receiving state selects the node from the received requests if the gap between the two nodes is the largest. The selected pairs of nodes will take average operations and update their values accordingly. The described process is called a stage. Iterate the average operations until the network converges and calculate the number of stages needed to be $\epsilon$-balanced.

Finally, a weighted graph is output. The values of the nodes in the graph have been updated to the values when the network is balanced. If a new node enters the network and breaks the balance, additional average operations are needed for network rebalance.

5 Analysis of the proposed randomized algorithm

In this section, we present detailed analysis of the proposed randomized distributed algorithm. The results of the upper and lower bounds are given.

The analysis of our randomized algorithm uses the well-known Chernoff bounds that are described below. All proofs of this paper are self-contained except the following famous theorems in probability theory and the existence of a polynomial time algorithm for linear programming.

Theorem 2

([33]) Let $X_{1},\ldots , X_{n}$be nindependent random 0–1 variables, where $X_{i}$takes 1 with probability $p_{i}$. Let $X=\sum _{i=1}^n X_{i}$, and $\mu =E[X]$. Then for any $\delta >0$,

• 1. $\Pr (X<(1-\delta )\mu )<e^{-{1\over 2}\mu \delta ^2}$, and

• 2. $\Pr (X>(1+\delta )\mu )<\left[ {e^{\delta }\over (1+\delta )^{(1+\delta )}}\right] ^{\mu }$.

We follow the proof of Theorem 2 to make the following versions (Theorems 3, 4, and Corollary 1) of Chernoff bounds for our algorithm analysis.

Theorem 3

Let $X_{1},\ldots , X_{n}$be nindependent random 0–1variables, where $X_{i}$takes 1 with probability at least pfor$i=1,\ldots , n$. Let $X=\sum _{i=1}^n X_{i}$, and $\mu =E[X]$. Then for any$\delta >0$, $\Pr (X<(1-\delta )pn)<e^{-{1\over 2}\delta ^2 pn}$.

Theorem 4

Let $X_{1},\ldots , X_{n}$be nindependent random 0–1 variables, where $X_{i}$takes 1 with probability at most pfor $i=1,\ldots , n$. Let $X=\sum _{i=1}^n X_{i}$. Then for any $\delta >0$, $\Pr (X>(1+\delta )pn)<\left[ {e^{\delta }\over (1+\delta )^{(1+\delta )}}\right] ^{pn}$.

Define $g_{1}(\delta )=e^{-{1\over 2}\delta ^2}$ and $g_{2}(\delta )={e^{\delta }\over (1+\delta )^{(1+\delta )}}$. Define $g(\delta )=\max (g_{1}(\delta ),g_{2}(\delta ))$. We note that $g_{1}(\delta )$ and $g_{2}(\delta )$ are always strictly less than 1 for all $\delta >0$. It is trivial for $g_{1}(\delta )$. For $g_{2}(\delta )$, this can be verified by checking that the function $f(x)=(1+x)\ln (1+x)-x$ is increasing and $f(0)=0$. This is because $f^{\prime }(x)=\ln (1+x)$ which is strictly greater than 0 for all $x>0$.

Corollary 1

([34]) Let $X_{1},\ldots , X_{n}$be nindependent random 0–1 variables and $X=\sum _{i=1}^n X_{i}$.

• 1. If $X_{i}$takes 1 with probability at most pfor $i=1,\ldots , n$, then for any ${1\over 3}>\epsilon >0$, $\Pr (X>pn+\epsilon n)<e^{-{1\over 3}n\epsilon ^2}$.

• 2. If $X_{i}$takes 1 with probability at least pfor $i=1,\ldots , n$, then for any $\epsilon >0$, $\Pr (X<pn-\epsilon n)<e^{-{1\over 2}n\epsilon ^2}$.

5.1 Upper bounds

Lemma 2

([10]) Let r(.) be a function from $S\rightarrow S$that r(x) generates a random element in S. Assume that Aand Bare two subsets of Swith $|A|\le |B|$, and $R(A)=\{x:x\in A, r(x)\in B\}$, $H(A)=\{r(x):x\in A, r(x)\in B\}.$Then with the probability at most

$$\begin{aligned} g(\epsilon )^{ |A||B|\over |S|}+((1-\gamma ))^{(2\gamma -1) {(1-\epsilon )\cdot {|B|\over |S|}\cdot |A|}}, \end{aligned}$$

we have

$$\begin{aligned} |H(A)|\le (1-\gamma )(1-\epsilon )\cdot {|B|\over |S|}\cdot |A|, \end{aligned}$$

where $\gamma$is a constant in (0, 1). Furthermore, if $|B|\ge \delta |S|$for some fixed $\delta \in (0,1)$, then the failureprobability is at most $2(1-a)^{|A|}$for some fixed $a\in (0,1)$.

Proof

Let $m=|R(A)|$. For each element in A, with probability ${|B|\over |S|}$, it sends a request to an element in B. By Chernoff bounds, we have $m< (1-\epsilon )\cdot {|B|\over |S|}\cdot |A|$ with small probability

$$\begin{aligned} \zeta _{1}\le g(\epsilon )^{ |A||B|\over |S|}. \end{aligned}$$

(1)

For each $x\in A$, define r(x) to be the element that x sends.

Let $\gamma$ have $e(1-\gamma )\le 1$ and $\gamma \in (0, 1)$.

Let $n=|B|$. The probability that $|H(A)|\le (1-\gamma )m$ is

$$\begin{aligned} \zeta _{2}\le & {} {n\atopwithdelims ()\left( 1-\gamma \right) m}\cdot \left( {(1-\gamma )m\over n}\right) ^m \end{aligned}$$

(2)

$$\begin{aligned}\le & {} {n^{(1-\gamma )m}e^{(1-\gamma )m}\over ((1-\gamma )m)^{(1-\gamma )m}}\cdot \left( {(1-\gamma )m\over n}\right) ^m \end{aligned}$$

(3)

$$\begin{aligned}\le & {} e^{(1-\gamma )m}\left( {(1-\gamma )m\over n}\right) ^{\gamma m} \end{aligned}$$

(4)

$$\begin{aligned}\le & {} \left( {e(1-\gamma )m\over n}\right) ^{(1-\gamma )m}\left( {(1-\gamma )m\over n}\right) ^{(2\gamma -1) m} \end{aligned}$$

(5)

$$\begin{aligned}\le & {} \left( {(1-\gamma )m\over n}\right) ^{(2\gamma -1) m} \end{aligned}$$

(6)

$$\begin{aligned}\le & {} ((1-\gamma ))^{(2\gamma -1) m}. \end{aligned}$$

(7)

The total failure probability is at most $\zeta _{1}+\zeta _{2}\le g(\epsilon )^{ |A||B|\over |S|}+((1-\gamma ))^{(2\gamma -1) {(1-\epsilon )\cdot {|B|\over |S|}\cdot |A|}}$ by inequalities (1) and (7). This proves the lemma.

$\square$

We need Lemma 2 to illustrate how the random average operations shrink the gap of a list of numbers. Meanwhile, the concepts of gap and $\alpha$-shrink are presented as Definitions 7 and 8, respectively. Then we have Lemma 3.

Definition 7

Let $L=a_{1},\ldots , a_{k}$ denote a set of real numbers. gap(L) is defined as $\max _{1\le i,j\le k}|a_{i}-a_{j}|$.

Definition 8

Let $\alpha >0$ and $L=a_{1},\ldots , a_{k}$ denote a set of real numbers. Assume iterative average operations transform L into $L^{\prime }=a_{1}^{\prime },\ldots , a_{k}^{\prime }$. If $gap(L^{\prime })\le (1-\alpha )gap(L)$, then $L^{\prime }$ is called $\alpha$-shrink of L.

Lemma 3

Let S be the list of all m elements that will take average operations. For some fixed $\alpha >0$ , with the failure probability at most ${1\over (\log m)^3}$ , we have the following facts:

• 1. After $O(\log m)$ stages of average operations, there is an $\alpha$ -shrink.

• 2. After $O(\log m)$stages of integer average operations, there is an$\alpha$-shrink if ${\mathrm{gap}}(L)$is at least H for some Hto be big enough.

Proof

Let $h=\max {S}-\min {S}$, $a=\min {\{S\}}$, and $b=\max {\{S\}}$. Apply Lemma 2. Let A be the set of elements greater than median (${\max {\{S\}}+\min {\{S\}}\over 2}$), and B be the set of elements smaller than or equal to the median ($a+{h\over 2}$) of a and b. Without loss of generality, assume $|A|\le |B|$. Let $A_{0}=A$, $B_{0}=B$, $S_{0}=S$, and $j=0$. We will discuss three periods of stages.

If $|A_{j}|\ge {\log m\over (\log \log m)^5}$, enter Period 1 below, otherwise, enter Period 3.

Period 1: O(1) stages

Let $A_{i+1}$ be the set of elements a that (1)$a\in A_{i}$ and a does not take any average operation; or (2) a is from one of the two elements after taking average between two elements c, d such that both c and d are in $A_{i}$.

Let $B_{i+1}$ be the set of elements a that (1)$a\in B_{i}$ and a does not take any average operation; or (2) a is from one of the two elements after taking average between two elements c, d such that at least one of c, d is in $B_{i}$.

Let $S_{j+1}^{(1)}=A_{j+1}\cup B_{j+1}$.

We will select three small constants $\tau _{1}>\tau _{2}>\tau _{3}>0$, and positive constants $\gamma _{1}, \gamma _{2}<1$. Let $\tau _{2}={\tau _{1}\over 2}$, and $\tau _{3}={\tau _{2}\over 2}$. Let $\gamma _{1}=0.05$, and $\gamma _{2}=2\gamma _{1}$. We assume $\epsilon \le \gamma _{1}$.

By Lemma 2, $|A_{i+1}|\le (1-\beta )|A_{i}|$ for some fixed $\beta \in (0,1)$ with the failure probability at most $2(1-a)^{|A_{i}|}\le 2(1-a)^{\log m\over (\log \log m)^5}$. Select a fixed integer i with $|A_{i}|\le (1-\beta )^i|A_{0}|\le \gamma _{1}|A_{0}|$. After i stages, we have

$$\begin{aligned} |A_{i}|\le & {} (1-\beta )^i|A_{0}|\le \gamma _{1}|S_{0}|, \end{aligned}$$

(8)

$$\begin{aligned} |B_{i}|\ge & {} (1-\gamma _{1})|S_{0}| {\mathrm{\ \ and,}} \end{aligned}$$

(9)

$$\begin{aligned} \max \{B_{i}\}\le & {} a+(1-\tau _{1})h\ \ {\mathrm{\ with\ }} \tau _{1}\in (0,1). \end{aligned}$$

(10)

Its failure probability is at most $2i(1-a)^{\log m\over (\log \log m)^5}$.

Claim

$\tau _{1}\ge {1\over 2^{i+1}}$.

Proof

It can be proved via a simple induction. For the case $i=0$, we can let $\tau _{1}={1\over 2}$. This is because $B_{0}$ contains all elements in S less than or equal to the median ($a+{h\over 2}$) by the definition of B, which is equal to $B_{0}$.

Assume it is true at $i=k$. The case at $i=k+1$ follows from the definition of $B_{i+1}$. When a number $x\in [a,a+h]$, takes average with a number $y\in [a, a+(1-{1\over 2^{k+1}})h]$, we have their average value ${x+y\over 2}\in [a, a+(1-{1\over 2^{k+2}})h]$. $\square$

Define $D_{3}$ to be the set of elements in $(a+(1-\tau _{3})h, a+h]$ in $S_{j}^{(1)}$. If $|D_{3}|\ge {\log m\over (\log \log m)^5}$, enter Period 2 below, otherwise, enter Period 3.

Period 2: $O(\log m)$ stages

Let $S_{i_{1}}^{(1)}$ be the final set generated from S in Period 1 via a series of average operations. Define $S_{0}^{(2)}=S_{i_{1}}^{(1)}$. Let $S_{j}^{(2)}$ be the set of elements after j stages in Period 2.

Define $D_{j,3}$ to be the set of elements in $(a+(1-\tau _{3})h, a+h]$ in $S_{j}^{(2)}$, $D_{j,3}^{\prime }$ to be the set of elements in $[a,a+(1-\tau _{3})h]$ in $S_{j}^{(2)}$, $D_{j,2}$ to be the set of elements in $(a+(1-\tau _{2})h, a+h]$ in $S_{j}^{(2)}$, and $D_{j,2}^{\prime }$ to be the set of elements in $[a,a+(1-\tau _{2})h]$ in $S_{j}^{(2)}$.

In Period 2, we always have inequality $|D_{j,3}|\ge {\log m\over (\log \log m)^5}$, otherwise, enter Period 3.

Since there are at most $\gamma _{1}\cdot m$ elements with value in the range $(a+(1-\tau _{1})h, a+h]$, they can help at most $\gamma _{1}\cdot m$ elements with value at most $a+(1-\tau _{1})h$ increase to at least $a+(1-\tau _{1/2})h=a+(1-\tau _{2})h$. This is because each one with value at most $a+h$ can contribute at most $\tau _{2h}$. With $\gamma _{1}\cdot m$ elements with value more than $a+(1-\tau _{1})h$, their total contribution is at most $\gamma _{1}\cdot m\cdot \tau _{2}$. Therefore, the number of elements in $[a, a+(1-\tau _{2})h]$ is always at least $(1-\gamma _{1})m-\gamma _{1}\cdot m=(1-2\gamma _{1})m=(1-\gamma _{2})m$.

Therefore, by Lemma 2, after each stage, the number of elements in $D_{3}$ is reduced by a constant factor. This is because each element in $D_{3}$ has larger probability to take average with the elements in $D_{j,2}^{\prime }$.

By Theorem 4, with the failure probability at most $g(\epsilon )^{|D_{j,3}|}$, there are more than $(\gamma _{2}+\epsilon )|D_{j,3}|$ elements in $D_{j,3}$ to select elements in $D_{j,2}$ to take average.

By Lemma 2, with the failure probability at most $g(\epsilon )^{|D_{j,3}|\over 2}+2(1-a)^{|D_{j,3}|}$, there are at least $(1-\gamma )(1-\epsilon )\cdot {|D_{j,2}^{\prime }|\over |S|}|D_{j,3}|$ elements in $D_{j,3}$ to select elements in $D_{j,2}^{\prime }$ to take average.

We note that if an element in $D_{j,3}$ takes average with another element in $D_{j,2}^{\prime }$, it will not stay in $D_{j+1,3}$ in the next stage. Therefore, the size of $D_{j+1,3}$ gets reduced.

Therefore, with the failure probability at most $2(1-a)^{|D_{j,3}|}+g(\epsilon )^{|D_{j,3}|\over 2}=o({1\over (\log m)^4})$ (we use the condition $|D_{j,3}|\ge {\log m\over (\log \log m)^5}$, otherwise, it enters Period 3), the elements in $D_{j,3}$ is reduced by at least

$$\begin{aligned}&(1-\gamma _{1})(1-\epsilon )\cdot {|D_{j,2}^{\prime }|\over |S|}|D_{j,3}|-(\gamma _{2}+\epsilon )|D_{j,3}|\\&\quad \ge (1-\gamma _{1})(1-\epsilon )(1-\gamma _{1})|D_{j,3}|-(\gamma _{2}+\epsilon )|D_{j,3}|\\&\quad \ge ((1-\gamma _{1})(1-\epsilon )(1-\gamma _{1})-(\gamma _{2}+\epsilon ))|D_{j,3}|\\&\quad \ge ((1-\gamma _{1})(1-\epsilon -\gamma _{1})-(\gamma _{2}+\epsilon ))|D_{j,3}|\\&\quad \ge ((1-\gamma _{1})(1-\epsilon -\gamma _{1})-2\gamma _{1}-\gamma _{1})|D_{j,3}|\\&\quad \ge ((1-\gamma _{1})(1-2\gamma _{1})-4\gamma _1-2\gamma _{1})|D_{j,3}|\\&\quad \ge (1-3\gamma _1-6\gamma _{1})|D_{j,3}|\\&\quad \ge (1-9\gamma _{1})|D_{j,3}|. \end{aligned}$$

The above inequalities are based on the setting for those parameters $\gamma _{1}, \gamma _{2}$ and $\epsilon$.

It takes $O(\log m)$ stages to stage j such that $|D_{j,3}|< {\log m\over (\log \log m)^5}$. We enter Period 3.

If $|D_{j,3}|< {\log m\over (\log \log m)^5}$, enter Period 3.

Period 3: $O((\log \log m)^2)$ stages

Let $S_{i_{2}}^{(2)}$ be the set generated from $S_{2}^{(2)}$ in Period 2 via a series of average operations. Define $S_{1}^{(3)}=S_{i_{2}}^{(2)}$. Let $A^*=D_{i_{2},3}$, and $B^*=D_{i_{2},2}^{\prime }$. We have $|A^*|< {\log m\over (\log \log m)^5}$, and $|B^*|\ge (1-\gamma _{2})|S|$.

Since almost all the elements belong to $B^*$ in Period 3, we can assume that with very small failure probability, the elements that sending requests will take average with the elements in B. Obviously, it holds that with probability at most ${3\over 4}$, the elements will not take average with the elements in $B^*$. Assume that an element has been under the condition that sends requests for u times, with probability at most $({3\over 4})^u$, it does not take average with an element in $B^*$. Let t be the number of stages in Period 3.

With probability at most $g({1\over 4})^{{t\over 2}}$, there are at most $({1\over 2}-{1\over 4})t={t\over 4}$ stages that an element is in sending status.

In this case, for each element in $A^*$, with probability at most $p_{3}=g({1\over 4})^{{t\over 2}}+({3\over 4})^{t\over 4}$, it does not get the chance to take an average operation with an element in $B^*$. There is the probability at most $O({(\log m)^3\over m^2})$ that two elements in $A^*$ select the same element to take average.

Therefore, the number of stages t in Period 3 is selected to be $(\log \log m)^2$ with probability at most $|A^*|p_{3}\le {1\over (\log m)^4}$.

Combining the analysis in above periods, we have the conclusion that the failure probability is at most ${1\over (\log m)^3}$. $\square$

Assume that the communication including c stages is $\alpha$-successful when there is an $\alpha$ shrink in terms of the gap. For further analysis, let parameter $\delta$ indicate the probability that fails to achieve an $\alpha$ shrink. Then we have Lemma 4.

Lemma 4

Let cbe a parameter. All stages are partitioned into multiple groups of cstages $G_{1},G_{2},\ldots , G_{k}$. Then there are kindependent 0, 1 random variables$r_{i}$for each group $G_{i}$such that

• 1. ${\mathrm{Prob}}(G_{i}$ is $\alpha$-successful$)\ge {\mathrm{Prob}}(r_{i}= 1)$

• 2. ${\mathrm{Prob}}(r_{i}=1)\ge 1-\delta$.

• 3. ${\mathrm{Prob}}($there are at least t$G_{i}$ to be $\alpha$-successful$)\ge {\mathrm{Prob}}(r_{1}+r_{2}+\cdots +r_{k}\ge t)$.

Proof

First, let $S_{1}, S_{2},\ldots , S_{m} \in \{1,2,\ldots , m\}$ denote the m random numbers in the range $\{1,2,\ldots , m\}$. Let $a_{i} \in {\{0,1\}}$ denote the status that whether a vehicle is receiving or sending requests.

Then, we have the 0,1 string $W_j=a_1S_1, a_2S_2,\ldots , a_mS_m$, which denotes an average operation among the m vehicles.

Let $D_i=W_1\ldots W_z$, $z=O(\log m)$. It means after $O(\log m)$ stages, the string $D_i$ will get an $\alpha$ shrink. There are $O(\log n)$ stages of $D_i$ which will get an $\alpha$ shrink.

Each $G_i$ corresponds to a random sequence $D_i$. Let T be the total number of random paths for group $G_i$.

Let $D_1, D_2,\ldots , D_T$ be an rearrangement of all the random paths such that $D_1,\ldots D_{H_{i}}$ are all $\alpha$-successful sorted by lexicographic order, and $D_{H_{i+1}+1}, \ldots , D_T$ sorted by lexicographic order. For each random sequence $D_i$ to be $\alpha$-successful, make it correspond to an integer in [1, T]. Assume that $G_i$ is $\alpha$-successful for $H_i$ random paths with $H_i\ge T\cdot (1-\delta )$. Without loss of generality, each $\alpha$-successful sequence corresponds to an unique integer in the range $[1, H_i]$. Then $G_i$ is $\alpha$-successful if and only if $r_i$ is an event with a random number $s_i$ in [1, T] with $s\le T\cdot (1-\delta )$. From Lemma 3, we can see the failure probability of an $\alpha$ shrink is quite small, which means $[H_{i+1}, T]$ is a very small interval.

It is proved by an induction on the number of groups k. It is trivial for the case $k=1$. Assume that it is true for k. Consider the case $k+1$. For each random sequence $D_1D_2\ldots D_k$, we consider the extension $D_1D_2\ldots D_kD$ for a random sequence D for $G_{k+1}$. The number of cases of D that $G_{k+1}$ is $\alpha$-successful for D random paths is $H_{k+1}\ge T\cdot (1-\delta )$. Then $G_{k+1}$ is $\alpha$-successful if and only if $r_{k+1}$ is an event with a random number $s_{k+1}$ in [1, T] with $s_{k+1}\le T\cdot (1-\delta )$. $\square$

Theorem 5

Let mbe the number of vehicles. Let $n_i^*$be the parameter for vehicle iin the final stage. There is a randomized algorithm that takes $O({(\log n)(\log m)\over \epsilon })$stages of integer average operations such that (1) If $m\ge (1+\epsilon )n$, then each$n_i^*$is either 1 or 0; (2) If $m\le (1-\epsilon )n$, then each$n_i\ge 1$, and the difference between every two nodes is at most two; (3) If $(1-\epsilon )n< m< (1+\epsilon )n$, then all parameters $n_i$are in the range [0, 2], and the number of iwith $n_i=0$is at most $\epsilon m$and the number of iwith $n_i=2$is at most $\epsilon m$.

Proof

The basic idea is that when the gap is large enough, we apply Lemma 3. By Lemma 4, and Chernoff bound, we need $O((\log n)(\log m))$ stages to get the case that the gap is O(1). It takes $O((\log n)(\log m))$ stages when the gap is bounded by a constant by Lemma 3. When the gap is O(1), we handle a bounded number of cases.

• $m\ge (1+\epsilon )n$: The number of elements with value zero is at least $\epsilon n$ when the number of elements with at least two is also at least $\epsilon n$.

  Assume that the largest element is bounded by a constant. In this case, the number of items with 0 and 1 is at least $(1+\epsilon )n/2$. When the largest element m takes average with an element at most $m-2$, it will never come back.

• $(1-\epsilon )n< m< (1+\epsilon )n$: When the number of nonzero elements is at least $(1-\epsilon )n$, most of their values are 1, and the number of elements with at least 3 get disappeared in $O(\log n)$ stages. Therefore, all the elements are in the range [0, 2] and there are at most $\epsilon n$ elements to be zero, and at most $\epsilon n$ elements to be 2.

• $m< (1-\epsilon )n$: After $O(\log n)$ stages, there are at least $\gamma n$ elements that are at least two for some fixed $\gamma >0$. Otherwise, it violates that condition $m< (1-\epsilon )n$.

  When the number of elements that are at least two is at least $\gamma n$, the number of zeros decreases by $\delta n$ for some fixed $\delta$. Eventually all elements with zero disappear after $O(\log n)$ stages. When two numbers with difference at least two take average, their gap will be reduced to at most 1.

  Let S be the multi-set of all elements left. Let $a=\max \{x:x\in S\}$, and $b=\min \{x: x\in S\}$. Define $||x||_S$ be the number of replicas of x in multi-set S. Without loss of generality, assume $||a||_S\le ||b||_S$. Assume ${\mathrm{gap}}(S)> 2$ and $|\{x: x\in S$ and $x\ge a+2\}|\ge \gamma k$. In each stage, there are $\delta m$ elements with value a to take average with the elements with value at least $a+2$. Therefore, after $O(\log m)$ stages, all elements with value a will be removed. Since ${\mathrm{gap}}(S)=O(1)$, we need only $O(\log m)$ stages.

$\square$

For the real average operations, we have the following theorem.

Theorem 6

Let mbe the number of vehicles. Then there is a randomized algorithm that takes$O({(\log n)(\log m)\over \epsilon })$stages of real average operations to enter into an $\epsilon$-balanced status.

5.2 Lower bounds

Theorem 7

It needs $\varOmega (\log n)$stages for the system to be$\epsilon$-balanced.

Proof

According to the algorithm, the number of nonzero elements is at most doubled in each stage. Therefore, it needs $\varOmega (\log n)$ stages if the number of vehicles $m\ge n$.$\square$

6 Performance evaluation

To evaluate the proposed replication-based randomized algorithm, a variety of simulations are executed. This section mainly presents simulation settings, describes the compared algorithms and evaluation criteria. Finally, simulation results are illustrated.

6.1 Simulation setup

Consider the complexity of the simulations, we select an area of San Francisco for simulation through the OpenSteetmap [35]. The size of the selected area is $2000\,{\mathrm{m}} \times 2000\,{\mathrm{m}}$. We choose this area for the reason that, it is densely populated and also a tourist attraction, therefore the daily traffic is heavy. The satellite map is shown in Fig. 1a. Then SUMO [36] is applied to transform the extracted area into road network, as shown in Fig. 1b. The movement trajectories of the vehicles are generated by SUMO. The output file will be input in NS-3 simulator to describe the movement of the nodes. Communications between vehicles follows Nakagami-m channel model.

Fig. 1

Selected area

Assume one vehicular node carries message M, the algorithm tries to disseminate the message to the vehicles in the target region. The destination of each data transmission is selected from the neighbor nodes. The communication range of vehicles is set to 300 m. The transmission frame duration is set to 1ms. The average encounter duration is related to the speed and density of the vehicles. According to reference [16], the simulation time is set to 1 h. The communication protocol adopts IEEE 802.11p to ensure the reliability of information transmission. To evaluate the effect of the number of vehicular nodes participating in data dissemination, we set different number of vehicular nodes, ranging from 600 to 800. We also evaluate the impact of allowed data replicas on network performance, and the number of replicas is set to 400–800. Table 3 gives a list of simulation parameters.

Table 3 Simulation settings

6.2 Compared algorithms

The proposed randomized algorithm is compared with several data dissemination algorithms in VANETs which are described as below.

• Epidemic routing: Epidemic is essentially a flooding algorithm. Each node carries information to all the neighbor nodes, which allows the information to be quickly forwarded to the vehicles in dissemination area.

• Randomized flooding (Random-flood): Each node randomly selects one node from its own neighbors to communicate. Through a series of communication operations, the network will converge to a consensus, that is, the states of the nodes are consistent.

• Constrained Capacity Replication (CCR): CCR is a distributed algorithm. According to available network capacity, the vehicles can autonomously determine data replication strategy.

• Replication algorithm in common urban and highway scenarios (EDDA): In EDDA, select all the independent pairs of vehicular nodes and take average operations. Iterate the average operations until the network converges.

• Replication-based Distributed Randomized Algorithm (R-DRA): The vehicular node in sending status selects one node from its neighbors randomly, and sends an average request. Then, each vehicular node in receiving status chooses the request with which the gap between the nodes is the largest. Finally, corresponding nodes take average with each other, then update their values accordingly.

6.3 Performance metrics

We evaluate the algorithms according to three metrics that are presented as below.

• Number of communication stages indicates the average operations for the network to be balanced. It can reflect the number of data transmissions for network balance and the network convergence complexity. Thus, communication stages can represent the communication overhead of data dissemination to a certain extent.

• Dissemination delay is utilized to measure the effectiveness of the compared algorithms. It presents the time consumed for the network to obtain an $\epsilon$-balanced status.

• Data delivery ratio is the proportion of vehicles that receive the replicas. It is also a way to evaluate the performance of data dissemination algorithms.

6.4 Simulation results

We implement and evaluate the proposed randomized algorithm by comparison with other data dissemination algorithms. The impacts of network size and allowed data replicas on the compared algorithms are illustrated. The network size is represented by the number of vehicular nodes, while the allowed maximum data replicas indicates the total quantity of message copies that can be spread in the network.

• 1. Effect of network size on network performance

Figure 2 describes the effect of number of vehicular nodes on communication stages consumed for the network convergence. As it can be seen, when compared with epidemic and randomized flooding, the proposed distributed randomized algorithm performs significantly fewer communication stages. Due to the strongly connected property, the proposed randomized algorithm applied in complete graph can achieve network balance with fewer stages when compared with the cases of arbitrary and linear graphs. When more vehicular nodes involve in data dissemination, the number of communication stages needed for network balance increases for all the compared algorithms.

Figure 3 depicts the changing trend of dissemination delay when the quantity of nodes that involve in data dissemination varies. In simulations, different numbers of vehicular nodes represent different vehicle densities. When there are fewer nodes in the network, the vehicle density is low, epidemic performs good dissemination delay. However, when the number of vehicles increases, epidemic would need much longer delay for messages dissemination, situation gets worse when more vehicles enter the network. Randomized flooding can improve the delay to some degree but still has to consume extra delay. As observed from the figure, the presented distributed randomized scheme achieves lower dissemination delay when compared with other algorithms and remains stable when the network size becomes larger.

Fig. 2

Communication stages versus number of vehicles

Fig. 3

Dissemination delay versus number of vehicles

Figure 4 shows data delivery ratio of the compared algorithms when the number of vehicles that involve in data dissemination varies. The results show that the delivery ratio increases with more vehicular nodes for the compared algorithms. The reason is that fewer vehicles in the dissemination area might increase the difficulty to carry and forward the message, which leads to more transmission failures. The situation would be improved with more vehicles in the network, as the network connectivity could become better and the frequent communications among the vehicles contribute to successful data transmissions. Replication-based algorithms profit from better network connectivity to achieve better delivery ratio.

Fig. 4

Delivery ratio versus number of vehicles

• 2. Effect of number of data replicas on network performance

Figure 5 evaluates the impact of increasing number of data replicas on communication stages that needed for the network to be balanced, while Fig. 6 presents the change of dissemination delay of the compared algorithms. From Fig. 5, we observe that the average operations will increase to achieve a balanced network status, when the quantity of allowed maximum data replicas becomes larger. Therefore, the compared algorithms need more communication stages when the number of data replicas increases. Epidemic and randomized flooding would consume more stages as they just do simple replication and do not take average. Benefiting from the strong connectivity of dense networks, the distributed randomized algorithm outperforms CCR and EDDA in terms of communication stages.

Figure 6 shows that the replication-based dissemination schemes perform pretty close dissemination delay if fewer data replicas are allowed to spread. This is because that fewer data replicas in the network would result in fewer redundant transmissions such that the dissemination delay is lower. With more data replicas disseminating to the target area, the dissemination delay of all compared schemes becomes higher. And the proposed randomized algorithm achieves lower dissemination delay than other schemes as the algorithm enables two nodes with the largest gap taking average operations, which can accelerate the dissemination. Additionally, when the number of data replicas increases, differences among the schemes become greater.

Figure 7 presents data delivery ratio of the compared algorithms when the quantity of allowed data replicas increases from 400 to 800. Compared with other algorithms, the randomized algorithm that takes advantage of average operations that each node can select a neighbor node with the largest gap to take average, presents the best delivery ratio. CCR and EDDA perform better than epidemic and randomized flooding, as in CCR, the replication strategy depends on the currently residual network capacity and better performance can be achieved, while EDDA benefits from the bounded number of message copies and distributed averaging operations. EDDA and CCR display poorer performance compared with data replication in complete graph under the same conditions. The reason is that due to the property of the strong connectivity in complete graph, the network consensus could be achieved in a quicker way, resulting in lower delay and higher delivery ratio. As is evident by the figure, with more data replicas allowed to spread in the network, the delivery ratio increases for all schemes.

Fig. 5

Communication stages versus number of replicas

Fig. 6

Dissemination delay versus number of replicas

Fig. 7

Delivery ratio versus number of replicas

7 Discussions and future remarks

To achieve efficient data dissemination for applications in vehicular networks, we study both data dissemination algorithms and average consensus problem. Graph theory is utilized to describe the network topology, and abstract the dense vehicular scenarios as complete graph. Then we propose a distributed randomized algorithm based on data replication for data dissemination in the case of complete graph. We prove that the network can enter into an $\epsilon$-balanced status after $O(\log {n\over \epsilon })$ stages. Upper and lower bounds of the proposed distributed randomized algorithm are derived through detailed analysis. Theoretical results of the proposed algorithm indicate the effectiveness of bounded number of data replication and average operations to achieve network balance. Finally, we implement the proposed randomized algorithm and demonstrate the rigorousness and effectiveness of the algorithm.

In this study, we mainly focus on homogeneous vehicles participating in data dissemination, and the vehicles are treated as nodes with the same capability of transmission and computation. However, there may exist different types of nodes with heterogeneous capabilities in a more complex scenario, in which the replication approach cannot simply be applied. In future work, we will consider new scenarios that the network infrastructures (e.g. buses, roadside units (RSUs) and unmanned aerial vehicles (UAVs)) work cooperatively with vehicles to facilitate data dissemination. Dissemination strategies will be adjusted according to different capabilities of nodes in terms of computation or processing due to their heterogeneity. Meanwhile, as a future prospect, we intend to enrich data dissemination mechanisms that can be adapted to complicated scenarios in wireless networks. Further, the efficiency of the proposed mechanism within different contexts in wireless networks deserves further examination.