Keywords

1 Introduction

A deployable mechanism (DM) is capable of configuration change which dramatically alters its shape and size. This property enables many potential applications [5, 6, 25]. With good design, DMs can be folded into a bundle and deployed into different shapes: the compact folding facilitates storage and transport.

DMs are often constructed as networks of simple component mechanisms called deployable units (DUs). Typically, identical units (of one or several types) can be added to the assembly without limit resulting in arbitrarily large deployed structures. A necessary condition for the compact folding of the network is that each DU can be reduced in size, ideally collapsed into a bundle. This is true for scissor-linkage elements, the most important subassembly used in DMs [15, 24]. Recently, the classic spatial overconstrained loops have been used as DUs. Pellegrino et al. studied a bundle-compacting form of the Bennett linkage with equal link lengths [17]. Similar research has also been done on the Myard [20] and Bricard linkages c [3, 4, 9, 17, 22]. In this study, we discuss the generalized construction of bundle folding mechanisms, focusing on 1-dof overconstrained hinged loops. Some general conditions and special cases are discussed and illustrated with examples and simulations.

Section 2 presents the geometric method for generating a bundle folding mechanism. Next, geometric conditions for a 1-dof loop with different numbers of revolute joints are analyzed. Case studies are performed on some typical overconstrained linkages; the obtained mechanisms have been simulated.

2 General Method for Obtaining Bundle Folding Mechanisms

In general, the geometric construction of R-jointed linkage with a given connectivity graph involves the determination of the spatial relationship among the hinge axes in each link. Beyond interference, the kinematics of the linkage is not affected by the geometric outlines of the links, yet these affect its physical appearance and utility.

The linkage is bundle-folding, if it has a configuration, in which the physical rigid links can be folded completely into a bundle without internal space gaps. We focus on single loops. A rigid bar which realizes a physical binary link should not be confused with the common normal used to geometrically represent the abstract link. The former can be any line segment with ends on the two joint axes sharing the link. The objective of the conceptual design of a maximally compact linkage is to find a line segment containing all rigid bars in some configuration.

Thus, a simple construction procedure can be proposed: choose a configuration and draw a line intersecting all joint axes. Then, take the segment of this line connecting the intersection points on any two adjacent R-axes as the physical rigid link. Thus, in the chosen configuration, the linkage will be compacted into a single line segment. Once the linkage moves to other configurations, (generally non-planar) polygons will be formed by these connecting link segments. Practically, the rigid links have finite cross section and so in the folded configuration, the physical shape of the mechanism will be a bundle. The mechanical design must ensure that this bundle is realized without gaps and interference.

3 Bundle Folding Conditions of 1-dof Overconstrained Mechanism

According to the Chebychev–Grübler–Kutzbach criterion, a spatial closed-loop linkage should have seven joints to be mobile. If realized with fewer hinges, the mechanism is called overconstrained. In the following, we will discuss the bundle folding conditions for loops with four, five, and six revolute joints.

3.1 4R Loops

Figure 1 [19] characterizes the Bennett linkage. Opposing links have the same length, a or b, and twist angle, \(\alpha \) or \(\beta \), respectively. All offsets are zero and \(a\sin \beta = b\sin \alpha \) [1].

Fig. 1
figure 1

The Bennett linkage and its geometric description [19]

Full size image

The linkage is mobile with one dof as in every configuration the four zero-pitch twists of the hinges are linearly dependent and span a three-system of screws. For general choices of the parameters a, b, \(\alpha \), \(\beta \), and a general configuration, this is a general three system with one positive, one negative, and no zero principal pitches. So four revolute joint axes will be in the same regulus on a hyperboloid of one sheet (the zero-pitch quadric of the system). Hence, every line of the second regulus of the same hyperboloid intersects all four hinge axes, and can be used to construct a bundle-folding Bennett four-bar. (See [8, 19] for the properties of the general three-system and the one spanned by the Bennett axes.)

Special or degenerate cases occur when for special geometries or configurations. Thus, when the common normals of the links align, the two reguli, of the R joints and of their intersectors, both rule a hyperbolic paraboloid.

When \(a=b \ne 0\), each pair of opposing revolute axes intersects at a point. The desired line can be the segment linking the two intersections, or any line passing through one of the points and lying in the plane of the two axes through the other. In this case the general three-system spanned by the joint twists has middle principal pitch equal to zero and the hyperboloid regulus of the four lines degenerates to a pair of intersecting planes.

When \(\alpha =\beta =0\), the mechanism becomes a planar parallelogram. In a general configuration no line intersects all axes (at finite points), but the four axes can become coplanar in a singularity of increased instantaneous mobility. Only in this configuration a bundle-generator line can be drawn.

Fig. 2
figure 2

Plane symmetric Myard linkage

Full size image

Analogously, when \(a=b=0\), the mechanism is a collapsible spherical four-bar. At the configuration where all the axes are coplanar, there are (infinitely many) bundle generators.

3.2 5R Loops

In a 5R loop with one dof, the screw system spanned by the rotational twists is of dimension 4. Any line intersecting all five hinges is the axes of a zero-pitch screw in the reciprocal two-system. (Two zero pitch screws are reciprocal if and only if their axes are coplanar.) Therefore, the existence and multiplicity of a bundle generator depends on the type of the co-determined two- and four-systems. A two-system may contain zero, one, two, or infinitely many zero-pitch screws. The most general cases are of two or zero solutions.

It is important to distinguish the special case when the candidate generator is parallel rather than intersecting an axis. To construct a physical bundle-folding linkage the intersection point must be finite. In practice, the angle at the intersection is preferred to be close to \(\pi /2\), although some useful solutions exist when the generator coincides with an axis.

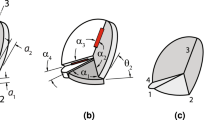
An example of 5R-loop is the plane-symmetric Myard linkage, in Fig. 2. The zero-pitch joint screws and their axes are denoted \(\varvec{\rho }_i\) and \(\ell (\varvec{\rho }_i)\), \(i = 1, \ldots , 5\), respectively. \(\ell (\varvec{\rho }_2)\) and \(\ell (\varvec{\rho }_5)\) always intersect, and so do \(\ell (\varvec{\rho }_3)\) and \(\ell (\varvec{\rho }_4)\). The two intersection points must be in the plane of symmetry, therefore, the line connecting the two points also intersects \(\varvec{\rho }_1\) (in some singular configurations, the two lines coincide). One more solution exists: the intersection of the plane defined by \(\ell (\varvec{\rho }_3)\) and \(\ell (\varvec{\rho }_4)\) and the one spanned by \(\ell (\varvec{\rho }_2)\) and \(\ell (\varvec{\rho }_5)\) intersects also with \(\ell (\varvec{\rho }_1)\), Fig. 2 [16, 19, 20, 23].

3.3 6R Loops

In a 6R 1-dof loop, the joint rotations span a 5-system of twists. The reciprocal (wrench) system is defined by a unique screw. A (unique) bundle generator exists only if the pitch of this screw is zero. (In addition this line must not be parallel to any of the axes.) Let \(\varvec{\rho }_i=(\varvec{\omega }_i, \mathbf {v}_i)\), \(i=1, \ldots , 5\), be five independent zero-pitch twists in the 5-system. A wrench, \(\psi = (\mathbf {f}, \mathbf {m})\), with on the screw reciprocal to the 5-system satisfies the five homogeneous linear equations

$$\begin{aligned} \mathbf {f}\cdot \mathbf {v}_i + \mathbf {m}\cdot \varvec{\omega }_i = 0 \end{aligned}$$
(1)

This defines a one-system of screws whose pitch is zero only if \(\mathbf {f}\cdot \mathbf {m} = 0\) for one (and every) solution. To avoid parallelism with a joint axis we need, for every i, either \(\mathbf {f}\times \varvec{\omega }_i \ne 0\) or \(\mathbf {m}/|\mathbf {f}|\ne \mathbf {v}_i/|\varvec{\omega }_i|\). In general, one cannot expect the additional conditions to be satisfied and therefore, for five lines in general position a sixth intersecting each of them does not exist.

However, the search for a bundle generator needs to succeed in only one configuration. If an IIM (increased instantaneous mobility) singularity exists, where no five of the lines are independent, finding a generator is easier. In particular, if the spanned system is three-dimensional, so is its reciprocal and then (usually) there will be infinitely many solutions, as explained above.

For instance, the systems of some Bricard linkages can degenerate in some configurations. Depending on the degree and type of the system, different numbers of solutions can be obtained. Examples are given in the following section.

4 Case Studies of Bundle Folding Loops

4.1 Bennett Linkage

We choose a Bennett linkage with parameters \(a=80\), \(b=128\), \(\alpha =30^\circ \), \(\beta =51.13^\circ \) as an example. The bundle is generated along the common intersecting line as shown in Fig. 3a. Here the folded configuration is the one where the joint axes have a common normal, which is the chosen bundle generators. There are infinitely many other common intersecting lines in this configuration, resulting in longer link segments. Bennett loops can be linked in a network forming intersting DMs. Bundle folding units are preferred; in particular the special case with \(a=b\) [2, 12, 17, 18].

Fig. 3
figure 3

Simulation of a bundle-folding Bennett linkage

Full size image

4.2 Type III Bricard Linkage

Figure 4 shows the definition of a type III Bricard linkage in one of its two collapsed configurations. The edges AB, BC, \(AC'\), \(A'B'\), \(B'C'\), \(A'C\) are the rotation axes of the mechanism. (For more details, see [7, 9].) In the example chosen, Figs. 4 and 5, the dimensions are: \(r=110\), \(l_{ OA}=l'_{ OA}=213.35\), \(\angle AOA'=27.93^\circ \), \(r=110\), \(R=179.47\).

Fig. 4
figure 4

Example of the type III Bricard linkage

Full size image
Fig. 5
figure 5

Simulation of a Bricard linkage

Full size image

In the collapsed configurations (where all hinge axes are coplanar), the rank of the system spanned by the joint twists drops to three. Then, there are infinitely many possible bundle generators, each intersecting all the revolute axes. Indeed, any line in the plain which is not parallel to any of the six axes can be used. Obviously, none of these generators can be a common normal to the hinges.

The segment \(BB'\) is the folded bundle of the linkage. In the other collapsed configuration, the link segments form a square, Fig. 4. A 3D CAD model of the Bricard linkage bundle has been build. The cross-section of each bar is nearly a rectangle, slightly modified to avoid collisions during the motion. Simulation of the movement is illustrated in Fig. 5. Bricard linkages have also been used as deployable units, usually bundle-folding [3, 4, 17, 22]. Type III Bricards can form indefinitely long chains [11] which can deploy and reconfigure in various ways [14].

4.3 Sarrus Linkage

The model and parameters of the Sarrus linkage [21] are shown in Fig. 6. The unit joint rotation twists are \(\varvec{\rho }_i\), \(i=1, \ldots , 6\). The adjacent axes of joints 1, 2 and 3 are parallel, and so are \(\ell (\varvec{\rho }_4)\), \(\ell (\varvec{\rho }_5)\), and \(\ell (\varvec{\rho }_6)\). The angle between the necessarily non-parallel directions of two groups of joint axes is \(\alpha \).

Fig. 6
figure 6

The Sarrus linkage

Full size image

As discussed in Sect. 3.3, the desired common intersecting line (a zero-pitch reciprocal screw) does not always exist for a 6R loop. In a Sarrus linkage configuration where the joint twists span a five-system, there cannot be a pure force exerting no power on any hinge rotation. Indeed, if this were the case, then the reciprocal system would be of dimension at least two because there is always an infinite-pitch reciprocal screw (in the direction perpendicular to all axes). However, for many Sarrus linkages there are singular configurations with instantaneous mobility two (or three) and then a bundle-generating line can be found.

For example suppose that the two planar 3R serial subchains of the Sarrus can be maximally extended simultaneously. That is, there is a configuration where the parallel triples \(\ell (\varvec{\rho }_i)\), \(i=1, 2, 3\) and \(i=4, 5, 6\), are coplanar in \(\pi _{123}\) and \(\pi _{456}\), respectively. Then the intersection \(\pi _{123}\cap \pi _{456}\) is the expected line. (The intersection line exists and is unique if the Sarrus is non-degenerate, allowing finite translation of link 3–4 with respect to 1–6.) An example mechanism is shown in Fig. 7.

Another example is when a Sarrus can be collapsed. Then, as with the type III Bricard, the joint twists span only a three-system, and any line on the plane not directed in either of the two joint-axis directions, can be the bundle generator, Fig. 8. Sarrus linkages can also be very useful when constructing deployable mechanisms : they can be used as equivalents of sliders in networks of scissor linkages [10, 13]. Bundle-folding Sarrus variants can be useful in such DM applications.

Fig. 7
figure 7

Bundle-folding Sarrus linkage

Full size image
Fig. 8
figure 8

Another bundle-folding Sarrus linkage

Full size image

5 Conclusions and Future Work

A simple general geometric method for the conceptual design of bundle-folding realizations of a spatial 1-dof overconstrained loop is presented. The procedure involves the construction of a bundle-generating line, which intersects all hinge axes in a chosen configuration. Geometric conditions are given for the existence of such a generator for linkages composed of four, five, and six revolute joints. Case studies of bundle-folding designs of different 4R and 6R loops are presented and validated using simulations.