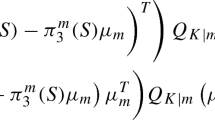1 Introduction

In supervised classification, the data are classified with respect to g known classes and the intent is to construct a discriminant rule or classifier on the basis of these classified data for assigning an unclassified individual to one of the g classes on the basis of its feature vector. Many real problems in supervised classification, however, involve high-dimensional feature vectors. While there is a vast literature on dimensional reduction and/or feature selection in supervised classification [4, 8, 13], some of the methods may become inapplicable or unreliable when the dimension of the feature vector is very large relative to the number of individuals [2, 10, 15, 24]. An example of such an application is the analysis of gene-expression data, where expression levels of genes (features) are available from patients in g known classes of distinct disease stages or outcomes and the aim is to identify a small subset of “marker” genes that characterize the different classes and construct a discriminant rule to predict the class of origin of an unclassified patient [11, 17]. One way to handle this high-dimensional problem is to identify genes that are differentially expressed among the g classes of tissue samples. In this context, multiple hypothesis test-based approaches [27–29] have been proposed to assess statistical significance of differential expression for each gene separately, with control for the false discovery rate (FDR) which is defined as the expected proportion of false positives among the genes declared to be differentially expressed [1]. Clustering-based approaches have also been considered, but these methods either work on gene-specific summary statistics [14, 23] or reduced forms of gene-expression data [6]. Alternatively, clustering methods that can handle full gene-expression data rely on the assumption that pure clusters of null (non-differentially expressed) genes and differentially expressed genes exist [12, 26]; see also [25]. More recently, a mixture model-based approach with random-effects terms was proposed to draw inference on differences between classes using full gene-expression data [22]. This method does not rely on the clusters being pure as to whether all cluster members are differentially expressed or null genes. In this paper, we propose a new three-step method that extends this mixture model-based approach in order to identify networks of correlated differential features (genes) for supervised classification of high-dimensional data.

The rest of the paper is organized as follows. In Sect. 2, we describe the mixture model with random-effects terms [20] that is adopted in the first step to cluster the genes using full gene-expression data. We also present the second step, where the relevance of each feature variable for differentiating the classes is formally tested and ranked on the basis of cluster-specific contrasts of mixed effects. In Sect. 3, we describe the final third step in which a non-parametric clustering approach is used to further explore the group structures of selected highly ranked differential features for each cluster identified in the first step. Section 4 presents the application of the proposed method to a publicly available gene-expression data set in cancer research for the discovery of correlated biomarkers relevant to the cancer prognosis. Discussion is given in Sect. 5.

2 Mixture Model with Random-Effects Terms

With supervised classification, it is supposed that an individual belongs to one of g classes, denoted by C 1, …, C g , and that there is a vector of p feature variables measured on each individual. Based on the observed feature vectors, represented by an n × p matrix, the intent is to construct a discriminant rule for allocating an unclassified individual to one of the g classes [15]. For applications in the context of supervised classification with gene-expression data, the number of individual tissue samples n is very small relative to the number of genes p. To handle this high-dimensional problem, it is proposed to adopt a mixture model with random-effects terms to firstly cluster the p genes and then identify those genes that are highly differentiated between the g classes of tissue samples.

Let \(\boldsymbol{y}_{j} = (\,y_{1j},\ldots,y_{nj})^{T}\) contain the measurements on the jth gene ( j = 1, …, p), where the superscript T denotes vector transpose and p is much greater than n. It is assumed that \(\boldsymbol{y}_{j}\) has a h-component mixture distribution with probability π i of belonging to the ith cluster (i = 1, …, h), where the π i sum to one. We let the h-dimensional vector \(\boldsymbol{z}_{j}\) denote the cluster membership of \(\boldsymbol{y}_{j}\), where \(z_{ij} = (\boldsymbol{z}_{j})_{i} = 1\) if \(\boldsymbol{y}_{j}\) belongs to the ith cluster and zero otherwise (i = 1, …, h). A mixture model with random-effects terms [20] is required because it is anticipated that repeated measurements of gene expression for a tissue sample and expression levels for a gene are both correlated; see also [19]. Specific random effects are thus considered in the mixture model to capture individual gene effects and the correlation between gene-expression levels among the tissue classes [22]. Conditional on its membership of the ith cluster, the distribution of \(\boldsymbol{y}_{j}\) is specified by the linear mixed model

$$\displaystyle{ \boldsymbol{y}_{j} = \boldsymbol{X}\boldsymbol{\eta }_{i} + \boldsymbol{U}\boldsymbol{b}_{ij} + \boldsymbol{V }\boldsymbol{c}_{i} + \boldsymbol{\varepsilon }_{ij}, }$$
(1)

where \(\boldsymbol{X},\boldsymbol{U}\), and \(\boldsymbol{V }\) denote the known design matrices corresponding to the fixed effects terms \(\boldsymbol{\eta }_{i}\) and to the random-effects terms \(\boldsymbol{b}_{ij}\) and \(\boldsymbol{c}_{i}\,(i = 1,\,\ldots,\,h;\,j = 1,\ldots,p)\), respectively. The vector \(\boldsymbol{b}_{ij} = (b_{1ij},\,\ldots,\,b_{gij})^{T}\) contains the unobservable gene-specific random effects for each of the g tissue classes, and \(\boldsymbol{c}_{i} = (c_{1i},\,\ldots,\,c_{ni})^{T}\) contains the random effects common to all genes from the ith cluster. The measurement error vector \(\boldsymbol{\epsilon }_{ij}\) is taken to be multivariate normal \(N_{n}(\boldsymbol{0},\,\boldsymbol{A}_{i})\), where \(\boldsymbol{A}_{i}\) is a diagonal matrix. The vectors \(\boldsymbol{b}_{ij}\) and \(\boldsymbol{c}_{i}\) of random-effects terms are taken to be multivariate normal \(N_{g}(\boldsymbol{0},\,\boldsymbol{B}_{i})\) and \(N_{n}(\boldsymbol{0},\,\boldsymbol{C}_{i})\), respectively, where the variance component \(\boldsymbol{C}_{i}\) is assumed to be diagonal and \(\boldsymbol{B}_{i}\) is a non-diagonal g × g matrix, where the correlation between gene-specific random effects b lij  (l = 1, …, g) is modelled via the off-diagonal elements in \(\boldsymbol{B}_{i}\); see, for example, [22]. The assignment of the p genes into h clusters is implemented using the estimated conditional posterior probabilities of cluster membership given \(\boldsymbol{y}_{j}\) and \(\hat{\mathbf{c}}_{l}(\,j = 1,\ldots,p;\,l = 1,\ldots,g)\):

$$\displaystyle{ \tau _{i}(\boldsymbol{\,y}_{j};\hat{\boldsymbol{\varPsi }},\hat{\mathbf{c}}) = \mbox{ pr}(Z_{ij} = 1\vert \boldsymbol{y}_{j},\hat{\mathbf{c}}) ={ \hat{\boldsymbol{\pi }}_{i}\,f(\boldsymbol{\,y}_{j}\vert z_{ij} = 1;\hat{\boldsymbol{\psi }}_{i},\hat{\mathbf{c}}_{i}) \over \sum _{m=1}^{h}\hat{\boldsymbol{\pi }}_{m}\,f(\boldsymbol{\,y}_{j}\vert z_{mj} = 1;\hat{\boldsymbol{\psi }}_{m},\hat{\mathbf{c}}_{m})}, }$$
(2)

where \(\boldsymbol{\psi }_{i}\) is the parameter vector for the ith component density containing the unknown parameters \(\boldsymbol{\eta }_{i}\) and distinct elements in \(\boldsymbol{A}_{i}\), \(\boldsymbol{B}_{i}\), and \(\boldsymbol{C}_{i}(i = 1,\,\ldots,\,h)\),and

$$\displaystyle{ \log f(\boldsymbol{\,y}_{j}\vert z_{ij} = 1;\hat{\boldsymbol{\psi }}_{i},\hat{\mathbf{c}}_{i}) = -\frac{1} {2}\bigg\{\log \vert \hat{\mathbf{D}}_{i}\vert + (\boldsymbol{\,y}_{j} -\boldsymbol{X}\hat{\boldsymbol{\eta }}_{i} -\boldsymbol{V }\hat{\mathbf{c}}_{i})^{T}\hat{\mathbf{D}}_{ i}^{-1}(\boldsymbol{\,y}_{ j} -\boldsymbol{X}\hat{\boldsymbol{\eta }}_{i} -\boldsymbol{V }\hat{\mathbf{c}}_{i})\bigg\} }$$

is the log density of \(\boldsymbol{y}_{j}\) conditioned on \(\hat{\mathbf{c}}_{i}\) and the membership of the ith cluster, apart from an additive constant, and where \(\hat{\mathbf{D}}_{i} = \hat{\mathbf{A}}_{i} + \boldsymbol{U}\hat{\mathbf{B}}_{i}\boldsymbol{U}^{T}\); see [20].

To quantify the relevance of each gene for differentiating the g classes, we consider an individual observation-specific contrast in the estimates of the fixed and random effects weighted by the estimated posterior probabilities (2) of cluster membership:

$$\displaystyle{ W_{j} =\sum _{ i=1}^{h}\tau _{ i}(\boldsymbol{\,y}_{j};\,\hat{\boldsymbol{\varPsi }},\hat{\mathbf{c}})\,\hat{S}_{ij}\qquad (\,j = 1,\ldots,p), }$$
(3)

where

$$\displaystyle{ \hat{S}_{ij} = \boldsymbol{d}_{j}^{T}(\hat{\boldsymbol{\eta }}_{ i}^{T},\hat{\mathbf{b}}_{ G_{i}}^{T},\hat{\mathbf{c}}_{ i}^{T})^{T}\bigg/\sqrt{\boldsymbol{d} _{ j}^{T}\hat{\boldsymbol{\varOmega }}_{i}\boldsymbol{d}_{j}} }$$
(4)

is the cluster-specific normalized contrast with the BLUP estimator of the mixed effects, and where \(\boldsymbol{d}_{j}\) is a vector whose elements sum to zero, \(\boldsymbol{b}_{G_{i}} = (\boldsymbol{b}_{i_{1}}^{T},\,\ldots,\,\boldsymbol{b}_{i_{p_{ i}}}^{T})^{T}\) contains the gene-specific random-effects terms for the p i genes belonging to the ith cluster G i  (i = 1, …, h), and \(\hat{\boldsymbol{\varOmega }}_{i}\) is the covariance matrix of the BLUP estimator of the mixed effects, which can be partitioned conformally corresponding to \(\boldsymbol{\eta }_{i}\vert \boldsymbol{b}_{G_{i}}\vert \boldsymbol{c}_{i}\), respectively, as described in [22].

Based on the weighted contrast W j  ( j = 1, …, p) given in (3), the p genes can be ranked in the order of their relevance for differentiating the g classes (with respect to the defined form of d j for the normalized contrast (4)). In the final step of the proposed method to be described in the next section, we intend to explore the group structure of top-ranked differentially expressed genes in each identified cluster G i (i = 1, …, h), say, for those genes with contrast W j more extreme than thresholds w 0u or w 0d for upregulated and downregulated genes, respectively. A guide to plausible values of w 0u and w 0d can be obtained using the percentile rank of W j ( j = 1, …, p), whereby the percentiles are taken to be the mixing proportions of the non-central portions of W j fitted by a three-component mixture of t-distributions (these two components are considered as representing the distribution of W j for upregulated and downregulated differentially expressed genes).

3 A Non-parametric Clustering Approach for Identification of Correlated Features

We consider the r i top-ranked genes with W j more extreme than either w 0u or w 0d in Cluster G i (i = 1, …, h) and adopt a non-parametric method to cluster the r i genes into networks of differentially expressed genes that are highly correlated. The method starts with the calculation of pairwise correlation coefficients for each pair of the r i genes in G i (i = 1, …, h). Significance of the pairwise correlation coefficients is then assessed with the use of a permutation method [21] to determine the null distribution of correlation coefficients. Precisely, the n class labels of tissue samples are randomly permuted separately for each gene. We pool the permutations for all \(N_{r_{i}} = r_{i}(r_{1} - 1)/2\) pairs of genes to determine the null distribution of correlation coefficients. In this paper, we consider the use of S = 100 repetitions of permutations and estimate the P-value for each pair of genes by

$$\displaystyle{ P_{l} =\sum _{ s=1}^{S}{\#\{m: R_{0m}^{(s)} \geq R_{ l},m = 1,\ldots,N_{r_{i}}\} \over N_{r_{i}}S} \qquad (l = 1,\ldots,N_{r_{i}}), }$$
(5)

where R 0m (s) is the null version of correlation coefficient for the mth pair of genes after the sth repetition of permutations \((m = 1,\ldots,N_{r_{i}};\,s = 1,\ldots,S)\). Let \(P_{(1)} \leq \cdots \leq P_{(N_{r_{ i}})}\) be the ordered observed P-values obtained from (5). The Benjamini–Hochberg procedure [1] is adopted to determine the cut-off \(\hat{k}\), where

$$\displaystyle{ \hat{k} = \mbox{ arg max}\{k: P_{(k)} \leq \alpha k/N_{r_{i}}\}, }$$
(6)

with control of the FDR at level α. Pairwise correlation coefficients corresponding to P-values \(P_{(1)} \leq \cdots \leq P_{(\hat{k})}\) are identified to be significant. Significance of the pairwise correlation coefficients is represented by an r i × r i symmetric binary matrix M with elements of one or zero indicating that the corresponding correlation coefficients are significance or not. Finally, we search in M to identify networks of differentially expressed genes in which all members in a group significantly correlate with one another [21]. This non-parametric clustering approach obtains overlapping groups (networks) of correlated differentially expressed genes.

4 Real Example

We consider the colorectal cancer gene-expression data set [5], which comprised expression values of 15,552 genes for plasma samples from 12 colorectal cancer patients and 8 healthy donors. The original study aims to validate the power of four randomly selected markers (from a list of 40 genes differentially upregulated in cancer patients) in enabling differentiation of the tumour from the healthy condition [5]. With the proposed three-step approach, we first fitted a mixture model with random-effects terms to the column-normalized gene-expression data set with h=3 to h=20 clusters, taking \(\boldsymbol{X} = \boldsymbol{U}\) to be a 20 × 2 zero-one matrix (the first 12 rows are (1, 0) and the next 8 rows are (0, 1)) and taking \(\boldsymbol{V }\) to be \(\boldsymbol{I}_{20}\). Based on the Bayesian information criterion (BIC) for model selection, we identified that there are 15 clusters of genes. The ML estimates of the unknown parameters are presented in Table 1. The ranking of differentially expressed genes is then implemented on the basis of the weighted estimates of a contrast in the mixed effects (3). For the case of g=2 classes of tissue samples (tumour versus healthy), we consider \(\boldsymbol{d}_{j}\) of the form as

$$\displaystyle{ \boldsymbol{d}_{j}^{T} = (1\ \ \mbox{ $-$1}\ \ \vdots\ \ 0\ \ 0,\ \ \ldots,\ \ 0\ \ 0,\ \ 1\ \ \mbox{ $-$1},\ \ 0\ \ 0,\ \ \ldots \ \ \vdots\ \ 0\ \ \ldots \ \ 0), }$$
(7)

where only one pair of (1  −1) exists in the second partition corresponding to \(\boldsymbol{b}_{G_{i}}\); see Eq. (4). We then fitted a three-component mixture of t-distributions [16] to W j and obtained the mixing proportions of the components corresponding to the non-central portion of W j , which are 11.5 and 7.2% for upregulated and downregulated genes in the tumour tissues, respectively. Thus we selected w 0u = 1. 661 (the 88.5th percentile of W j ) and w 0d = −2. 236 (the 7.2th percentile of W j ( j = 1, …, p)). There are a total of 2907 differentially expressed genes with W j more extreme than w 0u or w 0d (W j > 1. 661 or W j < −2. 236). Among them, 1581 genes have valid identifiers (1073 upregulated and 508 downregulated). Descriptive statistics of W j for these 1581 differentially expressed genes are provided in Table 2. It can be seen that Clusters 7–11 and 13–14 contain upregulated differentially expressed genes, Clusters 1, 3, 6, and 12 contain downregulated differentially expressed genes, and Clusters 5 and 15 contain both upregulated and downregulated differentially expressed genes.

Table 1 Estimates of the mixture model with random-effects terms for the colorectal cancer data set (15 clusters)
Full size table
Table 2 Descriptive statistics of W j for the differentially expressed genes with valid gene identifiers and W j more extreme than either w 0u or w 0d (15 clusters)
Full size table

In the final step, we applied the non-parametric method to identify networks of correlated differentially expressed genes from the r i genes in Cluster G i . We set α to be between 0.1 and 0.00005 such that the expected number of false positives among the pairs of genes identified to be significantly correlated is smaller than one; see [21]. With the matrix M, networks of differentially expressed genes were displayed using UCINET6 for Windows [3]. Figure 1 presents the identified networks of upregulated differentially expressed genes in Clusters 7, 9, 13, and 14, where the nodal size of a gene is proportional to the degree of the node (the number of genes that are significantly correlated with the gene). Networks of downregulated differentially expressed genes (Clusters 3, 6, and 12) were provided in Fig. 2. Clusters 5 and 15 had networks of up- and down regulated differentially expressed genes (Fig. 3).

Fig. 1
figure 1figure 1

Network of upregulated differentially expressed genes in (a) Cluster 7; (b) Cluster 9; (c) Cluster 13; and (d) Cluster 14. Nodal size is proportional to the degree (the number of genes that are significantly correlated with the gene). For Clusters 7, 9, and 13, only genes with the top 50 degrees were displayed

Full size image
Fig. 2
figure 2figure 2

Network of downregulated differentially expressed genes in (a) Cluster 3; (b) Cluster 6; and (c) Cluster 12. Nodal size is proportional to the degree (the number of genes that are significantly correlated with the gene). For Clusters 3 and 12, only genes with the top 50 degrees were displayed

Full size image
Fig. 3
figure 3

Network of upregulated and downregulated differentially expressed genes in (a) Cluster 5 and (b) Cluster 15. Nodal size is proportional to the degree (the number of genes that are significantly correlated with the gene). From (a), it can be seen that two separate networks were identified for genes belonging to Cluster 5. One of them contains upregulated genes HSPA12A, RTCA, PID1, C20orf194, ACAP2, PPP2R5C, COX11, and TRAFD1. Another one contains downregulated genes N62132, AA455350, and TRIP10. For Cluster 15 (b), the network contains genes that are downregulated except ARHGAP39 (upregulated), which significantly correlated with downregulated genes {H74004, AA417982} and {H74004, AA463454}

Full size image

A summary of the identified networks of correlated differentially expressed genes for each cluster is given in Table 3. Two isolated networks of differentially expressed genes were identified: {N62132, TRIP10, AA455350} downregulated genes network from Cluster 5 and {CLK2, ENSA, AA416971} upregulated genes network from Cluster 13. It is noted that four upregulated genes were considered in the original study and three of them (EPAS1, UBE2D3, KIAA0101) were validated to be significantly increased in cancer compared to healthy donors [5]. Our clustering results confirmed the same findings; these three genes were identified as differentially expressed genes in Cluster 14 (with contrast W j = 3.7, 3.3, and 2.0, respectively, and ranked the 2nd, 8th, and 156th among the 224 differentially expressed genes in Cluster 14). The original study could not validate the remaining upregulated gene DDX46. However, our method has sufficient power to identify DDX46 as a differentially expressed gene in Cluster 5, with W j = 2.4 and ranked the 1st among the 14 upregulated differentially expressed genes in Cluster 5.

Table 3 A summary of networks of highly correlated differentially expressed genes
Full size table

5 Discussion

We have presented a new approach to identify correlated differential features for supervised classification of high-dimensional data. The method adopts a mixture model with random-effects terms to cluster the feature variables and then ranks them in terms of their cluster-specific contrasts of mixed effects that quantify the evidence of differentiation between the known classes. The final step of the method adopts a non-parametric clustering approach to identify networks of differential features that are highly correlated in each identified cluster.

The proposed method is illustrated using an application on the analysis of gene-expression cancer data. The identified differentially expressed genes and their correlation structures can have significant contribution in the discovery of novel biomarkers relevant to the cancer diagnosis and prognosis; see also [7, 9] for the benefit of using the covariance information among genes for feature selection. Moreover, these differentially expressed genes can be included in a model to construct a classifier with a smaller subset of marker genes, using methods such as mixtures of factor analysers [15, 16] or mixtures of multivariate generalized Bernoulli distributions [18]. This work will be pursued in future research.