On New Fractional Inverse Matrix Projective Synchronization Schemes

Abstract

In this study, the problem of inverse matrix projective synchronization (IMPS) between different dimensional fractional order chaotic systems is investigated. Based on fractional order Lyapunov approach and stability theory of fractional order linear systems, new complex schemes are proposed to achieve inverse matrix projective synchronization (IMPS) between n-dimension and m-dimension fractional order chaotic systems. To validate the theoretical results and to verify the effectiveness of the proposed schemes, numerical applications and computer simulations are used.

1 Introduction

Fractional calculus, as generalization of integer order integration and differentiation to its non-integer (fractional) order counterpart, has proved to be valuable tool in the modeling of many physical phenomena [1,2,3,4,5] and engineering problems [6,7,8,9,10,11,12,13]. Fractional derivatives provide an excellent instrument for the description of memory and hereditary properties of various materials and processes [14, 15]. The main reason for using integer-order models was the absence of solution methods for fractional differential equations [16, 17]. The advantages or the real objects of the fractional order systems are that we have more degrees of freedom in the model and that a “memory”  is included in the model [18]. One of the very important areas of application of fractional calculus is the chaos theory [19, 20].

Chaos is a very interesting nonlinear phenomenon which has been intensively studied [21,22,23,24,25,26]. It is found to be useful or has great application potential in many fields such as secure communication [27], data encryption [28], financial systems [29] and biomedical engineering [30]. The research efforts have been devoted to chaos control [31,32,33] and chaos synchronization [34,35,36,37,38,39,40] problems in nonlinear science because of its extensive applications [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57].

Recently, studying fractional order systems has become an active research area. The chaotic dynamics of fractional order systems began to attract much attention in recent years. It has been shown that the fractional order systems can also behave chaotically, such as the fractional order Chua’s system [58], the fractional order Lorenz system [59], the fractional order Chen system [60, 61], the fractional order Rössler system [62], the fractional-order Arneodo’s system [63], the fractional order Lü system [64], the fractional-order Genesio-Tesi system [65], the fractional order modified Duffing system [66], the fractional-order financial system [67], the fractional order Newton–Leipnik system [68], the fractional order Lotka-Volterra system [69] and the fractional order Liu system [70]. Moreover, recent studies show that chaotic fractional order systems can also be synchronized [71,72,73,74,75,76,77,78]. Many scientists who are interested in this field have struggled to achieve the synchronization of fractional–order chaotic systems, mainly due to its potential applications in secure communication and cryptography [79,80,81].

A wide variety of methods and techniques have been used to study the synchronization of the fractional–order chaotic such as sliding mode controller [82,83,84], active and adaptive control methods [85,86,87], feedback control method [88, 89], linear and nonlinear control methods [90, 91], scalar signal technique [92, 93]. Many types of synchronization for the fractional-order chaotic systems have been presented [94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127]. Among all types of synchronization, projective synchronization (PS) has been extensively considered. In PS, slave system variables are scaled replicas of the master system variables. A variation of projective synchronization is the so-called matrix projective synchronization (MPS) (or full state hybrid projective synchronization) [128,129,130]. Also, matrix projective synchronization (MPS) between fractional order chaotic systems has been studied [131,132,133,134]. In this type of synchronization the single scaling parameter originally introduced in [135] is replaced by a diagonal scaling matrix [136, 137] or by a full scaling matrix [138]. Recently, an interesting scheme has been introduced [139], in which each master slave system state achieves synchronization with any arbitrary linear combination of slave system states. Since master system states and slave system states are inverted with respect to the MPS, the proposed scheme is called inverse matrix projective synchronization (IMPS). Obviously, the problem of inverse matrix projective synchronization (IMPS) is an attractive idea and more difficult than the problem of matrix projective synchronization (MPS). The complexity of the IMPS scheme can have important effect in applications.

Based on these considerations, this study presents new control schemes for the problem of IMPS in fractional-order chaotic dynamical systems. Based on Laplace transform and fractional Lyapunov stability theory, the study first analyzes a new IMPS scheme between $n-$dimensional commensurate fractional-order master system and $m-$dimensional commensurate fractional-order slave system. Successively, by using some properties of fractional derivatives and stability theory of fractional-order linear systems, IMPS is proved between $n-$dimensional incommensurate fractional-order master system and $m-$dimensional commensurate fractional-order slave system. Finally, several numerical examples are illustrated, with the aim to show the effectiveness of the approaches developed herein.

This study is organized as follow. In Sect. 2, some basic concepts of fractional-order systems are introduced. In Sect. 3, the master and the slave systems are described to formulate the problem of IMPS. In Sect. 4, two control schemes are proposed which enables IMPS to be achieved for commensurate master system and incommensurate master system cases, respectively. In Sect. 5, simulation results are performed to verify the effectiveness and feasibility of the proposed schemes. Finally, concluding remarks end the study.

2 Basic Concepts

In this section, we present some basic concepts of fractional derivatives and stability of fractional systems which are helpful in the proving analysis of the proposed approaches.

2.1 Caputo Fractional Derivative

The idea of fractional integrals and derivatives has been known since the development of the regular calculus, with the first reference probably being associated with Leibniz in 1695. There are several definitions of fractional derivatives [140]. The Caputo derivative [141] is a time domain computation method. In real applications, the Caputo derivative is more popular since the un-homogenous initial conditions are permitted if such conditions are necessary. Furthermore, these initial values are prone to measure since they all have idiographic meanings [142]. The Caputo derivative definition is given by

$$\begin{aligned} D_{t}^{p}f\left( t\right) =J^{m-p}f^{m}\left( t\right) , \end{aligned}$$

(1)

where $0<p\le 1,$ $m = [p]$, i.e., m is the first integer which is not less than $p, f^{m}$ is the m-order derivative in the usual sense, and $J^{q}$ $\left( q > 0 \right)$ is the q-order Reimann-Liouville integral operator with expression:

$$\begin{aligned} J^{q}f\left( t\right) =\frac{1}{{\varGamma \left( q\right) }}\int \limits _{0}^{t} {\left( {t-\tau }\right) ^{q-1}}f\left( \tau \right) d\tau , \end{aligned}$$

(2)

where $\varGamma$ denotes Gamma function.

Some basic properties and Lemmas of fractional derivatives and integrals used in this study are listed as follows.

Property 1

For $p=n$ , where n is an integer, the operation $D_{t}^{p}$ gives the same result as classical integer order n . Particularly, when $p=1$ , the operation $D_{t}^{p}$ is the same as the ordinary derivative, i.e., $D_{t}^{1}f\left( t\right) =\frac{df\left( t\right) }{dt}$ ; when $p=0$ , the operation $D_{t}^{p}f\left( t\right)$ is the identity operation: $D_{t}^{0}f\left( t\right) =f\left( t\right)$.

Property 2

Fractional differentiation (fractional integration) is linear operation:

$$\begin{aligned} D_{t}^{p}\left[ af\left( t\right) +bg\left( t\right) \right] =aD_{t}^{p}f\left( t\right) +bD_{t}^{p}g\left( t\right) . \end{aligned}$$

(3)

Property 3

The fractional differential operator $D_{t}^{p}$ is left-inverse (and not right-inverse) to the fractional integral operator $J^{p}$ , i.e.

$$\begin{aligned} D_{t}^{p}J^{p}f\left( t\right) =D^{0}f\left( t\right) =f\left( t\right) . \end{aligned}$$

(4)

Lemma 1

[143] The Laplace transform of the Caputo fractional derivative rule reads

$$\begin{aligned} \mathbf {L}\left( D_{t}^{p}f\left( t\right) \right) =s^{p}\mathbf {F}\left( s\right) -\sum _{k=0}^{n-1}s^{p-k-1}f^{\left( k\right) }\left( 0\right) ,{\ \ \ }\left( p>0,{\ \ }n-1<p\le n\right) . \end{aligned}$$

(5)

Particularly, when $0<p\le 1$, we have

$$\begin{aligned} \mathbf {L}\left( D_{t}^{p}f\left( t\right) \right) =s^{p}\mathbf {F}\left( s\right) -s^{p-1}f\left( 0\right) . \end{aligned}$$

(6)

Lemma 2

[144] The Laplace transform of the Riemann-Liouville fractional integral rule satisfies

$$\begin{aligned} \mathbf {L}\left( J^{q}f(t)\right) =s^{-q}\mathbf {F}\left( s\right) ,{\ \ \ } \left( q>0\right) . \end{aligned}$$

(7)

Lemma 3

[103] Suppose f(t) has a continuous kth derivative on [0, t] $(k\in N,$ $t>0)$, and let $p,q>0$ be such that there exists some $\ell \in N$ with $\ell \le k$ and p,  $p+q\in [\ell -1,\ell ]$. Then

$$\begin{aligned} D_{t}^{p}D_{t}^{q}f\left( t\right) =D_{t}^{p+q}f\left( t\right) , \end{aligned}$$

(8)

Remark 1

Note that the condition requiring the existence of the number $\ell$ with the above restrictions in the property is essential. In this work, we consider the case that $0<p,$ $q\le 1,$ and $0<p+q\le 1$. Apparently, under such conditions this property holds.

2.2 Stability of Linear Fractional Systems

Consider the following linear fractional system

$$\begin{aligned} D_{t}^{p_{i}}{x}_{i}(t)=\sum _{j=1}^{n}a_{ij}x_{j}(t), \qquad i=1,2,...,n, \end{aligned}$$

(9)

where $p_{i}$ is a rational number between 0 and 1 and $D_{t}^{p_{i}}$ is the Caputo fractional derivative of order $p_{i}$, for $i=1,2,...,n$. Assume that $p_{i}=\frac{\alpha _{i}}{\beta _{i}}$, $\left( \alpha _{i},\beta _{i}\right) =1,$ $\alpha _{i},\beta _{i}\in \mathbb {N}$, for $i=1,2,...,n$. Let d be the least common multiple of the denominators $\beta _{i}$’s of $p_{i}$’s.

Lemma 4

[145] If $p_{i}$’s are different rational numbers between 0 and 1, then the system (9) is asymptotically stable if all roots $\lambda$ of the equation

$$\begin{aligned} \det \left( diag\left( \lambda ^{dp_{1}},\lambda ^{dp_{2}},...,\lambda ^{dp_{n}}\right) -A\right) =0, \end{aligned}$$

(10)

satisfy $\left| \arg \left( \lambda \right) \right| >\frac{\pi }{2d} ,$ where $A=\left( a_{ij}\right) _{n\times n}$.

2.3 Fractional Lyapunov Method

Definition 1

A continuous function $\gamma$ is said to belong to class-K if it is strictly increasing and $\gamma \left( 0\right) =0$.

Theorem 1

[146] Let $X=0$ be an equilibrium point for the following fractional order system

$$\begin{aligned} D_{t}^{p}X\left( t\right) =F\left( X\left( t\right) \right) , \end{aligned}$$

(11)

where $0<p\le 1$. Assume that there exists a Lyapunov function $V\left( X\left( t\right) \right)$ and class-K functions $\gamma _{i}$ $\left( i=1,2,3\right)$ satisfying

$$\begin{aligned} \gamma _{1}\left( \left\| X\right\| \right) \le V\left( X\left( t\right) \right) \le \gamma _{2}\left( \left\| X\right\| \right) . \end{aligned}$$

(12)

$$\begin{aligned} D_{t}^{p}V\left( X\left( t\right) \right) \le -\gamma _{3}\left( \left\| X\right\| \right) . \end{aligned}$$

(13)

Then the system (11) is asymptotically stable.

Theorem 2

[147] If there exists a positive definite Lyapunov function $V\left( X\left( t\right) \right)$ such that $D_{t}^{p}V\left( X\left( t\right) \right) <0$, for all $t>0$, then the trivial solution of system (11) is asymptotically stable.

In the following, a new lemma for the Caputo fractional derivative is presented.

Lemma 5

[148] $\forall X(t)\in \mathbf {R}^{n},$ $\forall p\in \big ] 0,1\big ]$ and $\forall t>0$

$$\begin{aligned} \frac{1}{2}D_{t}^{p}\left( X^{T}(t)X(t)\right) \le X^{T}(t)D_{t}^{p}\left( X(t)\right) . \end{aligned}$$

(14)

3 System Description and Problem Formulation

We consider the following fractional chaotic system as the master system

$$\begin{aligned} D_{t}^{p}X\left( t\right) =AX\left( t\right) +f\left( X\left( t\right) \right) , \end{aligned}$$

(15)

where $X\left( t\right) =\left( x_{1}\left( t\right) ,x_{2}\left( t\right) ,...,x_{n}\left( t\right) \right) ^{T}$ is the state vector of the master system (15),  $A=\left( a_{ij}\right) _{n\times n}$ is a constant matrix,  $f=\left( f_{i}\right) _{1\le i\le n}$ is a nonlinear function,  $D_{t}^{p}=\left[ D_{t}^{p_{1}},\right. \left. D_{t}^{p_{2}},...,D_{t}^{p_{n}}\right]$ is the Caputo fractional derivative and $p_{i},$ $i=1,2,...,n,$ are rational numbers between 0 and 1.

Also, consider the slave system as

$$\begin{aligned} D_{t}^{q}Y\left( t\right) =g\left( Y\left( t\right) \right) +U, \end{aligned}$$

(16)

where $Y(t)=\left( y_{1}\left( t\right) , y_{2}\left( t\right) ,...,y_{m}\left( t\right) \right) ^{T}$ is the state vector of the slave system (16),  $g=\left( g_{i}\right) _{1\le i\le m}$, $D_{t}^{q}$ is the Caputo fractional derivative of order q, where q is a rational number between 0 and 1 and $U=\left( u_{i}\right) _{1\le i\le m}$ is a vector controller to be designed.

Before proceeding to the definition of inverse matrix projective synchronization (IMPS) for the coupled fractional chaotic systems (15) and (16), the definition of matrix projective synchronization (MPS) is provided.

Definition 2

The n-dimensional master system X(t) and the m-dimensional slave system Y(t) are said to be matrix projective synchronization (MPS), if there exists a controller $U=\left( u_{i}\right) _{1\le i\le m}$ and a given constant matrix $\varLambda =\left( \varLambda _{ij}\right) _{m\times n}$, such that the synchronization error

$$\begin{aligned} e(t)=Y(t)-\varLambda \times X(t), \end{aligned}$$

(17)

satisfies that $\lim$ $_{t\longrightarrow +\infty }\left\| e\left( t\right) \right\| =0.$

Definition 3

The n-dimensional master system X(t) and the m-dimensional slave system Y(t) are said to be inverse matrix projective synchronization (IMPS), if there exists a controller $U=\left( u_{i}\right) _{1\le i\le m}$ and a given constant matrix $M=\left( M_{ij}\right) _{n\times m}$, such that the synchronization error

$$\begin{aligned} e(t)=X(t)-M\times Y(t), \end{aligned}$$

(18)

satisfies that $\lim$ $_{t\longrightarrow +\infty }\left\| e\left( t\right) \right\| =0.$

Remark 2

The problem of inverse matrix projective synchronization in chaotic discrete-time systems have been studied and carried out, for example, in Ref. [149].

4 Fractional IMPS Schemes

In this section, we discuss two schemes of IMPS between the master system (15) and the slave system (16): The first scheme is proposed when the master system is commensurate system and the second one is constructed when the master system is incommensurate system. In this study, we assume that $n<m$.

4.1 Case 1

In this case, we assume that $p_{1}=p_{2}=...=p_{n}=p$ and $q<p$. The error system of IMPS, in scalar form, between the master system (15) and the slave system (16) is defined by

$$\begin{aligned} e_{i}(t)=x_{i}(t)-\sum _{j=1}^{m}M_{ij}\times y_{j}(t),\qquad i=1,2,...,n. \end{aligned}$$

(19)

Suppose that the controllers $u_{i},\ i=1,2,...,m,$ can be designed in the following form

$$\begin{aligned} u_{i}=-g_{i}\left( Y\left( t\right) \right) +J^{p-q}\left( v_{i}\right) , \qquad i=1,2,...,m, \end{aligned}$$

(20)

where $v_{i},$ $1\le i\le m,$ are new controllers to be determined later.

By substituting Eq. (20) into Eq. (16), we can rewrite the slave system as

$$\begin{aligned} D_{t}^{q}y_{i}\left( t\right) =J^{p-q}\left( v_{i}\right) , \qquad i=1,2,...,m. \end{aligned}$$

(21)

Now, applying the Laplace transform to (21) and letting

$$\begin{aligned} \mathbf {L}\left( y_{i}(t)\right) =\mathbf {F}_{i}(s),\qquad i=1,2,...,m, \end{aligned}$$

(22)

we obtain,

$$\begin{aligned} s^{q}\mathbf {F}_{i}(s)-s^{q-1}y_{i}(0)=s^{q-p}\mathbf {L}\left( v_{i}\right) , \qquad i=1,2,...,m, \end{aligned}$$

(23)

multiplying both the left-hand and right-hand sides of (23) by $s^{p-q},$ and again applying the inverse Laplace transform to the result, we obtain

$$\begin{aligned} D_{t}^{p}y_{i}(t)=v_{i},\qquad i=1,2,...,m. \end{aligned}$$

(24)

Now, the Caputo fractional derivative for order p of the error system (19) can be derived as

$$\begin{aligned} D_{t}^{p}e_{i}\left( t\right)= & {} D_{t}^{p}x_{i}(t)-\sum _{j=1}^{m}M_{ij}\times D_{t}^{p}y_{j}(t) \nonumber \\= & {} \sum _{j=1}^{n}a_{ij}x_{j}\left( t\right) +f_{i}\left( X\left( t\right) \right) -\sum _{j=1}^{m}M_{ij}\times v_{j},\qquad i=1,2,...,n. \end{aligned}$$

(25)

Furthermore, the error system (25) can be written as

$$\begin{aligned} D_{t}^{p}e_{i}\left( t\right) =\sum _{j=1}^{n}\left( a_{ij}-c_{ij}\right) e_{j}+R_{i}-\sum _{j=1}^{m}M_{ij}\times v_{j},\qquad i=1,2,...,n, \end{aligned}$$

(26)

where $\left( c_{ij}\right) \in \mathbf {R}^{n\times n}$ are control constants and

$$\begin{aligned} R_{i}=\sum _{j=1}^{n}\left( c_{ij}-a_{ij}\right) e_{j}+\sum _{j=1}^{n}a_{ij}x_{j}\left( t\right) +f_{i}\left( X\left( t\right) \right) , \qquad i=1,2,...,n. \end{aligned}$$

(27)

Rewriting the error system (26) in the compact form

$$\begin{aligned} D_{t}^{p}e\left( t\right) =\left( A-C\right) e\left( t\right) +R-M\times V, \end{aligned}$$

(28)

where $e\left( t\right) =\left( e_{1}\left( t\right) , e_{2}\left( t\right) ,...,e_{n}\left( t\right) \right) ^{T}$, $C=\left( c_{ij}\right) _{n\times n}$ is a control matrix to be selected later, $R=\left( R_{1},R_{2},...,R_{n}\right) ^{T}$ and $V=\left( v_{1},v_{2},...,v_{n},v_{n+1},...,v_{m}\right) ^{T}$.

Theorem 3

If the control matrix $C\in \mathbf {R}^{n\times n}$ is chosen such that $P=A-C$ is a negative definite matrix, then the master system (15) and the slave system (16) are globally inverse matrix projective synchronized under the following control law

$$\begin{aligned} \left( v_{1},v_{2},...,v_{n}\right) ^{T}=\hat{M}^{-1}\times R, \end{aligned}$$

(29)

and

$$\begin{aligned} v_{n+1}=v_{n+2}=...=v_{m}=0, \end{aligned}$$

(30)

where $\hat{M}^{-1}$ is the inverse matrix of $\hat{M}=\left( M_{ij}\right) _{n\times n}.$

Proof

By using (30), the error system (28) can be writtes as

$$\begin{aligned} D_{t}^{p}e\left( t\right) =\left( A-C\right) e\left( t\right) +R-\hat{M} \times \left( v_{1},v_{2},...,v_{n}\right) ^{T}, \end{aligned}$$

(31)

where $\hat{M}=\left( M_{ij}\right) _{n\times n}$. Applying the control law given in Eqs. (29) to (31) yields the resulting error dynamics as follows

$$\begin{aligned} D_{t}^{p}e\left( t\right) =\left( A-C\right) e\left( t\right) . \end{aligned}$$

(32)

If a Lyapunov function candidate is chosen as

$$\begin{aligned} V\left( e\left( t\right) \right) =\frac{1}{2}e^{T}\left( t\right) e\left( t\right) , \end{aligned}$$

(33)

then the time Caputo fractional derivative of order p of V along the trajectory of the system (32) is as follows

$$\begin{aligned} D_{t}^{p}V\left( e\left( t\right) \right) =\frac{1}{2}D_{t}^{p}\left( e^{T}\left( t\right) e\left( t\right) \right) , \end{aligned}$$

(34)

and by using Lemma 5 in Eq. (34) we get

$$\begin{aligned} \begin{array}{cl} D_{t}^{p}V\left( e\left( t\right) \right) &{} \le e^{T}\left( t\right) D_{t}^{p}e\left( t\right) \\ &{} =e^{T}\left( t\right) \left( A-C\right) e\left( t\right) =e^{T}\left( t\right) Pe\left( t\right) <0. \end{array} \end{aligned}$$

Thus, from Theorem 2, it is immediate that is the zero solution of the system (32) is globally asymptotically stable and therefore, systems (15) and (16) are globally inverse matrix projective synchronized.

4.2 Case 2

Now, in this case, we assume that $p_{1}\ne p_{2}\ne \ldots \ne p_{n}$ and $q<p_{i}$ for $i=1,2,...,n.$ The vector controller $U=\left( u_{i}\right) _{1\le i\le m}$ can be designed a

$$\begin{aligned} \left[ \begin{array}{c} u_{1} \\ u_{2} \\ \vdots \\ u_{n} \\ u_{n+1} \\ \ \vdots \\ u_{m} \end{array} \right] =\left[ \begin{array}{c} -g_{1}\left( Y\left( t\right) \right) +J^{p_{1}-q}\left( v_{1}\right) \\ -g_{2}\left( Y\left( t\right) \right) +J^{p_{2}-q}\left( v_{2}\right) \\ \vdots \\ -g_{n}\left( Y\left( t\right) \right) +J^{p_{n}-q}\left( v_{n}\right) \\ -g_{n+1}\left( Y\left( t\right) \right) \\ \ \vdots \\ -g_{m}\left( Y\left( t\right) \right) \end{array} \right] , \end{aligned}$$

(35)

where $v_{i},$ $i=1,...,n,$ are new controllers. By substituting Eq. (35) into Eq. (16), we can rewrite the slave system as

$$\begin{aligned} D_{t}^{q}y_{i}\left( t\right) =J^{p_{i}-q}\left( v_{i}\right) , \qquad i=1,...,n, \end{aligned}$$

(36)

and

$$\begin{aligned} D_{t}^{q}y_{i}\left( t\right) =0,\qquad i=n+1,n+2,...,m. \end{aligned}$$

(37)

By applying the Caputo fractional derivative of order $p_{i}-q$ to both the left and right sides of Eq. (36) and by using Lemma (3), we obtain

$$\begin{aligned} D_{t}^{p_{i}}y_{i}\left( t\right)= & {} D_{t}^{p_{i}-q}\left( D_{t}^{q}y_{i}\left( t\right) \right) \nonumber \\= & {} D_{t}^{p_{i}-q}J^{p_{i}-q}\left( v_{i}\right) \nonumber \\= & {} v_{i},\qquad i=1,...,n. \end{aligned}$$

(38)

In this case, the error system between the master system (15) and the slave system (16) can be derived as

$$\begin{aligned} D_{t}^{p_{i}}e_{i}\left( t\right)= & {} D_{t}^{p_{i}}x_{i}\left( t\right) -D_{t}^{p_{i}}\left( \sum _{j=1}^{m}M_{ij}y_{j}\left( t\right) \right) \nonumber \\= & {} \sum _{j=1}^{m}a_{ij}x_{j}\left( t\right) +f_{i}\left( X\left( t\right) \right) -\sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}} ^{m}M_{ij}D_{t}^{p_{i}}y_{j}(t)-M_{ii}v_{i},\qquad i=1,2,...,n. \end{aligned}$$

(39)

Furthermore, the error system (39) can be written as

$$\begin{aligned} D_{t}^{p_{i}}e_{i}\left( t\right) =\sum _{j=1}^{n}a_{ij}e_{j}+T_{i}-M_{ii}v_{i},\qquad i=1,2,...,n, \end{aligned}$$

(40)

where

$$\begin{aligned} T_{i}=-\sum _{j=1}^{n}a_{ij}e_{j}+\sum _{j=1}^{n}a_{ij}x_{j}\left( t\right) +f_{i}\left( X\left( t\right) \right) -\sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}} ^{m}M_{ij}D_{t}^{p_{i}}y_{j}(t). \end{aligned}$$

(41)

Rewriting the error system (41) in the compact form

$$\begin{aligned} D_{t}^{p}e\left( t\right) =Ae\left( t\right) +T-\text {diag}\left( M_{11},M_{22},...,M_{nn}\right) \times V, \end{aligned}$$

(42)

where $D_{t}^{p}{=}\left[ D_{t}^{p_{1}},D_{t}^{p_{2}},...,D_{t}^{p_{n}}\right] ,$ $e\left( t\right) {=}\left[ e_{1}\left( t\right) , e_{2}\left( t\right) ,...,e_{n}\left( t\right) \right] ^{T},$ $T=\left( T_{1},T_{2},...,T_{n}\right) ^{T}$ and $V=\left( v_{1},v_{2},...,v_{n}\right) ^{T}$.

To achieve IMPS between the master system (15) and the slave system (16), we assume that $M_{ii}\ne 0,$ $i=1,2,...,n.$ Hence, we have the following result.

Theorem 4

There exists a feedback gain matrix $L\in \mathbf {R}^{n\times n}$ to realize inverse matrix projective synchronization between the master system (15) and the slave system (16) under the following control law

$$\begin{aligned} V=\text {diag}\left( \frac{1}{M_{11}},\frac{1}{M_{22}},...,\frac{1}{M_{nn}} \right) \times \left( T+Le\left( t\right) \right) . \end{aligned}$$

(43)

Proof

Applying the control law given in Eq. (43) to Eq. (42), the error system can be described as

$$\begin{aligned} D_{t}^{p}e\left( t\right) =\left( A-L\right) e\left( t\right) . \end{aligned}$$

(44)

The feedback gain matrix L is chosen such that all roots $\lambda$, of

$$\begin{aligned} \det \left( \text {diag}\left( \lambda ^{dp_{1}},\lambda ^{dp_{2}},...,\lambda ^{dp_{n}}\right) +L-A\right) =0, \end{aligned}$$

(45)

satisfy $\left| \arg \left( \lambda \right) \right| >\frac{\pi }{2d} ,$ where d is the least common multiple of the denominators of $p_{i},$ $i=1,2,...,n$. According to Lemma 4, we conclude that the zero solution of the error system (44) is globally asymptotically stable and therefore, systems (15) and (16) are IMPS synchronized.

5 Numerical Examples

In this section, two numerical examples are used to show the effectiveness of the derived results.

5.1 Example 1

In this example, we consider the commensurate fractional order Lorenz system as the master system and the controlled hyperchaotic fractional order, proposed by Zhou et al. [151], as the slave system.

The master system is defined as

$$\begin{aligned} D^{p}x_{1}= & {} \alpha \left( x_{3}-x_{1}\right) , \\ D^{p}x_{2}= & {} \gamma x_{1}-x_{2}-x_{3}x_{1}, \nonumber \\ D^{p}x_{3}= & {} -\beta x_{3}+x_{2}x_{1}, \nonumber \end{aligned}$$

(46)

where $x_{1},x_{2}$ and $x_{3}$ are states. For example, chaotic attractors are found in [150], when $(\alpha , \beta , \gamma )=(10,\frac{8}{3} ,28)$ and $p=0.993.$ Different chaotic attractors of the fractional order Lorenz system (46) are shown in Figs. 1 and 2.

Fig. 1

Phase portraits of the master system (46) in 2-D

Fig. 2

Phase portraits of the master system (46) in 3-D

Compare system (46) with system (15), one can have

$$\begin{aligned} A=\left( \begin{array}{ccc} -10 &{} 10 &{} 0 \\ 28 &{} -1 &{} 0 \\ 0 &{} 0 &{} -\frac{8}{3} \end{array} \right) , \qquad f=\left( \begin{array}{c} 0 \\ -x_{1}x_{3} \\ x_{1}x_{2} \end{array} \right) . \end{aligned}$$

The slave system is described by

$$\begin{aligned} D^{q}y_{1}= & {} 0.56y_{1}-y_{2}+u_{1}, \\ D^{q}y_{2}= & {} y_{1}-0.1y_{2}y_{3}^{2}+u_{2}, \nonumber \\ D^{q}y_{3}= & {} 4y_{2}-y_{3}-6y_{4}+u_{3}, \nonumber \\ D^{q}y_{4}= & {} 0.5y_{3}+0.8y_{4}+u_{4}, \nonumber \end{aligned}$$

(47)

where $y_{1},y_{2},y_{3},y_{4}$ are states and $u_{i},$ $i=1,2,3,4,$ are synchronization controllers. The uncontrolled fractional hyperchaotic system (47) (i.e. the system (47) with $u_{1}=u_{2}=u_{3}=u_{4}=0$) exhibits hyperchaotic behavior when $q=0.95$. Attractors in 2-D and 3-D of the uncontrolled fractional hyperchaotic system (47) are shown in Figs. 3 and 4.

Fig. 3

Phase portraits of the slave system (47) in 2-D

Fig. 4

Phase portraits of the slave system (47) in 3-D

In this example, the error system of IMPS between the master system (46) and the slave system (47) is defined as

$$\begin{aligned} e_{1}= & {} x_{1}-\sum _{j=1}^{4}M_{1j}y_{j}, \\ e_{2}= & {} x_{2}-\sum _{j=1}^{4}M_{2j}y_{j}, \nonumber \\ e_{3}= & {} x_{3}-\sum _{j=1}^{4}M_{3j}y_{j}, \nonumber \end{aligned}$$

(48)

where

$$\begin{aligned} M=\left( M_{ij}\right) _{3\times 4}=\left( \begin{array}{cccc} 2 &{} 0 &{} 0 &{} 4 \\ 0 &{} 1 &{} 0 &{} 5 \\ 0 &{} 0 &{} 3 &{} 6 \end{array} \right) . \end{aligned}$$

So,

$$\begin{aligned} \hat{M}=\left( \begin{array}{ccc} 2 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 3 \end{array} \right) \text { and }\hat{M}^{-1}=\left( \begin{array}{ccc} \frac{1}{2} &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1}{3} \end{array} \right) . \end{aligned}$$

According to Theorem 3, there exists a control matrix $C\in \mathbf {R} ^{3\times 3}$ so that systems (46) and (47) realize the IMPS. For example, the control matrix C can be chosen as

$$\begin{aligned} C=\left( \begin{array}{ccc} 0 &{} 10 &{} 0 \\ 28 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

(49)

It is easy to show that $A-C$ is a negative definite matrix. Then the control functions are designed as

$$\begin{aligned} u_{1}= & {} -0.56y_{1}+y_{2}+J^{0.043}\left( -10y_{1}-20y_{4}+5x_{3}\right) , \\ u_{2}= & {} -y_{1}+0.1y_{2}y_{3}^{2}+J^{0.043}\left( -y_{2}-4y_{4}+28x_{1}-x_{3}x_{1}\right) , \nonumber \\ u_{3}= & {} -4y_{2}+y_{3}+6y_{4}+J^{0.043}\left( -\frac{8}{3}y_{3}-\frac{16}{3} y_{4}+\frac{1}{3}x_{2}x_{1}\right) , \nonumber \\ u_{4}= & {} -0.5y_{3}-0.8y_{4}. \nonumber \end{aligned}$$

(50)

Hence, the IMPS between the master system (46) and the slave system (47) is achieved. The error system can be described as follows

$$\begin{aligned} D^{0.993}e_{1}= & {} -10e_{1}, \\ D^{0.993}e_{2}= & {} -e_{2}, \nonumber \\ D^{0.993}e_{3}= & {} -\frac{8}{3}e_{3}. \nonumber \end{aligned}$$

(51)

For the purpose of numerical simulation, fractional Euler integration method has been used. In addition, simulation time $Tm=120\,\mathrm{s}$ and time step $h=0.005s$ have been employed. The initial values of the master system and the slave system are $[x_{1}(0),x_{2}(0),x_{3}(0)]=[3,4,5]$ and $[y_{1}(0),y_{2}(0),y_{3}(0),y_{4}(0)]=[-1,1.5,-1,-2],$ respectively, and the initial states of the error system are $[e_{1}(0),e_{2}(0),e_{3}(0)]=[13,12.5,20]$. Figure 5 displays the time evolution of the errors of IMPS between the master system (46) and the slave system (47).

Fig. 5

Time evolution of synchronization errors between the master system (46) and the slave system (47)

5.2 Example 2

In this example, we assumed that the incommensurate fractional order Liu system is the master system and the incommensurate fractional order hyperchaotic Liu system [153] is the slave system. The master system is defined as

$$\begin{aligned} D^{p_{1}}x_{1}= & {} a\left( x_{2}-x_{1}\right) , \\ D^{p_{2}}x_{2}= & {} bx_{1}-x_{1}x_{3}, \nonumber \\ D^{p_{3}}x_{3}= & {} -cx_{3}+4x_{1}^{2}, \nonumber \end{aligned}$$

(52)

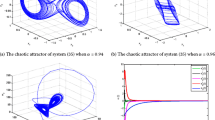
where $x_{1},x_{2}$ and $x_{3}$ are states. For example, chaotic attractors are found in [152], when $\left( p_{1},p_{2},p_{3}\right) =\left( 0.93,0.94,0.95\right)$ and $\left( a,b,c\right) =\left( 10,40,2.5\right)$. The Liu chaotic attractors are shown in Figs. 6 and 7.

Fig. 6

Phase portraits of the master system (52) in 2-D

Fig. 7

Phase portraits of the master system (52) in 3-D

Compare system (52) with system (15), one can have

$$\begin{aligned} A=\left( \begin{array}{ccc} -10 &{} 10 &{} 0 \\ 40 &{} 0 &{} 0 \\ 0 &{} 0 &{} -2.5 \end{array} \right) , \qquad f=\left( \begin{array}{c} 0 \\ -x_{1}x_{3} \\ 4x_{1}^{2} \end{array} \right) . \end{aligned}$$

The slave system is given by

$$\begin{aligned} D^{q}y_{1}= & {} 10\left( y_{2}-y_{1}\right) +y_{4}+u_{1}, \\ D^{q}y_{2}= & {} 40y_{1}+0.5y_{4}-y_{1}y_{3}+u_{2}, \nonumber \\ D^{q}y_{3}= & {} -2.5y_{3}+4y_{1}^{2}-y_{4}+u_{3}, \nonumber \\ D^{q}y_{4}= & {} -\left( \frac{10}{15}y_{2}+y_{4}\right) +u_{4}, \nonumber \end{aligned}$$

(53)

where $y_{1},y_{2},y_{3},y_{4}$ are states and $u_{i},$ $i=1,2,3,4,$ are synchronization controllers. The fractional order hyperchaotic Liu system (i.e. the system (53) with $u_{1}=u_{2}=u_{3}=u_{4}=0$) exhibits hyperchaotic behavior when $q=0.9$ [153]. Attractors in 2-D and 3-D of the fractional hyperchaotic Liu system are shown in Figs. 8 and 9.

Fig. 8

Phase portraits of the slave system (53) in 2-D

Fig. 9

Phase portraits of the slave system (53) in 3-D

In this example, the error system of IMPS between the master system (52) and the slave system (53) is defined as

$$\begin{aligned} e_{1}= & {} x_{1}-\sum _{j=1}^{4}M_{1j}y_{j}, \\ e_{2}= & {} x_{2}-\sum _{j=1}^{4}M_{2j}y_{j}, \nonumber \\ e_{3}= & {} x_{3}-\sum _{j=1}^{4}M_{3j}y_{j}, \nonumber \end{aligned}$$

(54)

where

$$\begin{aligned} M=\left( M_{ij}\right) =\left( \begin{array}{cccc} 6 &{} 3 &{} -2 &{} 4 \\ 0 &{} -5 &{} 0 &{} 5 \\ 2 &{} 1 &{} 4 &{} -1 \end{array} \right) . \end{aligned}$$

So,

$$\begin{aligned} \text {diag}\left( M_{11},M_{22},M_{33}\right) =\left( \begin{array}{ccc} 6 &{} 0 &{} 0 \\ 0 &{} -5 &{} 0 \\ 0 &{} 0 &{} 4 \end{array} \right) . \end{aligned}$$

According to Theorem 4, there exists a feedbak gain matrix $L\in \mathbf {R} ^{3\times 3}$ so that systems (52) and (53) realize the IMPS. For example, the feedbak gain matrix L can be selected as

$$\begin{aligned} L=\left( \begin{array}{ccc} 0 &{} 10 &{} 0 \\ 40 &{} 5 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$

and the control functions are constructed as follows

$$\begin{aligned} u_{1}= & {} 10\left( y_{1}-y_{2}\right) -y_{4}+J^{0.03}\frac{1}{6}\left( 10e_{1}+10\left( x_{2}-x_{1}\right) -3D_{t}^{0.93}y_{2} \right. \nonumber \\&+ \left. 2D_{t}^{0.93}y_{3}-4D_{t}^{0.093}y_{4}\right) , \qquad \\ u_{2}= & {} -40y_{1}-0.5y_{4}+y_{1}y_{3}-J^{0.04}\frac{1}{5}\left( 5e_{2}+40x_{1}-x_{1}x_{3}-5D_{t}^{0.94}y_{4}\right) , \nonumber \\ u_{3}= & {} 2.5y_{3}-4y_{1}^{2}+J^{0.05}\frac{1}{4}\left( 2.5e_{3}-2.5x_{3}+4x_{1}^{2}-2D_{t}^{0.95}y_{1}-D_{t}^{0.95}y_{2}+D_{t}^{0.95}y_{4}\right) , \nonumber \\ u_{4}= & {} \frac{10}{15}y_{2}+y_{4}. \nonumber \end{aligned}$$

(55)

The roots of $det\left( \text {diag}\left( \lambda ^{d0.93},\lambda ^{d0.94},\lambda ^{d0.95}\right) +L-A\right) =0,$ where d is the least common multiple of the denominators of the numbers 0.93,  0.94 and 0.95,  can be written as follows

$$\begin{aligned} \lambda _{1}= & {} 10^{\frac{1}{d0.93}}\left[ \cos \left( \frac{\pi }{d0.93} \right) +\mathbf {i}\sin \left( \frac{\pi }{d0.93}\right) \right] , \\ \lambda _{2}= & {} 5^{\frac{1}{d0.94}}\left[ \cos \left( \frac{\pi }{d0.94} \right) +\mathbf {i}\sin \left( \frac{\pi }{d0.94}\right) \right] , \\ \lambda _{3}= & {} 2.5^{\frac{1}{d0.95}}\left[ \cos \left( \frac{\pi }{d0.95} \right) +\mathbf {i}\sin \left( \frac{\pi }{d0.95}\right) \right] . \end{aligned}$$

Fig. 10

Time evolution of synchronization errors between the master system (52) and the slave system (53)

It is easy to see that $\arg \left( \lambda _{i}\right) >\frac{\pi }{2d},$ $i=1,2,3,$ and therefore, the IMPS between systems (52) and (53) is achieved.

The error system can be described as follows

$$\begin{aligned} D^{0.93}e_{1}= & {} -10e_{1}, \\ D^{0.94}e_{2}= & {} -5e_{2}, \nonumber \\ D^{0.95}e_{3}= & {} -2.5e_{3}. \nonumber \end{aligned}$$

(56)

For the purpose of numerical simulation, fractional Euler integration method has been used. In addition, simulation time $Tm=120\,\mathrm{s}$ and time step $h=0.005s$ have been employed. The initial values of the master system and the slave system are $[x_{1}(0), x_{2}(0), x_{3}(0)]=[0,3,9]$ and $[y_{1}(0),y_{2}(0),y_{3}(0),y_{4}(0)]=[2,-1,1,1],$ respectively, and the initial states of the error system are $[e_{1}(0),e_{2}(0),e_{3}(0)]=[-11,-7,3]$. Figure 10 displays the time evolution of the errors of IMPS between the master system (52) and the slave system (53).

6 Conclusions

In this study, two new complex schemes of the inverse matrix projective synchronization (IMPS) were proposed between a master system of dimension n and a slave system of dimension m. Namely, by exploiting the fractional Lyapunov technique and stability theory of fractional-order linear system, the IMPS is rigorously proved to be achievable including the two cases: commensurate and incommensurate master systems. Finally, the effectiveness of the method has been illustrated by synchronizing a three-dimensional commensurate fractional Lorenz system with four-dimensional commensurate hyperchaotic fractional Zhou-Wei-Cheng system, and a three-dimensional incommensurate fractional order Liu system with four-dimensional commensurate fractional order hyperchaotic Liu system

The proposed approach presents some useful features:

• (i) it enables chaotic (hyperchaotic) fractional system with different dimension to be synchronized;

• (ii) it is rigorous, being based on theorems;

• (iii) it can be applied to a wide class of chaotic (hyperchaotic) fractional systems;

• (iv) due to the complexity of the proposed scheme, the fractional IMPS may enhance security in communication and chaotic encryption schemes.