1 Introduction

Fractional calculus has been known since the early seventeenth century [1]. This concept generalizes the concepts of ordinary derivatives to some extent. It has been extensively applied in many fields which have been seen an overwhelming growth in the last three decades. A few examples are: mathematics [2], physics [3, 4], engineering [5], mathematical biology [6], and finance [7], life science [8]. Actually, fractional derivative based approaches establish far superior models of engineering systems than the ordinary derivative based approaches do in many applications. Thus, as mentioned in [1], there is no field that has remained untouched by fractional derivatives.

On the other hand, chaos and its applications have been studied and developed with much interest by scientists [9]. In recent years, studies of chaos and hyperchaos generation, control and synchronization have attracted considerable attentions due to their theoretical and practical applications in the fields of communications, laser, nonlinear circuit and neural network [10–15]. Many mathematical definitions of chaos exist but roughly, it may be described as a type of dynamic behavior with the following characteristics: extreme sensitivity to changes in initial conditions, random-like behavior, deterministic motion, trajectories of chaotic systems passing through any point infinite number of times. It is known that a regular chaotic system has one positive Lyapunov exponent. However, the system with more than one positive Lyapunov exponent is called hyperchaotic which has more complicated dynamics than a chaotic system. Consequently, hyperchaotic systems have important applications especially in secure communications. As mentioned above, in recent years, study on fractional-order dynamical systems has attracted increasing attention due to their great promise as a valuable tool in the modeling of many phenomena [16], and as a matter of fact, real world processes generally or most likely are fractional-order systems [17]. It has been found that fractional-order systems possess memory and displays much more sophisticated dynamics compared to its integral-order counterpart, which is of great significance in secure communication.

In the past two decades, a new direction of chaos research has emerged to address the more challenging problem of chaos synchronization due to its potential applications in laser physics, chemical reactors, secure communication, biomedicine and so on [18, 19]. The thrust of research within this area is aimed at achieving master–slave synchronization between two chaotic systems by choosing various kinds of methods with the pioneering work of Pecora and Carroll [20]. The master–slave synchronization has been naturally extended to the fractional-order system. For example, in [21], the authors studied the synchronization of a fractional-order unified system via one-way coupling method, while synchronization of fractional-order chaotic systems such as Chua system, Rössler system and Chen system are examined in [22]. Another recent work in synchronization of fractional chaotic systems [23] which used an active control methodology for synchronizing two Rössler systems.

A new synchronization [24] technique, known as Full State Hybrid Projective Synchronization (FSHPS), has been introduced and applied to chaotic and hyperchaotic systems [25]. In this paper we synchronize two fractional order systems in a master–slave configuration via FSHPS method. As another novelty of this work, we consider some parameter uncertainties in both master and slave systems, and under these uncertainties by using an adaptive control methodology, the asymptotical synchronization is achieved.

2 Numerical method for solving fractional differential equations

Numerical methods used for solving ordinary differential equations have to be modified for solving fractional differential equations (FDE).

A modification of Adams–Bashforth–Moulton algorithm is proposed to solve FDEs [26–28].

Consider for \( q \in (m - 1,m] \) the initial value problem:

$$ \begin{aligned}{}_{0}^{C} D_{t}^{q} x(t) = f(t,x(t));\quad 0 \le t \le T \\ & x^{k} (0) = x_{0}^{(k)} ,\quad k = 0, 1, \ldots , m - 1 \\ \end{aligned} $$
(1)

This equation is equivalent to the Volterra integral equation:

$$ x(k) = \sum\limits_{k = 0}^{m - 1} {x_{0}^{(k)} \frac{{t^{k} }}{k!}} + \frac{1}{\Upgamma (q)}\int\limits_{0}^{t} {(t - s)^{q - 1} f(s,x(s))ds} $$
(2)

Consider the uniform grid \( \left\{ {t_{n} = nh:\,n = 0, 1, \ldots, N} \right\} \) for some integer N and \( h = \frac{T}{N} \). Let \( x_{h} (t_{n} ) \) be approximation to \( x(t_{n} ) \). Assume that we have already calculated approximations \( x_{h} (t_{j} ),\quad j = 1,2, \ldots ,n \) and we want to obtain \( x_{h} (t_{n + 1} ) \) by means of the equation:

$$ x_{h} (t_{n + 1} ) = \sum\limits_{k = 0}^{m - 1} {x_{0}^{(k)} \frac{{t_{n + 1}^{k} }}{k!}} + \frac{{h^{q} }}{\Upgamma (q + 2)}f(t_{n + 1} ,x_{h}^{p} (t_{n + 1} )) + \frac{{h^{q} }}{\Upgamma (q + 2)}\sum\limits_{j = 0}^{n} {a_{j,n + 1} f(t_{j} ,x_{n} (t_{j} ))} $$
(3)

where

$$ a_{j,n + 1} = \left\{ {\begin{array}{ll} n^{q + 1} - (n - q)(n + 1)^{q} ;& j = 0 \\ (n - j + 2)^{q + 1} + (n - j)^{q + 1} - 2(n - j + 1)^{q + 1} ; & 1 \le j \le n \\ 1; & j = n + 1 \\ \end{array} } \right. $$
(4)

The preliminary approximation \( x_{h}^{p} (t_{n + 1} ) \) is called predictor and is given by:

$$ x_{h}^{p} (t_{n + 1} ) = \sum\limits_{k = 0}^{m - 1} {x_{0}^{(k)} \frac{{t_{n + 1}^{k} }}{k!}} + \frac{1}{\Upgamma (q)}\sum\limits_{j = 0}^{n} {b_{j,n + 1} f(t_{j} ,x_{n} (t_{j} ))} $$
(5)

where

$$ b_{j,n + 1} = \frac{{h^{q} }}{q}\left( {(n - j + 1)^{q} - (n - j)^{q} } \right) $$
(6)

The error in this method is:

$$ \mathop {\hbox{Max} }\limits_{j = 0,1, \ldots ,N} \left| {x(t_{j} ) - x_{n} (t_{j} )} \right| = O(h^{p} ) $$
(7)

where \( p = \hbox{Min} \,(2,1 + q) \).

The algorithm that is considered above can be interpreted as a fractional variant of the classical second-order Adams–Bashforth–Moulton method. It has been introduced and briefly discussed in [29]. More information is given in [30]. Some additional results for a specific initial value problem are contained in [31], a detailed mathematical analysis is provided in [32], and additional practical remarks can be found in [26]. Numerical experiments and comparisons with other methods are reported in [33].

3 System description

Usually a dynamical system with fractional order could be described by:

$$ \left\{ {\begin{array}{ll} {}_{0}^{C} D_{t}^{q} x(t) = f(x(t),t), & m - 1 < q < m \in {\mathbf{Z}}^{ + } ,\quad t > 0 \\ x^{(k)} (t)\left| {_{t = 0} } \right. = x_{0}^{k} ,& k = 1,2, \ldots ,m. \end{array} } \right. $$
(8)

where \( x \in {\mathbf{R}}^{n} ,\,f:{\mathbf{R}}^{n} \times {\mathbf{R}} \to {\mathbf{R}}^{n} ,\,q = \left( {\begin{array}{*{20}c} {q_{1} } & {q_{2} } & \ldots & {q_{n} } \\ \end{array} } \right)^{T} \) are vector state, nonlinear vector field, and differentiation order vector. If \( q_{1} = q_{2} = \cdots = q_{n} \) we call Eq. (8) commensurate fractional order dynamical system; otherwise we call it incommensurate one. Moreover, sum of the orders of all involved derivatives in Eq. (8), i.e. \( \sum\nolimits_{i = 1}^{n} {q_{i} } \) is called the effective dimension of Eq. (8) [34]. The size of vector x in state space form Eq. (8), i.e. n, is called the inner dimension of system given by Eq. (8) [35].

Theorem 1 [36].

Consider the following linear fractional order system:

$$ {}_{0}^{C} D_{t}^{q} x(t) = Ax(t),\,\;x(0) = x_{0} $$
(9)

with \( x \in {\mathbf{R}}^{n} ,\,A \in {\mathbf{R}}^{n \times n} ,\,q = \left( {\begin{array}{*{20}c} {q_{1} } & {q_{2} } & \ldots & {q_{n} } \\ \end{array} } \right)^{T} ,\,0 < q_{i} \le 1 \) and \( q_{i} = \frac{{n_{i} }}{{d_{i} }},\,\,\gcd (n_{i} ,d_{i} ) = 1 \). Let M be the lowest common multiple of the denominators \( d_{i} \)’s. The zero solution of system in Eq. (9) is globally asymptotically stable in the Lyapunov sense if all roots \( \lambda \)’s of the equation:

$$ \Updelta (\lambda ) = \det \,\left( {diag\,(\lambda^{{Mq_{i} }} ) - A} \right) = 0, $$
(10)

satisfy: \( \left| {\arg (\lambda_{i} )} \right| > \frac{\pi }{2M}. \)

Recently a novel hyperchaotic system is described by the following equations [37]:

$$ \begin{aligned} & \dot{x} = ax - yz \\ & \dot{y} = xz - by \\ & \dot{z} = cxy - dz + gxw \\ & \dot{w} = kw - hy \\ \end{aligned} $$
(11)

Here \( x,y,z,w \in {\mathbf{R}} \) are the pseudo-state variables, and \( a,b,c,d,g,h \) and \( k \) are positive constant parameters of the system. For \( a = 8,\,b = 43.75,\,c = 2,\,d = 10,\,g = 5,\,h = 0.2,\,k = 0.05 \) one can find five equilibria for this system as follows:

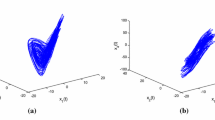
$$ \begin{aligned} & Q_{1} :\left( {0,0,0,0} \right) \\ & Q_{2} :\left( { - 4.4594,\, + 1.9069,\, - 18.7083,\, + 7.6277} \right) \\ & Q_{3} :\left( { + 4.4594,\, + 1.9069,\, + 18.7083,\, + 7.6277} \right) \\ & Q_{4} :\left( { + 4.4594,\, - 1.9069,\, - 18.7083, - \,7.6277} \right) \\ & Q_{5} :\left( { - 4.4594,\, - 1.9069,\, + 18.7083,\, - 7.6277} \right) \\ \end{aligned} $$
(12)

For each equilibrium point, one can compute the Jacobian matrix and then find the eigenvalues. As derived in [37] all of the above equilibria are unstable. Numerical simulations of this system are depicted in Figs. 1 and 2. It is mentioned that the system given by Eq. (11) can produce both chaotic and quasiperiodic behaviors.

Fig. 1
figure 1

Numerical simulations of trajectories of system of Eq. (13) with hyperchaotic natures

Full size image
Fig. 2
figure 2

Phase portrait of system of Eq. (13) with hyperchaotic natures

Full size image

Now consider the following fractional order dynamical system:

$$ \begin{aligned} & {}_{0}^{C} D_{t}^{{q_{1} }} x = ax - yz \\& {}_{0}^{C} D_{t}^{{q_{2} }} y = xz - by \\ &{}_{0}^{C} D_{t}^{{q_{31} }} z = cxy - dz + gxw \\ & {}_{0}^{C} D_{t}^{{q_{4} }} w = kw - hy \\ \end{aligned} $$
(13)

Note that the equilibria for this new fractional order hyperchaotic system are the same as for the integer order counterpart; i.e. Eq. (11). First let constitute the Jacobian matrix for Eq. (13) computed in equilibrium as follows:

$$ J_{Q} = \left( {\begin{array}{*{20}c} a & { - z^{*} } & { - y^{*} } & 0 \\ {z^{*} } & { - b} & {x^{*} } & 0 \\ {cy^{*} + gw^{*} } & {cx^{*} } & { - d} & {gx^{*} } \\ 0 & { - h} & 0 & k \\ \end{array} } \right) $$
(14)

For instance let focus on \( Q_{2} \). Since a natural symmetry exists in the structure of the system [37], a similar approach for other equilibria can be used. Evaluating Jacobian matrix in \( Q_{2} \), one can write:

$$ J_{Q} = \left( {\begin{array}{*{20}c} 8 & {18.7083} & { - 1.9069} & 0 \\ { - 18.7083} & { - 43.75} & { - 4.4594} & 0 \\ {41.9524} & { - 8.9188} & { - 10} & { - 22.2971} \\ 0 & { - 0.2} & 0 & {0.05} \\ \end{array} } \right) $$
(15)

The corresponding eigenvalues of \( Q_{2} \) can be easily obtained as follows:

$$\Lambda _{2} = (\lambda _{1} \,\lambda _{2} \,\lambda _{3} \,) = (\begin{array}{cccc} -40.6033 & 0.0912 & - 2.5940 + i13.4997 & -2.5940-i13.4997\end{array})$$
(16)

The equilibrium point \( Q_{2} \) is a saddle-focus point and therefore this equilibrium point is unstable. Because one of the associated eigenvalues of the aforementioned equilibria of Eq. (13) is real positive, the necessary condition derived in [38] has no meaningful result for the case. So it may exhibit chaos or hyperchaos for any order of fractional differentiation.

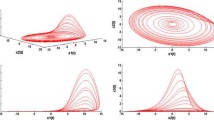
Now let consider the commensurate case; i.e. \( 0 < q{}_{1} = q_{2} = q_{3} = q_{4} < 1 \). If we take \( q_{i} = 0.98,\,i = 1, 2, 3,4, \) the hyperchaoticity behavior in the fractional order system can be observed as depicted in Figs. 3 and 4. Moreover, it may be that beside hyperchaotic phenomenon one can observe chaotic behavior. This can be seen in Fig. 5. It is mentioned that for identifying the chaoticity or hyperchaoticity for a fractional order nonlinear dynamical system one can utilize Lyapunov exponent criterion [39]. Using this technique the Lyapunov exponents are computed as \( ( + ,+ ,0 ,- ) \) for hyperchaotic behavior, and \( ( + ,0 ,- ,- ) \) for chaotic behavior. It is also mentioned that all following simulations are performed using the method discussed in the Sect. 2.

Fig. 3
figure 3

Numerical simulations of trajectories of system of Eq. (13) with order q = 0.98; hyperchaotic nature is cleared

Full size image
Fig. 4
figure 4

Phase portrait of system of Eq. (13) with order q = 0.98; hyperchaotic natures are cleared

Full size image
Fig. 5
figure 5

Phase portrait of system of Eq. (13) with order q = 0.85; chaotic natures are cleared

Full size image

4 Full state hybrid projective synchronization

Consider the master–slave (or drive-response) configuration of two autonomous different fractional order chaotic systems:

$$ \begin{array}{ll} Master{:}& {}_{a}^{C} D_{t}^{q} x_{m} (t) = f(x_{m} ) \\ Slave{:} & {}_{a}^{C} D_{t}^{q} y_{s} (t) = g(y_{s} ,x_{s} ) + u \end{array} $$
(17)

where q is the fractional order, \( x_{m} ,y_{s} \in {\mathbf{R}}^{n} \) represent the pseudo-states of the master and slave systems, respectively, \( f:{\mathbf{R}}^{n} \to {\mathbf{R}}^{n} ,\,g:{\mathbf{R}}^{n} \to {\mathbf{R}}^{n} \) are the vector fields of the master and slave systems, respectively. The aim of the FSHPS problem is to choose a suitable linear control function \( u = \left( {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{n} } \\ \end{array} } \right)^{T} \in {\mathbf{R}}^{n} \) such that the pseudo-states of the master and slave systems are synchronized, i.e. \( \mathop {\lim }\limits_{t \to \infty } \left\| {y_{s} (t) - \alpha x_{m} (t)} \right\| = 0 \), where \( \alpha = diag(\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} ) \) is a scaling matrix.

Consider a master–slave FSHPS scheme in which the master system is described as:

$$ \left\{ \begin{array}{l} {}_{0}^{C} D_{t}^{{q_{1} }} x_{m} = ax_{m} - y_{m} z_{m} \\ {}_{0}^{C} D_{t}^{{q_{2} }} y_{m} = x_{m} z_{m} - by_{m} \\ {}_{0}^{C} D_{t}^{{q_{3} }} z_{m} = cx_{m} y_{m} - dz_{m} + gx_{m} w_{m} \\ {}_{0}^{C} D_{t}^{{q_{4} }} w_{m} = kw_{m} - hy_{m} \\ \end{array} \right. $$
(18)

in which the subscript m is used for master variables. Slave system is described as follows:

$$\left\{ \begin{array}{l} {}_{0}^{C} D_{t}^{{q_{1} }} x_{m} = ax_{m} - y_{m} z_{m} \\ {}_{0}^{C} D_{t}^{{q_{2} }} y_{m} = x_{m} z_{m} - by_{m} \\ {}_{0}^{C} D_{t}^{{q_{3} }} z_{m} = cx_{m} y_{m} - dz_{m} + gx_{m} w_{m} \\ {}_{0}^{C} D_{t}^{{q_{4} }} w_{m} = kw_{m} - hy_{m} \\ \end{array} \right. $$
(19)

Note that in this configuration the constant parameters \( \left( {a,\,b,\,c,\,d,\,g,k,\,h} \right) \) are unknown and considered as the parameter uncertainties. Moreover, \( u = \left( {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } & {u_{4} } \\ \end{array} } \right)^{T} \in {\mathbf{R}}^{4} \) is the control vector which should be designed such that the two fractional order hyperchaotic systems can achieve FHSPS based on an adaptive mechanism.

As the first step in designing the control law, consider the control vector as:

$$ \begin{aligned} u_{1} = {}_{0}^{C} D_{t}^{{q^{\prime}_{1} }} x_{s} (t) - {}_{0}^{C} D_{t}^{{q_{1} }} x_{s} (t) + v_{1} \\ u_{2} = {}_{0}^{C} D_{t}^{{q^{\prime}_{2} }} y_{s} (t) - {}_{0}^{C} D_{t}^{{q_{2} }} y_{s} (t) + v_{2} \\ u_{3} = {}_{0}^{C} D_{t}^{{q^{\prime}_{3} }} z_{s} (t) - {}_{0}^{C} D_{t}^{{q_{3} }} z_{s} (t) + v_{3} \\ u_{4} = {}_{0}^{C} D_{t}^{{q^{\prime}_{4} }} w_{s} (t) - {}_{0}^{C} D_{t}^{{q_{4} }} w_{s} (t) + v_{4} \\ \end{aligned} $$
(20)

Thus inserting Eq. (20) in Eq. (19) yields slave system:

$$ \left\{ \begin{array}{l} {}_{0}^{C} D_{t}^{{q_{1} }} x_{s} = ax_{s} - y_{s} z_{s} + v_{1} \\ {}_{0}^{C} D_{t}^{{q_{2} }} y_{s} = x_{s} z_{s} - by_{s} + v_{2} \\ {}_{0}^{C} D_{t}^{{q_{3} }} z_{s} = cx_{s} y_{s} - dz_{s} + gx_{s} w_{s} + v_{3} \\ {}_{0}^{C} D_{t}^{{q_{4} }} w_{s} = kw_{s} - hy_{s} + v_{4} \\ \end{array} \right. $$
(21)

Now define the scaling errors as follows:

$$ \begin{aligned} & e_{1} = x_{s} - \alpha_{1} x_{m} \\ & e_{2} = y_{s} - \alpha_{2} y_{m} \\ & e_{3} = z_{s} - \alpha_{3} z_{m} \\ & e_{4} = w_{s} - \alpha_{4} w_{m} \\ \end{aligned} $$
(22)

Subtracting the dynamics of master system (Eq. (18)) from those of slave system (Eq. (21)), yields the following error dynamical system:

$$ \begin{aligned} & {}_{0}^{C} D_{t}^{{q_{1} }} e_{1} (t) = ae_{1} - (y_{s} z_{s} - \alpha_{1} y_{m} z_{m} ) + v_{1} \\ & {}_{0}^{C} D_{t}^{{q_{2} }} e_{2} (t) = - be_{2} + (x_{s} z_{s} - \alpha_{2} x_{m} z_{m} ) + v_{2} \\& {}_{0}^{C} D_{t}^{{q_{3} }} e_{3} (t) = - de_{3} + c(x_{s} y_{s} - \alpha_{3} x_{m} y_{m} ) + g(x_{s} w_{s} - \alpha_{3} x_{m} w_{m} ) + v_{3} \\ & {}_{0}^{C} D_{t}^{{q_{4} }} e_{4} (t) = ke_{4} - h(y_{s} - \alpha_{4} y_{m} ) + v_{4} \\ \end{aligned} $$
(23)

It is well-known that if the integer order counterpart of a fractional order dynamical system is stable, then the original fractional order system would be stable. Thus if the parameters of the master–slave systems are unknown, the control laws are proposed as follows:

$$ \begin{aligned}& v_{1} = (y_{s} z_{s} - \alpha_{1} y_{m} z_{m} ) - e_{1} (\hat{a} + 1) \\& v_{2} = - (x_{s} z_{s} - \alpha_{2} x_{m} z_{m} ) + (\hat{b} - 1)e_{2} \\ &v_{3} = (\hat{d} - 1)e_{3} - \hat{c}(x_{s} y_{s} - \alpha_{3} x_{m} y_{m} ) - \hat{g}(x_{s} w_{s} - \alpha_{3} x_{m} w_{m} ) \\& v_{4} = - (\hat{k} + 1)e_{4} + \hat{h}(y_{s} - \alpha_{4} y_{m} ) \\ \end{aligned} $$
(24)

and the parameter estimation update law is chosen as:

$$ \begin{aligned} & \dot{\hat{a}} = e_{1}^{2} ,\,\,\dot{\hat{b}} = - e_{2}^{2} , \\ & \dot{\hat{c}} = e_{3} (x_{s} y_{s} - \alpha_{3} x_{m} y_{m} ),\,\,\dot{\hat{d}} = - e_{2}^{3} ,\,\,\dot{\hat{g}} = e_{3} (x_{s} w_{s} - \alpha_{3} x_{m} w_{m} ), \\ & \dot{\hat{h}} = - e_{4} (y_{s} - \alpha_{4} y_{m} ),\,\,\dot{\hat{k}} = e_{4}^{2} \\ \end{aligned} $$
(25)

Theorem 2

For any given nonzero scaling matrix \( \alpha \), master system Eq. (18) and response system Eq. (19) can achieve FSHPS by the control law Eq. (24) and the update law Eq. (25) of parameters.

Proof

Consider the following Lyapunov function:

$$ V = \frac{1}{2}(e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + e_{4}^{2} + \tilde{a}^{2} + \tilde{b}^{2} + \tilde{c}^{2} + \tilde{d}^{2} + \tilde{g}^{2} + \tilde{h}^{2} + \tilde{k}^{2} ) $$
(26)

in which \( \tilde{a} = \hat{a} - a,\,\tilde{b} = \hat{b} - b,\,\tilde{c} = \hat{c} - c,\,\tilde{d} = \hat{d} - d,\,\tilde{g} = \hat{g} - g,\,\tilde{h} = \hat{h} - h,\,\tilde{k} = \hat{k} - k \). The time derivative of the Lyapunov function along the trajectory of Eq. (23) is:

$$ \begin{aligned} \dot{V} = & e_{1} \dot{e}_{1} + e_{2} \dot{e}_{2} + e_{3} \dot{e}_{3} + e_{4} \dot{e}_{4} + \tilde{a}\dot{\tilde{a}} + \tilde{b}\dot{\tilde{b}} + \tilde{c}\dot{\tilde{c}} + \tilde{d}\dot{\tilde{d}} + \tilde{g}\dot{\tilde{g}} + \tilde{h}\dot{\tilde{h}} + \tilde{k}\dot{\tilde{k}} \\ = & e_{1} (ae_{1} - (y_{s} z_{s} - \alpha_{1} y_{m} z_{m} ) + v_{1} ) + e_{2} ( - be_{2} + (x_{s} z_{s} - \alpha_{2} x_{m} z_{m} ) + v_{2} ) \\ & & + e_{3} ( - de_{3} + c(x_{s} y_{s} - \alpha_{3} x_{m} y_{m} ) + g(x_{s} w_{s} - \alpha_{3} x_{m} w_{m} ) + v_{3} ) \\ & + e_{4} (ke_{4} - h(y_{s} - \alpha_{4} y_{m} ) + v_{4} ) \\ & + \tilde{a}\dot{\hat{a}} + \tilde{b}\dot{\hat{b}} + \tilde{c}\dot{\hat{c}} + \tilde{d}\dot{\hat{d}} + \tilde{g}\dot{\hat{g}} + \tilde{h}\dot{\hat{h}} + \tilde{k}\dot{\hat{k}} \\ = & - e_{1}^{2} - e_{2}^{2} - e_{3}^{2} - e_{4}^{2} < 0. \\ \end{aligned} $$
(27)

Therefore based on the Lyapunov stability theory, the error dynamical system given by Eq. (23) with integer order is asymptotically stable at the origin with the proposed controller Eq. (24) and the parameter update law Eq. (25). Therefore, the fractional order error dynamical system is stable and the pseudo-states of the master system Eq. (18) and the pseudo-states of the response system Eq. (19) are ultimately hybrid projective synchronized.

Some recent works in projective synchronization which is a type of chaos-synchronization have been studied in the literature [40].

5 Simulation results

To verify the effectiveness of the proposed synchronization method in the previous section, we simulate the configuration with the numerical values. In the following simulations we consider the fractional orders of the master and slave:

$$ \begin{gathered} \left( {\begin{array}{*{20}c} {q_{1} } & {q_{2} } & {q_{3} } & {q_{4} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.98} & {0.99} & {0.99} & {0.98} \\ \end{array} } \right) \hfill \\ \left( {\begin{array}{*{20}c} {q^{\prime}_{1} } & {q^{\prime}_{2} } & {q^{\prime}_{3} } & {q^{\prime}_{4} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.90} & {0.93} & {0.94} & {0.97} \\ \end{array} } \right) \hfill \\ \end{gathered} $$
(28)

with the following scaling factors:

$$ \left( {\begin{array}{*{20}c} {\alpha_{1} } & {\alpha_{2} } & {\alpha_{3} } & {\alpha_{4} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 2 & 3 & 3 & 5 \\ \end{array} } \right) $$
(29)

The actual parameters of the systems are \( a = 8,b = 43.75,c = 2,d = 10,g = 5,h = 0.2,k = 0.05 \). For instance in Fig. 6 we present the time series of the variables \( w(t) \) and \( w_{s} (t) \). For the scaling factor \( \alpha_{4} = 5 \), the error time series is depicted in Fig. 7. Also in these simulations we have considered noise in the synchronization configuration.

Fig. 6
figure 6

Time series of the variables w and w s

Full size image
Fig. 7
figure 7

Error time series of the variable \( w_{s} (t) - 5w(t) \)

Full size image

6 Conclusions

This work discusses full state hybrid projective synchronization for two hyperchaotic systems with different incommensurate fractional orders. The fractional order hyperchaotic systems have attracted scientists and engineers from various fields. One of the main applications of such systems is secure communication system. Synchronization between receivers and transmitters in such communication systems is the most important work. We have presented an adaptive mechanism for full state hybrid projective synchronization (FSHPS) of two systems in which their parameters are assumed to be unknown. Under this uncertainty and some noise signals we present a complete FSHPS methodology. Some simulations support our analytic results.