Multibody System Modeling, Simulation, and 3D Visualization

Abstract

With the increase of power and wide availability of the computers the modeling and simulations become very capable approaches in solving complex engineering problems. Using modern modeling and simulation tools the needs for expensive experimental investigations of the real systems are significantly reduced. In this chapter we consider 3D multibody systems (MBS).

The basic topic presented in this chapter is modeling and analysis of MBS systems from two different points of view—dynamic and geometric (visual). Bond graph approach for modeling of dynamics of MBS is presented first. It is based on acausal bond graphs leading to implicit differential-algebraic equations (DAEs) models. This approach enables developing of complex velocity based Euler–Lagrange models of MBS in BondSim© environment and simulating their motions.

The MBS can also be seen as the geometric objects of interconnected bodies in virtual 3D space. Using advanced techniques of Visualization Toolkit (VTK) it is shown how such models can be constructed using MS Visual C++ techniques. It is implemented in a specially designed application BondSimVisual© developed by the first author.

The geometrical objects representing complex 3D scene are basically static. However, they can be driven by the bond graph models. Because these are two different modeling worlds and two different applications, in order to enable interconnection of these two worlds an inter-process communication technique is developed. It is based on named pipe technology.

To illustrate developed methods a rather complex robotic example was analyzed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

There is an extremely large body of literature dealing with the modeling and simulation of MBS . They mostly deal with kinematics and dynamics of 3D mechanical objects and systems. To enhance understanding of real behavior of such systems more attention was directed to the visualization of their motion in the virtual 3D scenes. These are often two separate approaches. Many well-known modeling and simulation software systems, which are quite capable of solving the dynamical side of the problem, support also the visualization. On other side 3D visualization tools often support also MBS kinematics. In this chapter the modeling and analysis of MBS systems from two different points of view are analyzed—dynamic and geometric (visual).

We start with dynamical modeling of MBS based on acausal component models based technique described in more detail in the recent book [3]. It is shown how a model of a complex MBS can be systematically developed. It leads essentially to implicit Euler–Lagrange models. It is well known that such models are higher index DAE s models. However, using bond graphs the corresponding models are velocity based and thus of a lower index and could be readily solved using available technique [3]. Such models can be systematically developed using BondSim© modeling and simulation environment.

The next topic is geometrical modeling of complex MBS such as robots, or other mechanisms, moving in 3D space. The approach used is based on visualization pipeline techniques implemented in VTK C++ library of Will Schroeder et al. [12]. The models can be constructed by assembling simple primitive objects such as cubes, cylinders, and spheres, or the CAD system created geometric objects. The visualization model of the system can be described by a simple script. This script is read by a special designed BondSimVisual© application. It constructs in the computer memory the corresponding visualization pipeline objects representing the system in the question. These basically show the corresponding mechanisms as the static objects in a 3D virtual scene.

In order to interconnect these two models—dynamical bond graph models and geometrical objects in 3D virtual scene an inter-process communication technique is developed. The technique used is based on named pipe technology . It enables that the dynamical model during the simulation drive the corresponding visual model in 3D virtual scene, thus gives to a user 3D view on the problem. In this way the dynamical and visual model behaves as a complex multi-physics model of the problem (see, e.g., Damic and Cohodar [2]).

2 Motion of Constrained Rigid Bodies in Space

2.1 Basic Kinematics

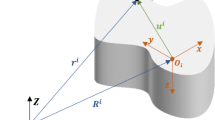
To describe motion of a body in space we use two fundamental coordinate frames (Fig. 17.1)—a base frame Oxyz and a body frame Cx′y′z. There can be a number of bodies and, hence, a number of body frames that are used for their description. On the other hand, there is a single base (inertial) frame. In robotics it is often convenient to introduce other frames, as well [13]. It is assumed that all frames are 3D Cartesian coordinate frames.

Fig. 17.1

The base and body frame

We assume that the position of a body frame with respect to the base is defined by a position vector r _C of the origin C of the body frame. The point C is the reference point for describing the body position—a body center (pole). It is usually the body mass center, but could also be some other point. The body orientation is defined by a rotation matrix R composed of the direction cosines of the body axes with respect to the base axes. The position of any point P fixed in the body with respect to the base is given by

$$ {\mathbf{r}}_P={\mathbf{r}}_C+\mathbf{R}{\mathbf{r}}_{CP}^{\mathbf{\prime}} $$

(17.1)

where r _CP ′ is the vector of its material coordinates, i.e., the coordinates with respect to the body frame.

This relation describes the position of rigid body in 3D space. If we assume that initially the both coordinate frames are coincident, then (17.1) show that a body can be moved into an arbitrary position in the space by rotation of the body frame about the common origin defined by rotation matrix R and translation of the body frame with respect to the base for vector r _C . Because the addition in (17.1) is a commutative operation it is also possible to exchange the rotation and translation transformations, i.e., first apply the translations and then the rotation about the translated frame (Fig. 17.1).

The relationship (17.1) can be described also in terms of the homogenous transformation. Thus, we introduce the homogenous four-dimensional vector corresponding to the common 3D vector $\mathbf{r}={\left(\begin{array}{ccc}\hfill x\hfill & \hfill y\hfill & \hfill z\hfill \end{array}\right)}^T$ by a

$$ \tilde{\mathbf{r}}=\left(\frac{\mathbf{r}}{1}\right) $$

(17.2)

The fourth component is a scale factor assumed here to be 1. We may introduce a matrix of homogenous transform defined by

$$ \mathbf{T}=\left(\begin{array}{l|l} \mathbf{R} & {\mathbf{r}}_C \\ \hline {} {\mathbf{0}}^T & 1 \end{array}\right) $$

(17.3)

Now (17.1) can be written compactly as

$$ {\tilde{\mathbf{r}}}_P=\mathbf{T}{\tilde{\mathbf{r}}}_{CP} $$

(17.4)

The homogenous transformations of position vectors are often used when dealing with geometric representation of body motion in 3D space (visualization). In dynamics we are more interested in the velocities.

During the motion, the positions of the body center r _C and its orientation—represented by matrix R—change with time. The material coordinates of a point fixed in the body do not change. The velocity of a point P, as seen from the base frame, can be found by differentiating (17.1) with respect to time, i.e.,

$$ {\mathbf{v}}_P={\mathbf{v}}_C+\frac{d\mathbf{R}}{dt}{\mathbf{r}}_{CP}^{\mathbf{\prime}} $$

(17.5)

The relative position of a point P with respect to the base frame can be found by multiplying its body frame coordinates by the rotation matrix R,

$$ {\mathbf{r}}_{CP}=\mathbf{R}{\mathbf{r}}_{CP}^{\mathbf{\prime}} $$

(17.6)

Note that the rotation matrix is an orthogonal matrix, i.e., ${\mathbf{R}}^T\mathbf{R}=\mathbf{R}{\mathbf{R}}^T=\mathbf{I}$, where subscript T denotes the transposition operator and I is the identity matrix. Substituting (17.6) into (17.5) yields

$$ {\mathbf{v}}_P={\mathbf{v}}_C+\frac{d\mathbf{R}}{dt}{\mathbf{R}}^T{\mathbf{r}}_{CP} $$

(17.7)

In analogy with vector product notation we may introduce the symbol (Borri et al. [1])

$$ \boldsymbol{\upomega} \times =\frac{d\mathbf{R}}{dt}{\mathbf{R}}^T $$

(17.8)

Thus, (17.7) can be written as

$$ {\mathbf{v}}_P={\mathbf{v}}_C+\boldsymbol{\upomega} \times {\mathbf{r}}_{CP} $$

(17.9)

This reminds us of common vector product operation between the vectors. The ω is really a vector, as can be easily shown.

The matrix in (17.8) is a skew-symmetric matrix (tensor). It has only three independent elements, and thus can be written in a familiar form

$$ \frac{d\mathbf{R}}{dt}{\mathbf{R}}^T=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -{\omega}_z\hfill & \hfill {\omega}_y\hfill \\ {}\hfill {\omega}_z\hfill & \hfill 0\hfill & \hfill -{\omega}_x\hfill \\ {}\hfill -{\omega}_y\hfill & \hfill {\omega}_x\hfill & \hfill 0\hfill \end{array}\right) $$

(17.10)

We may introduce now a vector composed of this components. This is the so-called axial vector corresponding to a skew-symmetric matrix

$$ \boldsymbol{\upomega} =\left(\begin{array}{c}\hfill {\omega}_x\hfill \\ {}\hfill {\omega}_y\hfill \\ {}\hfill {\omega}_z\hfill \end{array}\right)=\mathit{axial}\left(\frac{d\mathbf{R}}{dt}{\mathbf{R}}^T\right) $$

(17.11)

In the case of rotation matrix R, the axial vector ω is familiar the body angular velocity.

It could also be shown that the following well-known formula holds:

$$\small \boldsymbol{\upomega} \times \mathbf{r}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -{\omega}_z\hfill & \hfill {\omega}_y\hfill \\ {}\hfill {\omega}_z\hfill & \hfill 0\hfill & \hfill -{\omega}_x\hfill \\ {}\hfill -{\omega}_y\hfill & \hfill {\omega}_x\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill x\hfill \\ {}\hfill y\hfill \\ {}\hfill z\hfill \end{array}\right)=\left(\begin{array}{c}\hfill -y{\omega}_z+z{\omega}_y\hfill \\ {}\hfill x{\omega}_z-z{\omega}_x\hfill \\ {}\hfill -x{\omega}_y+y{\omega}_x\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill z\hfill & \hfill -y\hfill \\ {}\hfill -z\hfill & \hfill 0\hfill & \hfill x\hfill \\ {}\hfill y\hfill & \hfill -x\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\omega}_x\hfill \\ {}\hfill {\omega}_y\hfill \\ {}\hfill {\omega}_z\hfill \end{array}\right)=-\mathbf{r}\times \boldsymbol{\upomega} $$

The relations similar to (17.8) and (17.9) hold in the body frame as well. The components of the global velocity v _P expressed in the body frame are given by

$$ {\mathbf{v}}_P^{\mathbf{\prime}}={\mathbf{R}}^T{\mathbf{v}}_P $$

(17.12)

Multiplying (17.7) by R ^T yields

$$ {\mathbf{v}}_P^{\mathbf{\prime}}={\mathbf{v}}_C^{\mathbf{\prime}}+{\mathbf{R}}^T\frac{d\mathbf{R}}{dt}{\mathbf{r}}_{CP}^{\mathbf{\prime}} $$

(17.13)

Now we have

$$ {\mathbf{R}}^T\frac{d\mathbf{R}}{dt}={\boldsymbol{\upomega}}^{\mathbf{\prime}}\times $$

(17.14)

where ω′ is the vector of the rectangular components of body angular velocity in the body frame. Thus, (17.13) can be written as

$$ {\mathbf{v}}_P^{\mathbf{\prime}}={\mathbf{v}}_C^{\mathbf{\prime}}+{\boldsymbol{\upomega}}^{\mathbf{\prime}}\times {\mathbf{r}}_{CP}^{\mathbf{\prime}} $$

(17.15)

To represent these relationships compactly we introduce a generalized vector of 6D component composed of the linear velocity vector of the body center and the body angular velocity. In the base frame the generalized velocity is given by

$$ {\mathbf{f}}_C=\left(\begin{array}{c}\hfill {\mathbf{v}}_C\hfill \\ {}\hfill \boldsymbol{\upomega} \hfill \end{array}\right) $$

(17.16)

and similarly in the body frame as

$$ {\mathbf{f}}_C^{\mathbf{\prime}}=\left(\begin{array}{c}\hfill {\mathbf{v}}_C^{\mathbf{\prime}}\hfill \\ {}\hfill {\boldsymbol{\upomega}}^{\mathbf{\prime}}\hfill \end{array}\right) $$

(17.17)

These quantities are denoted by f because, as will be shown later, these are simply the flows of the bond graph component ports.

In a similar way, a generalized velocity of any other point P fixed in the body can be represented in the base frame by

$$ {\mathbf{f}}_P=\left(\begin{array}{c}\hfill {\mathbf{v}}_P\hfill \\ {}\hfill \boldsymbol{\upomega} \hfill \end{array}\right) $$

(17.18)

and in the body frame as

$$ {\mathbf{f}}_P^{\mathbf{\prime}}=\left(\begin{array}{c}\hfill {\mathbf{v}}_P^{\mathbf{\prime}}\hfill \\ {}\hfill {\boldsymbol{\upomega}}^{\mathbf{\prime}}\hfill \end{array}\right) $$

(17.19)

Note that the following holds:

$$ \mathbf{R}\left({\boldsymbol{\upomega}}^{\mathbf{\prime}}\times {\mathbf{r}}_{CP}^{\mathbf{\prime}}\right)=\boldsymbol{\upomega} \times {\mathbf{r}}_{CP}=-{\mathbf{r}}_{CP}\times \boldsymbol{\upomega} =\left(-{\mathbf{r}}_{CP}\times \mathbf{R}\right){\boldsymbol{\upomega}}^{\mathbf{\prime}} $$

Using (17.15) the corresponding transformation of flows between the body and base frames can be written compactly as

$$ {\mathbf{f}}_P=\left(\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill -{\mathbf{r}}_{CP}\times \mathbf{R}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{R}\hfill \end{array}\right){\mathbf{f}}_C^{\mathbf{\prime}} $$

(17.20)

The matrix

$$ \mathbf{C}=\left(\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill -{\mathbf{r}}_{CP}\times \mathbf{R}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{R}\hfill \end{array}\right) $$

(17.21)

can be termed a representation of the body frame configuration tensor [13]. Hence, (17.20) can be written as

$$ {\mathbf{f}}_P=\mathbf{C}{\mathbf{f}}_C^{\mathbf{\prime}} $$

(17.22)

The similar relationships hold in the body frame

$$ {\mathbf{f}}_P^{\mathbf{\prime}}={\mathbf{C}}^{\mathbf{\prime}}{\mathbf{f}}_C $$

(17.23)

where

$$ {\mathbf{C}}^{\mathbf{\prime}}=\left(\begin{array}{cc}\hfill {\mathbf{R}}^T\hfill & \hfill -{\mathbf{r}}_{CP}^{\mathbf{\prime}}\times {\mathbf{R}}^T\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill {\mathbf{R}}^T\hfill \end{array}\right) $$

(17.24)

The last equations imply also the flow relationships in the body frame:

$$ {\mathbf{f}}_P^{\mathbf{\prime}}=\left(\begin{array}{cc}\hfill \mathbf{I}\hfill & \hfill -{\mathbf{r}}_{CP}^{\hbox{'}}\times \hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \end{array}\right){\mathbf{f}}_C^{\mathbf{\prime}} $$

(17.25)

2.2 Bond Graph Representation of a Body Moving in Space

To develop a fundamental bond graph representation of the bodies moving in space we consider a single body interacting with its environment. The environment consists of the bodies the analyzed body is connected to. We model the body and its environment by two components—3DBody and Workspace (Fig. 17.2).

Fig. 17.2

Representation of a body moving in space

We assume that the body is connected to the other bodies at two points. We also assume that a body in the environment acts on the analyzed body by a force and moment. Likewise the body acts also to another body in the environment. In this way there is a transfer of power from the environment to the body and from the body back to the environment. In order to represent these interactions we assume that the 3DBody component has three ports. Two of these, the bottom and the upper ones in Fig. 17.2, correspond to the power interactions just described. We added the third one (the side port) to correspond to the body center of mass. It is possible to develop a model without the explicit use of the mass center port, but it simplifies the description of the body dynamics.

As explained previously, velocities seen at a port can be represented by the 6D flow vectors of (17.18) and (17.19). Similarly we can use 6D efforts to represent the resultant force and moment at a port. Such efforts can be represented in the base frame by

$$ {\mathbf{e}}_P=\left(\begin{array}{c}\hfill {\mathbf{F}}_P\hfill \\ {}\hfill {\mathbf{M}}_P\hfill \end{array}\right) $$

(17.26)

and, similarly, in the body frame as

$$ {\mathbf{e}}_P^{\mathbf{\prime}}=\left(\begin{array}{c}\hfill {\mathbf{F}}_P^{\mathbf{\prime}}\hfill \\ {}\hfill {\mathbf{M}}_P^{\mathbf{\prime}}\hfill \end{array}\right) $$

(17.27)

Here F _P and F ^′ _P are 3D representations of the resultant force at connection point P and M _P and M ^′ _P of the resultant moment.

To represent these 6D vector quantities, the ports of the 3DBody and Workspace components are assumed to consist of two subports. The first one corresponds to the linear velocity and resultant force, and the other to the body angular velocity and resultant moment. This way the ports can be used to access efforts and flows at the port by two ordered 6D efforts and flows. At the mass center port, however, as will be seen later, a 3D representation is sufficient. The flow is the mass center velocity and the effort is the resultant of the forces acting on the body at other ports (interconnection points) and reduced to the mass center. The gravity force (the body weight) acting there is not accounted for and is taken into account when dealing with the body translation dynamics. The reason for this is that body weight can be easily described in the base frame. However, this is not so in a body frame, because it is generally rotated with respect to the first.

We represent effort and flow vectors at body ports as seen in the body, i.e., with respect to a body fixed frame. Similarly at the workspace ports the corresponding quantities are expressed with respect to the base frame. Transformations between these two representations are given in Fig. 17.2 by the coordinate transformation component. This component transforms effort and flow at a body port to the corresponding base frame representation and vice versa. The transformation between efforts is given by

$$ {\mathbf{e}}_P=\left(\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{R}\hfill \end{array}\right){\mathbf{e}}_P^{\mathbf{\prime}} $$

(17.28)

and similarly for the flows,

$$ {\mathbf{f}}_P=\left(\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill \mathbf{0}\hfill \\ {}\hfill \mathbf{0}\hfill & \hfill \mathbf{R}\hfill \end{array}\right){\mathbf{f}}_P^{\mathbf{\prime}} $$

(17.29)

where R is the rotation matrix of the body frame with respect to the base.

We use Cartesian 3D frames only and, thus, the transformation matrix is orthogonal. It can be easily shown that the following relationship holds:

$$ {{\mathbf{f}}^{\mathbf{\prime}}}_P^T{\mathbf{e}}_P^{\mathbf{\prime}}={\mathbf{f}}_P^T{\mathbf{e}}_P $$

(17.30)

and thus the transformation does not change the power transfer.

The transformation of the port quantities can be represented by the 6D transform component of Fig. 17.3a. This component transforms the effort-flow pairs of the corresponding ports, according to (17.28) and (17.29), as shown in Fig. 17.3b. The transformations are represented by the Rot components that describe the transformation of 3D effort and flow vectors by the rotation matrix R. The transformation can be represented using transformer elements TF.

Fig. 17.3

6D transformation: (a) The component representation, (b) The structure

The velocities at a port are related to the velocity of the body mass center by (17.23) and (17.24). To find the relation between forces and moments, we evaluate the power transfer between the ports. We obtain the following relation:

$$ {{\mathbf{v}}^{\mathbf{\prime}}}_P^T{\mathbf{F}}_P^{\mathbf{\prime}}+{{\boldsymbol{\upomega}}^{\mathbf{\prime}}}^T{\mathbf{M}}_P^{\mathbf{\prime}}={{\mathbf{v}}^{\mathbf{\prime}}}_C^T{\mathbf{F}}_P^{\mathbf{\prime}}+{{\boldsymbol{\upomega}}^{\mathbf{\prime}}}^T\left({\mathbf{r}}_{CP}^{\mathbf{\prime}}\times {\mathbf{F}}_P^{\mathbf{\prime}}+{\mathbf{M}}_P^{\mathbf{\prime}}\right) $$

(17.31)

The last equation, jointly with (17.25), describes the basic velocity and force relationships for the rigid bodies. The structure of the 3D Body component following these relationships is given in Fig. 17.4.

Fig. 17.4

The model of 3D body motion

Component 1 is an array of the effort junctions corresponding to the center of mass velocity. The component Rotation defines the body rotational dynamic discussed later. The components 0 represent the array of flow junctions that describe the port velocities relationship given by the first 3D row of (17.25). It gives the linear velocity at a port as the sum of the velocity of the body mass center and the relative velocity due to the rotation of the body about the mass center. The joint variable is the force at the port. The body angular velocity, however, is a property of the body and it is directly transferred to the Rotation component.

The LinRot components represent transformations between linear and angular quantities. These transformations are defined by the skew-symmetric tensor operations in (17.25) and (17.31) and can be represented by transformers, as in Fig. 17.5.

Fig. 17.5

The representation of LinRot transformation

Every transformer in Fig. 17.5 corresponds to a nonzero entry of tensor −r _CP ′× or its transpose. The flow junctions on the left evaluate the relative velocities at the left port and the effort junctions on the right give the moment at the right port. The ratios of the transformers are the material coordinates of a body point corresponding to the port with respect to the mass center. Thus, they are parameters that depend on the geometry of the rigid body and don’t change with its motion.

2.3 Dynamic of Rigid Bodies

To complete the model, we need a dynamic equation governing rigid body motion. The simplest form of such an equation is given with respect to axes translating with the body mass center (Fig. 17.6). We assume that the base frame is an inertial.

Fig. 17.6

Motion of the body in space

The translational part of the motion is described by

$$ \left.\begin{array}{l}\mathbf{p}=m\mathbf{I}{\mathbf{v}}_C\\ {}\frac{d\mathbf{p}}{dt}=\mathbf{F}\end{array}\right\} $$

(17.32)

Here, m is the body mass and F is the resultant of the forces reduced to the mass center. We represent the dynamics of body translation in the Workspace (Fig. 17.7a) by CM component that describes the motion of the body mass center. This last component (Fig. 17.7b) consists of effort junctions corresponding to the x, y, and z components of the velocity of the body mass center with respect to the base frame. These junctions are connected to the Workspace port to which the resultant of the forces acting on the body is transferred.

Fig. 17.7

Rigid body translation: (a) Representation in the Environment (b) The CM component

Note that the weight of the body is added here represented by the source efforts defining the weight components with respect to the base frame axes. The momentum law in (17.32) is represented by the inertial elements I with the body mass as a parameter. Because it is used both in the SE and I components, it can be defined just once, at the CM document level.

The rotational part of the body dynamics is commonly described in the frame translating with the mass center of the body and is parallel to the base frame. In this frame it reads

$$ \left.\begin{array}{l}\mathbf{H}=\mathbf{J}\boldsymbol{\upomega } \\ {}\frac{d\mathbf{H}}{dt}=\mathbf{M}\kern0.5em \end{array}\right\} $$

(17.33)

where J is the mass inertia matrix and M is the resultant moment about the body mass center. Due to the body rotation the inertia matrix changes during the motion. Because of this the equations of the rotational dynamics are as a rule (at least for rigid bodies) represented with respect to a body fixed frame. It is not difficult to transform (17.33) to this form.

In the body frame the body moment of momentum is given by

$$ \mathbf{H}=\mathbf{R}{\mathbf{H}}^{\mathbf{\prime}} $$

(17.34)

Substituting from (17.33) we obtain

$$ {\mathbf{H}}^{\mathbf{\prime}}={\mathbf{R}}^T\mathbf{H}={\mathbf{R}}^T\mathbf{J}\boldsymbol{\upomega } ={\mathbf{R}}^T\mathbf{J}\mathbf{R}{\boldsymbol{\upomega}}^{\mathbf{\prime}}={\mathbf{J}}^{\mathbf{\prime}}{\boldsymbol{\upomega}}^{\mathbf{\prime}} $$

(17.35)

where

$$ {\mathbf{J}}^{\mathbf{\prime}}={\mathbf{R}}^T\mathbf{J}\mathbf{R} $$

(17.36)

is the body mass inertia matrix with respect to the central body axes. Multiplying second (17.33) by R ^T and substituting from (17.34), we obtain

$$ {\mathbf{R}}^T\frac{d}{dt}\left(\mathbf{R}{\mathbf{H}}^{\mathbf{\prime}}\right)={\mathbf{M}}^{\mathbf{\prime}} $$

(17.37)

or

$$ \frac{d{\mathbf{H}}^{\mathbf{\prime}}}{dt}+{\mathbf{R}}^T\frac{d\mathbf{R}}{dt}{\mathbf{H}}^{\mathbf{\prime}}={\mathbf{M}}^{\mathbf{\prime}} $$

(17.38)

Applying (17.14) the last equations can be written as

$$ \frac{d{\mathbf{H}}^{\mathbf{\prime}}}{dt}+{\boldsymbol{\upomega}}^{\mathbf{\prime}}\times {\mathbf{H}}^{\mathbf{\prime}}={\mathbf{M}}^{\mathbf{\prime}} $$

(17.39)

These are the famous Euler equations of body rotation in which the rate of change of the moment of momentum is represented by its local change and a part generated by the body rotation. This other part has a very elegant representation in a bond graph setting. This is the celebrated Euler Junction Structure (EJS) [6].

Now we can describe the ROTATION component of Fig. 17.4, which represents the body rotation dynamic about the center of mass with respect to the body frame (Fig. 17.8). The Torque balance component in the middle consists simply of an array of three effort junctions that corresponds to the x, y, and z components of the body angular velocity with respect to the body frame. The left and right ports transfer the moments of the forces and the moments acting on the body. In the center it is connected to Inertia and EJS components. The first of these consists of an array of inertial elements that describes the local rate of change of the moment of momentum. There is a control-out port that serves for the transfer of information on the moment of momentum vector H′ that the EJS component needs. This can be seen in (17.39). The EJS component is shown in Fig. 17.9.

Fig. 17.8

ROTATION component

Fig. 17.9

Euler junction structure (EJS)

It consists of three gyrators connected in a ring. Note that the power circulates inside the EJS, thus there is no net power generation or dissipation. The gyrators are modulated by the body moment of momentum.

This completes development of the component model of a body moving in 3D space. In BondSim© program the model is stored in the Models Library, under Word Model Components, from which it can be easily used by dragging it into the working window where the models are developed. Now we turn our attention to the modeling of interconnections between the bodies in space.

2.4 Modeling of Body Interconnection

Typical mechatronics systems, such as robots, consist of manipulators guided by controllers. The manipulators are multibody systems consisting of several members (links) interconnected by the suitable joints. They are powered by servo-actuators. In the previous sections we developed a fairly general component model of bodies that can be used for the representation of manipulator links. Now we develop models of the joints. Two types of joint are considered—revolute and prismatic. Based on these component models, a typical robotic manipulator can be represented in a way similar as how the real manipulators are assembled.

The approach is applicable to other multibody systems as well. Robot manipulators are chosen for several reasons. These are fascinating systems that have influenced development in many fields such as multibody mechanics, conventional and intelligent control, sensors and actuator technology, and have promoted mechatronics as design philosophy.

We consider here only the most common revolute joints . The analysis of the prismatic and the other joints can proceed in a similar way [3]. A typical revolute joint is shown in Fig. 17.10.

Fig. 17.10

Revolute joint in space

It consists of two bodies A and B, which can rotate about the common axis. The axis can have arbitrary position in space. The bodies could, for example, be two links of a robot manipulator joined by a revolute joint. We attach to body A the joint coordinate frame O _A x _A y _A z _A with axis z directed along the rotation axis. We assume further that there is also frame O _B x _B y _B z _B attached to the body B. The precise position of the frame is not prescribed and in a specific multibody system can be defined as is most convenient, e.g., using the Denavit–Hartenberg convention [2]. The frame Oxyz is the base frame.

Let P be the center point of the revolute joint used as the reference connection point. The joint can be represented as a word model component with two ports corresponding to body A and B. We consider flows and efforts at these ports expressed in their respective body frames. At A (the power-in) these are

$$ {\mathbf{f}}_P^A=\left(\begin{array}{c}\hfill {\mathbf{v}}_P^A\hfill \\ {}\hfill {\boldsymbol{\upomega}}_A^A\hfill \end{array}\right) $$

(17.40)

and

$$ {\mathbf{e}}_P^A=\left(\begin{array}{c}\hfill {\mathbf{F}}_P^A\hfill \\ {}\hfill {\mathbf{M}}_P^A\hfill \end{array}\right) $$

(17.41)

Similarly at B (the power-out) we have

$$ {\mathbf{f}}_P^B=\left(\begin{array}{c}\hfill {\mathbf{v}}_P^B\hfill \\ {}\hfill {\boldsymbol{\upomega}}_B^B\hfill \end{array}\right) $$

(17.42)

and

$$ {\mathbf{e}}_P^B=\left(\begin{array}{c}\hfill {\mathbf{F}}_P^B\hfill \\ {}\hfill {\mathbf{M}}_P^B\hfill \end{array}\right) $$

(17.43)

The linear velocities of bodies A and B at the connection point are common to both of the bodies. Hence

$$ {\mathbf{v}}_P^A={\mathbf{R}}_B^A{\mathbf{v}}_P^B $$

(17.44)

where R ^A _B is the rotation matrix of the body B frame with respect to the body A frame.

A similar relation holds for the forces. The linear velocities at the common point are equal, and the same is true for the power transferred across the joint during its translation, i.e.,

$$ {\left({\mathbf{v}}_P^A\right)}^T{\mathbf{F}}_P^A={\left({\mathbf{v}}_P^B\right)}^T{\mathbf{F}}_P^B $$

(17.45)

Substituting from (17.44) yields

$$ {\mathbf{F}}_P^B={\mathbf{R}}_A^B{\mathbf{F}}_P^A $$

(17.46)

Equations (17.44) and (17.46) describe the relationships between the linear parts of the flow-effort 3D vectors at the joint’s ports. We develop next the relationships between the angular parts, i.e., the angular velocities and moments.

The rotation matrices of the bodies A and B frames with respect to the base frame are related by composition of the rotations, i.e.,

$$ {\mathbf{R}}_B={\mathbf{R}}_A{\mathbf{R}}_B^A $$

(17.47)

Differentiating it with respect to time we get

$$ \frac{d{\mathbf{R}}_B}{dt}=\frac{d{\mathbf{R}}_A}{dt}{\mathbf{R}}_B^A+{\mathbf{R}}_A\frac{d{\mathbf{R}}_B^A}{dt} $$

(17.48)

From (17.8) and (17.14) we obtain

$$ {\boldsymbol{\upomega}}_B\times {\mathbf{R}}_B={\mathbf{R}}_A{\boldsymbol{\upomega}}_A^A\times {\mathbf{R}}_B^A+{\mathbf{R}}_A{\boldsymbol{\upomega}}_{AB}^A\times {\mathbf{R}}_B^A $$

(17.49)

where

$$ {\boldsymbol{\upomega}}_{AB}^A=\mathrm{axial}\left(\frac{d{\mathbf{R}}_B^A}{dt}{\mathbf{R}}_A^B\right) $$

(17.50)

is the relative angular velocity of body B with respect to body A expressed in body A frame. Simplifying (17.49) we get

$$ {\left({\mathbf{R}}_A\right)}^T{\boldsymbol{\upomega}}_B\times {\mathbf{R}}_A={\boldsymbol{\upomega}}_A^A\times +{\boldsymbol{\upomega}}_{AB}^A\times $$

(17.51)

Note that relative velocity of a point in body B with respect to the reference point P due to rotation of body B expressed in global frame is given by

$$ {\mathbf{v}}_{PB}=\boldsymbol{\upomega}_{B} \times {\mathbf{r}}_{PB} $$

The same velocity expressed in the body frame A defined by rotation matrix R _A can be found as

$$ {\mathbf{v}}_{PB}^A={\left({\mathbf{R}}_A\right)}^T{\mathbf{v}}_{PB}={\left({\mathbf{R}}_A\right)}^T{\boldsymbol{\upomega}}_B\times {\mathbf{R}}_A{\left({\mathbf{R}}_A\right)}^T{\mathbf{r}}_{PB}={\left({\mathbf{R}}_A\right)}^T{\boldsymbol{\upomega}}_B\times {\mathbf{R}}_A{\mathbf{r}}_{PB}^A $$

Note that ${\mathbf{r}}_{{}_{PB}}^A$ is a relative vector in body B expressed in body A frame. Therefore, the last expression implies that the axial vector

$$ {\boldsymbol{\upomega}}_B^A=\mathrm{axial}\left({\left({\mathbf{R}}_A\right)}^T{\boldsymbol{\upomega}}_B\times {\mathbf{R}}_A\right) $$

(17.52)

represents the angular velocity of body B expressed in body frame A. From (17.51) and (17.52) follows the relation between the relevant angular velocities of the revolute joint

$$ {\boldsymbol{\upomega}}_B^A={\boldsymbol{\upomega}}_A^A+{\boldsymbol{\upomega}}_{AB}^A $$

(17.53)

Note also that

$$ {\boldsymbol{\upomega}}_{AB}^A={\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \overset{.}{\varphi}\hfill \end{array}\right)}^T $$

(17.54)

where φ is the joint’s angle of the rotation.

We can now develop the bond graph component model of a revolute joint . Its word model is shown in Fig. 17.11. It has three power port and one control-out port. Two power point serves for connection to corresponding bodies, which rotate about the revolute joint (e.g., the robot links). The third one (shown on the left side) serves for actuating the joint. The signal port serves for extraction of information on the joint angle.

Fig. 17.11

Revolute joint component model

Its structure is shown in Fig. 17.12 and consists of two main parts: Revolute and Joint rotation. The Revolute represents the basic relations between the port variables in the frame of lower joint part (body A). The other component, Joint rotation, transforms the port variables from the frame of the upper body (body B) to the frame of the lower (body A).

Fig. 17.12

Structure of the revolute joint component model

The structure of the Revolute component is shown in Fig. 17.13 on the left. It consists of two components. The Tr component represents the translational part of the joint model and expresses the fact that the joint center point is common to the both bodies. Thus it consists solely of three effort junctions for the translation in the direction of x _A , y _A , and z _A axes. This ensures that the joined ends of the bodies move with the common velocity and that the corresponding forces are equal.

Fig. 17.13

The structure of: Revolute component, Rot subcomponent

The other component, Rot, whose structure is shown in Fig. 17.13 on the right, represents the relationship between the angular velocities as given by (17.53) and (17.54). The model is very simple and consists of two effort junctions in the x _A - and y _A -directions in which the angular components are the same for both of the joined bodies. There is also a flow junction that corresponds to the relative rotation about the z _A -axis. The 1-junction on the left in Fig. 17.13 is inserted to extract the joint relative angular velocity and to obtain the joint rotation angle by integration. It is not only used in the Joint rotation component, but is also transmitted to the output port (Fig. 17.12).

An important function of the joint is the rotation transformation between the two link frames (Fig. 17.12). This is depicted in Fig. 17.14. The transformations are applied to the linear effort-flow parts, and separately to the angular. These are represented by components RAB. The components represent transformations, as given by (17.44) and (17.46) for linear variables. The same transformations hold for the angular variables.

Fig. 17.14

Rotational transformations by the joint

We do not give here the general structure of the component because it depends on the structure of the kinematic links, which it is a part. Revolute joints play an important role in the design of robotic manipulators. They offer the simplest way to change the orientation of the robot links. The component model introduced here gives the main functionality of such joints. They are used later for the building of manipulator models.

3 Dynamics of an Anthropomorphic Robot Manipulator

In this section we apply modeling approach developed in the previous sections to modeling the dynamics of anthropomorphic robot manipulators. Many industrial manipulators are of this type. The first robot with anthropomorphic configuration was famous PUMA 560 released in 1978. As an example of such robots ABB IRB 1600 was chosen [5]. We concentrated on manipulator in open loop to show typical dynamic behavior of the robot. The closed model can be easily developed in a similar way as in Damic and Montgomery [3] for PUMA.

3.1 Kinematics Structure of ABB IRB 1600

The IRB 1600 is a six degree of freedom manipulator using revolute joints only. The robot coordinate frames are shown in Fig. 17.15. The links body frames are attached to the corresponding joint with one of the axes directed along the joint rotation axis. However, it is not required to choose for it the Z-axes, as in Denavit–Hartenberg scheme [9, 13].

Fig. 17.15

Kinematic structure of IRB 1600 robot

The joints and frames are numbered from the base to the robot tip. They are generated simply by translations from base X ₀ Y ₀ Z ₀. Thus, the first link frame X ₁ Y ₁ Z ₁ in the zero angle pose coincides with the base frame. The second frame can be obtained from the first by translation along X-axis for L ₂ and along Z-axis for L ₁. Similarly hold for the third and the fourth joint frame. The rotation axes of the last three joints intersect in the common point and are orthogonal. Therefore, the last three frames coincide in the zero angle pose. As is well known in anthropomorphic robot configurations the human-like terms are used for joints and robot links, i.e., body, upper- and fore-arms, the shoulder, elbow, and wrist.

The assumed values of the parameters in [m] are

• ${L}_1=0.4865,{L}_2=0.150,{L}_3=0.475,{L}_4=0.6,{L}_5=0.065$

The working range for IRB 1600 -x/1.2 is [5]

• $-180{}^{\circ}\le {\theta}_1\le 180{}^{\circ}$

• $-63{}^{\circ}\le {\theta}_2\le 136{}^{\circ}$

• $-235{}^{\circ}\le {\theta}_3\le 55{}^{\circ}$

• $-190{}^{\circ}\le {\theta}_4\le 190{}^{\circ}$

• $-115{}^{\circ}\le {\theta}_5\le 115{}^{\circ}$

• $-288{}^{\circ}\le {\theta}_6\le 288{}^{\circ}$

The kinematics is relatively simple. There are only three different rotation matrices: R _x (joints 4 and 6), R _y (joints 2, 3, and 5), and R _z (joint 1). The corresponding matrices read:

$$ {\mathbf{R}}_x=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill \cos \theta \hfill & \hfill - \sin \theta \hfill \\ {}\hfill 0\hfill & \hfill \sin \theta \hfill & \hfill \cos \theta \hfill \end{array}\right) $$

(17.55a)

$$ {\mathbf{R}}_y=\left(\begin{array}{ccc}\hfill \cos \theta \hfill & \hfill 0\hfill & \hfill \sin \theta \hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill - \sin \theta \hfill & \hfill 0\hfill & \hfill \cos \theta \hfill \end{array}\right) $$

(17.55b)

$$ {\mathbf{R}}_z=\left(\begin{array}{ccc}\hfill \cos \theta \hfill & \hfill - \sin \theta \hfill & \hfill 0\hfill \\ {}\hfill \sin \theta \hfill & \hfill \cos \theta \hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right) $$

(17.55c)

3.2 The Basic Structure of the Model

A brief description of Bond Graph model of the robot is given. The model has a hierarchical structure, which reminds of the structure of the real robot. The complete model can be downloaded from the web page¹ and analyzed using BondSim© program.

The system level model of robot ABB IRB1600 is shown in Fig. 17.16. It consists of three main components: Manipulator, Workspace, and Drives.

Fig. 17.16

System level model of IRB 1600 robot

The first two represent the model of the robot, and Drives represents simple open-loop drives of the robot actuators. The other components serve to post-process the signals and display them in the display components, which show changes with time of different variables of the interest during the simulation.

A special role in this model plays the component in the form of a ring (pipe). It is a component which enables inter-process communication between the robot dynamical model (within BondSim© program) and 3D geometric (visual) model of the same robot (within the corresponding BondSimVisual© application). It is really the client side of the communication (named) pipe. We will come to this topic later.

Model of the manipulator is shown in Fig. 17.17. It consists of Arm and Wrist components. On the left are two bonds, which deliver power to the arm and wrist actuators from the left multi-port connector. Similarly the connector on the right picks and further distributes the joint angles and angular velocities from these components.

Fig. 17.17

The structure of the manipulator model

The arm and wrist are interconnected by bond lines. It is assumed that power flows from the Workspace (Fig. 17.16) over Arm to Wrist. The wrist with a tool acts to the workspace. Therefore it delivers power to the workspace. However, the wrist and arm “feel” these interactions, and there is transfer of power from the Wrist (and tool) over Arm to Workspace. Thus, the model structure in Fig. 17.16 depicts what really happens in the robot and thus represents a pretty close physical model of it.

The models of Arm and Wrist are shown in Fig. 17.18. The Link 1 models the robot body, which can rotate about vertical the robot base axis (Fig. 17.15). Joint 2 is the shoulder, about which the upper arm (Link 2) can rotate. This arm is further connected by the elbow (Joint 3) to the forearm (Link 3), which carries the wrist. The wrist (Fig. 17.18 on right) represents a spherical joint (see [3] for details). It consists of Joint 4–6, and Link 4–6 that house the actuators driving the joints.

Fig. 17.18

Models of Arm (left) and Wrist (right)

Consider the bonds connecting the Joints and Links. The left ones we already have discussed. More interesting are bonds going down from the last Link 6 to the base. We remind of the modeling approach we discussed in Sect. 17.2.2, Fig. 17.2. We use three-port component models to represent space body models. Thus, the bond coming out of the upper port of Link 6 transfers 3D efforts and flows of the robot wrist (holding a tool) action to the workspace. In addition at it’s center of mass there are the resultant force and its velocity. All these quantities are described in the body (Joint 6) frame. There are different for an observer in the base. However, we do not know exact position and orientation of this frame in the base, and thus cannot transform them directly. Instead, we systematically transform these quantities from the joint to joint until the base. The same holds for the other links as well, only that there are smaller number of the quantities to transform as we approach the base.

Note how the bonds are gradually built. It is important because we need to unpack them later. At every joint to the already transformed quantities we add the corresponding link center of mass quantities and transform these new quantities further. This looks somewhat complicated, but if we apply this approach systematically there should be no problem. The similar effects appear in the reality. When we hold a heavy load in our hand, we feel it at every body parts to the foot.

To see these transformations in more detail we open, e.g., Joint 2 component (e.g., by double clicking). The model of Joint 2 on the left is similar to that of Fig. 17.12. There are, however, the additional two top right ports, which transfer the Link 2 center of mass quantities and the quantities from the previous joint, respectively (Fig. 17.18).

The Revolute component, which model the revolute joint, was already discussed in Sect. 17.2.4, Fig. 17.13. The Joint rotation model component is shown in Fig. 17.19 on the right. The R21 component describes the transformation corresponding to rotation about axis Y through the joint angle θ ₂, Fig. 17.15. The transformations are governed by matrix (17.55b) and are shown in Fig. 17.20.

Fig. 17.19

Structure of Joint 2 model component

Fig. 17.20

Component R21: rotation about Y-axis

We direct at the end our attention to Workspace component in Fig. 17.16. The model is shown in Fig. 17.21 left. We may first observe Robot base component. It is a simple component consisting of six source flows, which fix the base to the ground in its initial position, i.e., they imply zero linear and angular velocities of the base.

Fig. 17.21

The structure of model of the Workspace

The next component CM1 describes the dynamics of the Link1 center of mass. We have discussed it earlier in Sect. 17.2.3 (see Fig. 17.7). To establish the correct connection to the manipulator (Fig. 17.18) we add also a component called Other Part 6, indicating that it must contains six other components—the dynamic of centers of masses of other five links, and the robot wrist end component representing the TCP (the tool center point). The structure of the last component Other Part 2 is shown in Fig. 17.21 right. It contains CM6 component describing the dynamics of the center of the mass of the last link and the TCP component. The last component consists simply of three 1-junctions connected to the components port. They represent the nodes of TCP velocity components in the basic frame. Free End component defines the conditions at the robot end. It could be simply zero source efforts if the robot end moves freely in the environment. The bond at the right of TIP extracts its velocity. These signals go out from Other Part 6 in the Fig. 17.21 left and are integrated to obtain information on TCP position in the base frame.

One of the strong points in dealing with multibody dynamics as described above is a systematical use of compounded ports, i.e., the ports that consist of other subports, these of the others, and so on to the arbitrary depth. This enables representing of the complex interaction appearing in the devices of such a complexity in a straight and readable manner. Otherwise we should deal with forest of the signals. Of course the corresponding mathematical models could be difficult or even impossible to obtain by hand. BondSim© model build algorithm knows how to do it automatically without intervention of the modeler.

3.3 Simulation of the Robot Motion

We will now conduct the simulation of developed model of ABB IRB 1600 robot. We consider behavior of the robot in open loop. Thus, we will drive robot by the source flows, which generates the angular velocities of the joins defined by simple sinusoidal laws

$$ {\omega}_i=\alpha {}_i\omega_0 \cos \left({\omega}_0t\right),\kern0.5em \left(i=1,\dots, 6\right) $$

(17.56)

This correspond to rotations of the links given by

$$ {\theta}_i=\alpha {}_i\operatorname{sin}\left({\omega}_0t\right),\left(i=1,\dots, 6\right) $$

(17.57)

The circular frequency of the sinusoidal function was select relatively slow, e.g., ${\omega}_0=\pi /10$ rad/s, and the amplitudes are set to

• α ₁ = π, α ₂ = π/3, α ₃ = 0.25π, α ₄ = π, α ₅ = 0.6π, α ₆ = π

We run the robot joint angles for one period of the input sinusoid, i.e., the simulation time is t = 20 s. Figure 17.22 shows BondSim© program screen with open project ABB_IRB1600.

Fig. 17.22

BondSim© program screen with open ABB_IRB1600 project

The system level model of the project is shown in the central part of the screen. On the left is a window, which displays hierarchical structure of the model in the form of an Explorer style tree.

The enlarged part of this tabbed window is shown in Fig. 17.23 left. It shows the hierarchical structure of the model. The model project is at the root, and then the components. The components with the “folder” symbol denote the word model components, which contains the other components. By clicking the leading “+”, the corresponding component in the main windows opens. The same could be achieved by double clicking the component title in the main window. The components denoted by page symbols are elementary Bond Graph components.

Fig. 17.23

Enlarged parts of the BondSim© screen

The next tab contains Model Library (Fig. 17.23 in the middle). It is used often during development of models. It contains the complete projects, and different components, which are stored in the library (see [3] for details).

The basic editing tools are contained in Editing Box at the right side of the BondSim© screen (Fig. 17.22). Its enlarged view is shown in Fig. 17.23 right. It contains several tools for developing Bond Graphs, including the continuous and discrete time block diagrams. The development of the models is basically conducted by dragging the tools from Editing box and dropping them into the main windows (refer to [3] for details).

Before starting simulation we need to build the mathematical model of the system. This can be done by opening Simulation menu, and choosing Build command. The system starts reading all components the system consists of, checks the connections, generates the internal variables, and finally generates the mathematical model. The model is generated in symbolic form, which can be recompiled into a human readable form for inspection. We will not go in details here. Interested reader can consult [3] for details.

The current model consists of 959 implicit equations, and symbolically generated Jacobian matrix contains 2637 elements. Thus, it is very sparse, with on average less than 3 elements per row.

To start simulation, chose Simulation command Run. In the dialog that opens set the simulation interval to 20 s, the output interval, and maximum step size to 0.05 s. (The output delay interval is not important now.) For all other simulation parameters accept the default values (the method and error tolerances). Click Restart (if it is not already set) and select OK. Now simulation starts. System generates the messages in Output window at the bottom, which inform the user on simulation advance.

During a simulation run the model is repeatedly solved using a Backward Differentiation Formula (BDF) type solver. The solver successfully solved the model as the simulation statistics in Table 17.1 shows.

Table 17.1 Simulation statistics

Figure 17.24 shows the motion of the TCP during the simulation, and Fig. 17.25 shows how changes the absolute error in TCP position.

Fig. 17.24

Changes of coordinates of TCP with time

Fig. 17.25

Errors in TCP coordinates

These errors were calculated by comparing the values generating by the simulations and values calculated by the direct kinematics in component TCP. Diagram shows that these errors are of order of the simulation error tolerances in Table 17.1. Thus, the accuracy of the simulation is good.

4 Visualization of Robots in 3D

In the previous section we dealt with the dynamics of a robot. It gives a deeper insight into its behavior. However, it is rather an esoteric topic. Perhaps visualization of its motion in a virtual 3D space is more informative. We wish to stress that we are not speaking of animation of a robot motion, but on visual representation of simulated robot motion in 3D scene on computer screen. Thus, there is one-to-one correlation between the simulated robot motion of the last section and its visual 3D representation.

Many robot manufacturers use 3D robot models for off-line programming, e.g., ABB [11], Fanuc [10], KUKA [7], BYG [4], and others. These software applications were designed with the specific goals in mind and are based on geometric and kinematical models.

The geometrical models driven kinematically are useful for solving some problems, such as off-line programming, but cannot simulate the real behavior of the robots. It is quite complicated, however, to have in one application both the geometry and dynamics. Thus, we developed a separate application BondSimVisual© , which supports developing of 3D geometric models of robots and similar mechanical systems and their rendering on the computer screen in a 3D virtual scene. The simulated motion of a robot using BondSim© can be visualized in parallel in a separate window on the same or another computer by inter-process communications between these two. In this section we describe concept of visualization employed. Inter-process communication between the dynamical and virtual 3D space is discussed next.

4.1 Description of Robot System

The first step in generating 3D virtual scene is geometric description of the system that is the subject of the study. Usually it is the same system for which bond graph dynamical model was developed. The system is described in form of a relatively simple textual script written in ASCII code using corresponding commands. We will next describe the basic commands and show how a typical robot can be described. Note that in spite we are speaking of robots, the same is applicable to other mechanical objects like see-saws in children play grounds, the legged platforms, cranes, and similar 3D mechanisms.

Description of a robot or any other multibody mechanism can be done in two basic steps:

• Description of kinematic structure of the robot. This in essence defines all necessary coordinate frames and their relationships.

• Description of all main parts that robot consists of such as the base, links, tool, and its environment.

The description is given in form of a simple script, which is later used by the visualization program to create in the memory all objects that represent the 3D visual model of the robot. These objects draw itself on the computer screen as 3D picture of the robot. It is shown in a specified initial position.

4.1.1 Kinematic Structure of the Robot

The kinematic structure of a robot system defines relationships between different coordinate frames used to describe the geometry of a device. We use only the right Cartesian coordinate frames. There are three types of coordinate frames we use (Fig. 17.26). The first is the global World coordinate system X _w Y _w Z _w . The origin of the system is in the center of the screen with X _w -axis directed horizontally to the right, Y _w -axis vertically upward, and Z _w -axis out of the screen. To every mechanism in the scene there is attached a base coordinate frame.

Fig. 17.26

The coordinate frames

In addition to every link there is also attached a link frame. The origins of the frames are set at center point of the corresponding joint. The joints, and corresponding links and their frames, are ordered going from the base to the tip.

To define position between the coordinate frames the homogenous transforms are used (see Sect. 17.2.1). We assume that they are coincident at first. We rotate then first one frames with respect to the other about the common origin by a rotation matrix, and then translates it by a 3D vector. To define the rotation we use ZYZ Euler angles (Fig. 17.27).

Fig. 17.27

Euler ZYZ angles

The homogenous transform of one frame with respect to the other is defined in the form

( Shift x value1 y value2 z value 3 Euler angle1 angle2 angle3 )

Such a specification is used in different commands that we will encounter later.

The position of the base frame in the word coordinates and its kinematical structure is defined by the Device command, which has the form shown below. The specific command words are shown here in bold. They can be written in small, large, or mixed letters. The others are the parameters defined by the modeler. The terms in the command are separated by spaces. The command ends by semicolon. The same holds for the other commands as well.

Device Title (Shift x shx y shy z shz Euler eu1 eu2 eu3 LBox blen)

Joint 1 (Shift x shx y shy z shy Euler eu1 eu2 eu3)

Prismatic or Revolute x or y or z

(Shift x shx y shy z shy Euler eu1 eu2 eu3)        …    

Joint n (Shift x shx y shy z shy Euler eu1 eu2 eu3)

Prismatic or Revolute x or y or z

(Shift x shx y shy z shy Euler eu1 eu2 eu3)         

Tcp (shift x shx y shy z shy)                

Extend joint_index                    

Initial (value_1 value_2 … value_n);

The title of the device is specified first, then its position in the world frame, and the size of the bounding box. Next the first link frame is defined with respect to the base, then the second with respect to the first, and so on until the last link frame is defined.

Note that every joint is numbered going from 1 and up (the index 0 is reserved for the base). Every joint frame in the kinematic tree is defined first by specifying a pre-transform, then type of the joint, and finally a post-transform. Usually only pre-transform is enough, but sometimes we need both pre- and post-transforms. It assumes that joints are simple revolute or prismatic. Its rotation or sliding axis is aligned with one of the link coordinate axes.

The Tcp command defines position of the tool central point. The mechanisms often do not have the simple serial structure, but contains the parallelograms, or more than one arm. In that case subcommand Extend defines the index of the joint or base where the branching starts.

Finally there are subcommands that define the initial values of the joint variable (angle or displacement). The command defines only the initial position of the mechanism. It could be moved manually by a menu command or dynamically by another application (BondSim© ).

4.1.2 Geometric Representation of the Robot Parts

The geometric model of the device base or its links can be constructed in two ways—using the primitive forms or 3D CAD generated part files. The predefined primitive forms are shown in Fig. 17.28. To define the mechanism structure we used the corresponding commands, which are based on corresponding VTK classes [12].

Fig. 17.28

Primitive forms: (a) Cylinder, (b) Cone, (c) Cube, (d) Sphere, (e) Polyprism, and (f) Module

4.1.2.1 Cylinder

It serves to create a simple body in form of a cylinder (Fig. 17.28a). Its longitudinal axis is aligned with z axis. The parameters of the command are the dia[meter] of its base and its len[gth] (height) in millimeters. The cylinder bases are generated as regular polygons. The parameter res[olution] defines the number of divisions of the base circles. The cylinder center is on z-axis at a half of its height (length). The syntax of cylinder command is

Cylinder Title dia cdia res cres len clen;

4.1.2.2 Cone

A cone is defined in similar way (Fig. 17.28b). The base of the cone is circular with its center at the origin of the coordinates, but can be set to any other point. Similarly, direction vector from the center toward the apex is aligned with z-axis, but can be set to different directions. The other parameters are dia[meter] of the base and its len[gth]. The circle of the base is generated as a regular polygon whose number of divisions is defined by the res[olution] parameter. The syntax of cone command is

Cone Title (Center x value y value z value Direction x valuey value z value) dia cdia res cres len cH;

4.1.2.3 Cube

It serves to create a simple body whose three orthogonal edges are aligned with x, y, and z axes (Fig. 17.28c). The parameters of the command are the lengths of the edges xLen, yLen, and zLen. The coordinates of the cube center are (0.5 xLen, 0.5 yLen, and 0.5 zLen). The syntax of cube command is

Cube Title xLen yLen zLen;

4.1.2.4 Sphere

It serves to create a simple body with its center in the origin of the coordinates and radius (Fig. 17.28d). It is generated as a polygonal object with a res[olution]. The syntax of the sphere command is

Sphere Title radius sR res sres;

4.1.2.5 Polyprism

This command serves to create a prismatic body, which is generalization of a cylinder or cube (Fig. 17.28e). Its base is a closed polygon formed of the straight lines and circular arcs. The syntax of the command is

Polyprism Title Height value Coord1 coord2 … coord1 coord2 Arc to value1 value2 radius value res value Arc Large to value1 value2 radius value res value … ;

The Polyprism base lies in xy coordinate plane and its edges are orthogonal to the base and parallel to z axis. The command specifies the name of the polyprism and its height. The coordinates of the vertices are defined by its base-plane coordinates (Fig. 17.29).

Fig. 17.29

Definition of the coordinates

The arcs are drawn between the point specified by the previous vertex and the point defined by the x–y coordinates after to subcommands. The first form defines a (normal) short arc between the end points (Fig. 17.30a), its radius, and the resolution. The other form is similar but defines a large arc (Fig. 17.30b). The positive value of the radius denotes that the arc is drawn in clockwise direction Fig. 17.30a. If it is negative it is drawn in the opposite direction.

Fig. 17.30

The arcs of Polyprism: (a) Normal and (b) Large

4.1.2.6 Module

This command is used to define a general form of a body (Fig. 17.28f). It defines the name (title) of the body. The Points gives the list of vertices defined by their indices and the triplets of their x, y, and z coordinates in the local frame. The polygonal sides of the module are defined by Polygons, which consists of the list of indices of vertices enclosed in parentheses. To illustrate how such a form can be defined consider a body in form of a wedge in Fig. 17.31.

Fig. 17.31

Body in form of a wedge

To define the body by the module command, we define first its name, and an ordered list of the coordinates of the vertices (points), and finally the polygons (sides). The vertices are numbered from 0 to 7 and are defined by specifying its coordinates in the local coordinate frame. The polygonal sides are defined by listing the indices of their vertices. The corresponding command reads:

Module Wedge Points 0 0.0 0.0 0.0 1 50.0 15.0 0.0 2 50.0 75.0 0.0 3 0.0 75.0 0.0 4 50.0 15.0 15.0 5 50.0 75.0 15.0 6 0.0 75.0 20.0 7 0.0 0.0 20.0 Polygons (0 1 2 3) (1 2 5 4) (2 3 6 5) (3 6 7 0) (7 4 1 0) (4 5 6 7) ;

4.1.2.7 Parts

The bodies that make the robot can be generated using the part files generated by a Computer Aided Design (CAD) system such as Catia, Solid Works, ProEngeener, and the others. The robot manufacturers as a rule publish on their web sites the CAD files of the robot parts in the standard formats. BondSimVisual© supports the stl (stereo-lithography) format. This format is almost exclusively used for visualization and rapid prototyping. Even if original files are not in stl format but in some other public format, e.g., STEP, DXF, etc., they can be readily converted into it. Such files can be imported into BondSimVisual© program. To use parts defined in such way the Part command is used. It simply defines the filename of the imported part file (without extension .stl):

Part Filename;

4.1.2.8 Set

This command is used to create a complex body consisting of the simpler ones. We assign the name to the new assembly and add to it already defined bodies. These component bodies can be translated or rotated with respect to the local frame. This is described by the corresponding transforms enclosed in the parentheses. The syntax of the command is shown below.

The important application of the Set command is in creation of the device links. Because the links are associated with the joints, the same name is used for the both. In the command the link is defined by devicet_title#joint_index. Due to the fact that the link coordinate frame was already defined it is taken as the local frame of the assembly.

Set Title add comp_1 ( Shift x shx y shy z shy Euler eu1 eu2 eu3)

comp_2 ( Shift x shx y shy z shy Euler eu1 eu2 eu3)

…..

comp_n

…

;

Therefore, the Set commands are commonly used to assign the body assembles to the joints and thus create the links.

4.1.2.9 Render

All the previous commands serve to define the structure of the mechanism. The Render command is really a visualization command. It asks the system to render the corresponding component and shows it on the screen. Its format is

Render Title color red green blue;

The title defines the component which is the target of the command. It can be the base of the device, specified by its title, the links specified by the device title and its joint index attached by “#” sign (similarly as in Set command), e.g., IRB1600#2. The command also defines the RGB color values of the rendered component by specifying Red, Green, and Blue values in the range 0.0–1.0. Some common RGB values are given in Table 17.2 [12]. Note the “colour” is acceptable as well.

Table 17.2 Common colors defined by RGB values

4.1.2.10 Probe

This command is used to specify a point in the mechanism we are interested in. It can be a part of the mechanism, but can be a separate point. The program calculates its coordinates and outputs it. The syntax is:

Probe Title Frame_in ( Shift x shx y shy z shz) Refer Frame_to;

The position of the probe is specified by Shift command (within the brackets) with respect to Frame_in, which can be the mechanism base, or any of the joint coordinate frames. They are specified as in Set and Render commands. The values of probe’s coordinates are calculated with respect to the same or a different frame. It is specified by Refer and Frame_to, which can be World global frame, the robot base, or some of the joint frames. This command can be useful for visualization of the robot motion during its simulation. The visualization program returns the coordinates of the probe, which can be used by the connected (client) program, e.g., BondSim© .

In order to include the comments in the scripts the text line with leading ‘!’ is used. For more text the command ‘$’ followed with text lines and ended ‘$’ may be used. The comments are skipped when processing the scripts.

5 The Program Script

As application of the commands given above we analyze the script in Box 17.1, which defines the visual model of ABB IRB 1600 robot of Fig. 17.15. Device command defines the kinematical structure of the robot by defining the frames and initial position of the links. Note the robot title IRB_1600 may be different from the program name under which it was developed and stored. It is used locally inside the script only.

The origin of the base frame coincides with the global frame, but the axes are rotated first for −90° about global Z-axis (out of the screen), which moves x-axis downwards, and y-axis to the right. Next it is rotated for −90° about the new y-axis, which rotates x-axis out of the screen, and z-axis vertically up. This is the position we need and thus the third rotation is zero. The last item in the Device command is the size of the bounding box that defines the extent of the virtual screen. It is used by the windows system to properly scale the screen and do not rescale it every time the robot moves.

Next the joint coordinate frames are defined (Fig. 17.15). Starting from the base frame we have just defined, we assume that the first joint frame in zero angle pose is coincident with it. The joint is the revolute with z rotation axis. The second joint frame we obtain by translating along x-axis for L ₂ and for L ₁ along z-axis. It is again a revolute joint with y as the rotation axis. Next we translate upward for L ₃. The third joint is the revolute with y as the rotation axis. We proceed in the same way. Now we translate along x-axis for L ₄. The fourth joint is revolute about x-axis. Note the last three joint makes a spherical joint, which rotation axes are orthogonal in zero angles pose. Therefore, we assume that the last two frames coincide with the fourth joint frame. The fifth joint is revolute with y-axis as rotation axis, and the last joint is revolute again but about x-axis.

Tcp (tool center point) is displaced by L ₅ along x-axis. Finally the initial values of all joint angles are defined, which are simply equal to zeros.

The next six commands define the robot parts, the robot base, and six links. The Part names represent the filenames under which the stl parts are imported into the program from the manufacturer web page. This enormously simplifies building the visual model of the robot.

The first Set command attaches the Body0 part to the robot base frame and renders it in the gray color. Similarly the next Set command attaches the first link body to the first joint frame. In this way they define the robot body and its first link. The next commands did it with the other links. However, these commands incorporate the shifts, which we will explain.

The parts supplied by ABB are defined with respect to the base coordinate frame. Therefore to define them with respect to the local joint axes the parts must be first shifted back to the base frame and then set to the corresponding joint frame. Note also that all bodies are rendered gray. This follows the recent coloring scheme that ABB Robotics uses.

The final command is the Probe. It is shifted along x-axis of the last joint frame for L ₅ and hence coincides with TCP. Its motion is calculated with respect to the base robot coordinate frame. In the visual model of the robot it appears as yellow point, as the robot carries a tiny lamp.

5.1 Visualization Based on VTK

Among different systems that can be used for the visualization in 3D space a very interesting and powerful one is the Visualization Toolkit (VTK) by Kitware [12]. It is a large C++ open library. We use only a part of its capabilities. BondSimVisual© is written in MS VisualC++ and uses also Microsoft Foundation Class (MFC) library . The visual models of the systems which we are interested in are described in the form of script document as we discussed in the previous subsection. The management of script document is supported by the program. Thus, it is possible to create a new one, open and modify an existing one, delete copy and export them, etc. Because the scripts are simple text files, as the editor Notepad is used, which is called from the program directly.

To create a 3D virtual scene the corresponding menu command is issued, which offers to the user to select a robot script for which the scene will be generated. The script is then read and translated into series of the byte codes. During this translation phase the script is checked for eventual errors, which are returned to the user. When the translation phase was successfully completed, starts the final phase in which the visualization objects in computer memory are created and corresponding 3D scene, including the lights and camera, is generated.

Visualization in BondSimVisual© is based on VTK concept of visualization pipeline [12]. Thus, following the script the C++ objects are created in the memory and are interconnected as illustrated in Fig. 17.32.

Fig. 17.32

Visualization pipeline

The components in the upper part of the figure define the geometry of a link. Typically they use the sources of cubes, cylinders, and others forms, which define the parts the link is composed of. They are transformed and connected to the mapper objects, which defines the geometry of the link. It is also possible to use 3D CAD models of the parts, e.g., in stl format, and using the corresponding reader to read them into the memory. In the similar manner the base is created.

The outputs of the Mappers are connected to the Actors, which are responsible for rendering of the objects. Its properties can be defined, such as color, by Render script commands. Its input port is connected to the transform object, which describes rotation or sliding of the link by the revolute or prismatic joints. If the joint’s angles change, then all connected components are reevaluated and the robot changes its position on the screen.

Figure 17.33 shows BondSimVisual© screen showing ABB IRB1600 robot scene. It is shown in the initial zero angles pose.

Fig. 17.33

3D scene with ABB IRB1600 robot in the initial pose

Program BondSimVisual© is designed to work jointly with another program, which supplies the value of the joint variables, the revolute joint angles, or prismatic joint displacements. The primary dynamic modeling and simulation program is BondSim© , which supplies these data by the inter-process communication (IPC), Fig. 17.34.

Fig. 17.34

Concept of 3D visual and dynamic modeling and IPC

The BondSim© sends regularly, e.g., every 50 ms, the current values of joint variables to the BondSimVisual© , which processes them and redraws the virtual scene. In response it returns, e.g., the new position of the Probe to the BondSim© , which use it for its purposes. Currently, it plots it alongside with other variables. However, such information could be useful, e.g., for modeling and simulation of the crushes.

The interval for sending the data is defined at the start of the simulation. It is the output delay whose default value is 50 ms, which amounts to 1/0.050 = 20 frames/s. This is a common value, but could be set to a different value.

Inter-process communication is based on the named pipes [8] (Fig. 17.35). The server (BondSimVisual© ) is responsible for creating the pipe. It also creates a special listening thread, which enables that program simultaneously with the other tasks listen to messages from the client. The server also sends a message to the potential clients to connect to. The client BondSim© , after building the simulation model of the corresponding modeling project, connects to server using a command in the Simulation menu.

Fig. 17.35

The configuration of IPB using named pipe

When the two-way communication is established the simulation can start on the client side. As the simulation advances the robot starts moving its arm over the virtual scene. Figure 17.36 shows a sequence of IRB1600 postures during the simulation.

Fig. 17.36

The sequence of motion of ABB IRB1600 robot during the simulation

Figure 17.37 shows coordinates of TCP during the simulation. On the same plot are drawn the coordinates of the Probe returned by IPC from the server. Note that the probe was positioned exactly at the TCP (see Box 17.1). As can be seen the probe’s broken curve closely follows TCP simulation curve, displaced along the time axis for double output delay (0.1 s).

Fig. 17.37

Motion of TCP by: (a) Simulation (thin line) and (b) Visualization (probe, broken line)

Box 17.1 ABB IRB1600 Script

 !-------- ABB IRB1600_12 -------------------------------------  ! Characteristic lengths are L1 = 486.5 L2 = 150 L3 = 475 L4 = 600 L5 = 65 mm  Device IRB1600 (euler -90.0 -90.0 0.0 lbox 1200)  Joint 1 revolute Z  Joint 2 (shift x 150 z 486.5) revolute y  Joint 3 (shift z 475) revolute y  Joint 4 (shift x 600) revolute x  Joint 5 revolute y  Joint 6 revolute x  Tcp (shift x 65)  initial (0.0 0.0 0.0 0.0 0.0 0.0);  Part IRB1600_X-120_m2004_rev0_01-1_Body0;  Part IRB1600_X-120_m2004_rev0_01-7_Body1;  Part IRB1600_X-120_m2004_rev0_01-4_Body2;  Part IRB1600_X-120_m2004_rev0_01-5_Body3;  Part IRB1600_X-120_m2004_rev0_01-3_Body4;  Part IRB1600_X-120_m2004_rev0_01-2_Body5;  Part IRB1600_X-120_m2004_rev0_01-6_Body6;  Set IRB1600 add IRB1600_X-120_m2004_rev0_01-1_Body0 ;  Render IRB1600 color 0.5 0.5 0.5;  Set IRB1600#1 add IRB1600_X-120_m2004_rev0_01-7_Body1 ;  Render IRB1600#1 color 0.5 0.5 0.5 ;  Set IRB1600#2 add IRB1600_X-120_m2004_rev0_01-4_Body2 (shift x-150 z -486.5 );  Render IRB1600#2 color 0.5 0.5 0.5 ;  Set IRB1600#3 add IRB1600_X-120_m2004_rev0_01-5_Body3 (shift x-150 z -961.5 );  Render IRB1600#3 color 0.5 0.5 0.5 ;  Set IRB1600#4 add IRB1600_X-120_m2004_rev0_01-3_Body4 (shift x-750 z -961.5 );  Render IRB1600#4 color 0.5 0.5 0.5 ;  Set IRB1600#5 add IRB1600_X-120_m2004_rev0_01-2_Body5 (shift x-750 z -961.5 );  Render IRB1600_12#5 color 0.5 0.5 0.5 ;  Set IRB1600#6 add IRB1600_X-120_m2004_rev0_01-6_Body6 (shift x-750 z -961.5 );  Render IRB1600#6 color 0.5 0.5 0.5 ;  Probe Point1 IRB1600#6(shift x 65) refer IRB1600;  !------------- End -------------------------------------------

BondSimVisual© supports also creating avi files during the simulations. These files can be run by the most media players. More information can be found on BondSim© web site.