Path defined directed graph vector (Pgraph) method for multibody dynamics

Abstract

Dynamical modeling of complex systems may include multiple combinations of serial and tree topologies, as well as closed kinematic chain systems. Simulating of such systems is a costly task not only for run time but also for construction time when a model description and constraints are introduced. This paper presents a systematic framework of a construction time efficient modeling methodology for complex systems by introducing a path defined directed graph vector ($\mathit{Pgraph}$) and the associated methodology based on Linear Graph Theory (LGT). Updating of body coordinate frame vectors which can be a challenge in complex topology systems is easily performed using the proposed method. This technique is especially useful for systems changing topology, such as walking mechanisms where bilateral and unilateral constraints are conditionally embedded. Although this is a general methodology, to be combined with many dynamical modeling algorithms available in the literature, here we demonstrate it using Spatial Operator Algebra (SOA), which is a recursive algorithm based on the Newton–Euler formalism.

1 Introduction

During the mechanical design phase of a multibody system to achieve a desired motion, bodies are interconnected forming different topologies. Complex multibody systems are those that include multiple combinations of serial and tree topologies, as well as closed-chain systems. Simulating of such systems based on high fidelity modeling is a challenging and costly task not only for run time but also for construction time when a model description and constraints are introduced. Nevertheless, obtaining accurate yet computationally efficient models of multibody systems is crucial for model-based controller design processes. Without a systematic framework, however, modeling and formulating multibody dynamics can be too tedious depending on the complexity of the system.

Complex topology systems are likely to have a high number of degree of freedom. A number of computationally efficient programs were developed in the last couple of decades to analyze and simulate the dynamics of multibody systems dealing with a large size mass matrix whose inverse is computed in $\mathrm{O}(n)$ complexity [1–3, 5, 6, 15, 18]. Almost all of these programs include graph-theoretical approaches to the definition of the system topology. Among them Linear Graph Theory (LGT) has become a fundamental tool for solving complex systems. LGT is initially introduced by Euler to get the solution to the well-known “Königsberg bridge” problem in 1736. Since then, this approach has been widely used for modeling different physical systems. In 1977, Wittenburg [22] introduced a formulation to obtain the equation of motion of a complex multibody system. Later, McPhee et al. [14] stated that Wittenburg formulation can be considered in the scope of LGT. McPhee et al. also combined LGT with virtual work and symbolic computing methods to model a wide range of multibody systems [19–21]. In this regard, we want to emphasize Spatial Operator Algebra (SOA) [7, 10–13, 16, 17] on which this paper is based. Jain has combined SOA with LGT to develop methods for partitioning, aggregating and constraint embedding for multibody systems [8, 9].

All of these studies are done with a particular approach with some focus on optimizing run time. However, the construction time efficiency is one of the major current challenges in multibody dynamics, especially in the case of event-dependent changes in constraints as well as topology. Construction time also includes the effort it takes to set rules for updating of body coordinate frame vectors, which can be error prone.

In terms of describing the connectivity of the bodies, one of the important works done in this area was proposed by Featherstone [4], where undirected graphs describe the connectivity of the bodies by a parent array. Although this method is useful for describing the connectivity of the bodies, it uses also additional two arrays which represent the set of children of related body and the set of joints on the path between related body and root.

In this paper, we propose the $\mathit{Pgraph}$ method which is used for describing the connectivity of the bodies and branches based on LGT. Among the significant advantages of this method, obtaining spatial force and spatial velocity distributions as well as updating body coordinate frames in a systematic way should be emphasized. Furthermore, $\mathit{Pgraph}$ is used to incorporate the constraint forces into the equation systematically.

In this paper, we utilize Spatial Operator Algebra (SOA) with a minor difference. Although the original SOA uses an inboard numbering scheme where the numeration of the bodies is done in increasing order from the tip to the base, we use an outboard numbering scheme (from the base to the tip) to be compatible with common literature.

This paper is organized as follows. Section 2 is on the basics of Linear Graph Theory (LGT), Sect. 3 provides the mathematical basis of SOA with LGT. Section 4 presents the $\mathit{Pgraph}$ method. in Sect. 5, simulation results are presented. Finally, concluding remarks are given in Sect. 6.

2 Basics of linear graph theory (LGT)

A graph consists of nodes and edges at least one of which is subject to multiple branches as shown in Fig. 1. If the edges have directions, it is called a “directed graph” (digraph), where each edge defines parent/child relationship between sequential nodes. A root is the first node and a tip is the last node. Therefore, the root has no parent, while the tip has no child.

Fig. 1

A directed graph with seven nodes

Figure 1 demonstrates an example of a digraph with seven nodes. First node is the root node, and fourth, fifth and seventh nodes are the tip nodes of the digraph. The parent node of the $j$th node is denoted $\rho (j)$. In this example, $\rho (2)=1$, $\rho (5)=3$, $\rho (4)=2$ and so on. In the so-called canonical tree structure type digraph, the index of a parent node is always smaller than that of its child node. Two sequential nodes are defined as adjacent if they are connected to each other by an edge. The adjacency matrix is an $n\times n$ matrix that shows the connectivity of the nodes. The element in the $i$th row and the $j$th column of the adjacency matrix is 1, if and only if the $i$th node is the child of the $j$th node. Otherwise, it is 0.

The adjacency matrix of a digraph, $\mathbb{S}$, can be expressed as a sum of tensors in the following form:

$$ \mathbb{S}=\sum_{j=2}^{n} \sum_{\kappa \in \rho (j)} \mathbf{e}_{j} \mathbf{e}_{\kappa }^{T} $$

(1)

where $\mathbf{e}_{i}$ is the $i$th column of the $n\times n$ identity matrix. For the digraph given in Fig. 1, $\mathbf{e} _{i}$ ($_{i=1,2, \ldots ,7}$) vectors are defined as

$$ \mathbf{e}_{1}= \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix} , \quad \mathbf{e}_{2}= \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix} \quad ,\ldots , \quad \mathbf{e}_{7}= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ \end{bmatrix} . $$

(2)

Hence

$$ \mathbb{S}=\mathbf{e}_{2}\mathbf{e}_{1}^{T}+\mathbf{e}_{3}\mathbf{e}_{2}^{T}+ \mathbf{e}_{4}\mathbf{e}_{2}^{T}+\mathbf{e}_{5}\mathbf{e}_{3}^{T}+\mathbf{e}_{6} \mathbf{e}_{2}^{T}+\mathbf{e}_{7}\mathbf{e}_{6}^{T} , $$

(3)

$$ \mathbb{S}= \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&0&0&0&0&0&0 \\ 1&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0 \\ 0&1&0&0&0&0&0 \\ 0&0&1&0&0&0&0 \\ 0&1&0&0&0&0&0 \\ 0&0&0&0&0&1&0 \\ \end{array}\displaystyle \right] . $$

(4)

The adjacency matrix, $\mathbb{S}$, contains only one zero row corresponding to the root node and a zero column for each tip node.

3 Spatial operator algebra (SOA) with linear graph theory (LGT)

A full distribution of forces and torques in multibody system can be achieved in a Newton–Euler-based dynamical model. This makes Newton–Euler a better choice when coupling forces and torques matter as in the case of a controller design based on a reaction force. Most importantly, this has to be done in a computationally efficient and systematic way to make the method applicable to complex systems.

Spatial Operator Algebra (SOA) [9, 10] is a computationally efficient recursive algorithm to obtain systematic formulation of the dynamical model of multibody systems which may include serial, tree and closed topologies. SOA is based on Newton–Euler formalism and the full distribution of forces and torques in the multibody system is obtained with sparse operator matrices in a compact form. The algorithm is flexible for topology changes in multibody systems and capable of dealing with constraints. Spatial Kernel Operator (SKOs) and Spatial Propagation Operator (SPOs) represent the distribution of accelerations/forces throughout the bodies of a multibody system. SOA originally uses an inboard numbering scheme where the numeration of the bodies is done in increasing order from the tip to the base. For the sake of being compatible with common literature, we adopt the outboard numbering scheme to SOA as is done in [23].

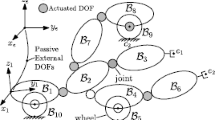
Let us consider Fig. 2 for representing a multibody system including seven rigid bodies connected by various type of joints in a tree topology structure. Within the scope of multibody system modeling, nodes and edges are replaced by body and joint notations, respectively. In Fig. 2, the first body ($\mathbf{B}_{1}$), which is the one connected to ground by the first joint ($\mathbf{J}_{1}$), is called the root body, $\mathbf{B}_{4}$, $\mathbf{B}_{5}$, $\mathbf{B}_{7}$ are the last bodies, which have no child body, they are called tip bodies. If $\mathbf{B}_{2}$ has more than one child body it is called the separation body.

Fig. 2

A multibody system including seven rigid bodies

We use a six-dimensional manifold to represent angular and linear motion of a rigid body. Therefore, a velocity vector in this manifold represents both angular and linear velocities called the “spatial velocity” vector. Within the same manifold the “spatial force” vector is also defined to represent a torque and force pair acting on the same point. The equation of motion of a multibody system can be obtained recursively in a three-sweep algorithm;

• Compute the velocity propagations from the root to tips (outboard).

• Compute the force propagations from the tips to root (inboard).

• Compute the acceleration propagations from the root to tips (outboard).

Figure 3 introduces the defined vectors for sequential bodies in a multibody system:

• $\mathbf{h}_{j}$ and $\mathbf{h}_{\kappa }$ are axis of rotation/translation vectors in 3D space,

• $O_{j}$ and $O_{\kappa }$ are the coordinate frame centers that are placed on bodies along the joints,

• $\mathbf{V}_{j}$ and $\mathbf{V}_{\kappa }$ are spatial velocity vectors at the coordinate frame centers,

• $\mathbf{V}_{jc}$ and $\mathbf{V}_{\kappa c}$ are spatial velocity vectors at the mass centers,

• $\mathbf{F}_{j}$ and $\mathbf{F}_{\kappa }$ are spatial force vectors at the coordinate frame centers,

• $\ell_{j,\kappa }$, is the link vector between the sequential parent and child body coordinate frames,

• $\ell _{j,c}$ and $\ell _{\kappa ,c}$ are the link vectors between the body coordinate frames and body centers.

Fig. 3

Defined vectors for sequential bodies in a multibody system

At this point of the paper, let us introduce a superscript–subscript notation. Let $\alpha_{c}$ indicate a variable, named $\alpha$, which belongs to the body $c$. To express the dimension of a variable, when necessary, we use left-subscript. If a variable $\alpha_{c}$ is of dimension $n\times m$, then we denote it as ${}_{n\times m}{\alpha} _{c}$. If its dimension is $b\times b$, we simply denote it as $_{b} \alpha_{c}$.

In the presence of an one rotational degree of freedom joint between the sequential bodies, the velocity propagation from the parent to child body can be written as

$$\begin{gathered} \mathbf{V}_{\kappa }=\phi _{\kappa ,j}\mathbf{V}_{j} +\mathbf{H}_{\kappa }\dot{\theta}_{\kappa }, \end{gathered}$$

(5)

$$\begin{gathered} {}_{6}\phi_{\kappa ,j}= \left[ \textstyle\begin{array}{c@{\quad}c} {}_{\mathbf{3}}\mathbf{I} & {}_{\mathbf{3}}\mathbf{0} \\ -\mathbf{\ell }_{j,\kappa }\times &{}_{\mathbf{3}}\mathbf{I} \end{array}\displaystyle \right], \qquad {}_{6\times 1}\mathbf{V}_{j} = \begin{bmatrix} \mathbf{\omega }_{j} \\ \mathbf{v}_{j} \end{bmatrix} ,\qquad {}_{6\times 1}\mathbf{H}_{\kappa }= \begin{bmatrix} \mathbf{h}_{\kappa } \\ \mathbf{0} \end{bmatrix} , \end{gathered}$$

(6)

where $\phi _{\kappa , j}$ is a link propagation matrix. ($\ell_{j,\kappa }\times$) is the skew symmetric matrix of the link vector between the body coordinate frames. $\mathbf{H}_{\kappa }$ is the axis of motion vector for a one degree of freedom joint. $\dot{\theta }_{\kappa }$ is the time derivative of the joint variable. It should be noted that the propagation equation can be written for a $q$ degree of freedom joint, using ${}_{6\times q}\mathbf{H}_{j}$. For a translational joint, all we have to do is to change $\mathbf{H}_{\kappa }$ in (5) as

$$ \mathbf{H}_{\kappa }= \begin{bmatrix} \mathbf{0} \\ \mathbf{h}_{\kappa } \end{bmatrix}. $$

(7)

In order to obtain the dynamical model of a multibody system, we need acceleration terms. To get the acceleration propagation between sequential bodies, we need to take the time derivative of the velocity propagation given in (5) and use the $j =\rho ( \kappa )$ parent–child relation as shown in Fig. 3. This yields

$$ \dot{\mathbf{V}}_{\kappa }=\phi_{\kappa ,j}\dot{\mathbf{V}}_{j}+ \mathbf{H} _{\kappa }\ddot{\theta }_{\kappa }+\mathbf{a}_{\kappa }, $$

(8)

where

$$ \mathbf{a}_{\kappa }= \begin{bmatrix} \mathbf{\omega }_{j} \times \mathbf{\omega }_{\kappa } \\ \mathbf{\omega }_{j} \times (\mathbf{\omega }_{j} \times \mathbf{\ell }_{j, \kappa }) \end{bmatrix} . $$

(9)

Although velocity and acceleration propagations are outboard; from the root body to a tip body, force propagation is inboard; from the tip body towards the root body. Torque propagation from child to parent body can be written as

$$ \tau_{j}=\tau_{\kappa }+ \mathbf{\ell }_{j,\kappa } \times \mathbf{f}_{ \kappa }+ \mathbf{\ell }_{j,c}\times \dot{\mathbf{v}}_{j} m_{j}+ \frac{d}{dt}(\mathcal {I}_{j} \mathbf{\omega }_{j}), $$

(10)

where the first two terms come from the child body and the last two terms are due to change in the parent body’s linear and angular momentum, respectively. Force propagation from child to parent body can be written as

$$ \mathbf{f}_{j}=\mathbf{f}_{\kappa }+m_{j} \frac{d}{dt} (\mathbf{v}_{j} + \mathbf{\omega }_{j} \times \mathbf{\ell }_{j,c}), $$

(11)

and (10) and (11) can be written in the matrix form

$$ \mathbf{F}_{j} = \phi_{\kappa ,j}^{T} \mathbf{F}_{\kappa }+ M _{j} \dot{\mathbf{V}}_{j} + \mathbf{b}_{j}, $$

(12)

where

$$ \mathbf{F}_{\kappa }= \begin{bmatrix} \mathbf{\tau }_{\kappa } \\ \mathbf{f}_{\kappa } \end{bmatrix} , \qquad M_{j}= \left[ \textstyle\begin{array}{c@{\quad}c} \mathcal {I}_{j} & m_{j} \mathbf{\ell }_{j,c} \times \\ -m_{j} \mathbf{\ell }_{j,c} \times &{}_{3\times 3}\mathbf{I} m_{j} \end{array}\displaystyle \right] , \qquad \mathbf{\mathbf{b}}_{j}= \begin{bmatrix} \mathbf{\omega }_{j}\times \mathcal {I}_{j} \mathbf{\omega }_{j} \\ m_{j} \mathbf{\omega }_{j} \times (\mathbf{\omega }_{j} \times \mathbf{\ell } _{j,c}) \end{bmatrix} . $$

Consider the multibody system shown in Fig. 2. In order to apply the propagations systematically on the branches of the digraph, an adjacency matrix is expanded to block the weighted adjacency matrix to include the link propagation matrices. Adjacency matrices have 1 or 0 scalar entries for the sequential nodes in a digraph, in the case of block weighted adjacency matrices, 1 or 0 scalar entries are expanded to a $6\times 6$ dimensional unit matrix or zero matrix and SKO (Spatial Kernel Operator) is obtained by using the following equation:

$$ \varepsilon_{\phi }= \sum\limits_{\kappa =2}^{n} \sum_{j \in \rho (\kappa )} \mathbf{e}_{\kappa }\phi_{\kappa ,j} \mathbf{e} _{j}^{T}, $$

(13)

where $\mathbf{e}_{i}$ is a $6n\times 6$ dimensional matrix which contains all zero matrix entries except for the $i$th block which is $6\times 6$ dimensional unit matrix. For the system given in Fig. 2, the $\mathbf{e}_{i}$ (${i=1,2,\ldots,7}$) matrices are defined as

$$ \mathbf{e}_{1}= \begin{bmatrix} {} _{\mathbf{6}}\mathbf{I} \\ {} _{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \end{bmatrix} , \quad \mathbf{e}_{2}= \begin{bmatrix} {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}\mathbf{I} \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \end{bmatrix} , \quad \ldots , \quad \mathbf{e}_{7}= \begin{bmatrix} {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}0 \\ {}_{\mathbf{6}}\mathbf{I} \end{bmatrix} . $$

(14)

Therefore

$$\begin{gathered} \varepsilon_{\phi } =\mathbf{e}_{2}\phi_{2,1}\mathbf{e}_{1}^{T}+\mathbf{e}_{3} \phi_{3,2}\mathbf{e}_{2}^{T}+\mathbf{e}_{4}\phi_{4,2}\mathbf{e}_{2}^{T} +\mathbf{e}_{5}\phi_{5,3}\mathbf{e}_{3}^{T}+\mathbf{e}_{6}\phi_{6,2}\mathbf{e} _{2}^{T}+\mathbf{e}_{7}\phi_{7,6}\mathbf{e}_{6}^{T}, \\ \varepsilon_{\phi }= \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0&0&0&0&0&0&0 \\ \phi_{2,1}&0&0&0&0&0&0 \\ 0&\phi_{3,2}&0&0&0&0&0 \\ 0&\phi_{4,2}&0&0&0&0&0 \\ 0&0&\phi_{5,3}&0&0&0&0 \\ 0&\phi_{6,2}&0&0&0&0&0 \\ 0&0&0&0&0&\phi_{7,6}&0 \end{array}\displaystyle \right] . \end{gathered}$$

(15)

The SPO matrix which includes $n$ bodies is obtained using the lemma in [17],

$$ \varPhi =({}_{6n}\mathbf{I}-\varepsilon_{\phi })^{-1} . $$

(16)

Using the $6n\times 6n$ dimensional $\varPhi$ SPO matrix, all spatial velocities of the bodies in a multibody system can be obtained:

$$ {}_{6n\times 1}\mathbf{V}=\varPhi \mathbf{H} \dot{\theta }, $$

(17)

where

$$\begin{aligned} \mathbf{V}= \begin{bmatrix} \mathbf{V}_{1} \\ \mathbf{V}_{2} \\ \vdots \\ \mathbf{V}_{n} \end{bmatrix} , \qquad {}_{6n\times n}\mathbf{H}= \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{H}_{1}& & & \\ &\mathbf{H}_{2}& & \\ & &\ddots & \\ & & &\mathbf{H}_{n} \end{array}\displaystyle \right] . \end{aligned}$$

The propagation matrix $\varPhi_{T}$ is employed to calculate the velocities of tip points of multibody system. For a system which has $n_{t}$ tip bodies, the propagation matrix $\varPhi_{T}$ is of dimension $6n_{t}\times 6n$. For the system in Fig. 2, the $^{i}\varPhi_{T}$ matrix is given as

$$ ^{i}\varPhi_{T}= \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {}_{\mathbf{6}}0&{}_{\mathbf{6}}0&{}_{\mathbf{6}}0&\phi_{t,4}&\phi_{t,5}& {}_{\mathbf{6}}0&\phi_{t,7} \end{array}\displaystyle \right] . $$

(18)

Hence, tip point velocity of an open-chain is

$$ \mathbf{V}_{T}=\varPhi_{T} \varPhi \mathbf{H} \dot{\mathbf{\theta }}= \mathbf{J} \dot{\theta }, $$

(19)

where $\mathbf{J}$ is the Jacobian operator defined as

$$ \mathbf{J}=\varPhi_{T} \varPhi H. $$

(20)

Spatial accelerations are obtained by taking the derivative of (17);

$$ \dot{\mathbf{V}}= \varPhi \mathbf{H}\ddot{\mathbf{\theta }} + \mathbf{a} . $$

(21)

Spatial forces are distributed inboard (from tip towards to root node) as

$$ \mathbf{F}= \varPhi^{T}\bigl(\mathbf{M} \dot{\mathbf{V}}+ \mathbf{b}+ \varPhi_{T}^{T} \mathbf{F}_{T} \bigr), $$

(22)

where

$$ \mathbf{F}= \begin{bmatrix} \mathbf{F}_{1} \\ \mathbf{F}_{2} \\ \vdots \\ \mathbf{F}_{n} \end{bmatrix} , \qquad \mathbf{M}= \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{M}_{1}& & & \\ &\mathbf{M}_{2}& & \\ & &\ddots & \\ & & &\mathbf{M}_{n} \end{array}\displaystyle \right] , \qquad \mathbf{b}= \begin{bmatrix} \mathbf{b}_{1} \\ \mathbf{b}_{2} \\ \vdots \\ \mathbf{b}_{n} \end{bmatrix} . $$

$\mathbf{F}_{T}$ is for the $6n_{t} \times 1$ dimensional external spatial forces that are applied to tip points.

Applied torques or forces are the projection of the body spatial forces along the axis of motion at the joints. This is stated as

$$ \mathbf{\mathcal {\tau }}=\mathbf{H}^{T} \mathbf{F} . $$

(23)

Therefore, the inverse dynamics of a multibody system is obtained:

$$ \mathbf{\tau }=\mathcal {M}\ddot{\mathbf{\theta }}+\mathbf{C} + \mathbf{J}^{T}\mathbf{F}_{T}, $$

(24)

where

$$\begin{aligned} \begin{aligned} \mathcal {M} &=\mathbf{H}^{T} \varPhi^{T} \mathbf{M}\varPhi \mathbf{H} , \\ \mathbf{C} &=\mathbf{H}^{T}\varPhi^{T}(\mathbf{M}\varPhi \mathbf{a}+\mathbf{b}) . \end{aligned} \end{aligned}$$

(25)

$\mathcal {M} \in \mathbb{R}^{n\times n}$ is a generalized mass matrix for a multibody system, $\mathbf{C} \in \mathbb{R}^{n}$ is the velocity dependent vector includes Coriolis and gravity terms.

The equation of motion regarding the forward dynamics is obtained using (24).

$$ \ddot{\mathbf{\theta }} = \mathcal {M}^{-1}\bigl( {\tau }- \mathbf{C}-\mathbf{J}^{T}\mathbf{F}_{T}\bigr) $$

(26)

4 Path defined directed graph vector ($\mathit{Pgraph}$) method

In the previous sections, the general concept of LGT (Linear Graph Theory) and canonical numeration of digraph were explained. Here we need to pay particular attention to (15) which deals with the interconnection of the bodies in a given system. Without a systematic approach, this equation needs to be manually implemented with a particular attention to connectivity of the bodies. On top of this error prone tedious work, then it comes to updating of coordinate frame vectors which may become a challenging task depending on the complexity of the topology of the system. To avoid all of these problems, we introduce a systematic approach under the name of $\mathit{Pgraph}$ method. $\mathit{Pgraph}$ is an automatic model configuration generator for multibody systems to provide a simplified standard structure for modeling as well as visualization with a significant advantage especially in construction time. Proposed $\mathit{Pgraph}$ algorithm is given by the flow chart in Fig. 4, where SBn is the separation body number, TBn is the tip (terminal) body number, SBS is the last-in-first-out (LIFO) type separation body stack, jdof is the joint degree of freedom vector and dof(i) is the degree of freedom between body i and its parent body.

Fig. 4

Flow chart of $\mathit{Pgraph}$ algorithm

The flow chart can be summarized in following steps.

• 1. Create an empty $\mathit{Pgraph}$ and $jdof$ vectors and assign the root body number to index $i$.

• 2. Add index number to $\mathit{Pgraph}$ and determine the joint DoF between the body $i$ and body $i-1$ (the first element of $jdof$ represents the joint DoF between the root body and ground).

• 3. If body $i$ is a separation body then push the index $i$ to SBS.

• 4. If body $i$ is a tip body then go to Step 5, otherwise assign an untraversed child body number to index $i$, and go to Step 2.

• 5. If the SBS is empty then go to Step 7, otherwise pull the index number from SBS and assign it to $i$, add this index value to $\mathit{Pgraph}$ and add zero element to $jdof$ vector. If separation body $i$ has more than one untraversed child body push the index number to SBS back again.

• 6. Assign an untraversed child body number to index $i$, and go to Step 2.

• 7. End of the algorithm.

$\mathit{Pgraph}$ may not be unique for the same multibody system, since one can choose the untraversed child of a separation body in Step 4. In this paper, left child priority has been adopted. Two examples are presented in Fig. 5 to demonstrate $\mathit{Pgraph}$ and $jdof$ vectors.

Fig. 5

Example multibody systems to demonstrate $\mathit{Pgraph}$ and $jdof$ vectors

In Newton–Euler dynamics, creating a propagation matrix plays a vital role to define the propagation of both spatial velocities and spatial forces in a multibody system. Once $\mathit{Pgraph}$ is obtained, (15) can now be constructed systematically as in the flow chart in Fig. 6. This flowchart makes the implementation of the presented multibody dynamics algorithm straightforward for computer programming.

Fig. 6

Flowchart for creating SPO matrix

During the run time of a simulation, axis of rotation and link vectors need to be updated. However, updating body coordinate frames of a complex topology system can be a complicated task depending on the complexity of the topology. Another important contribution of the proposed $\mathit{Pgraph}$ method is a systematic solution, introduced by the algorithm whose flow chart is given in Fig. 7, to this problem.

Fig. 7

Flowchart for updating body coordinate frames

Updating body coordinate frame algorithm, shown in Fig. 7, employs the following functions:

• $\mathit{Rot}(\mathbf{h},\Delta \theta )_{\kappa }$ is the rotation matrix function based on Rodriguez formulation: $\mathit{Rot}(\mathbf{h},\Delta \theta )_{\kappa }=I + (\mathbf{h}_{\kappa }\times ) \sin\Delta \theta_{\kappa }+ (\mathbf{h}_{\kappa }\times )^{2} (1-\cos\Delta \theta_{\kappa })$.

• The $\mathit{find}(\mathit{Pgraph}, \mathit{Pgraph}(\kappa ))$ function returns the index of the first place of the $\mathit{Pgraph}(k)$ element in $\mathit{Pgraph}$.

• $P$ is a list structure containing the body indices that were inserted to it. $F(P)$, on the other hand, is a function that returns the body coordinate frame vectors of the bodies whose index numbers are in the $P$ list.

Updating steps are demonstrated on a multibody system as an example in Fig. 8.

Fig. 8

Flowchart for updating body coordinate frames

4.1 Model description interface and constraint embedding

When modeling of multibody systems we do not envision people to write the $\mathit{Pgraph}$. Rather, we envision people to fill a simple table and let $\mathit{Pgraph}$ and $\mathit{jdof}$ vectors be created automatically. After all, the $\mathit{Pgraph}$ method is all about multibody system modeling with short construction time.

The name of the body, the name of the parent body, DoF, and the constraint type are the columns of this four column table. But, before this table, the first thing interface asks is the total number of bodies in the model. Once the users enters this number, the four column table gets automatically created with assumptions that the bodies are subject to holonomic constraints, bodies are connected with a single DoF joint in the form of a serial topology and the names of the bodies are sequential numbers starting from 1. Together with this table, digraph representation of the system is displayed on the screen. All the link vectors, axes of rotations, masses, and inertias are set at the default values. At this point the user may change the name of the bodies using alphanumeric characters, select a parent body from the body column (the first column) and change the number of DoF. The user can click on the bodies on the digraph representation to open a properties window to set the initial values of the axes of rotations and link vectors, mass and inertia matrix.

This interface is the foreground of the $\mathit{Pgraph}$ method. At the background, $\mathit{Pgraph}$ method-based multibody modeling software (MMS) will do the actual numbering of the bodies and the construction of the $\mathit{Pgraph}$ and $\mathit{jdof}$ vectors. Accordingly, MMS will obtain the propagation matrix, Jacobian matrix, generalized mass matrix and others. Updating of body coordinate frames will also be done using the $\mathit{Pgraph}$ method.

This interface also provides a separate list so that a user can define the constraints. The last column of the table is updated using this list of constraints. From the digraph representation display, by clicking on the bodies, the user can define conditions on these constraints. As closed kinematic chains, or closed topology systems, are particularly important in multibody dynamics from the force propagation point of view, dealing with such a system, we need to define cut-joints to decompose the closed topology into serial or tree topology system and then impose related constraints. Cut-joint motion constraints can represent both bilateral and unilateral constraints forces. Bilateral constraint forces can be categorized mainly into holonomic and nonholonomic motion constraints and they are constantly involved in the equation of motion. Unilateral constraint forces can occur in the case of body to body contact, body to ground contact or joint limits and these constraint forces are intermittently involved in the equation of motion. The main approaches for handling such constraints are soft contact, penalty and complementarity methods.

In the next section, simulations are performed for a cheetah-like multibody system including open and closed topology subsystems depending on the gait cycle, which is divided into swing, weight acceptance and stance phases. During the swing phase of the gait cycle, the multibody system includes an open topology in the form of serial and tree structures. During the weight acceptance phase when the tip bodies are contacted with ground, Coulomb friction and impact forces are introduced until the linear velocity at the contact point becomes zero. Next is the stance phase where multibody system becomes of closed topology due to the existence of closed kinematic chain, and ground contact forces are computed using holonomic constraints. Since a sticky type ground is not considered here, it is assumed that the ground cannot pull the foot. In other words, ground contact forces can only act in one direction, hence, they are unilateral. On the other hand, this force is only valid in the, so called, ground friction cone. This means that in the case the applied force from foot to ground is outside of the reversed of this cone, the ground friction force will remain on the border of the cone, causing them not to be equal and opposite to each other. Consequently, the foot will slide on the ground.

5 Simulations

Figure 9 shows the $\mathit{Pgraph}$ and $\mathit{jdof}$ vectors on 3D model of the quadruped and the parts of the model are given in Table 1.

Fig. 9

3D CAD model of quadruped

Table 1 Quadruped parts

As a case study, only the stance phase of the gait cycle of quadruped is considered so that simulation results can be compared with ADAMS software to verify. Simulation results of the other phases are not suitable for comparing since ADAMS uses graphical contact detection models, which is not in the scope of this paper. Constraint forces during the stance phase of the gait cycle are defined for the tip points of the quadruped to keep them at zero velocity by the following equation:

$$\begin{aligned} \begin{aligned} \mathbf{V}_{T} &=J\dot{\mathbf{\theta }}=\mathbf{0} , \\ \dot{\mathbf{V}}_{T} &=J\ddot{\mathbf{\theta }}+\dot{J}\dot{\mathbf{\theta }}= \mathbf{0}. \end{aligned} \end{aligned}$$

(27)

Multiplying the forward dynamics equation with $J$ leads to

$$ J\ddot{\mathbf{\theta }}=J\mathcal {M}^{-1}\bigl(\mathcal {T}-\mathbf{C}-J ^{T}\mathbf{F}_{T}\bigr). $$

(28)

Plugging (28) into (27), the constraint forces can be solved:

$$\begin{aligned} 0 &=J\mathcal {M}^{-1}\bigl(\mathcal {T}-\mathbf{C}-J^{T} \mathbf{F}_{T}\bigr)+ \dot{J}\dot{\theta} , \\ J\mathcal {M}^{-1}J^{T} \mathbf{F}_{T} &= J\mathcal {M}^{-1}( \mathcal {T}-\mathbf{C})+\dot{J}\dot{\mathbf{\theta }}, \\ \mathbf{F}_{T} &= \varOmega^{-1}\bigl(J\mathcal {M}^{-1}(\mathcal {T}- \mathbf{C}) + \dot{J}\dot{\mathbf{\theta }}\bigr), \end{aligned}$$

(29)

where

$$\begin{aligned} \varOmega =J\mathcal {M}^{-1}J^{T}. \end{aligned}$$

The 3D CAD model of the quadruped robot shown in Fig. 9 is formed in the solid commercial package CATIA v5 and it is imported to ADAMS software for analyzing and comparing the dynamical simulation results. The maximum difference between the two results (the one obtained using ADAMS and the one obtained using $\mathit{Pgraph}$-based MMS) is less than 4.0% as shown in Figs. 11 and 12.

Simulation results including tip point forces are obtained for 0.25 seconds. Angular accelerations of the bodies around $\mathbf{z}$ direction are shown in Figs. 11 and 12, comparing results obtained using ADAMS and $\mathit{Pgraph}$-based multibody modeling software (MMS). Figure 10 displays the pictorial representation of the configuration of the system in 50 ms intervals. Tip point forces for the left back paw are given in Fig. 13.

Fig. 10

Simulation frames (0–0.25 s)

Fig. 11

Angular accelerations of the bodies around $\mathbf{z}$ direction (Body 0–Body 8)

Fig. 12

Angular accelerations of the bodies around $\mathbf{z}$ direction (Body 9–Body 16)

Fig. 13

Tip point reaction forces from the ground on left back paw

6 Conclusions

The presented method of a path defined digraph vector ($\mathit{Pgraph}$) is a novel approach for the construction time efficient dynamical modeling of complex systems which may include multiple combinations of serial and tree topologies, as well as closed kinematic chain systems. Propagation matrix for spatial velocity and spatial force that plays a pivotal role in Newton–Euler-based multibody modeling can be obtained conveniently using the $\mathit{Pgraph}$ method. Similarly, systematic updating of body coordinate frame vectors, which can be a challenge in complex topology systems, is easily performed using the proposed method. Combining this technique with a model description interface and constraint embedding, the construction time of complex multibody system modeling is greatly reduced. This technique is especially useful for systems changing topology, such as a walking mechanisms where bilateral and unilateral constraints are conditionally embedded.