On the Mitigation of Interference Imposed by Intruders in Passive RFID Networks

Abstract

RFID networks are becoming an integral part of the emerging Internet of Things (IoT) era. Within this paradigm passive RFID networks have emerged as low cost energy-efficient alternatives that find applicability in a wide range of applications. However, such RFID networks and devices, due to their limited capabilities, can easily become vulnerable to several intrusive actions. In this paper, the problem of proactively protecting a passive RFID network from security threats imposed by intruders that introduce high interference to the system resulting in the possible disruption of the network’s proper operation is investigated. Passive RFID tags are associated with a well-designed utility function reflecting on one hand their goal to have their signal properly demodulated by the reader, and on the other hand their risk level of participating in the network, stemming from their hardware characteristics among others, thus characterizing them as normal or intruder tags. An interference mitigation risk aware (IMRA) problem is introduced aiming at maximizing each tag’s utility function, thus implicitly enforcing tags to conform to a more social behavior. Due to its nature, the proposed problem is formulated as a non-cooperative game among all the tags (normal and intruders) and its Nash equilibrium point is determined via adopting the theory of supermodular games. Convergence of the game to its Nash equilibrium is also shown. A distributed iterative and low-complexity algorithm is proposed in order to obtain the Nash equilibrium point and the operational effectiveness of the proposed approach is evaluated through modeling and simulation.

1 Introduction

Radio Frequency Identification (RFID) technology aims at tagging and identifying an object. The concept of RFID is envisioned as part of the Internet of Things and has been recently used in numerous applications from asset tracking to supply chain management and from medication compliance and home navigation for the elderly and cognitively impaired to military troop movements monitoring. RFID networks are exposed to a broader attack surface given their IoT nature, thus it is of great interest not only to develop security mechanisms that can protect critical data from harm (e.g. data encryption techniques), but also the application of intelligent control mechanisms that will enable an RFID network to work properly and in a reliable manner with minimum intervention [1].

An RFID basic characteristic is the conversion of a set of objects into a mobile network of nodes, which is of dense and ad-hoc nature and it is mainly utilized for objects tracking, environmental monitoring and events triggering [2]. The fundamental components of an RFID network are: (a) the RFID reader/interrogator and (b) the RFID tag, which can be either active or passive or semi-passive. The RFID reader communicates with the RFID tags via emitting radio waves and receiving signals back from the tags. The active RFID tags and semi-passive RFID tags embed a radio signal transceiver and an internal power source. The main advantages of active RFID tags are that they can activate themselves regardless of the presence of a reader in proximity, while providing greater operating range and supporting advanced functionalities compared to passive RFID tags. On the other hand, their main disadvantages are their high cost and significant environmental limitations due to the presence of the battery, i.e., large size, and their high transmission power [3]. Therefore, passive RFID tags emerge as the most energy-efficient, inexpensive solution to build an RFID network. Their low transmission power backscatter commands and low cost make them suitable for a wide range of IoT applications.

1.1 Motivation

A passive RFID network consists of a number of RFID readers and a number of passive RFID tags. The RFID tags have no on-board power source and derive their reflection power from the signal of an interrogating reader. A passive RFID tag is activated by the reader’s forward/transmission power, which is much more powerful than the reverse/reflection power sent back by the tag to the reader. Each tag must be able to reflect sufficient amount of power to the reader, which is mapped to a targeted signal-to-interference-plus-noise ratio (SINR), in order for its signal to be demodulated by the reader. The reflection power of all passive RFID tags within the RFID network contribute to the overall existing interference, which consequently drives the tags to reflect with even more power (while their maximum reflection power is limited) to ensure the demodulation of their signal at the reader.

Within such a passive RFID network, a security threat with respect to the reliable operation of the system is the presence of one or more intruding passive RFID tags that could act as interferers. In other words, such “attacker/intruder tags” can take advantages of their position in the network and their hardware characteristics may simply introduce strong interference in the rest of the passive RFID tags’ reflections rendering their signals hard or almost impossible to be demodulated at the RFID reader side. Taking into account the difficulty in identifying those intruder-tags and eventually removing them from the network an alternative strategy in dealing with this problem is to reduce the potential harm that they can impose on the system. This can be achieved by enforcing the tags to conform to a more social behavior with respect to their reflection behavior (for example, not using unnecessarily high reflection power), thus limiting the potential risks. The latter may range from simply wasting unnecessarily power to completely disturbing the proper operation of the system by making some objects impossible to be tracked.

Passive RFID tags share the same system bandwidth towards reflecting back their signal to the reader. Thus, increased level of interference caused by the rest of the tags will enforce a tag to increase also its reflection power in order to achieve a desired power level (which is translated to a target SINR value) that eventually will enable the demodulation of its signal by the reader. Therefore, passive RFID tags compete with each other to determine their optimal reflection powers that enable their signal demodulation. Masked or disguised intruder-tags pretending to act as normal passive RFID tags, tend to introduce high interference level to the passive RFID network, thus disrupting or even causing failure of its proper operation. Furthermore, due to the distributed nature of passive RFID networks and the absence of a single administrative entity to control tags’ reflection powers, while considering the potential risk level associated with the operation of each tag, distributed solutions should be devised in order to secure the reliable operation of the RFID networks and impose on participating entities to adhere to proper operation rules and behavior.

1.2 Contributions and Outline

In this paper, the problem of risk-aware mitigation of interference imposed by intruders in passive RFID networks is studied and treated via a game theoretic approach. Envisioning the Internet of Things (IoT) and battery-free wireless networks as key part of the emerging 5G era, the system model of a passive RFID network is initially introduced (Sect. 2.1). A utility-based framework is adopted towards representing passive RFID tag’s goal to have its signal being properly demodulated by the reader, while simultaneously considering its reflection power and its corresponding risk level – the latter being mapped to tag’s hardware related characteristics (Sect. 2.2). Due to the distributed nature of the proposed interference mitigation risk aware (IMRA) problem, it has been formulated as a non-cooperative game among passive RFID tags, which can be either normal or intruder-tags (Sect. 3.1) and IMRA game’s Nash equilibrium point is determined (Sect. 3.2). The convergence of the IMRA game to the Nash equilibrium is shown (Sect. 4), while a non-cooperative distributed low-complexity and iterative algorithm is presented to determine the Nash equilibrium of the IMRA game (Sect. 5). The performance of the proposed approach is evaluated in detail through modeling and simulation (Sect. 6), while related research work from the recent literature is presented in Sect. 7. Finally, Sect. 8 concludes the paper.

2 System Model

2.1 Passive RFID Networks

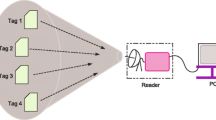
Figure 1 presents the considered topology of a passive RFID network. An RFID reader is assumed to activate the $N = N_{n} + N_{in}$ passive RFID tags, which reflect back their information in order for their signal to be demodulated by the reader. The number of normal passive RFID tags is denoted by $N_{n}$, while the number of intruder-tags is $N_{in}$. Respectively, the set of normal RFID tags is denoted by $S_{n}$ and the corresponding set of intruder-tags by $S_{in}$. The overall set of passive RFID tags within the network is $S = S_{n} \cup S_{in}$. Representative real life examples of this assumed topology include: (a) monitoring stock availability on retail shelves, (b) identifying books in shelves of library systems, and (c) monitoring the military equipment supply chain.

Fig. 1.

Passive RFID network – library system example.

RFID reader’s transmission power is assumed to be fixed, i.e. $P_{R}$, depending on its technical characteristics. In the examined topology, a simplified RFID network has been considered, consisting of one RFID reader and multiple passive RFID tags, which can be either normal or intruder-tags. The proposed framework can be easily extended to multiple RFID readers and multiple tags, while each one of the tags will be associated to its nearest RFID reader. Let $P_{i} , \, i = 1,2, \ldots \,N$ denote the reflection power of the i ^th, $i \in S = S_{n} \cup S_{in}$ passive RFID tag, where $P_{i} \in A_{i} ,A_{i} = \left[ {0,P_{i}^{Max} } \right]$. The maximum feasible reflection power $P_{i}^{Max}$ of each tag depends on: (a) the characteristics of the topology (e.g. distance $d_{i}$ between the RFID reader and the tag) and (b) tag’s hardware characteristics. Assuming single hop communication among the reader and the tag, the upper bound of passive RFID tag’s reflection power is:

$$ P_{i}^{Max} = P_{R} \cdot G_{R} \cdot G_{i} .K_{i} \left( {\frac{\lambda }{{4\pi d_{i} }}} \right)^{2} $$

(1)

where $P_{R}^{{}}$ is the transmission power of the RFID reader R communicating directly with the i ^th passive RFID tag, $G_{R}^{{}}$ and $G_{i}^{{}}$ are the RFID reader’s and passive RFID tag’s directional antenna’s gain, respectively, $K_{i}$ is the backscatter gain of the i ^th tag and the factor $\left( {\frac{\lambda }{{4\pi d_{i} }}} \right)^{2}$ describes the free space path loss.

In a backscatter communication system, i.e. communication from the N passive RFID tags to the reader, the signal-to-interference-plus-noise ratio (SINR), $\gamma_{i}$, must meet a required threshold $\gamma_{i}^{target}$ for the tag’s signal to be able to be demodulated by the reader. The SINR at the RFID reader R for each passive RFID tag $i,i \in S = S_{n} \cup S_{in}$ is given by [12]:

$$ \gamma_{i} = \frac{{h_{i} P_{i} }}{{\sum\limits_{j \ne i} {h_{j} P_{j} } + n}} $$

(2)

where $h_{i}$ represents the channel loss from the i ^th tag to the reader and $n$ contains the background noise. The term $\sum\limits_{j \ne i} {h_{j} P_{j} }$ denotes the RFID network interference at the RFID reader when receiving data from the i ^th tag.

2.2 Utility Function

Towards formulating passive RFID tag’s behavior under a common optimization framework, the concept of utility function is adopted. Each passive RFID tag (either normal or intruder) is associated with a utility function, which consists of two parts: (a) the pure utility function and (b) the risk function. The pure utility function represents the tag’s degree of satisfaction in relation to the achievement of the targeted SINR $\gamma_{i}^{target}$ and the corresponding power consumption. The risk function represents the risk level (with respect to its impact and potential harm to the system) of each passive RFID tag considering its reflection power and its hardware characteristics, i.e., directional antenna’s gain $G_{i}^{{}}$ and backscatter gain $K_{i}$. It is noted that a passive RFID tag is considered as a potential attacker/intruder of the overall RFID network if it introduces high level of interference due to its hardware characteristics, thus it should be penalized for its malicious and non-social behavior. The latter could result in increased reflection power $P_{i}$ from the rest of the tags. Considering that $P_{i}^{Max}$ is limited it could be the case that the tags cannot achieve their targeted SINR and consequently the reader will be unable to demodulate their signal. Therefore, the risk function provides the means to enforce the tags to conform to a more social behavior and limiting the potential impact of an intruder. Also note that an intruder will be masking its presence and behavior, and other than trying to impose high interference in the rest of the tags and therefore disrupt the normal system operation, its behavior will look normal to avoid being detected.

Based on the above discussion, each passive RFID tag’s utility function can be formulated as follows:

$$ U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} ) = U_{pure} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} ) - R\left( {G_{i}^{{}} ,K_{i} ,P_{i} } \right) $$

(3)

where $U_{pure} ( \cdot )$ denotes passive RFID tag’s pure utility function and $R\left( \cdot \right)$ its risk function. As it was discussed above, $U_{pure} ( \cdot )$ reflects the tradeoff between achieving the target SINR and the necessary corresponding reflection power, while considering the imposed interference by the rest of the tags. The risk function is introduced as a cost function penalizing the tags, which present non-social/malicious behavior and tend to damage/attack the RFID network via introducing high interference level due to their increased reflection power. Thus, the penalty increases for the tags that try to reflect with high power and have privilege against other tags due to their hardware characteristics.

Throughout the rest of the paper, without loss of generality and for presentation purposes, we consider the following passive RFID tag’s utility function:

$$ U(P_{i} ,\varvec{P}_{{\varvec{ - i}}} ) = \frac{{f_{i} (\gamma_{i} )}}{{P_{i} }} - G_{i} \cdot K_{i} \cdot P_{i} $$

(4)

where $f_{i} (\gamma_{i} )$ is a sigmoidal-like function with respect to $\gamma_{i}$, where the inflection point is mapped to the target SINR $\gamma_{i}^{target}$ of the $i,i \in S$ tag. For presentation purposes, we set $f_{i} (\gamma_{i} ) = \left( {1 - e^{{ - A\gamma_{i} }} } \right)^{M}$, where A, M are real valued parameters controlling the slope of the sigmoidal-like function.

3 Interference Mitigation Risk Aware (IMRA) Game

3.1 Problem Formulation

Let $G_{IMRA} = \left[ {S,\left\{ {A_{i} } \right\},\left\{ {U_{i} ( \cdot )} \right\}} \right]$ denote the corresponding non-cooperative interference mitigation risk aware game, where $S = \left\{ {1,2, \ldots ,N} \right\}$ is the index set of the passive RFID tags, $A_{i} = \left( {0,P_{i}^{Max} } \right] \subseteq\,\,R^{N}$ is the strategy set of the i ^th passive RFID tag and $U_{i} ( \cdot )$ is its utility function, as defined before. Each passive RFID tag aims at maximizing its utility via determining its reflection power $P_{i}$ in a non-cooperative manner. Thus, the Interference Mitigation Risk Aware (IMRA) game can be expressed as the following maximization problem:

$$ \left( {IMRA \, game} \right)\quad \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{{P_{i} \in A_{i} }} U_{i} = \mathop {\hbox{max} }\limits_{{P_{i} \in A_{i} }} U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} ), \, \forall i \in S} \hfill \\ {\quad s.t. \, 0 < P_{i} \le P_{i}^{Max} } \hfill \\ \end{array} $$

(5)

The solution of the IMRA game determines the optimal equilibrium for the RFID system, consisting of the individual decisions of each passive RFID tag (either normal or intruder-tag), given the decisions made by the rest of the tags in the passive RFID network. The solution of the IMRA game is a vector of passive RFID tags’ reflection powers $\varvec{P}^{ *} = (P_{1}^{*} ,P_{2}^{*} , \ldots ,P_{N}^{*} ) \in A$, $A = \cup A_{i} ,i \in S = S_{n} \cup S_{in}$, where $P_{i}^{*}$ is the reflection power of tag i. The Nash equilibrium approach is adopted towards seeking analytically the solution of the non-cooperative IMRA game. Based on this approach, which is most widely used for game theoretic problems, we have the following definition.

Definition 1.

The power vector $\varvec{P}^{ *} = (P_{1}^{*} ,P_{2}^{*} , \ldots ,P_{N}^{*} ) \in A$, $A = \cup A_{i} ,i \in S = S_{n} \cup S_{in}$, is a Nash equilibrium of the IMRA game, if for every $i \in S = S_{n} \cup S_{in}$ $U_{i} (P_{i}^{*} ,\varvec{P}_{{\varvec{ - i}}}^{*} ) \ge U_{i} (P_{i}^{{}} ,\varvec{P}_{{\varvec{ - i}}}^{*} )$ for all $P_{i}^{{}} \in A_{i}$.

The interpretation of the above definition of Nash equilibrium point is that no passive RFID tag, either normal or intruder-tag, has the incentive to change its strategy (i.e., reflection power), due to the fact that it cannot unilaterally improve its perceived utility by making any change to its own strategy, given the strategies of the rest of the tags. Moreover, it is concluded that the existence of a Nash equilibrium point guarantees a stable outcome of the IMRA game, while on the contrary the non-existence of such an equilibrium point is translated to an unstable and unsteady situation of the RFID system, stemming from high risk and interference levels imposed by the intruder-tags.

Furthermore, note that the utility function introduced in Eqs. (3) and (4) is generic enough to capture both normal and intruder-tags behavior, however it is not characterized by desirable properties, e.g., quasi-concavity. Therefore, alternative techniques from the field of game theory should be adopted in order to prove the existence of Nash equilibrium for the IMRA game.

3.2 Towards Determining the Nash Equilibrium

Towards proving the existence of at least one Nash equilibrium of the IMRA game, the theory of supermodular games is adopted. Supermodular games are of great interest as an optimization and decision making tool, due to the fact that they encompass many applied models, they tend to be analytically appealing since they have Nash equilibria and they have the outstanding property that many solutions yield the same predictions [13]. Moreover, supermodular games comply very well with intruder-tags’ behavior in the IMRA game, due to the fact that they are characterized by strategic complementarities, i.e., when one intruder-tag takes a more competitive and aggressive action (i.e., increase its reflection power), then the rest of the tags want to follow the same behavior, causing the RFID system to be led to borderline operation.

Considering the Interference Mitigation Risk Aware (IMRA) problem studied in this paper, we examine a single-variable supermodular game, which is defined as follows:

Definition 2.

A game $G = \left[ {S,\left\{ {A_{i} } \right\},\left\{ {U_{i} ( \cdot )} \right\}} \right]$ with strategy spaces $A_{i} \subset \Re$, $\forall i \in S = S_{n} \cup S_{in}$ is supermodular if for each $i,i \in S$, the utility function $U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ has non-decreasing differences (NDD) in $(P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ [13].

The property of non-decreasing differences (NDD) for the objective function $U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ is formally defined as follows.

Definition 3.

The objective function $U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ has non-decreasing differences (NDD) if for all $\varvec{P}_{{\varvec{ - i}}} \ge \varvec{P}_{{\varvec{ - i}}}^{{\mathbf{\prime }}}$, the difference $U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} ) - U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}}^{{\mathbf{\prime }}} )$ is non-decreasing in $P_{i}$. Moreover, if the objective function $U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ is smooth (i.e., it has derivatives of all orders), then it has non-decreasing differences in $(P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ if and only if

$$ \frac{{\partial^{2} U_{i} \left( \varvec{P} \right)}}{{\partial P_{i} \partial P_{j} }} \ge 0, \, j \ne i,\, \, j,i \in S $$

(6)

Examining the IMRA game as it has been formulated in relation (5), it is observed that it is not a supermodular game according to Definition 3, due to the exogenous risk factors $G_{i}^{{}} ,K_{i}$ included in the objective function. Therefore, the strategy space of each passive RFID tag should be slightly modified, in order to show that condition (6) holds true, so that the resulting game is supermodular.

Theorem 1.

The IMRA game’s utility function $U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$ as defined in (4) has non-decreasing differences (NDD) in $(P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$, i.e. $\frac{{\partial^{2} U_{i} \left( \varvec{P} \right)}}{{\partial P_{i} \partial P_{j} }} \ge 0, \, j \ne i,\, \, j,i \in S$, if and only if

$$ \gamma_{i} \in \left[ {\frac{\ln M}{A}, + \infty } \right) $$

(7)

Proof.

Towards showing that the IMRA game’s utility function has non-decreasing differences (NDD) in $(P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$, the sign of the second order partial derivative, i.e. $\frac{{\partial^{2} U_{i} \left( \varvec{P} \right)}}{{\partial P_{i} \partial P_{j} }}$, is examined as follows:

$$ \frac{{\partial^{2} U_{i} \left( \varvec{P} \right)}}{{\partial P_{i} \partial P_{j} }} = \frac{AM}{{P_{i}^{2} }}\frac{{h_{i} }}{{\sum\limits_{j \ne i} {h_{j} P_{j} } + n}}\gamma_{i}^{2} e^{{ - A\gamma_{i} }} \left( {1 - e^{{ - A\gamma_{i} }} } \right)^{M - 2} \left( {1 - Me^{{ - A\gamma_{i} }} } \right) $$

It is noted that the term $\frac{AM}{{P_{i}^{2} }}\frac{{h_{i} }}{{\sum\limits_{j \ne i} {h_{j} P_{j} } + n}}\gamma_{i}^{2} e^{{ - A\gamma_{i} }}$ is non-negative for all $\gamma_{i} \ge 0$. Moreover, considering the term $\left( {1 - e^{{ - A\gamma_{i} }} } \right)^{M - 2}$, we have: $\left( {1 - e^{{ - A\gamma_{i} }} } \right)^{M - 2} \ge 0 \Leftrightarrow \gamma_{i} \ge 0$. Furthermore, considering the sign of the term $\left( {1 - Me^{{ - A\gamma_{i} }} } \right)$, we have: $\left( {1 - Me^{{ - A\gamma_{i} }} } \right) \ge 0 \Leftrightarrow \gamma_{i} \ge \frac{\ln M}{A}$.

Based on the above, it is concluded that the IMRA game’s utility function $U(P_{i} ,\varvec{P}_{{\varvec{ - i}}} ) = \frac{{f_{i} (\gamma_{i} )}}{{P_{i} }} - G_{i} \cdot K_{i} \cdot P_{i}$ has non-decreasing differences in $(P_{i} ,\varvec{P}_{{\varvec{ - i}}} )$, if $\gamma_{i} \ge \frac{\ln M}{A}$.∎

Based on Definitions 2 and 3 and Theorem 1, we easily conclude the following.

Theorem 2.

The IMRA game $G_{IMRA} = \left[ {S,\left\{ {A_{i} } \right\},\left\{ {U_{i} ( \cdot )} \right\}} \right]$ is supermodular in a modified strategy space $A_{i}^{\prime } = \left[ {P_{i}^{Min} ,P_{i}^{Max} } \right] \subset A_{i}$, where $P_{i}^{Min}$ is derived from $\gamma_{i} \ge \frac{\ln M}{A}$.

At this point, it should be noted that the constraint $\gamma_{i} \ge \frac{\ln M}{A}$ is not an additional constraint to the initial formulation of the IMRA game, due to the fact that the target SINR value $\gamma_{i}^{target}$ introduced in Sect. 2 is equivalent to the value $\gamma_{i}^{target} = \frac{\ln M}{A}$. Specifically, it has already been explained in Sect. 2 that $\gamma_{i}^{target}$ is mapped to the inflection point of $f_{i} (\gamma_{i} )$. Thus, we have: $\frac{{\partial^{2} f_{i} (\gamma_{i} )}}{{\partial \gamma_{i}^{2} }} = 0 \Leftrightarrow \gamma_{i}^{target} = \frac{\ln M}{A}$. The meaning of the above description is that the passive RFID tag should have sufficient reflection power $P_{i} \in \left( {0,P_{i}^{Max} } \right]$ such that $\gamma_{i} \ge \gamma_{i}^{target}$ is ensured in order for its signal to be demodulated by the reader. Thus, assuming an ideal scenario where we do not have intruder-tags and the topology is favorable (i.e., not relatively extremely large distances for an RFID network) so as tag’s available power $P_{i} \in \left( {0,P_{i}^{Max} } \right]$ is sufficient in order to be read by the reader, then each tag’s goal is to achieve an SINR value greater or at least equal to the target one, i.e., $\gamma_{i} \ge \gamma_{i}^{target}$. Therefore, in the case that intruder-tags introduce high interference resulting in violation of the condition $\gamma_{i} \ge \gamma_{i}^{target} = \frac{\ln M}{A}$, this is essentially translated to no guarantee of Nash equilibrium existence (i.e., unstable situation of the RFID system), thus some or even all tags will not achieve $\gamma_{i}^{target}$ and consequently their signal will not be demodulated, and as a consequence the reader’s objective will not be fulfilled.

Theorem 2, i.e., proving that the IMRA game is supermodular in the modified strategy space $A_{i}^{\prime } \subset A_{i}$ $,\forall i \in S = S_{n} \cup S_{in}$, guarantees the existence of a non-empty set of Nash equilibria [13]. Therefore, the following holds true:

Theorem 3.

The modified IMRA game $G^{\prime}_{IMRA} = \left[ {S,\left\{ {A_{i}^{\prime } } \right\},\left\{ {U_{i} ( \cdot )} \right\}} \right]$ has at least one Nash equilibrium, which is defined as follows:

$$ P_{i}^{*} = \mathop {\arg \hbox{max} }\limits_{{P_{i} \in A_{i}^{\prime } }} U_{i} (P_{i} ,\varvec{P}_{{\varvec{ - i}}} ) $$

(8)

It should be noted that Theorem 3 guarantees the existence of at least one Nash equilibrium, while this point is not necessarily unique. Practically, the best response in (8) can be solved via single variable calculus utilizing the Extreme Value Theorem [14], and the most energy-efficient Nash equilibrium (i.e. the Nash equilibrium characterized by less reflection power $P_{i}$, while guaranteeing the target SINR $\gamma_{i}^{target}$) is adopted by each passive RFID tag.

4 Convergence of the IMRA Game

In this section, we prove the convergence of the interference mitigation risk aware (IMRA) game to a Nash equilibrium point, as this is determined by relation (8). Towards this direction, the best response strategy of each passive RFID tag $i,i \in S = S_{n} \cup S_{in}$ is denoted by $BR_{i}$ and is given as follows:

$$ BR_{i} \left( {P_{i} } \right) = \mathop {\arg \hbox{max} }\limits_{{P_{i} \in A_{i}^{\prime } }} U_{i} \left( {P_{i} ,\varvec{P}_{{\varvec{ - i}}} } \right) = P_{i}^{*} $$

(9)

As shown in [15], the fundamental step for showing the convergence of the IMRA game to a Nash equilibrium, as obtained by Eq. (8), is to show that the best response function $\varvec{BR(P)}$ is standard. In general, a function is characterized as standard if for all $\varvec{P} > \varvec{0}$, where $\varvec{P} = \left( {P_{1} ,P_{2} , \ldots ,P_{N} } \right)$, the following conditions/properties hold true:

• (i) Positivity: $\varvec{BR(P)} > \varvec{0}$;

• (ii) Monotonicity: if $\varvec{P}^{{\mathbf{\prime }}} \ge \varvec{P}$ then $\varvec{BR} (\varvec{P}^{{\mathbf{\prime }}} )\ge \varvec{BR(P)}$;

• (iii) Scalability: for all $\alpha$ > 1, $\alpha \varvec{BR(P)} \ge \varvec{BR(}\alpha \varvec{P)}$.

Theorem 4.

The modified IMRA game $G_{IMRA}^{{\prime }} = \left[ {S,\left\{ {A_{i}^{{\prime }} } \right\},\left\{ {U_{i} ( \cdot )} \right\}} \right]$ converges to a Nash equilibrium, as expressed in (8).

Proof.

As presented in Eq. (9) each passive RFID tag’s best response strategy is the argument of the maximum of the tag’s utility function with respect to the reflection power $P_{i} \in A_{i}^{{\prime }}$. Considering all the passive RFID tags participating in the IMRA game, we have $\varvec{BR(P)} = \left( {BR_{1} (P_{1} ),BR_{2} (P_{2} ), \ldots ,BR_{N} (P_{N} )} \right) = (P_{1}^{*} ,P_{2}^{*} , \ldots ,P_{N}^{*} )$. Towards proving that the best response function $\varvec{BR(P)}$ is standard, the corresponding aforementioned properties can be easily shown:

• (i) $\varvec{P} = \left( {P_{1} ,P_{2} , \ldots ,P_{N} } \right) > \varvec{0}$, thus $\varvec{BR(P)} > \varvec{0}$;

• (ii) if $\varvec{P}^{{\mathbf{\prime }}} \ge \varvec{P}$ then via Eq. (9), i.e., $BR_{i} \left( {P_{i} } \right) = P_{i}^{*}$ we conclude that $\varvec{BR(P}^{{\mathbf{\prime }}} \varvec{)} \ge \varvec{BR(P)}$;

• (iii) for all $\alpha$ > 1, then via Eq. (9), i.e., $BR_{i} \left( {P_{i} } \right) = P_{i}^{*}$ we conclude that $\varvec{BR(P^{\prime})} \ge \varvec{BR(}\varvec{P^{\prime})}$, where the equality holds true. ∎

Based on Theorem 4, it is guaranteed that the IMRA game converges to a stable situation, i.e. to a Nash equilibrium point. Detailed numerical results with respect to the convergence of the proposed IMRA game to a Nash equilibrium are presented in Sect. 6.

5 The IMRA Algorithm

Passive RFID networks, as part of the Internet of Things, are characterized by their distributed nature and the absence of any central entity that can take decisions about the actions of the passive RFID tags on their behalf. Thus, each RFID tag should determine in a distributed manner its equilibrium reflection power after being activated by the reader. Except for its hardware characteristics and its channel loss, which is customized/personal information already known by each tag, the only supplementary necessary information, towards determining the equilibrium powers, is the overall network interference which is broadcasted by the reader to the tags. Therefore, in this section we propose a distributed iterative and low complexity algorithm in order to determine the Nash equilibrium point(s) of the IMRA game. The proposed IMRA algorithm runs every time the RFID reader activates the passive RFID tags in order to collect their information.

6 Numerical Results and Discussions

In this section, we provide some numerical results illustrating the operation, features and benefits of the proposed overall framework and in particular the IMRA algorithm. Furthermore, the efficiency and effectiveness of the proposed approach is demonstrated via representative comparative scenarios.

Specifically, in Sect. 6.1 we initially demonstrate the convergence of the proposed Interference Mitigation Risk Aware (IMRA) algorithm. Moreover, the convergence time of the algorithm in terms of required iterations is studied and indicative real time-values are provided in order to show its applicability in realistic passive RFID scenarios. Then, in Sect. 6.2, the advantages of adopting the IMRA framework, in terms of controlling intruder-tags reflection power, are presented. The results obtained by the proposed IMRA approach are compared against two alternatives, namely: (a) the case where passive RFID tags reflect with their maximum available reflection power without considering any interference mitigation and/or power control scheme (in the following referred to as Max Reflection Scenario), and (b) the case where the IMRA adopts a more strict risk aware policy by the tags (e.g., convex risk function with respect to tag’s reflection power) enforcing intruders in a more strict manner, compared to a linear risk aware policy, to adopt a social behavior (in the following referred to as IMRA - Convex Risk Scenario). Finally, in Sect. 6.3, an evaluation of intruders’ impact on system’s reliability and effectiveness is provided for the IMRA framework and the results are compared to the corresponding outcome from the Max Reflection Scenario, described above.

Throughout our study, we consider a passive RFID network consisting of one RFID reader and $N = N_{n} + N_{in}$ passive RFID tags. RFID reader’s transmission power is fixed, i.e., $P_{R}^{{}} = 2W$ and also the gain of its antenna is considered to be $G_{R} = 6\,{\text{dBi}}$. The minimum received power by the RFID reader, in order to demodulate the received signal from the tags is assumed $P_{TH} = - 15\,{\text{dBm}}$ and corresponds to the passive RFID tag’s target SINR $\gamma_{i}^{target}$. The passive RFID network operates at $f = 915\,\text{MHz}$. The channel loss from the i ^th tag to the reader is formulated using the simple path loss model, $h_{i} = c_{i} /d_{i}^{a}$, where d _i is the distance of tag i from the reader, a is the distance loss exponent (e.g. a = 4) and c _i is a log-normal distributed random variable with mean 0 and variance $\sigma^{2} = 8({\text{dB)}}$ [12]. The normal passive RFID tags are characterized by their backscatter gain $K_{i,n} = 60\,\%$ and the gain of their directional antenna is $G_{i,n} = 12\,\text{dBi}$, while the corresponding values for the intruder-tags are: $K_{i,in} = 90\,\%$ and $G_{i,in} = 16\,\text{dBi}$. The topology that has been considered in Sects. 6.1 and 6.2, corresponds to a shelve of a library (equivalently it could be a part of any linear supply chain) containing N = 100 passive RFID tags and the distance d _i among the reader and each tag ranges in the interval [0.2 m, 1.5 m].

6.1 Convergence Evaluation of the IMRA Algorithm

We assume that the RFID network consists of N _n  = 100 = N passive RFID tags while for demonstration purposes only in the following we present the behavior of 10 tags that are placed in increasing distance from the RFID reader. Figure 2 illustrates tags’ reflection powers’ evolution as a function of the iterations required for the IMRA algorithm to converge at game’s $G_{IMRA}^{{\prime }}$ Nash equilibrium point. It should be noted that the same results hold true in terms of necessary iterations for convergence, if intruder-tags were residing in the network, while the absolute values of their reflection powers would be different.

Fig. 2.

IMRA algorithm’s convergence (10 selected tags presented in the graph).

The corresponding results reveal that the convergence of the proposed IMRA algorithm is very fast since less than thirty-five iterations are required in order to reach the equilibrium for all tags, starting from randomly selected feasible initial reflection powers. Moreover, for all practical purposes we notice that in less than twenty five iterations the values of the reflection powers have approximately reached their corresponding equilibrium values. The IMRA algorithm was tested and evaluated in an Intel (R) Core (TM) 2 DUO CPU T7500 @ 2.20 GHz laptop with 2.00 GB available RAM and its runtime was less than 0.5 ms, thus it can be easily adopted in a realistic scenario. Furthermore, given the distributed nature of the IMRA algorithm, i.e., the calculations are made by each RFID tag, its runtime does not depend on the number of passive RFID tags residing in the RFID network, therefore it is quite a scalable approach in single hop communication passive RFID networks.

6.2 Improving System Operational Efficiency Through Interference Mitigation

As it has been presented and discussed in detail in this paper, one of the main reasons that can disturb the proper operation of an RFID network (in terms of properly reading the passive RFID tags) is the presence of intruder-tags that are enabled with favorable hardware characteristics and thus being able to reflect with high reflection power and increase the network interference. Therefore, the IMRA framework can control the harm that intruder-tags can cause to the network via introducing a risk aware function, which penalizes more the intruders compared to the normal tags.

Figure 3 presents the sum of intruders’ reflection power as a function of the percentage of intruders within the network, while normal tags are replaced by intruders. As mentioned before, three comparative scenarios are presented:

Fig. 3.

Sum of Intruders’ reflection power as a function of the percentage of intruders.

• (i) Max Reflection Scenario: each tag (either normal or intruder) reflects with its maximum feasible reflection power.

• (ii) IMRA – Linear Risk Scenario: the IMRA framework presented in this paper, where the risk function is linear with respect to the reflection power, i.e., $R\left( {G_{i} ,K_{i} ,P_{i} } \right) = G_{i} \cdot K_{i} \cdot P_{i}$.

• (iii) IMRA – Convex Risk Scenario: the IMRA framework adopts a convex risk function which in essence penalizes more the intruder-tags, i.e., $R\left( {G_{i} ,K_{i} ,P_{i} } \right) = G_{i} \cdot K_{i} \cdot e^{{P_{i} }}$.

Based on the results of Fig. 3, it is clearly observed that the IMRA framework decreases considerably the impact of the intruder-tags on the network via keeping their reflection powers at low levels, thus mitigating the interference caused by them. Moreover, it is observed that as the risk function becomes more strict, thus imposing an even more social behavior to the intruders, the sum of intruders’ reflection powers can be further decreased. Therefore, based on the potential threat that an RFID network is expected to confront, different risk functions can be adopted, resulting in better level of protection.

6.3 Evaluation of Intruders’ Impact on System Reliability and Effectiveness

Towards studying the impact of intruders on system’s reliability and effectiveness, a detailed comparative study between the Max Reflection Scenario and the IMRA – Linear Risk Scenario is presented. A simplified topology has been considered as presented in Fig. 4 towards keeping most of the parameters the same among the passive RFID tags (e.g., distance from the reader), thus observing the impact of replacing normal RFID tags with intruders. The tags with x symbol refer to those tags that do not achieve their target SINR, while the tags with √ symbol are those that can be read by the reader. The star-tag depicts the intruder.

Fig. 4.

Circle topology with N = 10 passive RFID tags and d = 0.4 m.

In Fig. 5, the results reveal that in the Max Reflection Scenario, the intruder-tag that replaces a normal tag, dominates the rest of the tags and achieves to be read by the RFID reader, due to its comparatively larger reflection power. In parallel, it causes high interference to the network, thus normal RFID tags cannot be read, due to the fact that their maximum available reflection power is not sufficient to overcome the imposed interference. Observing the multiple examples in Fig. 5 for different number of intruders in the Max Reflection Scenario, we conclude that the intruder-tags achieve to be read, while the normal tags fail. However, this is completely undesirable due to the fact that an intruder-tag may reflect erroneous or misleading data, or alternatively few intruder-tags suffice to cause the non-reading of many normal tags.

Fig. 5.

Read (√) and non-read tags (x) for different numbers of intruders ().

On the other hand, the IMRA – Linear Risk Scenario achieves to isolate the intruder-tags and not read them, while it enables the RFID reader to properly read the normal tags. This observation stems from the fact that intruder tags are penalized via the linear risk function towards reducing their reflection power, which becomes quite low so that it is not sufficient to enable the intruder-tag to be read by the reader. This outcome is of great practical importance because it can be adopted as a methodology to isolate intruder-tags and support RFID network’s proper operation.

7 Related Work

Towards guaranteeing the non-disruptive reliable operation of a passive RFID network two critical dimensions should be considered: (a) energy-efficiency and (b) risk level of RFID devices, mainly for the following reasons:

• (i) The maximum RFID reader’s transmission power is limited by regulations [4] and it is the only source power enabling the RFID network’s operation, thus it should be utilized/spent in a sophisticated manner.

• (ii) RFID readers’ and tags’ emissions and reflections, respectively, can cause interference in the passive RFID network (resulting in limited read range and inaccurate reads) and in the neighboring systems.

• (iii) The optimization of readers’/tags’ transmission/reflection power contributes to readers’ energy saving, prolonging passive RFID network’s lifetime, building an energy-efficient network and extending passive RFID tags’ reflection range.

• (iv) Malicious passive RFID tags characterized by high risk level can cause great interference levels in the passive RFID network, thus threatening its proper operation.

Several frameworks have been proposed in the recent literature in order to deal with energy-efficiency and/or secure and reliable operation mainly in active RFID networks (i.e. including active or semi-passive RFID tags). In [5], a security solution for RFID supply chain systems has been proposed via classifying the supply chain environments in two categories, i.e. weak and strong security mode. A set of RFID protocols, e.g., tag reading, security mode switching, secret updating protocols, are introduced to enable the dual security modes. The authors in [6], propose a key management protocol to ensure the privacy of the RFID reader and tags in the communication channel among tags, reader and backend server. The European research project BRIDGE [7] has focused its efforts in providing security technology that supports RFIDs’ potential in mitigating existing business and security process risks. In [8], a trusted platform module is introduced only for the RFID readers, which constitute the core root of trust measurement for the overall framework.

Additional research works have targeted their efforts mainly to the power control and energy-efficiency improvement problem. In [9], a power control mechanism of RFID reader’s transmission power considering the proximity and motion sensors towards detecting an RFID tag in reader’s range is presented. In [10], an energy-efficient RFID tags inventory algorithm is proposed towards adjusting RFID reader’s transmission power via automatically estimating the number of tags in its coverage area. In [11], a dynamic power algorithm is introduced, where a Received Signal Strength Indication (RSSI) receiver is employed at RFID reader’s side to measure the strength of the received signal and adapt RFID reader’s transmission power accordingly. In [12], two heuristic power control algorithms are presented considering the interference measured at each RFID reader or its achieved signal-to-interference ratio (SIR), respectively, as local feedback parameters in order to adapt RFID readers’ transmission power.

The proposed framework in this paper differs from the aforementioned approaches associated with the secure and reliable operation of an RFID network in the sense that the IMRA framework capitalizes on power control and interference management techniques in order to mitigate potential risks introduced by intruding passive RFID tags. Its main novelty is that the IMRA approach proactively protects the RFID network from malicious behaviors of passive RFID tags, thus supporting its proper and non-disturbed operation. Based on an interference mitigation risk aware technique, masked or disguised intruder-tags pretending to act as normal within the RFID network are enforced to conform to a social-behavior, otherwise their existence can be a priori identified due to their increased reflection power levels. As such, the IMRA framework is able to contribute towards securing the proper and reliable operation of the RFID network reducing the threat and harm stemming from intruder-tags.

8 Concluding Remarks and Future Work

In this paper, the problem of mitigating the interference imposed by the intruders towards protecting the proper operation of passive RFID networks has been studied. Passive RFID networks are characterized by limited available power, thus they can become vulnerable to intruder-tags, which cause high interference to the network, resulting in inability of reading passive RFID tags. Passive RFID tags are characterized as normal or intruders and all of them adopt a well-designed utility function, which reflects their goal of being read by the reader, while it also captures their risk level depending on their hardware characteristics. An Interference Mitigation Risk Aware (IMRA) problem is formulated as a maximization problem of each tag’s utility function and solved based on a game theoretic approach, i.e., supermodular games. The Nash equilibrium of the IMRA game (i.e., vector of passive RFID tags’ reflection powers) is determined and a distributed algorithm towards calculating it is introduced. Indicative numerical results show the superiority of the proposed framework and more specifically its important attribute to identify and isolate the intruder-tags from the network.

Though in the current work as a proof of concept we focused on simple topologies where for example only one reader exists in the network, as part of our current research work we are performing additional extensive simulations in order to evaluate the performance of the proposed approach under more complex topologies, including additional variable (mobile) readers. The additional power overhead imposed to the tags by introducing the risk function can be further investigated and quantified. To further validate the applicability of our proposed interference mitigation risk aware framework, this framework should be also tested either in experimental IoT infrastructures or realistic large scale passive RFID networks, e.g., library systems, warehouses, etc. Furthermore, the IMRA framework can be extended in multi-hop (tag-to-tag communication) passive RFID networks, where the constraints of tags’ maximum reflection powers and the appropriate communication path/route should be considered and investigated. Moreover, the utility-based framework that has been proposed in this work can be utilized towards implementing a utility-based risk-aware/secure routing protocol in passive tag-to-tag RFID networks. In addition, different forms and/or expressions of the utility functions should be investigated in order to better represent scenarios where different RFID tags with different criticality and priority are included in the system or alternatively to express intruders’ utilities with differentiated forms compared to those of normal tags. Finally, part of our current and future research work in this area, considers additional game theoretic analysis where a team of intruders is strategically placing themselves and acting so as to induce maximum damage in the network, while the proposed network control and management framework attempts to react against such malicious attempts, by minimizing if not totally eliminating the potential damage. Given the distributed nature of the emerging IoT paradigm, additional types of attacks may be considered including localized ones that mainly aim at damaging a subset of RFIDs only.