Damage in Vascular Tissues and Its Modeling

Abstract

The present chapter reviews vessel wall histology and summarizes relevant continuum mechanical concepts to study mechanics-induced tissue damage. As long as the accumulated damage does not trigger strain localizations, the standard nonpolar continuum mechanical framework is applicable. As an example, a damage model for collagenous tissue is discussed and used to predict collagen damage in the aneurysm wall at supra-physiologic loading. The physical meaning of model parameters allow their straight forward identification from independent mechanical and histological experimental data. In contrast, if damage accumulates until the material’s stiffness looses its strong ellipticity, more advanced continuum mechanical approaches are required. Specifically, modeling vascular failure by a fracture process zone is discussed, such that initialization and coalescence of micro-defects is mechanically represented by a phenomenological cohesive traction separation law. Failure of ventricular tissue due to deep penetration illustrates the applicability of the model. Besides appropriate continuum mechanical approaches, laboratory experiments that are sensitive to constitutive model parameters and ensure controlled failure propagation are crucial for a robust parameter identification of failure models.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

4.1 Introduction

Understanding damage mechanisms of soft biological tissue is critical to the sensitive and specific characterization of tissue injury tolerance. Such knowledge may help improving clinical treatment planning by accurately assessing the rupture risk of Abdominal Aortic Aneurysms (AAAs) or the vulnerability of carotid plaques, for example. In addition, design optimization of medical devices critically depends on the proper understanding of short-term and long-term damage effects on the interaction of such devices with the biological tissue. Relating tissue chemical morphology to engineering concepts like constitutive models, i.e., histomechanical modeling is one promising way to better understanding tissue damage.

Mechanical force is transmitted from the macroscopic (tissue) length scale down to the atomistic length scale, and different microstructural constituents are loaded differently. Consequently, raising the macroscopic load leads to local stress concentrations in the tissue, and, if high enough, starts damaging it at specific spots. For example, micro-defects like breakage and/or pull-out of collagen fibrils gradually develop, which in turn weakens/softens the tissue. In healthy tissues at physiological stress levels, healing continuously repairs such defects in order to maintain the tissue’s structural integrity. For example in bones, osteoclasts remove damaged tissue which is then newly formed by osteoblasts. However, at supra-physiological stress level or for diseased tissues, healing cannot fully repair such micro-defects and the tissue continues to accumulate weak links, which in turn irreversibly diminish its strength. If the damage level, i.e., the numbers of defects per tissue volume exceeds a certain threshold, micro-defects join each other, and form macro-defects. Finally, a single macro-defect may propagate and finally rupture the tissue.

Despite increasing experimental and analytical efforts to investigate failure-related irreversible effects of soft biological tissue, the underlying mechanisms are still poorly understood. There is still no clear definition of what damage is, and conventional indicators of mechanical injury (such as visible failure and loss of stiffness) may not identify the tissue’s tolerance to injury appropriately. Micro-defects locally weaken the material and a Kachanov-like [1] damage parameter can only represent damage of inert material, but neglects all biological aspects of tissue damage. Consequently, a more complete definition of damage in a biological tissue is needed, and “a description of the mechanical and physiological changes that result in anatomical and functional damage” [2] defines more broadly damage of soft biological tissues. Clearly, damage mechanisms and specific injury tolerance is closely related to the individual tissue type.

This chapter adresses only the passive mechanical aspects of vascular tissue. Its first section outlines general consequences of damage and failure on the solution of (initial) boundary value problems. The second section reviews tissue histology with focus on the collagen in vessel walls. Then, a histologically motivated constitutive model for collagenous soft biological tissue for supra-physiological stress states is introduced. Finally, a continuum mechanics concept for strain localization problems is reviewed, and representative examples demonstrate the proposed modeling approaches.

4.2 Continuum Mechanical Consequences of Damage—The Basics

Local damage diminishes local tissue stiffness, and, if massively enough, defines a strain softening material. For a strain softening material the stress decreases with increasing strain, such that the tissue’s stiffness matrix is no longer positive definite. This changes the fundamental physics of the underlying mechanical problem, which is demonstrated by a simple rod under tension shown in Fig. 4.1. The rod of cross-section A is made of a material with a strain-dependent Young’s modulus $E(\varepsilon )$. Here, the strain $\varepsilon =u'=\partial u/\partial x$ depends on the displacement u, and the notations $\ddot{u}=\partial ^2 u/\partial t^2$ and $u''=\partial ^2 u/\partial x^2$ are used. Equilibrium along the axial direction, i.e., $-\rho A \text {d}x\ddot{u}-A [\sigma ]_x+A [\sigma ]_{x+\text {d}x}=0$, leads, with the Taylor series expansion $[\sigma ]_{x+\text {d}x}=[\sigma ]_{x}+[E(\varepsilon ){\text {d}}^2u/{\text {d}}x^2]_{x}{\text {d}}x+\mathcal {O}(2)$, to the governing equation

$$\begin{aligned} \ddot{u}- c u''=0 \quad \text { with } c= \frac{E(\varepsilon )}{\rho }\;, \end{aligned}$$

(4.1)

with $\mathcal {O}(2)$ denoting second-order terms. Most important, the parameter c renders the physics of the problem, i.e., for $c<0$ the problem is hyperbolic, while for $c>0$ it is elliptic. Consequently, for $E(\varepsilon )>0$ waves can propagate along the rod, while this is prohibited for $E(\varepsilon )<0$, i.e., at strain softening conditions. For the multidimensional small strain case the 1D condition $E(\varepsilon )>0$ relates to the strong ellipticity condition. This condition states that $\Delta \varvec{\varepsilon }:\mathbb {C}:\Delta \varvec{\varepsilon }>0$ for all possible strain increments $\Delta \varvec{\varepsilon }$, where $\mathbb {C}$ denotes the (nonconstant) elasticity tensor [3]. For finite strain problems a similar condition holds [4, 5].

Fig. 4.1

Forces acting on the material point of a rod under tension

4.2.1 Strain Localization

Following [6], strain localization is considered in a rod of length L that is discretized by n finite elements of equal lengths. The rod’s material follows the bilinear stress versus strain law as shown in Fig. 4.2. First, the stress increases linearly (at the stiffness E) until it reaches the elastic limit stress Y, and then it decreases linearly (at the softening h) until it is stress-free.

Fig. 4.2

Development of a strain localization in a rod of material with bilinear stress–strain properties and discretized by n finite elements. In the upper part of the figure different loading states are sketched and related to labeled points in the stress strain curve

The rod’s right end is pulled to the right, at the gradually increasing displacement $\Delta _0$. In response to that, the load F in the rod gradually increases to the maximum load $F=F_{\text {max}}$ (state (b) in Fig. 4.2), where all finite elements are strained equally $\varepsilon =\Delta /L$. Further increase in $\Delta$ causes a reduction of the load F and the solution bifurcates. Specifically, a single element (the one with the (numerically) smallest cross-section; in Fig. 4.2 this element is filled grey) follows the strain softening path, while all the other finite elements elastically unload (state (c) in Fig. 4.2) until the rod is completely stress-free (state (d) in Fig. 4.2). Consequently, the grey finite element in Fig. 4.2 accumulates the total strain, i.e., it developed a strain localization.

Next we introduce the averaged (smeared) strain

$$\begin{aligned} \bar{\varepsilon }=\Delta /L=\frac{h}{L}[(n-1)\varepsilon +\varepsilon ^*]=\frac{1}{n}\left[ \frac{(n-1)\sigma +Y}{k}+\frac{Y-\sigma }{h}\right] , \end{aligned}$$

(4.2)

all over the rod. Here, $\varepsilon =\sigma /k$ and $\varepsilon ^*=Y/k+(Y-\sigma )/h$ denote the strain in the $n-1$ non-localized and in the one localized finite elements, respectively. In order to derive this relation, the equilibrium, i.e., equal stress $\sigma$ in all finite elements, was used. Relation (4.2) is linear and can be inverted to express the stress versus averaged strain response

$$\begin{aligned} \sigma = \frac{\bar{\varepsilon } h k n - Y(h+k)}{h(n-1)-k}. \end{aligned}$$

(4.3)

Most importantly, Eq. (4.2) depends on the number n of finite elements, i.e., on the used discretization. Figure 4.3 illustrates this dependence.

Fig. 4.3

Stress–strain response of a rod discretized by n number of elements and using non-regularized (a) and regularized (b) approaches. The case uses an initial elastic stiffness $E=10$ MPa and a elastic limit $Y=1$ MPa. Localization is induced by linear softening $h=1$ MPa (a), and the regularized linear softening $h=1/n$ MPa (b), respectively

4.2.2 Dissipation

The dissipation for complete failure relates to the energy per reference volume that is dissipated until the force diminishes and reads

$$\begin{aligned} \mathcal {D}=\int \limits _0^{\bar{\varepsilon }_1}\sigma \text {d}\bar{\varepsilon }=\frac{Y^2}{2 k}+ \int \limits _{\bar{\varepsilon }_0}^{\bar{\varepsilon }_1}\sigma \text {d}\bar{\varepsilon } =\frac{Y^2}{2 n}\left( \frac{1}{h}+\frac{1}{k}\right) . \end{aligned}$$

(4.4)

Here, $\bar{\varepsilon }_0=Y/k$ and $\bar{\varepsilon }_1=Y(h + k)/(h k n)$ denote the strains at the elastic limit and at zero stress (complete failure), respectively. This relation can also be derived by taking the dissipation of the localized element $Y^2(1/k+1/h)/2$ and weighting it according to the volume ratio, i.e., by 1 / n.

Again, the total dissipation depends on the number n of finite elements used to discretize the rod. Most surprisingly, the dissipation vanishes for $n\rightarrow \infty$, i.e., the continuum solution of the problem. This was already indicated in Fig. 4.3a (case $n=10\;000$), where loading and unloading pathes were practically identical. This is an obviously nonphysical result (How can an inherently dissipative process like damage have no dissipation?) and direct consequence of localization. Specifically, for this (non-regularized) case the material volume that is affected by the localization tends to zero, such that also the dissipation vanishes. It is emphasized that this is not a problem of the finite element model but the hypothetical entity of a nonpolar continuum yields vanishing localization volume [7]. In contrast to the volume, the localization defines a surface, which area remains finite, i.e., for the above discussed rod problem, the localization area is equal to the rod’s cross-sectional area A.

4.2.3 Regularization

For every material, the material’s microstructure prevents from a vanishing localization volume. For example in collagenous tissues at tensile failure, the length of the pulled-out collagen fibers introduces an internal length scale, which in turn leads to a finite localization volume. Such an internal length scale can also be introduced in the model to prevent from a vanishing localization volume. The simplest solution is to relate the softening modulus h to the finite element size according to $h_{\text {reg}}=h/n$. Consequently, the regularized averaged strain and the regularized dissipation (i.e., regularized versions of Eqs. (4.2) and (4.4)) read:

$$\begin{aligned} \bar{\varepsilon }_{\text {reg}}=\frac{1}{n}\left[ \frac{(n-1)\sigma +Y}{k}+\frac{Y-\sigma }{h/n}\right] \;;\; \mathcal {D}_{\text {reg}}=\frac{Y^2}{2 n}\left( \frac{1}{h /n}+\frac{1}{k}\right) . \end{aligned}$$

(4.5)

The stress versus regularized strain is shown in Fig. 4.3b, and it is noted that the regularized dissipation of the continuum problem $\mathcal {D}_{{\text {reg}}\,n\rightarrow \infty }=Y^2/(2 h)$ yields the physically correct result. Despite such a regularization fully resolves the 1D problem, it leads to stress locking for general 3D problems that is discretized by an unstructured FE mesh. More advanced approaches will be discussed in Sect. 4.5 of this chapter.

4.2.4 Experimental Consequences

Experimental tensile testing into the strain softening region forms at least one localization (failure) zone, which is schematically illustrated in Fig. 4.4. Consequently, the data, that is recorded in the softening region (i.e., post the localization) is dependent on the marker positions, which were used to calculate the averaged strain $\bar{\varepsilon }=(l-L)/L$. Here, l and L denote the spatial and referential distances between two markers, see Fig. 4.4. Markers that are close to the localization zone (case (a) in Fig. 4.4) yield a rather ductile response, while markers that are far away from the localization zone (case (c) in Fig. 4.4) show much more brittle test results. Case (c) shows even snap-back, i.e., average strain and force decrease with failure progression. In such a case neither force-control nor clamp displacement-control can ensure stable failure progression, and other control mechanism are needed.

Fig. 4.4

Tensile experiment to complete tissue failure. Averaged strains $\bar{\varepsilon }$ are computed from three different sets of markers, i.e., $\bar{\varepsilon }_i=(l_i-L_i)/L_i\;i=1,2,3$ with l and L denoting deformed and undeformed distances between markers, respectively. To the right the schematic averaged strain versus stress curves that are associated with the three different sets of marker positions are shown

Summary   Mechanical damage triggers micro-defects, which diminishes tissue stiffness. Continuous accumulation of damage may lead to coalescence of micro-defects and the formation of strain localization. A strain localization is triggered as soon as the strong ellipticity condition is violated, and requires regularized computational models paired with properly controlled experimental designs.

4.3 Histology of the Vessel Wall

A sound histological understanding is imperative for the mechanical characterization of vascular tissue. The vessel wall is composed of intima, media, and adventitia (see Fig. 4.5), layers that adapt to their functional needs within certain physiologic limits.

The intima is the innermost layer of the artery. It comprises primarily a single layer of endothelial cells lining the arterial wall, resting on a thin basal membrane, and a subendothelial layer of varying thickness (depending on topography, age, and disease).

The media is the middle layer of the artery and consists of a complex three-dimensional network of Smooth Muscle Cells (SMCs), elastin and bundles of collagen fibrils, structures that are arranged in repeating Medial Lamellar Units (MLU) [8]. The thickness of MLUs is independent of the radial location in the wall and the number of units increases with increasing vessel diameter. The tension carried by a single MLU in the normal wall remains constant at about 2 + 0.4 N/m [8]. The layered structure is lost towards the periphery and clear MLUs are hardly seen in muscular arteries.

The adventitia is the outermost layer of the artery and consists mainly of fibroblasts and ExtraCellular Matrix (ECM) that contains thick bundles of collagen fibrils. The adventitia is surrounded by loose connective tissue that anchors the vessel in the body. The thickness of the adventitia depends strongly on the physiological function of the blood vessel and its topographical site.

Fig. 4.5

Histomechanical idealization of a young and normal elastic artery. It is composed of three layers: intima (I), media (M), adventitia (A). The intima is the innermost layer consisting of a single layer of endothelial cells, a thin basal membrane and a subendothelial layer. Smooth Muscle Cells (SMCs), elastin, and collagen are key mechanical constituents in the media arranged in a number of Medial Lamellar Units (MLUs). In the adventitia the primary constituents are collagen fibers and fibroblasts. Collagen fibers are assembled by collagen fibrils of different undulations that are interlinked by ProteoGlycan (PG) bridges

4.3.1 The Extracellular Matrix

The ECM provides an essential supporting scaffold for the structural and functional properties of vessel walls. The ECM mainly contains elastin, collagen, and proteoglycans (PGs) [9] and their three-dimensional organization is vital to accomplish proper physiological functions. The ECM, therefore, rather than being merely a system of scaffolding for the surrounding cells, is an active mechanical structure that controls the micro-mechanical and macro-mechanical environments to which vascular tissue is exposed.

While elastin in the ECM is a stable protein having half-life times of tens of years [10], collagen is normally in a continuous state of deposition and degradation [11] at a normal half-life time of 60–70 days [12]. Physiological maintenance of the collagen structure relies on a delicate (coupled) balance between degradation and synthesis. Fibroblasts, myofibroblasts, SMCs, and other cells perceive changes in the mechanical strains/stresses and adjust their expression and synthesis of collagen molecules in order to account for the changes in their micro-mechanical environment. In parallel, collagen is continuously degraded by matrix metalloproteinases (MMPs).

4.3.2 Collagen and Its Organization

Collagen determines the mechanics of the vessel wall at high loads, i.e., loading states that are of primary interest when studying mechanics-induced accumulation of damage. Collagen fibrils, with diameters ranging from fifty to a few hundreds of nanometers are the basic building blocks of fibrous collagenous tissues [13]. Clearly, the way how fibrils are organized into suprafibrilar structures has a large impact on the tissue’s macroscopic mechanical properties. Already 60 years ago Roach and Burton [14] reported that collagen mainly determines the mechanical properties of arterial tissue at high strain levels. Since that time a direct correlation between the collagen content and the tissue’s stiffness and strength has become generally accepted. Earlier observations indicated that the collagen-rich abdominal aorta was stiffer than the collagen-poor thoracic aorta [15, 16] and later regional variations of aortic properties were specifically documented, see [17] for example. Numerous further references were provided by the seminal works of Fung [18] and Humphrey [19]. Besides the amount of collagen fibers in the wall, also their spatial orientation [13] (and their spread in orientations [20]) are critical microstructural parameters with significant implications on the tissue’s macroscopic mechanical properties.

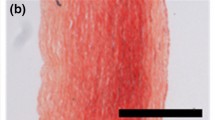
Collagen is intrinsically birefringent and Polarized Light Microscopy (PLM) provides an ideal method for its detection and analysis [21–23]. Combined with a Universal Rotary Stage (URS), PLM allows a quantitative analysis of collagen organization in the vessel wall [24–26]. Figure 4.6 shows a histological image of the AAA wall and illustrates a large mix bag of azimuthal alignment. Extinctions within the larger collagen fibers (see Fig. 4.6b) arose from the planar zigzag structure of collagen fibrils [27, 28]. The quantitative analysis of such images provides the 3D collagen fiber orientation density function $\rho _{\text {exp}}(\theta ,\phi )$, where $\theta$ and $\phi$ denote azimuthal and elevation angles, respectively. Specifically, these angels are defined by (in-plane) rotation and (out-of-plane) tilting of the URS until an individual collagen fiber lies perpendicular to the light ray of the PLM [24]. Finally, the experimentally identified collagen fiber orientations may be fitted to a statistical distribution, like the Bingham distribution [29]

$$\begin{aligned} \rho (\theta ,\phi )=c^{-1}\exp [\kappa _1(\cos \theta \cos \phi )^2+\kappa _2(\cos \phi \sin \theta )^2], \end{aligned}$$

(4.6)

where $\kappa _1$ and $\kappa _2$ denote distribution parameters to be identified from experimental data. In addition c serves a as normalization parameter, such that $\int _{\phi =0}^{\pi /2}\int _{\theta =0}^{2\pi }\rho \cos \phi {\text {d}}\phi \text {d}\theta =1$ holds, i.e., the total amount of collagen fibers remains constant. Further details are given elsewhere [26] and Fig. 4.7 illustrates the collagen fiber distribution in the AAA wall, for example.

Fig. 4.6

Polarized Light Microscopy (PLM) image taken from the Abdominal Aortic Aneurysm (AAA) wall. a Typically observed collagen organizations in the AAA wall, showing a large mix bag of azimuthal alignment. The horizontal sides of the images denote the circumferential direction. The collagen that is oriented perpendicular to the linear polarized light defines the extinctions seen in the image. Picrosirius red was used as a birefringent enhancement stain and the images were taken at crossed polars on the microscope. b Segmented portion of a single collagen fiber of diameter d that is formed by a bundle of collagen fibrils. Extinctions at distances of $\delta$ denote the wavelength of the collagen fibrils that form the collagen fiber

Fig. 4.7

Bingham distribution function (red) fitted to the experimentally measured fiber orientation distribution (light-blue) in the Abdominal Aortic Aneurysm (AAA) wall. Least-square optimization of Eq. (4.6) with experimental measurements taken from Polarized Light Microscopy (PLM) defined Bingham parameters of $\kappa _1=11.6$ and $\kappa _2=9.7$

4.3.3 Proteoglycans

Proteoglycan (PG) bridges may provide interfibrillar load transition [30, 31], a necessity for a load-carrying collagen fiber. Specifically, small proteoglycans such as decorin bind noncovalently but specifically to collagen fibrils and cross-link adjacent collagen fibrils at about 60 nm intervals [30]. Reversible deformability of the PG bridges is crucial to serve as shape-maintaining modules [30] and fast and slow deformation mechanisms have been identified. The fast (elastic) deformation is supported by the sudden extension of about 10 % of the L-iduronate (an elastic sugar) at a critical load of about 200 pN [32]. The slow (viscous) deformation is based on a sliding filament mechanism of the twofold helix of the glycan [30], and explains the large portion of macroscopic viscoelasticity seen when experimentally testing collagen.

PG-based cross-linking is supported by numerous experimental studies showing that PGs play a direct role in inter-fibril load sharing [30, 33–35]. This has also been verified through theoretical investigations [36–38]. However, it should also be noted that the biomechanical role of PGs is somewhat controversial, and some data indicates minimal, if any, PG contribution to the tensile properties of the tissue [36, 39, 40].

Summary   At higher strains collagen fibers, and their interaction with the ECM, are the dominant load-carrying structures in the vascular wall. Specifically, the amount and organization of these structures dominate vessel wall’s stiffness, strength, and toughness. Consequently, mechanical failure of soft biological tissues is often closely related to rupture, pull-out or plastic stretching of collagen fibers.

4.4 Irreversible Constitutive Modeling of Vascular Tissue

Constitutive modeling of vascular tissue is an active field of research and numerous descriptions have been reported. A phenomenological approach [41–45] may successfully fit experimental data, but it cannot allocate stress or strain to the different histological constituents in the vascular wall. Structural constitutive descriptions [20, 46–52] overcome this limitation and integrate histological and mechanical information of the arterial wall.

Specifically, one class of models, histomechanical constitutive models say, aims at integrating collagen fiber stress $\sigma$ and orientation density $\rho$ according to Lanir’s pioneering work [46]. This powerful approach assumes that the macroscopic Cauchy stress $\varvec{\sigma }$ is defined by a superposition of individual collagen fiber contributions, i.e.,

$$\begin{aligned} \varvec{\sigma }=\frac{2}{\pi }\int \limits _{\phi =0}^{\pi /2}\int \limits _{\theta =0}^{\pi /2} \rho (\phi ,\theta )\sigma (\lambda ){\text {d}ev}(\mathbf{m }\otimes \mathbf{m })\cos \phi \text {d}\phi \text {d}\theta + p\mathbf{I }, \end{aligned}$$

(4.7)

where $\mathbf{m }=\mathbf{F }\mathbf{M }/|\mathbf{F }\mathbf{M }|$ denotes the spatial orientation vector of the collagen fiber. In Eq. (4.7) the collagen fiber’s Cauchy stress $\sigma (\lambda )$ is related to its stretch $\lambda$. In addition, the term $p\mathbf{I }$ denotes the hydrostatic stress with p being a Lagrange parameter that is independent from the tissue’s constitution but is defined by the problem’s boundary conditions.

Equation (4.7) is numerically integrated by spherical t-designs, i.e., $\int _\omega (\bullet ) {\text {d}}\omega \approx (4\pi /l_{\text {int}}) \sum _{l=1}^{l_{\text {int}}} (\bullet )_l$, where $l_{\text {int}}$ denotes the total number of integration points. A spherical t-design integrates a polynomial expression $(\bullet )$ of degree $\le t$ exactly [53], and further details regarding the numerical integration are given elsewhere [54].

4.4.1 An Elastoplastic Damage Model for Collagenous Tissue

Exposing biological soft tissue to supra-physiological mechanical stresses rearranges the tissue’s microstructure by irreversible deformations. Damage-related effects (such as, for tendon and ligament [55, 56] and for vascular tissue [57–59]) and plasticity-related effects (such as, for skin [60], tendon and ligament [55, 61, 62] and vascular tissues [59, 63]) have been documented. These observations triggered the development of models that account for damage [64–66], plasticity [67, 68], and fracture [69–73]. Most commonly a macroscopic (single scale) view of tissues is followed, which cannot account for the (experimentally observed) localized structural rearrangement of collagen fibrils at supra-physiological mechanical stress. For example, in tendon tissue spatial micro-failure (most likely collagen fibril rupture) is seen already at $51\pm 12$ % of the ultimate tissue strength [74], which might even have been preceded by damage from intra-fibrillar sliding [75]. In contrast to a macroscopic metric, histomechanical modeling according to Eq. (4.7) naturally integrates localized damage of individual collagen fibers.

Modeling assumptions   Vascular tissue is regarded as a solid mixture at finite deformations, where collagen fibers are embedded in an isotropic matrix material. An orientation density function $\rho (\mathbf{M })=\rho (-\mathbf{M })$ defines the spatial alignment of collagen fibers with respect to the reference volume, see Sect. 4.3.2. Specifically, $\rho (\mathbf{M })$ defines the amount of collagen that is aligned along the direction $\mathbf{M }$ with $|\mathbf{M }|=1$, see [20, 46].

Fig. 4.8

Schematic load-carrying mechanisms of a collagen fiber assembled by a number of collagen fibrils. Load transition across collagen fibrils is provided by Proteglycan (PG) bridges. Antiparallel anionic glycosaminoglycan duplex binds non-covalently to the collagen fibrils at the proteglycan protein (P)

A particular collagen fiber is assembled by a bundle of collagen fibrils, and the model assumes that all such collagen fibrils engage simultaneously at the straightening stretch $\lambda _{\text {st}}$, i.e., no continuous engagement (as it has been suggested elsewhere [47, 49, 52]), has been regarded. Beyond $\lambda _{\text {st}}$, collagen fibrils are stretched and interfibrilar material is sheared, see Fig. 4.8. Specifically, the mechanical properties of the PG bridges determine sliding of collagen fibrils relatively to each other.

Sliding of the PG bridge becomes irreversible as soon as the overlap of the glycan chains decreases below a critical level (see [30] and references therein), which in turn causes irreversible (plastic) deformations that are observed in macroscopic experimental testing of vascular tissues, for example. At increasing stretch, PG bridges slide apart (rupture), and the loss of cross-links weakens (damages) the collagen fiber. PG filament sliding represents a slow (viscous) deformation mechanism [31], and the loss of PG bridges is regarded as a gradual and time-dependent process.

The above-discussed deformation mechanism of a collagen fiber motivates the introduction of a ‘stretch-based’ constitutive concept, where irreversible (plastic) sliding of the collagen fibrils not only defines the fiber’s irreversible elongation but also its state of damage. Consequently, plastic deformation of the collagen fiber is directly linked to fiber damage.

Kinematics   The assumed affine deformation between matrix and collagen fibers directly relates the total fiber stretch $\lambda =\sqrt{\mathbf{M }\cdot \mathbf{C }\mathbf{M }}=|\mathbf{F }\mathbf{M }|$ to the matrix deformation. Following multiplicative decomposition, the total stretch $\lambda =\lambda _{\text {el}}\lambda _{\text {st}}$ is decomposed into $\lambda _{\text {st}}$, a stretch that removes fiber undulation, and $\lambda _{\text {el}}$ that elastically stretches the fiber.

Constitutive model of the collagen fiber   The model assumes that collagen fibers (and fibrils) have no bending stiffness, and at stretches below $\lambda _{\text {st}}$ the fiber stress is zero. Exceeding $\lambda _{\text {st}}$, a linear relation between the effective second Piola-Kirchhoff stress $\widetilde{S}_{{\text {c}}}$ and the elastic stretch $\lambda _{\text {el}}$ holds, i.e., $\widetilde{S}_{{\text {c}}}=c_{\text {f}} \langle \lambda _{\text {el}}-1\rangle = c_{\text {f}} \langle \lambda /\lambda _{\text {st}}-1\rangle$, where $c_{\text {f}}$ and $\lambda$ denote the stiffness of the collagen fiber and its total stretch, respectively. The Macauley-brackets $\langle \bullet \rangle$ have been introduced to explicitly emphasize that a collagen fiber can only carry tensile load.

Considering incompressible elastic fiber deformation, the effective first Piola-Kirchhoff stress reads $\widetilde{P}_{{\text {c}}}=c_{\text {f}} \langle \lambda ^2_{\text {e}l}-\lambda _{\text {e}l}\rangle$, which reveals the constitutive relation using work-conjugate variables. Within reasonable deformations, this relation shows an almost linear first Piola-Kirchhoff stress versus engineering strain $\varepsilon _{\text {e}l}=\lambda _{\text {e}l}-1$ response, which is also experimentally observed [76, 77].

The state of damage of the collagen fiber is defined by an internal state (damage) variable d, such that the second Piola-Kirchhoff stress of the collagen fiber reads

$$\begin{aligned} S_{{\text {c}}}= (1-d)\widetilde{S}_{{\text {c}}}=(1-d)c_{\text {f}} \langle \lambda /\lambda _{\text {st}}-1\rangle . \end{aligned}$$

(4.8)

The damage variable d reflects the loss of stiffness according to slid apart (broken) PG bridges.

Plastic Deformation. Plastic deformation develops at large sliding of PG bridges, i.e., as soon as the overlap between the glycan chains of a PG bridge decrease below a critical level [30]. The proposed model records plastic deformation by a monotonic increase of the straightening stretch $\lambda _{{\text {st}}\,0}\le \lambda _{\text {st}}<\infty$, where $\lambda _{{\text {st}}\,0}$ denotes the straightening stretch of the initial (not yet plastically deformed) tissue. The initial straightening stretch $\lambda _{{\text {st}}\,0}$ is thought to be a structural property defined by the continuous turn-over of collagen and determined by the biomechanical and biochemical environment that the tissue experiences in vivo. Following the theory of plasticity [78, 79], we introduce an elastic threshold Y that classifies the following load cases,

$$\begin{aligned} \left. \begin{array}{cccl} \widetilde{S}_{\text {c}} &{}<&{} Y &{} \text{ elastic } \text{ deformation },\\ \widetilde{S}_{\text {c}} &{}=&{} Y &{} \text{ plastic } \text{ deformation },\\ \widetilde{S}_{\text {c}} &{}>&{} Y &{} \text{ to } \text{ be } \text{ ruled } \text{ out }.\\ \end{array} \right\} \end{aligned}$$

(4.9)

At quasi-static loading conditions an ideal plastic response is considered with $Y=Y_0$ reflecting the elastic limit (in an effective second Piola Kirchhoff setting) of the collagen fiber. In contrast, time-dependent plastic loading is thought to induce a hardening effect, i.e., $Y=Y_0+H$, where H reflects the increase of resistance against collagen fibril sliding due to the slow (viscous) sliding mechanism of the PG bridges. Consequently, a viscoplastic behavior of the collagen fibers is considered, and (for simplicity) the first-order rate equation

$$\begin{aligned} H= \eta \dot{\lambda }_{\text {st}} \end{aligned}$$

(4.10)

defines the viscous hardening, with $\eta$ denoting a material parameter.

Damage accumulation. As detailed above, larger irreversible (plastic) deformation of the collagen fiber causes failure of PG bridges, which in turn weakens the collagen fiber. The mechanical effect from ruptured PG bridges, i.e. the loss of stiffness of the collagen fiber is recorded by the damage parameter d, where an exponential relation

$$\begin{aligned} d= 1- \exp [-a(\lambda _{\text {st}}/\lambda _{{\text {st}}\,0}-1)^2] \end{aligned}$$

(4.11)

with respect to the plastic deformation (reflected by $\lambda _{\text {st}}/\lambda _{{\text {st}}\,0}$) is considered. Equation (4.11) has the properties $d(\lambda _{\text {st}}/\lambda _{{\text {st}}\,0}=1.0) = 0.0$ and $d(\lambda _{\text {st}}/\lambda _{{\text {st}}\,0}\rightarrow \infty ) = 1.0$, and a denotes a material parameter. Specifically, small and large values of a define ductile and brittle-like failure of the collagen fiber, respectively.

Details regarding the numerical implementation of this model are given elsewhere [50].

Basic model characteristics   A single finite element was used to investigate basic characteristics of the constitutive model. To this end constitutive parameters (listed in Table 4.1) were manually estimated from in vitro tensile test data of the AAA wall, and the histologically measured collagen orientation distribution was prescribed, see Sect. 4.3.2.

Table 4.1 Material and structural parameters used for computing a tensile test of tissue from the Abdominal Aortic Aneurysm (AAA) wall

The model captures the strongly nonlinear stiffening at lower stresses (toe region up to 50 kPa), where the initial straightening stretch $\lambda _{{\text {st}}\,0}$ allows to control the transition point from a matrix-dominated to a collagen-dominated tissue response, see Fig. 4.9.

By increasing the load beyond the toe region, a slightly nonlinear relation between the first Piola-Kirchhoff stress and stretch is observed, before collagen fibers gradually exceed their elastic limit, which in turn defines a concave stress–stretch response, see Fig. 4.9. Again, gradually exceeding the collagen fibers’ elastic limit defines a smooth transition from a convex to a concave curve, a response typically observed in experimental testing of vascular tissue.

Significant plastic deformation is required before the ultimate first Piola-Kirchhoff strength of about 0.18 MPa is reached. A further increase in stretch causes material instability, i.e., loss of ellipticity, and the deformation localizes. As outlined in Sect. 4.2, in the strain softening region the results strongly depend on the test specimen’s length. Here, neither the computational model used an internal length scale nor the experimental setup allowed controlled failure progression, such that these curves contain no constitutive information in the strain softening region. Influence of the strain rate and model response to cyclic loading are detailed in [50].

Fig. 4.9

Macroscopic constitutive response of Abdominal Aortic Aneurysm (AAA) wall tissue under uniaxial tension. Solid black curves denote tension responses along the circumferential and longitudinal directions, respectively. The grey curve illustrates the response from in vitro experimental stretching of a single AAA wall specimen along the longitudinal direction. The test specimen used for experimental characterization of AAA wall tissue is shown at the top right

Summary   Damage of vascular tissue can involve several interacting irreversible mechanisms. The presented model considered a coupling between plastic elongation and weakening of collagen fibers, irreversible mechanisms that can be explained by the deformation of PG bridges. The mechanical complexity of vascular tissue leads to descriptions that require many material parameters, which naturally complicates inverse parameter estimation—especially if parameters are mathematically not independent. A constitutive descriptions with model parameters of physical interpretation are particularly helpful for a robust model parameter identification.

4.5 Failure Represented by Interface Models

As shown in Sect. 4.2.1 of this chapter, stretching a rod until the strong ellipticity condition is violated, causes strains to localize within a small (infinitesimal) volume. For such a case the nonpolar continuum yields nonphysical post localization results. However, the cross-sectional area, within which strain localizes, remains finite. Consequently, introducing a failure surface, within which all inelastic processes take place, successfully resolves this issue. Such defined failure surface is then equipped with constitutive information, i.e., a cohesive traction separation law defines the traction that acts at the discontinuity as a function of its opening, i.e., the opening of the fracture. Such an approach goes back to the pioneering works for elastoplastic fracture in metals [80, 81], and for quasi-brittle failure of concrete materials [82].

Fig. 4.10

Discontinuous kinematics representing the reference configuration $\Omega _0=\Omega _{0+}\cup \Omega _{0-}\cup \partial \Omega _{0\,{\text {d}}}$ and the current configuration $\Omega =\Omega _{+}\cup \Omega _{-}\cup \partial \Omega _{\text {d}}$ of a body separated by a strong discontinuity. The associated three deformation gradients: (i) $\mathbf{F }_{\text {e}}=\mathbf{I }+\mathbf{Grad }\,\mathbf{u }_{\text {c}}+\mathbf{Grad }\,\mathbf{u }_{\text {e}}$, (ii) $\mathbf{F }_{\text {d}}=\mathbf{I }+\mathbf{Grad }\,\mathbf{u }_{\text {c}}+\mathbf{u }_{\text {e}}\otimes \mathbf{N }/2$ and (iii) $\mathbf{F }_{\text {c}}=\mathbf{I }+\mathbf{Grad }\,\mathbf{u }_{\text {c}}$

4.5.1 Continuum Mechanical Basis

Discontinous kinematics   As illustrated in Fig. 4.10, $\partial \Omega _{0\,{\text {d}}}$ denotes a strong discontinuity embedded in the reference configuration $\Omega _0$ of a body. The discontinuity separates the body into two sub-bodies occupying the referential sub-domains $\Omega _{0+}$ and $\Omega _{0-}$. The orientation of the discontinuity at an arbitrary point $\mathbf{X }_{\text {d}}$ is defined by its normal vector $\mathbf{N }(\mathbf{X }_{\text {d}})$, where $\mathbf{N }$ is assumed to point into $\Omega _{0+}$, see Fig. 4.10.

The discontinuous displacement field $\mathbf{u }(\mathbf{X })= \mathbf{u }_{\text {c}}(\mathbf{X }) + \mathcal {H}(\mathbf{X })\mathbf{u }_{\text {e}}(\mathbf{X })$ at a referential position $\mathbf{X }$ is based on an additive decomposition of $\mathbf{u }(\mathbf{X })$ into compatible $\mathbf{u }_{\text {c}}$ and enhanced $\mathcal {H}\mathbf{u }_{\text {e}}$ parts, respectively [83, 84]. Here, $\mathcal {H}(\mathbf{X })$ denotes the Heaviside function, with the values 0 and 1 for $\mathbf{X }\in \Omega _{0-}$ and $\mathbf{X }\in \Omega _{0+}$, respectively. Note that both introduced displacement fields, i.e., $\mathbf{u }_{\text {c}}$ and $\mathbf{u }_{\text {e}}$ are continuous and the embedded discontinuity is represented by the Heaviside function $\mathcal {H}$.

Following [85–87], we define a fictitious discontinuity $\partial \Omega _{\text {d}}$ as a bijective map of $\partial \Omega _{0\,{\text {d}}}$ to the current configuration. Specifically, $\partial \Omega _{\text {d}}$ is placed in between the two (physical) surfaces defining the crack, see Fig. 4.10. Therefore, we introduce an average deformation gradient $\mathbf{F }_{\text {d}}$ at $\mathbf{X }_{\text {d}}$ according to

$$\begin{aligned} \mathbf{F }_{\text {d}}(\mathbf{X }_{\text {d}})=\mathbf{I }+\mathbf{Grad }\,\left( \mathbf{u }_{\text {c}}+\frac{1}{2}\mathbf{u }_{\text {e}}\right) =\mathbf{I }+ \mathbf{Grad }\,\mathbf{u }_{\text {c}}+\frac{1}{2}\mathbf{u }_{\text {e}}\otimes \mathbf{N }, \end{aligned}$$

(4.12)

where the factor 1 / 2 enforces the fictitious discontinuity $\partial \Omega _{\text {d}}$ to be placed in the middle between the two (physical) surfaces defining the crack. Based on the deformation (4.12), the unit normal vector $\mathbf{n }$ to the fictitious discontinuity is defined by

$$\begin{aligned} \mathbf{n }= \frac{\mathbf{N }\mathbf{F }_{\text {d}}{}^{-1}}{|\mathbf{N }\mathbf{F }_{\text {d}}{}^{-1}|}, \end{aligned}$$

(4.13)

which can be interpreted as a weighted push-forward operation of the covariant vector $\mathbf{N }$.

Consequently, the introduced kinematical description of a strong discontinuity requires three deformations, as illustrated in Fig. 4.10, i.e., (i) the compatible deformation gradient $\mathbf{F }_{\text {c}} = \mathbf{I }+ \mathbf{Grad }\,\mathbf{u }_{\text {c}}$ (with $\det \mathbf{F }_{\text {c}}=J_{\text {c}}>0$), which maps $\Omega _{0-}$ into $\Omega _-$ as known from standard continuum mechanics; (ii) the enhanced deformation gradient $\mathbf{F }_{\text {e}} = \mathbf{I }+ \mathbf{Grad }\,\mathbf{u }_{\text {c}} + \mathbf{Grad }\,\mathbf{u }_{\text {e}}$ (with $\det \mathbf{F }_{\text {e}}=J_{\text {e}}>0$), which maps $\Omega _{0+}$ into $\Omega _+$, and finally, (iii) the average deformation gradient $\mathbf{F }_{\text {d}} = \mathbf{I }+\mathbf{Grad }\,\mathbf{u }_{\text {c}} + \mathbf{u }_{\text {e}}\otimes \mathbf{N }/2$ (with $\det \mathbf{F }_{\text {d}}=J_{\text {d}}>0$), which maps the referential discontinuity $\partial \Omega _{0\,{\text {d}}}$ into the (fictitious) spatial discontinuity $\partial \Omega _{{\text {d}}}$. Finally, any strain measure directly follows from the introduced deformation gradients, see elsewhere [86] for example.

Cohesive traction response   We assume the existence of a transversely isotropic (note that these type of models are denoted as isotropic elsewhere [88]) cohesive potential $\psi (\mathbf{u }_{\text {d}},\mathbf{n },\delta )$ per unit undeformed area over $\partial \Omega _{0\,\text {d}}$, which governs the material dependent resistance against failure in a phenomenological sense [88]. The cohesive zone’s properties are assumed to be dependent on the gap displacement $\mathbf{u }_{\text {d}}=\mathbf{u }_{\text {e}}(\mathbf{X }_{\text {d}})$, the current normal $\mathbf{n }$ and a scalar internal variable $\delta$. Finally, the cohesive potential is subjected to objectivity requirements, i.e., $\psi (\mathbf{u }_{\text {d}},\mathbf{n },\delta )=\psi (\mathbf{Q }\mathbf{u }_{\text {d}},\mathbf{Q }^{\text {-T}}\mathbf{n },\delta )$, where $\mathbf{Q }$ is an arbitrary proper orthogonal tensor, i.e., $\text{ Q }{}^{\mathrm {T}}=\mathbf{Q },\det \mathbf{Q }=1$.

The model is complemented by the introduction of a damage surface $\phi (\mathbf{u }_{\text {d}},\delta )$ in the gap displacement $\mathbf{u }_{\text {d}}$ space and Karush–Kuhn–Tucker loading/unloading $\dot{\delta }\ge 0,\phi \le 0,\dot{\delta }\phi =0$ and consistency $\dot{\delta }\dot{\phi }=0$ conditions are enforced.

Based on the procedure by Coleman and Noll [89] the cohesive traction $\mathbf T$ and the internal dissipation $\mathcal {D}_{\text {int}}$ take the form

$$\begin{aligned} \mathbf T =\frac{\partial \psi }{\partial \mathbf{u }_{\text {d}}}, \quad \mathcal {D}_{\text {int}}=-\frac{\partial \psi }{\partial \delta }\dot{\delta }\ge 0. \end{aligned}$$

(4.14)

An efficient application of a cohesive model within the FE method requires a consistent linearization of the cohesive traction $\mathbf T$ with respect to the opening displacement $\mathbf{u }_{\text {d}}$. In order to provide this, we introduce $\mathbf{C }_{\text{ u }_d} = \partial \mathbf T /\partial \mathbf{u }_{\text {d}}$, $\mathbf{C }_{\text{ n }} = \partial \mathbf T /\partial \mathbf{n }$, $\mathbf{C }_{\delta } = \partial \mathbf T /\partial \delta$, which describes the cohesive zone’s stiffness with respect to gap displacement opening, rotation and growing damage.

Variational formulation   In order to provide the variational basis for a quasi-static FE model, we start with a single-field variational principle [90], i.e., $\int \limits _{\Omega _0}\mathbf{Grad }\,\delta \mathbf{u }:\mathbf{P }(\mathbf{F }){\text {d}}V- \delta \Pi ^{\text {e}xt}(\delta \mathbf{u })=0$, where $\mathbf{P }(\mathbf{F })$ and $\delta \mathbf{u }$ denote the first Piola-Kirchhoff stress tensor and the admissible variation of the displacement field. The integration is taken over the reference configuration $\Omega _0$, where ${\text {d}}V$ denotes the referential volume element. In addition, the contributions from external loading, i.e., body force and prescribed traction on the von Neumann boundary, are summarized in the virtual external potential energy $\delta \Pi ^{\text {e}xt}(\delta \mathbf{u })$.

According to the introduced displacement field, its admissible variation reads $\delta \mathbf{u }\,{=}\, \delta \mathbf{u }_{\text {c}} + \mathcal {H}\delta \mathbf{u }_{\text {e}}$. Consequently, $\mathbf{Grad }\,\delta \mathbf{u }\,{=}\,\mathbf{Grad }\,\delta \mathbf{u }_{\text {c}}+\mathcal {H}\mathbf{Grad }\,\delta \mathbf{u }_{\text {e}}+ \delta _{\text {d}}(\delta \mathbf{u }_{\text {e}}\otimes \mathbf{N })$, which defines the two variational statements

$$\begin{aligned} \left. \begin{array}{rcl} \int \limits _{\Omega _0}\mathbf{Grad }\,\delta \mathbf{u }_{\text {c}}:\mathbf{P }(\mathbf{F }){\text {d}}V- \delta \Pi ^{\text {e}xt}_{\text {c}}(\delta \mathbf{u }_{\text {c}})&{}=&{}0,\\ \int \limits _{\Omega _{0+}}\mathbf{Grad }\,\delta \mathbf{u }_{\text {e}}:\mathbf{P }(\mathbf{F }){\text {d}}V+ \int \limits _{\partial \Omega _{0\,{\text {d}}}}\mathbf T \cdot \delta \mathbf{u }_{\text {e}}{\text {d}}S- \delta \Pi ^{\text {e}xt}_{\text {e}}(\delta \mathbf{u }_{\text {e}})&{}=&{}0,\\ \end{array} \right\} \end{aligned}$$

(4.15)

where $\delta \Pi ^{\text {e}xt}_{\text {c}}(\delta \mathbf{u }_{\text {c}})$ and $\delta \Pi ^{\text {e}xt}_{\text {e}}(\delta \mathbf{u }_{\text {e}})$ are external contributions associated with the compatible and enhanced displacements, respectively.

After some manipulations and a push-forward of Eq. (4.15), we achieve its spatial version [91],

$$\begin{aligned} \left. \begin{array}{rcl} \int \limits _{\Omega _-}\text {sym}(\mathbf{g rad}\,_{\text {c}}\delta \mathbf{u }_{\text {c}}): \varvec{\sigma }_{\text {c}}{\text {d}}v+ \int \limits _{\Omega _+}\text {sym}(\mathbf{g rad}\,_{\text {e}}\delta \mathbf{u }_{\text {c}}):\varvec{\sigma }_{\text {e}}{\text {d}}v- \delta \Pi ^{\text {e}xt}_{\text {c}}(\delta \mathbf{u }_{\text {c}})&{}=&{}0,\\ \int \limits _{\Omega _+}\text {sym}(\mathbf{g rad}\,_{\text {e}}\delta \mathbf{u }_{\text {e}}):\varvec{\sigma }_{\text {e}}{\text {d}}v+ \int \limits _{\partial \Omega _{\text {d}}}\mathbf{t }\cdot \delta \mathbf{u }_{\text {e}}{\text {d}}s- \delta \Pi ^{\text {e}xt}_{\text {e}}(\delta \mathbf{u }_{\text {e}})&{}=&{}0,\\ \end{array} \right\} \end{aligned}$$

(4.16)

where ${\text {d}}v$ and ${\text {d}}s$ are the spatial volume and surface elements, respectively. Moreover, $\varvec{\sigma }_{\text {c}}=J^{-1}_{\text {c}}\mathbf{P }(\mathbf{F }_{\text {c}})\mathbf{F }^{\text {T}}_{\text {c}}$ and $\varvec{\sigma }_{\text {e}}=J^{-1}_{\text {e}}\mathbf{P }(\mathbf{F }_{\text {e}})\mathbf{F }^{\text {T}}_{\text {e}}$ denote the Cauchy stress tensors and $\mathbf{t }= \mathbf T {\text {d}}S/{\text {d}}s$ is the Cauchy traction vector associated with a fictitious discontinuity $\partial \Omega _{\text {d}}$. The spatial gradients in (4.16) are defined according to $\mathbf{g rad}\,_{\text {c}}(\bullet )=\mathbf{Grad }\,(\bullet )\mathbf{F }_{\text {c}}{}^{-1}, \mathbf{g rad}\,_{\text {e}}(\bullet )=\mathbf{Grad }\,(\bullet )\mathbf{F }_{\text {e}}{}^{-1}$ and $\text {sym}(\bullet )=((\bullet )+(\bullet )^{\text {T}})/2$ furnishes the symmetric part of $(\bullet )$.

The consistent linearization of the variational statements can be found elsewhere [70, 86].

4.5.2 Formulation for the Cohesive Material Model

In order to particularize the transversely isotropic cohesive model introduced in Sect. 4.5.1, we restrict our considerations to the class of models $\psi = \psi (\mathbf{u }_{\text {e}}\otimes \mathbf{u }_{\text {e}},\mathbf{n }\otimes \mathbf{n },\delta )$ and apply the theory of invariants [92]. Hence, the cohesive potential can be expressed according to $\psi = \psi (i_1,i_2,i_3,i_4,i_5,\zeta )$, where $i_1,\ldots ,i_5$ are invariants, which depend on the symmetric tensors $\mathbf{u }_{\text {e}}\otimes \mathbf{u }_{\text {e}}$, and $\mathbf{n }\otimes \mathbf{n }$ [91].

As a special case the isotropic particularization

$$\begin{aligned} \psi (i_1,\zeta ) = \frac{t_0}{2\zeta }\exp (-a \delta ^b)i_1 \end{aligned}$$

(4.17)

is used. Here, $i_1=\mathbf{u }_{\text {e}}\cdot \mathbf{u }_{\text {e}}$ is the first invariant, $t_0$ denotes the cohesive tensile strength and the nonnegative parameters a and b aim to capture the softening response from failure progression.

In addition, we define a damage surface $\phi (\mathbf{u }_{\text {e}},\delta )=|\mathbf{u }_{\text {e}}|-\zeta = 0$ in the three-dimensional gap displacement space and assume $\dot{\zeta } = \dot{\overline{|\mathbf{u }_{\text {e}}|}}$ for the evolution of the internal (damage) variable $\zeta \in [0,\infty [$. A proof of nonnegativeness of the dissipation, i.e., $\mathcal {D}_{\text {int}}\ge 0$, of the introduced cohesive model is given elsewhere [91], and the underlying cohesive traction and associated stiffness measures read,

$$\begin{aligned} \mathbf T = c \mathbf{u }_{\text {e}} , \quad \mathbf{C }_{\text{ u }_e}=c\mathbf{I }, \quad \mathbf{C }_{\text{ n }}=\mathbf{0 }, \quad \mathbf{C }_{\delta }=-\gamma \mathbf{u }_{\text {e}}, \end{aligned}$$

(4.18)

where the two scalars

$$\begin{aligned} c=\frac{t_0}{\zeta }\exp (-a\zeta ^b), \quad \gamma = \frac{c}{\zeta }(1+ab\zeta ^b) \end{aligned}$$

(4.19)

uniquely describe the cohesive law at a certain state of damage $\delta$.

Initialization criterion.   The proposed FE implementation of the model assumes that the cohesive zone increases dynamically during the computation. In particular, the cohesive zone model is activated within a finite element if the initialization criterion $\mathcal {C}_{\text {init}}>0$ is satisfied. Herein, we use a Rankine criterion

$$\begin{aligned} \mathcal {C}_{\text {init}}=\mathbf{n }\cdot \varvec{\sigma }\mathbf{n }-t_0 \frac{{\text {d}}s}{{\text {d}}S}, \end{aligned}$$

(4.20)

where $\mathbf{n }$ denotes the perpendicular direction to the discontinuity in the spatial configuration. The formulation of the cohesive potential $\psi$ with respect to reference area, see Sect. 4.5.1, motivated the introduction of the area ratio ${\text {d}}s/{\text {d}}S$ in criterion (4.20).

Summary   The introduced model for tissue failure postulates the existence of a cohesive fracture process zone, a discrete surface (discontinuity) that represents initialization and coalescence of micro-cracks. A phenomenological traction separation law specifies the failure mechanics, i.e., how the traction across the discontinuity decreases with increasing crack opening. Such defined discontinuity has been embedded in the continuum, which effectively allows post-localization analyses.

4.6 Applications

4.6.1 Organ Level Simulation of Abdominal Aortic Aneurysm Rupture

The elastoplastic damage model for collagenous tissue detailed in Sect. 4.4 was deployed to simulate AAA inflation until structural collapse, i.e., until a quasi-static solution of the problem could no longer be computed. The observed structural collapse might also have caused material instability, i.e., loss of strong ellipticity [93, 94]. However, this was not further investigated.

Modeling assumptions   The AAA has been segmented from Computed Tomography-Angiography (CT-A) images (A4clinics Research Edition, VASCOPS GmbH), where deformable (active) contour models [95] supported an artifact-insensitive and operator-independent 3D reconstruction. The aneurysm was segmented between the renal arteries and about two centimeters distal the aortic bifurcation. The geometry was meshed by hexahedral finite elements, and the structural analysis was carried out in FEAP (University of California at Berkeley). Blood pressure was applied as a follower load, and all nodal degrees of freedom were locked at the aneurysm’s bottom and top slices. No contact with surrounding organs was considered, and further modeling details are given elsewhere [50].

Fig. 4.11

Maximum principal Cauchy stress (top row) and plastic deformation (bottom row) of an Abdominal Aortic Aneurysm (AAA) at inflation according to Load Case (a). FE predictions were based on material properties given in Table 4.1

Load case (a) increased the blood pressure at 10 mmHg/s until structural collapse was experienced. In contrast, load case (b) assumed a cyclic pulsatile blood pressure between 280 mmHg and 120 mmHg and at a frequency of one Hertz. Note that the investigated aneurysm was rather small, such that unrealistically high blood pressures were required to trigger AAA rupture.

Results

Load Case (a).   The development of the maximum principal Cauchy stress and the plastic deformation (in terms of the averaged straightening stretch $\overline{\lambda }_{\text {st}}=(1/l_{\text {int}})\sum _{l=1}^{l_{\text {int}}} \lambda _{{\text {st}}\,l}$) during inflation is illustrated in Fig. 4.11. The low loading rate of 10 mmHg/s caused localized plastic deformation and led to a rather brittle failure response. Finally, a single region of concentrated plastic deformation (and tissue damage) developed prior the structure collapsed.

Load Case (b).   The development of the plastic deformation (in terms of the averaged straightening stretch $\overline{\lambda }_{\text {st}}$) during cyclic inflation is illustrated in Fig. 4.12, where n denotes the cycle number. The high loading rate of ±320 mmHg/s spread plastic deformations all over the aneurysmatic bulge. Above 15 load cycles the numerical convergence of the problem was poor and the computation was terminated. Plastically deformed wall segments that could have been buckled during deflation, or the highly distorted mesh could also have caused such poor numerical convergence.

Fig. 4.12

Plastic deformation of an Abdominal Aortic Aneurysm (AAA) at cyclic inflation according to Load Case (b). AAA is shown at diastolic pressure, where n denotes the number of inflation cycles. FE predictions were based on material properties given in Table 4.1, and plastic deformation is expressed by the straightening stretch

4.6.2 Model Parameter Estimation from in Vitro Tensile Tests

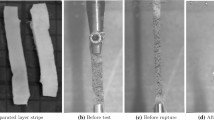
Cohort and specimen preparation   Tissue samples from the AAA wall (n=16; approximately 10 mm times 20  mm) and the Thoracic Aortic Aneurysm (TAA) wall (n=27; approximately 15 mm times 30  mm) were harvested during open surgical repair at Karolinska University Hospital, Stockholm, Sweden. Bone-shaped test specimens were punched-out from the dissected tissue patches using a custom-made pattern blade, see Fig. 4.13a. Test specimens from the AAA wall and from the TAA wall were aligned along the longitudinal and circumferential vessel directions, respectively. The length of the test specimens varied from 10 mm to 30 mm, and in order to improve specimen fixation in the testing machine, pieces of sand paper were glued to each end of the specimen (Super-adhesive glue, Loctite), see Fig. 4.13b. During specimen preparation the tissue was kept hydrated at any time. For the histological analysis, samples (taken from one part of each AAA test specimen and after the mechanical testing) were fixed, embedded in paraffin, sliced at a thickness of 7.0 $\upmu$m and stained with picrosirius red to enhance the birefringent properties of collagen. The use of material from human subjects was approved by the local ethics committee and further detail regarding the cohorts is given in [96, 97].

Fig. 4.13

Preparation of uniaxial test specimens. a Dimensions (in millimeters) of the pattern blade that was used to punch out test specimens from tissue patches. Typical specimens from the human Thoracic Aortic Aneurysm (TAA) wall (b) and from the porcine interventricular septum (c). Dimensions shown by the rulers are given in centimeters

Testing equipment and protocols   Prior to failure testing, the test specimen’s cross-section A at the neck, i.e., where the specimen was expected to rupture, was measured. Mechanical testing was performed with conventional testing systems (MTS for the AAA samples and Instron for the TAA samples). The load-displacement property of the test specimen was recorded during a displacement-controlled uniaxial tensile test at an elongation rate of 0.1  mm/s. During tensile testing, the test specimens remained entirely in Ringer solution at $37\pm 0.5$ $^\circ$C, and a load cell recorded the force that was applied to the specimen. Further details are given elsewhere [96, 97]. The ultimate first Piola-Kirchhoff strength $P_{\text {ult}}=F_{\text {ult}}/A$ was calculated, where $F_{\text {ult}}$ denotes the measured ultimate tensile load.

Identification of collagen fiber orientation and thickness   Collagen fiber orientations were identified from PicroSirius red stained histological slices. Measurements were taken with a BX50 polarized light microscope (Olympus) that was equipped with a URS (Carl Zeiss GmbH), as detailed in Sect. 4.3.2.

Numerical model, parameters estimation   For each bone-shaped test specimen, a plane-stress FE model with 96 Q1P0 mixed elements [98] was generated. The model was equipped with the elastoplastic constitutive model for collagenous tissue (see Sect. 4.4), and the specimen-individual collagen orientation was considered. The FE models were used to estimate the set $\{c_{\text {m}}, \lambda _{{\text {st}}\,0},c_{\text {f}}, a\}$ of material parameters for each wall sample. (For the AAA wall samples, the parameter $c_{\text {m}}$ that determines the matrix material was fixed to 0.012 MPa, i.e., a value reported in the literature [52].) The physical meaning of model parameters allowed their straight forward manual estimation. Specifically, parameters were alternated until FE model predictions matched the recorded stress–stretch curves in a least-square sense. Since the constitutive model is not suitable to predict strain localization, the strain softening region was disregarded. Finally, it is noted that a small amount of viscous hardening ($\eta =0.0001$ MPa s, see Sect. 4.4) was required to stabilize the FE model, which virtually did not alter the quasi-static result.

Fig. 4.14

Stress–stretch properties of a single Abdominal Aortic Aneurysm (AAA) wall specimen that is loaded along the axial vessel direction. Recordings from in vitro experiment is overlaid by FE predictions. Colored-coded images illustrate the Cauchy stress in tensile direction at two different stretch levels. Stretch is averaged over the length of the tensile specimen

Typical results   For all cases the applied FE models provided good approximations to the recorded stress–stretch curves, see the representative plot in Fig. 4.14, for example. By increasing the load beyond the toe region, a slightly nonlinear relation between the first Piola-Kirchhoff stress and stretch was observed. Then the collagen fibers gradually exceeded their elastic limit, which led to a concave stress–stretch response. Gradually exceeding the collagen fibers’ elastic limit defined a smooth transition from a convex to a concave curve, and significant plastic deformation accumulated before the ultimate strength $P_{\text {ult}}$ was reached. A further increase in stretch caused material instability (see Sect. 4.2), which is not covered by the applied constitutive model.

The Cauchy stress in tensile direction at two different deformations is shown in Fig. 4.14a, b. The irreversible overstretching of the tissue homogenizes the stress in the neck of the specimen (not seen for the selected color coding in Fig. 4.14). For AAA wall samples the highest Cauchy stress $\sigma _{\text {ult}}$= 569(SD 411) kPa appeared in the neck of the specimen and was recorded at a stretch of 1.436(SD 0.118). For TAA samples a stress of $\sigma _{\text {ult}}$= 1062(SD 736) kPa was reached at a stretch of 1.514(SD 0.214). Identified model parameters are summarized in Table 4.2, and further details are given elsewhere [96, 97].

Table 4.2 Numerically estimated constitutive parameters of Abdominal Aortic Aneurysm (AAA) and Thoracic Aortic Aneurysm (TAA) wall specimens

4.6.3 Ventricular Tissue Penetration

Tensile testing   Pig hearts (n=12) were taken from the butchery and bone-shaped specimens aligned in cross-fiber direction were prepared, see Fig. 4.13c. In total 64 specimens were prepared, using the preparation techniques detailed in Sect. 4.6.2.

Tensile testing was performed with a conventional MTS systems, where specimens were loaded at a prescribed elongation rate of 0.2 mm/s until they failed. Then the ultimate first Piola-Kirchhoff strength $P_{\text {ult}}=F_{\text {ult}}/A$ was calculated, where A denotes the initial cross-sectional area at the specimen neck. The studied myocardial tissue withstood a first Piola-Kirchhoff stress in cross-fiber direction of $P_{\text {ult}}=0.0326(SD~0.0159)$ MPa, and further details are given elsewhere [73].

Modeling the bulk material   In addition to direct failure-related energy dissipation (like collagen fiber breakage) also viscoelastic energy dissipation at the crack tip could be an important factor of failure propagation in vascular tissue, i.e., similar to observations made in rubber-like materials [99]. Consequently, ventricular tissue has been modeled as a viscoelastic material.

We assume an additive decomposition of the free-energy function $\Psi =\Psi _{\text {vol}}(J)+\Psi _{\text {iso}}(\mathbf {\overline{F}}, t)$ into volumetric $\Psi _{\text {vol}}$ and isochoric $\Psi _{\text {iso}}$ contributions, where $\mathbf {\overline{F}}=J^{-1/3}\mathbf {F}$ denotes the unimodular part of the deformation gradient $\mathbf {F}$, with $J=\text {det}\mathbf {F}$ and t being the time. In order to capture the non-linear mechanics of cardiac tissue, the polynomial free-energy

$$\begin{aligned} \Psi _{\text {iso}}^\infty =c_1(I_1-3)+c_2(I_1-3)^2, \end{aligned}$$

(4.21)

was used, where the invariant $I_1={\text {tr}}\overline{\mathbf{C }}$ of the modified right Cauchy-Green strain $\mathbf {\overline{C}}=\mathbf {\overline{F}^{\text {T}}}\mathbf {\overline{F}}=J^{-2/3}\mathbf {C}$ was introduced. This form of the constitutive relation has originally been proposed for rubber-like materials [100] and is frequently used in biomechanics to describe the mechanics of the aneurysm wall, for example [101, 102]. For the present study, the parameters $c_1=10.0$ kPa and $c_2=7.5$ kPa were estimated form the myocardial tissue in cross-fiber direction [73].

In order to equip the formulation with rate-dependent properties, the constitutive model (4.21) was extended to viscoelasticity, and the isochoric free-energy

$$\begin{aligned} \Psi _{\text {iso}}=\left\{ 1+\sum _{k=1}^{k}{\beta _k[1-\exp (-t/t_k)]}\right\} \Psi _{\text {iso}}^\infty \end{aligned}$$

(4.22)

was considered. Here, $\beta _k$ and $t_k$ are Prony series parameters defining the tissue’s rate-dependency. The model can be regarded as a generalized standard viscoelastic solid with k linear viscoelastic Maxwell elements [3].

This study considered two sets $\{\beta _k, t_k\}$ of constitutive parameters. Set I represented properties of the medial layer of arteries used in the literature [103], and Set II doubled the rate-effects by doubling the $\beta _k$ parameters of Set I.

Cohesive model of myocardial tissue splitting   Experimental penetration of biaxially stretched myocardial tissue indicated that crack faces were wedged open by the advancing punch [104], see Fig. 4.15. Such a splitting failure was modeled by a fracture process zone and captured by a traction separation law. Specifically, a triangular traction separation law related the traction $\mathbf {t}$ and the displacement $\mathbf {\delta }$ at the interface. The cohesive strength of the interface was set to $t_0=32.6$ kPa, i.e., the tissue strength identified from tensile testing in cross-fiber direction. Two different fracture energies $\mathcal {G}_0=6.32$ Jm$^{-2}$ and $\mathcal {G}_0=12.64$ Jm$^{-2}$ were used to investigate their influence on the punch force-displacement response.

Fig. 4.15

a Electron microscopy image taken from ventricular tissue penetration experiments [104]. Image illustrates a splitting mode (mode-I) failure together with remaining deformations at the penetration site. b Idealized failure mode of ventricular tissue due to deep penetration. Crack faces are wedged open by the advancing circular punch defining a splitting mode (mode-I) failure (The punch advances perpendicular to the illustration plane.)

FE model of deep penetration   A single penetration of biaxially stretched myocardial tissue [104] was modeled, where a punch of 1.32 mm in diameter penetrated a 10.0 mm by 10.0  mm tissue patch (ABAQUS/Explicit (Dassault Systèmes)), see Fig. 4.16(left). A cohesive zone was introduced in the middle of the domain, i.e., where tissue splitting was expected, and symmetry conditions of the problem were considered.

The investigated domain was discretized by 8120 hexahedral finite elements (b-bar formulation [6]), where the mesh was refined at the site of penetration. A penalty contact formulation [105] (with automatic adaptation of the penalty parameter) was used to model the rigid and frictionless contact problem.

Fig. 4.16

Left FE model to investigate myocardial penetration by an advancing circular punch. Numerically predicted crack tip deformation and tissue stress during the crack faces are wedged open by the advancing circular punch

Fig. 4.17

Penetration force-displacement response of myocardium against deep penetration. a Impact of the fracture energy of the cohesive zone. b Impact of the viscoelasticity of the bulk material

The numerically predicted Cauchy stress in cross-fiber direction at the crack tip is shown in Fig. 4.16 (right), while Fig. 4.17 presents the influence of model parameters on the penetration force versus displacement properties. Specifically, Fig. 4.17a illustrates that the energy release in the fracture process zone has almost no impact, while rate-dependent effects of the bulk material massively influence the penetration force versus displacement properties, see Fig. 4.17b. Compared to the experimentally recorded data [104], the FE predictions were too soft with the peak penetration force being about 2–4 times lower.

4.7 Conclusions

Vascular biomechanics is critical in order to define new diagnostic and therapeutic methods that could have a significant influence on healthcare systems and even on the life style of human beings. Despite continued advances in computer technology and computational methods, such simulations critically depend on an accurate constitutive description of vascular tissue. For many vascular biomechanics problems, robust modeling of damage accumulation and even tissue failure is required.

The present chapter summarized relevant continuum mechanical concepts and discussed parameter identification for such models. As long as the accumulated tissue damage does not trigger strain localization, such problems can be studied within the standard nonpolar continuum mechanics. However, if damage accumulation results in strain localization, the nonpolar continuum fails and tailored continuum approaches are needed. In addition, parameters for such failure models need to be identified from appropriate experimental setups at controlled failure progression. Failure in conventional engineering materials like steel has successfully been studied within Linear Fracture Mechanics (LFM) and related concepts. However, such concepts assume a sharp crack tip, which is not seen in failure of vascular tissue. Here, the crack tip is bridged by collagen fibers and other tissue ligaments bridge and motivates the application of cohesive failure models.

Difficulties to identify model parameters from experimental data increase with increasing number of parameters. However, at the same time a large number of constitutive parameters is needed to account for the complex elastic and irreversible mechanics of vascular tissues. Consequently, the application of constitutive models with parameters of physical meaning is recommended, such that tailored experiments can be designed, from which a subset of parameters can estimated independently. In addition, the experimental design should support parameter identification [106], i.e., experimental readings should be (i) sensitive to the model parameters and (ii) provide enough experimental information for a robust identification.

The present chapter regarded vascular tissue as an inert and passive material, which is clearly not the case. Like other biological tissues, the vascular wall responds to its mechanical environment and predictions based on passive constitutive models, i.e., suppressing tissue remodeling and growth, can only cover a limited time period. Understanding the tissue’s inherent properties to adapt to mechanical environments might improve vascular biomechanics predictions in the future.