1 Introduction

Carotid atherosclerotic plaque rupture and stroke are among the leading causes of death worldwide (Benjamin et al. 2017). Angioplasty, stenting and endarterectomy are the most common endovascular treatments to reopen atherosclerotic and narrowed arteries (Henry and Henry 2017; Moresoli et al. 2017). These treatments can apply supra-physiological loads on the vessel wall during the deployment of the intravascular device itself, or through external tissue clamping during surgery.

Healthy undamaged arterial tissues are composed of three distinct layers. The innermost layer is the tunica intima. It consists of a single layer of endothelial cells, a thin basal membrane and a subendothelial layer. The medial layer is composed of a three-dimensional network of smooth muscle cells, elastin and collagen fibres. This layer is separated from the intima and adventitia by internal and external elastic laminas. The outermost layer is the tunica adventitia. The adventitial layer consists of fibroblasts, fibrocytes, histological ground matrix and thick bundles of collagen fibres. For a more detailed description of the structure of the arterial wall, the reader is referred to, for example, Holzapfel et al. (2000). Although several constituents contribute to load bearing in arterial walls, collagen fibres are believed to play the most significant role in supporting physiological and supra-physiological loads (Holzapfel et al. 2000).

Experimental studies have revealed that passive damage accumulation in biological soft tissues is associated with four phenomena: (i) Mullins effect, (ii) hysteresis, (iii) permanent set and (iv) rupture. Mullins effect is due to microscopic softening in the tissue, and this phenomenon was first observed in experiments conducted on rubber-like material by Mullins (1948) and further investigated in studies such as Mullins (1969) and Mullins and Tobin (1965). Mullins effect describes the softening behaviour of soft biological tissues under cyclic loading and is governed by the maximum load level imposed on the vessel wall, and as such this behaviour is a discontinuous damage phenomenon (Balzani et al. 2006; Pena et al. 2009). Continuous softening or hysteresis describes the behaviour of soft tissues under cycling loading to the same load level until a saturation state is reached (Balzani et al. 2012; Pena et al. 2009). Hysteresis describes the difference between the loading and reloading paths in the preconditioning stages. Permanent set characterizes the inelastic behaviour of the tissue which results from accumulated strain in the tissue at high loads. This phenomenon has been investigated for soft tissues in studies such as Maher et al. (2011, 2012), Pena (2014). Finally, matrix failure and fibre rupture describe the ultimate failure behaviour of biological tissue at supra-physiological loads. This phenomenon has previously been explored for soft tissues in studies such as Calvo et al. (2009) and Pena (2014).

To capture the aforementioned damage-relevant phenomena in biological soft tissues, two common approaches have been used, namely the pseudo-elastic damage method and a continuum damage mechanics (CDM) method.

The theory of pseudo-elasticity was employed by Ogden and Roxburgh (1999) in order to capture the main features of Mullins effect in rubber-like materials. The formulation of this method is based on the concept of pseudo-elasticity which was used by Fung et al. (1979) to describe the behaviour of arterial tissue. This theory describes the behaviour of material as one elastic material in the loading path and another elastic material in the unloading path. Franceschini et al. (2006) used a pseudo-elastic damage model to capture the Mullins effect and permanent set in brain tissues using a series of uniaxial mechanical tests following the model proposed by Dorfmann and Ogden (2004). In arterial tissue, Weisbecker et al. (2011) implemented a pseudo-elastic damage model by defining different damage variables for the tissue matrix and collagen fibres. In that research, a neo-Hookean material model was used to describe the behaviour of matrix and the anisotropic energy function proposed by Holzapfel et al. (2000) was used for the fibrous tissue component. Pena and Doblare (2009) also used the theory of pseudo-elasticity to characterize the discontinuous softening in soft tissues.

The CDM method has been extensively employed to describe the progressive degradation of material before the initiation of micro-cracks (Simo and Ju 1987). This theory has been used to model damage in fatigue (Chaboche 1974; Lemaitre 1972), creep (Hult 1974; Rabotnov 1963) and creep–fatigue interaction (Lemaitre and Chaboche 1975). The theory of CDM is based on the thermodynamics of irreversible processes (Clausius–Duhem inequality for the internal dissipation) and the internal state variable theory (Miehe 1995; Simo and Ju 1987). According to this theory, the effect of the initiation or growth of micro-cracks can be modelled using internal damage variables, which can be defined as scalar variables for capturing isotropic damage or tensorial form for anisotropic damage when the evolution of damage depends on the orientation of the material constituents (Simo and Ju 1987).

Decoupled forms of CDM models have been applied to simulate damage accumulation phenomena in soft biological tissues. Balzani et al. (2006) demonstrated a constitutive model to capture damage phenomena in circumferentially overstretched atherosclerotic arteries, whereby different internal variables were assigned to the isotropic ground matrix and fibrous anisotropic strain energy functions. The model proposed by Balzani et al. (2006) for discontinuous damage has since been further developed by Famaey et al. (2013), who explored damage accumulation in smooth muscle cells at supra-physiological load levels. Using a CDM approach, Pena (2011) presented a structural constitutive model to capture discontinuous damage and inelastic deformation simultaneously within a soft tissue. However, relatively few studies have investigated the influence of stress softening and permanent set simultaneously in cyclic loading conditions (Alastrue et al. 2008; Munoz et al. 2008). The CDM approach was also used by Pena (2011) and Maher et al. (2012) to capture the discontinuous damage along with permanent set phenomenon in biological fibrous tissues. Balzani et al. (2012) used a decoupled form of CDM to propose a constitutive model that captures discontinuous and continuous softening along with the permanent set phenomenon; the main limitation of that study was that no damage was considered to accumulate in the matrix of the material. Pena (2014) employed CDM to capture Mullins effect simultaneously with continuous damage, permanent set and tissue rupture in arterial tissue. The number of material parameters required to define the model, however, was mentioned as a limitation of that study. For further information on existing damage models and their classifications, the reader is referred to, for example, Li (2016).

Although several constitutive models have been developed to model the damage-relevant phenomena in arterial tissue, there has been a lack of experimental data to distinguish the role of each constituent of arteries in damage accumulation phenomena. Whilst Weisbecker et al. (2013) performed a series of uniaxial experiments on intact, elastase-treated and collagenase-treated media of human thoracic aorta to explore the role of elastin and collagen fibres in the discontinuous and continuous softening of the tissue, they did not elucidate the role of each constituent of the arterial wall on damage-relevant phenomena such as permanent set or tissue failure.

The main aim of this research is to gain further insights into the contribution of matrix and fibres to damage accumulation in arteries under supra-physiological loading conditions. To achieve this aim, we have performed mechanical tests at high strain levels on intact and collagenase-treated media of porcine common carotid arteries in axial and circumferential directions. Using the obtained experimental data, we have developed a new computational framework to capture all passive damage-relevant phenomena in matrix and collagen fibres within arterial tissue.

1.1 Outline

Sections 2.1 to 2.3 outline the details of the sample preparation and the experimental protocol that we have applied for enzymatic digestion of the samples. The implementation of the constitutive model and the adjustment of the material model to the experimental data are outlined in Sects. 2.4 and 2.5, respectively. The outcome of our mechanical tests and fitting results of the proposed constitutive model are given in Sect. 3. Section 4 discusses the obtained experimental and computational results along with limitations of this study and future directions.

2 Materials and methods

2.1 Sample preparation

Fresh porcine common carotid arteries were harvested from 9 large white pigs aged 6 months and weighing approximately 80 kg. Carotid arteries were transported on ice and preparation began within 2 h of slaughter. The harvested arteries were washed with phosphate-buffered saline (PBS) to remove residual blood, and excess connective tissue was removed. The samples were stored in tissue-freezing medium (RPMI-60 Media, 1.8 M DMSO; and 0.1 M Sucrose), placed in a Mr. Frosty supplier cryosystem (containing isopropyl alcohol; VWR) and cryopreserved at − 80 °C. On the day of the experiments, samples were defrosted in PBS at ambient temperature. Arteries were cut into dog-bone-shaped specimens with a 2-mm width in the gauge region such that the gauge length \( l_{0} \ge 5.56 \times \sqrt {A } \), where A denotes the cross-sectional area of the specimens (Davis 2004). The thickness of each sample was then calculated by taking the average of three measurements using a Mitutoyo FS70Z microscope after carefully removing the adventitial layer using tweezers.

2.2 Enzyme treatment

Collagenase solution was prepared (500 U ml−1, chromatographically purified collagenase, Worthington Biochemical, NJ, USA) in buffer solution containing Dulbecco’s PBS with MgCl2 and CaCl2. The arterial samples were incubated in the collagenase solution at 37 °C for 42 h. Histological images were obtained to verify the digestion of collagen fibres at 0, 16 and 42 h using Picrosirius red staining, see Fig. 1.

Fig. 1
figure 1

Histology images obtained at different stages of collagen fibre digestion in samples of the porcine carotid arteries. a Control sample (0 h of collagenase treatment), b 16 h of collagenase treatment, c 42 h of collagenase treatment. Scale bar: 500 μm

Full size image

2.3 Tensile test

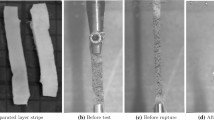
The mechanical tests were conducted on intact and digested specimens using a uniaxial test machine (Zwick ZO05, Zwick GmbH & Co. Ulm, Germany) equipped with a 20 N load cell. All the experiments were performed in a tissue bath of PBS at room temperature, see Fig. 2. A custom-designed video extensometer recorded the stretch in the gauge region of the specimen by tracking six black dots on the dog-bone strips in the direction of the applied force. The measured displacement between dots was then used only to calculate the stretch in the direction of loading of the specimen. A sequence of cyclic loading was imposed on the tissue at a constant displacement rate of 10 mm min−1 with stress limits for each load step. The mechanical tests started with five cycles of preconditioning at the beginning of the experiment and three cycles for each load step to monitor the discontinuous and continuous softening in the specimens. The cyclic mechanical tests continued in each sample until failure of the tissue. Only samples in which rupture occurred in the gauge length have been considered. The results obtained from our cyclic tensile tests on the intact and digested samples have been used to explore damage-relevant phenomena in the media layer of porcine common carotid arteries. A summary of the samples which have been used in different parts of this study is outlined in Table 1.

Fig. 2
figure 2

Representative images of the experimental set-up which was used for the uniaxial mechanical tests. The sample a before and b after rupture, scale bar: 12 mm

Full size image
Table 1 A summary of samples which have been used in different parts of this study
Full size table

2.4 Constitutive modelling

2.4.1 Kinematics

Arterial tissue is commonly considered an almost incompressible material, and therefore, a multiplicative decomposition of the deformation gradient tensor F into volumetric \( J^{{\frac{1}{3}}} {\mathbf{I}} \) and isochoric parts \( {\bar{\mathbf{F}}} \) is usually performed to characterize the deformation processes. Following Flory (1961), multiplicative decomposition of the deformation gradient tensor can be written as:

$$ {\mathbf{F}} = \left( {J^{{\frac{1}{3}}} {\mathbf{I}}} \right){\bar{\mathbf{F}}} $$
(1)

where I is the identity tensor. The right Cauchy–Green tensor, denoted by C, and its isochoric counterpart, denoted by \( {\bar{\mathbf{C}}} \), are then defined as follows:

$$ {\mathbf{C}} = {\mathbf{F}}^{T} {\mathbf{F}} = J^{{\frac{2}{3}}} {\bar{\mathbf{C}}},{\bar{\mathbf{C}}} = {\bar{\mathbf{F}}}^{T} {\bar{\mathbf{F}}} $$
(2)

The first deviatoric principal invariant of the right Cauchy–Green tensor takes the following representation.

$$ \bar{I}_{1} = tr\left( {{\bar{\mathbf{C}}}} \right) $$
(3)

The unit vector M can be used to define the direction of fibres with respect to the circumferential direction of the arterial wall in the undeformed state. The isochoric configuration of the vector M in the spatial coordinate system can then be written as follows:

$$ {\bar{\mathbf{M}}} = {\bar{\mathbf{F}}\mathbf{M}} $$
(4)

The deviatoric invariants associated with a unit vector M are represented as follows:

$$ \bar{I}_{M} = tr\left( {{\bar{\mathbf{C}}}{\bar{\mathbf{M}}} \otimes {\bar{\mathbf{M}}}} \right) = {\bar{\mathbf{M}}} \cdot \left( {{\bar{\mathbf{C}}}{\bar{\mathbf{M}}}} \right) $$
(5)

Generalized structure tensors have been used to represent the level of anisotropy of the fibres in the arterial tissue. Gasser et al. (2006) defined a structure tensor HM that accounts for the effect of angular distribution of the fibres in the direction of M.

$$ {\mathbf{H}}_{{\mathbf{M}}} = \kappa \bar{\varvec{I}} + \left( {1 - 3\kappa } \right)\left( {{\bar{\mathbf{M}}} \otimes {\bar{\mathbf{M}}}} \right) $$
(6)

where \( \kappa \) is a scalar value that represents the dispersion of fibres in the array of collagen fibres in the arterial tissue. The pseudo-invariants \( \bar{I}_{M}^{*} \) of HM can then be defined as follows (Gasser et al. 2006):

$$ \bar{I}_{M}^{*} = {\bar{\mathbf{C}}}:{\mathbf{H}}_{\text{M}} = \kappa \bar{I}_{1} + \left( {1 - 3\kappa } \right)\bar{I}_{M} $$
(7)

2.4.2 Response of arteries to physiological loading levels

The mechanical behaviour of arteries is commonly modelled using a hyperelastic anisotropic material model, whereby the existence of a Helmholtz free energy function is postulated per unit reference volume for the tissue. Following Holzapfel et al. (2000), the total strain energy function of arterial tissues can be additively decomposed into: volumetric \( \psi_{\text{vol}} \), isochoric isotropic \( \bar{\psi }_{\text{iso}} \) and isochoric anisotropic parts (\( \psi_{{\rm ef}} \) and \( \psi_{{\rm cf}} \) for elastin and collagen fibres, respectively):

$$ \psi = \psi_{\text{vol}} + \bar{\psi }_{\text{iso}} + \bar{\psi }_{\text{ef}} + \bar{\psi }_{\text{cf}} $$
(8)

The volumetric free energy \( \psi_{\text{vol}} \) can be expressed as follows:

$$ \psi_{\text{vol}} \left( J \right) = \frac{1}{2}\kappa_{0} \left( {J - 1} \right)^{2} $$
(9)

where \( \kappa_{0} \) serves as a penalty parameter that controls the compressibility of biological soft tissue (Gasser and Holzapfel 2002).

Isotropic material models have been widely used to represent the mechanical behaviour of the ground matrix. In this research, a neo-Hookean material model along with two families of elastin fibres at 45 degrees with respect to the circumferential direction of the vessel wall has been employed to describe the mechanical behaviour of the ground matrix and elastin fibres which constitute the elastin sheets, similar to Holzapfel et al. (2000).

$$ \bar{\psi }_{\text{iso}} \left( {{\bar{\mathbf{C}}}} \right) = \frac{1}{2}\mu \left( {\bar{I}_{1} - 3} \right) $$
(10)
$$ \bar{\psi }_{\text{ef}} \left( {{\bar{\mathbf{C}}}} \right) = \mathop \sum \limits_{{M_{\text{ef}} = M_{{4{\text{ef}},6{\text{ef}}}} }} \frac{{k_{{1{\text{ef}}}} }}{{2k_{{2{\text{ef}}}} }}\left( {\exp \left( {k_{{2{\text{ef}}}} \left( {\bar{I}_{{M_{\text{ef}} }} - 1} \right)^{2} } \right) - 1} \right) $$
(11)

where \( \mu \) is the shear modulus of the ground matrix and \( k_{{1{\text{ef}}}} \) and \( k_{{2{\text{ef}}}} \) are stress-like and dimensionless material parameters, respectively. \( \bar{I}_{{M_{{4{\text{ef}}}} }} \) and \( \bar{I}_{{M_{{6{\text{ef}}}} }} \) are the deviatoric invariants that indicate the square of stretch in elastin fibres and correspond to two unit vectors \( {\mathbf{M}}_{{4{\mathbf{ef}}}} = \left\{ {\cos \left( {\alpha_{\text{ef}} } \right),\sin \left( {\alpha_{\text{ef}} } \right),0} \right\} \) and \( {\mathbf{M}}_{{6{\mathbf{ef}}}} = \left\{ {\cos \left( {\alpha_{\text{ef}} } \right), - \sin \left( {\alpha_{\text{ef}} } \right),0} \right\} \), respectively, where \( \alpha_{\text{ef}} \) is the angle of elastin fibres which has been chosen to be equal to 45° with respect to the circumferential direction of the vessel wall.

Following Gasser et al. (2006), we have assumed that two symmetric families of collagen fibres contribute in bearing load in the arterial tissue. The contribution of these two families of collagen fibres in the overall mechanical behaviour of the tissue has been described using the strain energy function proposed in Gasser et al. (2006) as follows:

$$ \bar{\psi }_{\text{cf}} \left( {{\bar{\mathbf{C}}}} \right) = \mathop \sum \limits_{{M_{\text{cf}} = M_{{4{\text{cf}},6{\text{cf}}}} }} \frac{{k_{{1{\text{cf}}}} }}{{2k_{{2{\text{cf}}}} }}\left( {{ \exp }\left( {k_{{2{\text{cf}}}} \left( {\kappa \bar{I}_{1} + \left( {1 - 3\kappa } \right)\bar{I}_{{M_{\text{cf}} }} - 1} \right)^{2} } \right) - 1} \right) $$
(12)

where \( k_{{1{\text{cf}}}} \) and \( k_{{2{\text{cf}}}} \) are material parameters and \( \bar{I}_{{M_{{4{\text{cf}}}} }} \) and \( \bar{I}_{{M_{{6{\text{cf}}}} }} \) are the square of the stretch in the collagen fibres and correspond to two unit vectors \( {\mathbf{M}}_{{4{\text{cf}}}} = \left\{ {\cos \left( {\alpha_{\text{cf}} } \right),\sin \left( {\alpha_{\text{cf}} } \right),0} \right\} \) and \( {\mathbf{M}}_{{6{\text{cf}}}} = \left\{ {\cos \left( {\alpha_{{\rm cf}} } \right), - \sin \left( {\alpha_{{\rm cf}} } \right),0} \right\} \), respectively, where \( \alpha_{\text{cf}} \) is the angle of collagen fibres with respect to the circumferential direction.

2.4.3 Response of arteries to supra-physiological loading levels

To describe the response of arteries to supra-physiological loading conditions, a CDM-based approach was employed. As is common in CDM, to capture the energy dissipation in the vessel wall a reduction factor (1 − D) can be incorporated in the overall strain energy function of the tissue to simulate the energy dissipation, where D is a scalar damage function which may take any value between 0 and 1 and evolve according to the loading history of the vessel wall. The incorporation of the reduction factor in the total undamaged strain energy function \( \psi^{0} \left( {{\bar{\mathbf{C}}}} \right) \) may be expressed as follows (Holzapfel 2000):

$$ \psi \left( {{\bar{\mathbf{C}}},D} \right) = \left( {1 - D} \right)\psi^{0} \left( {{\bar{\mathbf{C}}}} \right) $$
(13)

Although prefixing the reduction factor to the intact strain energy function can describe discontinuous softening in soft tissue, this technique cannot provide an accurate insight into other damage-relevant phenomena such as hysteresis or permanent set. In order to model all of the damage-relevant phenomena in the arterial tissue, we have incorporated the reduction factor in the exponential part of the strain energy functions for both elastin and collagen fibres given in Eqs. (11) and (12); similar approaches have been employed in Balzani et al. (2012), Balzani and Schmidt (2015), Govindjee and Simo (1991).

$$ \bar{\psi }_{\text{ef}} \left( {{\bar{\mathbf{C}}},D_{\text{ef}} } \right) = \mathop \sum \limits_{{M_{\text{ef}} = M_{{4{\text{ef}}}} ,M_{{6{\text{ef}}}} }} \frac{{k_{{1{\text{ef}}}} }}{{2k_{{2{\text{ef}}}} }}\left( {\exp \left[ {k_{{2{\text{ef}}}} \left( {1 - D_{\text{ef}} } \right)\left( {\bar{I}_{{M_{\text{ef}} }} - 1} \right)^{2} } \right] - 1} \right) $$
(14)
$$ \begin{aligned} \bar{\psi }_{\text{cf}} \left( {{\bar{\mathbf{C}}},D_{\text{cf}} } \right) & = \mathop \sum \limits_{{M_{\text{cf}} = M_{{4{\text{cf}}}} ,M_{{6{\text{cf}}}} }} \frac{{k_{{1{\text{cf}}}} }}{{2k_{{2{\text{cf}}}} }}\\ &\quad \left( {{ \exp }\left( {k_{{2{\text{cf}}}} \left( {1 - D_{\text{cf}} } \right)\left( {\kappa \bar{I}_{1} + \left( {1 - 3\kappa } \right)\bar{I}_{{M_{\text{cf}} }} - 1} \right)^{2} } \right) - 1} \right) \end{aligned} $$
(15)

where Def and Dcf are the damage functions for elastin fibres and collagen fibres, respectively. These damage functions evolve according to structural pseudo-invariant functions over the loading history using two internal variables, \( \beta_{\text{ef,cf}} \) and \( \gamma_{\text{ef,cf}} \), to capture continuous and discontinuous softening, respectively. \( \beta_{\text{ef,cf}} \) is defined as follows:

$$ \beta_{\text{ef,cf}} = \left\langle {\tilde{\beta }_{\text{ef,cf}} - \tilde{\beta }_{\text{ef,cf}}^{\text{ini}} } \right\rangle $$
(16)

where \( \tilde{\beta }^{\text{ini}} \) is an internal variable at an initial damage state to ensure that the damage evolution starts when entering the supra-physiological domain, and Macaulay brackets, \( \left\langle {( \cdot )} \right\rangle = \frac{1}{2}\left[ {( \cdot ) + \left| {( \cdot )} \right|} \right] \), have been used to allow only positive values. \( \tilde{\beta }_{\text{ef,cf}} \) is defined according to changes in the pseudo-invariant \( \bar{I}_{{M_{\text{ef,cf}} }}^{*} \) over the total loading history, as follows:

$$ \tilde{\beta }_{\text{ef,cf}} = \mathop \smallint \limits_{0}^{t} \left\langle {\bar{I}_{{M_{\text{ef}} ,M_{\text{cf}} }}^{*} } \right\rangle {\text{d}}s $$
(17)

The internal variable \( \gamma_{\text{ef,cf}} \) is defined according to the maximum value \( \bar{I}_{\text{ef,cf}}^{*} \) experienced over the loading history up to the current loading state of the arterial tissue and defined as follows:

$$ \gamma_{\text{ef,cf}} = \mathop {\hbox{max} }\limits_{{S \in \left[ {0,S} \right]}} \left\langle {\bar{I}_{{M_{\text{ef}} ,M_{\text{cf}} }}^{*} - \bar{I}_{{M_{\text{ef}} ,M_{\text{cf}} }}^{{*{\text{ini}}}} } \right\rangle $$
(18)

The damage functions Def and Dcf can then be written as follows for both elastin and collagen fibres, similar to procedures shown in Balzani et al. (2012), Balzani and Schmidt (2015), Miehe (1995).

$$\begin{aligned} D_{\text{ef,cf}} & = D_{\infty_{{\text{ef,cf}}}} \left[ {1 - \exp \left( { - \frac{{\gamma_{\text{ef,cf}} }}{{\gamma_{\infty_{{\text{ef,cf}}}} }}} \right)} \right]\\ &\quad \left[ {1 - \exp \left( { - \frac{{\beta_{\text{ef,cf}} }}{{\beta_{s_{\text{ef,cf}}} }}} \right)} \right],D_{\text{ef,cf}} \in \left[ {0,1} \right)\end{aligned} $$
(19)

where \( D_{\infty_{{\text{ef,cf}}}} \) denotes a predefined limit for the overall damage values for elastin and collagen fibres which we have selected to be 0.99. \( \beta_{s_{\text{ef,cf}}} \) and \( \gamma_{\infty_{{\text{ef,cf}}}} \) are the only material parameters which have been used to capture continuous and discontinuous softening in the arterial tissue, respectively.

2.4.4 Finite element implementation

To implement this material model into a commercial finite element (FE) software, such as Abaqus (Dassault Systèmes Simulia corporations, Vèlizy-Villacoublay, France), the Cauchy stress tensor \( {\varvec{\sigma}} \) and the elasticity tensor \( {\mathbb{C}} \) (also referred to as the tangent modulus or the material Jacobian) should be defined. The Cauchy stress tensor is derived from the strain energy functions introduced in the preceding section (Eq. (8)), as follows:

$$ {\varvec{\upsigma}} = \frac{2}{J}{\mathbf{F}}\frac{\partial \psi }{{\partial {\mathbf{C}}}}{\mathbf{F}}^{T} $$
(20)

The corresponding Kirchhoff stress is defined as follows:

$$ {\varvec{\uptau}} = J{\varvec{\upsigma}} $$
(21)

In this research, following the procedure demonstrated by Sun et al. (2008), the material Jacobian has been derived by incrementally perturbing the deformation gradient tensor and performing a forward difference of the associated Kirchhoff stresses;

$$ {\mathbb{C}}^{{\left( {ij} \right)}} \approx \frac{1}{J\varepsilon }\left( {{\varvec{\uptau}}\left( {{\hat{\text{F}}}^{ij} } \right) - {\varvec{\uptau}}\left( {{\hat{\text{F}}}} \right)} \right) $$
(22)

where \( \varepsilon \) (10−8) is a small perturbation parameter and \( {\varvec{\uptau}} \) denotes the Kirchhoff stress tensor. The tensor \( {\hat{\mathbf{F}}}^{{\varvec{ij}}} \) describes the perturbed deformation gradient tensor which is;

$$ {\hat{\text{F}}}^{ij} = {\mathbf{F}} +\Delta {\text{F}}^{ij} $$
(23)

Following Miehe (1996) and Sun et al. (2008), \( \Delta {\mathbf{F}}^{ij} \) can be defined as follows:

$$ \Delta F^{ij} = \frac{\varepsilon }{2}\left( {e_{i} \otimes e_{j} {\mathbf{F}} + e_{j} \otimes e_{i} {\mathbf{F}}} \right) $$
(24)

where \( \left\{ {{\text{e}}_{\text{i}} } \right\}_{i = 1,2,3} \) denotes the unit vectors in the spatial configuration over which the perturbation has been performed, \( ij = \left\{ {11,22,33,12,23,31} \right\} \). A similar approach has also been employed by Creane et al. (2010). The algorithmic FE implementation of the demonstrated damage model along with required quantities is shown in Table 2.

Table 2 The summary of the quantities required for finite element implementation of the presented constitutive model
Full size table

2.5 Material calibration

To verify the proposed constitutive model, the response of the digested and intact samples has been obtained at different stages, namely (i) when no damage accumulates in the tissue, (ii) the stage at which damage starts to accumulate in the elastin fibres but no damage has accumulated in the collagen fibres and (iii) the stage at which damage is accumulating in both elastin and collagen fibres. Material parameters associated with capturing the damage accumulation in the elastin fibres only influence the stress calculation when the damage threshold for the elastin fibres has been passed (at this stage other material parameters such as c10, k1ef, k2ef remain constant), and damage parameters for the collagen fibres have only been incorporated in the response of the tissue when the damage threshold for collagen fibres has been exceeded. (At this stage, other material parameters such as c10, k1ef, k2ef, k1cf, k2cf, αcf remain constant.) Collagen fibres and elastin fibres have also been constrained to only contribute in the load bearing of the tissue under tension. The damage thresholds in the collagen and elastin fibres are functions of stretch in the fibres which has been captured by calculating the deviatoric invariants associated with the direction of the elastin and collagen fibres, \( I_{{M_{\text{ef}} }} \) and \( I_{{M_{\text{cf}} }} \), respectively, see Eq. (5). In order to set the damage threshold for damage accumulation in collagen fibres, the results of studies such as Converse et al. (2018) and Zitnay et al. (2017) were employed. In these studies, collagen hybridizing peptide (CHP) was utilized to detect damage initiation in collagen fibres under stretch. In addition, the difference in stiffness between elastin and collagen fibres is highlighted in studies such as Shadwick (1998), (1999). However, to the best of the authors’ knowledge, to date no specific damage threshold for elastin fibres has been presented in the literature. In this research, we assumed that damage accumulation in the elastin fibres starts as soon as their stretch is slightly greater than one (1.02). A sensitivity analysis has been performed to explore the influence of selecting different damage thresholds on damage accumulation and stress calculations for both collagen and elastin fibres. The results of this sensitivity analysis are included in supplementary material.

Stress–time curves from samples in the circumferential and axial directions of the vessel wall have been used simultaneously to account for the anisotropic behaviour of the non-collagenous and intact samples. Similar approaches have been used to adjust material models to experimental data in studies such as Balzani and Schmidt (2015), Maher et al. (2012), Pena (2014). It should be mentioned that data obtained for the values of permanent set have not been incorporated into the curve fitting process and have enabled us to further assess the suitability of this damage model for arterial tissue.

An inverse FE algorithm was implemented to adjust the parameters of our damage model to the experimental data using Isight 5.9 (Dassault Systèmes Simulia corporations, Vèlizy-Villacoublay, France). To simulate our cyclic mechanical tests, the stretch read from the video extensometer during the experimental tests was applied on one single element using displacement boundary conditions. An incompressibility constraint was also imposed by using a hybrid element type (C3D8H). A schematic of this simulation and boundary conditions is presented in Fig. 3.

Fig. 3
figure 3

A schematic of uniaxial mechanical tests simulated for specimens in a circumferential and b axial directions by applying the displacements boundary condition (u) in Abaqus

Full size image

Two sets of experimental data, one in the axial and the other one in the circumferential directions, were used to determine the material parameters for both intact and digested samples simultaneously. A combination of global and local optimization methods were employed to minimize the sum of the square difference of the measured stress between the experiments and the model, and the error is calculated as follows (Balzani et al. 2012):

$$ {\text{error}} = \mathop \sum \limits_{e = 1}^{{n_{e} }} \sqrt {\frac{1}{{n_{\text{mp}} }}\mathop \sum \limits_{m = 1}^{{n_{\text{mp}} }} \left( {\frac{{\sigma_{\text{mp}}^{\exp } - \sigma_{\text{mp}}^{\text{model}} }}{{\hbox{max} \left( {\sigma^{\exp } } \right)}}} \right)^{2} } $$
(25)

where ne is the number of experimental data sets (axial and circumferential), nmp is the total number of experimental points in the loading and reloading paths, \( \sigma^{ \exp } \) is the measured stress in the experiments and \( \sigma^{\text{model}} \) is the calculated stress from the model. In this research, we have used two sets of experimental data (\( n_{e} = 2 \)) simultaneously, with 100 points (\( n_{\text{mp}} = 100 \)) on each loading and reloading path.

In the first step of the minimization, a multi-objective genetic algorithm-based optimization method was used to characterize the material parameters of the media layer of the porcine common carotid arteries. One of the main benefits of using a genetic algorithm-based optimization method at this stage is that it examines a large population of random material parameter combinations in a certain domain to minimize the objective functions in each iteration. This technique can be particularly useful when no proper first estimation of the material parameters exists. This method also accelerates the process of finding the global minimum of the objective functions by adding penalty values to the local minimums. The general specifications of the genetic algorithm that we have used in this research are given in Table 3. For a more detailed description of the genetic algorithm and its application in identifying material parameters and inverse problems, the reader is referred to El Sayed et al. (2008). We have restricted all parameters to remain positive during the optimization process. The angle of collagen fibres is assumed to be between 10 and 80 degrees with respect to the circumferential direction of the vessel wall. The dispersion of collagen fibres was permitted to be between 0 and 0.33.

Table 3 Genetic algorithm options that have been used in this study
Full size table

The material parameters obtained in the first step of the optimization were then used as the preliminary material parameters for the second step of minimization where the Downhill simplex method was employed as the local optimization method. The Downhill simplex method is a gradient-free geometrically intuitive exploratory technique. For a detailed description of the Downhill simplex method and its implementation, the reader is referred to, for example, Press et al. (1987). The options that we have used for Downhill simplex method are given in Table 4. A schematic of the implemented optimization method is shown in Fig. 4.

Table 4 Options of the Downhill simplex method that have been used in this study
Full size table
Fig. 4
figure 4

A schematic presentation of the implemented inverse FE algorithm for material calibration of the media layer of porcine carotid arteries in Isight. Different parameterized Abaqus input files have been designated for the specimens in the axial and circumferential directions. The input files were imported into the Abaqus component of Isight and the material parameters selected as optimization variables. The results from the experiments and simulation have been imported into the data matching component where the sum of the stress difference for 100 points on each loading and reloading path has been defined as objective functions separately for samples in axial and circumferential directions. A hybrid optimization algorithm was then performed to characterize the material parameters of each specimen

Full size image

3 Results

The permanent deformation of the three intact and three digested arteries in the circumferential and axial samples is compared in Fig. 5. The summary of the samples which have been used for this study are shown in Table 1. The permanent set in each sample has been evaluated by reading the accumulated residual strain in each specimen at zero force in the reloading paths, similar to (Maher et al. 2012; Pena 2014). A linear relationship between the resulting permanent set and peak strain has been observed in the intact and digested samples in both the circumferential and axial directions. Our observations confirm that there is no statistically significant difference in the captured permanent set in either the circumferential and axial directions, or between the intact and digested samples.

Fig. 5
figure 5

The obtained permanent set in the cyclic mechanical tests at high strain levels in a axial and circumferential directions of intact samples, b circumferential samples of intact and digested arteries, c circumferential and axial directions of digested samples, d axial samples of intact and digested samples

Full size image

The stress–strain curves obtained from cyclic mechanical loading of one collagen fibre digested sample in the circumferential and axial directions have been compared with the response of the damage model in Fig. 6a, c. It should be mentioned that to calibrate this constitutive model only the stress computed by our damage model was compared with the stress obtained from experiments, and the error is calculated using Eq. (25). The values of the permanent set which was measured from the experiments and the predicted permanent set by the constitutive model are compared in Fig. 6b, d. It is worth mentioning that the data obtained for permanent set from experiments have not been incorporated in the calibration process, and Fig. 6b, d represents the prediction of the model.

Fig. 6
figure 6

Cyclic uniaxial tension tests of the collagen digested media layer of a porcine common carotid artery in axial (a, b) and circumferential (c, d) directions

Full size image

The material parameters to describe the mechanical behaviour of digested samples to supra-physiological loadings are shown in Table 5. Although a low level of anisotropic behaviour has been observed from the experimental data, the results computed by our damage model show that a material model with two families of elastin fibres at 45 degrees with respect to the circumferential direction of the vessel wall can successfully capture the low levels of discontinuous and continuous softening that occur in the ECM along with the associated permanent set in the soft tissue.

Table 5 Material parameters which have been used to capture the mechanical behaviour of digested samples shown in Fig. 6
Full size table

The stress–strain curves obtained from cyclic mechanical loading of axial and circumferential samples from two intact arteries at high strain levels have been compared with the response of the implemented CDM model, see Fig. 7. A summary of the samples which have been used in this study to explore the response of the intact samples to supra-physiological loads is shown in Table 1. The effect of continuous and discontinuous softening on the response of the arteries can be seen in Fig. 7a, d. The permanent set obtained from mechanical tests has been compared with the permanent set calculated using our FE simulation in Fig. 7b, c, e, f. It should be mentioned that, similar to collagen fibre digested samples, the data obtained for permanent set from experiments have not been incorporated in the curve fitting process. The material parameters to describe the mechanical behaviour of each artery are shown in Table 6.

Fig. 7
figure 7

Cyclic uniaxial tension tests of the intact media of two porcine common carotid arteries in the axial and circumferential directions

Full size image
Table 6 Material parameters which have been used to capture the mechanical behaviour of the two intact arteries in the axial and circumferential directions, as shown in Fig. 7
Full size table

4 Discussion

The obtained experimental results show that there is no significant difference between the resulting permanent set in the intact and digested samples in the circumferential and axial directions. These observations confirm the role of matrix, as opposed to fibres, in the inelastic deformation of arterial tissue at supra-physiological loads. To date, several constitutive models have assumed that damage in the arterial tissue occurs only within the collagen fibres (Balzani et al. 2012; Balzani and Schmidt 2015; Weisbecker et al. 2013), and as such, the model can adequately capture the damage accumulation in the collagen fibres, but not the overall inelastic behaviour of the tissue at supra-physiological loads.

Although constitutive models such as Balzani et al. (2012), Maher et al. (2012), Pena (2014) can mathematically capture the inelastic deformation of different biological soft tissues at high loading conditions, no specific structural element has been designated in those models to attribute the inelastic deformation of the artery to the matrix. In this study, we have adapted the constitutive model that was demonstrated in Holzapfel et al. (2000) to capture the behaviour of the matrix at supra-physiological loading conditions by incorporating two symmetric families of elastin fibres at 45 degrees with respect to the circumferential direction of the vessel wall. A reduction factor has then been incorporated in the exponential term of this constitutive model which enables the permanent set phenomenon in the media layer of the porcine common carotid arteries to be captured. Although some levels of anisotropy have been observed in the mechanical behaviour of the matrix, the proposed transversely isotropic strain energy function for elastin fibres can adequately predict all of the damage-relevant phenomena of the non-collagenase matrix. These findings are similar to the observations in Weisbecker et al. (2013) whereby they show that an isotropic neo-Hookean material model can sufficiently describe the behaviour of the extracellular matrix (ECM) at physiological loads.

Balzani and Schmidt (2015) compared different damage functions to determine their influence on the numerical stability of the tangent modulus tensor at the transition point between the undamaged and damaged states. In this research, the material Jacobian has been obtained by incrementally perturbing the deformation gradient tensor and performing a forward difference of the associated Kirchhoff stresses, following the method demonstrated in Miehe (1996) and Sun et al. (2008), which produces a concise mathematical formulation of the tangent modulus. Using this technique, we did not encounter any convergence issues.

To date, CDM has been extensively used to capture the mechanical behaviour of biological soft tissues, although one of the main limitations associated with this approach is calibrating the material parameters. In order to minimize the effect of the number of material parameters, in this research, only two material parameters for elastin fibres (\( \gamma_{\infty_{{\text{ef}}}} ,\beta_{s_{{\text{ef}}}} \)) and two material parameters for collagen fibres (\( \gamma_{\infty_{{\text{cf}}}} ,\beta_{s_{{\text{cf}}}} \)) have been employed in the constitutive model to control the damage accumulation in the arterial tissue. These material parameters are associated with two internal variables for both elastin and collagen fibres and evolve according to fictitious strain invariants as defined in Eq. (7). In this study, stretch in elastin and collagen fibres was used as the main metric to define the pre- and post-damage states of the fibres. The results of a sensitivity analysis, with regard to the threshold of stretch used for damage accumulation in collagen and elastin, show that selecting lower stretches as the damage thresholds for elastin and collagen fibres leads to increased accumulation of damage in the specimens and consequently a higher level of softening in the tissue. Further experimental studies are required to determine the values of these damage thresholds in elastin and collagen fibres.

A two-step optimization method has been employed to characterize the material parameters which have been used in the constitutive model for intact and digested samples. In the first step of the minimization, a large number of random material parameters have been examined using a multi-objective genetic algorithm-based optimization method to simultaneously minimize the sum of the square difference in stresses in the axial and circumferential directions from experiments and simulations. The results of the first step of the optimization have then been used as the first estimation for the local optimization method. This approach can be particularly useful when there is no clear first estimation of the material properties in the constitutive model.

Although this proposed two-constituent damage model can successfully capture all the passive damage-relevant phenomena in the arterial tissue, as shown in the preceding sections, some limitations still need to be addressed. Although the experimental tests in this study were performed on arterial samples of intima and media layers together, the contribution of the intima in supporting the loads has been neglected as the pigs were healthy and very young at the time they were slaughtered. For further information on the effect of age and disease on the stiffening of the intimal layer of arterial tissue and intimal thickening, the reader is referred to, for example, Holzapfel (2008). The proposed damage model does not relate the softening in the tissue with the viscoelastic response of the arterial tissue. The viscoelastic behaviour of soft tissue has been explored experimentally in studies such as Alastrue et al. (2008) and Armentano et al. (2006). Pena et al. (2010) also demonstrate a model to capture viscoelasticity and softening behaviour of biological soft tissue, although other damage-relevant phenomena such as permanent set and hysteresis were not investigated in that research. Although this damage model has been simultaneously calibrated for strips in the axial and circumferential directions, multi-axial mechanical tests would more accurately describe the mechanical behaviour of soft tissues (Holzapfel and Ogden 2009; Sommer et al. 2010).

Despite these limitations, the proposed model can accurately capture all of the passive damage-relevant phenomena in arterial tissue, namely Mullins effect, hysteresis, permanent set up to the level of rupture in the tissue. The proposed constitutive model is the only damage model that has been fit to cyclic mechanical tests at high strain levels on intact and collagenase digested samples that incorporates softening and permanent set. Such material models provide a means to better understand the mechanical response of arterial tissue under different loading conditions, such as the risk of atherosclerotic plaque rupture as a result of arterial tissue damage. Investigating the damage-relevant phenomena in arterial tissue is also important since they can be linked to arterial growth and remodelling responses where supra-physiological loading conditions are imposed, including stiffening of arterial walls following interventional procedures such as stenting and balloon angioplasty. The future goal of this research is to demonstrate the influence that progressive damage accumulation may have on collagen fibre remodelling in arterial tissue.