A Robust Leaky-LMS Algorithm for Sparse System Identification

Abstract

In this paper, a new Leaky-LMS (LLMS) algorithm that modifies and improves the Zero-Attracting Leaky-LMS (ZA-LLMS) algorithm for sparse system identification has been proposed. The proposed algorithm uses the sparsity of the system with the advantages of the variable step-size and l ₀ -norm penalty. We compared the performance of our proposed algorithm with the conventional LLMS and ZA-LLMS in terms of the convergence rate and mean-square-deviation (MSD). Additionally, the computational complexity of the proposed algorithm has been derived. Simulations performed in MATLAB showed that the proposed algorithm has superiority over the other algorithms for both types of input signals of additive white Gaussian noise (AWGN) and additive correlated Gaussian noise (ACGN).

1 Introduction

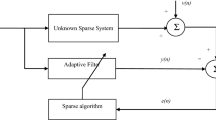
In adaptive filtering technology, the least-mean-square (LMS) algorithm is a commonly used algorithm for system identification (see Fig. 1), noise cancellation or channel equalization models [1]. Although it is a very simple and robust algorithm, its performance deteriorates for some applications which have high correlation, long filter length, sparse signals etc. In the literature, many different LMS-type algorithms were proposed to improve the performance of the standard LMS algorithm.

Fig. 1.

Block diagram of the system identification process.

Leaky-LMS algorithm was proposed [2, 3] to overcome the issues when the input signal is highly correlated, by using shrinkage in its update equation. Another LMS based algorithm VSSLMS uses a variable step-size in update equation of the standard LMS to increase the convergence speed at the beginning stages of the iterations and decrease MSD at later iterations [4, 5]. In order to improve the performance of the LMS algorithm when the system is sparse (most of the system coefficients are zeroes), ZA-LMS algorithm was proposed in [6].

In [7], the author proposed the ZA-LLMS algorithm which combines the LLMS algorithm and the ZA-LMS algorithm for sparse system identification. A better performance was obtained for AWGN and ACGN input signals. In [8], a high performance algorithm called zero-attracting function-controlled variable step-size LMS (ZAFC-VSSLMS) was proposed by using the advantages of variable step-size and l ₀-norm penalty. We were motivated by the inspiration of the combination of these two algorithms. So in this paper we proposed a new algorithm that combines the ZA-LLMS and ZAFC-VSSLMS algorithms. In the next section, a brief review of the LLMS and ZA-LLMS algorithms is provided. We describe the proposed algorithm in Sect. 3 with computational complexity and convergence analysis. In Sect. 4, the simulations are presented and the performance of the algorithm is compared. Conclusions are drawn in the last section.

2 Review of the Related Algorithms

2.1 Leaky-LMS (LLMS) Algorithm

In a system identification process, the desired signal is defined as,

$$ d(n) = {\mathbf{w}}_{0}^{T} {\mathbf{x}}(n) + \nu (n) $$

(1)

where ${\mathbf{w}}_{0} = [w_{0 0} , \ldots ,w_{0N - 1} ]^{T}$ are the unknown system coefficients with length N, ${\mathbf{x}}(n) = [x_{0} , \ldots ,x_{N - 1} ]^{T}$ is the input-tap vector and $v(n)$ is the additive noise. In addition to being independent of the noise sample $v(n)$ with zero mean and variance of $\sigma_{\upsilon }^{2}$, the input data sequence ${\mathbf{x}}(n)$ and the additive noise sample $v(n)$ are also assumed to be independent.

The cost function of the LLMS algorithm is given by,

$$ J_{1} (n) = \frac{1}{2}e^{2} (n) + \gamma {\mathbf{w}}^{T} (n){\mathbf{w}}(n) $$

(2)

where w(n) is the filter-tap vector at time n, $\gamma$ is a positive constant called ‘leakage factor’ and $e(n)$ is the instantaneous error and given by,

$$ e(n) = d(n) - {\mathbf{w}}^{T} (n){\mathbf{x}}(n) $$

(3)

The update equation of the LLMS algorithm can be derived by using the gradient method as,

$$ \begin{aligned} {\mathbf{w}}(n + 1) = & {\mathbf{w}}(n) + \mu \frac{\partial J(n)}{{\partial {\mathbf{w}}(n)}} \\ = (1 - \mu \gamma ){\mathbf{w}}(n) + \mu e(n){\mathbf{x}}(n) \\ \end{aligned} $$

(4)

where µ is the step-size parameter of the algorithm.

2.2 Zero-Attracting Leaky-LMS (ZA-LLMS) Algorithm

The cost function of the LLMS algorithm was modified by adding the log-sum penalty of the filter-tap vector as given below:

$$ J_{2} (n)) = \frac{1}{2}e^{2} (n) + \gamma {\mathbf{w}}^{T} (n){\mathbf{w}}(n) + \gamma^{\prime}\sum\limits_{i = 1}^{N} {(1 + } \frac{{\left| {w_{i} } \right|}}{{\xi^{\prime}}}) $$

(5)

where $\gamma^{\prime}$ and $\xi^{\prime}$ are positive parameters. Taking the gradient of the cost function and subtracting from the previous filter-tap vector iteratively, then the update equation was derived as follows [7]:

$$ {\mathbf{w}}(n + 1) = (1 - \mu \gamma ){\mathbf{w}}(n) + \mu e(n){\mathbf{x}}(n) - \rho \frac{{\text{sgn} [{\mathbf{w}}(n)]}}{{1 + \xi \left| {{\mathbf{w}}(n)} \right|}} $$

(6)

where $\rho = \frac{{\mu \gamma^{\prime}}}{{\xi^{\prime}}}$ is the zero-attracting parameter, $\xi = \frac{1}{{\xi^{\prime}}}$ and sgn(.) operation is defined as,

$$ \text{sgn} (x) = \left\{ {\begin{array}{*{20}c} {\frac{x}{\left| x \right|}\quad if\;x \ne 0} \\ {0\quad if\;x = 0} \\ \end{array} } \right. $$

(7)

3 The Proposed Algorithm

3.1 Derivation of the Proposed Algorithm

An improved sparse LMS-type algorithm was proposed in [8] by exploiting the advantages of variable step-size and recently proposed [9] l ₀-norm which gives an approximate value of $\left\| \cdot \right\|_{0}$. We modify the cost function of that algorithm by adding the weight vector norm penalty as,

$$ J_{3} (n)) = \frac{1}{2}e^{2} (n) + \gamma {\mathbf{w}}^{T} (n){\mathbf{w}}(n) + \varepsilon \left\| {{\mathbf{w}}(n)} \right\|_{0} $$

(8)

where ε is a small positive constant and $\left\| {{\mathbf{w}}(n)} \right\|_{0}$ denotes the l ₀-norm of the weight vector given as,

$$ \left\| {{\mathbf{w}}(n)} \right\|_{0} \simeq \sum\limits_{k = 0}^{N - 1} {(1 - e^{{ - \lambda \left| {{\mathbf{w}}(n)} \right|}} )} $$

(9)

where λ is a positive parameter. Deriving (8) with respect to w(n) and substituting in the update equation we get,

$$ {\mathbf{w}}(n + 1) = (1 - \mu (n)\gamma ){\mathbf{w}}(n) + \mu (n)e(n){\mathbf{x}}(n) - \rho (n)\text{sgn} [{\mathbf{w}}(n)]e^{{ - \lambda \left| {{\mathbf{w}}(n)} \right|}} $$

(10)

where $\rho (n) = \mu (n)\varepsilon \lambda$ is the sparsity aware parameter and depends on the positive constant λ and $\mu (n)$ which is the variable step-size and given in [6] as

$$ \mu (n + 1) = \alpha \mu (n) + \gamma_{s} f(n)\frac{{e(n)^{2} }}{{\hat{e}_{ms}^{2} (n)}} $$

(11)

where $0 < \alpha < 1,\;\gamma_{s} > 0$ are some positive constants and $e(n)$ is a mean value of the error vector. $\hat{e}_{ms}^{2} (n)$ is the estimated mean-square-error (MSE) and is defined as

$$ \hat{e}_{ms}^{2} (n) = \beta \hat{e}_{ms}^{2} (n - 1) + (1 - \beta )e(n)^{2} $$

(12)

where $\beta$ is a weighting factor given as $0 < \beta < 1\;{\text{and}}\;f(n)$ is a control function given below

$$ f(n) = \left\{ {\begin{array}{*{20}c} {1/n\quad n < L} \\ {1/L\quad n \ge L} \\ \end{array} } \right. $$

(13)

A summary of the algorithm is given in Table 1.

Table 1. Summary of the SBFC-VSSLMS algorithm.

It is seen that the update equation of the ZA-LLMS algorithm has been modified by changing the constant step-size µ with µ(n) given in [8] and the zero-attractor $\rho \frac{{\text{sgn} [{\mathbf{w}}(n)]}}{{1 + \xi \left| {{\mathbf{w}}(n)} \right|}}$ with $\rho (n)\text{sgn} [{\mathbf{w}}(n)]e^{{ - \lambda \left| {{\mathbf{w}}(n)} \right|}}$.

3.2 Computational Complexity

The update equation of the conventional LMS algorithm has O(N) complexity and has been calculated as 2N + 1 multiplications and 2N additions at each iteration [10]. For $(1 - \mu \gamma ){\mathbf{w}}(n)$ in LLMS N + 1 extra multiplications and one addition are required. In the update equation of the estimated MSE used in the algorithm proposed in [8], 3 multiplications and 2 additions are required additionally to compute the $\hat{e}_{ms}^{2} (n)$. For update equation of $\mu (n)$, we need 5 multiplications and one addition. The computational complexity of the zero attractor, $\rho (n)\text{sgn} [{\mathbf{w}}(n)]e^{{ - \lambda \left| {{\mathbf{w}}(n)} \right|}}$, requires N multiplications for $\lambda \left| {{\mathbf{w}}(n)} \right|$, N additions for $e^{{ - \lambda \left| {{\mathbf{w}}(n)} \right|}}$ (taking the first two terms of Taylor series), N multiplications for $\rho (n)\text{sgn} [{\mathbf{w}}(n)]$, N multiplications for one by one element product of $\lambda \left| {{\mathbf{w}}(n)} \right|$ by $\rho (n)\text{sgn} [{\mathbf{w}}(n)]$ and N comparisons for $\text{sgn} [{\mathbf{w}}(n)]$. So, overall complexity of the zero attractor is 3N multiplications, N additions and N comparisons. The overall computational complexity of the proposed algorithm requires 6N + 10 multiplications, 3N + 4 additions and N comparisons, that is, (O(N) complexity.

4 Simulation Results

In this section, we compare the performance of the proposed algorithm with LLMS and ZA-LLMS algorithms in high-sparse and low-sparse system identification settings. Two different experiments are performed for each of AWGN and ACGN input signals. To increase the reliability of the expected ensemble average, experiments were repeated by 200 independent Monte-Carlo runs. The constant parameters are found by extensive tests of simulations to obtain the optimal performance as follows: For LLMS: µ = 0.002 and γ = 0.001. For ZA-LLMS: µ = 0.002, γ = 0.001, ρ = 0.0005 and ξ = 30. For the proposed algorithm: ρ = 0.0005 and λ = 8.

In the first experiment, all algorithms are compared for 90 % high-sparsity and 50 % low-sparsity of the system with 20 coefficients having in the first part two ‘1’ and 18 ‘0’; in the second part ten ‘1’ and ten ‘0’ for 5000 iterations. Signal-to-noise ratio (SNR) is kept at 10 dB by regulating the variances of the input signal and the additive noise. The performance of the algorithm is compared in terms of convergence speed and $MSD = E\left\{ {\left\| {{\mathbf{w}}_{0} - {\mathbf{w}}(n)} \right\|^{2} } \right\}$. Figures 2 and 3 give the MSD vs. iteration number of the three algorithms for 90 % sparsity and 50 % sparsity levels respectively. In Fig. 2, the proposed algorithm has a convergence speed of around 1000 iterations and MSD about −37 dB, while the others are close to each other at a convergence speed of 2500 iterations and MSD of −26~28 dB. Figure 3 shows that the proposed algorithm has a convergence speed of 1100 iterations and MSD of −29.9 dB while the other algorithms have convergence speed and MSD about 3000 iterations and −26 dB, respectively. The figures show that, the proposed algorithm has a fairly fast convergence with lower MSD than that of the other algorithms.

Fig. 2.

Steady state behavior of the LLMS, ZA-LLMS and the proposed algorithm for 90 % sparsity with AWGN.

Fig. 3.

Steady state behavior of the LLMS, ZA-LLMS and the proposed algorithm for 50 % sparsity with AWGN.

In the second experiment, all conditions are kept as same as in the previous experiment except the input signal type. A correlated signal is created by the AR(1) process as $x(n) = 0.4x(n - 1) + v_{0} (n)$ and the normalized. Figures 4 and 5 shows that the proposed algorithm has a faster convergence and lower MSD than the other algorithms for 90 % sparsity and 50 % sparsity levels respectively.

Fig. 4.

Steady state behavior of the LLMS, ZA-LLMS and the proposed algorithm for 90 % sparsity with ACGN.

Fig. 5.

Steady state behavior of the LLMS, ZA-LLMS and the proposed algorithm for 50 % sparsity with ACGN.

5 Conclusions

In this work, we proposed a modified leaky-LMS algorithm for sparse system identification. It was derived by combining the ZA-LLMS and ZAFC-LMS algorithms. The performance of the proposed algorithm was compared with LLMS and ZA-LLMS algorithms for 90 % and 50 % sparsity levels of the system with AWGN and ACGN input signals in two different experiments performed in MATLAB. Additionally, the computational complexity of the proposed algorithm has been derived. It was shown that the computational complexity of the proposed algorithm is O(N) as same as in other LMS-type algorithms. Besides, the simulations showed that the proposed algorithm has a very high performance with a quite faster convergence and lower MSD than that of the other algorithms. As a future work, it is recommended that the proposed algorithm can be modified for transform domain or be tested for non-stationary systems.