Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Since the seminal paper of Nelder and Wedderburn (1972), the class of generalized linear models (GLM) has received wide acceptance in a host of applications (McCullagh and Nelder, 1989). Studies in these applications often involve covariates that cannot be measured precisely or directly. For example, in the Framingham Heart Study (Kannel et al., 1986), a logistic regression model was used to relate the indicator for the presence of coronary heart disease with covariates such as one’s smoking status, body mass index, age, serum cholesterol level, and long-term systolic blood pressure (SBP). Among these covariates, measures of one’s serum cholesterol level were imprecise, and the actual observed blood pressure of a subject is merely a noisy surrogate of the long-term SBP, which cannot be measured directly. Taking the structural model point of view to account for measurement error as opposed to the functional model point of view (Carroll et al., 2006, Sect. 2.1), one needs to assume a model for the latent true covariates in order to derive the observed data likelihood function. Together the latent-covariate model, the model that relates the true covariates with their noisy surrogates, and the GLM as the conditional model of the response given the true covariates, one has the complete specification of a structural measurement error model for the observed data. From that point on, one can draw parametric inference on the regression parameters straightforwardly.

Like most model-based inference, the validity of inference derived from the structure measurement error model relies on the assumed latent-variable model as well as the posited GLM. In the measurement error community there is a general concern about imposing models for unobserved covariates, as one can easily make inappropriate assumptions on unobservable covariates that often lead to misleading inference (Huang et al., 2006). The widely entertained GLMs for a binary response often assume one of the popular links such as logistic, probit, and complementary log-log. The choice of these popular links is mostly encouraged by ease of interpretation, the familiarity among practitioners, and its convenient implementation using standard statistical software. However, for one particular application, a link function outside of this popular suite of links may be able to capture the underlying association between the response and covariates more accurately. Li and Duan (1989) studied the properties of regression analysis under a misspecified link function in general regression settings. Czado and Santner (1992) focused on the effects of link misspecification on regression analysis based on GLMs for a binary response. Without considering measurement error in covariates, these authors provided theoretical and empirical evidence of the adverse effects of a misspecified link in GLM on likelihood-based inference. They showed that the maximum likelihood estimators (MLE) of regression coefficients obtained under an inappropriate link can be biased and inefficient.

In this article, we address both sources of model misspecification and propose diagnostic procedures to assess these model assumptions. There are only a handful of diagnostic methods available for testing either one of these assumptions (e.g., Pregibon, 1980; Brown, 1982; Stukel, 1988; Huang et al., 2009), and most existing tests for GLM, with or without error-prone covariates, are omnibus tests designed for testing overall goodness-of-fit (GOF) rather than assessing specific assumptions of a hierarchical model (e.g., Tsiatis, 1980; Fowlkes, 1987; Hosmer and Lemeshow, 1989; Le Cessie and van Houwelingen, 1991; Ma et al., 2011). To the best of our knowledge, there is no existing work that address the dual misspecification considered in our study. Huang et al. (2006) proposed the so-called remeasurement method, referred to as RM henceforth, to detect latent-variable model misspecification in structural measurement error models. This method also has successes in testing latent-variable model assumptions in the bigger class of joint models (Huang et al., 2009), and was later improved to adapt to more challenging data structures (Huang, 2009). To detect link misspecification without involving error-prone covariates, Pregibon (1980) proposed a test derived from linearizing the discrepancy between the assumed link and the true link. His test was developed under the assumption that the assumed link and the true link belong to the same family, which can be a stringent assumption. Moreover, his test fails easily if the local linear expansion of the true link about the assumed link is a poor approximation of the true link. For logistic regression models in the absence of measurement error, Hosmer et al. (1997) compared nine GOF tests for three types of model misspecification, including link misspecification, and found none of these tests have satisfactory power to detect link misspecification.

Inspired by the rationale behind RM, we propose a new diagnostic method initially aiming to detect link misspecification, called the reclassification method, or RC for short. This new method is described in Sect. 2, where we first define generic notations in a structural measurement error model, followed by a brief review of RM. Both RM and RC are motivated by theoretical findings on the effects of either type of misspecification on MLEs. For illustration purposes, we focus on one particular assumed structural measurement error model for the majority of the study and formulate a class of true flexible models. Under such formulation we present properties of the MLEs in the presence of one or both sources of misspecification in Sect. 3. In Sect. 4 we report finite-sample simulation studies to illustrate the performance of the proposed diagnostic procedures. Two real-life data examples are used to demonstrate the implementation of these methods in Sect. 5. Finally, discussions on our findings and follow-up research directions ensue in Sect. 6.

2 Models and Two Diagnostic Methods

2.1 Models

Denote by Y i the binary response of subject i, for i = 1, …, n, and the true distribution of Y i conditioning on covariates X i is specified by a GLM,

$$\displaystyle{ P(Y _{i} = 1\vert X_{i};\beta ) = H(\beta _{0} +\beta _{ 1}^{t}X_{ i}), }$$
(1)

where β = (β 0, β 1 t)t is the vector of regression coefficients, and H(s) is the inverse link function, assumed to be a nondecreasing and differentiable function of s. For a succinct exposition, we assume a scalar error-prone covariate X i in the sequel, and the observed covariate, W i , relates to X i via a classical measurement error model (Carroll et al., 2006, Sect. 1.2), for i = 1, …, n,

$$\displaystyle{ W_{i} = X_{i} + U_{i}, }$$
(2)

where U i  ∼ N(0, σ u 2) is the nondifferential measurement error (Carroll et al., 2006, Sect. 2.5). Estimation of σ u 2 is straightforward when replicate measures of each X i (i = 1, …, n) are available (Carroll et al., 2006, Eq. (4.3)). For notational simplicity, σ u 2 is assumed known in the majority of this article. Lastly, suppose that {X i } i = 1 n is a random sample from a distribution specified by the probability density function (pdf) f X (t)(x; τ), indexed by parameters τ. The three component models, (1), (2), and f X (t)(x; τ), constitute the structural measurement error model, based on which one has the correct likelihood function of the observed data for subject i, (Y i , W i ), given by \(f_{\mbox{ $Y,W$}}^{(t)}(Y _{i},W_{i};\varOmega ^{(t)},\sigma _{u}^{2}) =\int \left \{H(\beta _{0} +\beta _{1}x)\right \}^{Y _{i}}\left \{1 - H(\beta _{0} +\beta _{1}x)\right \}^{1-Y _{i}}\sigma _{u}^{-1}\phi \{(W_{i} - x)/\sigma _{u}\}f_{\mbox{ $X$}}^{(t)}(x;\tau )dx\), where ϕ(s) is the pdf of the standard normal distribution, and Ω (t) = (β t, τ t)t is the vector of all unknown parameters under the correct model specification.

Suppose that one assumes the link function to be J(s), which may differ from H(s) in (1), and one posits a model for X i with pdf give by f X(x; η), indexed by parameters η. Then one has the assumed likelihood function of the observed data for subject i, denoted by f Y,W(Y i , W i ; Ω, σ u 2), similarly derived as above, where Ω = (β t, η t)t is the p-dimensional vector of all unknown parameters under the assumed model.

2.2 Remeasurement Method and Reclassification Method

It was shown in Huang et al. (2006) that, when the model for the true covariate, that is, the X-model, is misspecified, the MLE of β is usually inconsistent with bias depending on the measurement error variance. By exploiting this dependence, they proposed further contaminating {W i } i = 1 n to generate \(W_{b,i}^{{\ast}} = W_{i} + \sqrt{\lambda }\sigma _{u}Z_{b,i}\), for b = 1, …, B, i = 1, …, n, where λ is a user-specified positive constant and Z b, i ’s are independent pseudo errors from N(0, 1). Note that the measurement error variance associated with {W b, i ∗, b = 1, …, B} i = 1 n is equal to (1 +λ)σ u 2. They then constructed a test statistic based on the difference between the MLE of β, \(\hat{\beta }\), computed using the raw data, {(Y i , W i )} i = 1 n, and the counterpart MLE, \(\hat{\beta }_{r}\), obtained from the remeasured data, {(Y i , W i ∗)} i = 1 n, where W i ∗ = (W 1, i ∗, …, W B, i ∗), for i = 1, …, n. Take β 1 as an example, the test statistic associated with β 1 is defined by \(T_{\beta _{1}} = (\hat{\beta }_{1} -\hat{\beta }_{1r})/\hat{\nu }_{\beta _{1}}\), where \(\hat{\nu }_{\beta _{ 1}}\) is an estimator of the standard error of \(\hat{\beta }_{1} -\hat{\beta }_{1r}\). Each so-constructed test statistic for a parameter in Ω follows a Student’s t distribution with n − p degrees of freedom asymptotically under the null hypothesis that the two MLEs being compared converge to the same limit as n → ∞. If the value of a test statistic deviates significantly from zero, one finds evidence that the assumed latent-variable model is inappropriate. Derivations of the standard error estimator and the proof of the null distribution, omitted here, are given in Huang et al. (2006).

It is assumed in this existing work that all aspects of the structural measurement error model are correctly specified except for the X-model. But one may legitimately question the adequacy of the assumed link in the GLM. And if the link is indeed misspecified, one may wonder if RM can also detect the link misspecification and how its ability to reveal latent-variable model misspecification is affected by this additional misspecification. As an important step in RM, pseudo measurement error are added to the observed covariates {W i } i = 1 n to produce the remeasured data. A natural extension of this idea is to add measurement error to the responses {Y i } i = 1 n. For binary data, measurement error lead to misclassified binary responses. Parallel with adding noise to W to detect latent-variable model misspecification, we propose to detect link misspecification by adding noise to Y, producing the so-called reclassified data. Now one may think of \(\hat{\beta }_{r}\) as the MLE of β obtained from the reclassified data. If \(\hat{\beta }\) is biased due to link misspecification, then \(\hat{\beta }_{r}\) is usually also biased. If the bias of \(\hat{\beta }_{r}\) depends on some parameter in the user-specified reclassification model according to which the reclassified data are created, then \(\hat{\beta }_{r}\) can differ noticeably from \(\hat{\beta }\). Such difference can serve as evidence of link misspecification. And test statistics like those constructed in RM can be used to quantify the significance of the difference. We refer to this strategy as the reclassification method, or, RC for short.

Under regularity conditions, the MLE of β follows a normal distribution asymptotically, despite the source of model misspecification (White, 1982) and the type of measurement error. Because both RM and RC rely on the discrepancy between the MLEs of β before and after pseudo measurement error are added (to W or Y ), one important clue to answering the question, “Does RM/RC work?”, is the means of these asymptotic normal distributions associated with the MLEs from data with measurement error (in X or Y ) in the presence of different model misspecification. The next section is devoted to studying these asymptotic quantities, i.e., the limiting MLEs of β.

3 Limiting Maximum Likelihood Estimators

3.1 Estimating Equations

Denote by β m and β c the limiting MLEs of β associated with the raw data and the reclassified data, respectively, as n → ∞. By the theory of maximum likelihood estimation in the presence of model misspecification (White, 1982), β m and β c uniquely satisfy the following score equations respectively,

$$\displaystyle\begin{array}{rcl} E_{\mbox{ $W$}}\left [E_{\mbox{ $Y\vert W$}}\left \{(\partial /\partial \beta )f_{\mbox{ $Y,W$}}(Y _{i},W_{i};\varOmega,\sigma _{u}^{2})\vert _{\beta =\beta _{m}}\right \}\right ]& =& 0,{}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} E_{\mbox{ $W$}}\left [E_{\mbox{ $Y^{{\ast}}\vert W$}}\left \{(\partial /\partial \beta )f_{\mbox{ $Y^{{\ast}},W$}}(Y _{i}^{{\ast}},W_{ i};\varOmega,\sigma _{u}^{2})\vert _{\beta =\beta _{c}}\right \}\right ]& =& 0,{}\end{array}$$
(4)

where \(f_{\mbox{ $Y^{{\ast}},W$}}(Y _{i}^{{\ast}},W_{i};\varOmega,\sigma _{u}^{2})\) is the likelihood of the reclassified data for subject i, (Y i ∗, W i ), and the subscripts attached to “E” signify that the expectations are defined with respect to the relevant true model.

In order to focus on inference for β, we treat the parameters in the assumed X-model, η, as known constants in (3) and (4). Although in practice one has to estimate η along with β, this seemingly unrealistic treatment of η does not make the follow-up theoretical findings less practically valuable if η can be estimated consistently (in some sense). Consistent estimation of η in the presence of model misspecification is often possible in many scenarios. For example, when both the assumed and the true X-models can be fully parameterized via some moments (included in η) up to a finite order, the interpretation of η remains meaningful even if the assumed X-model differs from the true model, and hence one can still conceptualize the “true” value of η, which are simply the moments of the true X-distribution. Moreover, such η usually can be consistently estimated, say, using the method of moments based on {W i } i = 1 n, even in the presence of dual misspecification.

In general, the above estimating equations cannot be solved explicitly, thus closed form expressions of their solutions, β m and β c , are usually unattainable. Without sacrificing too much the generality of the theoretical investigation, we next formulate the assumed model and true models that make these limiting MLEs more transparent.

3.2 Assumed and True Models

For tractability, we fix the assumed structural measurement error model at the probit-normal model, which is one of the favorite toy examples entertained in the measurement error literature. In this model, one posits a probit link in the primary model (1) and assumes X ∼ N(μ x , σ x 2). As for the true model, we formulate a class of the so-called mixture-probit-normal models, which contains the probit-normal model as a special member. In this class of true models, the link function H(s) is the cdf of a two-component mixture normal, referred to as the mixture probit. With a mixture probit link, the primary model is a GLM given by

$$\displaystyle{ P(Y _{i} = 1\vert X_{i};\beta ) =\alpha \varPhi \left (\frac{\beta _{0} +\beta _{1}X_{i} -\mu _{1}} {\sigma _{1}} \right ) + (1-\alpha )\varPhi \left (\frac{\beta _{0} +\beta _{1}X_{i} -\mu _{2}} {\sigma _{2}} \right ), }$$
(5)

where α ∈ [0, 1], μ k and σ k  > 0 (k = 1, 2) are chosen such that the corresponding mixture normal, α N(μ 1, σ 1 2) + (1 −α)N(μ 2, σ 2 2), is of zero mean and unit variance. The true X-model in this class is a mixture normal.

To achieve explicit likelihood for the reclassified data without being overly restrictive in the creation of reclassified data, we consider reclassification models of the form P(Y i ∗ = Y i  | W i ) = π i , for i = 1, …, n, according to which the reclassified responses, {Y i ∗} i = 1 n, are generated. Combining the assumed raw-data likelihood, f Y,W(Y i , W i ; Ω, σ u 2), and the reclassification model yields the likelihood of (Y i ∗, W i ) under the probit-normal model, \(f_{\mbox{ $Y^{{\ast}},W$}}(Y _{i}^{{\ast}},W_{i};\varOmega,\sigma _{u}^{2})\).

Under the formulated assumed and true models, all needed ingredients for deriving the score equations in (3) and (4) become available in closed form. These ingredients include the true mean of Y i and Y i ∗ given W i , the assumed-model likelihood for the raw data, f Y,W(Y i , W i ; Ω, σ u 2), and that for the reclassified data, \(f_{\mbox{ $Y^{{\ast}},W$}}(Y _{i}^{{\ast}},W_{i};\varOmega,\sigma _{u}^{2})\), the true-model likelihood for both types of data, f Y,W (t)(Y i , W i ; Ω (t), σ u 2) and \(f_{\mbox{ $Y^{{\ast}},W$}}^{(t)}(Y _{i}^{{\ast}},W_{i};\varOmega ^{(t)},\sigma _{u}^{2})\). The explicit expressions of these quantities are provided in Appendix 1. Some interesting findings regarding β m and β c are presented next, in which we only consider cases where β 1 ≠ 0. The special case with β 1 = 0 is discussed in Appendix 2, where the expressions of β m and β c are derived. This is a rare case where (3) and (4) can be solved explicitly, and also a rare case where the MLE of β 1 is consistent despite the type of model misspecification. When β 1 ≠ 0, although (3) and (4) cannot be solved explicitly, we are able to make use the aforementioned intermediate results in Appendix 1 to study the limiting MLEs.

3.3 Limiting MLEs from Data with Measurement Error Only in X

Fixing the assumed model at the probit-normal model, we consider combinations of five true links and five true X-distributions in the formulation of the true model. The five true links are, (L0) probit link, and four mixture probit links with the following parameter configurations: (L1) α = 0. 3, μ 1 = 0. 3, σ 1 = 0. 1; (L2) α = 0. 3, μ 1 = −0. 3, σ 1 = 0. 1; (L3) α = 0. 7, μ 1 = 0. 5, σ 1 = 0. 2; (L4) α = 0. 7, μ 1 = −0. 5, σ 1 = 0. 2. The upper panels of Fig. 1 depict these five links. For two link functions, H 1(s) and H 2(s), we say that H 1(s) and H 2(s) are symmetric of each other if H 1(s) = 1 − H 2(−s). Among the four mixture probit links, (L1) and (L2) are symmetric of each other, and (L3) and (L4) are symmetric of each other, with the latter two links deviating from probit more than the former two. The five true X-distributions are, (D0) N(0, 1), and four mixture normals with mean zero and variance one formulated by varying the mixing proportion ζ, skewness ξ, and excessive kurtosis κ as follows: (D1) ζ = 0. 3, ξ = −1, κ = 2; (D2) ζ = 0. 3, ξ = 1, κ = 2; (D3) ζ = 0. 1, ξ = −1. 5, κ = 2; (D4) ζ = 0. 1, ξ = 1. 5, κ = 2. The lower panels of Fig. 1 show the pdf’s of these five distributions. Among the four mixture normal distributions, (D1) and (D2) are symmetric of each other, and (D3) and (D4) are symmetric of each other, with the latter pair deviating from normal further than the former pair. In the true GLM in (5), we set β 0 = 0 and β 1 = 1. For ease of presentation, we use “\(\curlywedge\)” to connect a true X-model with a true link to refer to a true model specification. For example, (D1)\(\curlywedge\)(L3) refers to the true model with X following a distribution specified by (D1) and the link configured according to (L3).

Fig. 1
figure 1

Upper panels give four mixture probit links formulated in Sect. 3.3, where the upper left panel gives link (L1) (dashed line) and link (L2) (dot-dashed line), and the upper right panel gives link (L3) (dashed line) and link (L4) (dot-dashed line). Solid lines are the probit link. Lower panels show four mixture normal density functions formulated in Sect. 3.3, where the lower left panel gives distributions (D1) (dashed line) and (D2) (dot-dashed line), and the lower right panel gives distributions (D3) (dashed line) and (D4) (dot-dashed line). Solid lines are the density function of N(0, 1)

Full size image

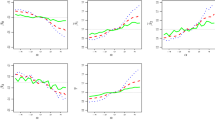
Under each of the above true model specifications, we numerically solve (3) for β m . Figure 2 presents β m under different true models as σ u 2 increases from 0 to 1. This range of σ u 2 yields a reliability ratio ω that drops from 1 to 0.5, where ω = σ x 2∕(σ x 2 +σ u 2). The top panels of Fig. 2, where the true X-model coincides with the assumed, show that β m only changes slightly as σ u 2 increases in the presence of link misspecification. This suggests that, unless information in both the raw data and the remeasured data are rich enough to allow detection of the weak dependence of β m on σ u 2, RM will have low power to detect link misspecification despite the amount of bias in β m due to link misspecification. When the true X-model deviates from normal (see the middle and the bottom panels of Fig. 2), although the dependence of β 1m on σ u 2 is stronger than before, β 1m changes noticeably mainly over a narrow range of σ u 2. This phenomenon for cases with dual misspecification indicates that, although RM has been shown to be effective in diagnosing latent-variable model misspecification, its power in this regard can be substantially compromised by the coexistence of link misspecification.

Fig. 2
figure 2

Plots of β 0m (left column) and β 1m (right column) versus σ u 2 when fixing the true X-model at N(0, 1) (top row), (D1) (middle row), and (D3) (bottom row), respectively, then varying the true link among the five links: probit (solid lines), (L1) (short dashed lines), (L2) (dotted lines), (L3) (dot-dashed lines), and (L4) (long dashed lines)

Full size image

Besides Fig. 2, we show analytically in Appendix 3 that, under certain conditions, β 1m is unchanged by a symmetric flip of either the true X-distribution or the true link, and only β 0m is affected. This property is stated next, with empirical justification relegated to Appendix 5.

Proposition 3.1.

Let f 1 (x) and f 2 (x) be two pdf’s specifying two true X-distributions that are symmetric of each other, and let H 1 (s) and H 2 (s) be two true links that are symmetric of each other. Denote by β m (jk) the limiting MLE of β based on data with measurement error only in X when the true model is \(f_{j}(x) \curlywedge H_{k}(s)\) , for j,k = 1,2. If E(X) = β 0 = 0, then β 0m (11) = −β 0m (22) and β 1m (11) = β 1m (22).

Note that Proposition 3.1 includes two special cases: one is when H 1(s) ≠ H 2(s) and f 1(x) = f 2(x) = f(x), where f(x) is a pdf symmetric around zero; the other is when f 1(x) ≠ f 2(x) and H 1(s) = H 2(s) = H(s), where H(s) is the cdf associated with a distribution symmetric around zero. This is because f 1(x) = f 2(x) = f(x) implies f 1(x) = f 2(−x), since f(x) = f(−x), and thus f 1(x) and f 2(x) are symmetric of each other. Similarly, H 1(s) = H 2(s) = H(s) implies H 1(s) = 1 − H 2(−s), as H(s) = 1 − H(−s), hence H 1(s) and H 2(s) are symmetric of each other. This proposition implies that β 0m can distinguish two true X-models that are symmetric of each other, and can also tell apart two true links that are symmetric of each other. For the purpose of model diagnosis, one can exploit this and other properties of β 0m to obtain a directional test based on RM that can identify the direction of model misspecification. This potential of RM is supported by the following observations of β 0m under the conditions stated in Proposition 3.1:

(M1):

Despite the skewness of the true link, when the true X-model is not normal, β 0m is increasing in σ u 2 when the true X-model is left-skewed, and it is decreasing in σ u 2 when the true X-model is right-skewed.

(M2):

When the true X-model is normal and the true link is not probit, β 0m is increasing in σ u 2 when the true link is right-skewed, and it is decreasing in σ u 2 when the true link is left-skewed.

The middle and bottom panels of Fig. 2, which are associated with two left-skewed true X-models, illustrate the first half of (M1), and the second half of (M1) is indicated by Proposition 3.1. Empirical evidence of (M1) is given in Appendix 5. Viewing a link function as a cdf, we say that a link function is left-skewed if the corresponding pdf is left-skewed. Among the four considered mixture probit links, (L1) and (L3) are left-skewed and (L2) and (L4) right-skewed. The top panel of Fig. 2 illustrates (M2). In Sect. 4.4, we propose a directional test based on RM that utilizes the properties of β 0m summarized in (M1) and (M2).

3.4 Limiting MLEs Based on Reclassified Data

Under the same configurations for the assumed/true models as in Sect. 3.3, we solve (4) numerically for β c based on reclassified data generated according to the reclassification model P(Y i ∗ = Y i  | W i ) = Φ(W i +γ), for i = 1, …, n, where γ is a constant. Figure 3 presents β c when γ = 0, which shows stronger dependence on σ u 2 compared to Fig. 2, especially for β 0c . This implies that, if one applies RM to the reclassified data, \(T_{\beta _{0}}\) can be much more significant than the counterpart test statistic from RM only (without adding noise to Y ).

Fig. 3
figure 3

Plots of β 0c (left column) and β 1c (right column) when P(Y i ∗ = Y i  | W i ) = Φ(W i ), for i = 1, …, n, versus σ u 2, with the true X-model being N(0, 1) (top), (D1) (middle), and (D3) (bottom), and the true link being probit (solid lines), (L1) (short dashed lines), (L2) (dotted lines), (L3) (dot-dashed lines), and (L4) (long dashed lines)

Full size image

Viewing β c as a function of γ and thinking of β c as β c (γ) symbolically, Fig. 4 presents β c (−2) −β c (0) as σ u 2 varies. This figure reveals that the changes in β c as γ changes can be substantial when σ u 2 is small. This phenomenon suggests that RC alone (without adding further noise to W) can have good power to detect X-model misspecification or link misspecification, and the power is higher when the error contamination in X is milder. If the X-model is correctly specified, both β 0c and β 1c can change substantially as γ varies when σ u 2 is fixed at a lower level, including 0. Hence, in the absence of measurement error in X, and thus without involving RM, RC alone is expected to possess some power to detect moderate to severe link misspecification.

Fig. 4
figure 4

Differences, β 0c (−2) −β 0c (0) (left column) and β 1c (−2) −β 1c (0) (right column), versus σ u 2 with the true X-model being N(0, 1) (top), (D1) (middle), and (D3) (bottom), and the true link being probit (solid lines), (L1) (short dashed lines), (L2) (dotted lines), (L3) (dot-dashed lines), and (L4) (long dashed lines)

Full size image

In Appendix 4, we show that, if the reclassification model is P(Y i ∗ = Y i  | W i ) = π(W i ), where π(t) is an even function or when π(t) satisfies π(−t) = 1 −π(t), then β c has the same property of β m under the same conditions stated in Proposition 3.1. Empirical justification of this finding are given in Appendix 5.

4 Testing Procedures

The investigation in Sect. 3 on the limiting MLEs of β based on data with measurement error in X or Y in the presence of X-model misspecification or link misspecification are helpful for understanding the operating characteristics of the test statistics, \(T_{\beta _{0}}\) and \(T_{\beta _{1}}\). When the true model is not in the class of mixture-probit-normal models, and the assumed model is probit-normal, the phenomena described in Sects. 3.3 and 3.4 that motivate the upcoming testing strategies are still observed in extensive simulations we carried out. Some of these simulation studies are presented in the upcoming subsections.

Similar comments apply to scenarios where the assumed model is the logit-normal model. This point is practically less relevant because, although one cannot choose a true model in reality, one can choose an assumed model and use it as a reference model for the purpose of exploring features of the unknown true model. Hence, with well-grounded and effective testing procedures developed with a probit-normal assumed model, using this particular assumed model serves the purpose of diagnosing model misspecification well enough. Regardless, for completeness, we present some simulation results in Appendix 5 where the assumed model is a logit-normal model. In this section, we keep the assumed model as probit-normal to first study via simulation the operating characteristics of the aforementioned test statistics resulting from three diagnostic methods: first, RM; second, RC; third, a hybrid method that combines RM and RC. Then we propose more informative testing procedures that can disentangle two sources of misspecification and point at the direction of misspecification.

4.1 Simulation Design

Fixing the sample size n at 500, we create the raw data, {(Y i , W i )} i = 1 n, from different true models resulting from varying three factors in the simulation experiments. The first factor is the true X-model, taking five levels (D0)–(D4) as defined in Sect. 3.3. The second factor is the true link function, for which we consider seven true links, (L0)–(L4), i.e., the probit and mixture-probit links formulated in Sect. 3.3, and two generalized logit links (Stukel, 1988), referred to as (L5) and (L6). These two generalized logit links are symmetric of each other, with (L5) left-skewed and (L6) right-skewed, as depicted in Fig. 5. The third factor is the value of σ u 2 used to generate {W i } i = 1 n according to (2), with four values leading to reliability ratio ω ranging from 0.7 to 1 at increments of 0.1. Under each simulation setting, 1000 Monte Carlo (MC) replicates are generated. After each replicate is generated, assuming a probit-normal model, we compute \(T_{\beta _{0}}\) and \(T_{\beta _{1}}\) associated with the aforementioned three diagnostic methods.

Fig. 5
figure 5

Two generalized logit links, (L5) (dashed line) and (L6) (dot-dashed line), in comparison with the logit link (solid line)

Full size image

When implementing RM, \(\hat{\beta }_{r}\) is the MLE from the remeasured data {(Y i , W i ∗)} i = 1 n, where W i ∗ = (W 1, i ∗, …, W B, i ∗), in which W b, i ∗ = W i +σ u Z b, i , with Z b, i  ∼ N(0, 1) independent across b = 1, …, B, i = 1, …, n, and B = 100. When carrying out RC, \(\hat{\beta }_{r}\) is the estimate computed from the reclassified data, {(Y i ∗, W i )} i = 1 n, where the reclassified responses, Y i ∗ = (Y 1, i ∗, …, Y B, i ∗), for i = 1, …, n, are generated according to P(Y b, i ∗ = Y i  | W i ) = Φ(W i ). When employing the hybrid method, we first generate {W b, i ∗, b = 1, …, B} i = 1 n as in RM above, then the reclassified responses are generated according to P(Y b, i ∗ = Y i  | W b, i ∗) = Φ(W b, i ∗); finally one obtains \(\hat{\beta }_{r}\) based on the hybrid data that have measurement error in both X and Y, {(Y b, i ∗, W b, i ∗), b = 1, …, B} i = 1 n. Using a significance level of 0.05, we monitor how often the value of a test statistic turns out significant, leading to rejection of a null hypothesis, which states that two MLEs being compared in the test statistic have the same limit as n → ∞.

4.2 Simulation Results

Table 1 presents the rejection rate of each test statistic under each simulation setting across 1000 MC replicates for a representative subset of all considered true-model configurations. This subset of true models includes five models belonging to the class of mixture-probit-normal models, (D3)\(\curlywedge\)(L0), (D0)\(\curlywedge\)(L3), (D3)\(\curlywedge\)(L3), (D4)\(\curlywedge\)(L3), and (D3)\(\curlywedge\)(L4); and four models in the class of generalized-logit-normal models, (D0)\(\curlywedge\)(L5), (D3)\(\curlywedge\)(L5), (D4)\(\curlywedge\)(L5), and (D3)\(\curlywedge\)(L6). Among these nine true-models configurations, (D3)\(\curlywedge\)(L0) represents the scenario where only the X-model is misspecified, (D0)\(\curlywedge\)(L3) and (D0)\(\curlywedge\)(L5) represent the case where only the link is misspecified, and the remaining six configurations represent cases with dual misspecification. Albeit not included in Table 1, we observe rejection rates for all tests well controlled at around 0.05 when the true model is (D0)\(\curlywedge\)(L0), that is, when there is no model misspecification. Some noteworthy observations regarding RM and RC from the simulation are summarized in the following three remarks.

Table 1 Rejection rates across 1000 Monte Carlo replicates of each test statistic under each testing procedure considered in Sect. 4 at different levels of reliability ratio ω when the assumed model is probit-normal
Full size table

Remark 1.

When σ u 2 = 0, that is, the covariate is measured without error (ω = 1), RM can detect neither source of misspecification. This is due to the definition of the remeasured data, \(W_{b,i}^{{\ast}} = W_{i} + \sqrt{\lambda }\sigma _{u}Z_{b,i}\), resulting in the remeasured data identical to the raw data when σ u 2 = 0. In contrast, when σ u 2 = 0, RC has impressive power to detect link misspecification, whether or not the X-model is also misspecified.

Remark 2.

When σ u 2 ≠ 0, the power of RM to detect X-model misspecification surpasses that of RC if this is the only source of misspecification; but when only the link is misspecified, the test based on \(T_{\beta _{0}}\) from RC is the clear winner in detecting link misspecification, whose power increases as σ u 2 decreases.

Remark 3.

Although RM is designed for detecting X-model misspecification, and RC is proposed aiming at detecting link misspecification, each of them can be influenced in nontrivial ways by the other source of misspecification. Take RM as an example. When only the X-model is misspecified, such as case (D3)\(\curlywedge\)(L0) in Table 1, RM is expectedly effective in picking up this type of misspecification. But its power is mostly weakened by the additional link misspecification as in case (D3)\(\curlywedge\)(L3). Note that, when the true model is (D3)\(\curlywedge\)(L3), the directions of the two misspecification are the same in the sense that the true X-model is left-skewed and so is the true link. This tampering effect on the power of RM due to the added link misspecification is not observed for \(T_{\beta _{0}}\) when the dual misspecification are of opposite directions, such as in cases (D3)\(\curlywedge\)(L4) and (D3)\(\curlywedge\)(L6). Similar nontrivial patterns are observed for RC when X-model misspecification is added on top of link misspecification. In summary, whether or not the added misspecification compromises the power of a method to detect the type of misspecification it is originally designed for depends on how the two types of misspecification interact.

Although the empirical power associated with \(T_{\beta _{1}}\) from RM lingers around 0.60 in the case (D3)\(\curlywedge\)(L3) when ω = 0. 7, 0.8, and 0.9, it drops to around 0.33 and 0.22 when ω = 0. 6 and 0.55 (not included in Table 1), respectively. This abrupt drop in power can be explained by the large-sample phenomenon in Sect. 3.3 depicted in Fig. 2. It is pointed out there that, in the presence of dual model misspecification, as in case (D3)\(\curlywedge\)(L3), β 1m changes noticeably mainly over a narrow (lower) range of σ u 2. For this case in particular, as shown in the lower right panel of Fig. 2 (with the dot-dashed line referring to case (D3)\(\curlywedge\)(L3)), β 1m stays nearly flat soon after σ u 2 passes 0.25 (i.e., soon after ω drops below 0.8). The (nearly) flat region of σ u 2 or ω is where \(T_{\beta _{1}}\) from RM exhibits low power.

Finally, the hybrid method is the same as RC when σ u 2 = 0. And, according to Table 1, when σ u 2 ≠ 0, the hybrid method performs similarly as RC when only the link is misspecified. In other cases, the power of the hybrid method mostly lies between that of RM and RC. We recommend use the hybrid method with caution due to the amount of information loss when creating the hybrid data.

4.3 Sequential Tests

Although we caution use of the hybrid method in practice, sequentially using test results from RM and those from RC can help to disentangle two types of misspecification. We now illustrate some sequential testing procedures when the covariate is measured with error. To distinguish the test statistics from two methods, denote by T θ (m) and T θ (c) the test statistics associated with RM and RC, respectively, where θ denotes a generic parameter. Suppose one implements RM, with only W-data further contaminated, and then implements RC, with only Y -data contaminated (and the W-data left as originally observed). Implementing these two methods sequentially yields four test statistics of interest, \(T_{\beta _{0}}^{(m)}\), \(T_{\beta _{1}}^{(m)}\), \(T_{\beta _{0}}^{(c)}\), and \(T_{\beta _{1}}^{(c)}\). In light of the operating characteristics of these test statistics revealed in Sect. 4.2, we consider the following three sequential testing strategies.

First, if \(T_{\beta _{0}}^{(m)}\) is highly significant and \(T_{\beta _{0}}^{(c)}\) is insignificant, one may interpret this as evidence that the X-model is misspecified and the assumed link may be adequate for the observed data. For instance, when the true model is (D3)\(\curlywedge\)(L0), using this testing criterion, one concludes “only the X-model is misspecified” 55, 70, and 84 % of the time when ω = 0. 7, 0. 8, 0. 9, respectively, based on the simulation results in Sect. 4.2. When summarizing the preceding rejection rates, we apply the Bonferroni correction for multiple testing and use a significance level of 0. 025( = 0. 05∕2) now that two test statistics are used simultaneously.

Second, if \(T_{\beta _{1}}^{(m)}\) turns out insignificant whereas \(T_{\beta _{0}}^{(c)}\) is highly significant, one may view this as indication that the assumed X-model may be appropriate but the assumed link is inadequate. Revisiting the simulation results in Sect. 4.2, when the true model is (D0)\(\curlywedge\)(L3), using this sequential testing strategy, one concludes “only the link is misspecified” 67, 86, and 94 % of the time when ω = 0. 7, 0. 8, 0. 9, respectively.

Third, having observed promising power from the above two sequential tests, one would hope that having both \(T_{\beta _{0}}^{(m)}\) and \(T_{\beta _{0}}^{(c)}\) significant can be interpreted as an indication of dual misspecification. Unfortunately, due to the complicated interaction between the two misspecification described in Remark 3 in Sect. 4.2, this criterion is a reliable indicator of dual misspecification only when two misspecification are of opposite directions. For example, when the true model is (D4)\(\curlywedge\)(L3), the criterion of both \(T_{\beta _{0}}^{(m)}\) and \(T_{\beta _{0}}^{(c)}\) being significant is met 79, 85, and 93 % of the time across 1000 MC replicates when ω = 0. 7, 0. 8, 0. 9, respectively. Similar high power is also observed when the true model is (D3)\(\curlywedge\)(L4), (D4)\(\curlywedge\)(L5), or (D3)\(\curlywedge\)(L6). However, if the true model is (D3)\(\curlywedge\)(L3), the rejection rates according to this same criterion drop to 1, 13, and 29 % when ω = 0. 7, 0. 8, 0. 9, respectively.

Despite the complication arising from dual misspecification, empirical evidence from the above three sequential tests give much encouragement to use the combination of two tests from two diagnostic methods, such as \(T_{\beta _{0}}^{(m)}\) (or \(T_{\beta _{1}}^{(m)}\)) and \(T_{\beta _{0}}^{(c)}\), in order to learn more from the data regarding the two model assumptions.

4.4 Directional Tests

The properties of β 0m described in (M1)–(M2) in Sect. 3.3 suggest that the sign of \(T_{\beta _{0}}^{(m)}\) can indicate in which direction the true X-model deviates from normal or the true link function deviates from probit (or logit). More specifically, if there is strong evidence against a normal X-distribution, then, despite what the true link is, a significantly negative (positive) \(T_{\beta _{0}}^{(m)}\) implies that the true X-distribution is left-skewed (right-skewed). This is supported by (M1). On the other hand, suppose one has evidence to suggest that the assumed normal X-model is likely appropriate, but suspects that the assumed probit link may be inadequate, then one further gains evidence to support a right-skewed link if \(T_{\beta _{0}}^{(m)} <0\), and left-skewed otherwise. This is justified by (M2).

As empirical evidence, Table 2 presents the rejection rates (at significance level 0.05) from the same simulation study described in Sect. 4.1 but associated with a one-sided test based on \(T_{\beta _{0}}^{(m)}\), assuming one knows a priori the right side of the test (as we do in simulations). The high rejection rates for the cases with X-model misspecification tabulated in Table 2 indicate that, if one is mostly interested in the skewness of the true X-distribution, the sign of \(T_{\beta _{0}}^{(m)}\) is indeed an effective indicator of the direction of skewness, regardless whether or not (and how) the link function is misspecified. In the absence of X-model misspecification, \(T_{\beta _{0}}^{(m)}\) requires milder error contamination in X in order to more effectively reveal the direction of skewness of the true link.

Table 2 Rejection rates associated with a one-sided test based on \(T_{\beta _{0}}^{(m)}\) at significance level 0.05 under different true model configurations defined in Sect. 3.3 at different levels of reliability ratio ω
Full size table

5 Application to Real Data Examples

We now apply the above testing procedures to two data examples, beginning with a data set from the Framingham Heart Study briefly described in Sect. 1.

5.1 Framingham Heart Study

The data considered in this example consist of information on 1615 subjects, who were followed for the development of coronary heart disease over six examination periods. Denote by Y i the binary indicator of the first evidence of coronary heart disease for subject i within an 8-year follow-up period from the second examination period, for i = 1, …, 1615. At each of the second and third examination periods, each subject’s SBP was measured twice. We first center all observed SBP measures from the second examination. Then, for subject i( = 1, …, 1615), we compute the average of the two (centered) SBP measures divided by 100 from the second examination, and use it as W i , the error-contaminated version of the unobservable (centered) long-term SBP, X i . Using the two replicate measures in the second exam and applying Eq. (4.3) in Carroll et al. (2006) gives an estimated ω for the so-defined W as around 0.92. Assuming a probit-normal structural measurement error model for the observed data {(Y i , W i )} i = 1 1615, we apply RM with λ = 1 and B = 100. The resulting test statistics are \(T_{\beta _{0}}^{(m)} \approx 2.349\) (0.019) and \(T_{\beta _{1}}^{(m)} \approx -2.387\) (0.017), with the corresponding p-values in parentheses. These test results yield significant evidence that the normality assumption on X is inadequate. This finding is not new (see, e.g., Huang et al., 2006; Huang, 2009). What is new here is that, because now \(T_{\beta _{0}}^{(m)}\) is significantly positive (at significance level 0.05), using the directional test described in Sect. 4.4, we also find evidence that the true X-distribution is right-skewed. This new finding (from a model diagnostics standpoint) agrees with the kernel density estimate for X in Wang and Wang (2011, Fig. 5), who applied the deconvoluting kernel density estimation (Stefanski and Carroll, 1990) to estimate the density of X based on W-data.

We also apply the RC method using the reclassification model, P(Y i ∗ = Y i  | W i ) = Φ(W i ), for i = 1, …, 1615, to generate the reclassified data. The resultant test statistics are \(T_{\beta _{0}}^{(c)} \approx -1.474\) (0.141) and \(T_{\beta _{1}}^{(c)} \approx 1.474\) (0.141), with the associated p-values in parentheses. Based on these we conclude that the current data do not give sufficient evidence to imply that the probit link is inappropriate for this application. To this end, we are comfortable with the probit link in the GLM and lean toward a right-skewed distribution for X as opposed to normal.

5.2 Beetle Mortality

Pregibon (1980) studied the association between mortality of adult beetles and exposure to gaseous carbon disulfide. Using his test for link specification, he found strong evidence to support an asymmetric link as opposed to the logit link. The data include logarithm of dosages of carbon disulfide exposure for a total of 481 adult beetles, and the status (being killed or surviving) of each beetle after 5 h exposure. Let Y i denote the indicator of being killed after exposure to carbon disulfide for the ith beetle, and denote by X i the standardized (via centering and scaling) logarithm of dosage this beetle was exposed to, for i = 1, …, 481. Here, the covariate of interest, log(dosage), is free of measurement error, making assumptions on X-model irrelevant to estimating β. Hence, we first focus on using RC to assess the adequacy of a probit GLM relating Y and X. The reclassification model used for this purpose is P(Y i ∗ = Y i  | X i ) = 0. 2, for i = 1, …, 481. The values of the test statistics of interest are, with the corresponding p-values in parentheses, \(T_{\beta _{0}}^{(c)} \approx 3.184\) (0.002) and \(T_{\beta _{1}}^{(c)} = 0.241\) (0.810). This round of test provides strong evidence that the assumed probit link may be inappropriate.

Log transformation is a popular transformation used by data analysts in biology and medicine to alleviate departure from normality of data. We are now curious about what RM can tell us about the normality assumption on the covariate, log(dosage), in this study. To make RM applicable, we create noisy surrogate covariate data, {W i } i = 1 481, according to (2) with an estimated ω to be 0.8. Using the new data, {(Y i , W i )} i = 1 481, treating them as the “raw” observed data, and assuming a probit-normal model, we implement RM, RC, and the hybrid method, successively. When carrying out RM, the remeasured data, {W b, i ∗, b = 1, …, 100} i = 1 481, are generated according to W b, i ∗ = W i +σ u Z b, i with Z b, i  ∼ N(0, 1), for b = 1, …, 100, i = 1, …, 481. For RC and the hybrid method, the reclassified responses are generated according to P(Y b, i ∗ = Y i  | W i ) = 0. 2 and P(Y b, i ∗ = Y i  | W b, i ∗) = 0. 2, respectively, for b = 1, …, 100, i = 1, …, 481. The resultant test statistics are listed below, with p-values in parentheses. From RM, \(T_{\beta _{0}}^{(m)} \approx -0.618\) (0.537) and \(T_{\beta _{1}}^{(m)} \approx -1.724\) (0.085); from RC, \(T_{\beta _{0}}^{(c)} \approx 2.904\) (0.004) and \(T_{\beta _{1}}^{(c)} \approx 0.090\) (0.929); and finally, from the hybrid method, \(T_{\beta _{0}} \approx 2.903\) (0.004) and \(T_{\beta _{1}} \approx 0.086\) (0.932). The pattern of these three sets of tests is mostly consistent with what is observed in Sect. 4.2 when only the link is misspecified. Following the sequential testing strategy proposed in Sect. 4.3, with the insignificant \(T_{\beta _{1}}^{(m)}\) and the highly significant \(T_{\beta _{0}}^{(c)}\) (at significance level 0.025), one can also conclude that the current data only provide strong evidence against the assumed link but not the normality assumption on log(dosage). In addition, using the directional test described in Sect. 4.4, although insignificant, the negative sign of \(T_{\beta _{0}}^{(m)}\) may be an indication that the true link is right-skewed.

For illustration purposes, we drop the log transformation on the dosage levels in the raw data and view the standardized dosage as the true covariate X. Then we repeat the same data generation procedure to create the (hypothetical) error-contaminated observed data, {(Y i , W i )} i = 1 481, based on which we further generate the remeasure data and the reclassified data as above, and implement RM, RC, and the hybrid method. The test statistics are: from RM, \(T_{\beta _{0}}^{(m)} \approx -1.192\) (0.234) and \(T_{\beta _{1}}^{(m)} \approx -4.067\) (0.000); from RC, \(T_{\beta _{0}}^{(c)} \approx 1.938\) (0.053) and \(T_{\beta _{1}}^{(c)} \approx -1.320\) (0.188); from the hybrid method, \(T_{\beta _{0}} \approx 1.253\) (0.211) and \(T_{\beta _{1}} \approx -0.843\) (0.400). Now the test based on \(T_{\beta _{1}}^{(m)}\) from RM indicates that the assumed normality on “dosage” is highly suspicious. The nearly significant \(T_{\beta _{0}}^{(c)}\) (at significance level 0.05) from RC may also suggest the probit link questionable, although the evidence is weaker than the previous round of testing from RC when log(dosage) is the true covariate. This seems to suggest that the power of RC to detect link misspecification is somewhat compromised by the coexistence of an inappropriate assumed X-model. Finally, using the directional test proposed in Sect. 4.4, the fact that \(T_{\beta _{0}}^{(m)} <0\), although insignificant, may be evidence that the true distribution of dosage is left-skewed.

6 Discussion

In this study we tackle the challenging problem of model diagnostics for GLM with error-prone covariates, where there are two potential sources of model misspecification. Motivated by the rationale behind the remeasurement method (RM) designed for assessing latent-variable model assumptions, we propose the reclassification method (RC) mainly for detecting a misspecified link in GLM. We carry out rigorous theoretical investigation to study the properties of MLEs for the regression coefficients in GLM when only the link is misspecified, and also when both the assumed link and the assumed latent-variable distribution differ from the truth. These estimators include MLEs resulting from data with measurement error only in the covariate, and also MLEs based on data with measurement error in the binary response. These properties of the estimators justify use of RM and RC for assessing different model assumptions, and further motivate more informative sequential/directional tests that can reveal how the true link or true latent-variable model deviates from the assumed one.

Although starting from Sect. 3.2 we focus on the (mixture-)probit-normal model as the assumed/true models, the theoretical findings in Sects. 3.3 and 3.4 have broader implications beyond this formulation. For example, when the assumed link is logit and/or the true link belongs to the class of generalized logit links, plenty empirical evidence (partly given in Sect. 4 and Appendix 5) suggest that most properties of β m and β c stated in Sects. 3.3 and 3.4 are still observed. Hence, the assumed/true models formulated in Sect. 3.2 help us make great strides toward understanding the asymptotic properties of MLEs in the presence of model misspecification, and the findings under this formulation provide answers to more general questions like “What happen to the MLE when one assumes a symmetric (not necessarily normal/probit) X-model/link whereas the true X-model/link is asymmetric?”. Because of the generality of their implications, similar operating characteristics of the proposed testing procedures described in Sect. 4.2 also carry over to cases outside of the (mixture-)probit-normal formulation, as evidenced in Table 1 and Appendix 5.

When multiple model assumptions are in question simultaneously, a potential obstacle for model diagnostics, and for inference in general, is non-identifiability. For example, in the framework of generalized linear mixed models (GLMM), it is only meaningful to test a posited model for the random effects when one assumes that the model for the response given the random effects is correct because these two models cannot be identified/validated simultaneously (Alonso et al., 2010; Verbeke and Molenberghs, 2010). In the context of our study, although the true covariate X in the primary model is a latent variable like random effects in GLMM, the existence of an observed surrogate W, which relates to X via a known model, clears the obstacle of non-identifiability encountered in GLMM, and thus it is possible to assess the assumed primary model and the assumed latent-variable model simultaneously. Concrete evidence of such identifiability is partly given by Proposition 1.

In the actual implementation of RC, one open question relates to the choice of reclassification model. In this work, we choose this model mostly for ease of deriving the reclassified-data likelihood and also try to avoid too much information loss in the reclassified responses. An interesting follow-up research topic is to find some optimal ways of creating reclassified data to maximize the power of RC. This direction of research will require involvement of the asymptotic variance of the MLE of β, a quantity yet to be studied besides the asymptotic means which we focus on in this article. Other practical concerns worth addressing in the future research are incorporation of multivariate error-prone covariates and relaxing the normality assumption on the measurement error.