Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Sparse matrix-vector multiply (SpMV) is the workhorse operation of many numerical simulations and has seen use in a wide variety of areas such as data mining [1] and graph analytics [2]. In these algorithms, a majority of the total processing is often spent on SpMV operations. Iterative computations such as the power method and conjugate gradient are commonly used in numerical simulations and require successive SpMV operations [3]. The use of GPUs has become increasingly common in computing these operations as they are, in principle, highly parallelizable. GPUs have both a high computational throughput and a high memory bandwidth. Operations on sparse matrices are generally memory bound; this makes the GPU a good target platform due to its higher memory bandwidth compared to that of the CPU, but it is still difficult to attain high performance with sparse matrices because of thread divergence and noncoalesced memory accesses.

Some applications require dynamic updates to the matrix; generally construed, updates may include inserting or deleting entries. Fully compressed formats such as compressed sparse row (CSR) cannot handle these operations without rebuilding the entire matrix. Rebuilding the matrix is orders of magnitude more costly than performing an SpMV operation. The ellpack (ELL) format allocates a fixed amount of space for each row, allowing fast insertion of new entries and fast SpMV, but limits each row to a predetermined number of entries and can be highly memory inefficient. The coordinate (COO) format stores a list of entries and permits both efficient memory use and fast dynamic updates but is unordered and slow to perform SpMV operations. The hybrid-ellpack (HYB) format attempts a compromise between these by combining an ELL matrix with a COO matrix for overflow. This compromise requires examination of the overflow matrix for SpMV operations and efficiency suffers.

Matrix representations of sparse graphs sometimes exhibit a power-law distribution (when the number of nodes with a given number of edges scales as a power of the number of edges). This distribution results in a long tail in which a few rows have a relatively high number of entries whereas the rest have a relatively low number. Important real-world phenomena exhibit the power-law distribution. Their corresponding matrices can represent adjacency graphs, web communication, and finite-state simulations. Such a matrix is also the pathological case for memory efficiency in the ELL format and requires significant use of the COO portion of a HYB matrix, making neither particularly well suited for dynamic sparse-graph applications.

One motivating application for our work is control-flow analysis (CFA): a general approach to static program analysis of higher-order languages [4, 5]. These algorithms use an approximate interpretation of their target code to yield an upper bound on the propagation of data and control through a program across all possible actual executions. A CFA involves a series of increasing operations on a graph (extending it with nodes and edges), terminating when a fixed point is reached (a steady state in which the analysis is self-consistent).

Recent work has shown how to implement this kind of static analysis as linear-algebraic operations on the sparse-matrix representation of a function [6, 7]. Other recent work shows how to implement an inclusion-based points-to analysis of C on the GPU by applying a set of semantic rules to the adjacency matrix of a sparse-graph [8]. These algorithms may be likened to finding the transitive closure of a graph encoded as an adjacency matrix. The matrix is repeatedly extended with new entries derived from SpMV until a fixed point is reached (no more edges need to be accumulated). Each of these approaches to static analysis on the GPU is very different; however, both require high performance sparse-matrix operations and dynamic insertion of new entries.

1.1 Contributions

Existing matrix formats are ill-suited for such dynamic allocation, with many being fully compressed or otherwise unable to be efficiently extended with new entries. Our contribution in this paper is to present a fast, dynamic method for sparse-matrix allocation:

  1. 1.

    We present a new sparse matrix format, dynamic compressed sparse row (DCSR), that allows for efficient dynamic updates, exhibits easy conversion with standard CSR, and has fast SpMV.

  2. 2.

    We implement an open-source library for DCSR and demonstrate its efficacy, benchmarking SpMV and insertions using the adjacency matrices for a suite of sparse-graph benchmarks.

2 Background

In this paper we are concerned with dynamic updates to sparse matrices. As SpMV is arguably the most important sparse-matrix operation, we want to maintain efficient times for the problem \(Ax = y\). A major goal of sparse-matrix formats is to reduce irregularity in the memory accesses. We provide a brief overview of some of the most commonly used sparse-matrix formats.

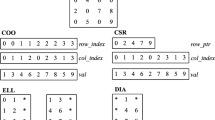
The coordinate (COO) format is the simplest sparse-matrix format. It represents a matrix with three vectors holding the row indices, column indices, and values for all nonzero entries in the matrix. The entries within a COO format must be sorted by row in order to efficiently perform an SpMV operation. SpMV operations are conducted in parallel through segmented reductions over the length of the arrays. Tracking which thread has processed the final entry in a row requires explicit inter-thread communication.

The compressed sparse row/column (CSR/CSC) formats are similar to COO in that they have arrays that fully store two of the three sets, either the column indices or the row indices in addition to the values. Either the rows or columns (in CSR or CSC, respectively) are compressed to store only offsets corresponding to the row/column locations in the other two arrays. For CSR, entry i and \(i+1\) in the row offsets array will store the starting and ending offsets for row i. CSR has been shown to be one of the best formats in terms of memory usage and SpMV efficiency due to its fully compressed nature, and thus it has become widely used [9]. CSR has a greater memory efficiency than COO, which is a significant factor in speeding up SpMV operations due to decreased memory bandwidth usage.

The ellpack (ELL) format uses two arrays, each of size \(m \times k\) (where m is the number of rows and k is a fixed width), to store the column indices and the values of the matrix [10, 11]. These arrays are stored in column-major order to allow for efficient parallel access across rows. This format is best suited for matrices that have a fixed number of entries per row.

Allocating enough memory in each row to store the entire matrix is prohibitively expensive for ELL when a matrix contains even one long row. The hybrid-ellpack (HYB) format offers a compromise by using a combination of ELL and COO. It stores as much as possible in an ELL portion, and the overflow from rows with a number of entries greater than the fixed ELL width is stored in a COO portion. ELL and HYB have become popular on SIMD architectures due to the ability of thread warps to look through consecutive rows in an efficient parallel manner [12].

The diagonal format (DIA) is best suited for banded matrices. It is formed by two arrays that store the nonzero data and the offsets from the main diagonal. The nonzero values are stored in an \(m \times k\) array where m is the number of rows in the matrix and k is the maximum number of nonzeros of any row in the matrix. The offsets are stored with respect to the main diagonal, with positive offsets to the right and negative offsets to the left. The SpMV parallelization of this format is similar to that of ELL with one thread/vector assigned to each row in the matrix. The values array is statically sized, similar to ELL, which restricts its ability to handle dynamic insertions.

A number of other specialized sparse-matrix formats have been developed, including diagonal (DIA), jagged diagonal storage (JDS), block diagonal (BDIA), skyline storage (SKS), tiled COO (TCOO), block ELL (BELL), and sliced-ELL (SELL) [13], which offer improved performance for specific matrix types. Blocked variants of these and other formats work by storing localized entries in blocks for better data locality and a reduction in index storage. “Cocktail” frameworks that mix and match matrix formats to fit specific subsets of the matrix have been developed, but they require significant preprocessing and are not easily modified dynamically [14]. Garland et al. have provided detailed reviews of the most common sparse-matrix formats [10, 11, 15], as well as an analysis of their performance on throughput-oriented many-core processors [16].

Block formats, such as BRC [17] and BCCOO [18] that use blocking, have limited ability to add in additional entries. BRC can add new entries only if those entries correspond to zeros within blocks that have been stored. BCCOO can handle the addition of new entries, but it suffers from many of the same problems as COO. Also, new insertions will not always follow a blocked structure, so additional blocks may be sparse, which lowers memory efficiency.

Many sparse-matrix formats are fully compressed and do not allow additional entries to be added to the matrix dynamically. Adding additional entries to a CSR matrix requires rebuilding the entire matrix, since there is no free space between entries. Of existing formats, COO is the most amenable to dynamic updates because new entries can be placed at the end of the data structure. However, updating a COO matrix in parallel requires atomic operations to keep track of currently available memory locations. The ELL/HYB formats allow for some additional entries to be added in a limited fashion. ELL cannot add in more entries per row than the given width of the matrix, and while the HYB format has a COO matrix to handle overflow from the ELL portion, it cannot be efficiently updated in parallel since atomic operations are required and the COO portion must maintain the sorted property.

A great deal of research has been devoted to improving the efficiency of SpMV, which has been studied on both multi-core and many-core architectures. Williams et al. demonstrated the efficacy of using architecture-specific data structures to optimize performance [19, 20]. As SpMV is a bandwidth-limited operation, research has also produced other methods, such as automatic tuning, blocking, and tiling, to increase cache hit rates and decrease bandwidth usage [21–23].

Graph applications often use sparse binary adjacency matrices to represent graphs and translate graph operations to linear algebraic operations [24]. A common graph algorithm is finding a transitive closure by repeated multiplication of its adjacency matrix. The transitive closure of an adjacency matrix R calculates \(R^+ = \!\!\!\!\!\! \underset{i\in \{1,2,3,...\}}{\cup }\!\!\!\!\!\!\!R^i\), where \(R^i\) is the \(i^{th}\) power of the matrix. This operation results in \(R^i\) having a nonzero between any pair of nodes that are connected by a path of length i. The union (addition/binary-or) of all \(R, \ldots R^n\) will have a nonzero entry for every pair of nodes that are connected by a path of length \(\le n\). This process of unioning successive powers of R can be continued until a fixed point is reached and all nodes that are connected by a path of any length will be marked in the matrix.

3 Dynamic Compressed Sparse Row (DCSR)

We present a dynamic sparse-matrix allocation method that allows for efficient dynamic updates while maintaining fast SpMV times. Our dynamic allocation uses a row offset array, representing a dense array of ordered rows, and for each a fixed number of segment offsets. The column indices and values are stored in arrays that are logically divided into these data segments in the same way that CSR row offsets partition the column indices and values. Each such segment is a contiguous portion of memory that stores entries within a row. Segments may contain more space than entries to allow for future insertions. The contiguous arrangement of entries within the set of segments for a given row is equivalent to the CSR format. In the following subsection we illustrate how dynamic allocation is performed, after which we provide details of how DCSR operations are implemented.

Initializing the matrix can be accomplished in one of two ways. Either a matrix can be loaded from another format (e.g., COO or CSR), or the matrix can be initialized as blank. In the latter case, each row is assigned an initial number of entries (an initial segment size) in the column indices and values arrays. The row offset array is initialized with space for k segment offset pairs, with either no allocated segments or a single allocated segment of size \(\mu \) per row. In the latter case this allocation consumes the same amount of memory as an ELL matrix with a row width of \(\mu \), except in row-major order instead of column-major order. A memory buffer with excess space maintained, using a simple bump-pointer allocation method to add new segments, to allow for dynamic allocation. This allocation pointer is set to the end of the currently used space (\(rows \times \mu \) in the case of a new matrix). A maximum size of memory buffer for the columns and values arrays is specified by the user. Figure 1 provides an illustrative comparison of CSR, HYB, and DCSR formats.

Fig. 1.
figure 1

Comparison of CSR, DCSR, and HYB formats. (Color figure online)

Full size image

In total, the format consists of four arrays for column indices, values, row offsets, and row sizes, in addition to a memory allocation pointer. The row offsets array functions in a manner similar to that of its CSR counterpart, except that both a beginning and ending offset are stored and space exists for up to k such pairs per row. This table is encoded as a strided array where the starting and ending offsets of segment k in row i are indexed by \((i*2 + k*pitch)\) and \((i*2 + k*pitch + 1)\), respectively. The pitch may be defined as a value convenient for cache performance such that \(pitch \ge 2*rows\). This pitch value is chosen to ensure memory aligned accesses. The number of memory segment offset pairs (the max k) is an adjustable parameter specified at matrix construction. The column indices and values correspond 1:1, just as in CSR. Unlike CSR, however, there may be more than one memory segment assigned to a given row and these segments need not be contiguous. As the last segment for a row may not be full, the actual row sizes are maintained so the used portion of each segment is known.

Explicitly storing row sizes allows for optimization techniques such as adaptive CSR (ACSR) [25] (of which we take advantage). This optimization implements customized kernels to process bins of specified row-lengths. During this binning process, we create a permuted set of row indices that are sorted according to these bin groupings. We launch each bin-specific kernel with these permuted indices on its own stream, which allows each kernel to easily access the rows that it needs to process without scanning over the matrix.

When inserting new elements within a row, the last allocated segment for that row is located, and if space is available the new elements are inserted in a contiguous fashion after the current entries. If that segment does not have enough room, a new segment will be allocated with the appropriate size plus an additional amount \(\alpha \). The \(\alpha \) value represents additional “slack space” and allows for a greater number of entries to be inserted without the creation of a new segment. Although we experimented with setting \(\alpha \) to be a factor of the previous segment size, for our tests we settled on a value of \(\mu \) (average row size of matrix). When a new segment is allocated, the memory allocation pointer is atomically increased by the size of the new segment. A hard limit on these additions, before defragmentation is required, is fixed by the number of segments k. The defragmentation operation always reduces the number of segments in each row to one, which allows the format to scale to an arbitrary number of allocations. Pseudo-code for new segment allocation is provided by Algorithm 1.

When inserting new elements into the matrix, it is possible that duplicate nonzero entries (i.e., two or more entries with the same row and column index) will be added. Duplicate entries are handled in one of two ways. The first method is to simply let the accumulation occur, as it does not pose a problem for many operations. SpMV operations are tolerant of duplicate entries since the reduction relies on associative operations. This result will be correct to within floating point tolerance. For binary matrices, the row-vector inner products will produce the same result irrespective of duplicate nonzeros. A second solution is to perform a segmented reduction on the entries after sorting by row and column. This operation combines all duplicate entries into a single entry but is generally not needed when performing only SpMV and addition operations. In our tests, we let the values accumulate for all formats as they do not hinder the SpMV operations that are performed. Pseudo-code for an insertion operation is given by Algorithm 2.

An SpMV operation works as follows. Initially the first pair of segment offsets is fetched. The entries within the corresponding segment are multiplied by the appropriate values in x according to the algorithm being used (CSR-scalar, CSR-vector, etc.). If the row size is greater than the capacity of the current memory segment, the next pair of offsets is fetched. If the size of the current segment plus the running sum of the previous segment sizes is greater than or equal to the row size, the final segment of that row has been found. If the final segment is not full, the location of the last entry can be determined by the difference of the row size and the running sum. This process continues until the entire row has been read. This is illustrated in Algorithm 3.

As the matrix accumulates more segments, SpMV performance decreases slightly. A fixed number of segments also means this process cannot continue forever. Our solution to both problems is to implement a defragmentation operation that compacts all entries within the column indices and values arrays, eliminating empty space. This operation compacts all segments in a row into a single segment. The defragmentation may be invoked periodically, or more conservatively when a row has reached its maximum capacity of segments. In practice we do the latter and set a flag when any row reaches its maximum segment count. At this point we consider defragmentation to be required.

figure a

Defragmentation performs the equivalent to a sort-by-row operation on the entries of the matrix; however, we formulated a method that does not require an actual sort and is significantly faster than doing so. We perform a prefix-sum operation on the row sizes to calculate the new row offsets in a compacted CSR form. After this, the entries are shuffled from their current indices to their new indices in newly allocated column indices and values buffers, after which we set a pointer in our data structure to these new arrays and free the old buffers (shallow copy). By using the knowledge of the row sizes to compute resulting offsets and indices, we eliminate the need to do any comparisons in this operation, which greatly improves performance. The defragmentation process is described by Algorithm 4.

Figure 2 illustrates an example of inserting new elements into a DCSR matrix. Initially the matrix has four populated rows with the memory allocation pointer being 16. Row 0 can insert one additional entry in its current segment before a new segment needs to be allocated. Rows 1 and 2 have enough room for two additional entries, and row 3 is full. Figure 2 shows a set of new entries that are inserted into rows 0, 2, and 3. In this case a new segment of size 4 is allocated for row 0 and row 3. The additional segments need not be consecutive nor in order of row since the exact offsets are stored for each segment. Finally, the defragmentation operation computes new segment offsets from the row sizes. The entries are shuffled to their new indices, which results in a single compacted segment for each row.

Fig. 2.
figure 2

Illustration of insertion and defragmentation operations with DCSR. (Color figure online)

Full size image
figure b
figure c
figure d

As CSR is the most commonly used sparse matrix format, we designed DCSR to be compatible with CSR algorithms and to allow for easy conversion between the formats. Minimal overhead is required to convert from CSR to DCSR and vice versa. When converting from CSR to DCSR, the column indices and values arrays are copied directly. For the row offsets array, the \(i^{th}\) element is copied to indices \(i*2-1\) and \(i*2\) for all elements except the first and last one. A simple subtraction must be performed to calculate the row sizes from the row offsets. Converting back to CSR is equally simple, assuming the matrix is first defragmented; the column indices and values arrays are copied back, and the starting segment offset from each row is copied to the row offsets array.

4 Experimental Results

In our tests we used an Intel Xeon E5-2640 processor running at 2.50 GHz, 128 GB of memory, and 3 NVIDIA Tesla K20c GPUs. For additional scaling tests, we used an Intel Xeon E5630 processor running at 2.53 GHz, 128 GB of memory, and 8 NVIDIA Tesla M2090 GPUs. We compiled using g++ 4.7.2, CUDA 5.5, and Thrust 1.8, comparing our method against modern implementations in Nvidia CUSP [26]. Table 1(a) provides a list of the matrices that we used in our tests as well as their sizes, number of nonzeros, and row entry distributions. All the matrices can be found in the University of Florida sparse-matrix database [27].

Memory consumption is a major concern for sparse matrix formats, as one of the primary reasons for eliminating the storage of zeros is to reduce the memory footprint. The ELL component of HYB is best suited to store rows with an equal number of entries. If there is a large variance in row size, much of the ELL portion may end up storing many zeros, which is inefficient. We provide a comparison of memory consumption for HYB, DCSR (using 2, 3, and 4 segments), and CSR formats in Table 1(b). We compute the storage size of the HYB format using an ELL width equal to the average number of nonzeros per row (\(\mu \)) for the given matrix. CSR has the smallest memory footprint since its row indices have been compressed to the number of rows in the matrix. We see that DCSR has a significantly smaller memory footprint in almost all test cases. Test cases such as AMA and DBL have lower memory consumption for HYB than for DCSR (with 3 and 4 segments), because these matrices have a low variance in row size. This low variance in row size makes them well suited for DCSR with 4 segments uses \(20\,\%\) less memory on average than HYB.

Table 1. (a): Matrices used in tests. NNZ: total number of nonzeros, \(\mu \): average row size, \(\sigma \): standard deviation of row sizes, max: maximum row size. (b): Comparison of memory consumption among HYB, CSR, and DCSR formats. Size of HYB is listed in bytes (using ELL width of \(\mu \)), and sizes for DCSR and CSR are listed as a percent of the HYB size.
Full size table

The conversion time between formats is often a key factor when determining the efficacy of a particular format. High conversion times can significantly hinder performance. Architecture-specific formats may provide better performance, but unless the rest of the code base uses that format, the conversion time must be accounted for. We provide the overhead required to convert to and from CSR and COO matrices in Table 2(a). The conversion times have been normalized against the time required to copy CSR \(\rightarrow \) CSR. The conversion times to DCSR are only slightly higher compared to that of CSR. HYB requires significant overhead as the entries must first be distributed throughout the ELL portion and the remaining overflow entries distributed to the COO portion.

Table 2. (a): Comparison of relative conversion times. Conversions are normalized against time to copy CSR\(\rightarrow \)CSR. (b): Overhead of DCSR defragmentation and HYB sorting is measured as the ratio of one operation against a single CSR SpMV. Update time is measured as the ratio of 1000 updates to a single CSR SpMV. (\(\infty \) means this test was unable to complete within machine resource limits)
Full size table

4.1 Matrix Updates

To measure the speed of dynamic updates, we ran two series of tests that involved streaming updates and iterative updates. In the streaming updates test, we incrementally build up the matrix by continuously inserting new entries. The elements are first buffered into three arrays for the rows, columns, and values. We initialize the matrix sizes according to the average number of nonzeros for the given input. Afterward, the entries are added in a streaming parallel fashion to the matrices.

Updating a HYB matrix first requires checking the ELL portion, and if the row in question is full, inserting the new entry into the COO portion. Any updates to the COO portion require atomic operations to ensure synchronous writes between multiple threads. These atomic updates are prohibitive to fast parallel updates as all threads are contending to insert entries onto the end of the COO matrix.

Updating a DCSR matrix requires finding the last occupied (current) segment within a row. If that segment is not full, the new entry is added into it and the row size is increased. When the current segment for a row fills up, a new segment is allocated dynamically. Since atomic operations are required only for the allocation of new segments, and not for each individual element, synchronization overhead is kept low. By allowing for dynamically sized slack space within a row, we dramatically reduce the number of atomic operations that are required to allocate new entries. In this way, DCSR was designed to be updated in an efficient parallel manner.

Fig. 3.
figure 3

Top: relative speedup of DCSR compared to HYB for iterative updates with SpMV operations. The speedup is compared to a normalized CSR baseline. Bottom: relative speedup of DCSR compared to HYB for matrix updates. (Color figure online)

Full size image

The number of segments, initial row width, and \(\alpha \) value can be tuned for the problem to give a reasonable limit on updates. In our tests we used four segments and \(\alpha \) value of \(\mu \) (average row size of the matrix). When a row nears its limit, a defragmentation is required in order to reduce that row to a single segment.

Figure 3 provides the results of our iterative and streaming matrix update tests. We do not compare to CSR in the latter case, since it is not possible to dynamically add entries without rebuilding the matrix. The goal of this operation is to load the matrix; insertion checks are not performed. DCSR saw an average speedup of 4.8\(\times \) over HYB with streaming updates. In the case of IND, only DCSR was able to perform the operation within memory capacity.

We also executed an iterative update test to compare the abilities of the formats to perform a combination of dynamic updates and SpMV operations. This test is analogous to what would be performed in a graph application (such as CFA) where the graph is updated at periodic intervals. In the iterative updates test we perform a series of iterations consisting of a matrix addition operation \((A = A + B)\) followed by several SpMV operations \(Ax = y\). Part (a) of Fig. 3 provides the results for our iterative updates. Within each iteration, the matrix is updated with an additional \(0.2\,\%\) random nonzeros followed by 5 SpMV operations, which is repeated 50 times, yielding a total increase of \(10\,\%\) to the number of nonzeros. We compare the DCSR and HYB results to a normalized CSR baseline. In the CSR case a new matrix must be created to update the original matrix, which causes a significant amount of overhead (in terms of computation and memory). In the cases of LJO and SOC, CSR was not able to complete within memory capacity, so we normalized against HYB.

DCSR shows significant improvement over HYB on streaming updates in all test cases (in some by as much as 8\(\times \)). DCSR also outperforms HYB in all test cases on iterative updates, and in some cases by as much as 2.5\(\times \). The Amazon-2008 matrix has a low standard deviation, and the majority of its entries fit nicely into the ELL portion, which greatly speeds up SpMV operations. However, even in this case DCSR slightly outperforms HYB on iterative updates due to having lower overhead for defragmentation. In all other cases DCSR exhibits noticeable performance improvements over HYB and CSR.

Fig. 4.
figure 4

FLOP ratings of SpMV operations for CSR, DCSR, and HYB. (Color figure online)

Full size image

4.2 SpMV Results

In the SpMV tests we take the same set of matrices and perform SpMV operations with randomly generated dense vectors. We performed each SpMV operation 100\(\times \) times and averaged the results. Figure 4 provides the results for these SpMV tests using both single and double-precision floating-point arithmetic. We implemented an adaptive binning optimization [25] (labeled ACSR), which requires relatively little overhead and provides noticeable speed improvements by using specialized kernels on bins of rows with similar row sizes. In these tests we compare across several variants of our format, including DCSR, defragmented DCSR, ADCSR, and defragmented ADCSR, in addition to standard implementations of HYB and CSR.

The fragmented DCSR times are \(8\,\%\) slower than the defragmented DCSR times on average. When the DCSR format is defragmented, it sees SpMV times competitive with those of CSR (\(1\,\%\) slower on average). With the adaptive binning optimization applied, we see that ADCSR outperforms HYB in many cases. On average, ADCSR performed \(9\,\%\) better than HYB across our benchmarks.

4.3 Post-processing Overhead

Post-processing overhead is a concern when dealing with dynamic matrix updates. Dynamic segmentation allows for DCSR to be updated with new entries without requiring the entries to be defragmented. SpMV operations can be performed on the DCSR format regardless of the order of the segments, unlike HYB matrices, where a sort is required anytime an entry is added to the COO portion. The SpMV operation for HYB matrices assumes the COO entries are sorted by row (without this property the COO SpMV would be dramatically slower). Table 2 provides post-processing times for HYB and DCSR formats relative to a single SpMV operation. In the case of IND, HYB was unable to sort and update due to insufficient memory overhead (represented as \(\infty \)).

The defragmentation operation can internally order rows by row size at no additional cost. This ordering is similar to the row sorting technique illustrated in [28], although we use a global sorting scope as opposed to a localized one. In addition, the internal order of segments may be changed arbitrarily, and this permutation remains invisible from the outside because starting and ending segment indices are managed explicitly. To accomplish this optimization we permute row sizes according to the permuted row indices (which have already been binned and sorted by row size). The permuted row sizes can then be used to create new offsets for the monolithic segments produced by defragmentation. This operation has the effect of internally reordering column and value data by row size at no additional cost. We observed this internal reordering provides a noticeable SpMV performance improvement of \(12\,\%\). This improvement is from an increased cache-hit rate via better correlation between bin-specific kernels and the memory they access.

The DCSR defragmentation incurs a lower overhead than HYB sort because entries can be shuffled to their new index without a sort operation. DCSR defragmentation is 2\(\times \) faster on average than HYB sorting, and this step is infrequently required (while HYB sorting must be performed at every insertion). These factors allow DCSR to have significantly lower post-processing overhead.

Fig. 5.
figure 5

Scaling results for SpMV with 1 and 2 K20 GPUs (upper) and 1, 2, 4, and 8 M2090 GPUs (lower). (Color figure online)

Full size image

4.4 Multi-GPU Implementation

DCSR can be effectively mapped to multiple GPUs. The matrix can be partitioned across n devices by dividing rows between them (modulo n) after sorting by row size. This mapping provides a roughly even distribution of nonzeros between the devices. Figure 5 provides scaling results for DCSR across two Tesla K20c GPUs and up to eight Tesla M2090 GPUs. We see an average speedup of 1.93\(\times \) for the single precision and 1.97\(\times \) for double precision across the set of test matrices. The RAL matrix sees a smaller performance gain due to our distribution strategy of dividing up the rows. The added parallelism is split across rows but, in this case, the matrix has few rows and many columns. We see nearly linear scaling for most test cases.

For the matrices INT and ENR we see reduced scaling due to small matrix sizes. In these cases the kernel launch times account for a significant portion of the total time due to a relatively small workload. The total compute time can be roughly represented as \(c + \frac{x}{n}\), where c is the kernel launch overhead, and the workload x is divided among n devices (assuming x can be fully parallelized). As the number of devices increases, the work per device decreases whereas the kernel launch time remains constant. In our tests we perform 100\(\times \) iterations of each kernel, which leads to poor scaling performance on small matrices. We performed additional tests in which we moved the iterations into the kernel itself and called the kernel once, eliminating the additional kernel launch times. In this case we see scaling for the INT matrix of 1.94\(\times \), 3.55\(\times \), and 6.03\(\times \), and for the ENR matrix we see scaling of 1.80\(\times \), 2.70\(\times \), and 3.76\(\times \) for 2, 4, and 8 GPUs, respectively. These results indicate that the poor performance of those cases was primarily due to the low amount of work done relative to the kernel launch overhead.

5 Conclusion

We have described a fast, flexible, and memory-efficient strategy for dynamic sparse-matrix allocation. The design of current formats limits the extension of an existing matrix with new entries. As many applications require or would benefit from efficient dynamic updates, we have proposed a strategy of explicitly managed dynamic segmentation that makes this operation inexpensive. Our approach is presented and evaluated using a new format (DCSR) that provides a robust method for allocating streaming updates while maintaining fast SpMV times on par with that of CSR. The format gracefully degrades in performance upon dynamic extension, but does not require a sort to be performed after inserting new entries (as opposed to COO-based formats such as HYB).

Without defragmentation, SpMV times are only marginally slower than that of a fully constructed CSR matrix, and after defragmentation they are roughly equal. With adaptive binning applied, DCSR gives faster overall SpMV times as compared to the HYB format. DCSR is significantly more efficient in terms of memory use as well. ELL must allocate enough room in every row for the longest row in a matrix. HYB is a vast improvement, allowing long rows to overflow into its COO portion; however, DCSR exhibited lower memory consumption on every benchmark when set to allow 2 segments per row, and still used \(20\,\%\) less memory on average when allowing 4 segments per row.

A key advantage of DCSR design is compatibility with CSR-scalar, CSR-vector, and other CSR algorithms. Only minor modifications are required to account for a difference in the format of the row offsets array. We have demonstrated how CSR-specific optimizations, such as adaptive binning, can be easily applied to DCSR. Other optimizations such as tiling and blocking could also be used. This compatibility also means that minimal overhead is required to convert to and from CSR. Numerous sparse-matrix formats have been developed that are specifically tailored to GPU architectures. These formats offer improved performance, but require converting from whatever previous format was being used. As CSR is the most commonly used sparse-matrix format, and large amounts of software already incorporate it into their code bases, it is often not worth the conversion cost to introduce another format. DCSR reduces this barrier to use with a low cost of conversion.

To the best of our knowledge, no other work has created a dynamic format such as DCSR for iterative updates to sparse matrices. Some dynamic graph algorithms, such as approximate betweenness centrality [29], require dynamic updates but do not specify how the graph should be represented and modified—a matrix encoding would require a dynamic format to be efficient. Dynamic insertion algorithms, like that described in [30], use a modified insertion sort that disperses gaps throughout the data in order to reduce insertion time from O(n) to \(O(log \; n)\) with high probability. This method probabilistically reduces the overall cost of the insertion sort from \(O(n^2)\) to \(O(n \; log \; n)\). The defragmentation operation we implement can be done in O(n) and insertions require O(1), which is better than insertion sort. Also, leaving many intermittent gaps between the data would slow SpMV times. We mitigate this problem by grouping entries contiguously within segments.

We believe our strategy lends itself well to certain operations and problems, such as graph algorithms that require periodically updating the graph with new entries. These applications have not previously been well addressed by sparse-matrix formats. Our work also opens up a number of interesting research questions as to whether existing algorithms that rebuild matrices between iterations could be improved by a matrix format that permits dynamic updates directly.