Resolving small random symmetric linear systems on graphics processing units

Abstract

This paper focuses on the resolution of a large number of small random symmetric linear systems and its parallel implementation in single precision on graphics processing units (GPUs). The computations involved by each linear system are independent from the others, and the number of unknowns does not exceed 64. For this purpose, we present the adaptation to our context of largely used methods that include: LDLt factorization, Householder reduction to a tridiagonal matrix, parallel cyclic reduction (PCR) that is not a power of two and the divide and conquer algorithm for tridiagonal eigenproblems. We not only detail the implementation and optimization of each method, but we also compare the sustainability of each solution and its performance which include both parallel complexity and cache memory occupation. In the context of solving a large number of small random linear systems on GPUs with no information about their conditioning, our research indicates that the best strategy requires the use of Householder tridiagonalization + PCR followed if necessary by a divide and conquer diagonalization.

1 Introdution

Several problems in physics and operations research can be divided into subproblems, solved independently, and processed using various communication steps to determine the global solution. This is also the case for simulations in mathematical finance, in particular for the challenging problem of credit valuation adjustment (CVA). When American contracts are involved, the CVA can be simulated thanks to a nested Monte Carlo (NMC) that performs a dynamic programming algorithm (DPA) on the inner trajectories. This procedure constitutes a straight extension of the square Monte Carlo presented in [1] as a benchmark method for CVA on European contracts. Basically, the main ingredient of this extension relies on the resolution of a large number of small random symmetric linear systems.

The CVA simulation is rather the origin and not the purpose of this paper. In this contribution, we are really focused on the computational effort of adapting to our context some well-known algorithms. Indeed, we are not aware of any work that deals with the resolution on graphics processing units (GPUs) of a large number of symmetric small linear systems whose common size $n = \text {(number of knowns)}$ does not exceed 64. The lack of research done in this direction could be due to the fact that large linear systems are more difficult to parallelize than smaller ones. Nevertheless, a good parallelization for small linear systems cannot be considered as straight simplification of the work done for large systems.

Actually, when targeting performance, we have to be aware that the paradigm of the parallel implementation changes according to the size. When $n \ge 8$, we should also be aware that the single instruction multiple data (SIMD) parallelization in our context is far from optimality. Indeed, because of the size of the cached memory available per block of threads, associating one thread per linear system reduces significantly the number of threads that can be launched in parallel. Consequently, the parallelization that we propose is neither SIMD nor straight simplification of known libraries developed for large linear systems like matrix algebra on GPU and multicore architectures (MAGMA) [23].

The solution that we propose is suited to the specific problem of solving a large number of small symmetric linear systems. It is based on the dependence classification of threads: the class of threads that are independent because involved in different linear systems, noted $\mathfrak {T_I}$, and the class of those that communicate because involved in the same linear system, noted $\mathfrak {T_C}$. The largest part of this paper is dedicated to the organization of communicating threads $\mathfrak {T_C}$ and to their use of CUDA shared memory. Regarding the independent groups of threads $\mathfrak {T_I}$, their number will be chosen to saturate the use of the shared memory size available per block or to have a sufficient work per streaming multiprocessors (SMs).

Our contribution can be summarized in the following points:

• We give the CUDA source code [24] associated with the adaptation of each algorithm: LDLt factorization, Householder reduction, parallel cyclic reduction (PCR) that is not necessary a power of two, and divide and conquer for eigenproblem. As one could expect, the adaptation of the divide and conquer was the trickiest one, since it requires some technicality due to: choosing the right indices for the division part, implementing the right algorithm for the solution of the secular equation, and tuning the deflation parameters to get sufficiently accurate results.

• We provide an in-depth description of each implementation.

• We compare the execution time of the different methods mentioned above.

• We propose an original method to further optimize the adaptation of LDLt factorization to our context.

• We provide an original PCR that can be used for any vector size and not only a power of two that requires a zero padding.

Although we are interested by small linear systems with $n \sim 32$, it is not reasonable to use LDLt factorization for all situations. In fact, in Sect. 2.2, we show that even when $n = 30$ some random linear systems turn out to be ill-conditioned for single floating-point precision as the one used on our Geforce GPU. For this reason, we found ourselves obliged to develop both the Householder tridiagonal reduction as well as the divide and conquer diagonalization of tridiagonal matrices. Subsequently, one could ask the following legitimate question:

Must we systematically use Householder tridiagonalization with divide and conquer when we suspect the random linear systems to be ill-conditioned?

Our answer is: Perform Householder tridiagonalization and solve the linear systems cheaply using parallel cyclic reduction, then take a decision according to the value of the residue error. If the residue error is small, then we already have good solutions. Otherwise, we must perform divide and conquer diagonalizations and discard the smallest eigenvalues. The next time we solve this same kind of linear systems: if they used to be well conditioned, then we just process LDLt; otherwise, we execute directly the combination of Householder tridiagonalization and divide and conquer diagonalization.

The answer above justifies the work detailed in this paper that is organized as follows. In Sect. 2, we give a brief description of NMC for CVA and we show a realistic example where the linear systems are ill-conditioned. Afterward, the presentation of each resolution algorithm is explained in a separate section: Sect. 3 for LDLt factorization, Sect. 4 for Householder and parallel cyclic reductions, and Sect. 5 for divide and conquer diagonalization. Sections 2, 3, 4, and 5 start with a subsection that describes the headlines of each problem and some references related to it. Section 6 concludes this paper with global remarks and the future work that is in preparation.

2 Brief description of NMC for CVA

2.1 Presentation of CVA and the references

The 2007 economic crisis raises the fear of systemic stability when the default of one financial institution could be the origin of a cascade of other defaults. To reduce this risk, several measures were established that include the calculation of the CVA as an important part of the Basel III prudential rules. Since the paper [6], the CVA can be viewed as an insurance contract that compensates for the no-recovered sum by the counterparty when it defaults.

For a comprehensive financial presentation of CVA, we refer to [5]. Regarding the mathematical aspects, the reference [10] can be viewed as the most recent and complete summary on the subject. However, little research has been dedicated to the development of numerical procedures that should be used to perform the computations. Book [7] is one of the first references that presents the industry practices in computing CVA. Among research papers, maybe the most devoted to computing CVA are [1, 15, 22].

Due to both mathematical and computational complexity, none of the previous references provide a benchmark procedure to deal with CVA when American contracts are involved. This is despite the fact that American contracts are widely exchanged, especially in some markets. As it will be shown, simulating CVA on American contracts can be overcome thanks to an efficient way of parallelizing the resolution of a large number of small symmetric systems on GPUs. This latter point is really the heart of this work. Before detailing the background NMC algorithm in the next subsection, we introduce below the simplest formulation of the CVA:

$$\begin{aligned} \text {CVA}_{0,T} = \displaystyle (1-R) E \left( P^+_\tau \mathbbm {1}_{t < \tau \le T} \right) , \end{aligned}$$

(1)

where R is the recovery made by the counterparty when it defaults, E denotes the expectation operator, $P_t$ is the process of the value exposure to the counterparty, $\tau$ is the random default time of the counterparty, T is the protection time horizon, and the positive part function is denoted by $^+$.

As already explained in [1], one of the most important challenges of the CVA comes from the fact that the exposure $P_t$ is generally the price of a basket of different contracts that are written with our counterparty. If these contracts can be priced by closed expressions, the CVA can be calculated thanks to a one-stage simulation using either the discretization of a partial differential equation or Monte Carlo method as in [11]. However, when the underlying contracts must be simulated, it is natural from expression (1) to perform a two-stage simulation: the inner stage to compute $P_t$ and the outer stage for the CVA. This two-stage simulation leads to the square Monte Carlo simulation used in [1] as a benchmark algorithm.

The square Monte Carlo proposed in [1] is developed for an exposure $P_t$ of European contracts which is a category of contracts that can be exercised only at maturity (${\le }{T}$). Unlike the European case, the American contracts allow an early exercise (${\le }{T}$) of the contract which can be solved using DPA. The most used implementation of this DPA is the Longstaff–Schwartz algorithm proposed in [27] and theoretically studied in [9]. For CVA simulation, this algorithm is implemented thanks to regressions performed on the inner trajectories providing a new NMC algorithm that extends the square Monte Carlo of [1].

2.2 Description of the matrices involved by our new NMC algorithm

As usual, expression (1) is discretized using a fixed number of time steps N that introduces the sequel $0=t_0<t_1<\cdots <t_N=T$ and the estimation

$$\begin{aligned} \text {CVA}_{0,T} = \sum _{k=0}^{N-1} E \left( P^+_{t_{k+1}} \mathbbm {1}_{\tau \in (t_{k},t_{k+1}]}\right) . \end{aligned}$$

(2)

To approximate the expectation E in (2), we simulate $M_0$ outer stage trajectories of the underlying asset $S=(S^1,\ldots ,S^d)$ on which the contracts are established. To compute the exposure P in (2) at each time $t_{k}$ of the outer trajectories, we simulate $M_k$ inner stage trajectories of the same underlying asset S. In these outer and inner simulations, the vector S is a given Markov process whose realizations could be drawn thanks to a given random number generator like those presented in [3]. An illustration of this NMC algorithm is given in Fig. 1.

Fig. 1

An example of a two-stage simulation with $M_0=2, M_6=8$, and $M_8=4$

When the exposure P includes American contracts, we perform Longstaff–Schwartz algorithm on the inner trajectories. This requires $N-k-1$ regressions at each time step $k \in \{1,\ldots ,N-1\}$ and for each outer trajectory $l \in \{1,\ldots ,M_0\}$. For a fixed couple (k, l), the regression is performed using a projection on the space generated by $\psi ^l(S_{t_k})=(\psi ^l_1(S_{t_k}),\ldots ,\psi ^l_n(S_{t_k}))$. The choice of the latter family should obviously depend on the considered problem, but generally practitioners use some family of polynomials.

The regression matrix is the Monte Carlo approximation $\widehat{A}_{k,l}$ of $A_{k,l} = E(\psi ^l(S_{t_k}) \psi ^l(S_{t_k})^t)$ given by

$$\begin{aligned} \widehat{A}_{k,l} = \frac{1}{M_k} \sum _{j=1}^{M_k} \psi ^l\left( S^{(j)}_{t_k}\right) \psi ^l\left( S^{(j)}_{t_k}\right) ^t \end{aligned}$$

(3)

where $^{(j)}$ is the inner trajectory index and $^t$ is the transpose operator.

Fig. 2

Condition numbers for linear regression associated with Black and Scholes model: $\sigma = 0.1, \mu =0.1, S_0=(1,\ldots ,1), t_k=0.1, n=30, M_k=300$ and $l\in \{ 1,\ldots ,1000 \}$

By definition, the correlation matrices $A_{k,l}$ are symmetric. Moreover, the family $\psi (S)$ is always chosen to make all $\{A_{k,l}\}_{1\le k \le N-1, 1\le l \le M_0}$ positive definite, i.e., $\forall A \in \{A_{k,l}, 1\le k \le N-1, 1\le l \le M_0\}$

$$\begin{aligned} X^tA X > 0,\quad \text {for every } X \in \mathbb {R}^n-\{(0,\ldots ,0)\}. \end{aligned}$$

(4)

However, the Monte Carlo approximations $\widehat{A}_{k,l}$, which are symmetric, do not necessary fulfill condition (4), since they depend on the convergence parameter $M_k$. Indeed, although the values taken by $M_k$ can be sufficient to have a good overall convergence of NMC, some small values produce either numerical indefiniteness or even negativity.

As already introduced in [17] and adapted to CVA in [2], $M_k$ should be of the order of $\sqrt{M_0}$. In Fig. 2, we give some condition values for the benchmark model of Black and Scholes ($d=29$) with independent coordinates. The parameters of this model are its volatility $\sigma$, interest rate $\mu$, and spot value $S_0$. The regressions performed in this figure are linear and include the constant 1, i.e., $\psi (S) = (1,S^1,\ldots ,S^{29})$ which makes $n=30$.

Although the value $n=30$ could be considered high by some practitioners, it is possible to use it especially for sufficiently large exposures to the counterparty, for instance, the exposure of a bank to another bank. Figure 2 shows, then, an example of matrices that can corrupt the DPA when implemented in a single precision. In fact, the number of trusted decimals is not sufficient to make a decision on the early exercise strategy computed by the DPA. When this kind of situation is confronted, one has to discard some smallest eigenvalues before resolving any linear system.

3 LDLt decomposition

3.1 Presentation of the algorithm and the references

The resolution of the linear system $A X = Y$ with A symmetric positive definite is divided into two steps: the factorization of the matrix A that leads to $A = LDL^t$ and the resolution of $LZ=Y$ as well as $DL^t X = Z$, where $L^t$ is the transpose of L. The matrix D is diagonal, and the matrix L is lower triangular with 1 on its diagonal. The factorization is performed because of the following expressions:

$$\begin{aligned} \displaystyle A= & {} LDL^t,\quad D_{j,j} = A_{j,j} - \sum _{k=1}^{j-1} L_{j,k}^2 D_{k,k} ,\nonumber \\ \displaystyle L_{i,j}= & {} \frac{1}{D_{j,j}} \left( A_{i,j} - \sum _{k=1}^{j-1} L_{i,k} L_{j,k} D_{k,k} \right) \quad \text {if } i>j . \end{aligned}$$

(5)

Because it prevents the computation of square roots, LDLt factorization is generally considered as a better alternative to the Cholesky decomposition. Both methods share the same important stability for symmetric positive definite matrices A characterized by (4). Furthermore, when the positive definiteness is numerically questioned, one should avoid the use of either LDLt or Cholesky decomposition. In addition, these two methods share the same complexity order and the same memory space occupation. Due to all these similarities and the fact that Cholesky’s literature is larger than LDLts, we will not distinguish between the references of each method.

The stability property of LDLt and Cholesky is quite important. In fact, when the correlation matrix is not numerically singular, these two methods are so stable that they do not need any pivoting like those performed for LU decomposition [29]. Escaping the pivoting phases makes a great advantage for the GPU implementation, since it reduces communications between threads. Furthermore, LDLt and Cholesky are the most efficient methods of factorization with a complexity given by $O(n^3/6)$, where $n\times n$ is the size of the matrix. They are also the ones that use the least memory space as they involve only $n(n+1)/2$ values. Once the LDLt factorization performed, the resolution of $LZ=Y$ and the resolution of $DL^t X = Z$ are straightforward. These resolutions are even quadratic in complexity with respect to n.

To the best of our knowledge, [30] is the first reference that implements Cholesky decomposition on GPUs. Paper [4] comes after, and it theorizes the minimization of the communication cost involved in Cholesky factorization. Even though both papers are very interesting, the extent of the work developed their is adapted to large matrices $n \ge 64$. The same can be said for the Cholesky’s code of MAGMA [23]. Indeed, MAGMA library is even dedicated to heterogeneous CPU/GPU implementations that are generally justified for sufficiently large sizes.

Actually, to deal with a large matrix, we need to divide it into smaller pieces and distribute the computations on the blocks of threads. In contrast, with a large number of small matrices, it is sufficient to distribute directly the matrices on the different blocks. Moreover, various techniques developed for matrices larger than 64 are not efficient for large number of matrices smaller than 64. We can cite the one presented in [30] Section 4.3 which produces another level of parallelism by splitting the dot product into partial sums. Nevertheless, this level of parallelism is less efficient for small matrices and increases the execution time, since it competes with the other more natural levels detailed in Sect. 3.2.

3.2 Adaptation and optimization

We present three different versions of the LDLt factorization:

• 1. an SIMD version that requires only threads of $\mathfrak {T_I}$, one for each linear system;

• 2. a collaborative version that involves n threads of $\mathfrak {T_C}$ for each linear system with n unknowns;

• 3. an optimal hybrid solution that involves $n^*\,(n^* <n)$ threads of $\mathfrak {T_C}$ for each linear system with n unknowns.

The number of the $\mathfrak {T_I}$-independent groups of threads is chosen to saturate the shared memory or at least to have sufficient work per SMs.

The SIMD version is straightforward and used only to convince the reader of its inefficiency. Regarding the collaborative and the hybrid versions, they are both based on a column after column processing. In fact, as shown in Fig. 3, for a fixed value of j, the different coefficients $\{ L_{i,j} \}_{j+1 \le i \le n}$ can be computed concurrently by at most $n-j$ independent threads. Thus, $\{ L_{i,1} \}_{2 \le i \le n}$ involve the largest number of possible concurrent threads equal to $n-1$. In the collaborative version, we use the maximum $n-1$ threads $+1$ additional thread that intervenes in the copy from global memory to shared memory and in the solution of the linear system after factorization. This makes n threads for the collaborative version, and one of these threads is also involved in the computation of $D_{j,j}$ which needs a synchronization before calculating $L_{i,j}$.

Fig. 3

Standard LDLt parallel strategy

For $j>n/2$ in the collaborative version, more than the half number of threads are in a wait state. This is not a problem when n is large enough, because the shared memory is sufficiently filled which limits the possibility of launching independent threads $\mathfrak {T_I}$ on other linear systems. Nevertheless, when n is small, the communicating threads $\mathfrak {T_C}$ in a wait state prevent the schedular from the execution of independent threads $\mathfrak {T_I}$, even though there is a sufficient shared memory space for other linear systems. This situation motivates the use of an hybrid solution that either employs about the half number $n^*(n) \simeq n/2$ of maximum number of communicating threads or all of it $n^*(n) \simeq n$. As we will see in Fig. 4 for some n, this hybrid solution is significantly better than the collaborative one. In Algorithm 1, we summarize the different steps of the hybrid LDLt factorization. $\lceil \cdot \rceil$ in Algorithm 1 is the ceiling function, i.e., For each real number, $x, \lceil x \rceil = \inf \{ a \in \mathbb {Z} ; a \ge x\}$.

Finally, we precise that we use $n(n+1)/2$ memory space for the LDLt factorization $+n$ for the resolution. To keep a coalesced access to the shared memory and reduce the bank conflicts, the matrices are also stored column after column and not row after row as it is generally done.

Fig. 4

The speedup of the collaborative and the hybrid versions when compared with the SIMD implementation

3.3 Comparison of the different versions

First, let us introduce the set of matrices used for the tests. The matrices introduced in Sects. 4.3 and 5.3 are related to the one presented here which are positive definite. It is straightforward to show that matrices $\varXi _\rho$ given by

$$\begin{aligned} \begin{array}{cc} \varXi _\rho = \left( \begin{array}{ccccc} 1 &{} \rho &{} \cdots &{} \rho &{} \rho \\ \rho &{} 1 &{} \rho &{} &{} \vdots \\ \rho &{} \ddots &{} \ddots &{} \ddots &{} \rho \\ \vdots &{} &{} \rho &{} 1 &{} \rho \\ \rho &{} \rho &{} \cdots &{} \rho &{} 1\\ \end{array}\right)&\text {with } 0< \rho < 1 \end{array} \end{aligned}$$

(6)

are positive definite. Because these matrices are strongly structured, we prefer to use randomized version given by $A = Q_{\varXi _{\rho }} R Q_{\varXi _{\rho }}'$, where R is a diagonally dominant tridiagonal symmetric random matrix and $Q_{\varXi _{\rho }}$ is the orthogonal matrix that results from the Householder tridiagonalization of $\varXi _{\rho }$. The components of R are set using uniform random variables and the multiplication of the diagonal elements by the appropriate factor to make R diagonally dominant.

We point out that all the results are obtained from an implementation on an NVIDIA Geforce 970.

Fig. 5

The optimal number of communicating threads in the hybrid version

Fig. 6

Number of linear systems that can be solved within a second

From Fig. 4, we notice that the hybrid solution outperforms the collaborative one when $n < 40$. Moreover, the SIMD version is clearly unsatisfactory for all sizes even when $n=4$. The speedup obtained when using communicating threads gets relatively high according to the size n, and it exceeds the speedup of 14 per linear system when $n=64$.

The optimal number of communicating threads in the hybrid version depends on the GPU used. In Fig. 5, we give the experimental values obtained for different sizes n when the implementation is performed on the Geforce 970. We distinguish two regimes:

$$\begin{aligned} n^*(n) \simeq \left\{ \begin{array}{l@{\quad }l} n/2 &{} \text {if } \quad n < 40 ,\\ n &{} \text {otherwise.}\\ \end{array}\right. \end{aligned}$$

(7)

Using the LDLt hybrid implementation, we establish Fig. 6 that shows the number of linear systems that can be solved per second. The curve obtained is almost proportional to $n^{-3}$ which coincides with the theoretical result. To push our study further, we compare, in Fig. 7, our CUDA implementation of the hybrid LDLt resolution to the OpenMP multithreaded implementation of the Cholesky resolution given in [29]. Since we are dealing with large number of small systems, the CPU parallelization is a simple SIMD implementation on an Intel I7-5930K that has 6 cores at 3.5 GHz with 15Mo memory cache.

Fig. 7

LDLt resolution: the speedup of CUDA/GPU implementation compared with OpenMP/CPU. This speedup is measured in terms of the number of solved systems per second

The decreasing behavior in Fig. 7 shows the superiority of independent threads $\mathfrak {T_I}$ when compared with communicating ones $\mathfrak {T_C}$. As a matter of fact, when n increases, there is less shared memory space for independent threads that are replaced by less effective communicating ones. That said, one can easily predict the better performances of our implementation on the new Nvidia Pascal architecture that contains twice the size of the shared memory.

4 Householder and parallel cyclic reductions

4.1 Presentation of the algorithms and the references

Householder tridiagonalization

Similar to the method based on LDLt, we propose here to solve the linear system $A X = Y$, with A symmetric, through two steps:

• The tridiagonal Householder decomposition $A=QUQ^t$ where Q is orthogonal and U is symmetric tridiagonal.

• The PCR associated with the problem $UZ = Q^tY$ that allows to recover X thanks to $X = QZ$.

When the linear system is symmetric, the Householder tridiagonalization is generally used as the first step of a diagonalization algorithm which could employ: QR factorization, bisection method, multiple relatively robust representations or divide and conquer. We refer to [14] for a sequential comparison between these four algorithms according to speed and accuracy.

As advised in the introduction, we would like to use the Householder tridiagonalization with PCR and check the residue error before looking for a diagonalization of the system. This procedure is justified by the fact that PCR is less complex than any of the four algorithms cited above with a theoretical ratio equal at least to $n/{\log _2(n)}$ in favor of PCR. Moreover, as already shown in [32], PCR is quite stable for symmetric and positive definite matrices and is suited to parallel architectures like GPUs.

Without going through details that can be found, for instance, in [13, 29], let us present the main points of the Householder tridiagonalization. The basic ingredient is the Householder matrix H whose expression, for some vector u different from the zero vector, is given by

$$\begin{aligned} H = I - uu^t/b, \quad b = u^t u /2. \end{aligned}$$

(8)

The idea then is to choose the right vectors $u_{n}$,..., $u_{3}$ associated with $H_{n}$,..., $H_{3}$. The product of these matrices yields to the orthogonal matrix $Q = H_{n} H_{n-1} \ldots H_{3}$, and their successive applications on A provide: $U = Q^tAQ = H^t_{3}\ldots H^t_{n}AH_{n} \ldots H_{3}$. In [31, p. 6], the authors discuss two solutions, for Householder reduction, that rely on CPU/GPU transfer. In our case, the CPU/GPU transfer is naturally harmful to the effectiveness of threads belonging to $\mathfrak {T_I}$.

Parallel cyclic reduction

Let us also give some highlights on PCR and refer to [21, 32] for more details on the subject. At this stage, we are interested by the resolution of the linear system $UZ = Q^tY$, where the value of $V = Q^tY = (v_1,\ldots ,v_n)$ is known and U is tridiagonal and symmetric, i.e.,

$$\begin{aligned} U = \left( \begin{array}{cccccc} d_1 &{} c_1 &{} &{} &{} &{} \\ c_1 &{} d_2 &{} c_2 &{} &{} 0 &{} \\ &{} c_2 &{} d_3 &{} \ddots &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} 0 &{} &{} \ddots &{} \ddots &{} c_{n-1} \\ &{} &{} &{} &{} c_{n-1} &{} d_{n} \end{array}\right) . \end{aligned}$$

(9)

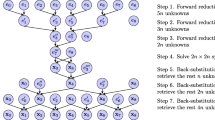
PCR comes from a simple modification of cyclic reduction (CR) which is schematized in Fig. 8 where the linear equations e1,..., e8 constitute the equality $UZ=V$ when $n=8$. Applied to this symmetric linear system of equations (e1,..., e8), the first step of CR reduces the number of 8 equations to 4 equations defined by:

$$\begin{aligned} \begin{array}{ll} \left\{ \begin{array}{ll} \text {e2': }~~~~~~~~d_2' z_2 + c_2' z_4 = v_2' \\ \text {e4':}c_ 2'z_2 + d_4' z_4 + c_4' z_6 = v_4' \\ \text {e6':}c_ 4'z_4 + d_6' z_6 + c_6' z_8 = v_8' \\ \text {e8': }~~~~~~~~c_ 6'z_6 + d_8' z_8 = v_8' \end{array}\right. &{} \text {with } \left\{ \begin{array}{c} \displaystyle d_i' = d_i - \frac{c^2_{i-1}}{d_{i-1}} - \frac{c^2_{i}}{d_{i+1}} \\ \displaystyle c_i' = - c_{i}c_{i+1}/d_{i+1} \\ \displaystyle v_i' = d_i - \frac{c_{i-1}v_{i-1}}{d_{i-1}} - \frac{c_{i}v_{i+1}}{d_{i+1}} \end{array}\right. \end{array}. \end{aligned}$$

(10)

On this new system, we perform another similar reduction that yields to a system of two equations that only involve $z_4$ and $z_8$. The resolution of the latter system makes possible the backward stage of resolving (10) and, finally, the original system of 8 equations.

Fig. 8

Cyclic reduction for $n=8$ unknowns: communication pattern showing the dataflow between equations. Letters $e{^\prime }$ and $e{^\prime {^\prime }}$ stand for updated equation

CR is specified by a forward reduction phase then a backward phase to recover the solution. CR suitability to GPU and its implementation were already studied in both [16, 32]. The authors of [16] propose a method to overcome shared memory bank conflicts during CR, but it uses 50 % more on-chip storage. Because of this extra storage, this trick must not be used in our case, since it reduces the number of independent groups of threads involved on different linear systems.

Unlike CR, PCR requires only forward reductions. In Fig. 8, for instance, the PCR version would apply two simultaneous reductions in Step 1: a reduction to obtain a new system involving $(z_2, z_4, z_6, z_8)$ and another reduction that provides a new system involving $(z_1, z_3, z_5, z_7)$. Generally speaking, for a system of size n, PCR reduces the system of n equations to 2 systems of n / 2 equations, then to 4 systems of n / 4 equations, and so on until reaching n / 2 systems of 2 equations that can be simply solved. This process makes PCR more suited to parallel architecture and prevent the bank conflicts of shared memory. Nevertheless, PCR can be improved for large systems $n>64$ by a combination with CR as detailed in [32].

4.2 Adaptation and optimization

Householder tridiagonalization

We present two different versions of the Householder tridiagonal factorization:

• 1. an SIMD version that requires only threads of $\mathfrak {T_I}$, one for each linear system;

• 2. a collaborative version that involves n threads of $\mathfrak {T_C}$ for each linear system with n unknowns.

The number of the $\mathfrak {T_I}$-independent groups of threads is taken to be the one that saturates the shared memory or that executes sufficient work per SMs.

The SIMD version is a single-threaded CUDA adaptation of the procedure proposed in [29, p. 470]. The collaborative version is also based on [29], but it provides a multi-threaded implementation of independent tasks which makes it much more efficient than the SIMD version. We begin by explaining the algorithmic steps of the common procedure. The first stage is to compute the tridiagonal form U through successive zeroing of the columns of matrix $A = (A_{i,j})_{i,j=1,\ldots ,n}$. This stage is processed at each step $i=n,\ldots ,3$ beginning by the vector

$$\begin{aligned} u_i^t=\left( A_{i,1},\ldots ,A_{i,i-1}\pm \sqrt{\sigma },0,\ldots ,0\right) , \quad \sigma = \sqrt{A_{i,1}^2+\cdots +A_{i,i-1}^2}, \end{aligned}$$

(11)

then calculating the intermediary variables

$$\begin{aligned} b_i = \frac{u_i^tu_i}{2}, p_i = \frac{U_{i+1} u_i}{b_i} , B_i = \frac{u_i^t p_i}{2b_i}, q_i = p_i - B_i u_i \end{aligned}$$

(12)

which allow us to set

$$\begin{aligned} U = U_3 \quad \text { with } U_i = U_{i+1} - q_i u_i^t - u_iq_i^t \text { and } U_{n+1} = A. \end{aligned}$$

(13)

Now that we have the tridiagonal form U, the second stage is to compute the orthogonal matrix Q defined by $Q = H_{n} H_{n-1} \ldots H_{3}$. Furthermore, we remind that a Householder matrix $H_i$ is completely specified by $u_i$. Consequently, during the first stage, the nonzero components of $u_i$ are stored in the ith row of the shared memory space allocated for A and $u_i/b_i$ in the ith column. Thus, the computation of Q is performed in the second stage using $Q = Q_n$ and the induction

$$\begin{aligned} Q_i = H_i Q_{i-1} \quad \text { for } i = 4,\ldots ,n \text { with } Q_3 = H_3. \end{aligned}$$

(14)

By definition, $Q_i$ is an identity matrix in the last i rows and columns, and only its elements up to row and column $i-1$ need to be computed. These then overwrite $u_i$ and $u_i/b_i$ stored in A in the first stage.

As far as the first stage is concerned, in addition to the $n\times n$ shared memory space allocated for A, we need $2n+1$ extra shared memory space. The latter space is used to store the diagonal and the off-diagonal plus 1 value needed for the synchronization between phases where only one thread can be used and the other phases. In addition, since $p_i$ is of size i, its components can be stored temporarily in the place of undetermined elements of the off-diagonal. Regarding $q_i$, it overwrites $p_i$ in the off-diagonal.

Let us now take a look at the multithreaded parts of the collaborative version. For the second stage, we can use $i-1$ threads of type $\mathfrak {T_C}$ that need synchronization only when the calculation of $Q_i$ is finished. As for the first stage, the computations of $p_i$ and $q_i$ in (12) and the induction performed in (13) are all parallelized using $i-1$ threads. The other parts of this stage are executed using only one thread. In Algorithm 2, we summarize the different steps of the collaborative Householder reduction.

Fig. 9

Modified parallel cyclic reduction for $n=8$: communication pattern showing the dataflow and permutation of equations. Letters $e{^\prime }$ and $e{^\prime {^\prime }}$ stand for updated equation

Parallel cyclic reduction

It is important to point out that CR and PCR implementations proposed in [16] and [32] cannot be used directly for any system size. Indeed, the first reference requires a size that is equal to a power of two plus one and the versions of the second paper are done for a size equal to a power of two. The simplest way to use both implementations for any size would be to perform a zero padding. In our case, using this latter technique is not a good option, since we fill a part of the shared memory with zeros instead of using it for the resolution of other systems. This fact motivates our version of the PCR presented below.

We propose to implement the PCR with permutations of equations in the way shown in Fig. 9. The idea is to gather the equations involved in the same system and to separate those that are independent. Indeed, using this simple idea one can deal with any size. Let us take the example $n=7$, the changes that occur on the matrix of the system are the following:

$$\begin{aligned} \begin{array}{ccc} \left( \begin{array}{ccccccc} d_1 &{} c_1 &{} &{} &{} &{} &{} \\ c_1 &{} d_2 &{} c_2 &{} &{} &{} &{}\\ &{} c_2 &{} d_3 &{} c_3 &{} &{} &{} \\ &{} &{} c_3 &{} d_4 &{} c_4 &{} &{}\\ &{} &{} &{} c_4 &{} d_5 &{} c_5 &{} \\ &{} &{} &{} &{} c_5 &{} d_6 &{} c_6 \\ &{} &{} &{} &{} &{} c_6 &{} d_7 \end{array}\right) &{}\begin{array}{c} (R) \\ \longrightarrow \end{array} &{} \left( \begin{array}{ccccccc} d_1' &{} 0 &{} c_2' &{} &{} &{} &{} \\ 0 &{} d_2' &{} 0 &{} c_3' &{} &{} &{} \\ c_2' &{} 0 &{} d_3' &{} 0 &{} c_4' &{} &{} \\ &{} c_3' &{} 0 &{} d_4' &{} 0 &{} c_5' &{}\\ &{} &{} c_4' &{} 0 &{} d_5' &{} 0 &{} c_6'\\ &{} &{} &{} c_5' &{} 0 &{} d_6' &{} 0 \\ &{} &{} &{} &{} c_6' &{} 0 &{} d_7' \end{array}\right) \\ \\ &{}\begin{array}{c} (P) \\ \longrightarrow \end{array} &{} \left( \begin{array}{ccccccc} d_1' &{} c_2' &{} &{} &{} &{} &{} \\ c_2' &{} d_3' &{} c_4' &{} &{} &{} &{}\\ &{} c_4' &{} d_5' &{} c_6' &{} &{} &{} \\ &{} &{} c_6' &{} d_7' &{} 0 &{} &{}\\ &{} &{} &{} 0 &{} d_2' &{} c_3' &{} \\ &{} &{} &{} &{} c_3' &{} d_4' &{} c_5' \\ &{} &{} &{} &{} &{} c_5' &{} d_6' \end{array}\right) \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ccc} \left( \begin{array}{ccccccc} d_1' &{} c_2' &{} &{} &{} &{} &{} \\ c_2' &{} d_3' &{} c_4' &{} &{} &{} &{}\\ &{} c_4' &{} d_5' &{} c_6' &{} &{} &{} \\ &{} &{} c_6' &{} d_7' &{} 0 &{} &{}\\ &{} &{} &{} 0 &{} d_2' &{} c_3' &{} \\ &{} &{} &{} &{} c_3' &{} d_4' &{} c_5' \\ &{} &{} &{} &{} &{} c_5' &{} d_6' \end{array}\right) &{}\begin{array}{c} (R) \\ \longrightarrow \end{array} &{} \left( \begin{array}{ccccccc} d_1'' &{} 0 &{} c_2'' &{} &{} &{} &{} \\ 0 &{} d_3'' &{} 0 &{} c_4'' &{} &{} &{}\\ c_2'' &{} 0 &{} d_5'' &{} 0 &{} &{} &{} \\ &{} c_4' &{} 0 &{} d_7' &{} 0 &{} &{}\\ &{} &{} &{} 0 &{} d_2'' &{} 0 &{} c_3''\\ &{} &{} &{} &{} 0 &{} d_4'' &{} 0 \\ &{} &{} &{} &{} c_3'' &{} 0 &{} d_6'' \end{array}\right) \\ \\ &{} \begin{array}{c} (P) \\ \longrightarrow \end{array} &{} \left( \begin{array}{ccccccc} d_1'' &{} c_2'' &{} &{} &{} &{} &{} \\ c_2'' &{} d_5'' &{} 0 &{} &{} &{} &{}\\ &{} 0 &{} d_3'' &{} c_4'' &{} &{} &{} \\ &{} &{} c_4'' &{} d_7' &{} 0 &{} &{}\\ &{} &{} &{} 0 &{} d_2'' &{} c_3'' &{} \\ &{} &{} &{} &{} c_3'' &{} d_6'' &{} 0 \\ &{} &{} &{} &{} &{} 0 &{} d_4'' \end{array}\right) \end{array} \end{aligned}$$

where (R) and (P) mean, respectively, reductions and permutations, and the empty parts of the matrices represent the null part. Obviously, one should also set the same kind of reductions and permutations on the vector of unknowns Z as well as on the vector of values V. To reorder the final solution, we use an array of size n in addition to the usual 3n memory space needed for PCR.

4.3 Comparison of versions and comparison with LDLt

In this section, we reuse the matrices $A = Q_{\varXi _{\rho }} R Q_{\varXi _{\rho }}'$ introduced in Sect. 3.3. Unlike LDLt and PCR, the Householder factorization does not require A to be definite positive, and thus, one can even take R to be only tridiagonal symmetric random matrix and not diagonally dominant.

As stated before, we ought to tridiagonalize $A: A=QUQ^t$ then use the PCR as well as two matrix/vector multiplications $UZ = Q^tY, X = QZ$ to recover the solution. The PCR and the multiplications are much faster than the tridiagonal factorization and, like for resolutions $LZ=Y$ and $DL^t X = Z$ in LDLt, can be neglected when compared with the overall execution time.

To make the previous affirmation more quantitative, Fig. 10 shows huge numbers of PCRs and matrix/vector multiplications that can be computed per second. These numbers generally exceed those associated to using LDLt shown in Fig. 6 of the previous section. However, they coincide for very small systems as we do much less computations on the shared memory compared to the time spent in accessing to the GPU global memory.

Regarding the benefits of using the collaborative solution instead of the SIMD version of Householder tridiagonalization, the continuous line in Fig. 11 shows a quite significant speedup that increases with respect to the size n. In addition, the dashed line in Fig. 11 shows the execution time superiority of the LDLt hybrid solution when compared with the collaborative version of the Householder tridigonalization + PCR. Basically, the LDLt hybrid solution is about 5 times faster than the collaborative Householder tridigonalization + PCR on our Geforce 970. Moreover, we already have a hybrid Householder factorization in our source code [24], but it does not perform better than the standard collaborative one.

Fig. 10

Number of “PCRs + two matrix/vector multiplications” that can be performed per second. Each PCR + matrix/vector multiplication couple are necessary to solve a system, once its Householder factorization is known

Fig. 11

The execution time ratio of: SIMD/collaborative and (tridiagonal + PCR)/LDLt

Like for LDLt factorization, we finish this section by comparing our CUDA implementation of the collaborative Householder solution to the OpenMP multithreaded implementation of Householder reduction given in [29]. This comparison is also done between a Geforce 970 and an I7-5930K, and the result is shown in Fig. 12. The speedup curve inherited its general shape from a combination of the LDLt speedup of Fig. 7 and the dashed line in Fig. 11. In addition, we remark that the Householder speedup of Fig. 12 outperforms the LDLt speedup of Fig. 12 when the size $n \gtrsim 16$. This fact can be explained by the fewer operations performed in LDLt which reduce the cache benefits of GPUs. However, when $n < 16$, the massive use of threads belonging to $\mathfrak {T_I}$ makes the LDLt speedup bigger than its Householder counterpart, which is more limited because it occupies a larger space in the shared memory. Moreover, compared with LDLt speedup at $n=4$, the Householder speedup does poorly and this can be explained by the fact that this method requires a larger memory copy between the shared and the global. The fact that Householder reduction executes more operations as well as needs more shared/global memory copies explains why the hybrid Householder solution is less effective than the collaborative one.

Fig. 12

Householder reduction + PCR: the speedup of CUDA/GPU implementation compared with OpenMP/CPU. This speedup is measured in terms of the number of solved systems per second

5 Divide and conquer algorithm for tridiagonal eigenproblems

5.1 Presentation of the algorithm and the references

We reuse here the Householder tridiagonalization of Sect. 4 as a first stage for the resolution of $A X = Y$ with A symmetric. This new resolution procedure is implemented through the following steps:

• We perform the tridiagonal Householder decomposition $A=QUQ^t$ where Q is orthogonal and U is symmetric tridiagonal.

• We use the divide and conquer algorithm for symmetric tridiagonal eigenproblems to establish the eigenvalues and eigenvectors of $U = ODO^t$ where O is orthogonal and D is diagonal. Consequently, we have $A=NDN^t$ where the orthogonal matrix $N = QO$.

• In the way that is usually done to solve a linear system with numerical singularities [29], we discard the smallest eigenvalues of D that provide a condition number larger than $10^5$.

Because the first step was already studied and the third step is quite standard, we are only interested by the divide and conquer part. This latter method goes back to the reference [12] and it became numerically sustainable, since the work presented in [19, 20]. In [13, p. 216], one can find a quite detailed presentation of divide and conquer algorithm for eigenproblems. Regarding a GPU version of this algorithm, the only works we know implement solutions for large matrices and use for that fine-grained parallel strategies involving both GPU ad CPU. In contrast to [8, 31], our GPU adaptation is dedicated to large number of small matrices and relies then on more effective coarse-grained parallel procedure.

As far as we are concerned, we study the important points that should be explored in our adaptation, which are the following:

• 1. Divide the diagonalization problem in two diagonalization subproblems with known diagonal factorization.

• 2. Solve the secular equation.

• 3. Use Löwner’s Theorem (see [13, 28]) for the stability of the overall procedure.

• 4. Perform a matrix multiplication to conquer the diagonalization problem from the diagonalized subproblems.

Let a matrix U given by (9), the first point would be to make the following division:

$$\begin{aligned} U= & {} \left( \begin{array}{cccc|cccc} d_1 &{} c_1 &{} &{} &{} &{} &{} &{} \\ c_1 &{} \ddots &{} \ddots &{} &{} &{} &{} &{} \\ &{} \ddots &{} \ddots &{} c_{m-1} &{} &{} &{} &{} \\ &{} &{} c_{m-1} &{} d_{m}-c_{m} &{} 0 &{} &{} &{} \\ \hline &{} &{} &{} 0 &{} d_{m+1} - c_{m} &{} c_{m+1} &{} &{} \\ &{} &{} &{} &{} c_{m+1} &{} \ddots &{} \ddots &{} \\ &{} &{} &{} &{} &{} \ddots &{} \ddots &{} c_{n-1}\\ &{} &{} &{} &{} &{} &{} c_{n-1} &{} d_{n}\\ \end{array}\right) \\&+\, c_m 1_{m,m+1} 1_{m,m+1}^t\nonumber \\= & {} \left( \begin{array} {c|c} U_1 &{} 0 \\ \hline 0 &{} U_2 \end{array}\right) + c_m 1_{m,m+1} 1_{m,m+1}^t \nonumber \end{aligned}$$

(15)

where $1_{m,m+1}=(0,\ldots ,0,1,1,0,\ldots ,0)$ with only the (m)th and $(m+1)$th coordinates equal to 1, and all the other coordinates are null. As assumed, $U_1$ and $U_2$ have known diagonal factorizations, i.e., there exist diagonal matrices $D_1, D_2$ and orthogonal matrices $O_1, O_2$, such that $U_1 = O_1D_1O_1^t$ and $U_2 = O_2D_2O_2^t$. Consequently, one can rewrite U as

$$\begin{aligned} U = \left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array}\right) \left( \left( \begin{array}{cc} D_1 &{} 0 \\ 0 &{} D_2 \end{array}\right) + c_m u u^t \right) \left( \begin{array}{cc} O_1^t &{} 0 \\ 0 &{} O_2^t \end{array}\right) \end{aligned}$$

where

$$\begin{aligned} u = \left( \begin{array}{cc} O_1^t &{} 0 \\ 0 &{} O_2^t \end{array}\right) 1_{m,m+1} = \left( \begin{array}{c} \text {last column of } O_1^t \\ \text {first column of } O_2^t \end{array}\right) . \end{aligned}$$

Denote now $\Lambda = \{\lambda _1, \ldots ,\lambda _n \}$ the ordered family of eigenvalues of $\left( \begin{array}{cc} D_1 &{} 0 \\ 0 &{} D_2 \end{array}\right)$. It is easy to show that if $c_m \ne 0$ and the eigenvalue $\lambda$ of U satisfy $\lambda \notin \Lambda$, then its value is obtained as a solution of the secular equation

$$\begin{aligned} \sum _{i=1}^n \frac{u^2_i}{\lambda _i - \lambda } + \frac{1}{c_m} = 0. \end{aligned}$$

(16)

The reference [26] provides a good summary on the different methods used for the solution of (16). It also proposes an hybrid procedure whose performances compete even with Gragg’s scheme [18] that has a cubic convergence. The major advantage of the hybrid scheme comes from the fact that it prevents additional computations due to the second order differentiation of the left term of equality (16).

Once we fix an eigenvalue $\lambda$ which is solution of (16), the eigenvector $V_\lambda$ of $\left( \begin{array}{cc} D_1 &{} 0 \\ 0 &{} D_2 \end{array}\right) + c_m u u^t$ is computed by

$$\begin{aligned} V_\lambda = \left( \left( \begin{array}{cc} D_1 &{} 0 \\ 0 &{} D_2 \end{array} \right) - \lambda I \right) ^{-1} \widetilde{u} \end{aligned}$$

(17)

where the vector $\widetilde{u}$ is defined in [19] and in [20] thanks to Löwner’s Theorem. Replacing u by $\widetilde{u}$ is quite important to ensure stability and sustainability of the algorithm, especially when some eigenvalues are almost equal.

Let us assume now that all eigenvectors $W = (V_\lambda )_{\lambda \text { eigenvalue of }U}$ are known. To conquer, we need to compute the eigenvectors of U using the product $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array}\right) W$. This last step is the heaviest numerically in the whole algorithm.

Finally, we voluntarily did not present the deflation that appears when $u_i$ or $\lambda _i - \lambda _{i+1}$ vanish numerically. This is due to the fact that deflation is already well presented in the references cited above and to the fact that deflation is not so important when matrices are small.

5.2 Adaptation and optimization

Let us study how the steps 1.$\rightarrow$4. should be and are implemented in our source code [24]. Because step 4. is the heaviest part, we start with it then we go decreasingly until the first step.

From step 3., we have at our disposal on the shared memory: the eigenvalues of U, the transpose matrix $W^t$ as well as $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right)$. Consequently, the computation of $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right) W$, at step 4., is done using $W^t\left( \begin{array}{cc} O_1^t &{} 0 \\ 0 &{} O_2^t \end{array} \right)$ then processing a transpose operation. Moreover, we do not need to transpose $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right)$ since $W^t\left( \begin{array}{cc} O_1^t &{} 0 \\ 0 &{} O_2^t \end{array} \right)$ involves the dot product of the rows of $W^t$ with the rows of $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right)$. Associating one thread for each row of the latter matrix, the memory access is coalescent during the successive multiplications. The result of the dot product performed by each thread is stored in the register memory, then it is copied, after a synchronization, to the shared memory space of each row of $W^t$. The complexity of step 4. is then $O(n^3)$, and we use $2n^2$ of the shared memory to perform the matrix multiplication. Because of the zeros in $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right)$, it is possible to decrease further the memory occupation but to the detriment of the readability of the code and shared memory bank conflicts.

From step 2., we have the eigenvalues of U and $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right)$ at our disposal on the shared memory. We would like to use one thread for the computation of each eigenvector of $\left( \begin{array}{cc} D_1 &{} 0 \\ 0 &{} D_2 \end{array}\right) + c_m u u^t$ to be stored in a column of W. This is performed thanks to expression (17) and each resulted eigenvector is saved in a row-form to keep the coalescent access of each thread. Subsequently, we obtain $W^t$ instead of W. The complexity of this step is $O(n^2)$, and it needs 3n shared memory space: n for the eigenvalues and 2n for both $\widetilde{u}$ and the diagonal $(D_1,D_2)$ involved in (17).

From step 1., we have the diagonal $(D_1,D_2), u$ and $\left( \begin{array}{cc} O_1 &{} 0 \\ 0 &{} O_2 \end{array} \right)$ at our disposal on the shared memory. Before starting the resolution of (16), we need to sort $(D_1,D_2)$ and build the ordered set $\Lambda = \{\lambda _1, \ldots ,\lambda _2 \}$. Although multithreaded, this sorting does not need to be optimized, because its complexity is at most $O(n^2)$. Moreover, the sorting result is stored in a new shared memory space of size n plus some variables stored temporarily in the memory space of $W^t$ (not used yet). Afterward, we solve (16) using Gragg’s scheme [18] that has the advantage of a cubic and monotonous convergence. The fact that this scheme requires a second order differentiation, of the left term of equality (16), is not an important drawback when the size n is small. In addition, because n is small, the complexity of the iterative Gragg’s scheme is rather $O(n^3)$ instead of $O(n^2)$, considered for big values of n.

Finally, we arrive to step 1. that represents the heart of the algorithm as it sets the division. One has then to choose a constant m and perform (15), such that $U_1$ and $U_2$ are already diagonalized. Otherwise, we have to reiterate the division (15) for $U_1$ and $U_2$ separately and so on till reaching a division that has a diagonal factorization. Assume now that for all $m \in \{2,\ldots ,n-2\}$, we do not know yet the diagonal factorization of $U_1$ and the diagonal factorization of $U_2$. What is then the best choice to do on the value of m?

There are two answers to the previous question depending on whether there exists $m_0$ such that $c_{m_0}=0$ or not:

• If yes, then set $m=m_0$. Moreover, we re-apply directly (15) on the sub-matrices.

• If no, then set $\displaystyle m=\lfloor n/2 \rfloor$ where $\lfloor \cdot \rfloor$ is the floor function i.e. For each real number $x, \lfloor x \rfloor = \sup \{ a \in \mathbb {Z} ; a \le x\}$.

The yes case is obvious, since the original linear system can be decomposed, without conquering, in two independent systems. Regarding the no case, the choice is set in such a way that the computations induced by each subproblem is comparable with the other. To make this latter fact possible, the best way is to impose the same size ($\pm 1$) for both problems.

To simplify the comparison between the Householder tridiagonalization and the divide and conquer algorithm, we consider only matrices with $c_m \ne 0$ for all $m \in \{1,\ldots ,n - 1\}$. Our division is then performed using the scheme given in Fig. 13 till reaching matrices of dimension $1\times 1$ or $2\times 2$ for which the diagonal form can be obtained easily. This division scheme requires an extra shared memory storage of size $2^{1+\lfloor \log _2(n-1) \rfloor }$, but it provides a pure divide and conquer algorithm (not a combination of divide and conquer with another method like QR). In particular, this pure divide and conquer prevents to have eigenvalues of multiplicity bigger than two at each conquering step.

Fig. 13

The division scheme

Thanks to what is explained above, it is not difficult to conclude that the overall shared memory occupation is given by $2n(n+2)+2^{1+\lfloor \log _2(n-1) \rfloor }$. In addition, the complexity t of the proposed implementation can be computed because of the induction

$$\begin{aligned} t(m) = 2t(m/2) + \alpha (m) m^3,\quad m \in \{2,\ldots ,n\} \end{aligned}$$

(18)

with $t(1)=1$ and $\alpha (m)$ is a decreasing sequence that is bigger than 2 for the sizes considered in this paper. Using (18), we check that $t(n) \le \frac{\alpha (n)4}{3} n^3$.

In Algorithm 3, we summarize the different steps of our divide and conquer implementation dedicated to small tridiagonal matrices. Without loss of generality, we assume that the first off-diagonal does not have any vanishing term. Otherwise, we have only to divide the original eigenproblem into various sub-eigenproblems. In Algorithm 3, we also simplify the matrix components’ notation from $A=(A_{i,j})_{m \le i,j\le M}$ to $A=(A_{m \le i,j\le M})$.

5.3 Comparison with Householder tridiagonalization

The complexity of the divide and conquer algorithm is generally considered as similar to the one of Householder tridiagonalization for large matrices (see [13]). This is not the case in our examples, because we deal with small ones (size does not exceed 64).

Moreover, the divide and conquer algorithm suffers from divergence problems when implemented on GPU. Indeed, the need for deflation in some cases can lead numerous threads to wait. The necessary use of more synchronization in this algorithm also reduces the performance. For instance, the resolution of the secular equation is iterative and, therefore, makes some threads wait for the others.

All the facts mentioned above justify the results obtained in Fig. 14. In particular, we see that for the largest matrices, $48 \le n \le 64$, the divide and conquer takes at most three $\times$ the execution time of a Householder collaborative factorization.

Fig. 14

The execution time of the divide and conquer when compared with the Householder tridiagonalization

6 Conclusion and future work

In this work, we explained the importance of proposing a GPU solution for large number of small systems, and we advocated it using a topical problem in mathematical finance. Because the small systems can be random, our goal was to know if the use of Householder tridiagonalization with divide and conquer is the best solution when we suspect the linear systems to be ill-conditioned.

The safest answer we provided is to first check the residual using Householder tridiagonalization + PCR. If the really fast PCR is not sufficient, performing a divide and conquer diagonalizations and discard the smallest eigenvalues becomes mandatory. If we are sure that the systems are well conditioned, then we just process an LDLt decomposition. If we are sure of the converse, we execute directly a combination of Householder tridiagonalization and divide and conquer diagonalization.

In addition to this answer, we explored, in terms of speedup and memory occupation, what we loose when we use the safest strategy instead of the simplest one based on LDLt. This study required us to implement and optimize our own code, since the work available in the literature is dedicated to large systems and thus not efficient for large number of small systems.

Beyond the source code and the main results above, we gave also some insights on various points including:

• A new version of PCR that can be used for any vector size and not only a power of two.

• A hybrid optimal LDLt that combines a good balance between communicating and independent threads.

• As Householder reduction involves more operations as well as needs more shared/global memory copies, its hybrid version is not optimal.

• Even though the non-optimality of the SIMD versions maybe obvious for systems larger than 16, it is not for tiny systems smaller than 16. Thus, we quantified to which extent the SIMD versions are not optimal.

• Comparison of the performance of our CUDA/GPU LDLt and Householder solutions to the standard OpenMP/CPU implementation.

• Although the divide and conquer is theoretically well suited to parallel architectures, the divergence within each wrap created by deflations reduces its benefit for small matrices.

As a future work, we plan to explore the accuracy of each method by studying the rounding errors and error propagation. For that, we aim to present a sufficiently consistent study of the residue errors as well as compare the results of CADNA [25] software obtained from the various solutions.