Keywords

1 Introduction

Multistability, i.e. the presence of multiple co-existing locally stable equilibria, is a critical concept in nonlinear dynamics, which has numberless and deep implications in biology and medicine. Two fields of biomedicine where this concept is increasingly gaining prominent are immunology and molecular biology. In the latter, in particular, the word bistability has became of quite common use also among experimental scientists.

For several decades the vast majority of mathematical epidemiology research has focused on monostable systems, and on their well-known paradigm that can be summarized as follows: there is an appropriate threshold parameter, often termed the reproduction number (RN) of the model, such that if the RN is smaller than one then the disease-free equilibrium (DFE) is unique and globally attractive, whereas if the RN it is larger than one then the DFE is unstable and a unique endemic equilibrium (EE) appears. Most often the EE is also globally attractive, in other cases, though far less frequently, it is surrounded by self-sustained oscillations [18].

In last twenty years, however, it has been shown that certain feedback loops, such as those stemming from vaccine imperfection or waning, may complicate this scenario since they may induce the onset of bistability through so called “backward bifurcations” (BB). This type of bifurcation is typically characterized as follows: there is a value \(b \in (0,1)\) such that, although the DFE is locally asymptotically stable (unstable) for \(RN<1\) (\(RN>1\)), nevertheless for values of the RN in the interval (b, 1) there are two endemic equilibria: one unstable and the other one locally stable. Therefore, for \(b<BRN<1\) bistability occurs, with the birth at \(RN=b\) of an endemic equilibrium that co-exists with the stable DFE. Note that for \(RN>1\) the DFE still exists but becomes unstable. This makes the BB deeply different from the more known hysteresis bifurcation, where there never is the coexistence of an even number of equilibria. Backward bifurcations have been found initially in a number of simple epidemic models [8, 16, 22, 23], in particular in models for infections without immunity, as the susceptible-infective-susceptible (SIS) model, when the vaccine is imperfect [23]. There is evidence that the phenomenon is also frequent in more realistic models, so that BB are also becoming important, due to their negative implications for infection elimination, from the public health viewpoint [20].

Classical epidemiological models are built upon some founding principles, namely the law of mass action of statistical mechanics, which is used to model at once social contacts between individuals and infection transmission. Though critical in promoting the take off of mathematical epidemiology as a discipline, the law of mass action is a gross simplification or reality whereby individuals entering into social contacts are represented as “collisions” between the particles of a perfect gas. This in turn implies that social contacts and transmission parameters are dealt with as “universal constants” which are therefore unaffected by e.g. the states of the infection and the disease. Said otherwise, individuals would continue to come into contact at the same rate, irrespective of how low or high is the risk of acquiring the infection, or of dying from it, that they might perceive from the available information on current and past infection prevalence and seriousness. The idea that human behavior is static is far distant from the reality and constitutes one of the strongest limitation of traditional epidemiological models. By their intimate nature, human beings are neither static nor passive. Changes in humans’ behavior in response to infection threats are indeed well documented already in outbreaks in historical epochs (where however they mostly occurred in the form of community-enforced measures), but seem to be a rule ([15] and references therein) in current societies, possibly stemming from the continued progress of scientific knowledge on diseases and communications technologies [6]. Modern individuals can therefore spontaneously change in a complicate manner their social behavior in response to a pandemic threat, as well documented for the 2009 H1N1 pandemics [15], or can shift their sexual activity towards partners that are perceived as being as less-at-risk in response to news about a threatening STI [21]. But they might also decide not to vaccinate their children after having compared perceived costs and benefits of a vaccination program, or to stop vaccinating after a rumour, thereby threatening the success of the program, as it has been the case for the pertussis whole-cell vaccine scare, and the persistent decline in MMR vaccine coverage in the UK due to the alert for the suspected relation between MMR and autism ([6] and references therein). From the latter standpoint human behavior is representing an increasing challenge not only for modelers but also for public health policies. Indeed, depending on not-easy-to-predict circumstances, the effects of human behavior on infection dynamics can range—and switch—from policy-enforcing to policy-threatening [7].

The importance of human behavior for the understanding of infection dynamics and for the development of resilient policy interventions has led in the last fifteen years to the take-off of the new branch that we termed the behavioral epidemiology (BE) of infectious diseases [6]. A major area of current behavioral epidemiology of infections deals with immunization choices, particularly in relation to childhood vaccine preventable infections. This interest in motivated not only by the aforementioned vaccine crises related to the big “vaccine scares” but also by the dramatically changed context of mass immunization in modern societies. This epochal change is the consequence of decades of successful mass immunization against traditionally threatening infections, within the overall changed landscape of infectious diseases in industrialized countries, due to the continued success of man in controlling diseases threats thanks to medical progress [6]. A major implication of these successes is for example the full overturning of perceived risks [28], with the perceived risk of vaccine adverse events becoming the major determinant of vaccination [12].

After a few forerunners [6, 17, 19], the last epoch has seen an explosion of studies of the interplay between the diffusion of information about perceived risks due to the infection on the one hand, and risks of vaccine adverse events on the other hand, and the infection dynamics and control. These investigations have resorted to a variety of different approaches, either “behavior implicit” or “behavior explicit” based e.g. on game-theoretic or other representations of behavior, to unfold the complicate relationship between human choices and infection control (e.g. [3–5, 10–14, 24–27, 29, 30] and references therein).

However, in this fast growing literature on the behavioral epidemiology of vaccination no studies have investigated, to the best of our knowledge, the dynamic implications of vaccinating behavior within the framework of models for imperfect vaccines showing backward bifurcations. Given the peculiar role played by vaccine characteristics in promoting or not BBs, it is of interest to investigate whether the interplay between vaccinating behavior and imperfect vaccines might trigger further interesting dynamic phenomena.

In this paper we study a model including a simple behavioral assumption about vaccination within one of the simplest framework capable to yield a backward bifurcation, namely the SIS model with imperfect vaccination (SISV) by Kribs-Zaleta and Velasco-Hernandez [23]. In particular vaccinating behavior is incorporated following the “behavior implicit” [6], phenomenologically-based, formulation proposed in [10] where the vaccine uptake at birth is specified as an increasing function of current infection prevalence.

2 The SISV Model with Prevalence-Dependent Vaccine Uptake and Its Disease-Free Equilibrium

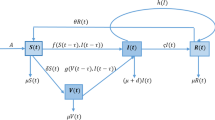
The modelling framework considered is that of a stationary and homogeneously mixing population where an infection without immunity can be controlled by immunization at birth (instead than [23] who considered vaccination at constant rate). The vaccine is assumed to be “imperfect” i.e. protection wanes over time and moreover vaccinated subjects can acquire infection, though at a reduced rate compared to fully susceptible individuals. Vaccination is assumed to be voluntary according to a prevalence-dependent schedule \(p(I) \in [0,1]\), where I denotes the relative infection prevalence and p an increasing function with \(p(0)\ge 0\). This formulation [10] amounts to assume that parents decide to vaccinate or not their children depending on the perceived risk of infection, possibly measured by the publicly available current information on infection prevalence. Though oversimplified, because behavior-implicit, this model can be shown to be consistent with more refined behavioral schemes, for example with a prevalence-dependent behavior-explicit vaccination schedule based on an imitation process [4], provided the social spread of behavior is fast compared to other processes [13]. These hypotheses yield the following SISV model:

$$\begin{aligned} S^{\prime }&= \mu (1-p(I)) -\mu S - \beta I S +\gamma I + \theta V, \nonumber \\ I^{\prime }&= I \left( \beta (S + \sigma V) -(\mu +\gamma ) \right) , \\ V^{\prime }&= \mu p(I) - \sigma \beta I V - (\mu +\theta ) V\nonumber \end{aligned}$$
(1)

where: S, I, V, \(S+I+V=1\), respectively denote the fractions of susceptible, infective, and vaccinated individuals, \(\mu \) denotes both the death and birth rates (taken equal to ensure that the population remains stationary over time), \(\beta \) the transmission rate for naive susceptibles, \(\sigma \beta \) (\(0<\sigma <1\)) the reduced transmission rate for vaccinated subjects, \(\gamma \) the rate of recovery from infection, \(\theta \) the vaccine waning rate. By the equality \(S+I+V=1\) one of the model equations can be eliminated yielding a 2-dimensional system. Using \(S=1-(I+V)\) we get:

$$\begin{aligned} I^{\prime }&= \beta I \left( p_{cr} - I - (1-\sigma ) V \right) , \end{aligned}$$
(2)
$$\begin{aligned} V^{\prime }&= \mu p(I) - (\mu +\theta + \sigma \beta I) V \end{aligned}$$
(3)

In (2) the constant \( p_{cr} \) is the critical immunization threshold [1] for infection elimination by a (hypothetical) perfect vaccine, in absence of behavioral effects:

$$ p_{cr} = 1- \frac{1}{R_0} $$

where \(R_0= \beta /(\mu +\gamma ) \) denotes the basic reproduction number of the infection, representing the number of secondary infections caused by a single infective case in a wholly susceptible population (therefore in the absence of any immunization).

As a preliminary step, note that from the differential inequality

$$ I^{\prime } \le \beta I (p_{cr} - I) $$

it is trivial to show that it asymptotically holds:

$$ 0< I(t) <p_{cr}. $$

Thus in the following we shall study system (2) and (3) in the set

$$ A = \left\{ (I,V) | I \in [0,p_{cr}] \ AND (V,I) \ge (0,0) \ AND \ I+V \le 1 \right\} $$

System (2) and (3) always admits the following disease free equilibrium (DFE):

$$ DFE = \left( 0, \frac{\mu }{\mu +\theta }p(0) \right) .$$

A linearization of system (2) and (3) straightforwardly yields that the local asymptotic stability (LAS) of the DFE is governed by the equation:

$$ i^{\prime } = \beta i \left( p_{cr} - (1-\sigma ) \frac{\mu }{\mu +\theta }p(0) \right) . $$

This means that the DFE will be LAS if the following condition holds:

$$\begin{aligned} p(0)> p_{cr}\frac{1}{1-\sigma }\left( 1 + \frac{\theta }{\mu }\right) , \end{aligned}$$
(4)

which can also be reformulated as \(R_V <1\) where \(R_V\) is the vaccine reproduction number:

$$\begin{aligned} R_{V} = R_{0} \frac{\theta + \mu (1-p(0)) + \sigma \mu p(0)}{\theta + \mu }, \end{aligned}$$
(5)

Condition (4) states that the local stability of the DFE requires that the “zero-prevalence” vaccine uptake, i.e. the vaccine uptake that spontaneously arises under conditions of minimal perceived risk of infection, must exceed the critical elimination threshold \(p_{cr}\) by a factor \((1-\sigma )^{-1} (1 + \theta /\mu )\). Note that this factor is increasing in both parameters (\(\sigma \) and \(\theta \)) tuning the degree of “imperfection” of the vaccine. Suppose now that the average length of vaccine-induced immunity (\(\theta ^{-1}\)) is significantly smaller than the average lifespan \(\mu ^{-1}\). In such a case, condition (4) might be fulfilled only for diseases that in the same time: (i) are characterized by a low critical threshold; (ii) can induce, also when their prevalence is low, a large perceived risk. This condition extends to the present SISV model the result that in our past work on behavior-implicit SIRV models we termed “elimination: mission impossible” [13].

In order to proceed further, let us rewrite system (2) and (3) in the following equivalent form that we will adopt in the next sections:

$$\begin{aligned} I^{\prime }&= \beta (1-\sigma ) I \left( L(I) - V \right) , \end{aligned}$$
(6)
$$\begin{aligned} V^{\prime }&= (\mu +\theta + \sigma \beta I) \left( \Psi (I) - V \right) \end{aligned}$$
(7)

where:

$$ L(I) = \frac{ p_{cr} - I}{(1-\sigma )} $$

is the nullcline \(I^{\prime } = 0\); and:

$$ \Psi (I) = \frac{ \mu p(I)}{(\mu +\theta + \sigma \beta I)} $$

is the nullcline \( V^{\prime } = 0\).

Endemic equilibria of (6) and (7) are the non-trivial intersections of the two nullclines.

3 Instability of the Disease-Free State: Mono Versus Multistability

In this section we shall assume that the baseline vaccination rate \(\mu p(0)\) is not sufficient to guarantee the elimination of the infection, i.e. we shall assume that

$$\begin{aligned} 0<p(0)< p_{cr}\frac{1}{1-\sigma }\left( 1 + \frac{\theta }{\mu }\right) . \end{aligned}$$
(8)

Note preliminarily that in the case of prevalence-independent vaccine uptake the following result holds:

Lemma

If p(I) is constant and (8) holds then (6) and (7) admit a unique endemic equilibrium point.

We now show that if \(\Psi \) is non-monotonic then there may be either a single or multiple equilibrium points.

As a first step, note that the local stability properties of all endemic equilibria of (6) and (7) depend on the following characteristic polynomial

$$\begin{aligned} \lambda ^2+(\mu +\theta +(1+\sigma )\beta I_e) \lambda + \beta I_e (\mu +\theta +\sigma \beta I_e)\left( 1 + (1-\sigma )\Psi ^{\prime }(I_e)\right) , \end{aligned}$$
(9)

The condition for the local stability of endemic states therefore reads as follows:

$$\begin{aligned} \Psi ^{\prime }(I_e) > -\frac{1}{1-\sigma }. \end{aligned}$$
(10)

i.e.

$$\begin{aligned} \Psi ^{\prime }(I_e) > L^{\prime }(I_e). \end{aligned}$$
(11)

The interpretation of condition (10) is immediate: if the linearized nullcline \(V^{\prime }=0\) at a generic endemic equilibrium (EE) of (6) and (7) is steeper than the linearized nullcline \(I^{\prime }=0\) at EE, then that particular endemic state EE is LAS, otherwise it is unstable.

As far as the V-nullcline \(\Psi (I)\) is concerned, it is worth to note that:

Lemma

Under condition (8), if \(\Psi (I)\) is monotone, i.e. if

$$ \mu p^{\prime }(I)> \sigma \beta \Psi (I) \ OR \ \mu p^{\prime }(I)< \sigma \beta \Psi (I), $$

or constant then system (6) and (7) has a unique equilibrium point.

Note, however, that uniqueness of the endemic state can also occur for some non-monotone \(\Psi (I)\).

If there is a unique endemic equilibrium point, the following proposition holds:

Proposition

If system (6) and (7) has a unique equilibrium point \(EE_u\) then it is globally stable in A.

Proof

First, it is straightforward to verify that \(EE_u\) cannot be unstable, otherwise it could not be the unique endemic equilibrium. Then, denoting as F the bi-dimensional vector field associated to system (6) and (7) and applying the Dulac–Bendixon theorem with weigth function 1 / I one gets:

$$ div\left( \frac{1}{I} F \right) = -\beta - \sigma \beta -\frac{\mu +\theta }{I} <0. $$

   \(\square \)

A necessary condition for the presence of multiple co-existing endemic equilibrium points, i.e. for endemic multistability, is that the V-nullcline \(\Psi (I)\) is non-monotone. Depending on the parameters of the system, for example \(\sigma \) or c, which are embedded in the functions L(I) and \(\Psi (I)\) these equilibria can vary, thus determining hysteresis or pitchfork bifurcations (see next subsection for a noteworthy example).

Note that the type of bifurcation described here differs from the backward bifurcation phenomenon well known in mathematical epidemiology. Indeed the backward bifurcation describes the onset of bistability where one of the two co-existing locally stable equilibria is the disease-free equilibrium. Here, instead all the coexisting LAS equilibria are endemic equilibria. In the next subsection we will develop the relevant bifurcation analysis based on a particular form of the vaccine uptake function p(I).

3.1 Bistable Endemicity Induced by a Linear-Saturated Vaccine Uptake p(I)

Let us consider the following linear-saturating vaccination rate:

$$\begin{aligned} p(I) = min( p(0) + c I,1) \end{aligned}$$
(12)

which increases for

$$ 0< I< I_*(c) = \frac{1-p(0)}{c}$$

and is constant thereafter.

It follows that for \( I > I_*(c)\) the function \(\Psi (I)\) is a decreasing hyperbolic function:

$$\begin{aligned} \Psi (I) = \frac{\mu }{\mu +\theta +\sigma \beta I} \end{aligned}$$
(13)

which does not depend on c. The latter fact is of relevance when considering c as the bifurcation parameter. Instead, for \( 0< I< I_*(c)\) the function \(\Psi (I)\) depends on c as follows:

$$\begin{aligned} \Psi (I) = \frac{\mu (p(0)+c I)}{\mu +\theta +\sigma \beta I} \end{aligned}$$
(14)

This implies that the condition for \(\Psi \) to be increasing in \( 0< I< I_*(c)\) is

$$ c > \sigma \beta \frac{p(0)}{\mu +\theta } .$$

Finally, if \(\Psi (I)\) is increasing in \( 0< I< I_*(c)\) then the condition for bistability is that the two solutions of the following equation

$$\begin{aligned} \frac{\mu }{\mu +\theta +\sigma \beta I}= \frac{p_{cr}-I}{1-\sigma } \end{aligned}$$
(15)

are both larger than \(I_*(c)\).

Taking c as the bifurcation parameter, makes it the analysis of the system quite simple. Note preliminarly that if the Eq. (15) has no real positive solutions (i.e. if the hyperbolic function (13) does not intersect the nullcline L(I)) then there is only a unique endemic equilibrium. The other case is that the hyperbolic function (13) intersect the linear nullcline L(I) in two points of positive abscissae \(I_{l}\) and \(I_{h} > I_{l}\). If

$$ I^*(c) \in (I_{l} , I_{h}) $$

then there is again a unique endemic equilibrium with

$$ I_e = I_{h}, $$

i.e. independent of c. On the contrary if

$$ I^*(c)< I_{l} $$

i.e. if

$$\begin{aligned} c> c_{l} = \frac{1-p_0}{I_{l}} \end{aligned}$$
(16)

then there is multistability with three co-existing endemic equilibria: (i) \(I_{h}\) which is LAS and constant, thus independent of c; (ii) \(I_{l}\) which is unstable and again constant, thus independent of c; (iii) a third equilibrium point \(I_{small}(c)\) that is LAS and decreasing function of c, with

$$ I_{small}(c_l) = I_{l}. $$

Finally, note that condition (16) for multistability is equivalent to state that

$$\begin{aligned} \Psi (I^*(c))> L(I^*(c)). \end{aligned}$$
(17)

In order to consider the role of \(\sigma \) as bifurcation parameter, it is useful to define the following functions

$$ (\Psi _1(I; \sigma ),L_1(I))=(1-\sigma )(\Psi (I),L(I)) $$

which have the following properties: \(L_1(I)\) does not depend any more on \(\sigma \), whereas \(\Psi _1(I;\sigma )\) is a strictly decreasing function of \(\sigma \).

As a consequence, let us consider a pair \((c_0,\sigma _0)\) where \(c_0 <c_{l}(\sigma _0)\). In such a case we have the above mentioned three equilibria, which also depend on \(\sigma \). If one increases \(\sigma \) then the function \(\Psi _1(I;\sigma )\) is pushed downward, the equilibrium \(I_{h}(\sigma )\) increases whereas the other two initially get closer and then both disappear. In other words we are describing a scenario of a classical hysteresis bifurcation (Figs. 1 and 2).

Fig. 1
figure 1

Impact of the behavior-related parameter c on the number and location of endemic equilibria. In all panels \(\sigma = 0.333\). Left panel for \(c=200\) the system exhibits three co-existing equilibria, as resulting from the intersection for the curves \(\Psi _I(I)\) and \(L_I(I)\); Central panel for \(c=10\) the central and the left endemic equilibria disappeared, whereas the right equilibrium was not affected at all by the change in the value of c; Right panel the full bifurcation diagram. Note that not only the largest equilibrium is constant, but also the central one (when it exists, i.e. for \(c>c_{l}\))

Full size image
Fig. 2
figure 2

Impact of the parameter \(\sigma \) on the number and location of endemic states: bifurcation diagram in the form \(I_e\) vs \(\sigma \), under \(c = 200\)

Full size image

4 Local Stability of the Disease-Free: Global Stability Versus Backward Bifurcations

In this section, for the sake of mathematical completeness, we shortly consider the issue of backward bifurcations, which is expected to occur in our model due to its SISV structure. We therefore focus on the case where the disease-free state is locally stable, i.e. the case where:

$$ p(0)> p_{cr}\frac{1}{1-\sigma }\left( 1 + \frac{\theta }{\mu }\right) ,$$

or equivalently

$$\begin{aligned} \Psi (0)> L(0). \end{aligned}$$
(18)

First let us consider the case where the DFE is the unique equilibrium. Not surprisingly, the following proposition holds:

Proposition

If \(\Psi (I)\ge L(I)\), i.e. if DFE is the unique equilibrium, then DFE is also Globally Asymptotically Stable (GAS) in A.

Proof

Let us define the following set:

$$ B= \left\{ (I,V) \in A | V \ge L(I) \right\} .$$

It is straightforward to show that if

$$\Psi (I)\ge L(I),$$

then B is a positively invariant set. The GAS of DFE in B then immediately follows by the following LaSalle–Liapunov function:

$$ \mathcal{L}(I)=I. $$

   \(\square \)

Remark

The above GAS condition yields:

$$ p(I)>\frac{(p_cr-I)(\mu +\theta +\sigma \beta I)}{\mu (1-\sigma )}, $$

i.e. if the vaccination behavioral response function is greater than the LHS function, then the global eradication is reachable.

Note however that, still under (18), if the two nullclines intersect then (excluding the trivial case of tangency) there must be an even number of intersections, as it follows by applying elementary analysis to the function

$$ D(I) = \Psi (I) - L(I) .$$

Thus we are dealing again with a multistable case where however one of the LAS equilibrium states involved is represented by the disease-free equilibrium. Therefore, the related bifurcation which appears when, due to appropriately varying the model parameters, the system makes a transition from the situation where the DFE is the unique and globally asymptotically stable equilibrium to such type of multistability is exactly a “backward bifurcation” of the type described for SISV systems in [23].

5 Concluding Remarks

In relation to the current epoch of development of behavioral epidemiology [25], a large part of the modeling investigations of the potential effects of immunizations choices on the dynamics and control of infectious diseases have focused on the case of vaccine preventable infections, such as measles, which confers permanent immunity. Consequently most efforts in the literature have concentrated on susceptible-infective-removed (SIR) frameworks [3–5, 9–14, 24–26, 29, 30], see also the review in [6] about the historical development of the subject, and references therein. In relation to this, much of the emphasis has concentrated, though not exclusively, on the issue of the difficulty to eliminate the infection, and possible ways to prevent this drawback, and on the complicate dynamic patterns (e.g. oscillations) that can be triggered by more appropriate, both behavior-implicit and explicit, modeling of individual behavioral responses. This emphasis on traditional vaccine preventable SIR-type infections by no means exhausts the range of infections for which complicate behavioral responses by agents might be triggered by the introduction of a vaccine. Many other important infections conform instead to the SISV-type framework that has been considered in this paper. Among the many instances in relation to this there are for example bacterial infections, such as Meningococcal Meningitis. Though characterised by a complex epidemiology, Meningococcal Meningitis does not impart immunity and both vaccines that have been introduced to protect against the two Meningococci types widely circulating in Europe, namely groups C and B, are “imperfect”. Another critical example, though based on a more complicate model structure, is tuberculosis [20]. As demonstrated in this paper the introduction of even the simplest possible hypothesis about human behavior, namely that of a behavior-implicit, prevalence-dependent vaccine uptake function, is capable to enrich the spectrum of possible dynamical behaviors of SISV-type models, by adding to the possibility of multi-stability on the sub-threshold side, the further possibility of multistability on the above-threshold side. The practical meaning of this finding is that the presence of agents’ behavioral responses to the introduction of the vaccine might cause the appearance and coexistence of a number of stable (over appropriate basins) endemic states. This was to our knowledge the first theoretical investigation in this direction, based on a very simple, almost trivial, hypothesis on the agents’ behavioral response. The follow-up of this first effort should therefore acknowledge a number of realistic features that just for the sake of simplicity had been neglected here. First of all one should, still within the boundary of behavior implicit models, consider the effects of time-delays, both in information supply and agents response, as opposed to the instantaneous adaptation of behavior postulated in this paper. These time-delays can generate complicate dynamical patterns even under simpler modeling frameworks, as the SIR model with information-dependent delay [10]. Even more interesting would be the inclusion of more structured, namely behavior explicit, behavioral responses, through e.g. imitation processes or their extensions [4, 5, 13, 14], or game-theoretic frameworks [2, 3, 27, 29, 30].