Computer-Aided Bifurcation Analysis for a Novel Car-Following Model with Relative Velocity Effect

Abstract

The global behaviour of mathematical models for traffic flow is important in order to understand their characteristics because of the bistable property observed in real traffic. This bi-stability can be discussed in a bifurcation analysis. In fact, bifurcation analysis of optimal velocity models in several studies has revealed the global bifurcation structure of the model, which shows a loss of stability due to the Hopf bifurcation and bistable property. Shamoto et al. proposed a novel car-following model with relative velocity effect (STNN model), which was not introduced into the optimal velocity model, but is important in real traffic scenarios. They discussed the linear stability of homogeneous traffic flow; however, they did not reveal the global bifurcation structure of the STNN model. In this paper, we numerically investigated the global bifurcation structure of the STNN model and observed that the strength of the relative velocity effect drastically changes the bifurcation structure. This result provides a possibility of implementing (semi-)automatic driving systems to alleviate traffic jams.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Various types of self-driven particle systems, such as vehicular traffic and pedestrian dynamics, have attracted a great deal of attention during the last few decades in a wide range of fields, such as natural sciences, applied sciences, and engineering, for the potential practical use of investigation results [2, 5, 9]. Especially, a better understanding of traffic flow has been achieved by developing sophisticated mathematical models. One of the common goals among these modelling approaches is to understand the spontaneous occurrence of traffic jams when the average density of vehicles exceeds a certain critical value. This transition in flow behaviour is considered as a dynamical phase transition and can be discussed in terms of instability of homogeneous flow. That is, jamming flow occurs as a result of the instability of homogeneous traffic flow due to fluctuations of the driving behaviour over the critical density; the instability leads to the transition of the homogeneous traffic flow to a jamming flow due to enhancement of fluctuations.

Linear stability analysis is very useful for detecting critical density. As the loss of stability is often accompanied by a bifurcation, one may expect a jamming flow to exist. The linear stability analysis, however, does not provide any information regarding a bifurcating solution. It is important to understand the global bifurcation structure of periodic solutions bifurcating from the critical density because bi-stability, which is regarded as one of the characteristics of transition to a jamming flow, is not a local property. Moreover, the features of a global bifurcation structure provide us with hints for controlling traffic flow by changing the parameters of a model. Thus, global bifurcation analysis is important from both theoretical and practical viewpoints. Several researchers have investigated the global bifurcation structure of a car-following type model by describing the dynamics of N vehicles on a circular road via special continuation codes [4, 6,7,8].

Gasser et al. [4] focused on an optimal velocity (OV) model, which is described as

$$\begin{aligned} \frac{d^2}{dt^2} x_j(t)&=a\Bigl \{V(h_j(t))-\frac{d}{dt}x_j(t)\Bigr \}, \end{aligned}$$

(1)

where $x_j~(j \in N)$ and $h_j=x_{j+1}-x_j$ are the position of the jth vehicle, and the headway distance between the jth vehicle and the vehicle in front, respectively. The function $V(h_j)$ is called the OV function, which provides an ideal velocity decided by the headway. This model (Eq. 1) was originally proposed by Bando et al. [1], and they considered the OV function as $V(h)=\tanh (h-2)+\tanh (2)$. In [4], they proved that the loss of stability is generally due to a Hopf bifurcation, and they analytically showed a quantity related to the first Lyapunov coefficient of the bifurcation, which determine if Hopf bifurcation is supercritical or subcritical for general OV function satisfying a few basic properties. This result mentioned that the type of Hopf bifurcation depends on the OV function, length of the circuit, and the number of vehicles. Moreover, they numerically investigated the global bifurcation structure for periodic solutions and revealed a complete picture of OV model dynamics. From these numerical results, the behaviour of a Hopf bifurcation is locally supercritical, but macroscopically subcritical under some situations, i.e., the OV model shows bi-stability. One of their conclusions was that the Hopf bifurcation is not necessarily subcritical, which depends on the optimal velocity function. Moreover, they concluded that a stable periodic solution may (co-)exist even in the stable region; in particular, this coexistence does not depend on the type of Hopf bifurcation, but on the global bifurcation structure.

Orosz et al. [6,7,8] proposed a novel OV model with driver reaction time delay, which is described as

$$\begin{aligned} \frac{d^2}{dt^2} x_j(t)&=a\Bigl \{V(h_j(t-\tau ))-\frac{d}{dt}x_j(t)\Bigr \}, \end{aligned}$$

(2)

where $\tau$ is the reaction time of the drivers in perception, which is different from the relaxation time $T=\frac{1}{\alpha }$ in action to adjust the vehicle’s velocity. They also showed the loss of stability due to Hopf bifurcation and the global behaviour of the system (Eq. 2) numerically, although their computational technique was different from the one in [4] because of the delay effect. As a result, they also observed branches of oscillating solutions connecting Hopf bifurcation points, where the OV function determines whether the Hopf bifurcation is supercritical or subcritical, and then they revealed the existence of the regions of bi-stability.

These investigations are very significant in order to understand the complete picture of each traffic model in detail; however, these models did not consider the relative velocity effect, and the parameters in these models were difficult to be estimated by real experiments, i.e., difficult to be controlled in practical use. Thus, in this paper, we investigate the global bifurcation structure of a model proposed by Shamoto et al. (STNN model) [10], in which the relative velocity effect is introduced, and the parameters are estimated by real experiments. Moreover, we show the changing the global bifurcation structure based on variation in the relative velocity effect as a possibility of the strategy to alleviate traffic jams, as the strength of relative velocity effect is varied.

This paper is organised as follows. In Sect. 2, we briefly review the STNN model proposed by Shamoto et al. [10] and modify the model to a suitable form for use with numerical bifurcation algorithm in AUTO [3]. The computational results are shown in Sect. 3. Finally, Sect. 4 is devoted to the concluding discussions.

2 STNN Model and Its Rewritten Form

Recently, Shamoto et al. proposed a novel car-following model (STNN model) in [10], which takes into account the relative velocity effect. Their model is described in the following form :

$$\begin{aligned} \frac{d}{dt} v_j&=a-b\frac{v_j}{(h_j-d)^2}\exp \Bigl (-c\varDelta v_j\Bigr )-\gamma v_j, \end{aligned}$$

(3)

where a, b, c, d and $\gamma$ are positive parameters. The parameter a represents the maximum acceleration. The initial acceleration of the vehicles, when they start to move forward, is determined by a. The parameter d indicates the headway when vehicles stop completely. The other parameters b, c, and $\gamma$ denote the strength of interaction with the vehicle in front, the weight of the relative velocity effect, and the strength of friction, respectively. The advantages of the STNN model are that it is experimentally accessible, and it is easy to understand the physical meaning, although the model has only five parameters. Actually, the parameter values were estimated by circuit experiments in [10]. They mentioned that their model showed a metastable homogeneous flow around the critical density from the linear stability analysis. That is, if the traffic density exceeded the critical density, the homogeneous flow became unstable because of a small perturbation that changes into another branch (a jamming flow). However, their results are local and do not give us any insight into the stability of the other branch and the changes in the global bifurcation structure, as a parameter is varied. We thus use the software AUTO [3] to numerically obtain and investigate the global behaviour of their model (Eq. 3).

The STNN model in the periodic system has a continuous family of solutions corresponding to the homogeneous traffic flow due to the translation symmetry. This feature is unsuitable for analysis by using AUTO, as AUTO can follow only a one-parameter family of solutions.

Fig. 1

The definition of the variables $y_j$ to suppress translation symmetry in the periodic condition

Let $N \in \mathbb {N}$ and $L > 0$. N is the number of vehicles, and L is the length of the circuit. We regard $x_{N+1} = x_1 + L$. Obviously, we have

$$\begin{aligned} \sum _{j=1}^{N} h_j = L. \end{aligned}$$

(4)

That is, the sum of headways is equal to the length of the entire circuit.

We suppress the translation symmetry by introducing variables $y=(y_1, \cdots , y_N)$ (see Fig. 1), which satisfy

$$\begin{aligned} y = (y_1, \dots , y_N) = (h_1, \dots , h_{N-1}, x_1). \end{aligned}$$

(5)

Note that this transformation of variables is regular. Indeed, the inverse is given by

$$\begin{aligned} x_j = y_N + \sum _{k=1}^{j-1} y_k,\quad j = 1,2, \dots , N, \end{aligned}$$

(6)

where the sum is taken only when $j-1>1$.

The STNN model can be written in the following form:

$$\begin{aligned} \ddot{x}_j = a - \dot{x}_j W(h_j, \dot{h}_j),\qquad j = 1, 2, \dots , N, \end{aligned}$$

(7)

where a is a positive parameter, which is the same as the original model. W is, for example,

$$\begin{aligned} W(h_j, \dot{h}_j) = \dfrac{b}{(h_j - d)^2} e^{-c\dot{h}_j} + \gamma . \end{aligned}$$

(8)

Here, we consider the case of N vehicles. In general, y is governed by

$$\begin{aligned} \ddot{y}_j&= -(\dot{y}_N + \sum _{k=1}^{j}\dot{y}_k) W(y_{j+1}, \dot{y}_{j+1}) + (\dot{y}_N + \sum _{k=1}^{j-1}\dot{y}_k) W(y_j, \dot{y}_j),\end{aligned}$$

(9)

$$\begin{aligned} \ddot{y}_{N-1}&= -\left( \sum _{k=1}^{N}\dot{y}_k \right) W(L-\sum _{k=1}^{N-1}y_k, -\sum _{k=1}^{N-1}\dot{y}_k) + (\dot{y}_N+\sum _{k=1}^{N-2}\dot{y}_k) W(y_{N-1}, \dot{y}_{N-1}),\\ \text {and}&\nonumber \end{aligned}$$

(10)

$$\begin{aligned} \ddot{y}_N&= a - \dot{y}_N W(y_1, \dot{y}_1), \end{aligned}$$

(11)

where $j = 1, 2, \dots , N-2$. $y_N$ is just an integral of $\dot{y}_N$. Note that the problem is reduced to a system on $\mathbb {R}^{2N-1}$.

3 Numerical Bifurcation Analysis

In this section, we show bifurcation diagrams of Eq. 3. In particular, we focus on the effect of relative velocity. First, we consider the case when $c=0$. Next, we consider the case when $c \ne 0$ by computing a two-parameter bifurcation diagram. We regard L and c as the primary and the secondary parameters, respectively. The remaining parameters are assigned the same values estimated in [10], that is, $a=0.73, b=3.25, d=5.25$, and $\gamma =0.0517$. Moreover, now we assign the number of vehicles $N = 30$.

3.1 Without Relative Velocity Effect ($c=0$)

First, we investigate a global bifurcation structure in the case of $c=0$, where the model has no relative velocity effect. Under this condition, the model should reflect the characteristics that are in common with the OV model.

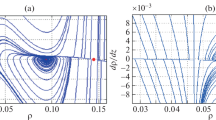
Figure 2 illustrates a bifurcation diagram, which has L on the horizontal axis and the relative velocity of the first vehicle on the vertical axis. The left image shows the entirety of the bifurcation diagram and the right image is the close-up picture at $L=1333.43$. The solid line (curve) and the dashed line (curve) indicate a stable solution and an unstable solution, respectively. From these figures, we reveal the birth of a supercritical Hopf bifurcation as the parameter L becomes small (density becomes large). That is, if one moves along the horizontal line ($\frac{dh_1}{dt}=0$) from right to left, one can find at first a stable equilibrium point ($L=1333.43$) that eventually loses its stability in favour of a periodic solution branch. Subsequent to that, two saddle-node bifurcations ($L=1333.41$ and $L=2619.25$) take place on this periodic solution branch. In the region $1333.43<L<2619.25$, both the homogeneous solution and the periodic solution are stable, that is the traffic flow shows bi-stability. This global bifurcation structure is qualitatively similar to the structure of the OV model shown in [4], that is, the behaviour of a Hopf bifurcation is locally supercritical, but macroscopically subcritical.

Fig. 2

Bifurcation diagram. Abbreviations: Stable Equilibrium (SE), Unstable Equilibrium (UE), Stable Cycle (SC), and Unstable Cycle (UC). Global bifurcation diagram of STNN model for the parameters $a=0.73$, $b=3.25$, $c=0$, $d=5.25$, and $\gamma =0.0517$ (a); close-up picture of the right Hopf bifurcation point (b)

3.2 With Relative Velocity Effect ($c\ne 0$)

Next, we consider the case when $c \ne 0$. A Hopf bifurcation point and a saddle-node bifurcation point draw a curve in two-parameter plane when an additional parameter is varied. We vary c as well as L to numerically compute the curves starting at two Hopf bifurcation points $((L, c)=(205.612, 0), (1333.41, 0))$ and two saddle-node bifurcation for Eq. 3 with $c=0$.

Figure 3 shows the two-parameter bifurcation diagram and its close-up view. The curve of Hopf bifurcation points turns down at $(L, c) = (395.55, 1.955)$, and no Hopf bifurcation is found for $c > 1.995$. From phenomenological point of view, this implies that the enhancement of relative velocity effect leads drivers to a good response and eventually makes the homogeneous flow stable for a fluctuation. Thus, we have found that homogeneous flow becomes stable in all densities in a parameter region $c > 1.955$. On the other hand, the curve of saddle-node bifurcation points meets at a cusp point $(L,c) = (1019.23, 0.6664)$. This implies that the bi-stability as shown in Fig. 2 does not appear when $c > 0.6664$. Thus, we have three intervals $0<c < 0.6664$, $0.6664< c < 1.955$, and $1.955 < c$ in which bifurcation diagrams are qualitatively different. It should be noted that here we discuss only two Hopf bifurcation points. Other Hopf bifurcation points exist at the region $205.612< L <1333.41$ and may show another stable periodic solution branch, which implies multi-stability. These features will be also investigated in the near future.

Fig. 3

Two-parameter bifurcation diagram: behaviours of Hopf Bifurcation points (HB) and Saddle-Node points (SN) on (L, c)-plane for the parameters $a=0.73$, $b=3.25$, $c=5.25$, $\gamma =0.0517$ (a); close-up picture at the cusp point (b)

4 Conclusion and Discussion

In this paper, we investigated the global bifurcation structure of the periodic solutions bifurcating from the critical density for STNN model, wherein the relative velocity effect is introduced. In the case when $c=0$, which corresponds to the model without the relative velocity effect, the global bifurcation structure shows features that are similar to the OV model; the model shows that the loss of stability in homogeneous flow is due to a Hopf bifurcation, and the behaviour of a Hopf bifurcation is locally supercritical, but macroscopically subcritical. Moreover, we have found that two Hopf bifurcation points turn down at a point on (L, c)-plane, and two saddle-node points merge and make a cusp point in the case of $c \ne 0$, where the model takes into account the relative velocity effect. In particular, this result shows that the instability of the homogeneous flow disappears, and the homogeneous flow becomes stable in a parameter region $c>1.955$. This situation might not be realistic in non-automatic driving, but could provide a solution in the near future for implementing (semi-)autonomous driving systems, such as the adaptive cruise control system, to alleviate traffic jams.