Stability, convergence and Hopf bifurcation analyses of the classical car-following model

Abstract

Reaction delays play an important role in determining the qualitative dynamical properties of a platoon of vehicles traversing a straight road. In this paper, we investigate the impact of delayed feedback on the dynamics of the classical car-following model (CCFM). Specifically, we analyze the CCFM in three regimes—no delay, small delay and arbitrary delay. First, we derive a sufficient condition for local stability of the CCFM in no-delay and small-delay regimes using control-theoretic methods. Next, we derive the necessary and sufficient condition for local stability of the CCFM for an arbitrary delay. We then demonstrate that the transition of traffic flow from the locally stable to the unstable regime occurs via a Hopf bifurcation, thus resulting in limit cycles in system dynamics. Physically, these limit cycles manifest as back-propagating congestion waves on highways. In the context of human-driven vehicles, our work provides phenomenological insight into the impact of reaction delays on the emergence and evolution of traffic congestion. In the context of self-driven vehicles, our work has the potential to provide design guidelines for control algorithms running in self-driven cars to avoid undesirable phenomena. Specifically, designing control algorithms that avoid jerky vehicular movements is essential. Hence, we derive the necessary and sufficient condition for non-oscillatory convergence of the CCFM. This ensures smooth traffic flow and good ride quality. Next, we characterize the rate of convergence of the CCFM and bring forth the interplay between local stability, non-oscillatory convergence and the rate of convergence of the CCFM. We then study the nonlinear oscillations in system dynamics that emerge when the CCFM loses local stability via a Hopf bifurcation. To that end, we outline an analytical framework to establish the type of the Hopf bifurcation and the asymptotic orbital stability of the emergent limit cycles using Poincaré normal forms and the center manifold theory. Next, we numerically bring forth the supercritical nature of the bifurcation that result in asymptotically orbitally stable limit cycles. The analysis is complemented with stability charts, bifurcation diagrams and MATLAB simulations. Thus, using a combination of analysis and numerical computations, we highlight the trade-offs inherent among various system parameters and also provide design guidelines for the upper longitudinal controller of self-driven vehicles.

1 Introduction

Intelligent transportation systems constitute a substantial theme of discussion on futuristic smart cities. A prospective solution to increase resource utilization is to use self-driven vehicles, which may also mitigate traffic congestion [1, Sect. 5.2], [2]. To that end, it is imperative to design stable control algorithms for these vehicles. Since a good design process requires an in-depth understanding of vehicular dynamics, a class of dynamical models—known as car-following models—have been developed and studied [3,4,5,6,7,8,9].

An important consideration in the study of car-following models is the delay in the dynamical variables. Delays arise due to various factors such as sensing, mechanical motions, communication and signal processing. These delays affect the properties of a dynamical system in many different ways [10]. Specifically, delays can readily lead to oscillations and instability [9, 11].

In this paper, we study the effect of delayed feedback on the qualitative dynamical properties of a platoon of vehicles traversing a straight road without overtaking. Specifically, we study the effect of delayed feedback on the classical car-following model (CCFM). In the context of human-driven vehicles, reaction delays can be fairly large (of the order of 1 second), with the physiological and the mechanical components being dominant [11]. In contrast, self-driven vehicles tend to have smaller reaction delays, and are typically due to sensing, computation and actuation [12]. Motivated by this, we study the CCFM in three regimes—no delay, small delay and arbitrary delay.

In addition to stability, non-oscillatory convergence and rate of convergence constitute two properties of practical interest, which we also explore for the case of the CCFM. Such conditions could aid in ensuring smooth traffic flow by avoiding jerky vehicular motion, thereby improving ride quality. The theoretic analyses could offer suggestions for design guidelines.

In the context of human-driven vehicles, our work enhances phenomenological insight into the emergence and evolution of traffic congestion. For instance, a peculiar phenomenon is observed on highways, wherein a congestion is formed—seemingly out of nowhere —which propagates backwards in space. This gives rise to a wave-like congestion pattern on highways that propagates backwards from the point of its origin [4, 5]. Such a phenomenon is known as a “phantom jam.” It is known that a sudden change in the driver’s sensitivity (such as a sudden deceleration) can result in such oscillatory behavior [4, 5]. In this paper, we show that an increase in the driver’s reaction delay may also lead to similar oscillations. More importantly, we show that the traffic flow transits into instability due to a Hopf bifurcation, thus resulting in limit cycles in system dynamics. These emergent limit cycles physically manifest as phantom jams. More generally, we show that the traffic flow may transit into instability due to a suitable variation in any combination of model parameters. To capture any complex relation between various parameters, we introduce a non-dimensional exogenous parameter in the CCFM, which is set to unity on the stability boundary. Indeed, we make use of this parameter to push the system beyond the stability region, thus resulting in a bifurcation.

In the context of self-driven vehicles, reaction delays are envisioned to be smaller than those of a human driver. Thus, the separation between consecutive self-driven vehicles in steady state is expected to be smaller [1, Sect. 5.2]. Hence, the resource utilization can be improved without any degradation in safety [2]. More importantly, the parameters of the control algorithm (called upper longitudinal control algorithm [1, Sect. 5.2]) in self-driven vehicles have to be appropriately tuned. It is known that a combination of stability and convergence analyses may be used to design several aspects of longitudinal control algorithms [1, Sect. 5.2]. Thus, based on a combination of analysis, numerical computations and simulations, our work may provide design guidelines for appropriate design of the control algorithm.

1.1 Related work

Stability properties of car-following models were studied initially by Chandler et al. [13] and Herman et al. [14]. The CCFM was proposed by Gazis et al. [3] with the intention of studying the macroscopic properties emerging from various drivers’ behavior. Several variants of the CCFM have since been studied in the literature; see [13,14,15]. These works consider the linearized models and predominantly use transform techniques to study their stability aspects. For a recent exposition of linear stability analysis as applied to car-following models, see [16].

In contrast, Zhang and Jarrett [9] and some of the references therein treat car-following models from a dynamical systems standpoint, and study their stability. Specifically, Zhang and Jarrett [9] studies some stability properties of the CCFM. However, the aforementioned works do not consider the delay in the self-velocity term. To make the model more realistic, we accounted for this delay in our previous work [6]. Therein, we studied a particular case of the CCFM called the reduced classical car-following model (RCCFM) and showed that it loses local stability via a Hopf bifurcation. This paper extends the results presented in [6] to the CCFM and also derives conditions that may ensure good ride quality, in addition to characterizing the time taken by a platoon to reach its equilibrium. Further, we show that oscillations in state variables are a manifestation of limit cycles, and not centers as asserted in [9]. For a recent review on stability analyses as applied to car-following models, see [17]. For an exposition on the use of time-delayed equations for traffic-flow modeling, see [18]. There has been a sustained research interest in the general direction of traffic modeling and analysis; see [17, 19,20,21] and references.

Note that several dynamical models have also been studied in the Physics literature beginning with the optimal velocity model (OVM) [8]. In fact, it is known that some of these models lose local stability via a Hopf bifurcation as well [7, 22]. Several extensions—such as multi-anticipation [23, 24]—have also been studied for the OVM. Studies have also tried to deduce macroscopic quantities [25] and macroscopic models [26] when drivers follow some variant of the OVM. However, this body of literature assumes the vehicles to be traveling on a single-lane circular loop, thus mathematically yielding periodic boundary conditions. In contrast, the CCFM and related models differ at a fundamental level by assuming the vehicular motion on a single-lane straight road. Thus, we do not attempt to compare our results with those derived for the OVM and related models.

From a vehicular dynamics perspective, most upper longitudinal controllers in the literature assume the lower controller’s dynamics to be well-modeled by a first-order control system, in order to capture the delay lag [1, Sect. 5.3]. The upper longitudinal controllers are then designed to maintain either constant velocity, spacing or time gap; for details, see [27] and the references therein. Specifically, Rajamani et al. [27] prove that synchronization with the lead vehicle is possible by using information only from the vehicle directly ahead. This reduces implementation complexity and does not mandate vehicles to be installed with communication devices.

However, in the context of autonomous vehicles, communication systems are required to exchange various system states required for the control algorithm. This information is used either for distributed control [27] or coordinated control [28]. Formation and platoon stabilities have also been studied considering information flow among the vehicles [29, 30]. For an extensive review, see [31].

In contrast to stabilizing platoons of autonomous vehicles (our scenario), it has been shown that well-placed, communicating autonomous vehicles may be used to stabilize platoons of human-driven vehicles as well [32]. More generally, the platooning problem has been studied as a consensus problem with delays [33]. Such an approach aids the design of coupling protocols between interacting agents (in this context, vehicles). In contrast, we provide design guidelines to appropriately choose protocol parameters, given a coupling protocol (the CCFM).

To the best of our knowledge, ours is the first work to study the practically relevant notions of time taken by a platoon to equilibrate, and the convergence of the CCFM in a non-oscillatory fashion, in the transportation setting. Further, although these are local properties, these (in addition to local stability) may help provide design guidelines for the upper longitudinal control algorithm. In the context of the OVM, Gasser et al. [22] have shown that the nonlinear system exhibits existence/coexistence of periodic solutions despite conforming to the local stability condition. However, for the CCFM, our simulations suggest that satisfying the local stability condition ensures stability of the nonlinear system as well. Thus, in this paper, we provide design guidelines for the upper longitudinal control algorithm using a combination of linear and nonlinear analyses and numerical computations.

1.2 Our contributions

Our contributions can be summarized as follows.

• (1) We make the CCFM a more realistic model by accounting for the delay in the self-velocity term.

• (2) We show that, in the absence of reaction delays, the CCFM is locally stable for all parameter values of practical interest. When the delays are rather small, we derive a sufficient condition for local stability of the CCFM using a linearization of the time variable.

• (3) We derive the necessary and sufficient condition for the local stability of the CCFM for an arbitrary delay. We then show that, upon violation of this condition, the CCFM loses local stability via a Hopf bifurcation. Indeed, this helps us understand that the oscillations emerge as a consequence of limit cycles, and centers as asserted in the literature.

• (4) In the case of human-driven vehicles, our work enhances phenomenological insights into the emergence and evolution of traffic congestion. For example, the notion of Hopf bifurcation provides a mathematical framework to offer a possible explanation for the observed “phantom jams.”

• (5) We derive the necessary and sufficient condition for non-oscillatory convergence of the CCFM. This is useful in the context of a transportation network since oscillations lead to jerky vehicular movements, thereby degrading ride quality and possibly causing collisions.

• (6) We characterize the rate of convergence of the CCFM, thereby gaining insight into the time required for the platoon to attain the desired equilibrium, when perturbed. Such perturbations occur, for instance, when a vehicle departs from a platoon.

• (7) We highlight the three-way trade-off between local stability, non-oscillatory convergence and the rate of convergence. Considering this trade-off, we suggest some guidelines to appropriately choose parameters for the upper longitudinal control algorithm in self-driven vehicles.

• (8) We outline an analytical framework to establish the type of the Hopf bifurcation and the asymptotic orbital stability of the limit cycles using Poincaré normal forms and the center manifold theory. Further, we numerically bring forth the supercritical nature of the bifurcation that result in asymptotically orbitally stable limit cycles.

• (9) We corroborate the analytical results with the aid of stability charts, numerical computations and simulations conducted using MATLAB.

The remainder of this paper is organized as follows. In Sect. 2, we introduce the CCFM. In Sects. 3, 4 and 5, we characterize the stable region for the CCFM in no-delay, small-delay and arbitrary-delay regimes, respectively. We understand the stable region by characterizing the region of non-oscillatory convergence of the CCFM in Sect. 6 and the rate of convergence of the CCFM in Sect. 7. In Sect. 8, we present the local Hopf bifurcation analysis for the CCFM. In Sect. 9, we present the simulation results before concluding in Sect. 10.

2 Models

We begin this section with an overview of the setting of our work. We then briefly explain the CCFM.

2.1 The setting

We consider a platoon of $N+1$ vehicles (having zero length) traveling on an infinitely long, single-lane road without overtaking. We number the lead vehicle with 0,  its follower 1,  and so on. The acceleration of each vehicle is updated based on the position, velocity and acceleration of that vehicle and the vehicle directly ahead. We denote the position of the ith vehicle at time t by $x_i(t)$. Following standard convention, we use ${\dot{x}}_i(t)$ and $\ddot{x}_i(t)$ to denote the corresponding velocity and acceleration. We assume that the acceleration and velocity profiles of the lead vehicle are known. Specifically, we consider only those leader profiles that converge, in finite time, to $\ddot{x}_0 = 0$ and $0< \text { } {\dot{x}}_0 < \infty$; that is, there exists a finite $T_0$ such that $\ddot{x}_0(t) = 0$, ${\dot{x}}_0(t) = {\dot{x}}_0 \, > \, 0,\,\forall \, t \ge T_0$. We use the terms “driver” and “vehicle” interchangeably throughout. Further, we use SI units throughout.

2.2 The classical car-following model (CCFM)

The CCFM is characterized by each vehicle updating its acceleration based on the following rule [3]

$$\begin{aligned} {\ddot{x}}_i(t) = \alpha _i \frac{ \left( {\dot{x}}_i(t) \right) ^m \left( {\dot{x}}_{i-1}(t - \tau ) - {\dot{x}}_{i}(t - \tau ) \right) }{\left( x_{i-1}(t - \tau ) - x_{i}(t - \tau )\right) ^l}, \end{aligned}$$

(1)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. Here, $\alpha _i \, > \, 0$ represents the ith driver’s sensitivity coefficient, for each $i \in \lbrace 1, 2, \ldots , N \rbrace$. The model parameters $m \in [-2,2]$ and $l \in {\mathbb {R}}_{+}$ capture the nonlinear dependence of the acceleration on the self-velocity term and the headway, respectively. It is interesting to note that, in its original form, the CCFM does not account for delay in the self-velocity term $\left( {\dot{x}}_i(t) \right) ^m$. While self-velocity might be available almost immediately, it takes some non-negligible time to execute the required control action. Also, from an analytical viewpoint, ignoring delays (in general) may generate inaccurate results. Thus, we account for the delay in the self-velocity term. Further, to make the model more realistic, we assume heterogeneity in reaction delays.

It is easy to see from (1) that the state variable $x_i(t) \rightarrow \infty$ as $t \rightarrow \infty$ for each i. That is, the positions of all vehicles become unbounded asymptotically. This is due to the infinite nature of the considered highway. However, to apply tools from dynamical systems theory, we require bounded state variable. Thus, similar to [9], we work with relative distances (headways) and relative velocities instead. Therefore, we make the following change of variables: $y_i(t) + b_i = x_{i-1}(t) - x_i(t)$ and $v_i(t) = {\dot{y}}_i(t) = {\dot{x}}_{i-1}(t) - {\dot{x}}_i(t)$ for $i \in \lbrace 1, 2, \ldots , N \rbrace$. Here, $b_i$ denotes the desired equilibrium separation for the ith pair of vehicles, $y_i(t) + b_i$ represents the separation between vehicles $i-1$ and i at time t,  and $v_i(t)$ corresponds to the relative velocity of the ith vehicle with respect to the $(i-1)$th vehicle at time t. Thus, the transformed model is

$$\begin{aligned} {\dot{v}}_i(t) =&\, \beta _{i-1}(t - \tau _{i-1}) v_{i-1}(t - \tau _{i-1}) \nonumber \\&- \beta _i( t - \tau _i) v_{i}(t - \tau _i),\nonumber \\ {\dot{y}}_i(t) =&\, v_i(t), \end{aligned}$$

(2)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. Here,

$$\begin{aligned} \beta _i(t) = \, \alpha _{i} \frac{ \left( {\dot{x}}_0(t) - v_0(t) - \cdots - v_{i}(t) \right) ^m}{\left( y_{i}(t) + b_i \right) ^l}. \end{aligned}$$

In the above equations, $y_0$, $v_0$, $\alpha _0$ and $\tau _0$ are introduced for notational brevity and are set to zero. In particular, note that $y_0$ and $v_0$ are not state variables.

Note that $y_i(t) + b_i,$ and not$y_i(t),$ represents the headway at time t. In fact, $y_i(t)$ represents the spacing error—the variation of the headway about its equilibrium $b_i$. Thus, $y_i(t)$ may become negative. However, the model breaks down when $y_i(t) + b_i$ becomes zero for $l > 0$ [9]. Also, the CCFM possesses an inherent “repulsion” property, which may be illustrated as follows. Suppose that the vehicle indexed i approaches the vehicle indexed $i-1$ at a relatively higher velocity. When the distance becomes very small (mathematically, $<1$ meter), the ith vehicle decelerates rather rapidly. This can be inferred from (1). This helps avoid collision (hence the term “repulsion”), thus ensuring $y_i(t) + b_i > 0$.

Since equations of form (2) are hard to analyze, we obtain sufficient conditions for their stability by analyzing them in the neighborhood of their equilibria. To that end, note that $v_i^* = 0,y_i^* = 0\,i = 1, 2, \ldots , N$ is an equilibrium for system (2). Linearizing (2) about this equilibrium, we obtain

$$\begin{aligned} \nonumber {\dot{v}}_i(t)&= \, \beta _{i-1}^* v_{i-1}(t - \tau _{i-1}) - \beta _i^* v_{i}(t - \tau _{i}), \nonumber \\ {\dot{y}}_i(t)&= \, v_i(t), \end{aligned}$$

(3)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. Here, $\beta _i^* = \alpha _{i} ({\dot{x}}_0)^m / (b_i)^l$ denotes the equilibrium coefficient for the ith vehicle.

Notice from (3) that the evolution of $v_i(t),$ in the vicinity of its equilibrium, is not affected by the evolution of $y_i(t)$. Further, $y_i(t)$ can be obtained by integrating $v_i(t)$. Thus, we drop the variables $\lbrace y_i(t) \rbrace _{i = 1}^{N}$ when dealing with the linearized system. This yields

$$\begin{aligned} {\dot{v}}_i(t) = \, \beta _{i-1}^* v_{i-1}(t - \tau _{i-1}) - \beta _i^* v_{i}(t - \tau _{i}). \end{aligned}$$

(4)

In Sects. 3 through 7 of this paper, we study system (4) to deduce various conditions for the CCFM. It may be noted that (4) is similar in form to the linearized RCCFM [6, Eq. (3)]. However, the equilibrium coefficient $\beta _i^*$ now accounts for the nonlinearity parameter $l \in {\mathbb {R}}_+$.

3 The no-delay regime

In this section, we consider the idealistic case of drivers that can react instantaneously to stimuli. This results in zero reactions delays, and hence the linear model described by system (4) boils down to the following system of ordinary differential equations (ODEs):

$$\begin{aligned} {\dot{v}}_i(t) = \, \beta _{i-1}^* v_{i-1}(t) - \beta _i^* v_{i}(t), \end{aligned}$$

(5)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. This can be succinctly written in matrix form as follows:

$$\begin{aligned} {\dot{\mathbf{V }}}(t) = \, A \mathbf{V }(t), \end{aligned}$$

(6)

where $\mathbf{V }(t) = [v_1(t) \, v_2(t) \, \ldots \, v_N(t)]^T \in {\mathbb {R}}^N,$ and $A \in {\mathbb {R}}^{N \times N}$. The matrix A,  known as the dynamics matrix [34, Sect. 2.2], is a lower-triangular matrix, given by:

$$\begin{aligned} A_{ij} = {\left\{ \begin{array}{ll} - \beta _i^*, &{} i = j, \\ \beta _j^*, &{} i = j+1, \\ 0, &{} \text {elsewhere}. \end{array}\right. } \end{aligned}$$

To characterize the stability of system (5), we require the eigenvalues of the dynamics matrix corresponding to system (6) to be negative [35, Theorem 5.1.1]. Since A is a lower-triangular matrix, the characteristic polynomial is given by the product of the diagonal elements of the matrix $(\lambda I - A)$ [36, Lemma 6.9.1]. Therefore, we have

$$\begin{aligned} f(\lambda ) = \text {det}(\lambda I - A) = \prod _{i = 1}^N \left( \lambda + \beta _i^*\right) = 0. \end{aligned}$$

(7)

That is, the eigenvalues corresponding to system (5) are located at $-\beta _i^*$, $i \in \lbrace 1, 2, \ldots , N \rbrace$. Note that, from physical constraints, $\alpha _i > 0$ and $b_i > 0\,\forall i$. This ensures $\beta _i^* > 0\,\forall i,$ for all physically relevant systems. Hence, the corresponding eigenvalues will lie in the open left half of the Argand plane, thereby ensuring the stability of system (4) for all physically relevant values of the parameters.

4 The small-delay regime

In this section, we analyze system (2) in the small-delay regime. A way to obtain insight for small delays is to conduct a linearization on the time variable. Thus, we obtain a system of ODEs, which serves as an approximation to the original infinite-dimensional system (4), for small delays. We derive the criterion for this system of ODEs to be stable, thereby emphasizing the design trade-off inherent among various system parameters and the reaction delay.

We begin by applying the Taylor series approximation to the time-delayed state variables thus: $v_i(t-\tau _i) \approx v_i(t) - \tau _i {\dot{v}}_i(t).$ Using this approximation for terms in (4), and re-arranging the resulting equations, we obtain

$$\begin{aligned} {\dot{v}}_i(t) + \frac{\beta _{i-1}^* \tau _{i-1}}{1- \beta _{i}^* \tau _{i}} {\dot{v}}_{i-1}(t) = \, \frac{\beta _{i-1}^*}{1- \beta _{i}^* \tau _{i}} v_{i-1}(t) - \frac{\beta _{i}^*}{1- \beta _{i}^* \tau _{i}} v_{i}(t), \end{aligned}$$

(8)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. This can be succinctly written in matrix form as

$$\begin{aligned} B \dot{\mathbf{V }}(t) = A_s \mathbf{V }(t), \end{aligned}$$

(9)

where $\mathbf{V }(t) = [v_1(t) \, v_2(t) \, \ldots \, v_N(t)]^T \in {\mathbb {R}}^N$. The matrix $A_s$ is as defined

$$\begin{aligned} A_{s_{ij}} = {\left\{ \begin{array}{ll} - \frac{\beta _i^*}{1-\beta _i^* \tau _i^*}, &{} i = j, \\ \frac{\beta _j^*}{1-\beta _i^* \tau _i^*}, &{} i = j+1, \\ 0, &{} \text {elsewhere}, \end{array}\right. } \end{aligned}$$

and B is given by

$$\begin{aligned} B_{ij} = {\left\{ \begin{array}{ll} 1, &{} i = j, \\ \frac{-\beta _j^* \tau _j}{1 - \beta _i^* \tau _i}, &{} i = j + 1, \\ 0, &{} \text {elsewhere}. \end{array}\right. } \end{aligned}$$

Note that B is a lower-triangular matrix with unit diagonal entries. Hence, it is invertible, and the inverse is also a lower-triangular matrix having unit diagonal elements. Also, since A is a lower-triangular matrix as well, the dynamics matrix corresponding to system (8), i.e.,${\tilde{A}} = B^{-1}A_s,$ is a lower-triangular matrix since it is the product of two lower-triangular matrices [37, Sect. 1.4]. Further, due to the said structures, the diagonal elements of ${\tilde{A}}$ are given by

$$\begin{aligned} {\tilde{A}}_{ii} = \frac{\beta _{i}^*}{1 - \beta _i^* \tau _i}, \, i \ge 1. \end{aligned}$$

(10)

Therefore, the characteristic polynomial corresponding to system (8) is the product of the diagonal entries of the matrix $(\lambda I - {\tilde{A}})$ [36, Lemma 6.9.1]. That is,

$$\begin{aligned} f(\lambda ) = \text {det } (\lambda I - {\tilde{A}}) = \prod _{i = 1}^{N} \left( \lambda + {\tilde{A}}_{ii}\right) = 0. \end{aligned}$$

(11)

This shows that the eigenvalues of system (8) are located at $-{\tilde{A}}_{ii}$, $i \in \lbrace 1, 2, \ldots , N \rbrace$. Hence, for system (8) to be stable, the diagonal entries of its dynamics matrix ${\tilde{A}}$ have to be positive. From (10), this is satisfied if and only if

$$\begin{aligned} \beta _i^* \tau _i < 1, \text { } i \in \lbrace 1, 2, \ldots , N \rbrace . \end{aligned}$$

(12)

Hence, the above equation represents the necessary and sufficient condition for stability of the time-linearized system (8). Further, as noted in Sect. 2, (12) is a sufficient condition for local stability of the CCFM, described by system (2).

5 Hopf bifurcation

Having studied system (2) in the no-delay and the small-delay regimes, in this section, we focus on the arbitrary-delay regime. We derive the necessary and sufficient condition for the local stability of system (2) and show that the corresponding traffic flow transits from the locally stable to the unstable regime via a Hopf bifurcation [38].

5.1 Transversality condition

Hopf bifurcation is a phenomenon wherein a nonlinear dynamical system loses/regains stability as a consequence of a pair of conjugate eigenvalues crossing the imaginary axis in the Argand plane [10, Chap. 11, Theorem 1.1]. Mathematically, a Hopf bifurcation analysis is a rigorous way of proving the emergence of limit cycles in nonlinear dynamical systems.

In order to ascertain whether the CCFM undergoes a stability loss via a Hopf bifurcation, we follow [39] and introduce an exogenous, non-dimensional parameter $\kappa \, > \, 0$. A general system of delay differential equations ${\dot{x}}(t) = f(x(t), x(t-\tau _1), \ldots , x(t-\tau _n))$ is modified to ${\dot{x}}(t) = \kappa f(x(t), x(t-\tau _1), \ldots , x(t-\tau _n))$ with the introduction of the exogenous parameter. Specific to the CCFM, introducing $\kappa$ in (2) yields

$$\begin{aligned} {\dot{v}}_i(t)&= \kappa \beta _{i-1}(t - \tau _{i-1}) v_{i-1}(t - \tau _{i-1}) \nonumber \\&- \kappa \beta _{i}(t - \tau _i) v_{i}(t - \tau _i), \nonumber \\ {\dot{y}}_i(t)&= \kappa v_i(t), \end{aligned}$$

(13)

for each $i \in \lbrace 1, 2, \ldots , N \rbrace$. Linearizing this about the all-zero equilibrium, and dropping $y_i$’s, we obtain

$$\begin{aligned} {\dot{v}}_i(t) = \, \kappa \beta _{i-1}^* v_{i-1}(t - \tau _{i-1}) - \kappa \beta _i^* v_{i}(t - \tau _{i}), \end{aligned}$$

(14)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. The characteristic equation associated with (14) is [6, Eq. (15)]

$$\begin{aligned} \lambda + \kappa \beta _i^* e^{- \lambda \tau _i} = \, 0. \end{aligned}$$

(15)

Ensuring that all roots of (15) lie in the open left half of the Argand plane guarantees the stability of system (14) [35, Theorem 5.1.1]. Thus, to characterize the local stability of system (13), we search for a conjugate pair of eigenvalues of (15) that crosses the imaginary axis in the Argand plane. This would, in turn, push the system into an unstable regime. Therefore, substituting $\lambda = j \omega$, where $j = \sqrt{-1}$, in (15) yields

$$\begin{aligned} \kappa \beta _i^* \text { cos}(\omega \tau _i) = 0, \text { and } \omega - \kappa \beta _i^* \text { sin}(\omega \tau _i) = 0. \end{aligned}$$

From the first equality, we infer that $\omega \tau _i$ = $(2n+1)\frac{\pi }{2}$ for $n = 0, 1, 2, \ldots$. Thus, the second equality implies that $\kappa \beta _i^*$ = $\omega$ for $n = 0, 2, 4, \ldots$. Therefore, the conditions that ensure the existence of a conjugate pair of eigenvalues on the imaginary axis are

$$\begin{aligned} \omega _0 =&\, (2n + 1) \frac{\pi }{2 \tau _i}, \text { } n = 0, 1, 2, \ldots , \end{aligned}$$

(16)

$$\begin{aligned} \kappa _{cr} =&\, (2n + 1) \frac{\pi }{2 \beta _i^* \tau _i}, \text { } n = 0, 2, 4, \ldots , \end{aligned}$$

(17)

where $\kappa _{cr}$ is the critical value of $\kappa$ at $\omega = \omega _0$.

Fig. 1

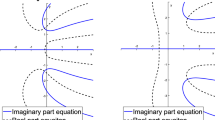
Variation in the locally stable regions of the CCFM as a function of the nonlinearity parameter l; a plot of (20) when $c=1$ and $b_i > 1$. a is for $m < 0$, whereas b is for $m > 0$. For visual clarity, we restrict m to the range [0.8, 2]. As l increases, the CCFM becomes resilient to instability since $b_i >1$

Note that using the change of variables $z = \lambda \tau _i,$ the characteristic equation (15) can be transformed to $z e^z + a = 0,$ where $a = \kappa \beta _i^* \tau _i$. From [40], it is known that for such a system, when $a < \pi / 2,$ the real part of all eigenvalues are negative. Further, for $a = \pi /2,$ there exists a simple conjugate pair of eigenvalues on the imaginary axis, whereas all other eigenvalues have negative real parts. For the CCFM, this translates to the following: (a) for $\kappa < \kappa _{cr},$ the system is stable, and (b) when $\kappa = \kappa _{cr},$ there is exactly one pair of conjugate eigenvalues on the imaginary axis, while the remaining eigenvalues have negative real parts. We next show that a further increase in the non-dimensional parameter would cause the eigenvalues to move right in the Argand plane, thus leading to a loss of local stability via a Hopf bifurcation. Indeed, this would also imply that $\kappa < \kappa _{cr}$ is then the necessary and sufficient condition for local stability of the CCFM.

To ascertain whether the eigenvalues cross the imaginary axis with increase in $\kappa ,$ we verify the transversality condition of the Hopf spectrum [10, Chap. 11, Theorem 1.1]. That is, we check if

$$\begin{aligned} \text {Re}\left[ \frac{\text {d} \lambda }{\text {d} \kappa } \right] _{\kappa = \kappa _{cr} } \ne \, 0 \end{aligned}$$

(18)

holds for each $n \in \lbrace 0, 2, 4, \ldots \rbrace$. To that end, we differentiate (15) with respect to $\kappa ,$ and perform algebraic manipulations to obtain

$$\begin{aligned} \text {Re}\left[ \frac{\text {d} \lambda }{\text {d} \kappa } \right] _{\kappa = \kappa _{cr} } = \frac{2 \beta ^*_i \tau _i^2 \omega _0^2 }{(2n + 1)(1 + \tau _i^2 \omega _0^2)\pi } > 0, \end{aligned}$$

(19)

for $n \in \lbrace 0, 2, 4, \ldots \rbrace$. This implies that system (13) undergoes a Hopf bifurcation at $\kappa = \kappa _{cr}$ for each $n \in \lbrace 0, 2, 4, \ldots \rbrace$. Hence, $\kappa < \kappa _{cr}$ when $n = 0$ is the necessary and sufficient condition for system (13) to be locally stable.

First, note that $\kappa = \kappa _{cr}$ represents the stability boundary (also called the Hopf boundary). To obtain the stability boundary of the CCFM, we set $\kappa _{cr} = 1$; that is, we tune the system parameters such that $2 \beta _i^* \tau _i = \pi$. Next, notice that the CCFM loses local stability when the very first pair of eigenvalues (the pair corresponding to $n = 0$) crosses the imaginary axis in the Argand plane. Since the derivative in (19) is positive for even values of n,  further increase in $\kappa$ cannot restore stability. And lastly, note that (17) captures the inverse relation between the reaction delay and the sensitivity parameter on the Hopf boundary. Hence, we set $\alpha _i \tau _i = c,$ a real constant, in order to study the trade-off between the leader’s profile ${\dot{x}}_0$, and the nonlinearity parameters l and m. The resulting necessary and sufficient condition for the local stability of system (2) is

$$\begin{aligned} \frac{( {\dot{x}}_0 )^m}{( b_i )^l} < \frac{\pi }{2c}. \end{aligned}$$

(20)

Notice that we recover the necessary and sufficient condition for the local stability of the RCCFM [6, Eq. (20)] if (i) the nonlinearity parameter l is set to zero, or (ii) the equilibrium headway $b_i$ is set to unity. For these cases, the inference drawn in [6] holds: When $m > 0,$ slow lead vehicles stabilize the system, and for $m < 0,$ fast lead vehicles are required to ensure system stability. From Fig. 1a, b, notice that the above inference holds for $l > 0$ as well. However, note that the nonlinearity parameter l affects the resilience of the CCFM to instability. Specifically, if the equilibrium headway $b_i > 1,$ then the locally stable region expands with an increase in l. However, when $b_i < 1,$ the locally stable region shrinks with an increase in l.

5.2 Discussion

A few comments are in order.

• (1) The foregoing analysis serves to clarify that the oscillations in state variables are a manifestation of limit cycles (isolated closed orbits in phase space) that emerge due to a Hopf bifurcation, and not centers (family of concentric closed orbits) as asserted in [9]. Further, as pointed out in the Introduction, these emergent limit cycles physically manifest themselves as back-propagating congestion waves, known as “phantom jams.” Thus, the analysis presented in this paper offers an explanation for this oft-observed phenomenon.

• (2) Note that $\kappa$ is an exogenous parameter introduced to aid the analysis. When the system operates on the edge of stability, this parameter is used to drive the system unstable in a controlled manner, as described in the foregoing analysis.

• (3) Feedback systems are known to lose stability when gain parameters are varied in a suitable manner [1, Sect. 3.7]. Therefore, to verify that the bifurcation phenomenon exhibited by the CCFM is not an artifact of the exogenous parameter, we prove the transversality condition of the Hopf spectrum with respect to a system parameter. For the CCFM, it can easily be shown, following the derivation in Sect. 5.1, that the CCFM undergoes a Hopf bifurcation when any of $\alpha _i$, $\tau _i$, ${\dot{x}}_0$, l or m is suitably varied.

• (4) Note that the D-partitioning and its “dual” $\tau$-decomposition approaches [41, Sect. 3.3] have been used extensively in the literature to study local stability properties of delay differential equations. While the former assumes the delay to be fixed and independent of other parameters, the latter allows only the delay to be varied. In contrast, our approach allows stability analysis to be conducted by a continuous variation of any parameter (including the exogenous parameter). Additionally, the use of an exogenous parameter as the bifurcation parameter captures any inter-dependence among model parameters, and generally simplifies the resulting algebra. Further, note that the bifurcation approach helps understand how local stability is lost and also approximates the trajectory of the CCFM in the vicinity of the equilibrium using nonlinear terms (up to third order in most cases)—key additions in comparison with other widely used approaches. This helps deduce the asymptotic orbital stability of the emergent limit cycles. Section 8 presents such an analysis for the CCFM.

• (5) Substituting $n = 0$ in (17), and letting $\kappa = 1$ on the stability boundary, the necessary and sufficient condition for the local stability of system (2) becomes

  $$\begin{aligned} \beta _i^* \tau _i < \frac{\pi }{2}. \end{aligned}$$

  (21)

  Note that when $\tau _i = 0,$ (21) is trivially satisfied. This, in turn, implies that the CCFM is stable for all parameter values, in the absence of reaction delays as seen in Sect. 3. However, as the delay increases, (21) will be violated, thus resulting in loss of local stability of the CCFM. This, in turn, validates our claim that delays play an important role in determining the qualitative behavior of the CCFM.

• (6) Note that the time linearization technique used in Sect. 4 may yield erroneous stability conditions; see [42, 43]. Therefore, the validity of any result obtained by using such a small-delay approximation should be verified on a case-by-case basis. For the CCFM, we note by comparing (12) and (21) that applying linearization to the time variable does yield a valid stability condition.

• (7) Note that (21) coincides with the necessary and sufficient condition derived in [9, Sect. 3.1]. In fact, the characteristic equation of form (15) (with $\kappa = 1$) arises in several applications including population dynamics [44], engineering [10], consensus dynamics [45] and vehicular dynamics [9]. In general, such equations have been analyzed using both time-domain [35, 44] and spectral-domain methods [9, 41]. However, to the best of our knowledge, none of these works apply the method used in this paper. Further, note that the evolution equations are nonlinear time-delay equations. Hence, the analysis goes beyond that of a linear time-delay system; see Sect. 8 for details.

6 Non-oscillatory convergence

In this section, we characterize the region corresponding to non-oscillatory convergence. Mathematically, this amounts to ensuring that the eigenvalues corresponding to system (4) are negative real numbers. Qualitatively, non-oscillatory convergence avoids jerky vehicular motion since relative velocities and headways constitute dynamical variables. Such results could help ensure the smooth flow of traffic and hence improve the ride quality.

In the above spirit, following [46], we derive the necessary and sufficient condition for non-oscillatory convergence of the CCFM. The characteristic equation pertaining to system (4), after dropping the subscript “i” for convenience, is $f(\lambda ) = \lambda + \beta ^* e^{-\lambda \tau } = 0$ [6, Eq. (8)]. Substituting $\lambda = - \sigma - j \omega$ and simplifying, we obtain

$$\begin{aligned} \sigma = \, \beta ^* e^{\sigma \tau } \cos (\omega \tau ), \text { and } \omega = \, \beta ^* e^{\sigma \tau } \sin (\omega \tau ). \end{aligned}$$

(22)

These, in turn, yield $\tan (\omega \tau ) = \omega /\sigma$. To ensure that $\omega = 0$ is the only solution of this equation, the necessary and sufficient condition is $\sigma \tau \ge 1$. Re-writing (22), we have

$$\begin{aligned} \beta ^* \tau e^{\sigma \tau } \left( \frac{\sin (\omega \tau )}{\omega \tau } \right) = 1. \end{aligned}$$

In the limit $\omega \rightarrow 0,$ the term within the brackets represents $\text {sinc}(0) = 1$. Moreover, the exponential term is bounded by e since $\sigma \tau \ge 1$. Hence, the boundary of non-oscillatory convergence is $\beta ^* \tau e = 1,$ and the corresponding necessary and sufficient condition for non-oscillatory convergence is

$$\begin{aligned} \beta ^* \tau \le \frac{1}{e}. \end{aligned}$$

(23)

Notice that the region in the parameter space described by (23) is a strict subset of the region described by (21). Therefore, from these two equations, we can summarize the conditions for the local stability of the CCFM as follows.

• (1) If $\beta ^* \tau \in [0,\pi /2),$ the system is locally stable.

• (2) Additionally, if $\beta ^* \tau \in [0,1/e],$ the system converges asymptotically to the equilibrium in a non-oscillatory fashion.

• (3) Contrarily, if $\beta ^* \tau \in (1/e,\pi /2),$ the state variable oscillates about the equilibrium, converging asymptotically.

Note that, despite differing in the method of derivation, (23) agrees with the condition for non-oscillatory condition derived in [9, Sect. 3].

7 Rate of convergence

Rate of convergence is an important performance metric that dictates the time a dynamical system takes to attain the desired equilibrium, when perturbed. In the context of a transportation network, it is related to the time required to attain the uniform traffic flow, once the traffic flow is perturbed (by events such as the departure of a vehicle from the platoon). Following [47], we characterize the rate of convergence for the CCFM.

The characteristic equation pertaining to system (4), with the subscript “i” dropped for ease of exposition, is $f(\lambda ) = \lambda + \beta ^* e^{-\lambda \tau } = 0$ [6, Eq. (8)]. In time domain, this corresponds to a system ${\dot{x}}(t) = - \beta ^* x(t - \tau ),$ where x is an arbitrarily chosen dynamical variable. The rate of convergence of such a system is the reciprocal of the smallest among $\sigma _1$, $\sigma _2$ and $\sigma _3,$ where these quantities are obtained by solving the equations [47, Theorem 2]

$$\begin{aligned}&\sigma \tau = \, 1, \\&\sigma \tau e^{-\sigma \tau } = \beta ^* \tau , \\&\frac{m}{\sin (m)} e^{-\frac{m}{\tan (m)}} = \beta ^* \tau , m = \sigma \tau \tan (m), \end{aligned}$$

respectively. The rate of convergence is maximum at $\tau ^* = 1/ (\beta ^* e)$. For $\tau < \tau ^*,$ the rate of convergence increases, whereas it decreases for $\tau > \tau ^*$ [47].

We solve the above equations using MATLAB to illustrate the variations in the rate of convergence for the CCFM, as the reaction delay is varied. To that end, we consider a tagged vehicle following a lead vehicle with an equilibrium velocity of 10. The tagged vehicle has a sensitivity coefficient of $\alpha = 0.7$ and tries to maintain an equilibrium headway of 20. We fix $m = 2,$ and consider $l \in \lbrace 0.8, 1, 1.2 \rbrace$.

The rate of convergence for this system is plotted in Fig. 2. It can be seen that the rate of convergence increases with $\tau$ for $\tau < \tau ^*,$ and decreases when the reaction delay is varied beyond $\tau ^*$. Also, note that the condition for the maximum rate of convergence coincides with the boundary for non-oscillatory convergence of the CCFM, $\beta ^* \tau ^* e = 1$. Hence, it would be optimal to choose parameters satisfying this equation. The said figure portrays $\tau ^*$ only for the $l = 1$ case.

Fig. 2

Variation in the rate of convergence of the CCFM as the reaction delay is increased, for $l \in \lbrace 0.8, 1, 1.2 \rbrace$

However, in practice, system parameters may vary. This will result in a shift of the operating point of the CCFM and may result in a trade-off between the rate of convergence and non-oscillatory convergence of the CCFM. Notice from Fig. 2 that, for a given value of nonlinearity parameter l,  the rate of convergence is not symmetric about $\tau ^*$. In the vicinity of $\tau ^*,$ if the operating point of the CCFM shifts to the left of $\tau ^*,$ the system retains its non-oscillatory behavior and the rate of convergence reduces drastically. On the other hand, if the operating point of the CCFM shifts to the right in the vicinity of $\tau ^*$, the system converges to the equilibrium in an oscillatory fashion, but the reduction in the rate of convergence is not as drastic. However, if the reaction delay increases considerably beyond $\tau ^*,$ then not only does the system exhibit oscillatory convergence, it may also converge to the equilibrium very slowly. This is portrayed in Fig. 2 using $\tau _1 = \tau ^*/3$ and $\tau _2 = 3 \tau ^*,$ for $l = 1$. Clearly, the rate of convergence at $\tau _2$ is much lesser than that at $\tau _1$.

Finally, notice from Fig. 2 that, an increase in l leads to a decrease in the rate of convergence. However, as discussed in Sect. 5.1, an increase in l makes the system relatively resilient to instability since $b_1 = 20 > 1$. Thus, there is a three-way trade-off involving the system’s resilience to instability, rate of convergence and non-oscillatory convergence. Note that Fig. 2 brings forth this trade-off for a fixed set of parameters. However, the same is true for other parameter values as well.

Note that the characteristic equation captures the closed-loop pairwise interaction in the platoon. To characterize the time taken by a platoon to reach an equilibrium (denoted by $T_{CCFM}^e$), we first define the time taken by the ith pair of vehicles in the platoon following the standard control-theoretic notion of “settling time.” That is, by $t_{i}^e(\epsilon ),$ we denote the minimum time taken by the time-domain trajectory of the ith pair to enter, and subsequently remain within, the $\epsilon$-band around its equilibrium. For simplicity, we drop the explicit dependence on $\epsilon$. Then, the platoon dynamics is said to converge to the uniform flow when the dynamics of each pair has settled inside the $\epsilon$-band of its respective equilibrium. Therefore, we have

$$\begin{aligned} T_{CCFM}^e = \max _{i = 1, 2, \dots , N} t_{i}^e. \end{aligned}$$

(24)

Here, given $\epsilon > 0$, $t_i^e$ is computed for the pair that has the least rate of convergence. This, in turn, yields $T_{CCFM}^e$. Note that the convergence of the CCFM is asymptotic, i.e., the system does not (strictly) converge to the equilibrium in finite time. Hence, we make use of the settling time concept.

8 Hopf bifurcation analysis

In the previous sections, we have characterized the stable region for the CCFM, and studied two of its most important properties; namely, non-oscillatory convergence and the rate of convergence. We have also proved, by means of the transversality condition of the Hopf spectrum (19), that system (2) loses stability via a Hopf bifurcation. In this section, we study the CCFM when it is pushed just beyond the stable region. We characterize the type of the bifurcation and the asymptotic orbital stability of the emergent limit cycles, following closely the style of analysis presented in [38], by using Poincaré normal forms and the center manifold theory.

We begin by defining $\mu = \kappa - \kappa _{cr}$. Thus, the system undergoes a Hopf bifurcation at $\mu =0,$ where $\kappa = \kappa _{cr}$. Henceforth, we consider $\mu$ as the bifurcation parameter. Note that changing $\kappa$ from $\kappa _{cr}$ to $\kappa _{cr} + \mu ,$ where $\mu >0,$ pushes the system in to its unstable regime.

Next, we expand the RHS of (13) about the all-zero equilibrium using Taylor’s series, to obtain

$$\begin{aligned} {\dot{v}}_i(t)&= - \kappa \beta ^*_i v_{i,t}( - \tau _i) + \kappa \beta ^*_{i-1} v_{(i-1),t}(- \tau _{i-1}) \nonumber \\&\quad - \frac{m}{{\dot{x}}_0} \beta _{i-1}^* v_{(i-1),t}^2(-\tau _{i-1}) + \frac{m}{{\dot{x}}_0} \beta _{i}^* v_{i,t}^2(-\tau _{i}) \nonumber \\&\quad - \frac{m}{{\dot{x}}_0} \beta _{i-1}^* \sum \limits _{n = 1}^{i-2} v_{n,t}(-\tau _{i-1}) v_{(i-1),t}(- \tau _{i-1}) \nonumber \\&\quad + \frac{m}{{\dot{x}}_0} \beta _{i-1}^* \sum \limits _{n = 1}^{i-1} v_{n,t}(-\tau _{i}) v_{i,t}(- \tau _{i}) \nonumber \\&\quad + \frac{l}{b_{i}} \beta _{i}^* v_{i,t}(-\tau _{i}) y_{i,t}(-\tau _{i}) \nonumber \\&\quad - \frac{m(m-1)}{2 ({\dot{x}}_0)^{2}} \beta _i^* v_{i}^3(-\tau _{i}) \nonumber \\&\quad - \frac{l}{b_{i-1}} \beta _{i-1}^* v_{(i-1),t}(-\tau _{i-1}) y_{(i-1),t}(-\tau _{i-1}) \nonumber \\&\quad - \frac{m(m-1)\beta _i^*}{2 ({\dot{x}}_0)^{2}} \sum \limits _{n,k = 1}^{i-1} v_{i,t}(-\tau _{i}) v_{n,t}(-\tau _{i}) v_{k,t}(-\tau _{i}) \nonumber \\&\quad + \frac{m(m-1)\beta _{i-1}^*}{2 ({\dot{x}}_0)^{2}} \sum \limits _{n,k = 1}^{i-2} ( v_{(i-1),t}(-\tau _{i-1}) \nonumber \\&\quad \times v_{n,t}(-\tau _{i-1}) v_{k,t}(-\tau _{i-1}) ) \nonumber \\&\quad - \frac{2m(m-1)}{3({\dot{x}}_0)^{2}} \beta _i^* \sum \limits _{n=1}^{i-1} v_{i,t}^2(-\tau _i) v_{n,t}(-\tau _i) \nonumber \\&\quad + \frac{2m(m-1)\beta _{i-1}^*}{3({\dot{x}}_0)^{2}} \sum \limits _{n=1}^{i-2} v_{(i-1),t}^*(-\tau _{i-1}) v_{n,t}(-\tau _{i-1}) \nonumber \\&\quad - \frac{l m}{3(b_{i})({\dot{x}}_0)} \beta _{i}^* \sum \limits _{n = 1}^{i-2} v_{i,t}(-\tau _{i}) v_{n,t}(-\tau _{i}) y_{i,t}(-\tau _{i}) \nonumber \\&\quad + \frac{l m \beta _{i-1}^*}{3(b_{i-1})({\dot{x}}_0)} \sum \limits _{n = 1}^{i-1} ( v_{(i-1),t}(-\tau _{i-1}) v_{n,t}(-\tau _{i-1}) \nonumber \\&\quad \times y_{(i-1),t}(-\tau _{i-1}) ) + \frac{m(m-1)}{2 ({\dot{x}}_0)^{2}} \beta _{i-1}^* v_{i-1}^3(-\tau _{i-1}) \nonumber \\&\quad - \frac{l m}{3({\dot{x}}_0)(b_i)} \beta _i^* v_{i,t}^2(-\tau _i) y_{i,t}(-\tau _i) \nonumber \\&\quad + \frac{l m}{3({\dot{x}}_0)(b_{i-1})} \beta _{i-1}^* v_{(i-1),t}^2(-\tau _{i-1}) y_{(i-1),t}(-\tau _{i-1}) \nonumber \\&{\dot{y}}_i(t) = \kappa v_i(t), \end{aligned}$$

(25)

where we use $v_{i,t}(-\tau _i)$ to denote $v_i(t - \tau _i)$.

Henceforth, we denote the space of all functions from A to B that are differentiable k times, with each derivative being continuous, by ${\mathcal {C}}^k\left( A;B\right)$. For convenience, we also use ${\mathcal {C}}$ to denote ${\mathcal {C}}^0$.

We define the state of the CCFM at time t as $\mathbf{S }(t) = [ v_1(t) \, v_2(t) \, \ldots \, v_N(t) \, y_1(t) \, y_2(t) \, \ldots \, y_N(t) ]$. Then, note that (2) can be written as:

$$\begin{aligned} \frac{\text {d}\mathbf{S }(t)}{\text {d}t} = {\mathcal {L}}_{\mu } \mathbf{S }_t(\theta ) + {\mathcal {F}}(\mathbf{S }_t(\theta ), \mu ), \end{aligned}$$

(26)

where t is positive and $\mu$ is a real quantity. Further, define $\tau = \underset{i}{\text {max }} \tau _i > 0$. Then, we have

$$\begin{aligned} \mathbf{S }_t(\theta ) = \mathbf{S }(t + \theta ), \text { } \mathbf{S }: [-\tau ,0] \longrightarrow {\mathbb {R}}^{2N}, \text { } \theta \in [-\tau , 0]. \end{aligned}$$

Here, ${\mathcal {L}}_{\mu }: {\mathcal {C}}\left( [-\tau ,0];{\mathbb {R}}^{2N}\right) \longrightarrow {\mathbb {R}}^{2N}$ is a one-parameter family of continuous, bounded linear functionals, while the operator ${\mathcal {F}}: {\mathcal {C}}\left( [-\tau ,0];{\mathbb {R}}^{2N}\right) \longrightarrow {\mathbb {R}}^{2N}$ is an aggregation of the nonlinear terms. Further, we assume that ${\mathcal {F}}(\mathbf{S }_t, \mu )$ is analytic, and that ${\mathcal {F}}$ and ${\mathcal {L}}_{\mu }$ depend analytically on $\mu$, when $|\mu |$ assumes small values. We now cast (26) in the standard form of an operator differential equation (OpDE):

$$\begin{aligned} \frac{\text {d}\mathbf{S }_t}{\text {d}t} = {\mathcal {A}}(\mu ) \mathbf{S }_t + {\mathcal {R}} \mathbf{S }_t, \end{aligned}$$

(27)

since the dependence here is on $\mathbf{S }_t$ alone rather than both $\mathbf{S }_t$ and $\mathbf{S }(t)$. Thus, we first transform the linear problem $\text {d}\mathbf{S }(t) / \text {d}t = {\mathcal {L}}_{\mu } \mathbf{S }_t(\theta )$. Riesz representation theorem [48, Theorem 6.19] guarantees the existence of a $2N \times 2N$ matrix-valued measure $\eta (\cdot , \mu )$ which takes in elements of ${\mathcal {B}}\left( {\mathcal {C}}\left( [-\tau ,0];{\mathbb {R}}^{2N}\right) \right)$ as an input, with the property that every component of this measure has bounded variation. Hence, for $\phi \in {\mathcal {C}}\left( [-\tau ,0];{\mathbb {R}}^{2N}\right) ,$ we can represent the linear problem as

$$\begin{aligned} {\mathcal {L}}_{\mu } \phi = \int \limits _{-\tau }^0 \text {d}\eta (\theta , \mu ) \phi (\theta ). \end{aligned}$$

(28)

Specifically for (26), we have

$$\begin{aligned} {\mathcal {L}}_{\mu } \mathbf{S }_t = \int \limits _{-\tau }^0 \text {d}\eta (\theta , \mu ) \mathbf{S }(t +\theta ). \end{aligned}$$

Keeping in mind the structure of the linearized system (4), we define

$$\begin{aligned} \text {d}\eta = \begin{bmatrix} {\tilde{A}}&0_{N \times N} \\ \kappa I_{N \times N}&0_{N \times N} \end{bmatrix} \text {d} \theta , \end{aligned}$$

where

$$\begin{aligned} ({\tilde{A}})_{ij} = {\left\{ \begin{array}{ll} -\kappa \beta _i^* \delta (\theta + \tau _i), &{} i = j,\\ \kappa \beta _i^* \delta (\theta + \tau _i), &{} i = j + 1, j \ge 1,\\ 0, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

For $\phi \in {\mathcal {C}}^1 \left( [-\tau ,0];{\mathbb {C}}^{2N}\right)$, we define

$$\begin{aligned} {\mathcal {A}}(\mu ) \phi (\theta ) = {\left\{ \begin{array}{ll} \frac{\text {d} \phi (\theta )}{\text {d} \theta }, &{} \theta \in [-\tau ,0),\\ \int \limits _{-\tau }^0 \text {d}\eta (s, \mu ) \phi (s) \equiv {\mathcal {L}}_{\mu }, &{} \theta = 0, \end{array}\right. } \end{aligned}$$

(29)

and

$$\begin{aligned} {\mathcal {R}} \phi (\theta ) = {\left\{ \begin{array}{ll} 0, &{} \theta \in [-\tau ,0),\\ {\mathcal {F}}(\phi , \mu ), &{} \theta = 0. \end{array}\right. } \end{aligned}$$

With the above definitions, we observe that $\text {d} \mathbf{S }_t / \text {d} \theta \equiv \text {d} \mathbf{S }_t / \text {d} t$. That is, we have cast (26) in the standard form of OpDE (27). Note that, going forward, it suffices to consider the aforementioned equations at the critical value of the bifurcation parameter. Therefore, we impose $\mu = 0$ hereon. We begin by finding the eigenvector of ${\mathcal {A}}(0)$ having an eigenvalue $\lambda (0) = j \omega _0$. That is, we look for a $2N \times 1$ vector (denoted by $q(\theta )$) such that ${\mathcal {A}}(0) q(\theta ) = j \omega _0 q(\theta )$ holds. We assume: $q(\theta ) = [1 \text { } \phi _1 \text { } \phi _2 \cdots \text { } \phi _{2N-1}]^T\,e^{j \omega _0 \theta }$. In order to solve the eigenvalue equations, we require the following assumption: $- \kappa \beta _1^* e^{- j \omega _0 \tau _1} = j \omega _0 \phi _0$. Then, for $i \in \lbrace 1, 2, \ldots N-1 \rbrace ,$ and $k \in \lbrace N, N+1, \ldots 2N-1 \rbrace ,$

$$\begin{aligned} \phi _i = \frac{\kappa \beta _i^* e^{- j \omega _0 \tau _i} \phi _{i-1}}{j \omega _0 + \kappa \beta _{i+1}^* e^{- j \omega _0 \tau _{i+1}}}, \text { and } \phi _k = \frac{\kappa \varTheta \phi _{2N-k}}{j \omega _0}, \end{aligned}$$

where we set $\phi _0 = 1$ for notational brevity. Here, $\varTheta = j ( e^{-j \omega _0 \tau } - 1) / \omega _0$.

Net, we define the adjoint operator of ${\mathcal {A}}$ as follows:

$$\begin{aligned} {\mathcal {A}}^*(0) \phi (\theta ) = {\left\{ \begin{array}{ll} -\frac{\text {d} \phi (\theta )}{\text {d} \theta }, &{} \theta \in (0, \tau ],\\ \int \limits _{-\tau }^0 \text {d}\eta ^T(s, 0) \phi (-s), &{} \theta = 0, \end{array}\right. } \end{aligned}$$

where d$\eta ^T$ is the transpose of d$\eta$.

The operator ${\mathcal {A}}^*$ maps real-valued functions defined over $[-\tau ,0]$ to a 2N-dimensional complex vector. Indeed, if $\nu$ is an eigenvalue of ${\mathcal {A}},$ then $\nu ^{*}$ is an eigenvalue of ${\mathcal {A}}^*$. Therefore, to find the eigenvector of ${\mathcal {A}}^*(0)$ corresponding to $-j \omega _0,$ we solve ${\mathcal {A}}^*(0) p(\theta ) = - j \omega _0 p(\theta )$. We assume: $p(\theta ) = B [\psi _{2N-1} \text { } \psi _{2N-2} \text { } \psi _{2N-3} \text { } \cdots \text { } 1 ]^T \text { } e^{j \omega _0 \theta }$. Simplifying the above operator equation, we obtain for $i \in \lbrace 1, 2, \cdots N-1 \rbrace ,$

$$\begin{aligned} \psi _N&= \frac{\kappa {\tilde{\varTheta }} \psi _0}{\kappa \beta _N^* e^{j \omega _0 \tau _{N}} - j \omega _0}, \text { } \psi _{i} = - j \omega _0, \text { and } \\ \psi _{N+i}&= \frac{\kappa \beta _{2N-i}^* e^{j \omega _0 \tau _{2N-i}} + \kappa {\tilde{\varTheta }} \psi _{N-i}}{\kappa \beta _{2N-i}^* e^{j \omega _0 \tau _{2N-i}} - j \omega _0}, \end{aligned}$$

where we set $\psi _0 = 1$ for notational brevity. Also, ${\tilde{\varTheta }} = j ( e^{j \omega _0 \tau } - 1) / \omega _0$.

We know that the inner product between p and q must be unity [38]. Evaluating this by using the above-mentioned expressions, we obtain an expression for B.

For any q in the domain of ${\mathcal {A}}$ and p in the domain of ${\mathcal {A}}^{*},$ we define the inner product as

$$\begin{aligned} \langle p, q \rangle \triangleq {\bar{p}} \cdot q - \int \limits _{\theta = - \tau }^0 \int \limits _{\zeta = 0}^{\theta } {\bar{p}}^T(\zeta - \theta ) \text {d}\eta q(\zeta ) \text { d}\zeta , \end{aligned}$$

(30)

where the overbar represents the complex conjugate and the “$\cdot$” represents the regular dot product. The value of B such that the inner product between the eigenvectors of ${\mathcal {A}}$ and ${\mathcal {A}}^*$ is unity can be shown to be

$$\begin{aligned} B = \frac{1}{\zeta _1 + \zeta _2 + \zeta _3 + \zeta _4}, \end{aligned}$$

where

$$\begin{aligned} \zeta _1&= {\overline{\varTheta }}^* \sum \limits _{i = 0}^{N-1} \kappa \psi _{N} {\bar{\phi }}_i, \text { } \zeta _2 = - \kappa \beta _N^* {\overline{\phi }}_{N-1} \psi _N \tau _N e^{j \omega _0 \tau _N} , \\ \zeta _3&= \sum \limits _{i = 1}^{N-1} \kappa \beta _i^* \tau _i e^{j \omega _0 \tau _i} {\overline{\phi }}_{i-1} ( \psi _{2N-i} - \psi _{2N-i-1} ) \text { and } \\ \zeta _4&= \sum \limits _{i = 0}^{2N-1} \psi _{2N-1-i} {\bar{\phi }}_i. \end{aligned}$$

In the above, we define $\phi _0 = \psi _0 = 0$ for notational brevity.

For $\mathbf{S }_t$, a solution of (27) at $\mu =0,$ we define

$$\begin{aligned} z(t)&= \langle p(\theta ), \mathbf{S }_t \rangle , \text { and }z \mathbf{w }(t, \theta ) \\&= \mathbf{S }_t(\theta ) - 2 \text {Real} ( z(t) q(\theta ) ). \end{aligned}$$

Then, on the center manifold $C_0$, we have $\mathbf{w }(t, \theta ) = \mathbf{w }(z(t), {\bar{z}}(t), \theta )$, where

$$\begin{aligned} \mathbf{w }(z(t), {\bar{z}}(t), \theta )&= \mathbf{w }_{20}(\theta ) \frac{z^2}{2} + \mathbf{w }_{02}(\theta ) \frac{{\bar{z}}^2}{2} \nonumber \\&\quad + \mathbf{w }_{11}(\theta ) z {\bar{z}} + \cdots . \end{aligned}$$

(31)

For the center manifold ${\mathcal {C}},$ the vectors z and ${\bar{z}}$ locally point along p and ${\bar{p}}$, respectively. Further, $\mathbf{w }$ is real if $\mathbf{S }_t$ is. And in such a case, we obtain only real solutions. As a consequence of the existence of $C_0,$ we can rewrite the standard form of an OpDE (27) as an ODE in one complex variable on the center manifold. Specifically, at the critical value of the bifurcation parameter, the said ODE can be written as

$$\begin{aligned} {\dot{z}}(t) =&\, \left\langle p, {\mathcal {A}} \mathbf{S }_t + {\mathcal {R}} \mathbf{S }_t \right\rangle , \nonumber \\ =&\, j \omega _0 z(t) + {\bar{p}}(0). {\mathcal {F}}\left( \mathbf{w }(z, {\bar{z}}, \theta ) + 2 \text {Real}( z(t) q(\theta ) ) \right) , \nonumber \\ =&\, j \omega _0 z(t) + {\bar{p}}(0). {\mathcal {F}}_0(z, {\bar{z}}), \end{aligned}$$

(32)

$$\begin{aligned} =&j \omega _0 z(t) + g(z, {\bar{z}}). \end{aligned}$$

(33)

The term g can be written as

$$\begin{aligned} g(z, {\bar{z}})&= \, {\bar{p}}(0). {\mathcal {F}}_0(z, {\bar{z}}) \nonumber \\&= \, g_{20} \frac{z^2}{2} + g_{02} \frac{{\bar{z}}^2}{2} + g_{11} z {\bar{z}} + g_{21} \frac{z^2 {\bar{z}}}{2} + \cdots . \end{aligned}$$

(34)

Note that, from the definition of $\mathbf{w },$ we have $\dot{\mathbf{w }} = \dot{\mathbf{S }}_t - {\dot{z}} q - \dot{{\bar{z}}} {\bar{q}}$. This can be simplified using (27) and (33) as:

$$\begin{aligned} \dot{\mathbf{w }} = {\left\{ \begin{array}{ll} {\mathcal {A}} \mathbf{w } - 2 \text {Real} ( {\bar{p}}(0). {\mathcal {F}}_0 q(\theta ) ), &{} \theta \in [-\tau , 0),\\ {\mathcal {A}} \mathbf{w } - 2 \text {Real} ( {\bar{p}}(0). {\mathcal {F}}_0 q(0) ) + {\mathcal {F}}_0, &{} \theta = 0. \end{array}\right. } \end{aligned}$$

Using (31), we rewrite this as

$$\begin{aligned} {\dot{\mathbf{w }}} = {\mathcal {A}} \mathbf{w } + H(z, {\bar{z}}, \theta ), \end{aligned}$$

(35)

where

$$\begin{aligned} H(z, {\bar{z}}, \theta )&= \, H_{20}(\theta ) \frac{z^2}{2} + H_{02}(\theta ) \frac{{\bar{z}}^2}{2} + H_{11}(\theta ) z {\bar{z}} \nonumber \\&\quad + H_{21}(\theta ) \frac{z^2 {\bar{z}}}{2} + \cdots . \end{aligned}$$

(36)

Note that $\dot{\mathbf{w }} = \mathbf{w }_z {\dot{z}} + \mathbf{w }_{{\bar{z}}} \dot{{\bar{z}}}$ is true in the vicinity of the origin, on the center manifold. Thus, we use (31) and (33) in place of $\mathbf{w }_z {\dot{z}}$. Further, we equate this to (35) and obtain

$$\begin{aligned}&(2 j \omega _0 - {\mathcal {A}}) \mathbf{w }_{20}(\theta ) = \, H_{20}(\theta ), \end{aligned}$$

(37)

$$\begin{aligned}&- {\mathcal {A}} \mathbf{w }_{11} = \, H_{11}(\theta ), \end{aligned}$$

(38)

$$\begin{aligned}&-(2 j \omega _0 + {\mathcal {A}}) \mathbf{w }_{02}(\theta ) = \, H_{02}(\theta ). \end{aligned}$$

(39)

Observe that

$$\begin{aligned} \mathbf{S }_t(\theta )&= \, \mathbf{w }_{20}(\theta ) \frac{z^2}{2} + \mathbf{w }_{02}(\theta ) \frac{{\bar{z}}^2}{2} + \mathbf{w }_{11}(\theta ) z {\bar{z}} \\&\quad + z q(\theta ) + {\bar{z}} {\bar{q}}(\theta ) + \cdots . \end{aligned}$$

In order to approximate the system dynamics, it suffices to use the coefficients of $z^2$, ${\bar{z}}^2$, $z^2 {\bar{z}}$, and $z {\bar{z}}$ [38]. Thus, henceforth, we only make use of these terms in various required expansions.

To understand the effect of quadratic and cubic terms of the Taylor’s series expansion, we substitute the aforementioned terms appropriately in the nonlinear terms of (25) and separate the terms as required. Therefore, for each $i \in \lbrace 1, 2, \dots , 2N \rbrace$, we have the nonlinearity term to be

$$\begin{aligned} {\mathcal {F}}_i = {\mathcal {F}}_{20i} \frac{z^2}{2} + {\mathcal {F}}_{02i} \frac{{\bar{z}}^2}{2} + {\mathcal {F}}_{11i} z {\bar{z}} + {\mathcal {F}}_{21i} \frac{z^2 {\bar{z}}}{2}, \end{aligned}$$

(40)

where, for $i \in \lbrace 1, 2, \ldots , N \rbrace ,$ the coefficients are given by

$$\begin{aligned} {\mathcal {F}}_{20i} =&- 4 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i-1}} \right) \beta _{i-1}^* e^{- 2 j \omega _0 \tau _{i-1}} \\&+ 4 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i}} \right) \beta _{i}^* e^{- 2 j \omega _0 \tau _{i}}, \\&- 4 \left( \frac{m}{{\dot{x}}_0} \right) \beta _{i-1}^* (i-2) e^{-2 j \omega _0 \tau _{i-1}} \\&+ 4 \left( \frac{m}{{\dot{x}}_0} \right) \beta _{i}^* (i-1) e^{-2 j \omega _0 \tau _{i}} \\ {\mathcal {F}}_{02i} =&- 4 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i-1}} \right) \beta _{i-1}^* e^{2 j \omega _0 \tau _{i-1}} \\&+ 4 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i}} \right) \beta _{i}^* e^{2 j \omega _0 \tau _{i}}, \\&- 4 \left( \frac{m}{{\dot{x}}_0} \right) \beta _{i-1}^* (i-2) e^{2 j \omega _0 \tau _{i-1}} \\&+ 4 \left( \frac{m}{{\dot{x}}_0} \right) \beta _{i}^* (i-1) e^{2 j \omega _0 \tau _{i}} \\ {\mathcal {F}}_{11i} =&- 2 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i-1}} \right) \beta _{i-1}^* + 2 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i}} \right) \beta _{i}^*, \\ {\mathcal {F}}_{21i} =&-2 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i-1}} \right) \beta _{i-1}^* w_{20(i-1)}(-\tau _{i-1}) e^{j \omega _0 \tau _{i-1}} \\&-4 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i-1}} \right) \beta _{i-1}^* w_{11(i-1)}(-\tau _{i-1}) e^{-j \omega _0 \tau _{i-1}} \\&+ 2 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i}} \right) \beta _{i}^* w_{20i}(-\tau _i) e^{j \omega _0 \tau _{i}} \\&+ 4 \left( \frac{m}{{\dot{x}}_0} + \frac{l}{b_{i}} \right) \beta _{i}^* w_{11i}(-\tau _{i}) e^{-j \omega _0 \tau _{i}} \\&- \left( \frac{m}{{\dot{x}}_0}\right) \beta _{i-1}^* \sum \limits _{n = 1}^{i-2} w_{20n}(-\tau _{i-1}) e^{j \omega _0 \tau _{i-1}} \\&- \left( \frac{m}{{\dot{x}}_0}\right) \beta _{i-1}^* \sum \limits _{n = 1}^{i-2} w_{20(i-1)}(-\tau _{i-1}) e^{j \omega _0 \tau _{i-1}} \\&- \left( \frac{2m}{{\dot{x}}_0}\right) \beta _{i-1}^* \sum \limits _{n = 1}^{i-2} w_{11n}(-\tau _{i-1}) e^{ -j \omega _0 \tau _{i-1}} \\&- \left( \frac{2m}{{\dot{x}}_0}\right) \beta _{i-1}^* \sum \limits _{n = 1}^{i-2} w_{11(i-1)}(-\tau _{i-1}) e^{ -j \omega _0 \tau _{i-1}} \\&+ \left( \frac{m}{{\dot{x}}_0}\right) \beta _{i}^* \sum \limits _{n = 1}^{i-1} (w_{20n}(-\tau _{i}) + w_{20i}(-\tau _{i})) e^{j \omega _0 \tau _{i}} \\&+ \left( \frac{2m}{{\dot{x}}_0}\right) \beta _{i}^* \sum \limits _{n = 1}^{i-1} (w_{11n}(-\tau _{i}) + w_{11i}(-\tau _{i})) e^{ -j \omega _0 \tau _{i}} \\&- ( 2 e^{- j \omega _0 \tau _{i}} \beta _{i}^*) \\&\quad \left( \frac{2m(m-1)(i-1)}{3({\dot{x}}_0)^2} + \frac{l m (i-1)}{3(b_{i}) ({\dot{x}}_0)} \right) \\&- (2 e^{- j \omega _0 \tau _{i}} \beta _{i}^*) \left( \frac{l m}{3(b_{i}) ({\dot{x}}_0)} \right) \\&+ (2 e^{- j \omega _0 \tau _{i-1}} \beta _{i-1}^*) \left( \frac{l m}{3(b_{i-1}) ({\dot{x}}_0)} \right) \\&- (2 e^{- j \omega _0 \tau _{i}} \beta _{i}^*) \\&\quad \left( \frac{m(m-1)}{2({\dot{x}}_0)^2} + \frac{m(m-1) (i-1)^2}{({\dot{x}}_0)^2} \right) \\&+ (2 e^{- j \omega _0 \tau _{i-1}} \beta _{i-1}^*) \\&\quad \left( \frac{m(m-1)}{2({\dot{x}}_0)^2} + \frac{m(m-1) (i-2)^2}{({\dot{x}}_0)^2} \right) \\&+ (2 e^{- j \omega _0 \tau _{i-1}} \beta _{i-1}^*) \\&\quad \left( \frac{2m(m-1)(i-2)}{3({\dot{x}}_0)^2} + \frac{l m (i-2)}{3(b_{i-1}) ({\dot{x}}_0)} \right) . \end{aligned}$$

Next, we write ${\mathcal {F}}_0 = [{\mathcal {F}}_1 \text { } {\mathcal {F}}_2 \text { } \text { } \cdots \text { } {\mathcal {F}}_N]^T$. From this, g is obtained as

$$\begin{aligned} g(z, {\bar{z}}) = {\bar{p}}(0).{\mathcal {F}}_0 = {\bar{B}} \sum \limits _{l = 1}^N {\bar{\psi }}_{N-l} {\mathcal {F}}_l. \end{aligned}$$

(41)

Plugging in ${\mathcal {F}}_i$’s from (40) in (41), we obtain

$$\begin{aligned} g_{x} = {\bar{B}} \sum \limits _{l = 1}^N {\bar{\psi }}_{N-l} {\mathcal {F}}_{xl}, \end{aligned}$$

(42)

where $x \in \lbrace 20, 02, 11, 21 \rbrace$. Using (42), the corresponding coefficients can be computed. Note that obtaining $g_{21}$ requires $\mathbf{w }_{20}(\theta )$ and $\mathbf{w }_{11}(\theta )$. To that end, we simplify H as

$$\begin{aligned} H(z, {\bar{z}}, \theta )&= - \text {Real} \left( {\bar{p}}(0). {\mathcal {F}}_0 q(\theta ) \right) , \\&= - \left( g_{20} \frac{z^2}{2} + g_{02} \frac{{\bar{z}}^2}{2} + g_{11} z {\bar{z}} + \cdots \right) q(\theta ) \\& - \left( {\bar{g}}_{20} \frac{{\bar{z}}^2}{2} + {\bar{g}}_{02} \frac{z^2}{2} + {\bar{g}}_{11} z {\bar{z}} + \cdots \right) {\bar{q}}(\theta ). \end{aligned}$$

This is true for $\theta \in [-\tau ,0)$. By comparing with (36), we obtain

$$\begin{aligned} H_{20}(\theta )&= - g_{20} q(\theta ) - {\bar{g}}_{20} {\bar{q}}(\theta ), \end{aligned}$$

(43)

$$\begin{aligned} H_{11}(\theta )&= - g_{11} q(\theta ) - {\bar{g}}_{11} {\bar{q}}(\theta ). \end{aligned}$$

(44)

From (29), (37) and (38), we obtain:

$$\begin{aligned} {\dot{\mathbf{w }}}_{20}(\theta ) =&\, 2 j \omega _0 \mathbf{w }_{20}(\theta ) + g_{20} q(\theta ) + {\bar{g}}_{02} {\bar{q}}(\theta ), \end{aligned}$$

(45)

$$\begin{aligned} \dot{\mathbf{w }}_{11}(\theta ) =&\, g_{11} q(\theta ) + {\bar{g}}_{11} {\bar{q}}(\theta ). \end{aligned}$$

(46)

The solution to above ODEs is given by

$$\begin{aligned} \mathbf{w }_{20}(\theta ) =&\, - \frac{g_{20}}{j \omega _0} q(0) e^{j \omega _0 \theta } - \frac{{\bar{g}}_{02}}{3 j \omega _0} {\bar{q}}(0) e^{-j \omega _0 \theta } + \mathbf{e } \text { } e^{2 j \omega \theta }, \end{aligned}$$

(47)

$$\begin{aligned} \mathbf{w }_{11}(\theta ) =&\, \frac{g_{11}}{j \omega _0} q(0) e^{j \omega _0 \theta } - \frac{{\bar{g}}_{11}}{ j \omega _0} {\bar{q}}(0) e^{-j \omega _0 \theta } + \mathbf{f }, \end{aligned}$$

(48)

where $\mathbf{e }$ and $\mathbf{f }$ are to be determined.

We define $\tilde{{\mathcal {F}}}_{20} \triangleq [{\mathcal {F}}_{201} \text { } {\mathcal {F}}_{202} \text { } \cdots \text { } {\mathcal {F}}_{20N}]^T$. Equating (37) and (43) yields $2 j \omega _0 \mathbf{e } - {\mathcal {A}} \left( \mathbf{e } \text { } e^{2 j \omega _0 \theta } \right) = \tilde{{\mathcal {F}}}_{20}$. On simplifying this operator equation, we obtain

$$\begin{aligned} \mathbf{e }_i = \frac{{\mathcal {F}}_{20i} - \kappa \beta _{i-1}^* \mathbf{e }_{i-1}}{2 j \omega _0 + \kappa \beta _i^* }, \text { and, } \mathbf{e }_{N+i} = \frac{{\mathcal {F}}_{20(N+i)} + \kappa \tau \mathbf{e }_i}{2 j \omega _0}, \end{aligned}$$

(49)

for $i \in \lbrace 1, 2, \ldots , N \rbrace$. Here, we set $\mathbf{e }_0 = 0$ for notational brevity.

We next define $\tilde{{\mathcal {F}}}_{11} \triangleq [{\mathcal {F}}_{111} \text { } {\mathcal {F}}_{112} \text { } \cdots \text { } {\mathcal {F}}_{11N}]^T$ and equate (38) to (44), to obtain ${\mathcal {A}} \mathbf{f } = -\tilde{{\mathcal {F}}}_{11}$. In order to solve this, we make the following assumption:

$$\begin{aligned} {\mathcal {F}}_{20i} \tau + \kappa \beta _{i-1}^* \mathbf{f }_{i-1} + \beta _i^* {\mathcal {F}}_{11(N+i)} = 0, \end{aligned}$$

for $i \in \lbrace 1, 2, \ldots , N-1 \rbrace$. With this assumption, solving the aforementioned operator equation yields, for $i \in \lbrace 1, 2, \ldots , N \rbrace ,$

$$\begin{aligned} \mathbf{f }_i = \frac{{\mathcal {F}}_{11i} + \kappa \beta _{i-1}^* \mathbf{f }_{i-1}}{\kappa \beta _i^*}, \text { and, } \mathbf{f }_{N+i} = c, \end{aligned}$$

(50)

where c is an arbitrary constant, set to zero for simplicity. We also set $\mathbf{f }_0 = 0$ for notational brevity.

Substituting for $\mathbf{e }$ and $\mathbf{f }$ from (49) and (50) in (47) and (48), respectively, we obtain $\mathbf{w }_{20}(\theta )$ and $\mathbf{w }_{11}(\theta )$. These help compute $g_{21}$. By $\alpha ^{'}(0),$ we denote the velocity of the eigenvalue in the Argand plane, given by (19). Thus, we can compute

$$\begin{aligned} c_1(0)&= \frac{j}{2 \omega _0} \left( g_{20} g_{11} - 2 | g_{11} |^2 - \frac{1}{3} | g_{02} |^2 \right) + \frac{g_{21}}{2}, \\ \mu _2&= - \frac{\text {Re}[c_1(0)]}{\alpha ^{'}(0)}, \text { } \beta _2 = 2 \text {Re}[c_1(0)]. \end{aligned}$$

Here, $c_1(0)$ is known as the Lyapunov coefficient and $\beta _2$ is the Floquet exponent. These quantities are useful since they help infer the type of the Hopf bifurcation and the asymptotic orbital stability of the emergent limit cycles [38]. Specifically, we have

(i):

If $\mu _2 > 0$, then the bifurcation is supercritical, while if $\mu _2 < 0$, then the bifurcation is subcritical.

(ii):

If $\beta _2 > 0$, then the limit cycle is asymptotically orbitally unstable, whereas if $\beta _2 < 0$, then the limit cycle is asymptotically orbitally stable.

Some details of the derivation can be found in the technical report [49].

To obtain some insight into the type of the Hopf bifurcation and the asymptotic orbital stability of the emergent limit cycles for the CCFM, we make use of the scientific computation software MATLAB to compute $\mu _2$ and $\beta _2$ using the above equations. The parameter values chosen and the corresponding values of $\mu _2$ and $\beta _2$ are as summarized below.

• (1) $N = 3$, $\alpha _1 = 0.8$, $\alpha _2 = 0.6$, $\alpha _3 = 0.5$, $\tau _1 = 0.2$, $\tau _2 = \tau _{cr} \approx 0.26$, $\tau _3 = 0.6$, $b_1 = 5$, $b_2 = 10$, $b_3 = 15$, $m = 2$, $l = 1$, ${\dot{x}}_0 = 5$. The computed values are $\mu _2 = 2.77 \times 10^{-48}$ and $\beta _2 = -1.51 \times 10^{-47}$. These values imply that the 2nd vehicle undergoes a supercritical Hopf bifurcation leading to asymptotically orbitally stable limit cycles.

• (2) $N = 4$, $\alpha _1 = 0.5$, $\alpha _2 = 0.6$, $\alpha _3 = 0.7$, $\alpha _4 = 0.8$, $\tau _1 = 0.5$, $\tau _2 = 0.4,$$\tau _3 = \tau _{cr} \approx 0.45,$$\tau _4 = 0.3$, $b_i = 20$, $i \in \lbrace 1, 2, 3, 4 \rbrace$, $l = 1$, $m = 2$, ${\dot{x}}_0 = 10$. The computed values are $\mu _2 = 5.39 \times 10^{-18}$ and $\beta _2 = -1.71 \times 10^{-17}$. Thus, the 3rd vehicle undergoes a supercritical Hopf bifurcation leading to asymptotically orbitally stable limit cycles.

• (3) $N = 10$, $\alpha _i = 0.6$, $i \in \lbrace 1, 2, \ldots , 10 \rbrace$, $\tau _i = 0.4$$\forall i \ne 5$, $\tau _5 = \tau _{cr} \approx 0.07$, $b_i = 25$, $i \in \lbrace 1, 2, \ldots , 10 \rbrace$, $l = 1$, $m = 2$, ${\dot{x}}_0 = 30$. The computed values are $\mu _2 = 1.6 \times 10^{-32}$ and $\beta _2 = -3.14 \times 10^{-31}$. Note that the 5th vehicle undergoes a supercritical Hopf bifurcation leading to asymptotically orbitally stable limit cycles.

• (4) $N = 50$, $\alpha _i = 0.6$, $i \in \lbrace 1, 2, \ldots , 50 \rbrace$, $\tau _i = 0.5$$\forall i \ne 25$, $\tau _{25} = \tau _{cr} \approx 1.05$, $b_i = 10$, $i \in \lbrace 1, 2, \ldots , 50 \rbrace$, $l = 1$, $m = 2$, ${\dot{x}}_0 = 5$. The computed values are $\mu _2 = 9.1 \times 10^{-39}$ and $\beta _2 = -1.24 \times 10^{-38}$. Therefore, the 25th vehicle undergoes a supercritical Hopf bifurcation leading to asymptotically orbitally stable limit cycles.

Indeed, computations for a wide range of parameter values show that the CCFM loses local stability via a supercritical Hopf bifurcation, and leads to asymptotically orbitally stable limit cycles. This is in line with results for the RCCFM presented in [49, Version 3], and generalizes them to the CCFM. Further, the supercritical nature of the bifurcation suggests that, if at all the CCFM were to lose stability, one could regain stability by an appropriate variation of any parameter as per the stability condition (21). In turn, this could help the upper longitudinal controller regain stability, in case the system were to lose stability.

Next, we present numerically constructed bifurcation diagrams to understand the effect of various parameters on the amplitude of the limit cycle.

Fig. 3

Bifurcation diagram: Variation in the amplitude of relative velocity of the CCFM as the non-dimensional parameter $\kappa$ is varied, for $l \in \lbrace 0.95, 1, 1.05 \rbrace$

8.1 Bifurcation diagrams

We next present bifurcation diagrams, numerically constructed using the scientific computation software MATLAB. We implement a discrete version of system (13) with update time $T_s = 0.01$ s. We then record the amplitude of the relative velocity in steady state by varying the non-dimensional parameter $\kappa$ in the range [1, 1.05]. The resulting plot of the envelope of the relative velocity as a function of the non-dimensional parameter is called a bifurcation diagram.

For illustration, we consider a single vehicle following a lead vehicle whose equilibrium velocity is 10. For the follower vehicle, we initialize the parameters as follows. $\alpha _1 = 0.7$, $b_1 = 20$ and $m = 2$. We set the reaction delay $\tau _1 = \tau _{cr} \approx 0.45$ to ensure that $\kappa _{cr} = 1$. Next, we vary the non-dimensional parameter in the vicinity of unity, and record the resulting amplitude of the relative velocity for $l = 0.95, 1, 1.05$. The resulting bifurcation diagram is portrayed in Fig. 3.

It can be inferred from Fig. 3 that, there is no monotonicity in the amplitude of relative velocity with an increase in the nonlinearity parameter l. This is unlike the result presented in [6], wherein monotonicity of the amplitude of relative velocity with an increase in m was shown numerically, for $l = 0$ (the RCCFM). While Fig. 3 was constructed for $m = 2,$ extensive computations reveal a lack of monotonicity in the amplitude of limit cycle with an increase in l.

9 Simulations

We now present the simulation results for the CCFM that serve to corroborate our analytical findings. We make use of the scientific computation software MATLAB to implement a discrete version of system (2) with update time $T_s = 0.01$ s, thus simulating the CCFM.

Fig. 4

Simulations: Emergence of limit cycles in the spacing error y(t) and the relative velocity v(t), as predicted by the analysis

We initialize the parameters with the following values. $N = 4$, $\alpha _1 = 0.5$, $\alpha _2 = 0.6$, $\alpha _3 = 0.7$, $\alpha _4 = 0.8$, $\tau _1 = 0.5$, $\tau _2 = 0.4$, $\tau _3 = \tau _{cr} \approx 0.45$ and $\tau _4 = 0.3$. The leader’s velocity profile is considered to be $10 (1 - e^{-10t}),$ thus ensuring an equilibrium velocity of 10. Further, we fix $m = 2$, $l = 1$ and desired headways $b_i = 20$$\forall i$. Figure 4 shows the emergence of limit cycles in the state variables of the third vehicle, as predicted by our analysis. Also notice the phase shift between the relative velocity and headway solutions, as a consequence of obtaining the latter by integrating the former.

Fig. 5

Simulations: Non-oscillatory and oscillatory solutions of the CCFM. a Portrays the relative velocity solutions, whereas b shows the spacing error solutions. These serve to validate our analytical insight

Next, we validate that the CCFM does indeed exhibit non-oscillatory convergence to the all-zero equilibrium, as predicted by (23). We also compare the rate of convergence when the reaction delay satisfies $\tau < \tau ^*$ and $\tau > \tau ^*,$ as discussed in Sect. 7. We make use of the same parameter values as above, except for reaction delays; these are identically set to $\tau _1 = 1/(3 e \beta ^*)$ and $\tau _2 = 3/( e \beta ^*)$. Figure 5a, b portray the solutions for relative velocity and headway, respectively. To ensure comparison with Fig. 2, these plots correspond to the third vehicle, i.e.,$\alpha = 0.7$$\text {s}^{-1}$ and $l = 1$. Notice that $\tau _1$ and $\tau _2,$ which are not in the vicinity of $\tau ^*$ corresponding to the third vehicle, as seen from Fig. 2. Hence, the solutions corresponding to $\tau _1$ attain their equilibria much faster than those pertaining to $\tau _2$.

10 Concluding remarks

In this paper, we highlighted the importance of delayed feedback in determining the qualitative dynamical properties of a platoon of vehicles traversing an infinite highway. Specifically, we analyzed the classical car-following model (CCFM) in three regimes—no delay, small delay and arbitrary delay. In the absence of delays, the CCFM was shown to be always locally stable. Then, the analysis for small-delay regime yielded a sufficient condition for the local stability of the CCFM, whereas we obtained the necessary and sufficient condition for the local stability of the CCFM in the arbitrary-delay regime.

We then proved that the CCFM undergoes a loss of local stability via a Hopf bifurcation, thus resulting in the emergence of limit cycles in system dynamics. Physically, these limit cycles manifest as back-propagating congestion waves on highways. Thus, in the context of human-driven vehicles, where parameters cannot be tuned, our work enhances the phenomenological insight into “phantom jams.” Therein, we used an exogenous and non-dimensional parameter to capture any inter-dependence among various parameters.

We then derived the necessary and sufficient condition for non-oscillatory convergence of the CCFM. Designing control algorithms that conform to this condition ensures that jerky vehicular motions are avoided, thus guaranteeing smooth traffic flow and improving ride quality. Next, we characterized the rate of convergence of the CCFM and highlighted the three-way trade-off between local stability, non-oscillatory convergence and the rate of convergence.

Finally, we studied the nonlinear oscillations in system dynamics that emerge as the CCFM undergoes a Hopf bifurcation. To that end, we outlined an analytical framework to establish the type of the Hopf bifurcation and the asymptotic orbital stability of the limit cycles using Poincaré normal forms and the center manifold theory. We then numerically brought forth the supercritical nature of the bifurcation resulting in stable limit cycles. Stability charts, numerically constructed bifurcation diagrams and MATLAB simulations were used to complement the analyses. Additionally, using a combination of numerics and analysis, we highlighted various trade-offs inherent among various parameters. Thus, we provided design guidelines for the upper longitudinal control algorithm of a self-driven vehicle.