Hidden Markov Models with Confidence

Abstract

We consider the problem of training a Hidden Markov Model (HMM) from fully observable data and predicting the hidden states of an observed sequence. Our attention is focused to applications that require a list of potential sequences as a prediction. We propose a novel method based on Conformal Prediction (CP) that, for an arbitrary confidence level $1-\varepsilon$, produces a list of candidate sequences that contains the correct sequence of hidden states with probability at least $1-\varepsilon$. We present experimental results that confirm this holds in practice. We compare our method with the standard approach (i.e.: the use of Maximum Likelihood and the List–Viterbi algorithm), which suffers from violations to the assumed distribution. We discuss advantages and limitations of our method, and suggest future directions.

1 Introduction

Hidden Markov Models (HMMs) are statistical models that have had a great impact in numerous fields since their introduction. They have been widely applied to diverse fields, ranging from Cryptanalysis to Speech Analysis, and they are the state-of-the-art in many applications such as Speech Recognition [4].

The idea behind HMMs is that there exists a time evolving “hidden” process, which we cannot directly observe, and an observable random variable, whose values are related in probability to those of the hidden process. HMMs can be discrete, if the observed process can only take a finite number of values, or continuous, if it takes values from an infinite set. This paper will focus on continuous HMMs. The following problems are of fundamental interest to real-world applications of HMMs: (i) what is the probability that a sequence of observations was generated by an HMM (evaluation); (ii) what is the hidden sequence that produced a sequence of observations (decoding); (iii) how can we estimate the parameters for an HMM from empirical observations (learning).

This paper considers the learning and decoding problems when fully observable data is available and a list of sequences is required as a prediction. That is, it assumes a training set that contains data from both the hidden and the observable processes, and it aims at producing, for a new observed sequence, a list of candidate hidden sequences.

The standard approach to this problem is to assume a distribution for the emission probabilities of the HMM, to estimate the parameters of the model by using Maximum Likelihood, and to use the List–Viterbi algorithm [5] to produce a list of candidate sequences. However, the standard approach: (i) requires to manually trim the size of the list in order to achieve the desired level of accuracy, and (ii) can have bad performances if the data does not follow the assumed probability distribution.

We propose a novel approach that: (i) guarantees the accuracy is as good as, or better than, a chosen confidence level, and (ii) makes no assumptions on the probability distribution of the examples, as long as they are exchangeable. The method works in two phases. In the first phase, it uses Conformal Prediction (CP) [9] to replace the estimation of emission probabilities. It accepts a significance level $\varepsilon$ as a parameter, and produces a list of candidate hidden sequences that is guaranteed to contain the correct sequence with probability of at least $1-\varepsilon$ (validity guarantee). In the second phase, it ranks the candidate sequences by their likelihood, using estimates of the initial and transmission probabilities. The method returns the list of candidate hidden sequences sorted with respect to their rank. While this paper focuses on continuous HMMs, this method can work on both discrete and continuous HMMs.

Originally, CP worked under the assumption of exchangeability, a weaker property than i.i.d., on training and test data. CP performs well, and gives valid confident prediction under this assumption. However, applying HMM goes beyond exchangeability. The book [9] suggests On-line Compression Models as an extension for various other assumptions including Markov Model (Chap. 8.6). However, this is not directly applicable to HMMs.

We perform experiments to verify the validity guarantee of the method. We also provide a comparison with the standard method. Experiments are made: (i) under optimal conditions for the standard method (i.e.: the data reflect the assumptions it made), (ii) violating the distribution assumed by the standard method. Results show that, while the standard method gives a better accuracy when the assumed emission probability distribution is correct, its performances strongly suffer when this assumption is violated. The method we propose does not depend on the underlying distribution, and provides the desired accuracy level under different distributions of data. Furthermore, it is able to keep the size of the prediction set small under both conditions (efficiency criterion).

We conclude our analysis discussing advantages and limitations of the method and suggesting future research directions.

2 Hidden Markov Models

We consider a discrete–time Markov chain $q_t$, with finite state space. That is, $q_t$ is a random process that at time $t=1,2, ...$ takes values in a finite set of states S, and for which holds the Markov property:

$$\begin{aligned} P(q_t=s_t|q_{t-1}=s_{t-1}, q_{t-2}=s_{t-2}, ..., q_{1}=s_1) = P(q_t=s_t|q_{t-1}=s_{t-1}), \end{aligned}$$

for $s_i \in S$; informally, this property means that the transition of $q_t$ from one state to the next one only depends on its current state.

In a Hidden Markov Model (HMM) there exists a “hidden” Markov chain $q_t$, as the one we described, whose values are generally unobservable. Whilst we cannot directly observe $q_t$, we have access to a random variable $v_t$, whose value at time t depends in probability on the state of $q_t$. The variable $v_t$ takes values in a measurable space O. In a discrete HMM O is finite, in a continuous one it is infinite. This paper will focus on the continuous case. Figure 1 shows the structure of an HMM.

A continuous HMM is defined by a transition probability matrix A, emission probability densities B, and initial probabilities $\varPi$. Follows a description of them. A transition probability matrix is a matrix $A=\{\alpha _{ij}\}$, where $\alpha _{ij}$ is the probability that the hidden process makes a transition from state $s_i$ to state $s_j$:

$$\begin{aligned} \alpha _{ij} = P(q_t=s_j|q_{t-1}=s_i). \end{aligned}$$

We assume that, for each hidden state $s_j \in S$, the conditional distribution:

$$\begin{aligned} P(v_t|q_t=s_j) \end{aligned}$$

has a density function $b_j$ on O. $B=\{b_{j}\}$, for all $s_j \in S$, is the set of emission probability densities. We also define the initial probabilities $\varPi =\{\pi _{i}\}$, where:

$$\begin{aligned} \pi _{i} = P(q_1=s_i). \end{aligned}$$

Fig. 1.

Structure of an HMM, observed at time $t=1, 2, ..., \ell$. A Markov chain $q_t$ is hidden, and makes transitions between states $s_i \in S$ with respect to a transition probability matrix A. We can observe a random variable $v_t$, whose values $o_i \in O$ depend in probability on the current state of $q_t$; B defines the emission probabilities from a state to the observation.

We call observations the values $o_t \in O$ taken by the observable random variable $v_t$. We refer to a sequence of contiguous observations as

$$\begin{aligned} x=(o_1, o_2, ...), \end{aligned}$$

where $o_t \in O$ is the value taken by $v_t$ at time t. Analogously, we write

$$\begin{aligned} h=(s_1, s_2, ...), \end{aligned}$$

to indicate a sequence of hidden states. We use the notation $x^{(j)}$ when referring to the j-th element of a sequence x; for example, $x^{(j)}=o_j$ for the sequence mentioned above. Similarly, $h^{(j)}$ is the j-th element of the sequence h. In the formulation of the problem (Sect. 3) we will assume that we can fully observe an HMM for $\ell$ time during a training phase. This operation produces an observable sequence $x=(o_1, o_2, ..., o_\ell )$, and a hidden sequence $h=(s_1, s_2, ..., s_\ell )$.

3 Problem Setting and Evaluation Criteria

We assume we can fully observe an HMM in a training phase. In this phase we collect a multiset of n pairs:

$$\begin{aligned} \{(x_i, h_i)\}, \end{aligned}$$

where $x_i=(o_1, o_2, ..., o_{\ell _i})$, $o_t \in O$, is a sequence of observations, and $h_i=(s_1, s_2, ..., s_{\ell _i})$, $s_t \in S$, is the respective sequence of hidden states. We assume $|x_i| > 1$, for $i=1, 2, ..., n$, but we do not require that $|x_i| = |x_j|$ for $i \ne j$.

In a test phase we are given a new sequence of observations $x_{n+1}$, whose corresponding hidden sequence $h_{n+1}$ is unknown to us. Our goal is to predict a list of candidate hidden sequences $\hat{H}$, sorted by their likelihood, that contains the correct hidden sequence.

We consider three evaluation criteria for the problem:

Accuracy: an error is made when the correct sequence is not in the prediction set $\hat{H}$. Let $\eta$ be the number of errors committed in n predictions, accuracy is:

$$\begin{aligned} 1-\frac{\eta }{n}. \end{aligned}$$

Efficiency: is the average size of the prediction set (see N criterion in [8]). This criterion is crucial to the problem: a perfect accuracy can be achieved by trivially returning the list of all the possible sequences of length $\ell =|x_{n+1}|$; however, it is more difficult to achieve a good accuracy while keeping small the size of $|\hat{H}|$.

Average Position (AP): this criterion evaluates the goodness of the ranking scores we associate with the predicted sequences. AP is the average position that the correct sequence takes within the sorted prediction list $\hat{H}$.

4 Standard Approach

The standard approach to the problem is as follows: a family of probability distributions is assumed for emissions; the parameters of these distributions and initial and transition probabilities are estimated from training data by using Maximum Likelihood; then, the List–Viterbi algorithm is applied, for a certain value of k, to predict the sequence of hidden states. The List–Viterbi algorithm returns a list of k candidate sequences. If the application requires some confidence that the correct sequence is in the predicted list, experiments need to be done to determine which value of k gives the desired accuracy.

This section presents the Maximum Likelihood method to estimate the parameters of an HMM from fully observed data (observations and hidden states), and the List–Viterbi algorithm [5], an extension of the Viterbi algorithm [1, 7], which outputs the k best sequences.

4.1 Maximum Likelihood Method for Estimating A, B, $\varPi$

Let $Z=\{(x_i, h_i)\}$, for $i=1, 2, ..., n$, be a multiset of observed sequences $x_i$ and corresponding hidden sequences $h_i$. We shall use this multiset for estimating A, B, $\varPi$. Let S be the set of hidden states, and N its size.

Initial Probabilities. Initial probabilities $\varPi$ can be estimated as follows:

$$\begin{aligned} \varPi = \{\pi _j\} = \left\{ \frac{|\{i : h^{(1)}_i = s_j \quad (x_i, h_i) \in Z\}|}{n} \right\} \quad j=1, 2, ..., N. \end{aligned}$$

Transition Probabilities. Let $Z'$ be a multiset of pairs composed of the hidden state at time t and the hidden state at time $t+1$. We derive $Z'$ as:

$$\begin{aligned} Z' = \{(x^{(t)}_i, x^{(t+1)}_i)\} \quad t=1, 2, ..., (\ell _i-1) \quad (x_i, h_i) \in Z, \end{aligned}$$

where $\ell _i=|x_i|$. The probability of transitioning from $s_i$ to $s_j$ is estimated as:

$$\begin{aligned} \alpha _{ij} = \frac{| \{ (s_t, s_{t+1}) \in Z' : s_t = s_i \wedge s_{t+1} = s_j \} |}{ | \{ (s_t, s_{t+1}) \in Z' : s_t = s_i \} | }, \end{aligned}$$

and is done for all $i=1, 2, ..., N$ and $j=1,2, ..., N$. The transition probability matrix is $A=\{\alpha _{ij}\}$.

Emission Probabilities. Estimation of emission probability densities $B=\{b_{j}\}$, for $s_j \in S$ depends on the chosen probability density. A typical choice is the Normal density function: $b_{j} \sim \mathcal {N}(\mu _j, \sigma _j)$, for some mean $\mu _j$ and standard deviation $\sigma _j$.

Let $Z''$ be a multiset of pairs composed of an observable state and the corresponding hidden state:

$$\begin{aligned} Z'' = \{(x^{(j)}_i, h^{(j)}_i)\} \quad j=1, 2, ..., \ell _i \quad (x_i, h_i) \in Z, \end{aligned}$$

where $\ell _i=|x_i|$. We estimate the parameters for $b_{j}$ (e.g.: $\mu _j$, $\sigma _j$ for a Normal density) on the multiset:

$$\begin{aligned} \{ o : (o, s) \in Z'' \wedge s=s_j \}. \end{aligned}$$

4.2 Viterbi Algorithm

The Viterbi algorithm computes the most likely sequence of states $\hat{h}$ for an observed sequence $x=(o_1, o_2, ..., o_\ell )$, given an HMM $(A, B, \varPi )$.

At each step $t=1, 2, ..., \ell$ the Viterbi algorithm computes, for each state $s_i\in S$, the probability $V_t(s_i)$ of the most likely sequence for which $q_t=s_i$. It first initialises:

$$\begin{aligned} V_1(s_i) = P(o_1| q_1 = s_i)P(q_1 = s_i) \quad s_i \in S, \end{aligned}$$

where $P(o_1| q_1 = s_i)=b_{s_i}(o_1)$, and $P(q_1 = s_i) = \pi _i$. Then, for each step $t>1$, it sets the probability of being at state $s_i$ at time t, $V_t(s_i)$ to:

$$\begin{aligned} V_t(s_i) = P(o_t|q_t=s_i) \max _{s_j \in S} P(q_t=s_i|q_{t-1}=s_j) V_{t-1}(s_j), \end{aligned}$$

for all $s_i \in S$. We remark that $P(o_t|q_t=s_i) = b_{s_i}(o_t)$ and $P(q_t=s_i|q_{t-1}=s_j)=\alpha _{ji}$. $V_t(s_i)$ represents the probability of being in state $s_i$ at time t, given that the most likely path to reach $s_i$ was followed by the HMM.

The most likely sequence can be obtained by using back pointers to the best path taking to each state, for time $t=1, 2, ..., \ell$.

4.3 List–Viterbi Algorithm

The List–Viterbi algorithm is an extension of the Viterbi algorithm, which outputs the k most likely hidden sequences for the observed sequence x.

The algorithm works as the Viterbi algorithm, but each variable $V_t(s_i)$, for $t>1$, is a vector of length k; the j-th element of vector $V_t(s_i)$ is the likelihood of the j-th most likely sequence that takes to state $s_i$ at time t. At each step $t>2$, all the k|S| likelihoods are considered, and only the best k are kept for the next step. The List–Viterbi algorithm returns a list of the most likely sequences, which are obtained by using back pointers to the k best paths. The sequences of the prediction list are sorted by their likelihood.

5 Prediction with Confidence for HMMs

This section introduces a method to train an HMM from fully observable data and to make a prediction for a new observed sequence. The method outputs a list of candidate hidden sequences $\hat{H}$, sorted with respect to their likelihood; $\hat{H}$ contains the correct sequence with probability at least $1-\varepsilon$, for a chosen significance level $\varepsilon$.

The method operates in two phases. In the first phase, the algorithm:

• 1. uses training data to create a training set $Z_{train}$ of pairs $(o_i, s_i)$, for observations $o_i \in O$ and respective hidden states $s_i \in S$;

• 2. considers each observation $o_j$ of the test sequence individually, and uses CP and the training set $Z_{train}$ to determine a set of candidate hidden states $\hat{H}_j$ for that observation; when doing this, hidden states are considered as the labels to predict;

• 3. produces the list $\hat{H}$ of all the hidden sequences that can be generated by using one state from $\hat{H}_1$ as a first state, one from $\hat{H}_2$ as a second state, and so on;

Figure 2 offers a graphical overview of the first phase.

The second phase is concerned with sorting the list of candidate hidden sequences $\hat{H}$ by their likelihood. In this phase the algorithm computes Maximum Likelihood estimates of initial and transition probabilities. It computes a ranking score for each sequence, using the Maximum Likelihood estimates, as the probability of the hidden Markov chain $q_t$ to produce that sequence. The algorithm returns a list $\hat{H}$ of sequences, sorted with respect to their ranking scores.

We introduce CP, and present the method into details.

5.1 Conformal Prediction

CP is a statistical framework that allows to edge predictions with respect to a confidence level [2, 6, 9]. Let $z_i = (o_i, s_i)$, for $i=1, 2, ..., n$, be pairs of observation and respective hidden state, and $\varepsilon \in [0,1]$ a significance level. We identify a hidden state with the label to predict. CP produces, for a new observation $o_{n+1}$, a set of candidate labels $\varGamma ^\varepsilon$. The validity property of CP guarantees that $\varGamma ^\varepsilon$ contains the correct label, $s_{n+1}$, with probability $1-\varepsilon$, for an arbitrary significance level¹. We call $1-\varepsilon$ confidence level.

Nonconformity Measure. CP works for a nonconformity measure:

$$\begin{aligned} A: O^{(*)} \times O \mapsto \mathbb {R}. \end{aligned}$$

The function A accepts a multiset of observations and a new observation, and returns a scalar (nonconformity score) that indicates how strange the new observation is respect to the multiset. Any function in the form of A guarantees the validity of the method. However, some functions may provide a better efficiency in the terms described in Sect. 3.

In our analysis, we consider the k-Nearest Neighbours (k-NN) nonconformity measure, which is computed as follows. Let $\mathcal {O}$ be a multiset of observations, $o_{n+1}$ a new observation, and $\delta _i$ the i-th smallest distance between $o_{n+1}$ and the observations in $\mathcal {O}$. The k-NN nonconformity measure is:

$$\begin{aligned} A(\mathcal {O}, o_{n+1}) = \sum _{j=1}^k \delta _{i}, \end{aligned}$$

where k is the chosen number of neighbours. In experiments we will use the k-NN nonconformity measure with $k=1$.

CP in Multi–label Setting. Different formulations of CP exist. We consider the multi–label setting, where we are given examples $(o_i, s_i)$ of observation $o_i \in O$ and label $s_i \in S$, and CP returns, for a new observation, a set of candidate labels $\varGamma ^\varepsilon \subseteq S$.

Algorithm 1 describes CP in this setting. We write:

$$\begin{aligned} \varGamma ^\varepsilon = CP(o_{n+1}, Z, A, \varepsilon ) \end{aligned}$$

to indicate a call to this algorithm for a new observation $o_{n+1}$, a training set Z, nonconformity measure A, and significance level $\varepsilon$. Thanks to the validity property of CP, $\varGamma ^\varepsilon$ is guaranteed to contain the correct label for $o_{n+1}$ with probability $1-\varepsilon$.

5.2 Prediction with Confidence for HMMs

We are provided with a multiset of pairs $Z=\{(x_i, h_i)\}$, for $i=1, 2, ..., n$, of observable and respective hidden sequences (Sect. 3). We are also given a test sequence $x_{n+1}=(o_1, o_2, ..., o_\ell )$, whose corresponding hidden sequence $h_{n+1}$ is unknown to us. Follows a description of the method for making a prediction with confidence for $h_{n+1}$.

The method is composed of two phases, that we shall call Confident Prediction and Ranking. The former aims at producing a list of candidate sequences $\hat{H}$ that contains $h_{n+1}$. The latter computes the likelihoods (ranking scores) of the sequences in $\hat{H}$, and returns the list sorted with respect to them.

Confident Prediction. The first phase uses information about the relation between hidden states and observations to make a list prediction for a new sequence.

We create a multiset of pairs of observation and respective hidden state:

$$\begin{aligned} Z_{train} = \{(x^{(k)}_i, h^{(k)}_i)\} \quad k=1, 2, ..., \ell _i \quad (x_i, h_i) \in Z, \end{aligned}$$

where $\ell _i$ is the length of the i-th sequence. We will consider $Z_{train}$ as a training set, where hidden states are the labels to predict from observations.

We individually consider each observation $o_j = x^{(j)}_{n+1}$ from the sequence $x_{n+1}$, for $j=1, 2, ..., \ell$, and look for candidate hidden states for it. Specifically, we use CP and the training set $Z_{train}$ to predict a set of labels (hidden states) $\hat{H}_j$ for the observation $o_j$:

$$\begin{aligned} \hat{H}_j = CP\left( o_j, Z_{train}, A, \frac{\varepsilon }{\ell }\right) , \end{aligned}$$

where CP is Smooth CP in multi–label setting (Algorithm 1). Any nonconformity measure A in the form described in Sect. 5.1 is allowed, but some nonconformity measures may provide a better efficiency. The result of this operation is a set $\hat{H}_j$ containing candidate hidden states for the observation $o_j$. We assume exchangeability on the elements of the multiset:

$$\begin{aligned} Z_{train} \cup (x^{(j)}_{n+1}, h^{(j)}_{n+1}). \end{aligned}$$

Then, thanks to the validity property of CP, $\hat{H}_j$ contains the correct hidden state $h^{(j)}_{n+1}$ with probability $1-\frac{\varepsilon }{\ell }$.

We iterate this operation for each observation $o_j$ of the sequence $x_{n+1}=(o_1, o_2, ..., o_\ell )$, obtaining the sets $\hat{H}_1, \hat{H}_2, ..., \hat{H}_\ell$. We obtain $\ell$ sets of candidate hidden states, each one indicating candidate states for a position in the sequence.

We produce all the sequences of length $\ell$ having as a first state one state from $\hat{H}_1$, as a second state one from $\hat{H}_2$, and so on. This means we take the Cartesian product of these sets:

$$\begin{aligned} \hat{H} = \hat{H}_1 \times \hat{H}_2 \times ... \times \hat{H}_\ell . \end{aligned}$$

We call $\hat{H}$ the prediction list. The probability that $h_{n+1}$ is in $\hat{H}$ is:

$$\begin{aligned} P(h_{n+1} \in \hat{H}) \ge 1-\varepsilon , \end{aligned}$$

for an arbitrary significance level $\varepsilon \in [0,1]$. A proof of this is given in Appendix.

Ranking. The second phase of the algorithm focuses on ranking the sequences of $\hat{H}$ with respect to their likelihood.

We estimate initial and transition probabilities $(A, \varPi )$ using Maximum Likelihood (Sect. 4.1). Then we compute a ranking score $\sigma (\hat{h})$, for the hidden sequence $\hat{h} \in \hat{H}$, $\hat{h} = (s_1, s_2, ..., s_{\ell })$, as the probability that the hidden process of the HMM produced that sequence:

$$\begin{aligned} \sigma (\hat{h})&= P(\hat{h} | \varPi , A) = P(s_1) \cdot \prod ^{\ell -1}_{t=1} P(s_t | s_{t-1}) \\&= \pi _{s_1} \cdot \prod ^{\ell -1}_{t=1} \alpha _{s_{t-1}s_t}; \end{aligned}$$

here $\pi _{s_1}$ is the initial probability for state $s_1$, $\alpha _{s_{t-1}s_t}$ is the probability of transitioning from state $s_{t-1}$ to state $s_t$.

We return the list $\hat{H}$ sorted with respect to the ranking scores of its sequences. A larger score gives a higher position in the list.

Fig. 2.

The first phase of prediction with confidence for HMMs. A test sequence $o_1, o_2, ..., o_\ell$ is observed. We apply CP individually to each observation $o_j$ using a training multiset of observations and respective hidden states. This returns, for each $o_j$ of the sequence, a list of candidate hidden states $\hat{H}_j$. We produce the list $\hat{H}$ of all the sequences that can be generated by using one of $\hat{H}_1=\{s_1, s_2\}$ as the first state, one of $\hat{H}_2=\{s_1, s_2, s_3\}$ as the second state, and so on. In the second phase the sequences are ranked with respect to their initial and transition probability estimates.

6 Experiments

In this section we show that the validity property of our method holds in practice. This means that, for different significance levels $\varepsilon$, the method keeps an error which is always smaller or equal to $\varepsilon$. Furthermore, we present an experimental comparison of our method with the standard approach. Similarly to what [3] did when comparing the Bayes approach and CP, we experiment with these methods under two settings: (i) emission probabilities follow the distribution assumed by the standard approach (optimality for the standard approach), (ii) emissions violate this distribution. This approach needs generating two datasets that fulfill these requirements. We refer to these datasets as HMM-NORM and HMM-GMM. HMM-NORM was generated by a continuous HMM, for which emission probabilities were normally distributed. HMM-GMM was generated by a continuous HMM, which used mixtures of Normal distributions (GMM) as emission probability densities. Construction details are in Appendix.

In experiments, we consider an on–line setting, where the correct sequence is provided after prediction, and the predicted example is added to the training set. Our training set starts from 4 observed sequences and reaches 2000.

6.1 Validity of the Method

The method we propose is valid, in the sense that it produces a prediction set that contains the correct sequence with probability at least $1-\varepsilon$, for an arbitrary significance level $\varepsilon$. A proof of this is Appendix.

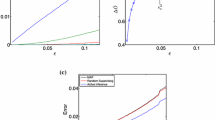
We apply our method to the data for significance levels: (0.01, 0.05, 0.1), and nonconformity measure k-NN, for $k=1$. Figure 3 shows the cumulative error of the method in this setting. We observe that the validity property holds empirically: the error tends to be equal or smaller than the significance levels, for a chosen level.

Figure 4 compares the significance level and the respective empirical error that was achieved. This plot shows that the empirical error is smaller than the significance level for each value.

Fig. 3.

Cumulative error of our method on the HMM-NORM dataset. The validity is respected empirically for each significance level. We refer to our method as CP-HMM.

6.2 Comparison with the Standard Approach

We compare our method with the standard approach on datasets HMM-NORM and HMM-GMM. We assume Normal distribution for the emission probabilities of the standard approach. Consequently, HMM-NORM represents the optimal conditions for the standard approach. HMM-GMM violates its assumptions.

Fig. 4.

Average error achieved by our method, for different significance levels. The empirical error tends to be smaller than $\varepsilon$. We refer to our method as CP-HMM.

Accuracy for the Same Size of Prediction Set. We measure the accuracy of our method and of the standard approach when producing a set of predictions of the same size. In order to do this we first run our method for some significance level ($\varepsilon =0.01$), we record the size of the prediction list $\hat{H}$, and we run the List–Viterbi algorithm for $k=|\hat{H}|$. Results of this experiment on HMM-NORM and HMM-GMM are shown in Fig. 5.

We observe that the standard approach achieves the best accuracy under optimal conditions (Fig. 5(a)). In this case, our method achieves a slightly worse accuracy than the standard approach. However, when the assumptions of the standard approach are violated (i.e.: emission probabilities are not normally distributed), its error increases considerably (Fig. 5(b)). Nonetheless, our method is able to keep the same accuracy as before (see Fig. 5(b)). This suggests that our method may be applied to a wider range of cases, where estimating the probability distribution of emissions is non–trivial.

Fig. 5.

Cumulative error of our method (which we call, for brevity, CP-HMM) and the standard approach, when they produce a prediction set of the same size. The left figure shows results under optimal conditions for the standard approach. The right figure shows what happens when its assumptions are violated.

Average Position. In this experiment we determined the Average Position (AP) of our method and of the standard method. Namely, we determined which of the two methods puts the correct prediction closer to the top of their prediction lists. This criterion helps to understand what is the smallest size of the prediction list that achieves perfect accuracy. A smaller AP indicates a better performance.

Table 1 reports the average position taken by the correct prediction in the prediction list, when using the List–Viterbi algorithm, and confidence prediction for HMMs (for significance levels (0.01, 0.05, 0.1)).

We notice that AP of our method tends to get better for higher significance levels. The standard approach under its optimal conditions is better, in terms of AP. However, we observe that its AP gets much worse when the data violates its assumptions (HMM-GMM). In this case our method is able to perform better.

Table 1. AP for our method with different $\varepsilon$ and for the standard approach. For brevity, we refer to our method as CP-HMM. The left–hand table shows the results for the HMM-NORM dataset, when the assumptions of the standard method are satisfied; the right–hand table shows AP when these are violated (HMM-GMM dataset).

7 Conclusions

We proposed a method that trains an HMM from fully observable data and that outputs a list of candidate hidden sequences for a new observed sequence. The method guarantees validity, in the sense that its probability of error is smaller or equal than $\varepsilon$, for an arbitrary $\varepsilon \in [0,1]$.

We discuss advantages and limitations of the method with respect to the standard approach, and suggest future research directions.

7.1 Comparison with the Standard Approach

The standard approach to the problem we considered is to assume probability distributions for the emissions of the HMM, to estimate the parameters using Maximum Likelihood, and to use the List–Viterbi algorithm.

One limitation of the List–Viterbi algorithm is that it does not allow to directly control the accuracy. We thus need trim on experimental data the parameter k, that indicates the size of the prediction list, and choose the value that gives the desired level of accuracy. The method we propose accepts a significance level $\varepsilon$, and guarantees that its error is upper–bounded by $\varepsilon$. This means that our method gives a direct control over the errors.

The standard approach is optimal when the correct distributions are assumed, and the parameters are correctly estimated. However, if the data assume different probability distributions, its performances strongly deteriorate. Results on both optimal and non–optimal conditions for the standard method show that the method we propose is robust independently of the distributions. For this reason, we suggest that our method may have a wider applicability to complex cases, where estimating the correct distributions is non–trivial.

As an advantage with respect to the standard method, our method reduces the state space (first phase of the method, Sect. 5.2). While the standard method needs to consider any state as a candidate, given an observation, our method allows to consider only those that conform the distribution. Future work may try to apply variants of the Viterbi and List–Viterbi algorithms to the result of the first phase of our method, as a way of reducing their complexity.

One disadvantage of our method is that CP might return an empty set as a prediction for an observation. This would cause an empty prediction list. To overcome this problem, we may modify Algorithm 1 to output some states, even when none of them conforms. Future research may experiment with this option, and perhaps verify if this would affect the validity of the method.

7.2 Future Work

Future work may apply our method to real–world problems. The method is applicable to both discrete and continuous HMMs, and it has the advantages of: (i) being independent of the probability distributions, and (ii) providing a direct control on the errors.

Our experiments focused on the k-NN nonconformity measure, but the method can work for any nonconformity measure (Sect. 5.1). However, as for CP, some nonconformity measures may provide tighter predictions. Future research may consider other nonconformity measures, such as Kernel Density Estimation, and determine if they can achieve better performances.

Our method, in its current form, uses information about transition and emission probabilities in two separate phases. CP is used in the emission phase only. Although the method made the prediction better, the following challenge appears for the future. If an observation of the hidden sequence does not look to come from its true hidden state (e.g.: there is noise between the hidden process and the random variable), the method will not consider further information (e.g.: transition probabilities) when making a prediction. Future research may attempt to solve this problem. One way is using probabilistic Venn–Machines [9], which may substitute CP in our method. One advantage of them would be a probabilistic output, which may be combined with initial and transition probabilities.

Future work may also consider other ways to rank the predicted sequences, in order to improve the Average Position of the method. The use of Venn–Machines may be helpful also in this case.

Finally, future research may try to limit the size of the training data to reduce the complexity of the method (e.g.: Inductive CP).

Appendices

A Validity of the Method

We are given a multiset (training set) of sequences $\{(x_i, h_i)\}$, for $i=1, 2, ..., n$. We select a significance level $\varepsilon \in [0,1]$. Let $x_{n+1}$ be a test sequence and $h_{n+1}$ the corresponding sequence of hidden states. Our method outputs a prediction set $\hat{H}=\{h_1, h_2, ...\}$. We show that the probability that $\hat{H}$ contains the correct sequence is at least $1-\varepsilon$.

Let us construct the following multiset:

$$\begin{aligned} Z_{train} = \{(x^{(j)}_i, h^{(j)}_i)\} \quad j=1,2,...\ell _i \quad i=1,2,...,n, \end{aligned}$$

where $\ell _i = |x_i| = |h_i|$.

Let $\ell =|x_{n+1}|=|h_{n+1}|$. Let us consider the j-th element of the sequence $x_{n+1}$. We assume exchangeability on the multiset

$$\begin{aligned} Z_{train} \cup \{(x^{(j)}_{n+1},h^{(j)}_{n+1})\}. \end{aligned}$$

We run:

$$\begin{aligned} \hat{H}_j = CP\left( x^{(j)}_{n+1}, Z_{train}, A, \frac{\varepsilon }{\ell }\right) , \end{aligned}$$

as defined in Algorithm 1. Thanks to the validity property of Smooth CP [9], the following holds:

$$\begin{aligned} P(h^{(j)}_{n+1} \notin \hat{H}_j) = \frac{\varepsilon }{\ell }. \end{aligned}$$

We repeat this for all the observations in $x_{n+1}$. We define $\hat{H}$ as the set of all the sequences of length $\ell$ that can be generated by using elements from $\hat{H}_1$ as a first element, elements from $\hat{H}_2$ as a second one, and so on. Then we can derive the probability of error of our method as the probability of the correct sequence $h_{n+1}$ of not being in the prediction set as:

$$\begin{aligned} {\begin{matrix} P(h_{n+1} \notin \hat{H}) &{} = P(h_{n+1}^{(1)}\notin \hat{H}_1 \vee h_{n+1}^{(2)}\notin \hat{H}_2 \vee ... \vee h_{n+1}^{(\ell )}\notin \hat{H}_\ell ) \\ &{} \le \sum _{j=1}^\ell P(h_{n+1}^{(j)}\notin \hat{H}_j) = \ell \frac{\varepsilon }{\ell } = \varepsilon \end{matrix}} \end{aligned}$$

$\qquad \blacksquare$

Follows that $1-\varepsilon$ is a lower–bound to the probability of error of the method.

Fig. 6.

Distribution of the emission probabilities for the three hidden states in HMM-NORM (left–hand figure), and in HMM-GMM (right–hand figure).

B Datasets

1.1 B.1 HMM-NORM Dataset

We sampled 2000 sequences of length $\ell =10$. The sequences were generated by using a continuous HMM with 3 hidden states, $S=\{s_1,s_2,s_3\}$, start probabilities $\varPi = \{0.6, 0.3, 0.1\}$, transition probabilities:

$$\begin{aligned} A = \{\alpha _{ij}\} = \left( \begin{array}{ccc} 0.7 &{} 0.2 &{} 0.1 \\ 0.3 &{} 0.5 &{} 0.2 \\ 0.3 &{} 0.3 &{} 0.4 \end{array} \right) , \end{aligned}$$

and emission probabilities: $b_{o}{s_1} \sim \mathcal {N}(-2,0.7)$, $b_{o}{s_2} \sim \mathcal {N}(0,0.7)$, $b_{o}{s_3} \sim \mathcal {N}(2,0.7)$. Figure 6(a) graphically shows the distribution of $b_{o}{s_1}$, $b_{o}{s_2}$, and $b_{o}{s_3}$.

1.2 B.2 HMM-GMM Dataset

We sampled 2000 sequences of length $\ell =10$. The sequences were generated by using a continuous HMM with 3 hidden states, $S=\{s_1,s_2,s_3\}$, start probabilities $\varPi = \{0.6, 0.3, 0.1\}$, transition probabilities:

$$\begin{aligned} A = \{\alpha _{ij}\} = \left( \begin{array}{ccc} 0.7 &{} 0.2 &{} 0.1 \\ 0.3 &{} 0.5 &{} 0.2 \\ 0.3 &{} 0.3 &{} 0.4 \end{array} \right) . \end{aligned}$$

Emission probabilities where given by one mixture of two Normal distributions. Let $\mathcal {G}(\mu ,\sigma ,w)$ be a mixture of two Normal distribution with means $\mu =(\mu _1, \mu _2)$, standard deviations $\sigma =(\sigma _1, \sigma _2)$, and weights $w=(w_1, w_2)$. That is:

$$\begin{aligned} \mathcal {G}(\mu ,\sigma ,w) = \sum ^2_{i=1} w_i \mathcal {N}(\mu _i, \sigma _i). \end{aligned}$$

The model we used had emission probabilities: $b_{o}{s_1} \sim \mathcal {G}((0,2),(0.7,0.7),(0.7,0.3))$, $b_{o}{s_2} \sim \mathcal {G}((-2,-1),(0.25,0.25),(0.5,0.5))$, $b_{o}{s_3} \sim \mathcal {G}((2,3),(0.5,0.3),(0.7,0.3))$. Figure 6(b) graphically shows the distribution of $b_{o}{s_1}$, $b_{o}{s_2}$, and $b_{o}{s_3}$.