Active Inference for Binary Symmetric Hidden Markov Models

Abstract

We consider active maximum a posteriori (MAP) inference problem for hidden Markov models (HMM), where, given an initial MAP estimate of the hidden sequence, we select to label certain states in the sequence to improve the estimation accuracy of the remaining states. We focus on the binary symmetric HMM, and employ its known mapping to 1d Ising model in random fields. From the statistical physics viewpoint, the active MAP inference problem reduces to analyzing the ground state of the 1d Ising model under modified external fields. We develop an analytical approach and obtain a closed form solution that relates the expected error reduction to model parameters under the specified active inference scheme. We then use this solution to determine most optimal active inference scheme in terms of error reduction, and examine the relation of those schemes to heuristic principles of uncertainty reduction and solution unicity.

1 Introduction

In a typical statistical inference problem, we want to infer the true state of some hidden variables based on the observations of some other related variables. The quality of statistical inference is generally improved with adding more data or prior information about the hidden variables. When obtaining such information is costly, it is desirable to select this information optimally so that it is most beneficial to the inference task.

This notion of active inference (or active learning) [1], where one optimizes not only over the models, but also over the data, has been used in various inference problems including Hidden Markov Models (HMMs) [2, 3], network inference [4–7], etc.

The efficiency of active inference is naturally determined from the error reduction of the inference method [8]. Since this quantity is not readily available in practice, several heuristic methods were developed [1]. For instance, a class of methods seeks to implement active inference in a way of obtaining possibly unique solution (or reducing the set of available solutions) [1, 9]. A related family of methods tries to learn those variables whose uncertainty is large [1, 10]. Both heuristics have intuitive rationale and can do well in practice, but theoretical understanding of how exactly those heuristics relate to error reduction is largely lacking. In particular, most existing theoretical results are concerned with sub-modular cost functions that allow to establish certain optimality guarantees [11, 12] on active selection strategies. However, these cost functions do not usually refer directly to the error reduction of some inference method.

Here we consider the active maximum a posteriori (MAP) inference problem for the binary symmetric HMMs, or BS-HMM (see [3] for a brief review of active estimation methods in HMM). BS-HMM is sufficiently simple so it allows to study active MAP inference analytically [13, 14], yet it still contains all the essential features of HMMs that make them a flexible and widely used tool for probabilistic modeling in various fields [15, 16]. We emphasize that even for the simple BS-HMM model considered here, obtaining analytical insights about active inference strategies is a non-trivial problem, as we demonstrate below.

Similar to other inference problems, the active MAP-estimation for BS-HMM can be reduced to a properly defined statistical physical system; see [17–19] for general surveys on the relationship between statistical physics and probabilistic inference. For the present case, the statistical structure of BS-HMM can be mapped to one-dimensional (1d) Ising model in random external fields [20, 21]. As we show below, active MAP inference can be reduced to the problem of selecting a ground state of the corresponding 1d Ising model under modified external conditions (fields). We develop an analytical approach for studying the active MAP inference problem for BS-HMM, and use it to determine the most efficient schemes of uncertainty reduction, where labeling a small number of states results in the largest expected error reduction in the estimation of the remaining (unlabeled) states. Our analysis allows us to examine how the active inference in BS-HMM relates to the heuristic principles of uncertainty reduction and solution unicity. Specifically, we obtain a closed form expression for the expected error reduction as a function of model parameters, and use it to assess the optimality of active inference schemes. Finally, we compare our analytical predictions with numerical simulations and obtain excellent agreement within the validity range of the proposed analysis.

The rest of the paper is organized as follows: Sect. 2 defines generalities of active MAP-inference. Sections 3 and 4 introduce the BS-HMM and its MAP analysis, respectively. Section 5 presents our the main analytical findings on active inference, and is followed by experimental validation of those findings in Sect. 6. We conclude by discussing our main findings, their relationships to the existing heuristics for active inference, and identifying some future directions of research in Sect. 7.

2 Active Inference: Generalities

2.1 MAP Inference

Let $\mathbf{x}=(x_1,\ldots ,x_N)$ and $\mathbf{y}=(y_1,\ldots ,y_N)$ be realizations of discrete-time random processes $\mathcal{X}$ and $\mathcal{Y}$, respectively. $\mathcal{Y}$ is the noisy observation of $\mathcal{X}$. We assume a binary alphabet $x_i=\pm 1$, $y_i=\pm 1$ and write the probabilities as $p (\mathbf{x})$ and $p (\mathbf{y})$. The influence of noise is described by the conditional probability $p(\mathbf{y}|\mathbf{x})$. Given an observation sequence $\mathbf{y}$, the MAP estimate $\hat{\mathbf{x}}(\mathbf{y})=(\hat{x}_1(\mathbf{y}),..., \hat{x}_N(\mathbf{y}))$ of $\mathbf{x}$ is found from maximizing over $\mathbf{x}$ the posterior probability $p(\mathbf{x}|\mathbf{y})={p(\mathbf{y}|\mathbf{x})p(\mathbf{x})}/ {p(\mathbf{y})}$:

$$\begin{aligned} {\hat{\mathbf{x}}}(\mathbf{y}) = \mathop {{{\mathrm{arg\,max}}}}\limits _{\mathbf{x}}p(\mathbf{x}|\mathbf{y}). \end{aligned}$$

(1)

In general, the maximization can produce ${\mathcal {N}}(\mathbf{y})$ outcomes. Since they are equivalent, each of them is chosen (for a given $\mathbf{y}$) with probability $1/{\mathcal {N}}(\mathbf{y})$, which defines a realization ${\hat{\mathbf{x}}}$ of a random variable $\mathcal{\hat{X}}$.

The estimation accuracy is measured using the overlap (larger O means better estimate)

$$\begin{aligned} \bar{O}= & {} \sum _{\mathbf{y}}p(\mathbf{y})\frac{1}{{\mathcal {N}}(\mathbf{y})}\sum _{{\hat{\mathbf{x}}}(\mathbf{y})} O [{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y}], \end{aligned}$$

(2)

$$\begin{aligned} O [{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y}]= & {} \sum _{\mathbf{x}}\sum _{i=1}^N {\hat{x}}_i(\mathbf{y})x_i\, p(\mathbf{x}|\mathbf{y}), \end{aligned}$$

(3)

Note that the definition of $\bar{O}$ involves averaging over $\mathcal{X}$, $\mathcal{Y}$ and $\mathcal{\hat{X}}$. The error probability is expressed through the overlap as $P_\mathrm{e}=\frac{1}{2}[1-\frac{\bar{O}}{N}]$. Below we are interested by the conditional–over a fixed $\mathbf{y}$ and ${\hat{\mathbf{x}}}$–overlap $O [{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y}]$.

2.2 Active MAP Inference

Given $\mathbf{y}$ and $\hat{\mathbf{x}}(\mathbf{y})$ we request the true value of one of the variables (say $x_1$, generalization to many variables is straightforward). Below we refer to this procedure as supervising. After supervising $x_1$, we re-estimate other variables:

$$\begin{aligned} (\hat{x}_2(\mathbf{y}),..., \hat{x}_N(\mathbf{y})) \rightarrow (\tilde{x}_2(x_1,\mathbf{y}),..., \tilde{x}_N(x_1,\mathbf{y})), \end{aligned}$$

(4)

where $\tilde{x}_i(x_1,\mathbf{y})$ is obtained under the MAP estimation with the fixed value of $x_1$. Let us define the overlap gain

$$\begin{aligned} \varDelta O[{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y};1]=\sum _{\mathbf{x}}\sum _{i=2}^N [\tilde{x}_i(x_1,\mathbf{y})-\hat{x}_i(\mathbf{y})] x_i\,p(\mathbf{x}|\mathbf{y}), \end{aligned}$$

(5)

Then supervising $x_1$ is meaningful if this gain is positive, $\varDelta O >0$. Note that the sum $\sum _{i=2}^N$ is taken over the non-supervised variables [cf. (2)]. In $\varDelta O [{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y}]$ the average is taken also over all possible values $\mathbf{x}=(x_1,...,x_N)$. The fully averaged overlap gain $\varDelta \bar{O}$ is determined from $\varDelta O [{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y};1]$ as in (2).

If $x_1$ was already correctly recovered using the initial MAP estimation, then supervising $x_1$ does not change anything: $\{\tilde{x}_i(\hat{x}_1(\mathbf{y}),\mathbf{y})\}_{i=2}^N =\{\hat{x}_i(\mathbf{y})\}_{i=2}^N$. Hence, we get from (5):

$$\begin{aligned} \varDelta O[{\hat{\mathbf{x}}}(\mathbf{y}),\mathbf{y};1]= & {} \sum _{x_2,...,x_N}\sum _{i=2}^N [\tilde{x}_i(-\hat{x}_1(\mathbf{y}),\mathbf{y})-\hat{x}_i(\mathbf{y})] \nonumber \\&\times x_i\, p(-\hat{x}_1(\mathbf{y}),x_2,...,x_N|\mathbf{y}). \end{aligned}$$

(6)

3 Reducing HMMs to the Ising Model

We now consider a binary symmetric HMM. $\mathcal{X}$ is a Markov process given by the following state-transition probabilities

$$\begin{aligned} p(\mathbf{x})={\prod }_{k=2}^N\, p(x_{k}|x_{k-1})p(x_1), \qquad x_k=\pm 1, \end{aligned}$$

(7)

where $p(x_{x}|x_{k-1})$ is the transition probability parameterized by a single number $0<q<1$:

$$\begin{aligned} p(+1|+1)= & {} p(-1|-1)=1-q, \\ p(+1|-1)= & {} p(-1|+1)=q. \end{aligned}$$

The noise is memory-less and unbiased:

$$\begin{aligned} p(\mathbf{y}|\mathbf{x}) = {\prod }_{k=1}^N \pi (y_k|x_k), \qquad y_k=\pm 1 \end{aligned}$$

(8)

where

$$\begin{aligned} \pi (-1|+1)= & {} \pi (+1|-1)=\epsilon , \\ \pi (+1|+1)= & {} \pi (-1|-1)=1-\epsilon , \end{aligned}$$

and $\epsilon$ is the probability of error. Here memory-less refers to the factorization in (8), while unbiased means that the noise acts symmetrically on both realizations of the Markov process: $\pi (1|-1)=\pi (-1|1)$.

Recall that the composite process $\mathcal{X}\mathcal{Y}$ is Markovina, but $\mathcal{Y}$ is generally not a Markovian process [15, 16].

To proceed further, we use the following parametrization of the HMM [20]:

$$\begin{aligned} p(x_{k}|x_{k-1})= & {} \frac{e^{J x_{k} x_{k-1} }}{2\cosh J} ,\quad J=\frac{1}{2}\ln \left[ \frac{1-q}{q } \right] , \end{aligned}$$

(9)

$$\begin{aligned} \pi (y_{i}|x_{i})= & {} \frac{e^{h y_i x_i}}{2\cosh h},\quad h=\frac{1}{2}\ln \left[ \frac{1-\epsilon }{\epsilon } \right] , \end{aligned}$$

(10)

MAP estimation is then equivalent to minimizing the Hamiltonian defined as $H(\mathbf{y},\mathbf{x})\equiv -\ln [\, p(\mathbf{y}|\mathbf{x})p(\mathbf{x})\,]$ [20]:

$$\begin{aligned} H(\mathbf{y},\mathbf{x})=-J{\sum }_{k=1}^N x_{k} x_{k+1} - h{\sum }_{k=1}^Ny_kx_k, \end{aligned}$$

(11)

where we have omitted irrelevant factors that are either additive or vanish for $N\gg 1$. The Hamiltonian Eq. 11 formally describes a 1d Ising model with random external fields [22], where the distribution of those fields is governed by $p(\mathbf{y})=\sum _{\mathbf{x}} p(\mathbf{x},\mathbf{y})$. We note that one dimensional Ising-type models have been also used to study error correcting codes [21, 23].

We find it convenient to introduce the following gauge transformation:

$$\begin{aligned} z_i=x_iy_i, \qquad \tau _i=y_iy_{i+1}. \end{aligned}$$

(12)

For a given $\mathbf{y}$, the role of observations will be played by ${\varvec{\tau }}=\{\tau _i \}$, while the original hidden variables now correspond to $\mathbf{z}=\{ z_i \}$. Hence, (11) reads

$$\begin{aligned} H(\varvec{\tau },\mathbf{z})= & {} -J{\sum }_{k=1}^N\tau _k z_{k} z_{k+1} -h{\sum }_{k=1}^Nz_k, \end{aligned}$$

(13)

$$\begin{aligned} p(\varvec{\tau },\mathbf{z})\propto & {} \exp [- H(\varvec{\tau },\mathbf{z})]. \end{aligned}$$

(14)

We shall refer to $\tau _k=\pm 1$ as bond (plus or minus), and to $z_k=\pm$ as spin (up and down). Eq. 13 describes the Hamiltonian of a one-dimensional Ising model with random bonds $\tau _k$ in an external field h [20]. The MAP inference reduces to minimizing this Hamiltonian for a given $\varvec{\tau }$, i.e. to taking the zero-temperature limit $T\rightarrow 0$ [24]. Note also that Eq. 14 is the Gibbs distribution at temperature $T=1$ [24].

In the new variables, the overlap gain given by Eq. 6 reads:

$$\begin{aligned} \varDelta O[{\hat{\mathbf{z}}},\varvec{\tau };1]= & {} \sum _{z_2,...,z_N}\sum _{i=2}^N [\tilde{z}_i(-\hat{z}_1(\varvec{\tau }),\varvec{\tau })-\hat{z}_i(\varvec{\tau })] \nonumber \\&\quad z_i\, p(-\hat{z}_1(\varvec{\tau }),z_2,...,z_N|\varvec{\tau }). \end{aligned}$$

(15)

Below we suppress the arguments of $\varDelta O$, if they are clear from the context.

4 Domain Structure of MAP

The MAP estimation for BS-HMMs is characterized by (countably infinite) numbers of operational regimes that are related to each other via first-order phase transitions [13]. Those transitions occur at the parameter values

$$\begin{aligned} h_c^{m}=2J/m, \end{aligned}$$

(16)

or alternatively, at the critical noise intensities [13]

$$\begin{aligned} \epsilon _c^{m}=1/[1+\epsilon ^{4J/m}] \ , \ m=1,2,.. \end{aligned}$$

(17)

Furthermore, for any noise intensity above the critical value $\epsilon >\epsilon _c^1$, the MAP solution is macroscopically degenerate: For any observation sequence of length N, there are exponentially many (in N) sequences that simultaneously maximize the MAP objective [13].

Let us focus on the structure of the MAP solution. A straightforward analysis (first carried out in [25] for the one-dimensional Ising model) shows that the dependence of $\hat{\mathbf{z}}(\varvec{\tau })$ on $\varvec{\tau }$ is local: $\varvec{\tau }$ is factorized into non-overlapping domains $\varvec{\tau }=(\varvec{\tau }_1,\mathbf{w}_1,\varvec{\tau }_2,\mathbf{w}_2,...)$, where $\mathbf{w}_k$ are the walls separating domains. Walls are sequences of two or more up spins joined by positive bonds; see below. The estimated sequence $\hat{\mathbf{z}}$ admits similar factorization $\hat{\mathbf{z}}=(\hat{\mathbf{z}}_1,\mathbf{w}_1,\hat{\mathbf{z}}_2,\mathbf{w}_2,...)$, such that $\hat{\mathbf{z}}_k$ has the same length as $\varvec{\tau }_k$, and is determined solely from $\varvec{\tau }_k$ (non-uniquely in general).

We now proceed to describe the domain structure for those different regimes as characterized by h / J. Without loss of generality we assume $J>0,\, h>0$.

4.1 The Maximum Likelihood Regime

For sufficiently weak noise [cf. (10)]

$$\begin{aligned} h>2J, \end{aligned}$$

(18)

the MAP estimation coincides with the observed sequence $\hat{\mathbf{x}}=\mathbf{y}$. Hence, $\hat{z}_i=1$ for all i; see (13). The prior probability $p(\mathbf{x})$ is irrelevant in this regime: on can take $J=0$, i.e. the MAP estimation reduces to the maximum-likelihood estimation, where the noise probability $p(\mathbf{y}|\mathbf{x})$ is maximized for a fixed $\mathbf{y}$; see (8).

The overlap gain (15) nullifies for (18), because supervising a spin does not change other spins: $\hat{z}_i=\tilde{z}_i$.

4.2 First Non-trivial Regime

We now focus on the following regime:

$$\begin{aligned} J<h<2J, \end{aligned}$$

(19)

Here $2J>h$ ensures that there are $\hat{z}$-spins equal to $-1$ [otherwise we are back to (18)], while $h>J$ means that two spins joined by a positive bound are both equal to 1. To verify it consider

$$\begin{aligned}&\uparrow ~ - ~ \uparrow ~ + ~ \uparrow ~ - ~ \uparrow , \end{aligned}$$

(20)

$$\begin{aligned}&\uparrow ~ - ~ \downarrow ~ + ~ \downarrow ~ - ~ \uparrow , \end{aligned}$$

(21)

where $z_i=1$ and $z_i=-1$ are represented as $\uparrow$ and $\downarrow$, respectively, while $\pm$ refer to $\tau _i =\pm$.

The energy of (20) is $J-4h$ which is smaller than the energy $-3J$ of (21) precisely when $h>J$. Hence, the minimal size of the wall in the regime (19) is just two ($+1$) spins joined by a positive bond.

In the regime (19) there are the following domains [25].

• A frustrated $2n+1$-domains consists of an odd (and larger than one) number $2n+1$ of consequitive minus bonds (i.e. bonds with $\tau _k=-1$) that are bound from both ends by positive bonds. Frustrated means the correspondence between $\{\tau _k\}$ and $\{\hat{z}_k\}$ is not unique, e.g. the following two configurations have the same energy

  $$\begin{aligned}&+ ~ \uparrow ~ - ~ \uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~+, \end{aligned}$$

  (22)
  $$\begin{aligned}&+ ~ \uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~ - ~ \uparrow ~+. \end{aligned}$$

  (23)

  Both (22) and (23) have the same values of $\{\tau _k\}_{k=1}^5$. However, the sequences $\{\hat{z}_k\}_{k=1}^4$ are different, though they have exactly the same energy. More generally, a frustrated $2n+1$-domain supports $n+1$ equivalent sequences [25]; see also below. This non-uniqueness is reflected via a zero-temperature entropy [13, 25].

• Non-frustrated domains consist of an even number of consecutive minus bonds bound from both ends by positive bonds. In this case, the correspondence between $\{\tau _k\}$ and $\{\hat{z}_k\}$ is unique, e.g. $( + ~ \uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~ +)$.

It is worthwhile to note that the notion of frustration described above is inherently related to the exponential degeneracy (in the number of observations N) of the MAP solution above the first critical noise intensity [13]. Indeed, consider, for instance, the frustrated 3-domain shown in (20) and (21). In any observation sequence $\mathbf{y}$ of length N, the expected number of such frustrated 3-domains $n_d$ scales linearly with $N,\; n_d=\alpha N$, where $\alpha$ is a (possibly small) constant. And since each such domain multiplies the number of MAP solution by two (i.e., simultaneously flipping both frustrated spins is still a solution), there overall number of solutions will scale as $\propto 2^{\alpha N}$, thus indicating exponential degeneracy.

4.3 Further Regimes

Now lets us focus on the third regime defined by

$$\begin{aligned} 2J/3<h<J, \end{aligned}$$

(24)

In this regime, the walls are formed by two (or more) up-spins joined together by two (or more) positive bonds. Thus $2J/3<h$ is precisely the condition why three spins joined by two positive bonds always look up, while $h<J$ means that two spins joined by one positive bonds can both look down.

• The old domains stay intact if they are separated (from both ends) by (at least) three up-looking spins joined by (at least) two positive bonds.

• New domains are formed by pair(s) of spins joined by a positive bond, which are immersed into a set of negative bonds. In the new domains only the pairs of spins joined by positive bond can be frustrated. The frustration rule follows the above pattern, where now the pairs (super-spin) play the role of single spins in the previous regime (19), while the odd (even) number of negative spins built up into one negative (positive) superbond [25]. Here is an example of this situation

  $$\begin{aligned} \underbrace{+\uparrow +\uparrow }_{\uparrow } \underbrace{ - \downarrow - \uparrow -}_{-} \underbrace{\downarrow + \downarrow }_{\downarrow } \underbrace{-}_{-} \underbrace{\uparrow +\uparrow +}_{\uparrow }, \end{aligned}$$

  (25)

  where the super-spins and super-bonds are shown in the second line. This domain is not frustrated. Note that in the regime (19, 25) breaks down into two separate domains, the first of which is frustrated.

The domain structure for $h<2J/3$ (and smaller values of h) is constructed recursively following the above pattern [25].

5 Active Estimation of Basic Domains

We implement active estimation for separate domains, i.e. in each domain we supervise one spin $z_1$. Advantages of this implementation are as follows: (i) properly choosing already one spin (and finding out that it is incorrect) allows to get rid of the non-uniqueness of the MAP estimate; (ii) the re-estimation $\hat{\mathbf{z}}(\varvec{\tau })\rightarrow \tilde{\mathbf{z}}(x_1,\varvec{\tau })$ is restricted to one domain only; (iii) (15) can be calculated approximately.

5.1 Frustrated 3-domain

In the domain (22) we supervise the second spin. If it is opposite to the MAP estimate, then we move to the configuration (23) that has the same energy:

$$\begin{aligned} {\hat{\mathbf{z}}}(\varvec{\tau })= & {} (+ ~ \uparrow ~ - ~ \Uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~+), \end{aligned}$$

(26)

$$\begin{aligned} {\tilde{\mathbf{z}}}(\varvec{\tau })= & {} (+ ~ \uparrow ~ - ~ \Downarrow ~ - ~ \uparrow ~ - ~ \uparrow ~+), \end{aligned}$$

(27)

where $\Uparrow$ shows the supervised spin. Hence, the active estimation removes the non-uniqueness of the MAP solution. The overlap gain is calculated from (15):

$$\begin{aligned} \varDelta O=2{\sum }_{z_3}z_3 p(-1,z_3|\varvec{\tau }), \end{aligned}$$

(28)

where $z_3$ is the third spin in (26, 27); the one that changes after the re-estimation. The marginal probability $p(-1,z_3|\varvec{\tau })$ in (28) cannnot be determined in a closed analytic form [13, 14].

We calculate $p(z_2,z_3|\varvec{\tau })$ in a impenetrable wall approximation: when J and h are sufficiently large, then one can neglect fluctuations of the spins within the walls separating domains as compared to spins located within the domains. Hence, we write for n-domain ($n=3,5,7,...$ and normalization is omitted)

$$\begin{aligned} p(z_2,...,z_n|\varvec{\tau })\propto e^{-J(z_2+z_n)-J\sum _{k=2}^{n-1} z_k z_{k+1} +h\sum _{k=2}^{n}z_k }. \end{aligned}$$

(29)

We checked numerically that even for thinnest two-spin walls the approximation works well already for $J\simeq 1$; see below. Using (29) with $n=3$ in (28) we get

$$\begin{aligned} \varDelta O= \frac{2(1-e^{-2h})}{2+e^{-2h}+e^{-4J+2h}}. \end{aligned}$$

(30)

Likewise, if the originally estimate sequence is given by (31), then upon supervising the second spin we obtain

$$\begin{aligned}&\hat{z}(\varvec{\tau })=(+ ~ \uparrow ~ - ~ \Downarrow ~ - ~ \uparrow ~ - ~ \uparrow ~+), \end{aligned}$$

(31)

$$\begin{aligned}&\tilde{z}(\varvec{\tau })=(+ ~ \uparrow ~ - ~ \Uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~+). \end{aligned}$$

(32)

Instead of (28), we need to use

$$\begin{aligned} \varDelta O=-2{\sum }_{z_3}z_3 p(1,z_3|\varvec{\tau }), \end{aligned}$$

(33)

which yields

$$\begin{aligned} \varDelta O=\frac{2(1-e^{-2(2J-h)})}{2+e^{-2h}+e^{-4J+2h}}. \end{aligned}$$

(34)

Remarkably, (34) and (30) are different. This seems surprising, since given the apparent symmetry between (26, 27) and (31, 32), one would expect that the overlap gain should be the same in both cases. This is not the case, however, since (33) and (28) are defined differently, e.g. (33) involves $p(1,z_3|\varvec{\tau })$, while (28) has $p(-1,z_3|\varvec{\tau })$.

Both (30) and (34) are positive in the regime (19), but (30)$>$(34): when the supervised spin (initially) agrees with the observation, the expect gain due to active inference is larger.

For $h<J$ we can employ the same two domains (26, 27) and (31, 32) provided that they are surrounded by sufficiently thick walls; see Sect. 4.3. Now the opposite relation holds: (30)$<$(34).

Note finally that whenever the supervising shows that the true value of the spin was already recognized correctly, the overlap does not change, but it is still useful, since the number of solutions decreases, i.e. instead of two solutions in (22, 23) we have only one.

5.2 Frustrated 5-domain

There are 3 MAP sequences for the 5-domain

$$\begin{aligned} \hat{\mathbf{z}}= & {} (+ ~ \uparrow ~ - ~ \uparrow ~ - ~ \downarrow ~ - ~ \Uparrow ~ - ~ \downarrow ~ - ~\uparrow ~ +), \end{aligned}$$

(35)

$$\begin{aligned} \tilde{\mathbf{z}}= & {} (+ ~ \uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~ - ~ \Downarrow ~ - ~ \uparrow ~ - ~\uparrow ~ +), \end{aligned}$$

(36)

$$\begin{aligned}&(+ ~ \uparrow ~ - ~ \downarrow ~ - ~ \uparrow ~ - ~ \uparrow ~ - ~ \downarrow ~ - ~\uparrow ~ +). \end{aligned}$$

(37)

The following scenarios are the most efficient ones, i.e. they lead to the largest $\varDelta O$ (under (19)): (i) going from (35) to (36) by supervising the fourth spin (denoted by $\Uparrow$ in (35)). (ii) going from (36) to (35) by supervising the third spin. Both these cases have the same overlap gain (38) due to the mirror symmetry with respect to the center of the domain that is shared also by (29).

The optimal overlap gain is calculated from (29)

$$\begin{aligned} \varDelta O= & {} 2\sum _{z_2,z_3,z_5}(z_3+z_5-z_2)p(z_2,z_3,-1,z_5|\varvec{\tau })\nonumber \\= & {} \frac{2 e^{4 J} \left( e^{2 h} \left( \left( 3 e^{2 h}+1\right) e^{4 J}-2 e^{2 h}+e^{4 h}-2\right) -1\right) }{\left( 3 e^{2 h}+2\right) e^{2 h+8 J}+\left( 2 e^{2 h}+3 e^{4 h}+4 e^{6 h}+1\right) e^{4 J}+e^{8 h}}. \end{aligned}$$

(38)

It can be shown that (38) is larger than (30), which is the best overlap gain for a 3-domain. In (37) there are no spins whose supervision can lead to the maximal overlap gain.

For the 5-domain we meet a situation that was absent in the previous 3-domain case. While (38) calculates the average overlap gain for supervising the fourth spin in (35), it is possible that this spin was recovered by the MAP correctly, i.e. it does not flip after supervising. Then we are left with no overlap gain and also with uncertainty between (35) and (37), since they both have the correct fourth spin. We can now supervise an additional spin, so as to recover the unique original sequence. It is seen from (35, 37) that when starting from (35) there are 2 possibilities: to supervise the second spin or the third one. Additional 2 possibilities exist when supervising from (37). Out of these 4 possibilities the largest overlap gain is achieved for supervising the second spin in (35):

$$\begin{aligned} \varDelta O= & {} 2 \sum _{z_3,z_5}z_3 p(-1,z_3,1,z_5|\varvec{\tau })\nonumber \\= & {} \frac{8 e^{4 h+6 J} \sinh (h) \cosh (h-2 J)}{\left( 3 e^{2 h}+2\right) e^{2 h+8 J}+\left( 2 e^{2 h}+3 e^{4 h}+4 e^{6 h}+1\right) e^{4 J}+e^{8 h}}, \end{aligned}$$

(39)

where $p(-1,z_3,1,z_5|\varvec{\tau })$ shows that the fourth spin is fixed to its correct MAP value 1. The same $\varDelta O$ as in (39) is reached when supervising the third spin in (37). The remaining two possibilities are inferior.

Our analysis shows that the gain described by Eq. 39 is smaller than both (38) and (30). Thus, one can turn to the situation described by (39), only if some budget is left after supervising 3-domains; cf. the discussion after (50).

5.3 Frustrated 7-domains

In this case there are four MAP sequences defined as follows:

$$\begin{aligned} \hat{\mathbf{z}}= & {} (+ ~ \uparrow - \uparrow - \downarrow - \Uparrow - \downarrow - \uparrow - \downarrow - \uparrow ~ +), \end{aligned}$$

(40)

$$\begin{aligned} \tilde{\mathbf{z}}= & {} (+ ~ \uparrow - \downarrow - \uparrow - \Downarrow - \uparrow - \uparrow - \downarrow - \uparrow ~ +), \end{aligned}$$

(41)

$$\begin{aligned} \hat{\mathbf{z}}= & {} (+ ~ \uparrow -\downarrow - \uparrow - \downarrow - \Uparrow - \downarrow - \uparrow - \uparrow ~ +), \end{aligned}$$

(42)

$$\begin{aligned} \tilde{\mathbf{z}}= & {} (+ ~ \uparrow - \downarrow - \uparrow - \uparrow - \Downarrow - \uparrow - \downarrow - \uparrow ~ +). \end{aligned}$$

(43)

Two most efficient active inference schemes are realized by transitions from (40) to (41) and from (42) to (43). They are again related to each other by the mirror symmetry, hence their overlap gains are equal and is calculated from (29). Furthermore, tedious but straightforward calculations demonstrate that the overlap gain for those scheme is larger than the one given by (38), the best overlap gain for a 5-domain. We also note that the most efficient supervision is absent if one starts from (41) or from (43).

Similar to 5-domain, it is possible that a spin does not flip after semi-supervising (e.g., it was recovered correctly in the original MAP inference). In this case, one should consider supervising other spins in the domain. The analysis of possible strategies can be performed as explained in Sect. 5.2.

5.4 Non-frustrated Domains

A simple analysis suggests that it is meaningless to supervise a spin inside a non-frustrated domain (even number of negative bonds surrounded by two walls). Indeed, consider

$$\begin{aligned} {\hat{\mathbf{z}}}= & {} (+ ~ \uparrow - \downarrow - \Uparrow - \downarrow - \uparrow ~ +), \end{aligned}$$

(44)

$$\begin{aligned} {\tilde{\mathbf{z}}}= & {} (+ ~ \uparrow - \uparrow - \Downarrow - \uparrow - \uparrow ~ +), \end{aligned}$$

(45)

where the third spin is supervised. Calculating the overlap gain following to the above method, we confirm that this gain is zero.

5.5 Supervising Inside a Wall

It is possible that even after supervising all the frustrated domains, one still has budget for supervising additional spins. Hence, we study supervising of a spin inside a wall. Consider the thinnest wall (two spins joined by a positive bond) in the regime (19), and assume that it is surrounded by larger walls (at least two positive bonds).

$$\begin{aligned}&{\hat{\mathbf{z}}}=(+\uparrow + ~ \uparrow ~ - ~ \Uparrow ~ + ~ \uparrow ~ - ~ \uparrow ~ + \uparrow +), \end{aligned}$$

(46)

$$\begin{aligned}&{\tilde{\mathbf{z}}}=(+\uparrow + ~ \uparrow ~ - ~ \Downarrow ~ + ~ \downarrow ~ - ~ \uparrow ~+\uparrow +), \end{aligned}$$

(47)

where, as above, $\Uparrow , \Downarrow$ indicate on the supervised spin. We have [cf. (28)]

$$\begin{aligned} \varDelta O=-2{\sum }_{z_4}z_4 p(-1,z_4|\varvec{\tau }). \end{aligned}$$

(48)

We employ [cf. (29)]

$$\begin{aligned} p(z_3,z_4|\varvec{\tau })\propto e^{-Jz_3+Jz_3z_4-Jz_4+h(z_3+z_4)} \end{aligned}$$

(49)

and get for (48)

$$\begin{aligned} \varDelta O =\frac{2(e^{2(2J-h)}-1)}{2+e^{2h}+e^{4J-2h}}. \end{aligned}$$

(50)

This is smaller than both (30) and (34): it is less efficient to supervise a spin inside a (two-spin) wall than inside a (two-spin) domain. In the regime (19), (50) can be both smaller or larger than (39) depending on concrete values of h and J.

5.6 Summary

To summarize this section, we converge to the following picture of active inference: given the unsupervised MAP-sequence, one fixes the walls and factorizes the sequence over frustrated domains of odd-numbered bonds. Starting from the longest domain (as it corresponds to the largest overlap gain) one supervises the spin (or spins) in each domain that yield maximum expected overlap gain, as described above. Thereby, a unique supervised MAP-sequence is gained. Once all the domains are supervised in this way, one should spend the remaining “budget” for supervising spins inside the walls.

6 Comparison with Numerical Results

We now report on our experiments aimed at validating our analytical predictions. We will focus on the non-trivial regime of sufficiently high noise intensities ($\epsilon > \epsilon _c^1)$, for which there are exponentially many (in the number of observations) MAP solutions corresponding to a given observation sequence [13]. Recalling our discussion of the frustrated domains, it is clear that all those solutions correspond to permuted configurations of the frustrated spins.

In our experiments, we generate random HMM sequences, then run the Viterbi algorithm to find one of the MAP sequences. We then apply the active inference strategies described above, and compare the numerical findings with the analytic predictions. For simplicity, here we focus on our prediction for 3-domains; see Sect. 5.1. Recall that our analytical results are obtained under the impenetrable wall approximation (29), which requires that the constant J is not very small; cf. (10). In the experiments below we set $J=1.5$.

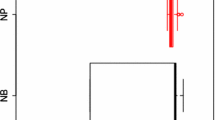
First, we study the statistics of different domains as a function of noise. Figure 1a shows the fraction $f_i$ of spins that belong to frustrated domains of size i, for $i=3,5,7,9$. We observe that the overall fraction of spins inside those domains is rather small. For instance, for $\epsilon =0.1$, only $2\,\%$ of spins belong to 3-domains, and less then $0.01\,\%$ belong to 9-domains. Thus, for the parameter range considered here, any gain in active inference will be mostly due to 3, 5, and 7-domains.

Fig. 1

a Fraction of spins belonging to different domains plotted against noise; b The average overlap gain plotted against noise obtained from simulations (open symbols) and analytical predictions given by Eqs. 30 and  34 (solid lines); c Inference error for different methods plotted against noise. In all three figures we use $J=1.5$. For b and c, we used sequences of size $10^5$, and averaged the results over 1000 random realizations

Next, we compare our analytical prediction with simulation results for two active inference strategies applied to 3-domains. For the simulations, we generated sufficiently long sequences ($10^5$), identified all 3-domains, and applied two active inference strategies as described in Sect. 5.1. For the first strategy, we always supervise one of two spins that is looking up (i.e., the inferred hidden state is aligned with the observation). The expect gain in overlap for this strategy is given by Eq. 30. And for the second strategy, we supervise the spin that is looking down (i.e., the inferred hidden state is misaligned with the observation). In this case, the expected overlap gain is given by Eq. 34.

The results are shown in Fig. 1b, where we plot the expected overlap gain as a function of noise, in the range $\epsilon _c{^1}\le \epsilon \le \epsilon _c^{3}$; cf. (17). The agreement between the prediction and the simulations is near-perfect when the noise intensity is in the range $\epsilon _c{^1}\le \epsilon \le \epsilon _c^{2}$. In particular, the switching of the optimal supervising strategy, as predicted from Eqs. 30 and  34, is reproduced in the experiments. Interestingly, for one of the “branches” (given by Eq. 34), the agreement remains near-perfect even for larger noise intensities. However, the agreement with the other branch (given by Eq. 34) deteriorates with increasing noise. We recall that the analytical predictions are obtained under the impenetrable wall approximation, which assumes that domains are surrounded by sufficiently thick walls. When increasing noise, the assumptions starts to gradually break down, and the approximation becomes less accurate.

Finally, Fig. 1c compares inference errors for the original MAP, MAP with random supervising, and MAP with active inference. We see that the active inference strategy yields lower inference error over the whole range of noise intensities. In fact, this difference becomes more pronounced for large noise intensities. We also note that the slight kinks in the curves corresponding to the phase transition between different domains [13].

7 Conclusion

7.1 Discussion of the Main Results

We have developed an analytical approach to study active inference problem in binary symmetric HMMs. We obtained a closed-form expression that relates the expected accuracy gain to model parameters within the impenetrable domain approximation, specified the validity range of the analysis, and tested our analytical predictions with numerical simulations. Based on the analytical insights, we suggest an optimal active inference strategies for BS-HMM, that can be summarized as follows: Given an observation sequence $\mathbf{y}$ and a corresponding (unsupervised) MAP-sequence $\hat{\mathbf{x}}(\mathbf{y})$, we first find all the frustrated domains composed of odd-numbered bonds. Then, starting from the longer domains, we supervise one of the spins inside the domain, according to the optimality criteria outline in (30, 38). Only after supervising all the frustrated domains (and subject to budget constraints), one can consider supervising schemes described in (39) and (50).

Note that while our focus was on batch active inference, our results are also applicable to the online settings (e.g., active filtering), owing to the separation of the estimated hidden sequence into separate weakly interacting domains.

7.2 Relationship to Existing Heuristics for Active Inference

Here we discuss to which extent solutions studied above relate to heuristic methods for active inference; see Sect. 1. Below we always assume the regime of parameters, where (29) applies.

Within the uncertainty reduction heuristics we supervise $x_l$ if some suitable measure of uncertainty, e.g. $1-\sum _{x_k=\pm 1} p^2(x_k|\mathbf{y})$, maximizes at $k=l$. For the 3-domain (26, 27) both spins of the domain are equally uncertain [see (29)], but we saw that their supervising leads to different results. Thus, the uncertainty reduction does not correlate with the optimal scheme.

For the 5-domain (35–37) the third spin (and due to the mirror symmetry the fourth one) is the most uncertain one. This correlates with the optimal scheme (35, 36), but does not allow to recover this scheme, e.g. supervising the third spin in (37) is not optimal. The same correlation is seen for the 7-domain, where the fourth spin is the most uncertain one; see (40–43).

Consider now another (related) heuristic principle for active inference that tries to supervise spins in such a way that it leads to a unique solution. This principle does not apply 3-domain, since here the choice of either spin leads to a unique solution. It partially holds for the optimal solution of the 5-domain: if in (35) the supervised spin was found to be wrong, then we are left with only one possible configuration (36), e.g. supervising the third spin in (35) does lead to unique sequence: it can be either (36) or (37). However, if the supervised spin in (35) was found to be correct, we are not left with a unique configuration [an additional supervising is necessary to achieve a unique configuration, but it is beneficial to supervise instead another 3-domain of 5-domain; see the discussion after (39)]. Likewise, for the 7-domain, no correlation exists between the optimal supervising and the uniqueness of the resulting configuration: even if the optimally supervised is found to be wrong, we do not automatically appear in a unique configuration; see (40, 41).

7.3 Open Problems

There are several interesting directions for extending the presented results. First, here we focused on the inference task, assuming that the model parameters are known. In more realistic scenarios, those parameters ($(q,\epsilon )$, or (J, h)) are unknown and need to be estimated from the data, e.g., using Baum–Welch algorithm [16]. While developing a full analytical solution for the joint active inference/learning problem might be challenging even for the simple BS-HMM considered here, it should be possible to extend the methods presented here for studying the robustness of optimal inference strategies with respect to misspecified parameters. In particular, a regime where $J\gg h$ [cf. (9, 10)] was left open in our consideration. This case is realized when, in particular, the noise is very strong $\epsilon \rightarrow 1/2$. It is known from the experience of the 1d random-field Ising model that this case is rather non-trivial due to the presence of (partially hidden) non-analytic features [26]. We hope to account for this regime in future.

Another interesting and important question is to what extent the optimal active inference schemes analyzed here apply to more general class of HMMs. We believe that the answer to this question can be examined via a generalized definition of frustration. In the context of MAP estimation, this implies looking at generalized (k-best) Viterbi algorithm that return several candidates solutions having approximately equal likelihoods or energies [27, 28]. In this scenario, we can intuitively define frustrated variables as those that change from one solution to sanother.

Also, using the analogy with statistical physics, we believe that the active MAP inference via domains and walls can be generalized beyond the (one-dimensional) HMM models, and it possibly applies to active recognition of two-dimensional patterns. Now instead of one-dimensional Ising model, one has a two-dimensional (2d) random Ising spin system. We note that 2d Ising-type models have been used extensively in various pattern recognition tasks such as computer vision [29].

Finally, there are several interesting analogies between the optimal inference strategies uncovered here and human heuristics in information processing [30, 31]. Note that the optimal scheme in the regime (19) amounts to supervising the up-spins, e.g., the ones that agree with observations. This point can be related to falsifiability [30], where one looks at cases when the existing (prior) knowledge can be challenged. In contrast, people often show confirmation bias, i.e. they tend to confirm the existing knowledge rather than question it; see [31] for a review. Further development of those ideas may provide interesting connections with cognitive aspects of active inference strategies.