Snap-Through Buckling of Micro/Nanobeams in Bistable Micro/Nanoelectromechanical Systems

Abstract

In this chapter, we investigate the instability behavior of an initially curved micro/nanobeam subject to an electrostatic force. The general governing equations of the curved beam are developed using Euler-Bernoulli beam theory and are solved using the Galerkin decomposition method. Firstly, the size effect on the symmetric snap-through buckling of the microbeam is studied. The size effect is accounted for in the beam model using the modified couple stress theory. The fringing field effect and the intermolecular effects, such as van der Waals and Casimir forces, are also included in the snap-through formulations. The model simulations reveal the significant effect of the beam size, and to a much lesser extent the effect of fringing field and intermolecular forces, upon the snap-through criterion for the curved microbeam. Secondly, the surface effects on the asymmetric bifurcation of the nanobeam are studied. The surface effects, including the surface elasticity and the residual surface tension, are accounted for in the model formulation. The results reveal the significant size effect due to the surface elasticity and the residual surface tension on the symmetry-breaking criterion for the considered nanobeam.

9.1 Introduction

Micro/nano-electro-mechanical systems (MEMS/NEMS) have aroused great interest for their unique advantages such as small size, high precision, and low power consumption. One benchmark of MEMS/NEMS is the initially straight micro/nanobeam system driven by electrostatic force, whose static and dynamic behaviors have been largely investigated in the literature (Carr et al. 1999; Dequesnes et al. 2002; Jia et al. 2011; Ke et al. 2005; Kinaret et al., 2003; Li et al., 2013; Ruzziconi et al., 2013; Tilmans and Legtenberg, 1994; Verbridge et al., 2007 among many others). Recently, the bistable MEMS/NEMS based on initially curved micro/nanobeams have drawn more and more attention from the scientific community for their various potential applications such as optical switches, micro-valves, and non-volatile memories (Charlot et al., 2008; Goll et al., 1996; Intaraprasonk and Fan (2011); Roodenburg et al., 2009).

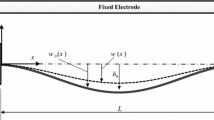
The initially curved beam (arch) under transverse forces may exhibit two main instabilities: symmetric snap-through buckling and asymmetric bifurcation. The symmetric snap-through buckling is the transition between two stable states (Medina et al. 2012). After the snap-though, the arch shape is symmetric, as depicted in Fig. 9.1a. However, for the asymmetric bifurcation, the arch may exhibit one of the asymmetric deformations shown in Fig. 9.1b.

Fig. 9.1

Schematics of instability behaviors of arch under transverse force

The existence of snap-through buckling and asymmetric bifurcation depends on various factors, e.g., initial arch rise and beam thickness. Pippard (1990) conducted experiments to develop a phase diagram of instability in terms of the arch span and the initial angle at the clamped ends. This work was followed by Patricio et al. (1998) in which they developed theoretical model simulations to derive a similar phase diagram. As a result of the earlier experiments and model simulations, Krylov et al. (2008) revealed that the symmetric snap-through buckling occurs at large initial deflections. Pane and Asano (2008) conducted energy analysis and further found that the existence of bistable states in an initially curved beam depends on the ratio of its initial deflection to its thickness. Park and Hah (2008) conducted theoretical investigations and showed that the existence of bistable states also depends on the residual axial stress in the beam. Das and Batra (2009a) developed a finite element model to study the transient snap-through behavior of the initially curved beam, and found that at high loading rates (i.e., voltage is applied at a high rate), the snap-through buckling is suppressed. Moghimi Zand (2012) also developed a finite element model and found the significant inertia effect on the dynamic snap-through behavior. Medina et al. (2012, 2014a) examined the symmetric snap-through buckling and the asymmetric bifurcation of an electrostatically actuated mircobeam with/without residual stress. They derived the criteria of symmetric snap-through and symmetry breaking for quasi-static loading conditions.

Careful literature review indicates that many studies consider a uniform mechanical force as the applied load. However, the electrostatic force applied on the curved micro/nanobeam is highly nonuniform and strongly depends on the beam deflection. Several studies consider the electrostatic force, but they fail to examine the fringing field effect and/or the influence of the intermolecular forces such as Casimir and van der Waals forces. Furthermore, the size effect at the microscale and the surface effects at the nanoscale are neglected in almost all the existing studies.

For the microstructures, the size effect on deformation behaviors has already been observed experimentally (Fleck et al. 1994; Lam et al. 2003; Ma and Clarke 1995; McFarland and Colton 2005), and such size dependency is attributed to the non-local effects, which cannot be described by the classical continuum theories of local character. Various nonclassical continuum theories with additional material length scale parameters have been proposed (Eringen 1983; Fleck and Hutchinson 2001; Lam et al. 2003; Mindlin 1965; Toupin 1962; Yang et al. 2002). Among them, the modified couple stress theory developed by Yang et al. (2002) with a length scale parameter is one of the most used. Determining the microstructure-dependent length scale parameters is difficult, so it is desirable to use the theories with only one length scale parameter (Reddy 2011). Based on the nonclassical continuum theories, the size effect on various behaviors of microbeams has been theoretically studied, including bending, buckling, free vibration, and pull-in instability (Belardinelli et al. 2014; Farokhi et al. 2013; Kong 2013; Ma et al. 2008).

For the nanostructures, experiments have shown that their elastic properties are size dependent (Cuenot et al. 2004; Jing et al. 2006; Li et al. 2003; Poncharal et al. 1999; Sadeghian et al. 2009; Salvetat et al. 1999; Shin et al. 2006), and such size dependency can be explained by the associated surface effects (Cuenot et al. 2004; Dingreville et al. 2005; Jing et al. 2006; Miller and Shenoy 2000; Sadeghian et al. 2011; Zhu 2010). The surface elasticity theory of Gurtin and Murdoch (1975, 1978) can predict the size-dependent effective elastic properties of the nanostructures, which has been extensively validated by experiments (Asthana et al. 2011; Fu et al. 2010; He and Lilley 2008; Xu et al. 2010). Based on this theory, the surface effects on various deformation behaviors of nanobeams have been investigated, such as bending, buckling , free vibration, and pull-in instability (Fu and Zhang 2011; He and Lilley 2008; Wang and Feng 2007, 2009).

In this chapter, we extend the earlier studies to investigate the size effect and the surface effects on the instability behaviors of the initially curved micro- and nanobeams under electrostatic force. Section 9.2 is devoted to the size effect on the symmetric snap-through buckling of microbeam. The beam model is developed considering the modified couple stress theory (Yang et al. 2002). The fringing field effect is taken into account by Meijs-Fokkema formula (van der Meijs and Fokkema 1984), and the influence of the intermolecular forces is also examined. In Sect. 9.3, the surface effects on the asymmetric bifurcation of nanobeam are studied. The surface elasticity and the residual surface tension are accounted for in the beam model by using the surface elasticity theory of Gurtin and Murdoch (1975, 1978) and the generalized Young–Laplace equation (Chen et al. 2006; Gurtin et al. 1998). Based on the models and simulation results, the criteria for the existence of snap-through buckling and asymmetric bifurcation are derived, which can be used for the design of the bistable MEMS/NEMS.

9.2 Size Effect on Symmetric Snap-Through Buckling of Microbeam

9.2.1 Formulation

9.2.1.1 Governing Equations

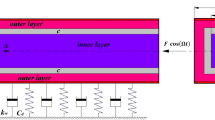
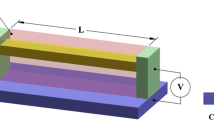
Consider an initially curved rectangular microbeam of span L, width b, and thickness h undergoing in-plane bending (x − z plane in Fig. 9.2). The respective displacements u _x , u _y , and u _z along x-, y-, and z-coordinates are assumed to be dependent only on x and z. u _y is further assumed to be 0. For a thin beam (h < < L), the Euler-Bernoulli beam theory is applied:

Fig. 9.2

Initially curved double-clamped micro/nanobeam under electrostatic force. The directions of electrostatic and intermolecular forces are indicated by arrows

$$ {u}_x\left(x,z\right)=u(x)-z{w}^{\prime }(x) $$

(9.1a)

$$ {u}_z\left(x,z\right)=w(x) $$

(9.1b)

where u(x) and w(x) are, respectively, the axial (along x-coordinate) and transverse (along z) displacements of a point on the midplane of the beam; a superimposed apostrophe denotes a derivative with respect to x. During the snap-through buckling, the midplane stretching can be important. To consider this effect, the von Karman nonlinear strain is used. With the aid of Eq. (9.1a, b), the nonzero strain component (i.e., axial strain ε ^* _xx ) can be obtained as (Reddy 2011)

$$ {\varepsilon}_{xx}^{*}={u}^{\prime }-z{w}^{{\prime\prime} }+\frac{1}{2}{\left({w}^{\prime}\right)}^2 $$

(9.2)

Considering the initial strain ε ⁰ _xx related to the initial deflection w ₀(x) by ${\varepsilon}_{xx}^0=-z{w}_0^{{\prime\prime} }+{\left({w}_0^{\prime}\right)}^2/2$, we calculate the axial strain change ε _xx from Eq. (9.2) as

$$ {\varepsilon}_{xx}={\varepsilon}_{xx}^{\ast }-{\varepsilon}_{xx}^0={u}^{\prime }-z\left({w}^{\prime \prime }-{w}_0^{\prime \prime}\right)+\frac{1}{2}\left({\left({w}^{\prime}\right)}^2-{\left({w}_0^{\prime}\right)}^2\right) $$

(9.3)

The symmetric curvature tensor $\underline {\underline{\chi}}$ conjugated to the deviatoric couple stress tensor $\underline {\underline{\psi}}$ in the modified couple stress theory is (Yang et al. 2002)

$$ \underline {\underline{\chi}}=\frac{1}{2}\left(\nabla \underline{\omega}+{\left(\nabla \underline{\omega}\right)}^{\mathrm{T}}\right) $$

(9.4)

where $\underline{\omega}\left(=\left(\nabla \times \underline{u}\right)/2\right)$ is the rotation vector, with $\underline{u}\left(={\left({u}_x,{u}_y,{u}_z\right)}^{\mathrm{T}}\right)$ being the displacement vector; the superimposed T denotes the transpose of the matrix. With the aid of Eq. (9.1a, b), the nonzero curvature components in Eq. (9.4) are calculated as

$$ {\chi}_{xy}^{*}={\chi}_{yx}^{*}=-\frac{1}{2}{w}^{{\prime\prime} } $$

(9.5)

Considering the initial nonzero curvature ${\chi}_{xy}^0={\chi}_{yx}^0=-{w}_0^{\prime \prime }/2$ due to the initial deflection w ₀, we obtain the curvature change χ _xy and χ _yx from Eq. (9.5) as

$$ {\chi}_{xy}={\chi}_{yx}={\chi}_{xy}^{*}-{\chi}_{xy}^0=-\frac{1}{2}\left({w}^{{\prime\prime} }-{w}_0^{{\prime\prime}}\right) $$

(9.6)

To derive the governing equations , the theorem of minimum potential energy is used:

$$ \delta {U}_{\mathrm{elas}}-\delta {W}_{\mathrm{ext}}=0 $$

(9.7)

where δU _elas and δW _ext are, respectively, the variations of the elastic strain energy, and the work done by the external forces. Considering the nonzero strain component ε _xx and the nonzero curvature components χ _xy and χ _yx , we can calculate δU _elas as (Yang et al. 2002)

$$ \delta {U}_{\mathrm{elas}}={\displaystyle {\int}_0^L{\displaystyle {\int}_S\left(\underline {\underline{\sigma}}:\delta \underline {\underline{\varepsilon}}+\underline {\underline{\psi}}:\delta \underline {\underline{\chi}}\right)}\mathrm{d}s\ \mathrm{d}x}={\displaystyle {\int}_0^L{\displaystyle {\int}_S\left({\sigma}_{xx}\delta {\varepsilon}_{xx}+2{\psi}_{xy}\delta {\chi}_{xy}\right)}\mathrm{d}s\ \mathrm{d}x} $$

(9.8)

where ${\displaystyle {\int}_S\mathrm{d}s}$ is the integral over the cross section (y–z plane in Fig. 9.2). Introduce Eqs. (9.3) and (9.6) into Eq. (9.8), integrate the resulting equation by parts with respect to x, and we obtain

$$ \begin{array}{l}\delta {U}_{\mathrm{elas}}=-{\displaystyle {\int}_0^L{N}^{\mathrm{\prime}}\delta u\mathrm{d}x}-{\displaystyle {\int}_0^L\left({M}^{\mathrm{\prime}\mathrm{\prime }}+{C}^{\mathrm{\prime}\mathrm{\prime }}+{\left(N{w}^{\mathrm{\prime}}\right)}^{\mathrm{\prime}}\right)\delta w\mathrm{d}x}\\ {} -N(0)\delta u(0)+N(L)\delta u(L)-({M}^{\mathrm{\prime}}(0)+{C}^{\mathrm{\prime}}(0)+N(0){w}^{\mathrm{\prime}}(0))\delta w(0)\\ {} +({M}^{\mathrm{\prime}}(L)+{C}^{\mathrm{\prime}}(L)+N(L){w}^{\mathrm{\prime}}(L))\delta w(L)+(M(0)+C(0))\delta {w}^{\mathrm{\prime}}(0)\\ {}\kern3.5em -(M(L)+C(L))\delta {w}^{\mathrm{\prime}}(L)\end{array} $$

(9.9)

where the stress resultants N, M, and C are defined as

$$ N={\displaystyle {\int}_S{\sigma}_{xx}\ \mathrm{d}s} $$

(9.10a)

$$ M={\displaystyle {\int}_Sz{\sigma}_{xx}\ \mathrm{d}s} $$

(9.10b)

$$ C={\displaystyle {\int}_S{\psi}_{xy}\ \mathrm{d}s} $$

(9.10c)

Neglecting the gravity , we can calculate the variation δW _ext of the work done by the external forces as

$$ \delta {W}_{\mathrm{ext}}={\displaystyle {\int}_0^L{f}_z(x)\delta w\ \mathrm{d}x} $$

(9.11)

where the distributed transverse load f _z is composed of

$$ {f}_z={f}_{\mathrm{elec}}+{f}_{\mathrm{casi}}+{f}_{\mathrm{VDW}} $$

(9.12)

f _elec, f _casi, and f _VDW are, respectively, the electrostatic force, Casimir force, and van der Waals force per unit length.

The electrostatic force f _elec per unit length can be calculated using (Batra et al. 2006; Dequesnes et al. 2002)

$$ {f}_{\mathrm{elec}}=\frac{1}{2}{V}^2\frac{\mathrm{d}{C}_{\mathrm{cap}}}{\mathrm{d}g} $$

(9.13)

where the sign of the force depends on the coordinate system , V is the applied voltage between the beam and the rigid electrode, C _cap is the capacitance per unit length of the capacitor composed of the beam and the electrode, and g is the gap between the beam and the electrode as being

$$ g(x)={g}_0+w(x) $$

(9.14)

with g ₀ being the initial gap (i.e., distance between the clamped beam ends and the rigid electrode (see Fig. 9.2)). For a small gap g (<< beam length), the beam with the electrode can be regarded as a parallel-plate capacitor. To further take into account the fringing fields at the edges of the microbeam, the capacitance C _cap is estimated using the Meijs-Fokkema formula (van der Meijs and Fokkema 1984):

$$ C(g)={\varepsilon}_0\left(\frac{b}{g}+0.77+1.06{\left(\frac{b}{g}\right)}^{0.25}+1.06{\left(\frac{h}{g}\right)}^{0.5}\right) $$

(9.15)

where ε ₀ is the vacuum permittivity. It is noted that the error of the estimated capacitance using Eq. (9.15) is within 6 % for the microbeam systems satisfying beam-width-to-gap ratio (b/g) larger than 0.3 and beam-thickness-to-gap ratio (h/g) smaller than 10 (van der Meijs and Fokkema 1984). So to ensure the proper application of Eq. (9.15), this chapter only studies the microbeam systems with the width-to-initial-gap ratio (b/g ₀) larger than 0.5 (considering w _max = 0.5 g ₀ in Eq. (9.14)) and the thickness-to-initial-gap ratio (h/g ₀) smaller than 5 (considering w _min = −0.5 g ₀). Introduce Eqs. (9.14) and (9.15) into Eq. (9.13), and after several calculations we obtain (Krylov et al. 2008)

$$ {f}_{\mathrm{elec}}=-\frac{1}{2}\frac{\varepsilon_0b{V}^2}{{\left({g}_0+w\right)}^2}\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{g_0+w}{h}\right)}^{0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{g_0+w}{h}\right)}^{0.5}\right) $$

(9.16)

The intermolecular forces can be described by Casimir and van der Waals forces. The former force is attributed to the attraction between two closely spaced conducting surfaces, and the latter one is due to the electrostatic interactions among dipoles at the atomic scale (Batra et al. 2007; Lifshitz 1956). For a small gap (<< beam length), the parallel-plate approximation is applied (Casimir 1948; Israelachvili 2011):

$$ {f}_{\mathrm{casi}}=-\frac{\pi^2\hslash cb}{240{\left({g}_0+w\right)}^4} $$

(9.17a)

$$ {f}_{\mathrm{VDM}}=-\frac{Ab}{6\pi {\left({g}_0+w\right)}^3} $$

(9.17b)

where ℏ is the reduced Planck constant; c is the speed of light; A is the Hamaker constant.

Introducing Eqs. (9.9) and (9.11) into Eq. (9.7), we arrive at

$$ \begin{array}{l}{\displaystyle {\int}_0^L{N}^{\mathrm{\prime}}\delta u\mathrm{d}x}+{\displaystyle {\int}_0^L\left({M}^{\mathrm{\prime}\mathrm{\prime }}+{C}^{\mathrm{\prime}\mathrm{\prime }}+{\left(N{w}^{\mathrm{\prime}}\right)}^{\mathrm{\prime}}+{f}_z\right)\delta w\mathrm{d}x}+N(0)\delta u(0)-N(L)\delta u(L)\\ {}+({M}^{\mathrm{\prime}}(0)+{C}^{\mathrm{\prime}}(0)+N(0){w}^{\mathrm{\prime}}(0))\delta w(0)-({M}^{\mathrm{\prime}}(L)+{C}^{\mathrm{\prime}}(L)+N(L){w}^{\mathrm{\prime}}(L))\delta w(L)\\ {}-(M(0)+C(0))\delta {w}^{\mathrm{\prime}}(0)+(M(L)+C(L))\delta {w}^{\mathrm{\prime}}(L)=0\end{array} $$

(9.18)

To satisfy Eq. (9.18) with arbitrary variations of displacements δu and δw, we obtain the following governing equations:

$$ \delta u:\kern1.25em {N}^{\prime }=0 $$

(9.19a)

$$ \delta w:\kern1em {M}^{\prime \prime }+{C}^{\prime \prime }+{\left(N{w}^{\prime}\right)}^{\prime }+{f}_z=0 $$

(9.19b)

With Eq. (9.19a), Eq. (9.19b) can be reduced to

$$ {M}^{{\prime\prime} }+{C}^{{\prime\prime} }+N{w}^{{\prime\prime} }+{f}_z=0 $$

(9.20)

Suppose the beam material is elastically isotropic with Young’s modulus E and Poisson’s ratio ν. For an Euler-Bernoulli beam undergoing in-plane bending, the 1D constitutive relation is

$$ {\sigma}_{xx}=E{\varepsilon}_{xx} $$

(9.21)

The deviatoric couple stress ψ _xy is related to the symmetric curvature χ _xy by (Yang et al. 2002):

$$ {\psi}_{xy}=\frac{E{l}^2}{\left(1+\nu \right)}{\chi}_{xy} $$

(9.22)

where l is a length scale parameter. With Eqs. (9.3), (9.6), (9.21), and (9.22), Eq. (9.10a, b, c) is changed to

$$ N(x)=ES\left({u}^{\prime }+\frac{1}{2}{\left({w}^{\prime}\right)}^2-\frac{1}{2}{\left({w}_0^{\prime}\right)}^2\right) $$

(9.23a)

$$ M(x)=-EI\left({w}^{{\prime\prime} }-{w}_0^{{\prime\prime}}\right) $$

(9.23b)

$$ C(x)=-\frac{ES{l}^2}{2\left(1+\nu \right)}\left({w}^{{\prime\prime} }-{w}_0^{{\prime\prime}}\right) $$

(9.23c)

where S (=bh) is the cross-sectional area (y–z plane in Fig. 9.2); I (=bh ³/12) is the second moment of area. Introduce Eq. (9.23a, b, c) into Eq. (9.20), and we have

$$ EI\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right)\left(w\hbox{'}\hbox{'}\hbox{'}\hbox{'}-{w}_0\kern-.25em \hbox{'}\hbox{'}\hbox{'}\hbox{'}\right)-ES\left(\left({u}^{\prime }+\frac{1}{2}{\left({w}^{\prime}\right)}^2-\frac{1}{2}{\left({w}_0^{\prime}\right)}^2\right){w}^{\prime}\right)\hbox{'}-{f}_z=0 $$

(9.24)

Equation (9.19a) shows that the axial force N is constant. So N can be estimated as the average value calculated from Eq. (9.23a): $\frac{ES}{L}\left({\displaystyle {\int}_0^L\left({u}^{\prime }+\frac{1}{2}{\left({w}^{\prime}\right)}^2-\frac{1}{2}{\left({w}_0^{\prime}\right)}^2\right)\mathrm{d}x}\right)$. In Eq. (9.24), replace N with the average value , consider the boundary conditions of double-clamped beam, and we obtain

$$ EI\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right)\left(w\hbox{'}\hbox{'}\hbox{'}\hbox{'}-{w}_0\kern-.25em \hbox{'}\hbox{'}\hbox{'}\hbox{'}\right)-\frac{ES}{2L}\left({\displaystyle {\int}_0^L\left({\left({w}^{\prime}\right)}^2-{\left({w}_0^{\prime}\right)}^2\right)\mathrm{d}x}\right){w}^{{\prime\prime} }-{f}_z=0 $$

(9.25)

Introducing Eqs. (9.12), (9.16), and (9.17a, b) into Eq. (9.25), and we have

$$ \begin{array}{l}EI\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right)\left(w\hbox{'}\hbox{'}\hbox{'}\hbox{'}-{w}_0\kern-.25em \hbox{'}\hbox{'}\hbox{'}\hbox{'}\right)-\frac{ES}{2L}\left({\displaystyle {\int}_0^L\left({\left({w}^{\prime}\right)}^2-{\left({w}_0^{\prime}\right)}^2\right)\mathrm{d}x}\right){w}^{{\prime\prime}}\\ {}\kern1em +\frac{1}{2}\frac{\varepsilon_0b{V}^2}{{\left({g}_0+w\right)}^2}\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{g_0+w}{h}\right)}^{0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{g_0+w}{h}\right)}^{0.5}\right)\\ {}\kern1em +\frac{\pi^2\hslash cb}{240{\left({g}_0+w\right)}^4}+\frac{Ab}{6\pi {\left({g}_0+w\right)}^3}=0\end{array} $$

(9.26)

It is seen from Eq. (9.26) that the length scale parameter l has the effect of increasing the effective Young’s modulus (E)_eff for bending, being

$$ {(E)}_{\mathrm{eff}}=E\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right) $$

(9.27)

For thin beams (beam thickness h close to l), the effective Young’s modulus for bending can be as large as $\left(1+\frac{6}{\left(1+\nu \right)}\right)$ (≈5.7 at ν = 0.27) times the conventional Young’s modulus (E), while for thick beams (h ≫ l) the effective Young’s modulus is nearly equal to the conventional one, indicating that the size effect is negligible.

Rewrite Eq. (9.26) in the following non-dimensional form:

$$ \begin{array}{l}\left(\overline{w}\hbox{'}\hbox{'}\hbox{'}\hbox{'}-\overline{w_0}\hbox{'}\hbox{'}\hbox{'}\hbox{'}\right)-\alpha \left({\displaystyle {\int}_0^1\left({\left(\overline{w}\hbox{'}\right)}^2-{\left(\overline{w_0}\hbox{'}\right)}^2\right)\mathrm{d}\overline{x}}\right)\overline{w}\hbox{'}\hbox{'}+{\lambda}_{\mathrm{VDW}}\frac{1}{{\left(1+\overline{w}\right)}^3}+{\lambda}_{\mathrm{casi}}\frac{1}{{\left(1+\overline{w}\right)}^4}\\ {}\kern0.75em =-\frac{\beta_v}{{\left(1+\overline{w}\right)}^2}\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{1+\overline{w}}{\overline{h}}\right)}^{0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{1+\overline{w}}{\overline{h}}\right)}^{0.5}\right)\end{array} $$

(9.28)

where the non-dimensional quantities are defined in Table 9.1; a superimposed apostrophe in the non-dimensional equations denotes a derivative with respect to the normalized coordinate $\overline{x}$. The non-dimensional boundary conditions of double-clamped beam are

Table 9.1 Non-dimensional quantities adopted in this chapter

$$ \delta \overline{w}:\kern1.5em \overline{w}(0)=0,\kern1.25em \overline{w}(1)=0 $$

(9.29a)

$$ \delta {\overline{w}}^{\prime }:\kern1.25em {\overline{w}}^{\prime }(0)=0,\kern1em {\overline{w}}^{\prime }(1)=0 $$

(9.29b)

9.2.1.2 Influence of Intermolecular Forces

In the non-dimensional governing equation (Eq. (9.28)), we can identify the dimensionless van der Waals force $\overline{f_{\mathrm{VDW}}}$, Casimir force $\overline{f_{\mathrm{casi}}}$, and electrostatic force $\overline{f_{\mathrm{elec}}}$ as

$$ \overline{f_{\mathrm{VDW}}}=-{\lambda}_{\mathrm{VDW}}\frac{1}{{\left(1+\overline{w}\right)}^3} $$

(9.30a)

$$ \overline{f_{\mathrm{casi}}}=-{\lambda}_{\mathrm{casi}}\frac{1}{{\left(1+\overline{w}\right)}^4} $$

(9.30b)

$$ \overline{f_{\mathrm{elec}}}=-\frac{\beta_v}{{\left(1+\overline{w}\right)}^2}\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{1+\overline{w}}{\overline{h}}\right)}^{0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{1+\overline{w}}{\overline{h}}\right)}^{0.5}\right) $$

(9.30c)

where λ _VDW, λ _casi, and β _v are, respectively, the van der Waals force parameter, the Casimir force parameter, and the voltage parameter. With the aid of Table 9.1, we can compare λ _VDW and λ _casi with β _v as follows:

$$ \frac{\lambda_{\mathrm{VDW}}}{\beta_v}=\frac{A}{3\pi {\varepsilon}_0}\frac{1}{g_0{V}^2} $$

(9.31a)

$$ \frac{\lambda_{\mathrm{casi}}}{\beta_v}=\frac{\pi^2\hslash c}{120{\varepsilon}_0}\frac{1}{g_0^2{V}^2} $$

(9.31b)

Consider ${g}_0\approx {10}^{-6}\mathrm{m}$ for the microscale systems and $V\approx {10}^1\mathrm{V}$ for the order of applied voltage , and with the values of the constants in Table 9.2 we calculate Eq. (9.31a, b) as

Table 9.2 Values of constants

$$ \frac{\lambda_{\mathrm{VDW}}}{\beta_v}\approx {10}^{-5} $$

(9.32a)

$$ \frac{\lambda_{\mathrm{casi}}}{\beta_v}\approx 3\times {10}^{-6} $$

(9.32b)

With Eqs. (9.30a, b, c) and (9.32a, b), the force ratios can be estimated as

$$ \left|\overline{f_{\mathrm{VDW}}}/\overline{f_{\mathrm{elec}}}\right| < {10}^{-5}\frac{1}{1+\overline{w}} $$

(9.33a)

$$ \left|\overline{f_{\mathrm{casi}}}/\overline{f_{\mathrm{elec}}}\right| < 3\times {10}^{-6}\frac{1}{{\left(1+\overline{w}\right)}^2} $$

(9.33b)

The maximum force ratios are determined by the minimum stable deflection, i.e., deflection at pull-in instability, which is roughly half gap ($\overline{w}=-0.5$) (Ballestra et al. 2010; Dequesnes et al. 2002; Hu et al. 2004). Then Eq. (9.33a, b) leads to

$$ \max \left|\overline{f_{\mathrm{VDW}}}/\overline{f_{\mathrm{elec}}}\right|\approx 2\times {10}^{-5} $$

(9.34a)

$$ \max \left|\overline{f_{\mathrm{casi}}}/\overline{f_{\mathrm{elec}}}\right|\approx 1\times {10}^{-5} $$

(9.34b)

Equation (9.34a, b) shows that the intermolecular forces (van der Waals and Casimir forces) are negligible with respect to the electrostatic force when studying the snap-through buckling of microbeams.

9.2.1.3 One Degree of Freedom Reduced-Order Model

In the previous subsection, we have proved that the intermolecular forces can be neglected in the study of snap-through buckling of microbeams. So the governing equation (Eq. (9.28)) can be further reduced to

$$ \begin{array}{l}\left(\overline{w}\hbox{'}\hbox{'}\hbox{'}\hbox{'}-\overline{w_0}\hbox{'}\hbox{'}\hbox{'}\hbox{'}\right)-\alpha \left({\displaystyle {\int}_0^1\left({\left(\overline{w}\hbox{'}\right)}^2-{\left(\overline{w_0}\hbox{'}\right)}^2\right)\mathrm{d}\overline{x}}\right)\overline{w}\hbox{'}\hbox{'}\\ {}\kern0.5em =-\frac{\beta_v}{{\left(1+\overline{w}\right)}^2}\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{1+\overline{w}}{\overline{h}}\right)}^{0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{1+\overline{w}}{\overline{h}}\right)}^{0.5}\right)\end{array} $$

(9.35)

Equation (9.35) with the boundary conditions expressed in Eq. (9.29a, b) can be solved using the Galerkin decomposition of the dimensionless deflection $\overline{w}\left(\overline{x}\right)$ (Das and Batra 2009b; Krylov et al. 2008; Medina et al. 2012):

$$ \overline{w}\left(\overline{x}\right)\approx {\displaystyle \sum_{k=1}^n{q}_k{\phi}_k\left(\overline{x}\right)} $$

(9.36)

where ϕ _k (k = 1, 2, …, n) is the kth eigenmode of the straight beam, and q _k is its generalized coordinate. The buckling eigenmodes are taken here, which have been found more suitable for the studies on the buckling behaviors (Medina et al. 2014a, b):

$$ {\phi}_k\left(\overline{x}\right)={A}_k\left(\frac{ \cos \left({\lambda}_k\right)-1}{ \sin \left({\lambda}_k\right)-{\lambda}_k} \sin \left({\lambda}_k\overline{x}\right)- \cos \left({\lambda}_k\overline{x}\right)-{\lambda}_k\frac{ \cos \left({\lambda}_k\right)-1}{ \sin \left({\lambda}_k\right)-{\lambda}_k}\overline{x}+1\right) $$

(9.37)

where A _k is a constant satisfying $\underset{\overline{x}\in \left[0,1\right]}{ \max}\left|{\phi}_k\left(\overline{x}\right)\right|=1$, and λ _k is the eigenvalue satisfying ${\lambda}_k \sin \left({\lambda}_k\right)+2 \cos \left({\lambda}_k\right)=2$.

It is shown by Das and Batra (2009b) that the numerical simulations using n ≥ 6 in Eq. (9.36) are indistinguishable from each other. They also found that a reasonably accurate prediction of the symmetric snap-through behavior can be given by considering only the first mode, which indicates that the first mode approximation of the deflection can capture the characteristics of the symmetric snap-through behavior. So in order to simplify our study for an analytical snap-through criterion , we decided to make the first mode approximation here. Suppose that the dimensionless initial deflection $\overline{w_0}\left(\overline{x}\right)$ is also in the first mode, then we have

$$ \overline{w}\left(\overline{x}\right)={q}_1{\phi}_1\left(\overline{x}\right) $$

(9.38a)

$$ \overline{w_0}\left(\overline{x}\right)={q}_0{\phi}_1\left(\overline{x}\right) $$

(9.38b)

where q ₁ is the dimensionless midpoint deflection; q ₀ (= r/g ₀) is the dimensionless initial arch rise, with r being the initial arch rise (i.e., initial deflection at the midpoint). Introduce Eq. (9.38a, b) into Eq. (9.35), multiply the result by ϕ ₁, and then integrate over the domain [0, 1]. Further integrate by parts with respect to $\overline{x}$ and consider the boundary conditions (Eq. (9.29a, b)); we obtain the following reduced-order model with one degree of freedom:

$$ {\beta}_v=-\frac{\alpha {s}_{11}^2}{I_1\left({q}_1\right)}{q}_1^3-\frac{b_{11}-\alpha {s}_{11}^2{q}_0^2}{I_1\left({q}_1\right)}{q}_1+\frac{b_{11}{q}_0}{I_1\left({q}_1\right)} $$

(9.39)

where the values of b ₁₁ and s ₁₁ are given in Table 9.3, and the expression of I ₁ is

Table 9.3 Values of coefficients related to first and second buckling eigenmodes

$$ \begin{array}{c}{I}_1\left({q}_1\right)={\displaystyle {\int}_0^1\frac{\phi_1}{{\left(1+{q}_1{\phi}_1\right)}^2}\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{1+{q}_1{\phi}_1}{\overline{h}}\right)}^{0.75}\right.}\\ {}\kern10pc {\displaystyle \left.+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{1+{q}_1{\phi}_1}{\overline{h}}\right)}^{0.5}\right)\ \mathrm{d}\overline{x}}\end{array} $$

(9.40)

9.2.2 Results and Discussions

9.2.2.1 Influence of Initial Arch Rise on Snap-Through Behavior

Let us consider an electrostatically actuated microbeam system described by the dimensional quantities in Table 9.4, which is obtained from Krylov et al. (2008) for the experiments, and Zhang et al. (2007) for the material properties. Taking the material length scale parameter l = 10⁻¹ μm for silicon (Rokni et al. 2013), and with the aid of Tables 9.1 and 9.4, we calculate the corresponding dimensionless quantities, and introduce them into Eq. (9.39). The obtained equation is plotted in Fig. 9.3 at different levels of q ₀ (0 ~ 0.5). The experimental results from Krylov et al. (2008) are also shown. It is seen that the model (Eq. (9.39)) can approximately describe the snap-through behavior observed from the experiments. The difference in the critical voltages (i.e., voltage parameters at the extreme points) is possibly due to the non-ideal clamping conditions, residual stresses, initial imperfections in the beam shape, and variations of beam geometry due to the low fabrication tolerances (Krylov et al. 2008).

Table 9.4 Dimensional quantities of electrostatically actuated microbeam system obtained from Krylov et al. (2008) and Zhang et al. (2007)

Fig. 9.3

Evolution of voltage parameter β _v with dimensionless midpoint deflection q ₁ at different levels of dimensionless initial arch rise q ₀. The extreme points q _s, q _r, and q _p correspond, respectively, to the critical points of the snap-through buckling, the release (snap-back), and the pull-in instability. The insets show the evolutions of the deformed beam

Figure 9.3 shows that the existence of the snap-through buckling depends on the level of the dimensionless initial arch rise q ₀. For very small q ₀ (e.g., q ₀ = 0 in Fig. 9.3a), there is only one extreme point q _p on the β _v −q ₁ curve. With the increase of the voltage (β _v increases), the microbeam bends towards the rigid electrode due to the electrostatic force. The equilibrium position of the beam can be determined by the balance of the elastic and electrostatic forces. Therefore, the beam deflection decreases gradually (see the loading path A → q _p in Fig. 9.3a). When the critical point q _p is reached, the microbeam becomes unstable (i.e., the elastic force can no longer resist the electrostatic force), so it collapses onto the rigid electrode (q _p → B). This behavior is called pull-in instability.

For a larger value of q ₀ (e.g., 0.35 in Fig. 9.3b), two more extreme points q _s and q _r appear, which correspond, respectively, to the snap-through buckling and the release (snap-back). With the increase of β _v , the beam deflection decreases gradually (C → q _s in Fig. 9.3b) until reaching the critical point q _s where two stable states (q _s and D) coexist. A slight increase in β _v makes the state at q _s unstable, which results in a sudden transition from q _s to the second stable state D. Such transition is called snap-through buckling. After the snap-through buckling, the beam deflection continues to decrease gradually with β _v (D → q _p) until reaching the pull-in instability where the beam collapses onto the rigid electrode (q _p → E).

9.2.2.2 Size and Fringing Field Effects on Necessary Snap-Through Criterion

The extreme points q _s, q _r, and q _p on β _v  − q ₁ curve (refer to Fig. 9.3) can be obtained by solving the following equation with the aid of Eq. (9.39):

$$ \frac{\mathrm{d}{\beta}_v}{\mathrm{d}{q}_1}=0\Rightarrow \alpha {s}_{11}^2{I}_2{q}_1^3-3\alpha {s}_{11}^2{I}_1{q}_1^2+{I}_2\left({b}_{11}-\alpha {s}_{11}^2{q}_0^2\right){q}_1-\left({b}_{11}-\alpha {s}_{11}^2{q}_0^2\right){I}_1-{b}_{11}{I}_2{q}_0=0 $$

(9.41)

where I ₂ is calculated from Eq. (9.40) as

$$ \begin{array}{c}{I}_2=\frac{\mathrm{d}{I}_1}{\mathrm{d}{q}_1}={\displaystyle {\int}_0^1\frac{-2{\phi}_1^2}{{\left(1+{q}_1{\phi}_1\right)}^3}\left(1+0.165625{\left(\frac{b}{h}\right)}^{-0.75}{\left(\frac{1+{q}_1{\phi}_1}{\overline{h}}\right)}^{0.75}\right.}\\ {}{\displaystyle \kern6pc \left.+0.3975{\left(\frac{b}{h}\right)}^{-1}{\left(\frac{1+{q}_1{\phi}_1}{\overline{h}}\right)}^{0.5}\right)\mathrm{d}\overline{x}}\end{array} $$

(9.42)

Equation (9.41) containing integrals (I ₁, I ₂) cannot be solved analytically. So we solve the equation numerically, and show the typical results in Fig. 9.4. It is seen that q ₀ must be larger than a critical value q ^min₀ for the existence of the snap-through points q _s and q _r. At q ₀ = q ^min₀ , both q _s and q _r are near 0. So for a first approximation , we take q ₁ = 0 in Eq. (9.41) and find

Fig. 9.4

Evolutions of the extreme points (q _s, q _r, q _p) with the dimensionless initial arch rise q ₀ at different levels of stretching parameter α and width-to-thickness ratio b/h

$$ {q}_0^{\min }=\sqrt{\frac{b_{11}}{\alpha {s}_{11}^2}+{\left(\frac{b_{11}{m}_{11}^{*}}{\alpha {s}_{11}^2{f}_1^{*}}\right)}^2}-\frac{b_{11}{m}_{11}^{*}}{\alpha {s}_{11}^2{f}_1^{*}} $$

(9.43)

where the values of b ₁₁ and s ₁₁ are given in Table 9.3; f ^*₁ and m ^*₁₁ are

$$ {f}_1^{*}=\left(1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\overline{h}\right)}^{-0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\overline{h}\right)}^{-0.5}\right){\displaystyle {\int}_0^1{\phi}_1\mathrm{d}\overline{x}} $$

(9.44a)

$$ {m}_{11}^{*}=\left(1+0.165625{\left(\frac{b}{h}\right)}^{-0.75}{\left(\overline{h}\right)}^{-0.75}+0.3975{\left(\frac{b}{h}\right)}^{-1}{\left(\overline{h}\right)}^{-0.5}\right){\displaystyle {\int}_0^1{\phi}_1^2\mathrm{d}\overline{x}} $$

(9.44b)

Introducing Eq. (9.44a, b) into Eq. (9.43) and replacing the non-dimensional quantities (α, q ₀) with the expressions in Table 9.1, we obtain the following necessary criterion for the existence of snap-through buckling:

$$ \begin{array}{l}{\left(\frac{r}{h}\right)}_{\min }=\sqrt{\frac{b_{11}}{6{s}_{11}^2}\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right)+{\left(\frac{b_{11}{m}_{11}}{6{s}_{11}^2{f}_1}\overline{h}\right)}^2{\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right)}^2{\left(\frac{1+0.165625{\left(\frac{b}{h}\right)}^{-0.75}{\left(\overline{h}\right)}^{-0.75}+0.3975{\left(\frac{b}{h}\right)}^{-1}{\left(\overline{h}\right)}^{-0.5}}{1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\overline{h}\right)}^{-0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\overline{h}\right)}^{-0.5}}\right)}^2}\\ {}\kern10.75em -\frac{b_{11}{m}_{11}}{6{s}_{11}^2{f}_1}\overline{h}\left(1+\frac{6}{\left(1+\nu \right)}{\left(\frac{l}{h}\right)}^2\right)\left(\frac{1+0.165625{\left(\frac{b}{h}\right)}^{-0.75}{\left(\overline{h}\right)}^{-0.75}+0.3975{\left(\frac{b}{h}\right)}^{-1}{\left(\overline{h}\right)}^{-0.5}}{1+0.265{\left(\frac{b}{h}\right)}^{-0.75}{\left(\overline{h}\right)}^{-0.75}+0.53{\left(\frac{b}{h}\right)}^{-1}{\left(\overline{h}\right)}^{-0.5}}\right)\end{array} $$

(9.45)

where the values of b ₁₁, s ₁₁, f ₁, and m ₁₁ are given in Table 9.3. Eq. (9.45) is plotted in Fig. 9.5 to show the size effect (by introducing the length scale parameter l, normalized as l/h) and the fringing field effect (considering the finite beam width b, normalized as b/h) on the minimum allowable ratio (r/h)_min. It is seen that both effects increase (r/h)_min and the size effect is much more significant. Eq. (9.27) shows that the size effect (l/h) increases the effective Young’s modulus for bending, so the microbeam becomes stiffer and more difficult to exhibit snap-through buckling. As a result, the minimum allowable ratio (r/h)_min increases.

Fig. 9.5

(a) Size effect (l/h) on the minimum allowable ratio (r/h)_min at b/h = +∞. No size effect at l/h = 0 (i.e., beam thickness h ≫ l). (b) Fringing field effect (b/h) on the minimum allowable ratio (r/h)_min at l/h = 0. No fringing field effect at b/h = +∞ (infinitely wide beam)

9.3 Surface Effects on Asymmetric Bifurcation of Nanobeam

9.3.1 Formulation

9.3.1.1 Surface Effects

In the surface elasticity theory of Gurtin and Murdoch (1975, 1978), the surface layer is regarded as a thin film of negligible thickness . In the surface layer, there exists a surface stress ${\underline {\underline{\sigma}}}^{\mathrm{s}}\left(\mathrm{N}/\mathrm{m}\right)$, which is related to the surface energy density γ (J/m²) by (Cammarata 1994)

$$ {\underline {\underline{\sigma}}}^s=\gamma \underline {\underline{\delta}}+\frac{\partial \gamma }{\partial {\underline {\underline{\varepsilon}}}^s} $$

(9.46)

where $\underline {\underline{\delta}}$ is the Kronecker delta; ${\underline {\underline{\varepsilon}}}^{\mathrm{s}}$ is the strain tensor in the surface layer. Assuming an elastic surface, we can derive a linear constitutive equation from Eq. (9.46) as (Miller and Shenoy 2000)

$$ {\underline {\underline{\sigma}}}^{\mathrm{s}}={\underline {\underline{\tau}}}^0+{\underline {\underline {\underline {\underline{C}}}}}^{\mathrm{s}}:{\underline {\underline{\varepsilon}}}^{\mathrm{s}} $$

(9.47)

where ${\underline {\underline{\tau}}}^0$ is the residual surface stress tensor; ${\underline {\underline {\underline {\underline{C}}}}}^{\mathrm{s}}\ \left(\mathrm{N}/\mathrm{m}\right)$ is the surface elasticity tensor. Both ${\underline {\underline{\tau}}}^0$ and ${\underline {\underline {\underline {\underline{C}}}}}^{\mathrm{s}}$ can be calculated by atomistic simulations, and they can be either positive or negative depending on the crystallographic structures of the materials (Miller and Shenoy 2000; Wang and Feng 2009). We only consider the axial stress here. Then Eq. (9.47) can be reduced to the following 1D form (He and Lilley 2008; Wang and Feng 2009):

$$ {\sigma}^{\mathrm{s}}={\tau}^0+{E}^{\mathrm{s}}{\varepsilon}^{\mathrm{s}} $$

(9.48)

where τ ⁰ is the residual surface tension; E ^s (N/m) is the surface elastic modulus, which is related to the surface Lame constants μ ^s and λ ^s by E ^s = 2μ ^s + λ ^s in 1D condition.

It is seen from Eq. (9.48) that there are two contributions to the surface effects: the residual surface tension (τ ⁰) and the surface elasticity (E ^s). The surface elasticity (E ^s) introduces an additional axial elastic stress σ* being

$$ {\sigma}^{\ast }={E}^{\mathrm{s}}{\varepsilon}^{\mathrm{s}} $$

(9.49)

And the residual surface tension τ ⁰ results in a distributed transverse load f ^s, which can be determined by the generalized Laplace-Young equation (Chen et al. 2006; Gurtin et al. 1998). This equation relates the stress jump [$\left[\kern-.25em ,\left[\underline {\underline{\sigma}}\right],\kern-.25em \right]$] across an interface to the curvature $\underline {\underline{\kappa}}$ and the surface stress ${\underline {\underline{\sigma}}}^{\mathrm{s}}$ of that interface, from which we have (Chen et al. 2006; Miller and Shenoy 2000; Wang and Feng 2007)

$$ \underline{n}: \underline {\underline{\sigma}} :\underline{n}={\underline {\underline{\sigma}}}^{\mathrm{s}}:\underline {\underline{\kappa}} $$

(9.50)

where $\underline{n}$ is the interface unit normal. By only considering the axial stress, we can simplify the right-hand side of Eq. (9.50) to σ ^s κ, where κ is the beam curvature. Suppose that the slope of the beam is small compared with the unity; then κ can be approximated as w″, with w being the beam deflection (transverse displacement). Considering a rectangular beam of width b, we can obtain the distributed transverse load f ^s from Eq. (9.50) as (He and Lilley 2008; Wang and Feng 2007, 2009)

$$ {f}^{\mathrm{s}}=2{\tau}^0b{w}^{{\prime\prime} } $$

(9.51)

9.3.1.2 Governing Equations

Consider an initially curved rectangular nanobeam subjected to an electrostatic force (Fig. 9.2). For a thin beam (h ≪ L), the axial strain change ε _xx is given in Eq. (9.3). Then the variation δU _elas of the elastic strain energy including the surface elasticity can be calculated as

$$ \delta {U}_{\mathrm{elas}}={\displaystyle {\int}_0^L({\displaystyle {\int}_S{\sigma}_{xx}\delta {\varepsilon}_{xx}ds}+{\displaystyle {\int}_{\mathrm{\partial}S}{\sigma}^{\ast}\delta {\varepsilon}_{xx}\mathrm{d}l})\mathrm{d}x} $$

$$ \begin{array}{l}\kern3.7em =-{\displaystyle {\int}_0^L{N}^{\mathrm{\prime}}\delta u\mathrm{d}x}-{\displaystyle {\int}_0^L({M}^{\mathrm{\prime}\mathrm{\prime }}+{(N{w}^{\mathrm{\prime}})}^{\mathrm{\prime}})\delta w\mathrm{d}x}\kern1.00em \\ {}\kern4.8em -N(0)\delta u(0)+N(L)\delta u(L)-({M}^{\mathrm{\prime}}(0)+N(0){w}^{\mathrm{\prime}}(0))\delta w(0)\kern1.00em \\ {}\kern4.8em +({M}^{\mathrm{\prime}}(L)+N(L){w}^{\mathrm{\prime}}(L))\delta w(L)+M(0)\delta {w}^{\mathrm{\prime}}(0)-M(L)\delta {w}^{\mathrm{\prime}}(L)\kern1.00em \end{array} $$

(9.52)

where stress resultants N and M are defined as

$$ N={\displaystyle {\int}_S{\sigma}_{xx}\mathrm{d}s}+{\displaystyle {\int}_{\partial S}{\sigma}^{\ast}\mathrm{d}l} $$

(9.53a)

$$ M={\displaystyle {\int}_Sz{\sigma}_{xx}\mathrm{d}s}+{\displaystyle {\int}_{\partial S}z{\sigma}^{\ast}\mathrm{d}l} $$

(9.53b)

σ* is the additional axial stress from surface elasticity (Eq. (9.49)), and ${\displaystyle {\int}_{\partial S}\mathrm{d}l}$ is the integral over the boundary of the cross section . Neglecting the gravity and the intermolecular forces, we can calculate the variation δW _ext of the work done by the external forces as

$$ \delta {W}_{\mathrm{ext}}={\displaystyle {\int}_0^L\left(\kern.18em {f}_{\mathrm{elec}}+{f}^{\mathrm{s}}\right)\delta w\mathrm{d}x} $$

(9.54)

where f ^s is the distributed load due to the residual surface tension (Eq. (9.51)); f _elec is the distributed electrostatic force. Suppose that the beam is infinitely wide (width b ≫ thickness h); then the fringing field can be neglected , and Eq. (9.16) can be reduced to

$$ {f}_{\mathrm{elec}}=-\frac{1}{2}\frac{\varepsilon_0b{V}^2}{{\left({g}_0+w\right)}^2} $$

(9.55)

Introducing Eqs. (9.52) and (9.54) into the theorem of minimum potential energy given in Eq. (9.7), we obtain the following governing equations:

$$ \delta u:\kern1.25em {N}^{\prime }=0 $$

(9.56a)

$$ \delta w:\kern1.25em {M}^{\prime \prime }+{\left(N{w}^{\prime}\right)}^{\prime }+{f}_{\mathrm{elec}}+{f}^{\mathrm{s}}=0 $$

(9.56b)

With Eq. (9.56a), Eq. (9.56b) can be rewritten as

$$ {M}^{{\prime\prime} }+N{w}^{{\prime\prime} }+{f}_{\mathrm{elec}}+{f}^{\mathrm{s}}=0 $$

(9.57)

Suppose that the beam material is elastically isotropic with Young’s modulus E and Poisson’s ratio ν. Then the 1D constitutive equation for an infinitely wide beam becomes

$$ {\sigma}_{xx}={E}^{*}{\varepsilon}_{xx} $$

(9.58)

where the effective elastic modulus E ^* is

$$ {E}^{*}=\frac{E}{1-{\nu}^2} $$

(9.59)

Introduce Eqs. (9.3), (9.49), and (9.58) into Eq. (9.53a, b), and consider b ≫ h; we have

$$ N(x)={E}^{*}S\left(1+2\frac{E^{\mathrm{s}}}{E^{*}}\kern.15em \frac{1}{h}\right)\left({u}^{\prime }+\frac{1}{2}{\left({w}^{\prime}\right)}^2-\frac{1}{2}{\left({w}_0^{\prime}\right)}^2\right) $$

(9.60a)

$$ M(x)=-{E}^{*}I\left(1+6\frac{E^{\mathrm{s}}}{E^{*}}\kern.15em \frac{1}{h}\right)\left({w}^{{\prime\prime} }-{w}_0^{{\prime\prime}}\right) $$

(9.60b)

The effective axial stiffness (ES)_eff can be derived from Eq. (9.60a) as

$$ {(ES)}_{\mathrm{eff}}={E}^{*}bh+2{E}^{\mathrm{s}}b $$

(9.61)

And the effective Young’s modulus (E)_eff for bending can be derived from Eq. (9.60b) as

$$ {(E)}_{\mathrm{eff}}={E}^{*}\left(1+6\frac{E^{\mathrm{s}}}{E^{*}}\kern.15em \frac{1}{h}\right) $$

(9.62)

It is seen that the surface elasticity (E ^s) has the effect of increasing or decreasing (E)_eff, depending on the sign of E ^s.

Introduce Eqs. (9.51), (9.55), and (9.60b) into Eq. (9.57), replace the axial force by the average value calculated from Eq. (9.60a), and we obtain the following governing equation :

$$ \begin{array}{l}{E}^{\ast }I\left(1+6\frac{E^{\mathrm{s}}}{E^{\ast }}\kern.15em \frac{1}{h}\right)\left({w}^{\prime \prime \prime \prime }-{w_0}^{\prime \prime \prime \prime}\right)-\frac{E^{\ast }S}{2L}\left(1+2\frac{E^{\mathrm{s}}}{E^{\ast }}\kern.15em \frac{1}{h}\right)\left({\displaystyle {\int}_0^L\left({\left({w}^{\prime}\right)}^2-{\left({w}_0^{\prime}\right)}^2\right)\mathrm{d}x}\right)\\ {}\kern8pc \cdot {w}^{\prime \prime }-2{\tau}^0b{w}^{\prime \prime }=-\frac{1}{2}\frac{\varepsilon_0b{V}^2}{{\left({g}_0+w\right)}^2}\end{array} $$

(9.63)

Rewrite Eq. (9.63) in the non-dimensional form as

$$ \left({\overline{w}}^{\prime \prime \prime \prime }-{\overline{w_0}}^{\prime \prime \prime \prime}\right)-\left({\lambda}_s+{\alpha}^{\ast}\left({\displaystyle {\int}_0^1\left({\left({\overline{w}}^{\prime}\right)}^2-{\left({\overline{w_0}}^{\prime}\right)}^2\right)\mathrm{d}\overline{x}}\right)\right){\overline{w}}^{\prime \prime }=-\frac{\beta_v^{\ast }}{{\left(1+\overline{w}\right)}^2} $$

(9.64)

with the non-dimensional quantities given in Table 9.1, and the non-dimensional boundary conditions given in Eq. (9.29a, b).

9.3.1.3 Two Degrees of Freedom Reduced-Order Model

Equations (9.64) and (9.29a, b) can be solved using the Galerkin decomposition method (see Eq. (9.36)). For the asymmetric deformations, the participation of the second mode is more than that of the fourth and sixth modes (Das and Batra 2009b). So we decided to focus on the first two modes (i.e., n = 2 in Eq. (9.36)). The dimensionless initial deflection $\overline{w_0}\left(\overline{x}\right)$ is assumed to be in the first mode state; then we have

$$ \overline{w}\left(\overline{x}\right)={q}_1{\phi}_1\left(\overline{x}\right)+{q}_2{\phi}_2\left(\overline{x}\right) $$

(9.65a)

$$ \overline{w_0}\left(\overline{x}\right)={q}_0{\phi}_1\left(\overline{x}\right) $$

(9.65b)

where q ₁ is the dimensionless midpoint deflection (since ${\phi}_1(0.5)=1$, ${\phi}_2(0.5)=0$); q ₀ (= r/g ₀) is the dimensionless initial arch rise, with r being the initial arch rise (deflection at the midpoint). Introduce Eq. (9.65a, b) into Eq. (9.64), multiply the result by ϕ ₁ and ϕ ₂, respectively, and then integrate over the domain [0, 1]. Further integrate by parts and take into account the orthogonality of ϕ ₁ and ϕ ₂; we obtain the reduced-order model with two degrees of freedom:

$$ {\phi}_1:\kern0.5em {\alpha}^{*}{s}_{11}^2{q}_1^3+\left({b}_{11}-{\alpha}^{*}{s}_{11}^2{q}_0^2+{\lambda}_s{s}_{11}\right){q}_1+{\alpha}^{*}{s}_{11}{s}_{22}{q}_1{q}_2^2-{b}_{11}{q}_0=-{\beta}_v^{*}{I}_1^{*}\left({q}_1,{q}_2\right) $$

(9.66a)

$$ {\phi}_2:\ {\alpha}^{*}{s}_{22}^2{q}_2^3+\left({b}_{22}-{\alpha}^{*}{s}_{11}{s}_{22}{q}_0^2+{\lambda}_s{s}_{22}\right){q}_2+{\alpha}^{*}{s}_{11}{s}_{22}{q}_1^2{q}_2=-{\beta}_v^{*}{I}_2^{*}\left({q}_1,{q}_2\right) $$

(9.66b)

where b ₁₁, b ₂₂, s ₁₁, s ₂₂, and f ₁ are given in Table 9.3; the integrals I ^*₁ and I ^*₂ are given below:

$$ {I}_1^{*}\left({q}_1,{q}_2\right)={\displaystyle {\int}_0^1\frac{\phi_1}{{\left(1+{q}_1{\phi}_1+{q}_2{\phi}_2\right)}^2}\ \mathrm{d}\overline{x}} $$

(9.67a)

$$ {I}_2^{*}\left({q}_1,{q}_2\right)={\displaystyle {\int}_0^1\frac{\phi_2}{{\left(1+{q}_1{\phi}_1+{q}_2{\phi}_2\right)}^2}\ \mathrm{d}\overline{x}} $$

(9.67b)

9.3.2 Results and Discussions

9.3.2.1 Influence of Initial Arch Rise on Asymmetric Bifurcation Behavior

Introducing α ^* = 600 and λ _s = 2 into Eq. (9.66a, b), we plot the obtained equation in Fig. 9.6 at different levels of the dimensionless initial arch rise q ₀. The dimensionless residual surface tension λ _s is calculated using the expression in Table 9.1 with the surface parameters ${\tau}^0=0.6056\ \mathrm{N}\cdot {\mathrm{m}}^{-1}$ and ${E}^{\mathrm{s}}=-10.036\ \mathrm{N}\cdot {\mathrm{m}}^{-1}$ from Miller and Shenoy (2000), and the beam dimensions and bulk material properties L = 15 μm, b = 400 nm, h = 200 nm, E = 185 GPa, and ν = 0.28 from Intaraprasonk and Fan (2011).

Fig. 9.6

Bifurcation diagram of nanobeam actuated by electrostatic force. ② and ③ are bifurcation points. The insets show the evolutions of the deformed beam

It is seen from Fig. 9.6 that when q ₀ is small (e.g., 0.1 in Fig. 9.6a), the solution of the asymmetric deformation doesn’t exist (i.e., q ₂ ≡ 0), so the beam always deforms symmetrically. When q ₀ is large enough (0.3 in Fig. 9.6b), the solution of the asymmetric deformation exists. With the decrease of the midpoint deflection (q ₁ decreases), the beam deforms symmetrically (① → ② in Fig. 9.6b) until reaching the bifurcation point ② where there are two asymmetric deformations given by Eq. (9.66a, b). By following one of the asymmetric deformations, the beam deforms asymmetrically (② → ③) until reaching another bifurcation point ③. After ③, the beam returns to deform symmetrically with the decrease of the midpoint deflection.

9.3.2.2 Surface Effects on Necessary Symmetry-Breaking Criterion

Near the asymmetric bifurcation points (② and ③ in Fig. 9.6b), q ₂ is about 0. So we linearize the governing equations (Eq. (9.66a, b)) around q ₂ = 0 as (Medina et al. 2014a)

$$ {\phi}_1:\kern0.5em {\alpha}^{*}{s}_{11}^2{q}_1^3+\left({b}_{11}-{\alpha}^{*}{s}_{11}^2{q}_0^2+{\lambda}_s{s}_{11}\right){q}_1-{b}_{11}{q}_0=-{\beta}_v^{*}{I}_1^{*}\left({q}_1,0\right) $$

(9.68a)

$$ {\phi}_2:\ \left({b}_{22}-{\alpha}^{*}{s}_{11}{s}_{22}{q}_0^2+{\lambda}_s{s}_{22}+{\alpha}^{*}{s}_{11}{s}_{22}{q}_1^2\right){q}_2=2{\beta}_v{I}_3^{*}\left({q}_1\right){q}_2 $$

(9.68b)

with I ^*₃ being

$$ {I}_3^{*}\left({q}_1\right)={\displaystyle {\int}_0^1\frac{\phi_2^2}{{\left(1+{q}_1{\phi}_1\right)}^3}\ \mathrm{d}\overline{x}} $$

(9.69)

To obtain Eq. (9.68a, b), the following relations are used: ${\displaystyle {\int}_0^1\frac{\phi_1{\phi}_2}{{\left(1+{q}_1{\phi}_1\right)}^3}\ \mathrm{d}\overline{x}}=0$, ${\displaystyle {\int}_0^1\frac{\phi_2}{{\left(1+{q}_1{\phi}_1\right)}^2}\ \mathrm{d}\overline{x}}=0$. For the asymmetric deformations (q ₂ ≠ 0), Eq. (9.68b) can be further reduced to

$$ {\phi}_2:\ {b}_{22}-{\alpha}^{*}{s}_{11}{s}_{22}{q}_0^2+{\lambda}_s{s}_{22}+{\alpha}^{*}{s}_{11}{s}_{22}{q}_1^2=2{\beta}_v^{*}{I}_3^{*}\left({q}_1\right) $$

(9.70)

Express β ^* _v , respectively, from Eqs. (9.68a) and (9.70), equilibrate these expressions, and we obtain the following equation for the asymmetric bifurcation points:

$$ \begin{array}{l}2{\alpha}^{*}{s}_{11}^2{I}_3^{*}{q}_1^3+{\alpha}^{*}{s}_{11}{s}_{22}{I}_1^{*}\left({q}_1,0\right){q}_1^2+2\left({b}_{11}-{\alpha}^{*}{s}_{11}^2{q}_0^2+{\lambda}_s{s}_{11}\right){I}_3^{*}{q}_1\\ {}\kern0.5em +\left({b}_{22}+{\lambda}_s{s}_{22}\right){I}_1^{*}\left({q}_1,0\right)-2{b}_{11}{I}_3^{*}{q}_0-{\alpha}^{*}{s}_{11}{s}_{22}{I}_1^{*}\left({q}_1,0\right){q}_0^2=0\end{array} $$

(9.71)

Taking λ _s = 2 in Eq. (9.71), we solve the obtained equation numerically and show the results in Fig. 9.7. It is seen that the dimensionless initial arch rise q ₀ should be larger than a critical value q ^min₀ for the existence of the asymmetric bifurcation points. It is also seen that at q ^min₀ , q ₁ is near 0. So as a first approximation of q ^min₀ , we take q ₁ = 0 in Eq. (9.71) and find

Fig. 9.7

Evolutions of asymmetric bifurcation points (② and ③) with dimensionless initial arch rise at different levels of the stretching parameter α ^*

$$ {q}_0^{\min }=\sqrt{\frac{b_{22}+{\lambda}_s{s}_{22}}{\alpha^{*}{s}_{11}{s}_{22}}+{\left(\frac{b_{11}{m}_{22}}{\alpha^{*}{s}_{11}{s}_{22}{f}_1}\right)}^2}-\frac{b_{11}{m}_{22}}{\alpha^{*}{s}_{11}{s}_{22}{f}_1} $$

(9.72)

where b ₁₁, b ₂₂, s ₁₁, s ₂₂, f ₁, and m ₂₂ are given in Table 9.3. In Eq. (9.72), replace the non-dimensional quantities (q ₀, α ^*, λ _s) with the expressions in Table 9.1, and we obtain the necessary symmetry-breaking criterion as follows:

$$ \begin{array}{l}{\left(\frac{r}{h}\right)}_{\min }=\sqrt{\frac{b_{22}}{6{s}_{11}{s}_{22}}\left(1+4\frac{1}{\frac{h}{E^{\mathrm{s}}/{E}^{*}}+2}\right)+\frac{4}{s_{11}}{\left(\frac{L}{h}\right)}^2\left(\frac{1}{\frac{h}{E^{\mathrm{s}}/{E}^{*}}+2}\right)\frac{\tau^0}{E^{\mathrm{s}}}+{\left(\frac{b_{11}{m}_{22}}{6{s}_{11}{s}_{22}{f}_1}\left(1+4\frac{1}{\frac{h}{E^{\mathrm{s}}/{E}^{*}}+2}\right)\right)}^2{\left(\frac{h}{g_0}\right)}^2}\\ {}\kern12em -\frac{b_{11}{m}_{22}}{6{s}_{11}{s}_{22}{f}_1}\left(1+4\frac{1}{\frac{h}{E^{\mathrm{s}}/{E}^{*}}+2}\right)\frac{h}{g_0}\end{array} $$

(9.73)

Equation (9.73) is plotted in Fig. 9.8, from which it is found that the positive residual surface tension (τ ⁰/E ^s > 0 in Fig. 9.8a, τ ⁰/E ^s < 0 in Fig. 9.8b) increases (r/h)_min, while the negative one decreases it. The positive surface tension (traction) reduces the arch rise, so larger initial arch rise (larger (r/h)_min) is required for the existence of asymmetric bifurcation, and vice versa for the negative surface tension (compression).

Fig. 9.8

Minimum allowable ratio (r/h)_min between the initial arch rise r and the beam thickness h for the asymmetric bifurcation at different levels of beam thickness h (normalized as h/(E ^s/E ^*)) and residual surface tension τ ⁰ (normalized as τ ⁰/E ^s). The beam length-to-thickness ratio L/h = 25

It is also found from Fig. 9.8 that the beam size (thickness h, normalized as h/(E ^s/E ^*)) affects (r/h)_min. Such size dependency of (r/h)_min can be explained by the influences of the effective Young’s modulus (E)_eff and the residual surface tension τ ⁰. In the case of positive surface Young’s modulus E ^s (refer to Fig. 9.8a), the effective Young’s modulus (E)_eff increases with the decrease of h (see Eq. (9.62)), so the nanobeam becomes stiffer, which will lead to an increase of (r/h)_min. On the other hand, since the effective axial stiffness decreases when decreasing h (see Eq. 9.61), the negative surface tension τ ⁰ will induce more arch rise, so the required initial arch rise ((r/h)_min) for asymmetric bifurcation is reduced. When τ ⁰ is small (i.e., negative residual surface tension is large enough), the influence of τ ⁰ is dominant, so (r/h)_min appears to decrease when reducing h (see the curve at τ ⁰/E ^s = −0.04 in Fig. 9.8a). When τ ⁰ is large, (E)_eff is dominant, so (r/h)_min increases when reducing h (see the curve at τ ⁰/E ^s = −0.01). Both positive τ ⁰ and (E)_eff have the effect of increasing (r/h)_min when reducing h (see the curves at τ ⁰/E ^s = 0.02 and 0.04). The size effect on (r/h)_min in the case of negative surface Young’s modulus (refer to Fig. 9.8b) can be explained in the similar way.

It is noted that in Fig. 9.8, (r/h)_min is plotted in the range (i.e., h/(E ^s/E ^*) ≤ −6 and ≥ 0) where the effective Young’s modulus (Eq. (9.62)) is nonnegative. Moreover, if (r/h)_min is negative or an imaginary number, the asymmetric bifurcation may take place in an initially straight beam. In this case, (r/h)_min is taken to be 0 in the figure.

9.4 Conclusions

In this chapter, we examine the instability behaviors of the electrostatically actuated micro/nanobeam. The governing equations are developed with the aid of Euler-Bernoulli beam theory and are solved using Galerkin decomposition method. The symmetric snap-through of the microbeam is studied first. The fringing field effect, the beam size effect , and the intermolecular forces are accounted for in the model formulation. Our results, which are based on the first mode approximation, reveal that the size of the microbeam plays a major role in dictating the existence of the snap-through behavior of the beam , while the fringing field and intermolecular forces play an insignificant role. In the second part, the asymmetric bifurcation of the nanobeam is investigated. The surface effects at nanoscale are accounted for in the beam model. Our results, which are based on the reduced-order model of two degrees of freedom, show that the beam size and the residual surface tension play significant roles in the symmetry-breaking criterion .